湖北省黄冈中学惠州学校高一数学下学期期中试题 理 新人教A版
湖北省黄冈中学2018年高一下学期数学(理)期中试卷及答案

湖北省黄冈中学2016年春季期中联考高一数学试题(理)考试时间:4月27日上午8:00—10:00 试卷满分:150分一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、下列关于x的不等式解集是实数集R的为()A.B.4x2+4x+1>0C.3x-1>0 D.2、在△ABC中,a,b,c分别为角A,B,C对应的边,若,则角C等于()A.60°B.45°C.120° D.30°3、等比数列{a n}各项均为正数,且a5a6+a4a7=54,则log3a1+log3a2+…+log3a10=()A.8 B.10C.15 D.204、在△ABC中,a,b,c分别为角A,B,C对应的边,则满足A=45°,c=8,a=6的△ABC的个数为m,则a m的值为()A.36 B.6C.1 D.不存在5、已知数列{a n}首项,则a2016=()A.-2 B.C. D.36、对任意实数x,不等式2kx2+kx-3<0恒成立,则实数k的取值范围是()A.-24<k<0 B.-24<k≤0C.0<k≤24 D.k≥247、数列{a n}满足a1=1,,且,则a n等于()A.B.C.D.8、在300米高的山顶上,测得山下一塔顶与塔底的俯角分别是30°,45°,则塔高为()A.B.C.D.9、若等差数列{a n}中,|a5|=|a11|,公差d<0,则使前n项和S n取得最大值的n是()A.8 B.7或8C.8或9 D.710、设实数x,y满足约束条件,若目标函数z=ax+by(a>0,b>0)的最大值为1,则的最小值为()A.B.49C.35 D.11、两千多年前,古希腊毕达哥拉斯学派的数学家们曾经在沙滩上研究数学问题.他们在沙滩上画点或用小石子表示数,按照点或小石子能排列的形状对数进行分类.如下图中实心点的个数5,9,14,20,……为梯形数.根据图形的构成,记此数列的第2016项为a2016,则a2016-5=()A.2023×2016 B.2015×2022C.2023×1008 D.2015×101112、己知等差数列{a n}的公差d≠0,且a1,a3,a13成等比数列,若a1=1,S n为数列{a n}的前n项和,则的最小值为()A.B.C.D.第Ⅱ卷非选择题二、填空题:本大题共4小题,每小题5分,共20分.13、已知a>0,b>0,2a+b=16,则ab的最大值为__________.14、中国古代数学巨著《九章算术》中有“分钱问题”:现有5人分五钱,5人所得数依次成等差数列,前两人分的数与后三人分的数相等,问第二人分__________钱.15、在△ABC中,已知A=60°,b=1,其面积为,则__________.16、设a>0,b>0,称为a,b的调和平均数.如图,线段AC过⊙O的圆心与圆交于点C,E,AB 为圆的切线,B为切点,BD⊥OA于D,F在圆上且FO⊥OA于O.AC=a,AE=b,线段__________的长度是a,b的几何平均值,线段__________的长度是a,b的调和平均值.三、解答题:本大题共6小题,共70分.解答题应写出文字说明,证明过程或演算步骤.17、(本小题满分10分)求下列关于实数x的不等式的解集:(1)-x2+5x-6≤0;(2).18、(本小题满分12分)在等差数列{a n}中,a2=4,a3+a8=15.(1)求数列{a n}的通项公式;(2)设,求b1+b2+b3+…+b10的值.19、(本小题满分12分)已知a,b,c分别是△ABC的三个内角A,B,C的对边,.(1)求角B的大小;(2)求函数的值域.20、(本小题满分12分)某市人民广场立有一块巨大的电子显示屏,如图,为测量它的上下宽度(即AB 的长度).一名学生站在如图C处测得A,B的仰角分别为60°,45°,从C点出发,沿着直线OC再前进20米到达D点,在D点测得A的仰角为30°.不考虑测角仪的高度和人的高度(即C,D视为测角仪所在的位置,E视为人的眼睛所在位置)(1)求电子显示屏的上下宽度AB;(2)该生站在E点观看电子显示屏,为保证观看节目的视觉效果最佳,即人的眼睛与A,B连线所成角最大,求O,E两点间的距离.(第二问结果保留一位小数,参考数据:)21、(本小题满分12分)定义:在平面直角坐标系中落在坐标轴上的整点(即横坐标和纵坐标均为整数的点)称为“轴点”.设不等式|x|+|y|≤n(n∈N+)所表示的平面区域为D n,记D n内的“轴点”个数为a n.(1)求a1,a2,a3,并猜想a n的表达式(不需要证明);(2)利用(1)的猜想结果,设数列{a n-1}的前n项和为S n,数列的前n项和为T n,若对一切n∈N+,恒成立,求实数m的取值范围.22、(本小题满分12分)若数列{a n}的前n项和S n满足:S n=2a n-2,记b n=log2a n.(1)求数列{b n}的通项公式;(2)若c1=1,,求证:c n<3;(3)记,求的值.(注:[x]表示不超过x的最大整数,例:[2.1]=2,[-1.3]=-2)答案与解析:1、C解析:A中的解集是{x|x>1或x<-1},B中的解集是,C中的解集是R,D中的解集是{x|x ≠-1},故答案为C.2、D解析:由余弦定理得,又0°<C<180°,∴C=30°,故答案为D.3、C解析:{a n}是等比数列,∴a5a6=a4a7=27,log3a1+log3a2+...+log3a10=log3(a1a2 (10)=log3(a1a10)5=5log3a1a10=5log3a5a6=5log327=5×3=15,故答案为C.4、A解析:∵csinA<a<c,∴这样的三角形有2个,即m=2,∴a m=62=36.5、C解析:故数列{a n}是周期数列且周期T=4,,故选择C.6、B解析:当k=0时不等式即为-3<0,不等式恒成立,当k≠0时,若不等式恒成立,则,即,即-24<k<0,综合知-24<k≤0,故选择B.7、D解析:由题知是等差数列,又,∴公差为.,故答案为D.8、A解析:如图,山高为AB=300m,塔高为CD.∴BC=300,∵∠EAB=60°,.Rt△ECD中,,,故选择A.9、B解析:∵|a5|=|a11|,∴a5+a11=0,又a5+a11=a8+a8,∴a8=0.又公差d<0,∴a7>0,a9<0,∴S n中S7=S8最大,故选择B.10、A解析:画出可行域,如图,可知z=ax+by在A(3,4)处取得最大值,故3a+4b=1.,当时取最小值,故选A.11、D解析:……归纳出..,故选D.12、A13、3214、15、16、AB,AD17、解:(1)不等式变形为:(x-2)(x-3)≥0,所以不等式解集为(-∞,2]∪[3,+∞).(5分)(2)不等式等价于2(x-a)(x-a2-1)<0,,所以不等式解集为(a,a2+1).(10分)18、解:(1)由a2=a1+d=4,a3+a8=2a1+9d=15得a1=3,d=1.∴a n=a1+(n-1)d=n+2(6分)(2)b n=2n+2n+1(12分)19、解:(1)由正弦定理得:20、解:(1)设OB=x,则由∠OCB=45°,∠OCA=60°,∠ODA=30°,得OC=x,,OD=3x.则由OD=OC+CD,得3x=x+20,所以x=10所以电子屏的宽度.(6分)(2)设OE=y,则,当且仅当即y≈13.2时,tan∠AEB最大,即∠AEB最大.答:(1)电子屏的宽度为米.(2)当OE为13.2米时,观看节目的视觉效果最佳.(12分)21、解:(1)a1=5,a2=9,a3=13,故猜想a n=4n+1.(4分)22、解:(1)当n=1时,S1=2a1-2,解得a1=2当n≥2时,a n=S n-S n-1=(2a n-2)-(2a n-1-2)=2a n-2a n-1即a n=2a n-1所以数列{a n}是以a1=2为首项,公比为2的等比数列∴a n=2·2n-1=2n,从而b n=log2a n=n.(3分)(2)由(1)知∴c n=(c n-c n-1)+(c n-1-c n-2)+…+(c2-c1)+c1(n≥2)11。
湖北省黄冈市蕲春一中2013-2014学年高一数学下学期期中试题 理 新人教A版

某某省黄冈市蕲春一中2013-2014学年高一数学下学期期中试题 理新人教A 版试卷满分:150分 时间:120分钟一、选择题(本大题共10个小题;每小题5分,共50分.在每小题给出的四个选项中,只有一个符合题目要求,请将正确选项的代号填入答题卡的相应位置.) 1.已知数列的一个通项公式为113(1)2n n n n a +-+=-,则5a = ( ) A .12B .12-C .932D .932-2.不等式xx x x 22->- 解集是 ( ) A .(0,2)B .(-∞,0)C .(2,+∞)D .(-∞,0)∪(0,+∞)3.下列命题中正确的是( )A .若a b >,则22ac bc > B .若0ab >,a b >,则11a b < C .若a b >,c d >,则a c b d ->- D .若a b >,c d <,则a bc d>4.在ABC ∆中,角,A B 分别满足tan 2,tan 3A B ==,则角C 为 ( ) A .34π B .4π C . 6π D . 3π 5.已知数列121,,,4a a --成等差数列,1231,,,,4b b b --成等比数列,则212a ab -=( ) A .12B .12-C.1122-或D.146.在钝角三角形ABC 中,a=1,b=2,则最大边c 的取值X 围是 ( ) A .(3,3)B .(2,3)C .(5,3)7.如图,已知正方形ABCD 的边长为2, P 、Q 分别为边AB 、DA 上的点。
设,,BCP DCQ αβ∠=∠=若APQ ∆的周长为4,则αβ+=( ) A .15︒B .30︒ C .45︒D .60︒8.已知数列{}n a 为21,3231+,434241++,54535251+++,…,若2+n n 的前n 项和S n = ( )A .)2)(1(532+++n n n nB .)3)(1(522+++n n n nC .)3)(2(232+++n n n nD .)2)(1(322+++n n nn9.若ABC ∆内接于单位圆,且ABC ∆面积为S ,则长为sin ,sin ,sin A B C 的三条线段( )A .不能构成三角形B .能构成一个三角形,其面积为2SC .能构成一个三角形,其面积大于2S D .能构成一个三角形,其面积小于 2S 10.把数列{}12+n 依次按第一个括号一个数,第二个括号两个数,第三个括号三个数,第四个括号四个数,第五个括号一个数,…循环分为:(3) (5,7) (9,11,13) (15,17,19,21) (23) (25,27) (29,31,33) (35,37,39,41)…则第60个括号内各数之和为( ) A.1112B.1168C.1176D. 1192二、填空题(本大题共5小题,每小题5分,共25分,把答案填在答题卡的相应位置.)11.不等式ax 2+4x +a >1-2x 2对一切x ∈R 恒成立,则实数a 的取值X 围是________. 12.{}n a 为等差数列,若a 1>0,a 2013+a 2014>0,a 2013a 2014<0,则使前n 项0n S >的最大自然数n 是.13.设α为锐角,若cos ⎝ ⎛⎭⎪⎫α+π6=45,则sin ⎝⎛⎭⎪⎫2α+π12的值为______. 14.已知一个三角形的三边长为连续的三个自然数,且最大角是最小角的2倍,则这个三角形的面积为________.15.下列说法中正确的有(填写你认为正确的命题的序号)________.①若数列{}n a 是等差数列,且*)(N t s n m a a a a t s n m ∈+=+、、、,则t s n m +=+;②若n S 是等差数列{}n a 的前n 项的和,则n n n n n S S S S S 232--,,成等差数列; ③若n S 是等比数列{}n a 的前n 项的和,则n n n n n S S S S S 232--,,成等比数列;④若n S 是等比数列{}n a 的前n 项的和,且B Aq S nn +=;(其中B A 、是非零常数,*N n ∈),则B A +为零 三、解答题:(本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤.) 16.(本题满分12分)若关于x 的不等式-12x 2+2x >mx +1的解集为{x | 1<x <2},求m 的值.17.(本题满分12分)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c 分,且满足2cos cos c b Ba A-=. (1)求角A 的大小;(2)若25a =,求△ABC 面积的最大值.18.(本题满分12分)在塔底的水平面上某点测得塔顶的仰角为θ,由此点向塔底沿直线行走30米,测得塔顶的仰角为2θ,再向塔前进310米,又测得塔顶的仰角为4θ,求塔高。
湖北省黄冈市2019-2020学年高一下学期期中考试数学(理)测试题-附答案(精校版)

湖北省黄冈中学2019年春季期中联考高一数学试题(理)考试时间:4月27日上午8:00—10:00 试卷满分:150分一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、下列关于x的不等式解集是实数集R的为()A.B.4x2+4x+1>0C.3x-1>0 D.2、在△ABC中,a,b,c分别为角A,B,C对应的边,若,则角C等于()A.60°B.45°C.120° D.30°3、等比数列{a n}各项均为正数,且a5a6+a4a7=54,则log3a1+log3a2+…+log3a10=()A.8 B.10C.15 D.204、在△ABC中,a,b,c分别为角A,B,C对应的边,则满足A=45°,c=8,a=6的△ABC 的个数为m,则a m的值为()A.36 B.6C.1 D.不存在5、已知数列{a n}首项,则a2016=()A.-2 B.C. D.36、对任意实数x,不等式2kx2+kx-3<0恒成立,则实数k的取值范围是()A.-24<k<0 B.-24<k≤0C.0<k≤24 D.k≥247、数列{a n}满足a1=1,,且,则a n等于()A.B.C.D.8、在300米高的山顶上,测得山下一塔顶与塔底的俯角分别是30°,45°,则塔高为()A.B.C.D.9、若等差数列{a n}中,|a5|=|a11|,公差d<0,则使前n项和S n取得最大值的n是()A.8 B.7或8C.8或9 D.710、设实数x,y满足约束条件,若目标函数z=ax+by(a>0,b>0)的最大值为1,则的最小值为()A.B.49C.35 D.11、两千多年前,古希腊毕达哥拉斯学派的数学家们曾经在沙滩上研究数学问题.他们在沙滩上画点或用小石子表示数,按照点或小石子能排列的形状对数进行分类.如下图中实心点的个数5,9,14,20,……为梯形数.根据图形的构成,记此数列的第2016项为a2016,则a2016-5=()A.2023×2016 B.2015×2022C.2023×1008 D.2015×101112、己知等差数列{a n}的公差d≠0,且a1,a3,a13成等比数列,若a1=1,S n为数列{a n}的前n项和,则的最小值为()A.B.C.D.第Ⅱ卷非选择题二、填空题:本大题共4小题,每小题5分,共20分.13、已知a>0,b>0,2a+b=16,则ab的最大值为__________.14、中国古代数学巨著《九章算术》中有“分钱问题”:现有5人分五钱,5人所得数依次成等差数列,前两人分的数与后三人分的数相等,问第二人分__________钱.15、在△ABC中,已知A=60°,b=1,其面积为,则__________.16、设a>0,b>0,称为a,b的调和平均数.如图,线段AC过⊙O的圆心与圆交于点C,E,AB为圆的切线,B为切点,BD⊥OA于D,F在圆上且FO⊥OA于O.AC=a,AE=b,线段__________的长度是a,b的几何平均值,线段__________的长度是a,b的调和平均值.三、解答题:本大题共6小题,共70分.解答题应写出文字说明,证明过程或演算步骤.17、(本小题满分10分)求下列关于实数x的不等式的解集:(1)-x2+5x-6≤0;(2).18、(本小题满分12分)在等差数列{a n}中,a2=4,a3+a8=15.(1)求数列{a n}的通项公式;(2)设,求b1+b2+b3+…+b10的值.19、(本小题满分12分)已知a,b,c分别是△ABC的三个内角A,B,C的对边,.(1)求角B的大小;(2)求函数的值域.20、(本小题满分12分)某市人民广场立有一块巨大的电子显示屏,如图,为测量它的上下宽度(即AB的长度).一名学生站在如图C处测得A,B的仰角分别为60°,45°,从C点出发,沿着直线OC再前进20米到达D点,在D点测得A的仰角为30°.不考虑测角仪的高度和人的高度(即C,D视为测角仪所在的位置,E视为人的眼睛所在位置)(1)求电子显示屏的上下宽度AB;(2)该生站在E点观看电子显示屏,为保证观看节目的视觉效果最佳,即人的眼睛与A,B连线所成角最大,求O,E两点间的距离.(第二问结果保留一位小数,参考数据:)21、(本小题满分12分)定义:在平面直角坐标系中落在坐标轴上的整点(即横坐标和纵坐标均为整数的点)称为“轴点”.设不等式|x|+|y|≤n(n∈N+)所表示的平面区域为D n,记D n内的“轴点”个数为a n.(1)求a1,a2,a3,并猜想a n的表达式(不需要证明);(2)利用(1)的猜想结果,设数列{a n-1}的前n项和为S n,数列的前n项和为T n,若对一切n∈N+,恒成立,求实数m的取值范围.22、(本小题满分12分)若数列{a n}的前n项和S n满足:S n=2a n-2,记b n=log2a n.(1)求数列{b n}的通项公式;(2)若c1=1,,求证:c n<3;(3)记,求的值.(注:[x]表示不超过x的最大整数,例:[2.1]=2,[-1.3]=-2)答案与解析:1、C解析:A中的解集是{x|x>1或x<-1},B中的解集是,C中的解集是R,D中的解集是{x|x≠-1},故答案为C.2、D解析:由余弦定理得,又0°<C<180°,∴C=30°,故答案为D.3、C解析:{a n}是等比数列,∴a5a6=a4a7=27,log3a1+log3a2+...+log3a10=log3(a1a2 (10)=log3(a1a10)5=5log3a1a10=5log3a5a6=5log327=5×3=15,故答案为C.4、A解析:∵csinA<a<c,∴这样的三角形有2个,即m=2,∴a m=62=36.5、C解析:故数列{a n}是周期数列且周期T=4,,故选择C.6、B解析:当k=0时不等式即为-3<0,不等式恒成立,当k≠0时,若不等式恒成立,则,即,即-24<k<0,综合知-24<k≤0,故选择B.7、D解析:由题知是等差数列,又,∴公差为.,故答案为D.8、A解析:如图,山高为AB=300m,塔高为CD.∴BC=300,∵∠EAB=60°,.Rt△ECD中,,,故选择A.9、B解析:∵|a5|=|a11|,∴a5+a11=0,又a5+a11=a8+a8,∴a8=0.又公差d<0,∴a7>0,a9<0,∴S n中S7=S8最大,故选择B.10、A解析:画出可行域,如图,可知z=ax+by在A(3,4)处取得最大值,故3a+4b=1.,当时取最小值,故选A.11、D解析:……归纳出..,故选D.12、A13、3214、15、16、AB,AD17、解:(1)不等式变形为:(x-2)(x-3)≥0,所以不等式解集为(-∞,2]∪[3,+∞).(5分)(2)不等式等价于2(x-a)(x-a2-1)<0,,所以不等式解集为(a,a2+1).(10分)18、解:(1)由a2=a1+d=4,a3+a8=2a1+9d=15得a1=3,d=1.∴a n=a1+(n-1)d=n+2(6分)(2)b n=2n+2n+1(12分)19、解:(1)由正弦定理得:20、解:(1)设OB=x,则由∠OCB=45°,∠OCA=60°,∠ODA=30°,得OC=x,,OD=3x.则由OD=OC+CD,得3x=x+20,所以x=10所以电子屏的宽度.(6分)(2)设OE=y,则,当且仅当即y≈13.2时,tan∠AEB最大,即∠AEB最大.答:(1)电子屏的宽度为米.(2)当OE为13.2米时,观看节目的视觉效果最佳.(12分)21、解:(1)a1=5,a2=9,a3=13,故猜想a n=4n+1.(4分)22、解:(1)当n=1时,S1=2a1-2,解得a1=2当n≥2时,a n=S n-S n-1=(2a n-2)-(2a n-1-2)=2a n-2a n-1即a n=2a n-1所以数列{a n}是以a1=2为首项,公比为2的等比数列∴a n=2·2n-1=2n,从而b n=log2a n=n.(3分)(2)由(1)知∴c n=(c n-c n-1)+(c n-1-c n-2)+…+(c2-c1)+c1(n≥2)。
湖北省黄冈市高一下学期期中数学试卷

湖北省黄冈市高一下学期期中数学试卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分) (2019高三上·鹤岗月考) 点是角终边上一点,则的值为()A .B .C .D .2. (2分) (2020高一上·长春期末) 的值为()A .B .C .D .3. (2分) (2015高三上·石家庄期中) 已知点P(,﹣)在角θ的终边上,且θ∈[0,2π),则θ的值为()A .B .C .D .4. (2分)(2016·潍坊模拟) 已知向量,的夹角为60°,且| |=1,|2 ﹣ |= ,则| |=()A . 1B .C .D . 25. (2分)(2020·海南模拟) 已知为第二象限角,且,则()A .B .C .D .6. (2分)已知函数f,若f(x+θ)是周期为2π的偶函数,则θ的一个可能值是()A .B .C . πD .7. (2分)(2017·黄陵模拟) 在△OAB中,O为坐标原点,,则当△OAB 的面积达最大值时,θ=()B .C .D .8. (2分) (2015高一下·河北开学考) 向量 =(,tanα), =(cosα,1),且∥ ,则cos (+α)=()A .B . ﹣C . ﹣D . ﹣9. (2分)已知tanα=4,cotβ=,则tan(α+β)等于()A .B .C .D .10. (2分)若,则sin2θ=()A .B .D .11. (2分)若的最小值为-2,其图像相邻最高点与最低点横坐标之差为,且图像过点(0,1),则其解析式是()A .B .C .D .12. (2分) (2019高二下·上海月考) 在四边形()A .B .C .D .二、填空题 (共4题;共4分)13. (1分)若向量 =(1,﹣2),向量 =(x,1),且⊥ ,则x=________.14. (1分)已知cosα= ,cos(α+β)= ,α,β均为锐角,则cosβ=________.15. (1分)已知x>0,y>0,a=x+y,,,若存在正数m使得对于任意正数x,y,可使a,b,c为三角形的三边构成三角形,则m的取值范围是________.16. (1分) (2016高一下·滑县期末) 若函数y=sin(2x﹣)(a<x<b)的值域是[﹣1,),则b﹣a的最大值是________.三、解答题 (共6题;共45分)17. (10分)已知向量 =(), =().(1)若 =1,求cos(﹣x)的值;(2)记f(x)= 在△ABC中角A,B,C的对边分别为a,b,c,且满足(2sinA﹣sinC)cosB=sinBcosC,求f(A)的取值范围.18. (5分) (2020高一下·济南月考) 已知,, .(Ⅰ)求证:向量与垂直;(Ⅱ)若与的模相等,求的值(其中为非零实数).19. (5分)已知函数,F(x)=sinx•f(cosx)+cosx•f(sinx)且.(Ⅰ)将函数F(x)化简成Asin(ωx+φ)+B(其中A>0,ω>0,φ∈[0,2π))的形式;(Ⅱ)求函数F(x)的值域.20. (5分)已知函数f(x)=asinx•cosx﹣ acos2x+ a+b(a>0).(Ⅰ)写出函数的单调递增区间;(Ⅱ)设x∈[0, ],f(x)的最小值是﹣,最大值是2,求实数a,b的值.21. (10分)计算下列各式:(1)已知tanα=2,求值;(2)化简f(α)= .22. (10分)(2020·定远模拟) 在中,角 , , 的对边分别为 , , .(1)若,且为锐角三角形, , ,求的值;(2)若 , ,求的取值范围.参考答案一、选择题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题;共45分)17-1、17-2、18-1、19-1、20-1、21-1、21-2、22-1、22-2、。
2023-2024学年广东省惠州中学高一(下)期中数学试卷(含答案)

2023-2024学年广东省惠州中学高一(下)期中数学试卷一、单选题:本题共8小题,每小题5分,共40分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合A ={−2,−1,0,1,2},B ={x|lnx >0},则A ∩B =( )A. {1}B. {2}C. {−2,2}D. {−1,0,1}2.已知α,β是平行四边形的两个内角,则“α=β”是“sinα=sinβ”的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件3.已知互相垂直的平面α,β交于直线l ,若直线m ,n 满足m//α,n ⊥β,则( )A. m//lB. m//nC. n ⊥lD. m ⊥n 4.如图,在△ABC 中,AN =12NC ,P 是BN 上的一点,若AP =(m +13)AB +19AC ,则实数m 的值为( )A. 19B. 29C. 23D. 135.若函数f(x)={x 2−2ax +1,x >1ax,x ≤1在其定义域内是一个单调递增函数,则实数a 的取值范围是( )A. (0,1]B. (0,23]C. [0,1]D. [0,23]6.已知一个圆锥的底面半径为3,其侧面积是底面积的2倍,则圆锥的体积为( )A. 6πB. 6 3πC. 9 3πD. 12π7.心理学家有时用函数L(t)=A(1−e −kt )测定在时间t(单位:min)内能够记忆的量L ,其中A 表示需要记忆的量,k 表示记忆率.假设一个学生需要记忆的量为200个单词,此时L 表示在时间t 内该生能够记忆的单词个数.已知该生在5min 内能够记忆20个单词,则k 的值约为( )(ln0.9≈−0.105,ln0.1≈−2.303)A. 0.021B. 0.221C. 0.461D. 0.6618.如图,O 是锐角三角形ABC 的外心,角A ,B ,C 所对的边分别为a ,b ,c ,且A =π3,若cosB sinCAB +cosCsinB AC =2m AO ,则m =( )A. 12 B. 22C. 32D. 1二、多选题:本题共3小题,共18分。
湖北省黄冈市高一下学期期中数学试卷
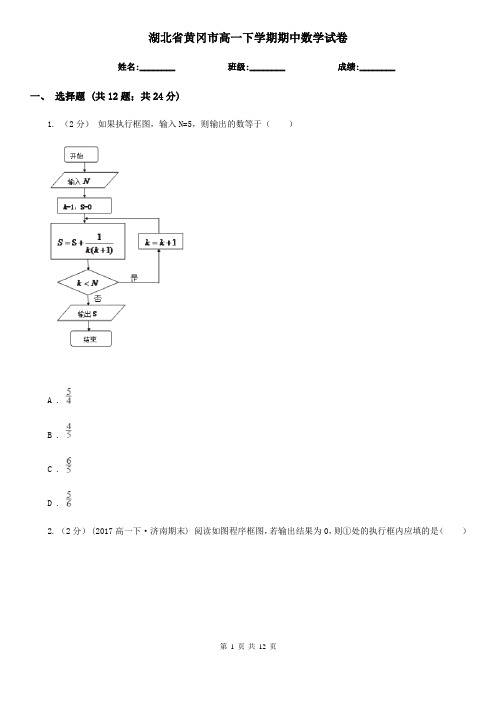
湖北省黄冈市高一下学期期中数学试卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分)如果执行框图,输入N=5,则输出的数等于()A .B .C .D .2. (2分) (2017高一下·济南期末) 阅读如图程序框图,若输出结果为0,则①处的执行框内应填的是()A . x=﹣1B . b=0C . x=1D . a=3. (2分)某初级中学领导采用系统抽样方法,从该校800名学生中抽50名学生做牙齿健康检查.现将800名学生从1到800进行编号,求得间隔数k=16,即每16人抽取一个人.在1~16中随机抽取一个数,如果抽到的是7,则从65~80这16个数中应取的数是()A . 71B . 68C . 69D . 704. (2分)某校1000名学生中,O型血有400人,A型血有250人,B型血有250人,AB型血有100人,为了研究血型与色弱的关系,要从中抽取一个容量为40的样本,按照分层抽样的方法抽取样本,则O型血、A型血、B型血、AB型血的人要分别抽的人数为()A . 16、10、10、4B . 14、10、10、6C . 13、12、12、3D . 15、8、8、95. (2分)下列事件中:①任取三条线段,这三条线段恰好组成直角三角形;②从一个三角形的三个顶点各任画一条射线,这三条射线交于一点;③实数a,b都不为0,但a2+b2=0;④明年12月28日的最高气温高于今年12月10日的最高气温,其中为随机事件的是()A . ①②③④B . ①②④C . ①③④D . ②③④6. (2分)设是A的对立事件,是B的对立事件。
若和事件A+B发生的概率为0.4,则积事件·发生的概率为()A . 0.24B . 0.36C . 0.4D . 0.67. (2分) (2016高一下·烟台期中) “勾股定理”在西方被称为“毕达哥拉斯定理”,三国时期吴国的数学家赵爽创制了一幅“勾股圆方图”,用数形结合的方法给出了勾股定理的详细证明.如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个边长为2的大正方形,若直角三角形中较小的锐角,现在向该正方形区域内随机地投掷一枚飞镖,飞镖落在小正方形内的概率是()A .B .C .D .8. (2分) (2016高二上·孝感期中) 已知数据x1 , x2 , x3 ,…,x100是杭州市100个普通职工的2016年10月份的收入(均不超过2万元),设这100个数据的中位数为x,平均数为y,方差为z,如果再加上马云2016年10月份的收入x101(约100亿元),则相对于x、y、z,这101个月收入数据()A . 平均数可能不变,中位数可能不变,方差可能不变B . 平均数大大增大,中位数可能不变,方差也不变C . 平均数大大增大,中位数一定变大,方差可能不变D . 平均数大大增大,中位数可能不变,方差变大9. (2分)设集合A={x|x2-2x-3≤0},集合B={x|≤0},如果A B= ()A . {x|-1≤x<0}B . {x|0≤x<2}C . {x|0≤x≤2}D . {x|0≤x≤1}10. (2分)已知sinα+cosα=-,,则tanα的值是()A . -B . -C .D .11. (2分)已知α是三角形的内角,且cosα=-,则tanα等于()A . -B . -C .D .12. (2分)函数的图象大致是()A .B .C .D .二、填空题: (共4题;共4分)13. (1分) (2019高一上·忻州月考) 如图所示的程序的运行结果为________.14. (1分) (2017高二下·枣强期末) 已知圆直线,圆上任意一点到直线的距离小于2的概率为________.15. (1分) (2017高二下·蕲春期中) 一个口袋中装有6个小球,其中红球4个,白球2个,如果不放回地依次摸出2个小球,则在第一次摸出红球的条件下,第2次摸出红球的概率为________.16. (1分)将分针拨慢5分钟,则分针转过的弧度数是1三、解答题 (共6题;共65分)17. (15分) (2016高一下·汉台期中) 袋中有大小相同的红、黄两种颜色的球各1个,从中任取1只,有放回地抽取3次.求:(1) 3只全是红球的概率;(2) 3只颜色全相同的概率;(3) 3只颜色不全相同的概率.18. (10分)西安世园会志愿者招骋正如火如荼进行着,甲、乙、丙三名大学生跃跃欲试,已知甲能被录用的概率为,甲、乙两人都不能被录用的概率为,乙、丙两人都能被录用的概率为.(1)乙、丙两人各自能被录用的概率;(2)求甲、乙、丙三人至少有两人能被录用的概率.19. (10分) (2016高二上·孝感期中) 一个盒子中装有标号为1,2,3,4的4张标签,随机地选取两张标签,根据下列条件求两张标签上的数字为相邻整数的概率:(1)标签的选取是无放回的;(2)标签的选取是有放回的.20. (10分) (2018高二下·临汾期末) 某市政府为了节约生活用电,计划在本市试行居民生活费定额管理,即确定一户居民月用电量标准,用电量不超过的部分按平价收费,超出的部分按议价收费.为此,政府调查了100户居民的月平均用电量(单位:度),以,,,,,,分组的频率分布直方图如图所示.(1)根据频率分布直方图的数据,求直方图中的值并估计该市每户居民平均用电量的值;(2)用频率估计概率,利用(1)的结果,假设该市每户居民月平均用电量服从正态分布(i)估计该市居民月平均用电量介于度之间的概率;(ii)利用(i)的结论,从该市所有居民中随机抽取3户,记月平均用电量介于度之间的户数为,求的分布列及数学期望 .21. (5分)(2017·河西模拟) 如图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图(Ⅰ)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以说明;(Ⅱ)建立y关于t的回归方程(系数精确到0.01),预测2017年我国生活垃圾无害化处理量.参考数据: =9.32, =40.17, =0.55,≈2.646.参考公式:相关系数r= 回归方程 = + t 中斜率和截距的最小二乘估计公式分别为: = , = ﹣.22. (15分) (2020高一下·平谷月考) 已知函数.(1)把函数解析式化为的形式;(2)求函数的最小正周期及值域;(3)若时,函数有两个零点,求实数的取值范围.参考答案一、选择题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题: (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题;共65分) 17-1、17-2、17-3、18-1、18-2、19-1、19-2、20-1、20-2、21-1、22-1、22-2、22-3、。
湖北省黄冈市高一下学期数学期中考试试卷(C)
湖北省黄冈市高一下学期数学期中考试试卷(C)姓名:________ 班级:________ 成绩:________一、单选题 (共10题;共20分)1. (2分) (2016高三上·黑龙江期中) 已知实数x,y满足,其中a= (x2﹣1)dx,则z=2|x ﹣1|+|y|的最小值是()A . 5B . 3C . 6D . 22. (2分)如果N=a2(a>0且a≠1),则有()A . log2N=aB . log2a=NC . logNa=2D . logaN=23. (2分) (2019高一上·长春月考) 设集合,,则()A .B .C .D .4. (2分) (2016高二上·宁远期中) 在△ABC中,若a2+b2﹣c2<0,则△ABC是()A . 钝角三角形B . 直角三角形C . 锐角三角形D . 都有可能5. (2分)的展开式的常数项是()A . -3B . -2C . 2D . 36. (2分) (2016高二上·重庆期中) 一束光线从点A(﹣1,1)出发,经x轴反射到圆C:(x﹣2)2+(y﹣3)2=1上的最短路程是()A . 3 ﹣1B . 2C . 4D . 57. (2分)向量对应的复数是5-4i,向量对应的复数是-5+4i,则+对应的复数是()A . -10+8iB . 10-8iC . 0D . 10+8i8. (2分) (2017高三上·漳州期末) 在平面直角坐标系中,不等式组,(a是常数)表示的平面区域面积是9,那么实数a的值为()A . 3 +2B . ﹣3 +2C . ﹣5D . 19. (2分) (2019高一上·长春期中) 设,,,则此三个数大小关系是()A .B .C .D .10. (2分)函数y=Asin(ωx+φ)(A>0,ω>0,﹣<φ<)的部分图象如图所示,则此函数的解析式可为()A . y=2sin(2x﹣)B . y=2sin(2x﹣)C . y=2sin(4x﹣)D . y=2sin(4x+)二、填空题 (共5题;共5分)11. (1分)当x∈{x|(log2x)2﹣log2x﹣2≤0}时,函数y=4x﹣2x+3的最小值是________12. (1分) (2016高一上·沭阳期中) 函数y= 的定义域是________13. (1分)设集合A={|2a﹣1|,2},B={2,3,a2+2a﹣3}且∁BA={5},则实数a的值是________.14. (1分) (2017高一下·淮安期中) 已知点(﹣3,﹣1)和(4,﹣6)在直线3x﹣2y﹣a=0的两侧,则a 的取值范围是________.15. (1分)(2017·山东模拟) 对于实数m,n,定义一种运算:,已知函数f(x)=a*ax ,其中0<a<1,若f(t﹣1)>f(4t),则实数t的取值范围是________.三、解答题 (共6题;共50分)16. (10分) (2019高一上·忻州月考) 已知函数在上有最大值1和最小值0,设 .(1)求m,n的值;(2)若不等式上有解,求实数的取值范围。
湖北省黄冈市高中联校2023-2024学年高一下学期期中教学质量抽测数学试题
湖北省黄冈市高中联校2023-2024学年高一下学期期中教学质量抽测数学试题一、单选题1.在ABC V 中,30ABC ∠=︒,AB =3BC =,则AB BC ⋅=u u u r u u u r( )A .3B .92C .3-D .92-2.若向量()2,1a x x =-r 与向量(4,6)b =-r 方向相同,则实数x =( )A .12B .12-C .2D .-23.已知cos()cos sin()sin 1αβαβαα---=,则sin 2β=( )A .1B .0C .1±D .-14.将函数πcos 26y x ⎛⎫=+ ⎪⎝⎭的图象向右平移π4个单位长度,得到函数()y f x =的图象,则曲线()y f x =的一条对称轴为( ) A .π12x = B .π6x =C .π3x =D .5π12x =5.3π7πtantan 4125π1tan12+=-( )AB.C.D6.在ABC V 中,内角,,A B C 的对边分别为a ,b ,c,已知2sin b A =3a =,B ∠为钝角,2b c -=,则b =( ) A .5B .6C .7D .87.函数()sin cos (0,0)f x x a x a ωωω=+>>的部分图象如图所示,A,π,2B ⎛ ⎝,则ω=( )A .1B .2C .3D .48.在ABCD Y 中,BE EC =u u u r u u u r,2CF FD =u u u r u u u r ,若A C E AF A λμ=+u u u r u u u r u u u r ,则实数λμ+等于( )A .73B .32C .75D .76二、多选题9.已知函数44()2sin cos cos sin f x x x x x =-+,则下列关于函数()f x 的说法正确的是( ) A .函数()f x 的最小正周期为π B .函数()f x 的图像关于点π,08⎛⎫⎪⎝⎭对称C .函数()f x 在π0,2⎡⎤⎢⎥⎣⎦上单调递增D .函数()1y f x =+在区间[0,]a 上至少有3个零点,则a 的最小值为π10.已知平面向量a r,b r 满足|||2a a b =-=rr r ,则下列命题正确的是( )A .若()b a b ⊥-r rr ,则||b r B .若a b r r ∥,则||2b rC .若|2|2a b -=r r,则||b r D .向量a r,b r 的夹角的最大值为π411.在ABC V 中,内角A ,B ,C 的对边分别为a ,b ,c ,1cos sin 2tan A B C==,则( ) A .π2A B += B .22πA C +=C .a c =D .b =三、填空题12.在ABC V 中,π4A =,sinBC =,则角C =.13.已知ππcos ,sin 1212a ⎛⎫= ⎪⎝⎭r ,(1,1)b =-r ,()a a b λ⊥+rr r ,则λ=.14.函数()|sin ||cos ||sin 2|f x x x x =++的值域为.四、解答题15.已知tan 2tan αβ=.(1)若α,β均为锐角,满足2παβ+=,求tan α. (2)若1sin()4-=αβ,求sin()αβ+; 16.在ABC V 中,内角,,A B C 的对边分别为a ,b ,c ,已知sin 2sin A B =,3c =,4cos 5C =. (1)求ABC V 的周长; (2)求A B -的值.17.在四边形ABCD 中,1AB =,2BC =,90ABC ∠=︒,120BAD ∠=︒ (1)若A ,B ,C ,D 四点共圆,求线段CD 的长;(2)若BD ABCD 的面积.18.在平面直角坐标系xOy 中,角α以原点O 为顶点,x 轴非负半轴为始边,终边OA 与单位圆交于A 点,角π3α+的终边与单位圆交于B 点.(1)若(0,2)P ,求PA PB ⋅u u u r u u u r的取值范围;(2)若()111,e x y =r ,()222,e x y =r ,定义向量()121221,e e x y x y ⊕=++r r设向量OA OB ⊕u u u r u u u r 的模为T ,当T ≥α的取值范围.19.已知直线12l l ∥,M ,N 分别为1l ,2l 上的两个定点,点A 在线段MN 上,1AM =,2AN =,B 为直线1l 上一动点,C 为直线2l 上一动点,B ,C 两点均在直线MN 的同一侧,π3MNC ∠=.设ACN α∠=.ABC V 面积为()S α.(1)若∠BAC =π2,求()S α的最小值;(2)若π3BAC ∠=,且()S α ①求CN 的长;②若线段AC 与BN 交与点D ,CD CA λ=u u u r u u u r,求实数λ的值.。
湖北省黄冈市高一下学期数学期中考试试卷
湖北省黄冈市高一下学期数学期中考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分)若,则下列结论不正确的是()A . a2<b2B . ab<b2C . >2D . |a|﹣|b|=|a﹣b|2. (2分)的内角A,B,C的对边分别为a,b,c,若,则边a等于()A .B .C .D . 23. (2分)不等式的解()A .B .C .D .4. (2分)等比数列中, 则的前项和为()A . 45D . 525. (2分)(2020高一下·长春期中) 在中所对的边分别是,若,则()A . 37B . 13C .D .6. (2分)(2018·张家口期中) 已知等比数列的各项都是正数,且,,成等差数列,则()A . 9B . 8C . 7D . 67. (2分)已知a=log23,b=8﹣0.4 , c=sinπ,则a,b,c的大小关系是()A . a>b>cB . a>c>bC . b>a>cD . c>b>a8. (2分)(2019·浙江模拟) 已知数列{an},满足an+1=3an ,且a2a4a6=9,则log3a5+log3a7+log3a9=()C . 8D . 119. (2分)(2017·齐河模拟) 已知x、y满足则4x﹣y的最小值为()A . 4B . 6C . 12D . 1610. (2分)在数列{an}中,a1=2,an+1=2an+2,则a100的值为()A .B .C .D .11. (2分)在中,角的对边分别是若,则的最小值为()A .B .C .D .12. (2分)(2013·新课标Ⅰ卷理) 设等差数列{an}的前n项和为Sn ,若Sm﹣1=﹣2,Sm=0,Sm+1=3,则m=()A . 3B . 4C . 5D . 6二、填空题 (共4题;共4分)13. (1分) (2019高三上·上海期中) 方程的解是________14. (1分) (2020高一下·武汉期中) 如图,在平面四边形中,,,,则的取值范围是________.15. (1分) (2019高一下·苏州月考) 在中,若,,,则 ________.16. (1分)(2018·长沙模拟) 已知各项都为整数的数列中,,且对任意的,满足,,则 ________.三、解答题 (共6题;共60分)17. (10分) (2020高一下·元氏期中) 设函数 .已知不等式的解集为(1)求m和n的值.(2)若对任意恒成立,求a的取值范围.18. (10分) (2020高一下·乌拉特前旗月考) 设的内角A,B,C所对的边分别为a,b,c,且,, cosB= .(1)求a,c的值;(2)求的值.19. (10分) (2017高三上·宜宾期中) 已知在等差数列{an}中,Sn为其前n项和,a2=2,S5=15;等比数列{bn}的前n项和.( I)求数列{an},{bn}的通项公式;( II)设cn=an•bn ,求数列{cn}的前n项和Cn .20. (5分) (2017高一下·庐江期末) 某厂生产甲、乙两种产品每吨所需的煤、电和产值如下表所示.用煤(吨)用电(千瓦)产值(万元)甲产品35012乙产品7208但国家每天分配给该厂的煤、电有限,每天供煤至多47吨,供电至多300千瓦,问该厂如何安排生产,使得该厂日产值最大?最大日产值为多少?21. (15分)(2020·大庆模拟) 已知函数, .(1)若,且,,求的值;(2)在中,角的对边分别为,满足, ,求的取值范围.22. (10分) (2017高一下·孝感期末) 已知公差不为零的等差数列{an}中,a1=1且a1 , a3 , a9成等比数列,(Ⅰ)求数列{an}的通项公式(Ⅱ)设bn=n•2 求数列[bn}的前n项和Sn .参考答案一、单选题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题;共60分) 17-1、17-2、18-1、18-2、19-1、20-1、21-1、21-2、22-1、。
湖北省黄冈市蕲一中高一数学下学期期中试题 理 新人教
湖北省黄冈市蕲春一中2013-2014学年高一数学下学期期中试题 理新人教A 版试卷满分:150分 时间:120分钟一、选择题(本大题共10个小题;每小题5分,共50分.在每小题给出的四个选项中,只有一个符合题目要求,请将正确选项的代号填入答题卡的相应位置.) 1.已知数列的一个通项公式为113(1)2n n n n a +-+=-,则5a = ( ) A .12B .12-C .932D .932-2.不等式xx x x 22->- 解集是 ( ) A .(0,2)B .(-∞,0)C .(2,+∞)D .(-∞,0)∪(0,+∞)3.下列命题中正确的是( )A .若a b >,则22ac bc > B .若0ab >,a b >,则11a b < C .若a b >,c d >,则a c b d ->- D .若a b >,c d <,则a bc d>4.在ABC ∆中,角,A B 分别满足tan 2,tan 3A B ==,则角C 为 ( ) A .34π B .4π C . 6π D . 3π 5.已知数列121,,,4a a --成等差数列,1231,,,,4b b b --成等比数列,则212a ab -=( ) A .12B .12-C.1122-或D.146.在钝角三角形ABC 中,a=1,b=2,则最大边c 的取值范围是 ( ) A .(3,3)B .(2,3)C .(5,3)7.如图,已知正方形ABCD 的边长为2, P 、Q 分别为边AB 、DA 上的点。
设,,BCP DCQ αβ∠=∠=若APQ ∆的周长为4,则αβ+=( )A .15︒B .30︒C .45︒D .60︒8.已知数列{}n a 为21,3231+,434241++,54535251+++,…,若2+n n 的前n 项和S n = ( )A .)2)(1(532+++n n n nB .)3)(1(522+++n n n nC .)3)(2(232+++n n n nD .)2)(1(322+++n n nn9.若ABC ∆内接于单位圆,且ABC ∆面积为S ,则长为sin ,sin ,sin A B C 的三条线段( )A .不能构成三角形B .能构成一个三角形,其面积为2SC .能构成一个三角形,其面积大于2S D .能构成一个三角形,其面积小于 2S 10.把数列{}12+n 依次按第一个括号一个数,第二个括号两个数,第三个括号三个数,第四个括号四个数,第五个括号一个数,…循环分为:(3) (5,7) (9,11,13) (15,17,19,21) (23) (25,27) (29,31,33) (35,37,39,41)…则第60个括号内各数之和为( ) A.1112B.1168C.1176D. 1192二、填空题(本大题共5小题,每小题5分,共25分,把答案填在答题卡的相应位置.)11.不等式ax 2+4x +a >1-2x 2对一切x ∈R 恒成立,则实数a 的取值范围是________. 12.{}n a 为等差数列,若a 1>0,a 2013+a 2014>0,a 2013a 2014<0,则使前n 项0n S >的最大自然数n 是 .13.设α为锐角,若cos ⎝ ⎛⎭⎪⎫α+π6=45,则sin ⎝⎛⎭⎪⎫2α+π12的值为______. 14.已知一个三角形的三边长为连续的三个自然数,且最大角是最小角的2倍,则这个三角形的面积为________.15.下列说法中正确的有(填写你认为正确的命题的序号)________.①若数列{}n a 是等差数列,且*)(N t s n m a a a a t s n m ∈+=+、、、,则t s n m +=+;②若n S 是等差数列{}n a 的前n 项的和,则n n n n n S S S S S 232--,,成等差数列; ③若n S 是等比数列{}n a 的前n 项的和,则n n n n n S S S S S 232--,,成等比数列;④若n S 是等比数列{}n a 的前n 项的和,且B Aq S nn +=;(其中B A 、是非零常数,*N n ∈),则B A +为零 三、解答题:(本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤.) 16.(本题满分12分)若关于x 的不等式-12x 2+2x >mx +1的解集为{x | 1<x <2},求m 的值.17.(本题满分12分)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c 分,且满足2cos cos c b Ba A-=. (1)求角A 的大小;(2)若25a =,求△ABC 面积的最大值.18.(本题满分12分)在塔底的水平面上某点测得塔顶的仰角为θ,由此点向塔底沿直线行走30米,测得塔顶的仰角为2θ,再向塔前进310米,又测得塔顶的仰角为4θ,求塔高。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高一年级数学学科(理科)期中考试命题说明
一、试卷题型题量
1、选择题(共8题,每题5分)
2、填空题(共6题,每题5分)
3、解答题(共6题,前两道大题每题12分,后四道大题每题14分)
二、命题范围
人教A 版《必修5》全册
三、难度系数
难:中:易=1 : 3 : 6
四、预估成绩
预期平均分95分左右,优秀率25%左右,合格率90%左右
高一年级数学学科(理科)试题
说明:1、本卷总分 150 分,考试时间 120分钟。
2、考生必须用黑色钢笔或签字笔在答题卷指定范围内作答。
一、选择题(本大题共8小题,每小题5分,共40分. 在每小题给出的四个选项中,只有一项是符合题目要求的)
1、 已知0a b >>,那么下列不等式成立的是( )
()A a b ->- ()B a c b c +<+ ()()()22C a b ->- ()
11D a b
>
2.,的一个通项公式是( )
A. n a =n a =n a n a =
3、在△ABC 中,a =3,b =7,c =2,那么B 等于(
) A . 30°
B .45°
C .60°
D .120°
4. 在等差数列{}n a 中,已知1234520a a a a a ++++=,则3a 等于 ( )
A. 4
B. 5
C. 6
D. 7
5、已知x ,y 满足约束条件⎩⎪⎨⎪⎧ x -y +5≥0,x +y ≥0,
x ≤3,
则z =2x +4y 的最小值为( ) A .5 B .-6 C .10 D .-10
6. 设△ABC 的内角A , B , C 所对的边分别为a , b , c , 若cos cos sin b C c B a A +=, 则△ABC 的形状为( )
(A) 锐角三角形 (B) 直角三角形 (C) 钝角三角形 (D) 不确定
7、数列{a n }中,a 1=1,a n +1=22+n n a a (n ∈N *),则101
2是这个数列的第几项( ) A.100项 B.101项 C.102项 D.103项
8、在R 上定义运算⊗:(1)x y x y ⊗=-,若不等式1)()(<+⊗-a x a x 对任意实数x 成立,则a 的取值范围为 ( )
A .11<<-a
B .20<<a
C .2123<<-a
D .2321<<-a
二.填空题(本大题共6小题,每小题5分,共30分)
9、在△ABC 中,===B c a ,2,33150°,则b =
10、在等比数列{}n a 中,已知12324,a a +=3436,a a +=则56a a +=_____________
11、 在等腰三角形 ABC 中,已知sinA ∶sinB=1∶2,底边BC=10,则△ABC 的周长是__ __.
12、设的最小值为则
且y
x y x y x 11,120,0+=+>> .
13. 数列1
21,241,38
1,4161,…的前n 项和为 . 14、在数列}{n a 中,已知11=a ,52=a ,)N (*12∈-=++n a a a n n n ,则
=2008a _________
三、解答题(本大题共6小题,共80分. 解答应写出文字说明、证明过程或演算步骤)
15. (本小题满分12分)
在△ABC 中,已知b =2,c =1,B =45°,求a 、A 、C .
16.(本小题满分12分)
设f (x )=(m +1)x 2-mx +m -1.
(1)、当m =1时,求不等式f (x )>0的解集;
(2)、若不等式f (x )+1>0的解集为(32
,3),求m 的值.
17. (本小题满分14分)
已知A 、B 、C 为ABC ∆的三内角,且其对边分别为a 、b 、c , 若2
1sin sin cos cos =-C B C B . (Ⅰ)求A ; (Ⅱ)若4,32=+=c b a ,求ABC ∆的面积.
18、(本小题满分14分)
设}{n a 为正项等比数列,满足256,151==a a ;n S 为等差数列}{n b 的前n 项
和,,21=b 8525S S =.(1)求}{n a ,}{n b 的通项公式.(2)设n T n n b a b a b a ++=2211,求n T .
19、(本小题满分14分)
某公司的仓库A 存有货物12吨,仓库B 存有货物8吨.现按7吨、8吨和5吨把货物分别调运给甲、乙、丙三个商店,从仓库A 运货物到商店甲、乙、丙,每吨货物的运费分别为8元、6元、9元、从仓库B 运货物到商店甲、乙、丙,每吨货物的运费分别为3元、4元、5元.设仓库A 运给甲、乙商店的货物分别为x 吨,y 吨,从两个仓库运货物到三个商店的总运费为z
(1)、试用x 与y 来表示z .
(2)、求从两个仓库运货物到三个商店的总运费z 的最小值?
20. (本题满分14分)
已知二次函数c bx ax x f ++=2)(经过坐标原点,当31=x 时有最小值3
1-,数列}{n a 的前n 项和为n S ,点))(,(*N n S n n ∈均在函数)(x f y =的图象上。
(1)求函数)(x f 的解析式; (2)求数列}{n a 的通项公式;
(3)设n n n n T a a b ,11
+=是数列}{n b 的前n 项和,求使得20m T n <对所有*N n ∈都成立的最小正整数m 。
