圆的单元检测(一).doc
(必考题)小学数学六年级上册第五单元《圆》检测题(包含答案解析)(1)

(必考题)小学数学六年级上册第五单元《圆》检测题(包含答案解析)(1)一、选择题1.把一个直径10厘米圆分成两个相等的半圆,两个半圆的周长的和是()A. 31.4B. 62.8C. 41.4D. 51.4 2.在长4厘米,宽3厘米的长方形内画最大半圆,这个半圆的周长是()A. 6.28厘米B. 7.71厘米C. 10.28厘米D. 12.56厘米3.两个圆的周长不相等,是因为它们的()。
A. 圆心位置不同B. 半径不相等C. 圆周率不相等4.东方公园有一个圆形的喷水池,经测量得出这个喷水池的周长是37 .68m。
这个喷水池占地()m2。
A. 37.68B. 113.04C. 452.165.下图是一个半圆,它的半径是5cm,周长是()cm。
A. 5π +10B. 5πC. 10πD. 10π+106.把一个直径是2cm的圆平分成2个半圆后,每个半圆的周长是()。
A. 6.28cmB. 3.14cmC. 4.14cmD. 5.14cm 7.长方形、正方形、圆的周长都相等,则面积最大的是()。
A. 长方形B. 正方形C. 圆D. 无法比较8.周长相等的长方形、正方形、圆中,()的面积最大。
A. 长方形B. 正方形C. 圆9.一个圆形花坛的半径是2.5米,在花坛一周铺了一条宽0.5米的碎石小路,小路的面积是()平方米。
A. 27.475B. 9.42C. 8.635D. 28.26 10.下面两个图形阴影部分的周长和面积的大小关系是()。
A. 周长相等,面积不相等B. 周长和面积都相等C. 周长和面积都不相等D. 周长不相等,面积相等11.大圆的半径是小圆半径的3倍,则大圆面积是小圆面积的()。
A. 3倍B. 4倍C. 6倍D. 9倍12.一个圆的半径是6厘米,它的周长是()厘米。
A. 18.84B. 37.68C. 113.04二、填空题13.用圆规画一个周长是12.56dm的圆,圆规两脚之间的距离是________dm,这个圆的面积是________dm2。
新北师大版六年级数学上册1.圆单元测试(含答案)

六年级上册数学圆单元测试一、单选题1.一个圆至少对折( )次才能找到圆心.A. 1B. 2C. 32.给一个直径1米的圆桌选一块方形桌布,选一块方形桌布,选()块最合适.A. 1.3米×1.3米.B. 1.3米×1.1米C. 1.2米×0.9米D. 1.1米×1.1米3.小红用彩色纸剪了一个半圆(如图),半径是6cm,求周长,列式是( )。
A. 3.14×6×2÷2B. 3.14×62÷2C. 3.14×6×2÷2+6×2D. 3.14×6×2÷2+64.下列说法:()①圆锥的体积等于圆柱体积的三分之一;②长方体有12条棱和8个顶点;③圆的半径扩大5倍,周长也扩大5倍;④直线外一点与直线上各点连接的所有线段中,垂线段最短。
其中正确的有多少个?A. 1个B. 2个C. 3个D. 4个二、判断题5. 一个圆的半径扩大3倍,它的面积扩大6倍()6.圆的半径扩大3倍,面积扩大9倍.()7.任何一个圆的周长都是它直径长度的π倍.()8.6个圆心角都是60°的扇形一定可以拼成一个圆。
()三、填空题9.求图中涂色部分的面积.(单位:cm)(保留两位小数)(1)面积是________cm2(2)面积是________cm2(3)面积是________cm2(4)面积是________cm210.圆的位置由________确定;圆的半径决定圆的________;画圆时圆规两脚间的距离是圆的________.11.用一根铁丝围成一个圆,半径正好是5分米,如果把这根铁丝改围成一个正方形,它的边长是________分米。
(π=3.14)12.一个直径为4米的半圆,它的周长是________ 米。
四、解答题13.一张圆桌的直径达到1.8米,按照每人占有位置70厘米计算(如图),这张圆桌大约可以坐几个人?14.求下图中阴影部分的面积。
九年级上学期数学《圆》单元检测题含答案

A.5B. C.5 D.5
[答案]D
[解析]
试题解析:连接OA、OB、OP,
∵∠C=30°,∴∠APB=∠C=30°,∵PB=A B,∴∠PA B=∠APB=30°
A.π+1B.π+2C.2π+2D.4π+1
8.如图,△A B C是⊙O的内接三角形,∠C=30°,⊙O的半径为5,若点P是⊙O上的一点,在△A BP中,PB=A B,则PA的长为()
A. 5B. C. 5 D. 5
9.如图是某公园的一角,∠AOB=90°,弧A B的半径OA长是6米,C是OA的中点,点D在弧A B上,C D∥OB,则图中休闲区(阴影部分)的面积是()
23.如图,点I是△A B C的内心,AI的延长线和△A B C的外接圆相交于点D,与B C相交于点E.
(1)求证:DI=D B;
(2)若AE=6Cm,ED=4Cm,求线段DI的长.
24.如图,已知扇形AOB的圆心角为直角,正方形OC DE内接于扇形AOB.点C、E、D分别在OA、OB、弧A B上,过点A作AF⊥DE交ED的延长线于F,如果正方形的边长为1,求阴影部分M、N的面积和.
点睛:本题考查了圆周角定理,圆周角的度数等于它所对的弧所对的圆心角度数的一半,圆的弦所对的圆周角分两种,一种是优弧所对的圆周角,一种是劣弧所对的圆周角,它们是互补的关系.
4.⊙O的半径r=5Cm,直线l到圆心O的距离D=4,则l与⊙O的位置关系是( )
A.相离B.相切C.相交D.重合
[答案]C
[解析]
3.正六边形内接于圆,它的边所对的圆周角是( )
《常考题》小学数学六年级上册第五单元《圆》检测(有答案解析)(1)
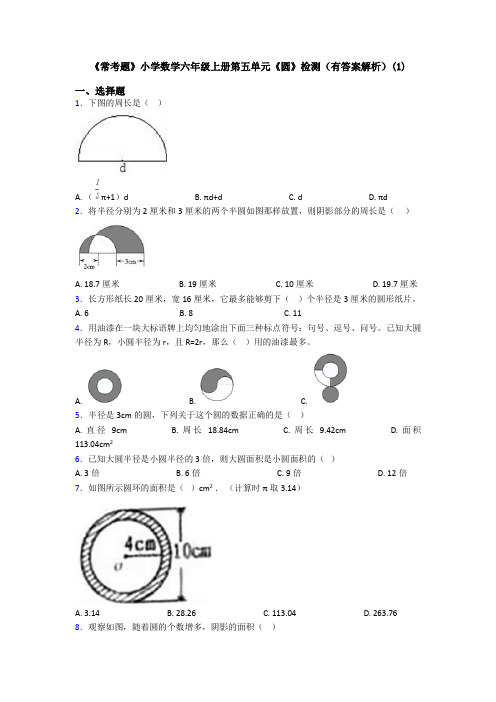
3.长方形纸长 20 厘米,宽 16 厘米,它最多能够剪下( )个半径是 3 厘米的圆形纸片。
A. 6
B. 8
C. 11
4.用油漆在一块大标语牌上均匀地涂出下面三种标点符号:句号、逗号、问号。已知大圆
半径为 R,小圆半径为 r,且 R=2r,那么( )用的油漆最多。
A.
B.
C.
5.半径是 3cm 的圆,下列关于这个圆的数据正确的是( )
《常考题》小学数学六年级上册第五单元《圆》检测(有答案解析)(1)
一、选择题
1.下图的周长是( )
A. ( π+1)d
B. πd+d
C. d
D. πd
2.将半径分别为 2 厘米和 3 厘米的两个半圆如图那样放置,则阴影部分的周长是( )
A. 18.7 厘米
B. 19 厘米
C. 10 厘米
D. 19.7 厘米
10.A
解析: A
【解析】【解答】解: ×5×2÷2+5×2=5 +10(cm)。
故答案为:A。
【分析】半圆的周长包括所在圆周长的一半加上直径的长度,由此根据周长公式计算即
可。
11.C
解析: C
【解析】【解答】解:设直径是 1,则周长是: ×1+1,(
)÷1=
。
故答案为:C。
【分析】半圆的周长是圆周长的一半加上直径的长度,设直径是 1,计算出半圆的周长,
24.街心花园有一个圆形花坛,花坛的直径是 10m。要在花坛的外围修一条宽 1.5m 的小 路,这条小路的面积是多少平方米? 25.在一个长 20cm、宽 10cm 的长方形里,剪一个最大的圆,这个圆的周长是多少?面积 是多少? 26.求下图中阴影部分的周长和面积。
北师大版数学六年级上册第一单元《圆的面积》练习.doc

圆的面积练习精选一、填空1.一个圆形桌面的直径是2米,它的面积是()平方米。
2.已知圆的周长c,求d=(),求r=()。
3.圆的半径扩大2倍,直径就扩大()倍,周长就扩大()倍,面积就扩大()倍。
4.环形面积S=()。
5.用圆规画一个周长50.24厘米的圆,圆规两脚尖之间的距离应是()厘米,画出的这个圆的面积是()平方厘米。
6.大圆半径是小圆半径的4倍,大圆周长是小圆周长的()倍,小圆面积是大圆面积的()。
7.圆的半径增加1/4圆的周长增加(),圆的面积增加()。
8.一个半圆的周长是20.56分米,这个半圆的面积是()平方分米。
9.将一个圆平均分成1000个完全相同的小扇形,割拼成近似的长方形的周长比原来圆周长长10厘米,这个长方形的面积是()平方厘米。
10.在一个面积是16平方厘米的正方形内画一个最大的圆,这个圆的面积是()平方厘米;再在这个圆内画一个最大的正方形,正方形的面积是()平方厘米。
11.大圆半径是小圆半径的3倍,大圆面积是84.78平方厘米,则小圆面积为()平方厘米。
12.大圆半径是小圆半径的2倍,大圆面积比小圆面积多12平方厘米,小圆面积是()平方厘米。
13.鼓楼中心岛是半径10米的圆,它的占地面积是()平方米。
14.小华量得一根树干的周长是75.36厘米,这根树干的横截面大约是()平方厘米15.一只羊栓在一块草地中央的树桩上,树桩到羊颈的绳长是3米。
这只羊可以吃到()平方米地面的草。
16.一根2米长的铁丝,围成一个半径是30厘米的圆,(接头处不计),还多()米,围成的面积是()17.用一根10.28米的绳子,围成一个半圆形,这个半圆的半径是(),面积是()18.从一个长8分米,宽5分米的长方形木板上锯下一个最大的圆,这个圆的面积是()19.大圆的半径等于小圆的直径,大圆的面积是小圆面积的()20.一个圆的周长扩大3倍,面积就扩大()倍。
21.用三根同样长的铁丝分别围成一个长方形、一个正方形、和一个圆,其中()面积最小,()面积最大二、应用题1.一个环形的外圆半径是8分米,内圆半径5分米,求环形的面积?2.环形的外圆周长是18.84厘米,内圆直径是4厘米,求环形的面积?3.校园圆形花池的半径是6米,在花池的周围修一条1米宽的水泥路,求水泥路的面积是多少平方米?4.(1)轧路机前轮直径1.2米,每分钟滚动6周。
(必考题)小学数学六年级上册第五单元《圆》检测(有答案解析)(1)

解析: 3:4;9:16 【解析】【解答】周长之比:(2π×3):(2π×4) =6π:8π =3:4; 面积之比:(π×32):(π×42) =9π:16π =9:16。 故答案为;3:4;9:16。 【分析】此题主要考查了圆的周长与面积公式的应用,C=2πr,S=πr2 , 两个圆的半径之比 是 x:y,则两个圆周长的最简整数比是 x:y,两个圆的面积的最简整数比是 x2:y2 , 据 此解答。
二、填空题
13.2;1256【解析】【解答】解:1256÷314÷2=2dm 所以圆规两脚之间的距离 是 2dm2×2×314=1256dm2 故答案为:2;1256【分析】圆规两脚之间的距离是 所画圆的半径;圆的半径=圆的
解析: 2;12.56 【 解 析 】 【 解 答 】 解 : 12.56÷3.14÷2=2dm , 所 以 圆 规 两 脚 之 间 的 距 离 是 2dm , 2×2×3.14=12.56dm2。 故答案为:2;12.56。 【分析】圆规两脚之间的距离是所画圆的半径; 圆的半径=圆的周长÷π÷2;圆的面积=πr2。
选项 C, ×[π×(2r)2-πr2]+πr2
= ×3πr2+πr2
= πr2。
因为 >3>2,所以?用的油漆最多。 故答案为:C。 【分析】选项 A,句号用的油漆=大圆的面积-小圆的面积; 选项 B,逗号用的油漆=大圆面积的一半;
选项 C,问号用油漆=大圆的面积减去小圆的面积得出的结果的 , 再加上小圆的面积; 计算出各个选项的值再进行比较即可得出答案。 注意圆的面积=π×半径的平方。
五年级下册数学单元测试卷-第一单元 完美的图形——圆-青岛版五四制(含答案)
五年级下册数学单元测试卷-第一单元完美的图形——圆-青岛版五四制(含答案)一、选择题(共5题,共计20分)1、下面各圆中的线段,()是圆的半径.A. B. C. D.2、两个大小不同的圆.如果这两个圆的半径都增加3厘米,那么,它们周长增加的部分相比()A.大圆增加的多B.小圆增加的多C.增加的同样多D.无法比较3、把一张长为5分米、宽为4分米的长方形纸片剪成一个最大的圆,这个圆的周长是()分米.A.6.28B.15.7C.12.564、周长为800m的正方形铁片,要在其上截出一个圆,该圆最大面积是()A.100π平方米B.1000π平方米C.10000π平方米D.100000π平方米5、在草地中心栓着一头牛,绳长4米,这牛最多吃到的面积是多少?正确的列式是()A.3.14×4 2B.2.14×4C.2×3.14×4D.2×3.14×42二、填空题(共8题,共计24分)6、同学们围成一个圆圈做游戏,老师站在中心点上,已知这个圆圈的周长是18.84米,每个同学与老师的距离大约是________米。
7、一只大钟,它的分针长40厘米.这根分针的尖端转动一周所走的路程是________厘米,从1 时到2时分针扫过的面积是________平方厘米.8、某赛车的左、右轮子的距离为2米,赛车车轮绕一半径为8米的圆形场地行走一圈时,外轮比内轮多走了________米(结果保留π).9、用圆规画一个周长是9.42cm的圆,圆规两脚间的距离是________cm,这个圆的面积是________cm2。
10、半径是3厘米的圆,这个圆的周长是________厘米,面积是________平方厘米。
11、求下面圆的面积.面积是________dm2.12、运动场是由一个________和两个________组成。
A.长方形 B.平行四边形 C.半圆 D.圆13、把一根6.28m长的铁丝围成一个正方形,则正方形的面积是________ m2;若围成一个圆,则圆的面积是________ m2。
《易错题》小学数学六年级上册第五单元《圆》检测卷(含答案解析)(1)
《易错题》小学数学六年级上册第五单元《圆》检测卷(含答案解析)(1)一、选择题1.把一个直径10厘米圆分成两个相等的半圆,两个半圆的周长的和是()A. 31.4B. 62.8C. 41.4D. 51.4 2.长方形纸长20厘米,宽16厘米,它最多能够剪下()个半径是3厘米的圆形纸片。
A. 6B. 8C. 113.用油漆在一块大标语牌上均匀地涂出下面三种标点符号:句号、逗号、问号。
已知大圆半径为R,小圆半径为r,且R=2r,那么()用的油漆最多。
A. B. C.4.如图,正方形的周长是16分米,则这个圆的面积是()A. 50.24平方分米B. 12.56平方分米C. 25.12平方分米D. 803.84平方分米5.下面图()中的阴影部分可能是圆心角为100°的扇形.A. B. C.D.6.如图所示圆环的面积是()cm2.(计算时π取3.14)A. 3.14B. 28.26C. 113.04D. 263.76 7.如图,两只蚂蚁分别选择甲、乙两条线路从A地爬向B地.下面说法正确的是()A. 甲线路路程多B. 乙线路路程多C. 两条线路的路程一样多D. 不能确定8.在圆内剪去一个圆心角为45的扇形,余下部分的面积是剪去部分面积的()倍.A. 9 B. 8 C. 79.下图是一个半圆,它的半径是5cm,周长是()cm。
A. 5π +10B. 5πC. 10πD. 10π+10 10.周长相等的长方形、正方形、圆中,()的面积最大。
A. 长方形B. 正方形C. 圆11.一个圆形花坛的半径是2.5米,在花坛一周铺了一条宽0.5米的碎石小路,小路的面积是()平方米。
A. 27.475B. 9.42C. 8.635D. 28.26 12.大圆的半径是小圆半径的3倍,则大圆面积是小圆面积的()。
A. 3倍B. 4倍C. 6倍D. 9倍二、填空题13.一个圆形花坛的半径4米,周长是________米,面积是________平方米.14.一个正方形边长10厘米,在这个正方形里画一个最大的圆,这个圆的周长是________厘米,面积是________平方厘米.15.半径为4cm的圆比直径为6cm的圆周长多________cm;面积多________cm2.16.圆心角为90°,半径为6米的扇形,它的面积是________平方米.17.两圆的半径长分别是3cm和4cm,那么它们的周长比为________,面积比为________.18.如图,用一张边长是8cm的正方形纸剪一个最大的圆,那么这个圆的周长是________cm,面积是________cm2。
(常考题)人教版初中数学九年级数学上册第四单元《圆》检测卷(包含答案解析)(1)
一、选择题1.下列说法正确的是( )A .圆是轴对称图形,任何一条直径都是圆的对称轴B .平分弦的直径垂直于弦C .长度相等的弧是等弧D .在同圆或等圆中,相等的圆心角所对的弦相等2.如图,一块直角三角板的30°角的顶点P 落在O 上,两边分别交圆O 于A ,B 两点,若O 的直径为6,则弦AB 的长为( )A .3B .2C .2D .33.下列说法:(1)三点确定一个圆;(2)直径所对的圆周角是直角;(3)平分弦的直径垂直于弦,并且平分弦所对的弧;(4)相等的圆心角所对的弧相等;(5)圆内接四边形的对角互补.其中正确的个数为( ) A .1个B .2个C .3个D .4个4.已知⊙O ,如图,(1)作⊙O 的直径AB ;(2)以点A 为圆心,AO 长为半径画弧,交⊙O 于C ,D 两点;(3)连接CD 交AB 于点E ,连接AC ,BC .根据以上作图过程及所作图形,有下面三个推断:①CE DE =;②3BE AE =;③2BC CE =.其中正确的推断的个数是( )A .0个B .1个C .2个D .3个 5.如图,PA 切O 于点,A PB 切O 于点B PO ,交O 于点C ,下列结论中不一定成立的是( )A .PA PB =B .PO 平分APB ∠C .AB OP ⊥D .2PAB APO ∠=∠ 6.如图,PA 、PB 、CD 是O 的切线,切点分别是A 、B 、E ,CD 分别交PA 、PB 于C 、D 两点,若60APB ∠=︒,则COD ∠的度数( )A .50°B .60°C .70°D .75°7.如图△ABC 中,∠C =90°,∠B =28°,以C 为圆心,CA 为半径的圆交AB 于点D ,则AD 的度数为( )A .28°B .56 °C .62°D .112°8.如图,在菱形ABCD 中,60A ∠=︒ ,3AB = ,A ,B 的半径分别为2和1,P ,E ,F 分别是CD 边、A 和B 上的动点,则PE PF +的最小值是( )A .333B .2C .3D .339.如图,⊙O 的半径为1,点 O 到直线 a 的距离为2,点 P 是直线a 上的一个动点,PA 切⊙O 于点 A ,则 PA 的最小值是( )A .1B .3C .2D .510.如图,半径为1cm 的P 在边长为9πcm ,12πcm ,15πcm 的三角形外沿三遍滚动(没有滑动)一周,则圆P 所扫过的面积为( )cm 2A .73πB .75πC .76πD .77π11.如图,四边形ABCD 内接于O ,若108B ∠=︒,则D ∠的大小为( )A .36°B .54°C .62°D .72°12.如图,在平行四边形ABCO 中,45C ∠=︒,点A ,B 在O 上,点D 在ADB 上,DA DB =,则AOD ∠的度数为( )A .112.5°B .120°C .135°D .150°二、填空题13.如图,有一半径为6cm 的圆形纸片,要从中剪出一个圆心角为60︒的扇形ABC ,AB ,AC 为⊙O 的弦,那么剪下的扇形ABC (阴影部分)的面积为 ___________.14.如图,⊙O 的直径16AB =,半径OC AB ⊥,E 为OC 的中点, DE OC ⊥,交⊙O 于点D ,过点D 作DF AB ⊥于点F .若 P 为直径AB 上一动点,则PC PD +的最小值为 ________ .15.如图,已知O 是以数轴上原点O 为圆心,半径为2的圆,45AOB ∠=︒,点P 在x正半轴上运动,若过点P 与OA 平行的直线与O 有公共点,设P 点对应的数为x ,则x 的取值范围是______.16.在ABC 中,90,3,4C AC BC ∠===,则ABC 的内切圆的周长为___________.17.如图,△ABC 中,∠A=60°,若O 为△ABC 的内心,则∠BOC 的度数为______度.18.如图,已知点,,A B C 在O 上,若50ACB ∠=,则AOB ∠=_____________________度.19.如图,ABC 是等边三角形,180BAD BCD ∠+∠=︒,8BD =,2CD =,则AD =________.20.如图,⊙O 的半径为3,点A 是⊙O 外一点,OA =6,B 是⊙O 上的动点,线段AB 的中点为P ,连接 OA 、OP .则线段 OP 的最大值是______.三、解答题21.如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,ABC 的顶点均在格点上,点C 的坐标为()2,1-.(1)画出将ABC 关于y 轴对称的111A B C △;(2)画出ABC 绕点O 的逆时针旋转90°得到的图形222A B C △,并求出在此旋转过程中点A 运动到点2A 所经过路径的长.22.如图,AB 是⊙O 的直径,弦CD AB ⊥于点H ,30A ∠=︒,43CD =⊙O 的半径的长.23.对于平面上两点,A B ,给出如下定义:以点A 或B 为圆心,AB 长为半径的圆称为点,A B 的“共径圆”.点,A B 的“共径圆”的示意图如图所示.(1)已知点A 的坐标为(0,0),点B 的坐标为(3,4),则点,A B 的“共径圆”的面积为_______________;(2)已知点A 在以坐标原点为圆心,以1为半径的圆上,点B 在直线4y x =-+上,求点,A B 的“共径圆”的半径最小值;(3)已知点A 的坐标为(0,0),点B 是x 轴及x 轴上方的点,如果直线y x b =+上存在两个点B ,使得点,A B 的“共径圆”的面积为4π,直接写出满足条件的b 的取值范围.24.如图,AB 为⊙O 的直径,C ,D 是⊙O 上的点,P 是⊙O 外一点,AC ⊥PD 于点E ,AD 平分∠BAC .(1)求证:PD是⊙O的切线;(2)若DE=3,,∠BAC=60°,求⊙O的半径.25.如图,ABC内接于O,60∠=︒,点D是BC的中点.BC,AB边上的高BACAE,CF相交于点H.试证明:∠=∠;(1)FAH CAO(2)四边形AHDO是菱形.26.如图,在平面直角坐标系xOy中,A(0,1),点P(t,0)为x轴上一动点(不与原点重合).以P为圆心,PA为半径的⊙P与x轴正半轴交于点B,连接AB,以AB为直角边在AB的右上方作等腰直角三角形ABC,且∠BAC=90°,直线BC于⊙P的另一个公共点为F,连接PF.(1)当t = 2时,点C的坐标为(,);(2)当t >0时,过点C作x轴的垂线l.①判断当点P运动时,直线l的位置是否发生变化?请说明理由;②试说明点F到直线l的距离始终等于OP的长;(3)请直接写出t为何值时,CF=2BF.【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【分析】根据对称轴的定义对A进行判断;根据垂径定理的推论对B进行判断;根据等弧定义对C 进行判断;根据圆心角定理对D进行判断.【详解】解:A、圆是轴对称图形,任何一条直径所在的直线都是它的对称轴,所以A选项错误;B、平分弦(非直径)的直径垂直于弦,并且平分弦所对的弧,所以B选项错误;C、长度相等的弧不一定能重合,所以不一定是等弧,所以C选项错误;D、在同圆或等圆中,相等的圆心角所对的弦相等,所以D选项正确.故选:D.【点睛】本题考查了圆的有关性质,掌握相关定理是解题关键.2.A解析:A【分析】连接AO并延长交O于点D,连接BD;根据同弦所对的圆周角相等可得30∠=∠=︒;再说明AD=6,然后根据在直角三角形中30°所对的直角边为斜边的一D P半.【详解】解:如图:连接AO并延长交O于点D,连接BD,30P ∠=︒,30D P ∴∠=∠=︒,∵AD 是O 的直径,6AD =,90ABD ∠=︒,132AB AD ∴==. 故答案为A .【点睛】本题考查了圆周角定理以及直角三角形的性质,掌握直径所对的圆周角为直角是解答本题的关键.3.B解析:B【分析】根据确定圆的条件、直径的性质、垂径定理、圆周角定理、圆内接四边形的性质一一判断即可.【详解】解:(1)任意三点确定一个圆;错误,应该是不在同一直线上的三点可以确定一个圆; (2)直径所对的圆周角是直角;正确;(3)平分弦的直径垂直于弦;并且平分弦所对的弧,错误,直径与直径互相平分,但不一定互相垂直;(4)相等的圆心角所对的弧相等;错误,应该是在同圆或等圆中;(5)圆内接四边形对角互补;正确;故选:B .【点睛】本题考查确定圆的条件、直径的性质、垂径定理、圆周角定理、圆内接四边形的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.4.D解析:D【分析】①根据作图过程可得AC AD =,根据垂径定理可判断;②连接OC ,根据作图过程可证得△AOC 为等边三角形,由等边三角形的性质即可判断; ③根据直角三角形中30°角所对的直角边等于斜边的一半即可判断.【详解】解:①∵以点A 为圆心,AO 长为半径画弧,交⊙O 于C ,D 两点,∴AC AD,根据垂径定理可知,AB⊥CE,CE=DE,∴①正确;②连接OC,∵AC=OA=OC,∴△AOC为直角三角形,∵AB⊥CE,∴AE=OE,∴BE=BO+OE=3AE,∴②正确;③∵AB为直径,∴∠ACB=90°,∵∠CAB=60°,∴∠ABC=30°,∴BC=2CE,∴③正确,故选:D.【点睛】本题考查了垂径定理、圆周角定理、等边三角形的判定与性质、含30°角的直角三角形的性质,理解基本作图知识,熟练掌握各基本性质和综合运用是解答的关键.5.D解析:D【分析】利用切线长定理证明△PAG≌△PBG即可得出.【详解】解:连接OA,OB,AB,AB交PO于点G,由切线长定理可得:∠APO=∠BPO,PA=PB,又∵PG=PG,∴△PAG ≌△PBG ,从而AB ⊥OP .因此A .B .C 都正确.无法得出AB =PA =PB ,可知:D 是错误的.综上可知:只有D 是错误的.故选:D .【点睛】本题考查了切线长定理、全等三角形的判定和性质,关键是利用切线长定理解答. 6.B解析:B【分析】连接AO ,BO ,OE 由切线的性质可得90PAO PBO ︒∠=∠=,结合已知条件和四边形的内角和为360°可求出AOB 的度数,再由切线长定理即可求出COD 的度数.【详解】如图,连接AO ,BO ,OE ,∵PA 、PB 是O 的切线,∴∠PAO =∠PBO =90∘,∵60APB ∠=︒,∴36029060120AOB ∠=︒-⨯︒-︒=︒,∵PA 、PB 、CD 是⊙O 的切线,∴∠ACO =∠ECO ,∠DBO =∠DEO ,∴∠AOC =∠EOC ,∠EOD =∠BOD , ∴1602COD COE EOD AOB ∠=∠+∠=∠=︒, 故选B.【点睛】本题考查了切线的性质及切线长定理,解答本题的关键是熟练掌握:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线,平分两条切线的夹角.7.B解析:B【分析】连接CD ,如图,利用互余计算出∠A=62°,则∠A=∠ADC=62°,再根据三角形内角和定理计算出∠ACD=56°,然后根据圆心角的度数等于它所对弧的度数求解.【详解】解:连接CD,如图,∵∠C=90°,∠B=28°,∴∠A=90°-28°=62°,∵CA=CD,∴∠A=∠ADC=62°,∴∠ACD=180°-2×62°=56°∴AD的度数为56°;故选:B.【点睛】本题考查了同圆的半径相等、直角三角形的两锐角互余、等腰三角形的性质,熟练进行逻辑推理是解题关键.8.C解析:C【分析】的最小值,进而求解即可.利用菱形的性质及相切两圆的性质得出P与D重合时PE PF【详解】解:作点A关于直线CD的对称点A´,连接BD,DA´,∵四边形ABCD是菱形,∴AB=AD,∵∠BAD=60°,∴△ABD是等边三角形,∴∠ADB=60°,∵∠BDC=∠ADB=60°,∴∠ADN =60°,∴∠A´DN=60°,∴∠ADB+∠ADA´=180°,∴A´,D,B在一条直线上,+最小,由此可得:当点P和点D重合,E点在AD上,F点在BD上,此时PE PF∵在菱形ABCD中,∠A=60°,∴AB=AD,则△ABD为等边三角形,∴BD=AB=AD=3,∵⊙A,⊙B的半径分别为2和1,∴PE=1,DF=2,+的最小值为3.∴PE PF故选C.【点睛】本题考查了菱形的性质,等边三角形的性质,点与圆的位置关系等知识.根据题意得出点P位置是解题的关键.9.B解析:B【分析】因为PA为切线,所以△OPA是直角三角形.又OA为半径为定值,所以当OP最小时,PA 最小.根据垂线段最短,知OP=2时PA最小.运用勾股定理求解.【详解】解:作OP⊥a于P点,则OP=2.根据题意,在Rt△OPA中,AP=2221=3--=22OP OA故选:B.【点睛】此题考查了切线的性质及垂线段最短等知识点,如何确定PA最小时点P的位置是解题的关键,难度中等偏上.10.A解析:A【分析】圆在三角形的三个角的顶点处旋转的路线是弧,通过观察可以发现圆转动时在三个角上共转动了圆心角360°,所以在三个顶点处转了一个圆的面积,在三个边上滚过的图形是以三角形边长为长,圆的直径为宽的矩形,然就分别计算,最后求和.【详解】解:根据运动特点可知三个顶点处转了一个圆的面积,在三个边上滚过的图形矩形 ∴圆P 所扫过的面积=π+(9π+12π+15π)×2=73π故选:A【点睛】解答本题的关键是,找出圆滚动一周的图形,并将图形进行分割,拼组,化难为易,列式解答即可.11.D解析:D【分析】运用圆内接四边形对角互补计算即可.【详解】∵四边形ABCD 内接于⊙O ,∠B =108°,∴∠D =180°−∠B =180°−108°=72°,故选:D .【点睛】本题主要考查了圆内接四边形的性质,熟练掌握圆内接四边形对角互补是解答此题的关键.12.C解析:C【分析】延长DO 交AB 于点H ,连接OB ,证明△△AOD BOD ≅,OD 是AOB ∠的角平分线,求得290345∠=︒-∠=︒,进行求解即可;【详解】延长DO 交AB 于点H ,连接OB ,∵四边形ABCD 是平行四边形,45C ∠=︒,∴345∠=︒,∵DA DB =,OA OB =,∴△△AOD BOD ≅,∴OD 是AOB ∠的角平分线,又∵AO BO =,∴DH AB ⊥,∴290345∠=︒-∠=︒,又∵221∠=∠,∴18045135AOD ∠=︒-︒=︒.故选:C .【点睛】本题主要考查了与圆有关的计算,结合全等三角形的性质和角平分线的性质计算即可.二、填空题13.【分析】如图(见解析)先根据等边三角形的判定与性质可得再根据圆周角定理可得然后根据垂径定理勾股定理可得BC 的长从而可得AB 的长最后利用扇形的面积公式即可得【详解】如图连接OBOCBC 过点O 作于点D 由 解析:218cm π【分析】如图(见解析),先根据等边三角形的判定与性质可得AB BC =,再根据圆周角定理可得120BOC ∠=︒,然后根据垂径定理、勾股定理可得BC 的长,从而可得AB 的长,最后利用扇形的面积公式即可得.【详解】如图,连接OB 、OC 、BC ,过点O 作OD BC 于点D ,由题意得:,60,6AB AC A OB OC cm =∠=︒==,ABC ∴是等边三角形,AB BC ∴=,由圆周角定理得:2120BOC A ∠=∠=︒,OD BC ⊥,160,22BOD BOC BC BD ∴∠=∠=︒=, 30OBD ∴∠=︒,在Rt BOD 中,13,2OD OB cm BD ====,2AB BC BD ∴===,则剪下的扇形ABC (阴影部分)的面积为(()226018360cm ππ⨯=,故答案为:218cm π.【点睛】本题考查了等边三角形的判定与性质、圆周角定理、垂径定理、扇形的面积公式等知识点,通过作辅助线,利用到垂径定理是解题关键.14.【分析】延长CO 交⊙O 于G 连接GD 交AB 于P 根据两点之间线段最短可知PC+PD 的最小值为GD 由勾股定理分别求得DEDG 即可解答【详解】解:延长CO 交⊙O 于G 连接GD 交AB 于P 则PC+PD 的最小值为G 解析:83【分析】 延长CO 交⊙O 于G ,连接GD 交AB 于P ,根据两点之间线段最短可知PC+PD 的最小值为GD ,由勾股定理分别求得DE 、DG 即可解答.【详解】解:延长CO 交⊙O 于G ,连接GD 交AB 于P ,则PC+PD 的最小值为GD ,连接OD ,则OD=OG=OC= 12AB=8, ∵E 为OC 的中点,∴OE=12OC=4, ∴EG=4+8=12,∵DE OC ⊥,∴在Rt △OED 中,22228443OD OE -=-=,在Rt △GED 中,DG=2222(43)1283ED EG +=+=,故答案为:83.【点睛】本题考查勾股定理、最短路径问题、圆的有关概念与性质,熟练掌握勾股定理和圆的性质是解答的关键.15.【分析】根据题意知直线和圆有公共点则相切或相交相切时设切点为C 连接OC 根据等腰直角三角形的直角边是圆的半径2求得斜边是2所以x 的取值范围是0<x≤2【详解】解:设切点为C 连接OC 则圆的半径OC=2O解析:022x <≤【分析】根据题意,知直线和圆有公共点,则相切或相交.相切时,设切点为C ,连接OC .根据等腰直角三角形的直角边是圆的半径2,求得斜边是22.所以x 的取值范围是0<x≤22.【详解】解:设切点为C ,连接OC ,则圆的半径OC=2,OC ⊥PC ,∵∠AOB=45°,OA//PC ,∴∠OPC=45°,∴PC=OC=2,∴OP=2222+=22,所以x 的取值范围是0<x≤22,故答案为0<x≤22.【点睛】此题主要考查了直线与圆的位置关系,勾股定理,作出切线找出直线与圆有交点的分界点是解决问题的关键.16.【分析】先根据勾股定理求出斜边AB 的长再根据直角三角形内切圆的半径公式求出半径再算出周长【详解】解:根据勾股定理内切圆半径内切圆周长故答案是:【点睛】本题考查三角形的内切圆解题的关键是掌握直角三角形 解析:2π【分析】先根据勾股定理求出斜边AB 的长,再根据直角三角形内切圆的半径公式求出半径,再算出周长.【详解】解:根据勾股定理,5AB ==, 内切圆半径345122AC BC AB +-+-===, 内切圆周长22r ππ==.故答案是:2π.【点睛】本题考查三角形的内切圆,解题的关键是掌握直角三角形内切圆半径的求解方法. 17.120【分析】根据三角形的内心是三角形角平分线的交点结合公式求出即可【详解】解:为的内心故答案是:120【点睛】注意此题中的结论:若是内心则熟记公式可简化计算解析:120【分析】 根据三角形的内心是三角形角平分线的交点,结合公式1902BOC A ∠=+∠︒求出即可. 【详解】解:60A ∠=︒,O 为ABC ∆的内心, 1190906012022BOC A , 故答案是:120.【点睛】注意此题中的结论:若O 是内心,则1902BOC A ∠=+∠︒.熟记公式可简化计算. 18.【分析】直接根据圆周角定理即可得出结论【详解】解:∵∠ACB 与∠AOB 是同弧所对的圆周角与圆心角∠ACB=50°∴∠AOB=100°故答案是:100°【点睛】本题考查的是圆周角定理熟知在同圆或等圆中解析:100【分析】直接根据圆周角定理即可得出结论.【详解】解:∵∠ACB 与∠AOB 是同弧所对的圆周角与圆心角,∠ACB=50°,∴∠AOB=100°.故答案是:100°.【点睛】本题考查的是圆周角定理,熟知在同圆或等圆中,一条弧所对的圆周角等于这条弧所对的圆心角的一半是解答此题的关键.19.6【分析】在线段BD 上取一点E 使得BE=CD 连接AE 由四点共圆得∠再证明△是等边三角形得再由线段的和差关系可得结论【详解】解:在线段BD 上取一点E 使得BE=CD 连接AE ∵∴四点共圆∴∠∴∠∵△是等边解析:6【分析】在线段BD 上取一点E ,使得BE=CD ,连接AE ,由,,,A B C D 四点共圆得∠ABE ACD =∠,再证明ABE ACD ≅∆,△ADE 是等边三角形,得AD DE AE ==,再由线段的和差关系可得结论.【详解】解:在线段BD 上取一点E ,使得BE=CD ,连接AE ,∵180BAD BCD ∠+∠=︒∴,,,A B C D 四点共圆,∴∠ABD ACD =∠∴∠ABE ACD =∠∵△ABC 是等边三角形,∴AB AC BC ==,60DAE ∠=︒,∴△ABE ACD ≅∆,∠60BAE CAF +∠=︒,∴,BAE CAD BAF CAD ∠=∠∠=∠,∴∠60CAD CAE +∠=︒,即60DAE ∠=︒,∴△ADE 是等边三角形,∴AD DE AE ==,∵=8BD ,2CD =,∴6DE BD BE BD CD =-=-=,∴6AD DE ==.【点睛】此题主要考查了全等三角形的判定与性质,以及四点共圆的判定,证明∠ABE ACD =∠是解答此题的关键.20.【分析】如图连接OB 设OA 交⊙O 于点T 连接PT 利用三角形中位线定理求出PT 根据OP≤PT+OT 可得结论【详解】如图连接OB 设OA 交⊙O 于点T 连接PT ∵OA=6OT=3∴OT=TA ∵AP=PB ∴PT= 解析:92【分析】如图,连接OB ,设OA 交⊙O 于点T ,连接PT .利用三角形中位线定理求出PT ,根据OP≤PT+OT ,可得结论.【详解】如图,连接OB,设OA交⊙O于点T,连接PT.∵OA=6,OT=3,∴OT=TA,∵AP=PB,∴PT=12OB=32,∵OP≤PT+OT,∴OP≤92,故答案为:92.【点睛】本题考查点与圆的位置关系,三角形中位线定理等知识,解题的关键是学会添加常用辅助线,构造三角形的中位线解决问题.三、解答题21.(1)见解析;(2)图见解析,5 2【分析】(1)依据轴对称的性质,即可得到△ABC关于y轴对称的△A1B1C1;(2)依据旋转中心、旋转方向和旋转角度,即可得到△A2B2C2,再根据弧长计算公式,即可得出旋转过程中点A运动到点A2所经过路径的长.【详解】解:(1)如图所示,△A1B1C1即为所求;(2)如图所示,△A 2B 2C 2即为所求;∵OA=22345+=,∠AOA 2=90°,∴在此旋转过程中点A 运动到点A 2所经过路径的长为:90551802ππ⨯⨯=. 【点睛】本题主要考查了利用轴对称变换以及旋转变换进行作图,勾股定理,以及弧长公式,熟练掌握旋转变换与轴对称变换的定义和性质是解题的关键.22.4【分析】连接OC, 根据垂径定理可得∠CHO=90°,CD=2CH ,求出CH 的长,根据30°的直角三角形的特征以及勾股定理求出OC=2OH 即可.【详解】连接OC ,则OA =OC .∴∠A =∠ACO =30°.∴∠COH =60°.∵AB 是⊙O 的直径,弦CD ⊥AB 于点H ,∴∠CHO=90°,CD=2CH∴∠OCH=30°,∴2OC OH =,∵CD 3∴CH =23∴在Rt OCH 中,222OH HC OC +=∴OH =2.∴OC =4.【点睛】本题考查了垂径定理及30度的直角三角形的性质以及勾股定理得应用,解题的关键是掌握垂径定理及30度的直角三角形的性质.23.(1) 25π;(2)221-;(3)222b ≤<【分析】(1)由点A 、B 的坐标知,22345,=+=AB 由圆的面积公式得:“共径圆”的面积πr 2=25π;(2)如下图,当O 、A 、B 三点共线,且OB ⊥直线l 时,共径圆”的半径最小,即可求解; (3)设点B 的坐标为(x ,x+b ),设AB 之间的距离为r ,则πr 2=4π,解得r=2(负值已舍去),则AB=x 2+(x+b )2=22=4,满足条件的B 点有2个,故△=(2b )2-2×4(b 2-4)>0,进而求解.【详解】解:(1)A 的坐标为(0,0),点B 的坐标为(3,4),∴22345,=+=AB由圆的面积公式得:“共径圆”的面积πr 2=25π,故答案为25π;(2)作OB ⊥直线l 于B 交圆O 于点A ,此时点,A B 的“共径圆”的半径最小值; 设直线4y x =-+与,x y 轴交于点,M N .()4,00,4()M N ∴,),则ON=OM=4,∴ MON △等腰直角三角形,∴224244=+=MN∴О点到直线MN 的距离为22A 点在O 上,B 点在直线4y x =-+上,A B ∴间的最短距离是221-即,A B 的“共径圆”的最小半径是221-(3)设点B 的坐标为(x ,x+b ),设AB 之间的距离为r ,则πr 2=4π,解得r=2(负值已舍去),则AB=x 2+(x+b )2=22=4,化简得:2x 2+2bx+b 2-4=0,∵满足条件的B 点有2个,故△=(2b )2-2×4(b 2-4)>0, 解得:2222,-<<b∵点B 是x 轴及x 轴上方的点,故b >0,而当b=2时,点B 在x 轴上,∴222b ≤<【点睛】本题为圆的综合题,涉及到一次函数的性质、根的判别式等,这种新定义类的题目,通常按照题设的顺序逐次求解,一般比较容易解答.24.(1)见解析;(2)2【分析】(1)连接OD ,根据角平分线的定义得到∠BAD=∠DAE ,根据等腰三角形的性质得到∠ODA=∠OAD ,由垂直的定义得到∠AEP=90°,根据切线的判定定理即可得到结论; (2)连接BD ,根据角平分线的定义得到∠BAD=∠DAE=30°,推出AB=2BD ,设BD=x ,则AB=2x ,根据勾股定理即可得到结论.【详解】(1)证明:连接OD ,∵AD 平分∠BAC ,∴∠BAD=∠DAE ,∵OA=OD ,∴∠ODA=∠OAD ,∴∠ODA=∠DAE ,∴OD ∥AE ,∵AC ⊥PD ,∴∠AEP=90°,∴∠ODP=∠AEP=90°,∴OD ⊥PE ,∵OD 是⊙O 的半径,∴PD 是⊙O 的切线;(2)解:连接BD ,∵AD 平分∠BAC ,∠BAC=60°,∴∠BAD=∠DAE=30°,∵AC ⊥PE ,∴AD=2DE=∵AB 为⊙O 的直径,∴∠ADB=90°,∴AB=2BD ,设BD=x ,则AB=2x ,∵AD 2+BD 2=AB 2,∴()222(2x x += ∴BD=2,AB=4,∴AO=2,∴⊙O 的半径为2.【点睛】本题考查了切线的判定和性质,勾股定理,角平分线的定义,圆周角定理,含30度角的直角三角形的性质,正确的作出辅助线是解题的关键.25.(1)见详解;(2)见详解【分析】(1)连接AD ,根据题意易得,BAD CAD OD BC ∠=∠⊥,则有∠DAE=∠ODA ,∠DAO=∠ODA ,然后根据角的等量关系可求解;(2)过点O 作OM ⊥AC 于M ,由题意易得AC=2AM ,AC=2AF ,进而可证△AFH ≌△AMO ,然后可得四边形AHDO 是平行四边形,最后问题可证.【详解】证明:(1)连接AD ,如图所示:∵点D 是BC 的中点,∴,BAD CAD OD BC ∠=∠⊥,∵AE ⊥BC ,∴AE ∥OD ,∴∠DAE=∠ODA ,∵OA=OD ,∴∠DAO=∠ODA ,∴∠BAD-∠DAE=∠CAD-∠DAO ,∴∠FAH=∠CAO ;(2)过点O作OM⊥AC于M,∴AC=2AM,∵CF⊥AB,∠BAC=60°,∴AC=2AF,∴AF=AM,∵∠AFH=∠AMO=90°,∠FAH=∠OAM,∴△AFH≌△AMO(ASA),∴AH=AO,∵OA=OD,∴AH//CD,∴四边形AHDO是平行四边形,∵OA=OD,∴四边形AHDO是菱形.【点睛】本题主要考查圆周角定理、垂径定理及菱形的判定,熟练掌握圆周角定理、垂径定理及菱形的判定是解题的关键.26.(1)1,35+2)①不变,理由见解析;②见解析;(3)4 3±【分析】(1)过C作y轴的垂线交y轴与D点,先根据题意求得PA、OB的长,然后再证明△ACD≌△AOB,最后根据图形即可解答;(2)①过点C作CH⊥y轴,垂足为点H,先证明△HAC≌△OBA,进一步得到C点的横坐标恒为1,即可说明;②过F作FM⊥l交l与M,过点F作FN⊥x轴,垂足为点N,即∠APF=90°,再说明∠APF、=90°,再证得△AOP≌△PBF,最后根据图形运用线段的和差即可解答;(3)分t>0和t<0两种情况分别求解即可【详解】解:(1)如图:过C作y轴的垂线交y轴与D点∵t=2,P(2,0),A(0,1)∴225OA OB+=∴∵∠BAC=90°,∠CDA=90°,∴∠DAC+∠OAB=90°, ∠DAC+∠DCA=90°,∴∠OAB=∠DCA在△ACD 和△AOB 中∠OAB=∠DCA ,∠CDA=∠AOB=90°,AC=AB∴△ACD ≌△AOB (AAS )∴∴C (1,3+);(2)①不变、理由如下:过点C 作CH ⊥y 轴,垂足为点H ,易证△HAC ≌△OBA ,得HC =OA =1,∴点C 的横坐标是定值为1,∴直线l 是过点(1,0)且垂直于x 轴的直线,直线l 的位置不发生变化;②如图:过F 作FM ⊥l 交l 与M,过点F 作FN ⊥x 轴,垂足为点N ,即∠APF =90°, ∵△ACB 为等腰直角三角形,∠CAB=90°∴∠ABC=45°∴∠APF=2∠ABC=90°同理(1)可得△AOP ≌△PBF ,∴PN =OA ,OP=FN∴ON=OP+PN=OP+OA∵直线l 为l=1∴FM=OP ;(3)∵CF=2BF∴当t >0,如图,23MF OP BQ OB OQ ===- ∴3t=22t +,即:()3340t t -=,解得t=43 或t=0(舍去) 同理可得t <0时,可得t=-43. 综上,当t=43±时,CF=2BF .【点睛】本题属于几何综合题,主要考查了圆的性质、全等三角形的判定与性质、勾股定理、一元二次方程的解法等知识点,灵活应用所学知识成为解答本题的关键.。
小学数学新六年级上册第一单元 圆 单元检测卷(附答案)
小学数学六年级上册第一单元圆单元检测卷一、填空题。
1.一个圆有( )条直径,所有的直径都( ),直径的长度是半径的( )倍。
2. 一个圆的半径是1分米,直径是( )分米,周长是( )分米,面积是( )平方分米。
3. 圆有( )条对称轴,长方形有( )条对称轴。
4.要画一个周长是12.56厘米的圆,圆规两脚间的距离应定为( )厘米,这个圆的面积是( )平方厘米。
5.用一张长8分米、宽6分米的纸剪一个最大的圆,这个圆的面积是( )平方分米。
6.一个时钟的时针长5厘米,它转动一周形成的图形是( ),这个时针的尖端转动一昼夜所走的路程是( )厘米。
二、判断题。
(对的画“√”,错的画“✕”)1.把圆形纸片按不同的方向对折,折痕一定都经过圆心。
( )2.圆的周长是这个圆的直径的3.14倍。
( )3.圆越大,圆周率也越大。
( )4.一个半圆只有一条对称轴。
( )5.若大圆半径等于小圆的直径,则大圆面积是小圆面积的4倍。
( )三、选择题。
(把正确答案的序号填在括号里)1.要画一个直径是5厘米的圆,圆规两脚之间的距离是( )厘米。
A.5B.2.5C.10D.152.一个圆的直径和一个正方形的边长相等,这个圆的面积和这个正方形的面积的关系为( )。
A.圆的面积大B.正方形的面积大C.两者的面积相等D.不能比较3.一个圆的半径由2厘米增加到3厘米,那么这个圆的面积增加了( )平方厘米。
A.12.56B.28.26C.15.7D.3.144.车轮滚动一周,求所行的路程就是求车轮的( )。
A.直径B.周长C.面积D.半径四、计算题。
1.求下面各图形的面积和周长。
2.求下图中阴影部分的面积。
五、解决问题。
1.一块圆形桌布,半径是6分米,给它的周围缝上花边,花边长多少分米?这块桌布用料多少平方分米?2.一个直径为18米的圆形花坛,周围有一条宽1米的小路,这条小路的面积是多少平方米?3.一根圆柱形木材,它的横截面的周长是 1.884米,这根木材的横截面的面积是多少平方米?(得数保留两位小数)4.一台压路机前轮的半径是0.4米,如果前轮每分转动6周,10分可以从路的一端行到另一端,这条路大约有多长?5.公园里有一个圆形的养鱼池,量得养鱼池的周长是100.48米,养鱼池的中间有一个圆形小岛,半径是6米。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆的单元检测(一)
一、选择题(每小题3分,共30分)
1. 下列说法:(1)直径是弦;(2)弦是直径;(3)
半圆是弧,但弧不一定是半圆;
(4)半 径相等的两个圆是等圆;(5)
长度相等的两条弧是等弧.其中错误的个数是()
A、1个 B、2个 C、3个 D、4
个
2. 如图,是一个单心圆曲隧道的截面,若路面AB宽为10米,净高CD为7
米,则此隧
道单心圆的半径OA是( )
37 37
A
、
5米 B、—米 C、一米 D、7
米
7 5
3. 如图,小华从一个圆形场地的A点出发,沿着与半径OA夹角为a
的方向行走,走到
场地边缘B后,再沿着与半径OB夹角为a的方向折向行走.按照这种方式,小华第五次 走到
场地边缘时处于孤AB上,此时ZAOE=56° ,则。的度数是( )
A、52° B、60° C、72° D、76°
4. 如图,OO中,ABDC是圆内接四边形,ZBOC=HO° ,则ZBDC
的度数是( )
A、110° B、70° C、55° D、125°
5.
小明不慎把家里的圆形玻璃打碎了,其中四块碎片如图所示,为配到与原来大小一样的
圆形玻璃,小明带到商店去的一块玻璃碎片应该是( )
A、第①块 B、第②块 C、第③块 D
、第④块
6. 若。。所在平面内一点P到(DO上的点的最大距离为m,最小距离为n(m>n),
则此
圆的半径为( )
+ 〃 m-n m + n m - n ,
A、 ----- B、 ---------- C、 ------------ 或 ----- D、m+n 或 m・n
2 2 2 2
7. 如图,C是以AB为直径的OO上一点,已知AB=5, BC=3,则圆心O到弦BC
的距离
是( ) A、1.5 B、2 C、2.5 D、
3
8. 如图,在RtAABC中,ZC=90° , ZB=30° , BC=4cm,以点C为圆心,以2cm
的长
第(2)题图 第(3)题图 第(4)题图 第(5)题图
A、相离 B、相切 C、相交 D
、相切或相交
成的圆环的面积为( )A、16 n B、2兀
C、16 D、4n
第(9)题图
为半径作圆,则。C与AB的位置关系是(
9. 已知两个同心圆:大圆的弦AB与小圆相切于点C,若AB=4cm,
则由大圆和小圆所形
10. 如图,PA、PB切。O于点A、B,直线FG切于点E,交PA于F,交PB于点G,
二、填空题(每小题3分,共16分)
11. 在直径为20cm的圆柱形油槽内装入一些油后,截面如图所示,若油槽面宽AB=16cm,
则油的最大深度为
12. 如图,点A, B是。0上两点,AB=10,点P是。O上的动点(P与A, B
不重合),
连接AP, PB,过点O分别作OE1AP于E, OF1PB于F,则
EF=
13. 如图,。0的直径CD过弦EF的中点G, ZEOD=40° ,则ZFCD
的度数为
14. 如图,已知A、B两点的坐标分别为(2V3 , 0)、(0, 2), ?是左AOB
外接圆上的一
点,且ZAOP=45° ,则点P的坐标为
15. 如图,在RtAABC中,ZC=90° , O是斜边AB上的一点,圆O过点A并与边BC
相切于点D,与边AC相交于点E.若圆O的半径为
4, ZB=30° , AC=.
16. 如图,已知。0是以数轴的原点为圆心,半径为1的圆,ZAOB=45° ,点P
在数轴上
若PA=4cm,则Z\PFG的周长是( )
第(10)题图
笫(14)题图
运动,若过点P且与OB平行的直线于。。有公共点,设
P (x, 0),
则x的取值范围是
第(16)题
三、解答题(共72分)
17. 如图,已知三角形ABC中,ZB=90° , O是AB ±一点,以O为圆心,OB
为半径
的圆与AB交于点E,与AC切于点D,求证:
DE〃OC;
18. (10分)如图,OO的直径AB=4, ZABC=30° , BC=4A/3 ,D是线段BC
的中点.
(1) 试判断点D与。0
的位置关系,并说明理由;
(2) 过点D作DE1AC,垂足为点E,求证:直线DE是。O
的切线.
19. (10分)某地有一座圆弘形拱桥,圆心为O,桥下水面宽度为7.2m,
过。作
O C±AB
于D,交圆弧于C, CD=2.4m (如图所示).现有一艘宽3m、船舱顶部为方
第(15)题
第(17)题图
形并高出水面
2m
的货船要经过拱桥,此货船能否顺利通过这座拱桥?
第(19)题图
20. (12分)如图,。0的直径AB=2, AM和BN是它的两条切线,DE切。O于E,交AM
于 D,交 BN 于 C.设
AD=x, BC=y.
(1) 求证:AM//BN;
(2) 求y关于x
的关系式;
(3) 求四边形ABCD的面积S,并证明:SN2.
21、(12分)已知,如图,OD交y轴于A、B,交x轴于C,过点C的直线:y=—2 V2 x-8
与y轴交于P,且D的坐标
(0, 1).
(1)求点C、点P的坐标;(2)求证:PC是。D
的切线;
(3) 判断在直线PC上是否存在点E,使得EOPMSACDO.
若存在,
标;若不存在,请说明理由.
第(21)题图
第(20)题图
