两次相遇及“多次相遇”问题
“多次相遇问题”解题技巧

“多次相遇问题”解题技巧“多次相遇”问题有直线型和环型两种模型。
相对来讲,直线型更加复杂。
环型只是单纯的周期问题。
一、直线型直线型多次相遇问题宏观上分“两岸型”和“单岸型”两种。
“两岸型”是指甲、乙两人从路的两端同时出发相向而行;“单岸型”是指甲、乙两人从路的一端同时出发同向而行。
(一)两岸型两岸型甲、乙两人相遇分两种情况,可以是迎面碰头相遇,也可以是背面追及相遇。
题意如果没有明确说明是哪种相遇,对两种情况均应做出思考。
1、迎面碰头相遇:如下图,甲、乙两人从A、B两地同时相向而行,第一次迎面相遇在a处,(为清楚表示两人走的路程,将两人的路线分开画出)则共走了1个全程,到达对岸b后两人转向第二次迎面相遇在c处,共走了3个全程,则从第一次相遇到第二次相遇走过的路程是第一次相遇的2倍。
之后的每次相遇都多走了2个全程。
所以第三次相遇共走了5个全程,依次类推得出:第n次相遇两人走的路程和为(2n-1)S,S为全程。
而第二次相遇多走的路程是第一次相遇的2倍,分开看每个人都是2倍关系,经常可以用这个2倍关系解题。
即对于甲和乙而言从a到c走过的路程是从起点到a的2倍。
相遇次数全程个数再走全程数1 1 12 3 23 5 24 7 2………n 2n-1 22、背面追及相遇与迎面相遇类似,背面相遇同样是甲、乙两人从A、B两地同时出发,如下图,此时可假设全程为4份,甲1分钟走1份,乙1分钟走5份。
则第一次背面追及相遇在a处,再经过1分钟,两人在b处迎面相遇,到第3分钟,甲走3份,乙走15份,两人在c处相遇。
我们可以观察,第一次背面相遇时,两人的路程差是1个全程,第二次背面相遇时,两人的路程差为3个全程。
同样第二次相遇多走的路程是第一次相遇的2倍,单看每个人多走的路程也是第一次的2倍。
依次类推,得:第n次背面追及相遇两人的路程差为(2n-1)S。
(二)单岸型单岸型是两人同时从一端出发,与两岸型相似,单岸型也有迎面碰头相遇和背面追及相遇两种情况。
多次相遇行程问题的多种解答

多次相遇行程问题的多种解答!哈尔滨市经纬小学何华数学竞赛有这样一道题:小明和小英各自在公路上往返于甲、乙两地。
假设开始时他们分别从两地同时相向而行,若在距甲地!千米处,他们迎面相遇。
第二次迎面相遇时,地点在距乙地"千米处。
求甲、乙两地的距离为多少千米?分析与解:本题是常见的多次相遇行程问题。
可分几种情况讨论。
草量是#$#%$&’()。
!牧场每周新长出的青草量是((&*())+(,*&)’!。
"牧场原有的青草量是(&*!$,’-"或(()*!$&)。
#"#头牛每周吃掉原有的青草量是#$"#*!’#,。
$供"#头牛吃完全部青草的时间是-"+#,’.(周)。
以上解题过程说明,解决“牛吃草”问题的关键是先求出单位时间内新长出的青草量和牧场原有的青草量,解题方法一般用比较法。
具体解题思路是:%算出两种吃法所产生的两个青草总量;&通过比较,用差与差对应的方法求出单位时间里新长出的青草量。
!求出原有的青草量。
"根据问题求出答案。
."!人的天职在勇于探索真理。
———哥白尼图!一般情况下:两人速度相差不大,第一次相遇后,双方在返回的途中第二次迎面相遇(如图"),可知第一次相遇两人合行"个甲乙全程。
小明行了!千米。
从第一次相遇到第二次迎面相遇,两人又合行#个甲乙全程(也就是第二次相遇所用时间为第一次相遇所用时间的#倍)。
小明行了!$#%&(千米)。
两次相遇小明共行!’!$#%((千米)。
比一个甲乙全程多#千米。
因此,甲、乙两地间距离为!’!$#)#%*(千米)。
特殊情况:!小明乘坐交通工具,速度比小英快。
结果小明在第二次往返时迎面遇上小英(如图#)。
小英两次相遇共行#千米。
其中两次相遇之间所行路程是第一次相遇时所行路程的#倍。
因此小英第一次相遇时行#+(#’")%#!(千米)。
行测备考辅导:多次相遇问题

⾏测备考辅导:多次相遇问题 ⾏测中多次相遇问题还是⽐较难的,⼩编为⼤家提供⾏测备考辅导:多次相遇问题,希望⼤家能耐⼼研究例题,总结好这类题型的特点! ⾏测备考辅导:多次相遇问题 ⾏测考试中的数量关系是⼤多数考⽣头疼的部分甚⾄是放弃的专项,尤其是⾏程问题,这⼀题型的考点较多,过程复杂,难上加难的是碰到多次相遇问题。
但是相信⼤家也都知晓不管是在事业单位还是在国省考中,⾏程问题⼀定是必考题型,甚⾄在2017年的浙江省省考考试中出现4道题,可想⽽知这⼀问题的重要性啦。
但是也别害怕,⾏程问题也是有章可循的。
今天⼩编就来攻破下多次相遇这个硬⾻头。
在正式做题前,我们要知道做多次相遇问题要记牢两个结论,今天我们主要学习其中⼀个:从出发点到第N次相遇,甲⾛的路程,⼄⾛的路程,甲⼄⾛的路程和以及所⽤的时间均是第⼀次相遇的(2N-1)倍。
接下⾥我们通过题⺫来看下这个结论如何运⽤: 例1、在⼀次航海模型展⽰活动中,甲⼄两款模型在⻓100⽶的⽔池两边同时开始相向匀速航⾏,甲款模型航⾏100⽶要72秒,⼄款模型航⾏100⽶要60秒,若调头转⾝时间忽略不计,在12分钟内甲⼄两款模型相遇次数是:A.9次B.10次C.11次D.12次 ⾸先通过题⺫的阅读我们不难发现这是在考察多次相遇这个考点,可能很多⼩伙伴对于2-3次的相遇问题还能忍⼀忍、画下⾏程图什么的来算⼀算,这是这道题⼀看就是10次左右的相遇,难免会头⼤甚⾄在考场直接跳过放弃。
但是当我们知晓上⾯的那个结论,对于此类问题也就迎刃⽽解啦。
通过典型例题的讲解,不难发现即便我们没有画⾏程图,但是知道多次相遇的结论,很多问题都可以有⽅法可循,不过在解题的时候要注意:1.单位的统⼀(时间或路程单位)2.核⼼要了解第n次相遇和第⼀次相遇的关系,求出第⼀次相遇所使⽤的的时间t,甲所⾛的路程,⼄所⾛的路程,以及甲⼄所⾛的路程和。
现在,让我们带着这个结论再来⼩试⽜⼑。
例2:甲⼄两⻋同时从A、B两地相向⽽⾏,在距B地54千⽶处相遇,他们各⾃到达对⽅⻋站后⽴即返回,在距A地42千⽶处第⼆次相遇。
“多次相遇问题”解题技巧

“多次相逢问题”解题本领之阳早格格创做“多次相逢”问题有曲线型战环型二种模型.相对付去道,曲线型越收搀杂.环型不过简朴的周期问题.一、曲线型曲线型多次相逢问题宏瞅上分“二岸型”战“单岸型”二种.“二岸型”是指甲、乙二人从路的二端共时出收相背而止;“单岸型”是指甲、乙二人从路的一端共时出收共背而止.(一)二岸型二岸型甲、乙二人相逢分二种情况,不妨是迎里碰头相逢,也不妨是反里逃及相逢.题意如果不精确证明是哪种相逢,对付二种情况均应搞出思索.1、迎里碰头相逢:如下图,甲、乙二人从A、B二天共时相背而止,第一次迎里相逢正在a处,(为领会表示二人走的路途,将二人的门路分启绘出)则共走了1个齐程,到达对付岸b后二人转背第二次迎里相逢正在c 处,共走了3个齐程,则从第一次相逢到第二次相逢走过的路途是第一次相逢的2倍.之后的屡屡相逢皆多走了2个齐程.所以第三次相逢共走了5个齐程,依次类推得出:第n次相逢二人走的路途战为(2n-1)S,S为齐程.而第二次相逢多走的路途是第一次相逢的2倍,分启瞅每部分皆是2倍闭系,时常不妨用那个2倍闭系解题.即对付于甲战乙而止从a到c走过的路途是从起面到a的2倍.相逢次数齐程个数再走齐程数1 1 12 3 23 5 24 7 2… … …n 2n-1 22、反里逃及相逢取迎里相逢类似,反里相逢共样是甲、乙二人从A、B二天共时出收,如下图,此时可假设齐程为4份,甲1分钟走1份,乙1分钟走5份.则第一次反里逃及相逢正在a处,再通过1分钟,二人正在b 处迎里相逢,到第3分钟,甲走3份,乙走15份,二人正在c处相逢.咱们不妨瞅察,第一次反里相逢时,二人的路途好是1个齐程,第二次反里相逢时,二人的路途好为3个齐程.共样第二次相逢多走的路途是第一次相逢的2倍,单瞅每部分多走的路途也是第一次的2倍.依次类推,得:第n次反里逃及相逢二人的路途好为(2n-1)S.(二)单岸型单岸型是二人共时从一端出收,取二岸型相似,单岸型也有迎里碰头相逢战反里逃及相逢二种情况. 1、迎里碰头相逢:如下图,假设甲、乙二人共时从A端出收,假设齐程为3份,甲每分钟走2份,乙每分钟走4份,则甲乙第一次迎里相逢正在a处,此时甲走了2份,乙走了4份,再过1分钟,甲共走了4份,乙共走了8份,正在b处迎里相逢,则第二次相逢多走的跟第一次相逢相共,依次类推,可得出:当第n次碰头相逢时,二人的路途战为2ns.2、反里逃及相逢取迎里相逢相似,假设齐程为3份,甲每分钟走1份,乙每分钟走7份,则第一次反里相逢正在a处,2分钟后甲走了2份,乙走了14份,二人正在b处相逢.第一次相逢,二人走的路途好为2S,第二次相逢二人走的路途好为4S,依次类推,不妨得出:当第n次逃及相逢时,二人的路途好为2ns.“曲线型”归纳(死记)①二岸型:第n次迎里碰头相逢,二人的路途战是(2n-1)S.第n次反里逃及相逢,二人的路途好是(2n-1)S.②单岸型:第n次迎里碰头相逢,二人的路途战为2ns.第n次反里逃及相逢,二人的路途好为2ns.底下列出几种以后大概会考到的曲线型多次相逢问题罕睹的模型:{模型一}:根据2倍闭系供AB二天的距离.【例1】甲、乙二人正在A、B二天间往返集步,甲从A,乙从B共时出收,第一次相逢面距B60米,当乙从A处返回时走了10米第二次取甲相逢.A、B相距几米?A、150B、170C、180D、200【问案及剖析】B.如下图,第一次相逢正在a处,第二次相逢正在b处,aB的距离为60,Ab的距离为10.以乙为钻研对付象,根据2倍闭系,乙从a到A,再到b共走了第一次相逢的2倍,即为60×2=120米,Ab为10,则Aa的距离为120-10=110米,则AB距离为110+60=170米.{模型二}:报告二人的速度战给定时间,供相逢次数.【例2】甲、乙二人正在少30米的泳池内游泳,甲每分钟游37.5米,乙每分钟游52.5米.二人共时分别从泳池的二端出收,触壁后本路返回,如是往返.如果不计转背的时间,则从出收启初估计的1分50秒内二人共相逢频频?D、5B、3C、4A、2【问案及剖析】B.题目出道是迎里仍旧反里,所以二种相逢的次数皆该当估计.分启计划,如是是迎里相次,走的齐程为个,根据迎里相逢逢,则走的齐程的个数为n 1=5-2n,供得;如果是反里相逢,则走的齐程数为n=31,故正在分50秒内,不克不迭反里相逢.所以共相逢3次. {模型三}:报告二人的速度战任性二次迎里相逢的距离,供AB二天的距离.【例3】甲、乙二车分别从A、B二天共时出收,正在A、B间不竭往返止驶.甲车每小时止20千米,乙车每小时止50千米,已知二车第10次取第18次迎里相逢的天面相距60千米,则A、B相距几千米?D、110B、100C、105A、95【问案及剖析】C.走相共时间内,甲乙走的路途比为20:50=2:5.将齐程瞅成7份,则第一次相逢走1个齐程时,甲走2份,乙走5份.以甲为钻研对付象(也不妨以乙),第10次迎里相逢走的齐程数为2×10-1=19个,甲走1个齐程走2份,则走19个齐程可走19×2=38份.7份是一个齐程,则38份公有38÷7=5…3份(当商是奇数时从甲的一端数,0也是奇数;当商是奇数时从乙的一端数,比圆第1个齐程正在乙的一端,第2个齐程正在甲的一端)从乙端数3份.共该当第18次相逢,甲走的份数为(2×18-1)×2=70份.公有70÷7=10个齐程,10为奇数正在甲的端面.如下图:则第10次相逢取第18次相逢公有4份为60千米,所以AB少为千米.w面评:对付于给定任性二次的距离,主假如根据速度转移为齐程的份数,找一个为钻研对付象,瞅正在相逢次数内走的齐程数,进而转移为份数,而后根据一个齐程的份数,将钻研对付象走的总份数去掉齐程的个数瞅结余的份数,注意由齐程的个数决断结余的份数从哪一端数.【例4】甲、乙二车分别从A、B二天共时出收,正在A、B间不竭往返止驶.甲车每小时止45千米,乙车每小时止36千米,已知二车第2次取第3次迎里相逢的天面相距40千米,则A、B相距几千米?A、90B、180C、270D、110【问案及剖析】A.法一:共上题.相共时间,甲、乙路途比为45:36=5:4,则将齐程分成9份.则一个齐程时甲走5份,乙走4份.以甲为钻研对付象,第2次相逢,走的齐程数为2×2-1=3个,则甲走的份数为3×5=15份,一个齐程为9份,则第2次相逢甲走的份数转移为齐程的个数为15÷9=1…6份,则从乙端数6份.第3次相逢走的份数为(2×3-1)×5=25份,转移为齐程的个数为25÷9=2…7,则从甲端数7份.如下图:由图第2次战第3次相逢之间公有4份为40千米,则AB相距=90千米.法二:正在此引进“沙漏模型”.利用沙漏模型解题的前提是题搞中已知二人的速度.将速度转移为相共路途的条件下二人的时间比,则以时间为刻度,绘出二人到达对付岸的门路图,二人走的门路图相接的面即为二人相逢的天面.s-t图中的门路果像古代记时间的沙漏故称为“沙漏模型”.本题中,甲、乙走到端面用的时间比为36:45=4:5.如下图:根据门路图瞅出甲乙第2次相逢战第3次相逢的接面E战O,根据三角形相似,可得CE:EG=3:6=1:2,则供得第2次相逢距A天的比率为S/3,共理DO:ON=7:2,则第3次相逢距A天的比率为7S/9,则二次相逢比率为为40千米,则S=90千米.w面评:考死如果能掌握“沙漏”模型,则会曲瞅赶快的普及解题速度.用接面推断是迎里相逢仍旧反里相逢的本领:瞅相接的二条线是由共一岸引出仍旧二岸,共一岸则证明是反里相逢,分歧岸则证明是迎里相逢.用时注意:普遍题搞波及到的相逢次数较少时可绘,相逢次数太多,则会耗费洪量时间,不利于普及速度;绘时的单位刻度要瞅时间比,如果时间比中的数据较大可把刻度绘大.{模型四}:报告二人的速度,相逢次数较少时,利用s-t图产死“沙漏”模型速解.【例5】A、B二天相距950米.甲、乙二人共时由A天出收往返锻炼半小时.甲步止,每分钟走40米;乙跑步,每分钟止150米.则甲、乙二人第频频迎里相逢时距B天迩去.A、1B、2C、3D、4【问案及剖析】B.利用“沙漏模型”.甲乙走到端面用的时间比为150:40=15:4,半小时二人共走的齐程数为个.对付于单岸型,相逢6个齐程,则是迎里第三次相逢(由前边公式推出)绘出s-t图:瞅察上图可知,可第3次迎里相逢的历程中,甲乙有一次反里相逢(接面由共一面引出).而正在三次迎里相逢中第2次相逢离B天迩去,而且可根据三角形相似供出离B天的距离.【例6】河道赛道少120米,火流速度为2米/秒,甲船静火速度为6米/秒,乙船静火速度为4米/秒.角逐举止二次往返,甲、乙共时从起面出收,先顺火航止,问几秒后甲、乙船第二次迎里相逢?D、54A、48B、50C、52【问案及剖析】C.由题知,得出如下闭系:顺流顺流甲8(15)4(30)乙6(20)2(60)注:()中为走实足程的时间.假设A到B是顺流,由上表可知甲、乙二人第2次迎里相逢公有4个齐程.由于甲的速度快,则第2次相逢前甲已走了2个齐程.共15+30=45秒.当第45秒时乙走了一个顺流齐程20秒战25秒的顺流,走的路途为25×2=50米,则正在结余的70米内,甲乙分别以顺流战顺流相逢时间为t,则有70=(8+2)×t,供得t=7秒,则共用时间45+7=52秒.本题共样可用“沙漏模型”办理.根据上表中的速度闭系,可得出一个齐程时的时间闭系如下:顺流顺流甲 3 6乙 4 12根据时间的闭系,得出s-t图像,如下:瞅察上图,可瞅出第二次迎里相逢正在P面,以甲为钻研对付象估计时间,此时甲走了一个顺流,一个顺流,其余EP段为顺流,根据三角形相似可供出走EP用的时间EP:PN=EF:MN=7:8,由上表,供出走EP用的时间为,则甲共走的时间为15+30+7=52.二、环型环型主要分二种情况,一种是甲、乙二人共天共时反背迎里相逢(不可能反里相逢),一种是甲、乙二人共天共时共背反里逃及相逢(不可能迎里相逢).分启计划如下:(一)甲、乙二人从A天共时反背出收:如下图,一个周少分成4份,假设甲是顺时针每分钟走1份到B,乙是顺时针每分钟走3份到B,则第一次相逢二人走了1个周少,则再过1分仲,甲再走1份到C,共样乙走3份也到C,则第二次相逢共走了2个周少,依次类推,可得出:第n次迎里相逢共走了n圈.(二)甲、乙二人从A天共时共背出收:如下图,齐程分成4份.假设甲、乙二人皆是顺时针共时出收,甲每分钟走1份,乙每分钟走5份,则1分钟后二人正在B处第一次反里逃及相逢,二人走的路途好为1个周少.再过1分钟后,甲到C 处,乙也到C处,二人第二次反里逃及相逢,多走的路途好共样为一个周少,依次类推,不妨得出:第n次反里逃及相逢,路途好为n圈.环型多次相逢问题相对付比较简朴,当甲、乙不正在共一天面出收时相对付具备易度.比圆正在曲径二端出收.考死可通过底下的例题掌控.【例1】老弛战老王二部分正在周少为400米的圆形池塘边集步.老弛每分钟走9米,老王每分钟走16米.当前二部分从共一面反目标止走,那么出收后几分钟他们第三次相逢?A、33B、45C、48D、56【问案及剖析】C.第一次迎里相逢时间为400÷(9+16)=16,则第三次迎里相逢时间为16×3=48.【例2】小明、小明从400米环形跑道的共一面出收,背背而止.当他们第一次相逢时,小明转身往回跑;再次相逢时,小明转身往回跑;以去的屡屡相逢分别是小明战小明二人接替调转目标,小明速度3米/秒,小明速度5米/秒,则正在二人第30次相逢时小明共跑了几米?A、11250B、11350C、11420D、11480【问案及剖析】A.由题意知,第1次是迎里相逢,第2次是反里逃及相逢,之后皆是迎里取反里相逢接替.则正在30次相逢中,迎里相逢15次,反里相逢15次.迎里相逢一次用时为400÷(3+5)=50,反里相逢一次用时为400÷(5-3)=200,则30次相逢共用时为15×(50+200)=3750s,则小时正在那段时间里跑的路途为3750×3=11250米.【例3】甲、乙二人分别从一圆形场合的曲径二端面共时启初以匀速按好异目标绕此圆形路线疏通,当乙走了100米以去,他们第一次相逢,正在甲走完一周前60米处又第二次相逢,则那个圆形场合的周少为几米?A、320B、360C、420D、480【问案及剖析】D.如下图,假设甲、乙分别正在曲径A、B二端以顺时针战顺时针疏通.第1次相逢正在C面距B面100米,第2次相逢正在D面,距A面60当正在曲径端面二岸止走时,可将环型转移为曲线型,则第2次相逢每部分走的路皆是第1次相逢的2倍.以乙为钻研对付象,则从C到D走的路是B到C的2倍,即200米,果AD为60米,则CA为200-60=140米,所以半个周少为100+140=240米,周少为240×2=480米.归纳对付于多次相逢问题,要蓄意识的培植上述几种模型的解题本领,越收是曲线型的多次相逢问题,对付于给定二者速度的题目,且相逢次数较少时能流利使用“沙漏模型”解题,可曲瞅灵验天普及解题的速度.对付于环型,不像曲线型那么搀杂,注意处理佳相逢次数,是迎里仍旧逃及相逢,使用公式可赶快解题.。
小学四年级行程多次相遇问题

多次相遇问题1.甲村、乙村相距6千米,小张与小王分别从甲、乙两村同时出发,在两村之间往返行走(到达另一村后马上返回).在出发后40分钟两人第一次相遇.小王到达甲村后返回,在离甲村2千米的地方两人第二次相遇.小张和小王行走时的速度?2.小张与小王分别从甲、乙两村同时出发,在两村之间往返行走(到达另一村后就马上返回),他们在离甲村3500米处第一次相遇,在离乙村2000米处第二次相遇,问他们两人第四次相遇的地点离乙村多少米?(相遇指迎面相遇)3.甲乙二人分别从A、B两地同时出发,在A、B之间往返跑步.甲每秒跑3米,乙每秒跑7米,如果他们第四次迎面相遇点与第五次迎面相遇点之间相距150米,求A、B间相距多少米?4.甲乙两地之间有一条公路,李明从甲地出发步行往乙地;同时张平从乙地出发骑摩托车往甲地,80分后两人在途中相遇.张平到达甲地后马上折回往乙地,在第一次相遇后又经过20分张平在途中追上李明.张平到达乙地后又马上折回往甲地,这样一直下去,当李明到达乙地时,张平追上李明的次数是多少?5.甲乙二人分别从A、B两地同时出发,并在两地间往返行走。
第一次二人在距离B点400米处相遇,第二次二人又在距离B点100米处相遇,问两地相距多少米?6.甲乙两人分别从AB两地相向往返而行,第一次相遇在离A地92米处,第二次相遇在离B地63米处,求全程。
7.湖中有A、B两岛,甲、乙二人都要在两岛间游一个来回。
两人分别从A、B两岛同时出发,他们第一次相遇时距A岛700米,第二次相遇时距B岛400米。
问:两岛相距多远?8.甲乙两车同时从A、B两地相向而行,在距B地54千米处相遇。
他们各自到达对方车站后立即返回原地,途中又在距A地42千米处相遇。
求两次相遇地点的距离。
9.甲乙丙三辆车同时从A地出发到B地去,甲、乙两车的速度分别为每小时60千米和48千米。
有一辆迎面开来的卡车分别在他们出发后6小时、7小时、8小时先后与甲、乙、丙三辆车相遇。
行测:简单又复杂的“多次相遇”问题

在历年公务员考试中,行程问题都是一个必考知识点,而在考察的行程问题中,多次相遇问题出现频率非常高,对于很多考生而言,这部分知识难度大,变化形式多,因此很多考生在考场上就会放弃这类题目,其实了解这部分题型的本质后,就会将复杂问题简单化,很容易求解选出正确答案。
万变不离其宗,要想快速求解多次相遇问题,首先要了解其基本模型,了解了基本模型,在此基础上所做的变化也难逃大家的法眼。
多次相遇的三个前提条件为:1、往返运动;2、匀速行驶;3、迎面相遇。
一、基本模型考察的最基本模型为:甲从A地、乙从B地两人同时出发,在两地之间往返行走(到达另一地后就马上返回)。
在往返的过程中两人实现多次相遇。
如下图示。
\图中简单画出了前三次相遇情况,以此向下类推,从图中不难看出:㈠相邻两次相遇从出发到第一次相遇,两人走过的路程和S0-1=AB;从第一次相遇到第二次相遇,两人走过的路程和S1-2=2AB;从第二次相遇到第三次相遇,两人走过的路程和S2-3=2AB;从第三次相遇到第四次相遇,两人走过的路程和S3-4=2AB;……因此,两人走过的路程和存在以下比例关系:S0-1 : S1-2 : S2-3 : …… : Sn-1-n =1:2:2 : …… :2路程和=速度和×时间,由于两人是匀速行驶,速度和不变,时间与路程和成正比:T0-1 : T1-2 : T2-3 : …… : Tn-1-n =1:2:2 : …… :2甲乙两人速度不变,各自所走路程与时间成正比:S甲0-1 : S甲1-2 : S甲2-3 : …… : S甲n-1-n =1:2:2 : …… :2S乙0-1 : S乙1-2 : S乙2-3 : ...... : S乙n-1-n =1:2:2 : (2)㈡从出发到第N次相遇从出发到第一次相遇,两人走过的路程和S0-1=AB;从出发到第二次相遇,两人走过的路程和S0-2=3AB;从出发到第三次相遇,两人走过的路程和S0-3=5AB;从出发到第四次相遇,两人走过的路程和S0-4=7AB;……因此,两人走过的路程和存在以下比例关系:S0-1 : S0-2 : S0-3 : …… : S0-n =1:3:5 : …… :(2n-1)路程和=速度和×时间,由于两人是匀速行驶,速度和不变,时间与路程和成正比:T0-1 : T0-2 : T0-3 : …… : T0-n =1:3:5 : …… :(2n-1)甲乙两人速度不变,各自所走路程与时间成正比:S甲0-1 : S甲0-2 : S甲0-3 : …… : S甲0-n =1:3:5 : …… :(2n-1)S乙0-1 : S乙0-2 : S乙0-3 : …… : S乙0-n =1:3:5 : …… :(2n-1)二、模型变式考察的模型变式为:甲、乙两人同时从A地出发前往B地,在两地之间往返行走(到达另一地后就马上返回)。
一道多次相遇问题
一道多次相遇问题
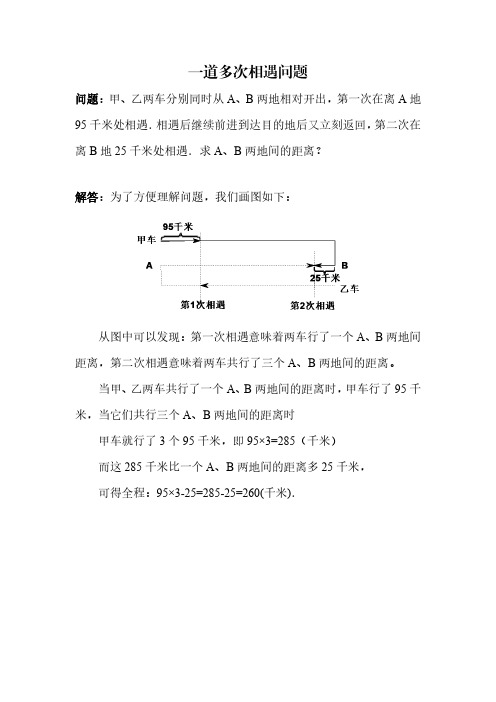
问题:甲、乙两车分别同时从A、B两地相对开出,第一次在离A地95千米处相遇.相遇后继续前进到达目的地后又立刻返回,第二次在离B地25千米处相遇.求A、B两地间的距离?
解答:为了方便理解问题,我们画图如下:
从图中可以发现:第一次相遇意味着两车行了一个A、B两地间距离,第二次相遇意味着两车共行了三个A、B两地间的距离。
当甲、乙两车共行了一个A、B两地间的距离时,甲车行了95千米,当它们共行三个A、B两地间的距离时
甲车就行了3个95千米,即95×3=285(千米)
而这285千米比一个A、B两地间的距离多25千米,
可得全程:95×3-25=285-25=260(千米).。
2020国考行测数量关系:多次相遇问题

2020国考行测|数量关系:多次相遇问题相信大家在备考行测时经常会遇到行程问题,而行程问题往往思路不够清晰、对应情景比较复杂,如经常看到有多者相遇、追及的情景,甚至还会出现多次相遇。
一、什么叫多次相遇:
所谓多次相遇,即在题干中出现两个主体,在运动中不断地相遇的题型。
我们都知道,如果在直线异地相遇的情景中,两者同时相对出发,会相遇一次,那如果想要出现多次相遇,则需要两者“到达对方出发点后立即返回,在两地间往返运动”,这就是直线异地多次相遇的题型特征。
二、解题思路
想要分析直线异地多次相遇的解题思路,需要借助行程图,我们一起来看看每次相遇时的具体情况。
到这里我们不难看出,如果继续往后分析,第三次到第四次相遇之间,总路程、时间和各自路程依旧会是之前的2倍。
如此,我们会发现,在直线异地多次相遇的题型中,路程和、时间和各自的路程,会有一个明确的比例关系:每相邻两次相遇之间的总路程、时间和各自的路程,都为二者出发到第一次相遇时总路程、时间、各自路程的2倍。
简单就记为1:2:2:2:2……。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
两次相遇及“多次相遇”问题两次相遇问题核心公式:单岸型S=(3S'+S'')/2;两岸型S=3S'-S''(S 表示两岸的距离)一:单岸型:这里S'代表第一次相遇,S''第二次相遇距离A地的距离。
1:例题:两车同时从A、B两地相向而行,在距A地80千米处相遇,相遇后两车继续前进,甲车到达B地、乙车到达A地后立即原路返回,第二次在距A 地60千米处相遇,则A、B两地路程为多少?解:S=(3S'+S'')/2=(3x80+60)/2=150千米向左转|向右转二:两岸型:这里S'代表第一次相遇,S''第二次相遇距离B地的距离。
1:例题:甲从A地、乙从B地同时以均匀速度相向而行,第一次相遇离A 地6千米,继续前进,到达对方起点后立即返回,在离B地3千米处第二次相遇,则AB两地距离多少?解:S=3S'-S''=3x6-3=15千米向左转|向右转“多次相遇”问题有直线型和环型两种模型。
相对来讲,直线型更加复杂。
环型只是单纯的周期问题。
一、直线型直线型多次相遇问题宏观上分“两岸型”和“单岸型”两种。
“两岸型”是指甲、乙两人从路的两端同时出发相向而行;“单岸型”是指甲、乙两人从路的一端同时出发同向而行。
(一)两岸型两岸型甲、乙两人相遇分两种情况,可以是迎面碰头相遇,也可以是背面追及相遇。
题意如果没有明确说明是哪种相遇,对两种情况均应做出思考。
1、迎面碰头相遇:如下图,甲、乙两人从A、B两地同时相向而行,第一次迎面相遇在a处,(为清楚表示两人走的路程,将两人的路线分开画出)则共走了1个全程,到达对岸b后两人转向第二次迎面相遇在c处,共走了3个全程,则从第一次相遇到第二次相遇走过的路程是第一次相遇的2倍。
之后的每次相遇都多走了2个全程。
所以第三次相遇共走了5个全程,依次类推得出:第n次相遇两人走的路程和为(2n-1)S,S为全程。
而第二次相遇多走的路程是第一次相遇的2倍,分开看每个人都是2倍关系,经常可以用这个2倍关系解题。
即对于甲和乙而言从a到c走过的路程是从起点到a的2倍。
相遇次数全程个数再走全程数1 1 12 3 23 5 24 7 2………n 2n-1 22、背面追及相遇与迎面相遇类似,背面相遇同样是甲、乙两人从A、B两地同时出发,如下图,此时可假设全程为4份,甲1分钟走1份,乙1分钟走5份。
则第一次背面追及相遇在a处,再经过1分钟,两人在b处迎面相遇,到第3分钟,甲走3份,乙走15份,两人在c处相遇。
我们可以观察,第一次背面相遇时,两人的路程差是1个全程,第二次背面相遇时,两人的路程差为3个全程。
同样第二次相遇多走的路程是第一次相遇的2倍,单看每个人多走的路程也是第一次的2倍。
依次类推,得:第n次背面追及相遇两人的路程差为(2n-1)S。
(二)单岸型单岸型是两人同时从一端出发,与两岸型相似,单岸型也有迎面碰头相遇和背面追及相遇两种情况。
1、迎面碰头相遇:如下图,假设甲、乙两人同时从A端出发,假设全程为3份,甲每分钟走2份,乙每分钟走4份,则甲乙第一次迎面相遇在a处,此时甲走了2份,乙走了4份,再过1分钟,甲共走了4份,乙共走了8份,在b处迎面相遇,则第二次相遇多走的跟第一次相遇相同,依次类推,可得出:当第n次碰头相遇时,两人的路程和为2ns。
2、背面追及相遇与迎面相遇相似,假设全程为3份,甲每分钟走1份,乙每分钟走7份,则第一次背面相遇在a处,2分钟后甲走了2份,乙走了14份,两人在b 处相遇。
第一次相遇,两人走的路程差为2S,第二次相遇两人走的路程差为4S,依次类推,可以得出:当第n次追及相遇时,两人的路程差为2ns。
“直线型”总结(熟记)①两岸型:第n次迎面碰头相遇,两人的路程和是(2n-1)S。
第n次背面追及相遇,两人的路程差是(2n-1)S。
②单岸型:第n次迎面碰头相遇,两人的路程和为2ns。
第n次背面追及相遇,两人的路程差为2ns。
下面列出几种今后可能会考到的直线型多次相遇问题常见的模型:{模型一}:根据2倍关系求AB两地的距离。
【例1】甲、乙两人在A、B两地间往返散步,甲从A,乙从B同时出发,第一次相遇点距B60米,当乙从A处返回时走了10米第二次与甲相遇。
A、B相距多少米?A、150B、170C、180D、200【答案及解析】B。
如下图,第一次相遇在a处,第二次相遇在b处,aB的距离为60,Ab的距离为10。
以乙为研究对象,根据2倍关系,乙从a到A,再到b共走了第一次相遇的2倍,即为60×2=120米,Ab为10,则Aa的距离为120-10=110米,则AB距离为110+60=170米。
{模型二}:告诉两人的速度和给定时间,求相遇次数。
【例2】甲、乙两人在长30米的泳池内游泳,甲每分钟游37.5米,乙每分钟游52.5米。
两人同时分别从泳池的两端出发,触壁后原路返回,如是往返。
如果不计转向的时间,则从出发开始计算的1分50秒内两人共相遇多少次?A、2B、3C、4D、5【答案及解析】B。
题目没说是迎面还是背面,所以两种相遇的次数都应该计算。
分开讨论,如是是迎面相遇,则走的全程的个数为个,根据迎面相遇n次,走的全程为2n-1=5,求得n=3;如果是背面相遇,则走的全程数为,故在1分50秒内,不能背面相遇。
所以共相遇3次。
{模型三}:告诉两人的速度和任意两次迎面相遇的距离,求AB两地的距离。
【例3】甲、乙两车分别从A、B两地同时出发,在A、B间不断往返行驶。
甲车每小时行20千米,乙车每小时行50千米,已知两车第10次与第18次迎面相遇的地点相距60千米,则A、B相距多少千米?A、95B、100C、105D、110【答案及解析】C。
走相同时间内,甲乙走的路程比为20:50=2:5。
将全程看成7份,则第一次相遇走1个全程时,甲走2份,乙走5份。
以甲为研究对象(也可以以乙),第10次迎面相遇走的全程数为2×10-1=19个,甲走1个全程走2份,则走19个全程可走19×2=38份。
7份是一个全程,则38份共有38÷7=5…3份(当商是偶数时从甲的一端数,0也是偶数;当商是奇数时从乙的一端数,比如第1个全程在乙的一端,第2个全程在甲的一端)从乙端数3份。
同理当第18次相遇,甲走的份数为(2×18-1)×2=70份。
共有70÷7=10个全程,10为偶数在甲的端点。
如下图:则第10次相遇与第18次相遇共有4份为60千米,所以AB长为千米。
点评:对于给定任意两次的距离,主要是根据速度转化为全程的份数,找一个为研究对象,看在相遇次数内走的全程数,从而转化为份数,然后根据一个全程的份数,将研究对象走的总份数去掉全程的个数看剩余的份数,注意由全程的个数决定剩余的份数从哪一端数。
【例4】甲、乙两车分别从A、B两地同时出发,在A、B间不断往返行驶。
甲车每小时行45千米,乙车每小时行36千米,已知两车第2次与第3次迎面相遇的地点相距40千米,则A、B相距多少千米?A、90B、180C、270D、110【答案及解析】A。
法一:同上题。
相同时间,甲、乙路程比为45:36=5:4,则将全程分成9份。
则一个全程时甲走5份,乙走4份。
以甲为研究对象,第2次相遇,走的全程数为2×2-1=3个,则甲走的份数为3×5=15份,一个全程为9份,则第2次相遇甲走的份数转化为全程的个数为15÷9=1…6份,则从乙端数6份。
第3次相遇走的份数为(2×3-1)×5=25份,转化为全程的个数为25÷9=2…7,则从甲端数7份。
如下图:由图第2次和第3次相遇之间共有4份为40千米,则AB相距=90千米。
法二:在此引入“沙漏模型”。
利用沙漏模型解题的前提是题干中已知两人的速度。
将速度转化为相同路程的条件下两人的时间比,则以时间为刻度,画出两人到达对岸的路线图,两人走的路线图相交的点即为两人相遇的地点。
s-t图中的路线因像古代记时间的沙漏故称为“沙漏模型”。
本题中,甲、乙走到端点用的时间比为36:45=4:5。
如下图:根据路线图看出甲乙第2次相遇和第3次相遇的交点E和O,根据三角形相似,可得CE:EG=3:6=1:2,则求得第2次相遇距A地的比例为S/3,同理DO:ON=7:2,则第3次相遇距A地的比例为7S/9,则两次相遇比例为为40千米,则S=90千米。
点评:考生如果能掌握“沙漏”模型,则会直观快速的提高解题速度。
用交点判断是迎面相遇还是背面相遇的技巧:看相交的两条线是由同一岸引出还是两岸,同一岸则说明是背面相遇,不同岸则说明是迎面相遇。
用时注意:一般题干涉及到的相遇次数较少时可画,相遇次数太多,则会花费大量时间,不利于提高速度;画时的单位刻度要看时间比,如果时间比中的数据较大可把刻度画大。
{模型四}:告诉两人的速度,相遇次数较少时,利用s-t图形成“沙漏”模型速解。
【例5】A、B两地相距950米。
甲、乙两人同时由A地出发往返锻炼半小时。
甲步行,每分钟走40米;乙跑步,每分钟行150米。
则甲、乙二人第几次迎面相遇时距B地最近。
A、1B、2C、3D、4【答案及解析】B。
利用“沙漏模型”。
甲乙走到端点用的时间比为150:40=15:4,半小时两人共走的全程数为个。
对于单岸型,相遇6个全程,则是迎面第三次相遇(由前边公式推出)画出s-t图:观察上图可知,可第3次迎面相遇的过程中,甲乙有一次背面相遇(交点由同一点引出)。
而在三次迎面相遇中第2次相遇离B地最近,并且可根据三角形相似求出离B地的距离。
【例6】河道赛道长120米,水流速度为2米/秒,甲船静水速度为6米/秒,乙船静水速度为4米/秒。
比赛进行两次往返,甲、乙同时从起点出发,先顺水航行,问多少秒后甲、乙船第二次迎面相遇?A、48B、50C、52D、54【答案及解析】C。
由题知,得出如下关系:注:()中为走完全程的时间。
假设A到B是顺流,由上表可知甲、乙两人第2次迎面相遇共有4个全程。
由于甲的速度快,则第2次相遇前甲已走了2个全程。
共15+30=45秒。
当第45秒时乙走了一个顺流全程20秒和25秒的逆流,走的路程为25×2=50米,则在剩余的70米内,甲乙分别以顺流和逆流相遇时间为t,则有70=(8+2)×t,求得t=7秒,则共用时间45+7=52秒。
本题同样可用“沙漏模型”解决。
根据上表中的速度关系,可得出一个全程时的时间关系如下:根据时间的关系,得出s-t图像,如下:观察上图,可看出第二次迎面相遇在P点,以甲为研究对象计算时间,此时甲走了一个顺流,一个逆流,另外EP段为顺流,根据三角形相似可求出走EP用的时间EP:PN=EF:MN=7:8,由上表,求出走EP用的时间为,则甲共走的时间为15+30+7=52。
