近年高考理科立体几何大题汇编.docx

近几年高考理科立体几何大题汇编

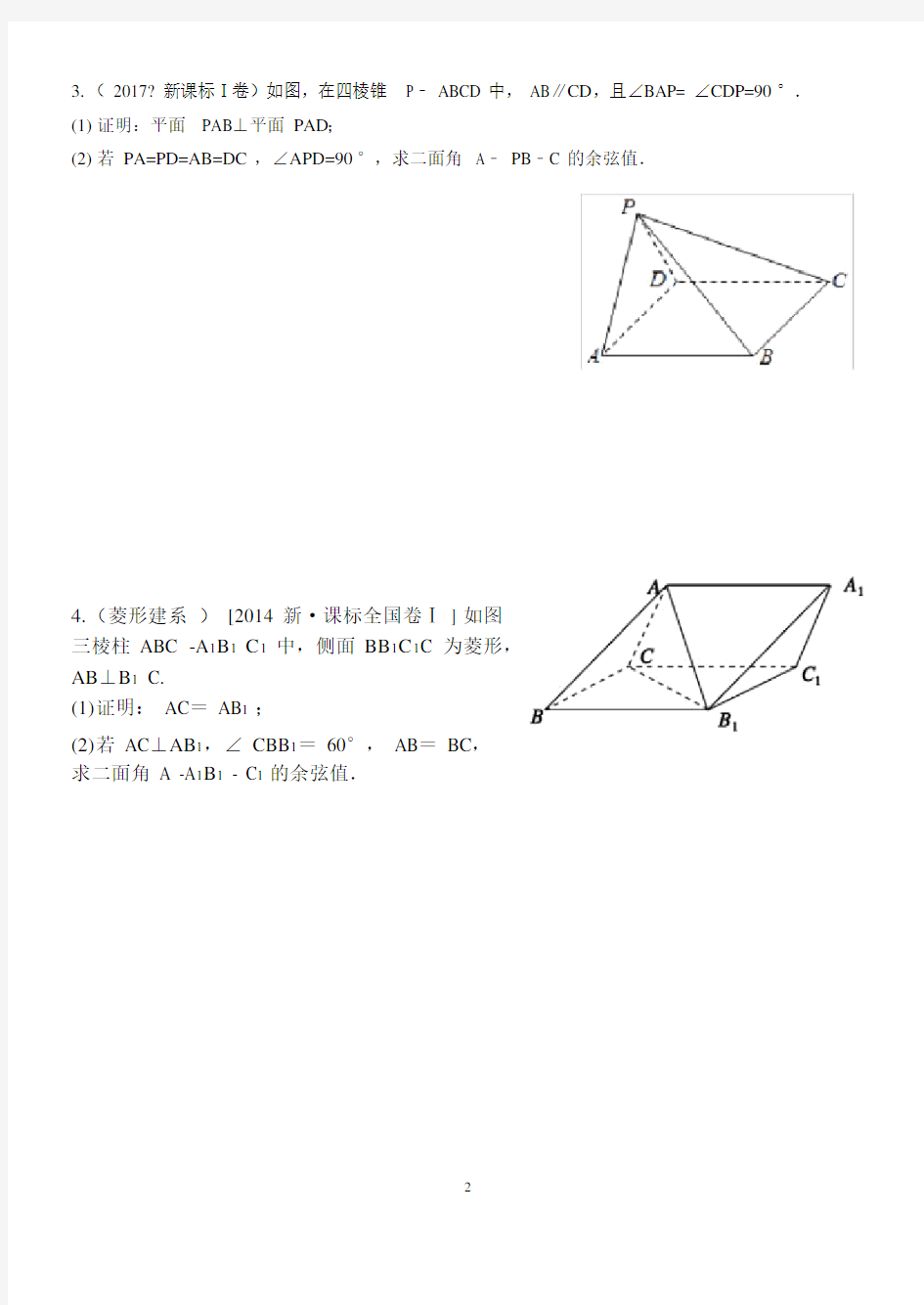
1.（2018 年 III 卷）如图，边长为 2 的正方形

ABCD 所在的平面与半圆弧?

M 是CD 所在平面垂直，

?

CD 上异于 C ，D的点．

（1）证明：平面 AMD ⊥平面BMC；

（2）当三棱锥M ABC体积最大时，求面 MAB 与面MCD所成二面角的正弦值．

2、[2014 ·新课标全国卷Ⅱ ] 四棱锥 P-ABCD 中，底面

ABCD 为矩形， PA⊥平面 ABCD， E 为 PD 的中点．

(1)证明： PB∥平面 AEC；

(2)设二面角 D-AE-C 为 60°， AP＝1， AD＝ 3，求

三棱锥 E-ACD 的体积．

1

3.（ 2017? 新课标Ⅰ卷）如图，在四棱锥 P﹣ ABCD 中， AB∥CD，且∠BAP= ∠CDP=90°．

(1)证明：平面 PAB⊥平面 PAD；

(2)若 PA=PD=AB=DC ，∠APD=90°，求二面角 A﹣ PB﹣C 的余弦值．

4.（菱形建系） [2014 新·课标全国卷Ⅰ ] 如图

三棱柱ABC -A1B1C1中，侧面BB1C1C 为菱形，

AB⊥B1 C.

(1)证明： AC＝ AB1；

(2)若 AC⊥AB1，∠ CBB1＝ 60°， AB＝ BC，

求二面角 A -A1B1 - C1的余弦值．

2

5.（菱形建系）【 2015 高考新课标 1】如图，四边形 ABCD 为菱形，∠ ABC=120 °，

E，F 是平面 ABCD 同一侧的两点， BE⊥平面 ABCD， DF⊥平面 ABCD，BE=2 DF，AE⊥EC. （Ⅰ）证明：平面 AEC⊥平面 AFC；

（Ⅱ）求直线 AE 与直线 CF 所成角的余弦值 .

6.（翻折） (2018 年 I 卷 )如图，四边形ABCD为正方形，E, F分别为AD , BC的中点，以

DF 为折痕把△ DFC 折起，使点 C 到达点 P 的位置，且 PF BF .

（ 1）证明：平面 PEF 平面 ABFD ；

（ 2）求 DP 与平面 ABFD 所成角的正弦值.

3

7.（翻折）（2016 年全国 II 高考）如图，菱形ABCD 的对角线 AC 与 BD 交于点 O ，

AB 5, AC 6 ，点 E, F 分别在 AD , CD 上， AE CF 5

，EF交BD于点H．将4

DEF 沿 EF 折到D' EF 位置，OD10 ．（Ⅰ）证明： D H平面ABCD；

（Ⅱ）求二面角 B D A C 的正弦值．

8. （动点问题）（ 2018 年 II 卷）如图，在三棱锥P ABC

中，

AB BC 2 2

，

PA PB PC AC 4

，

O

为

AC

的中点．P

（ 1）证明：PO平面 ABC ；

（ 2）若点 M 在棱BC上，且二面角M PA C 为 30，求 PC 与平面PAM所成角的正弦值．

A

O

C

M

B

4

近几年高考理科立体几何大题汇编

1.（2018 年 III 卷）如图，边长为 2 的正方形

ABCD 所在的平面与半圆弧?

M 是CD 所在平面垂直，

?

CD 上异于 C ，D的点．

（ 1）证明：平面AMD ⊥平面BMC；

（ 2）当三棱锥M ABC 体积最大时，求面MAB 与面MCD所成二面角的正弦值．

1.解：（ 1）由题设知 ,平面CMD⊥平面ABCD,交线为CD.因为BC⊥CD,BC平面ABCD,

所以 BC⊥平面 CMD,故 BC⊥ DM.

?

因为 M 为 CD 上异于 C， D 的点,且 DC为直径，所以DM⊥ CM.

又BC I CM= C,所以 DM⊥平面 BMC.

而DM 平面 AMD,故平面 AMD⊥平面 BMC.

uuur

（2）以D为坐标原点 , DA的方向为x轴正方向 ,建立如图所示的空间直角坐标系

D- xyz.

?

当三棱锥 M- ABC体积最大时， M 为 CD 的中点.

由题设得 D (0,0,0), A(2,0,0), B(2,2,0), C(0,2,0), M (0,1,1) ，

uuuur uuur uuur

AM ( 2,1,1), AB (0, 2,0), DA(2,0,0)

设 n ( x, y, z) 是平面 MAB 的法向量,则

5

n uuuur

0,2x y z 0, AM

n uuur

0.

即

0. AB 2 y

可取 n(1,0,2) .

uuur

DA 是平面 MCD 的法向量,因此

uuur

uuur

5 n DA

cos n, DA uuur，

| n || DA |5

sin

uuur 2 5 n, DA，

5

所以面 MAB与面 MCD所成二面角的正弦值是2 5 .

5

2、[2014 ·新课标全国卷Ⅱ ] 如图 1-3，四棱锥 P-ABCD 中，底面 ABCD 为矩形， PA⊥平面 ABCD，E 为 PD 的中点．

(1)证明： PB∥平面 AEC；

(2)设二面角 D-AE-C 为 60°， AP＝1，AD＝3，求三棱锥 E-ACD 的体积．

图 1-3

2，解： (1)证明：连接 BD 交 AC 于点 O，连接 EO.

因为 ABCD 为矩形，所以 O 为 BD 的中点．

又E 为 PD 的中点，所以 EO∥ PB.

因为 EO? 平面 AEC， PB?平面 AEC，所以 PB∥平面 AEC.

(2)因为 PA⊥平面 ABCD，ABCD 为矩形，

所以 AB，AD，AP 两两垂直．

→→如图，以 A 为坐标原点， AB， AD， AP 的方向为 x 轴、 y 轴、 z 轴的正方向， |AP

|

D (0，31→

为单位长，建立空间直角坐标系A-xyz，则3，0)， E 0，2，2， AE ＝31

0，2，2 .

6

→

3，0)．

设 B(m ，0，0)(m>0)，则 C(m ， 3，0)，AC ＝(m ，

设 n 1＝ ，

， z) 为平面 ACE 的法向量，

(x y

n 1 →

mx ＋ 3y ＝0，

·AC ＝0，

即 3

则

→

1

1

＝0， y ＋ z ＝ 0，

2

2

n ·AE

可取 n 1＝ m 3

，－ 1， 3 .

又 n 2＝(1， 0，0)为平面 DAE 的法向量，

1

由题设易知 |cos 〈n 1，n 2〉|＝2，即

3 1 3 .

2＝ ，解得 m ＝ 3＋4m 2 2

因为 E 为 PD 的中点，所以三棱锥 E-ACD 的高为

1

三棱锥

E-ACD 的体积

V ＝1

×

2

.

3

1 3 1 3 2× 3×2×2＝ 8 .

3. （ 2017? 新课标Ⅰ卷）如图，在四棱锥 P ﹣ ABCD 中，

AB ∥CD ，且∠BAP= ∠CDP=90°．

(1) 证明：平面 PAB ⊥平面 PAD ；

(2) 若 PA=PD=AB=DC ，∠APD=90°，求二面角 A ﹣ PB ﹣C

的余弦值．

3. 【答案】 （ 1 ）证明：∵∠ BAP=∠ CDP=90°，∴ PA ⊥ AB ， PD ⊥ CD ， ∵ AB ∥ CD ，∴ AB ⊥ PD ， 又 ∵ PA ∩PD=P ， 且 PA ?

平 面 PAD ，

PD ? 平 面PAD

， ∴ AB

⊥ 平

面

PAD ，

又 AB ?

平 面

PAB

， ∴

平

面

PAB

⊥

平

面

PAD

；

（ 2）解：∵ AB ∥ CD ， AB=CD ，∴四边形 ABCD 为平行四边形， 由（ 1）知 AB ⊥平面 PAD ，∴ AB ⊥

AD

， 则 四 边 形

ABCD

为

矩

形

，

7

在△ APD中，由PA=PD，∠ APD=90°，可得△ PAD为等腰直角三角形，

设PA=AB=2a，则

取AD 中点 O， BC 中点以O 为坐标原点，分别以

AD=．

E ，连接PO、 OE，

OA、 OE、 OP 所在直线为x 、 y、 z轴建立空间直角坐标系，

则： D （），B（），P（0，0，），C（）．

，，．设平面PBC的一个法向量为，

由，得，取y=1 ，得．∵AB ⊥平面PAD ，AD ?平面PAD ，∴AB ⊥AD ，又PD⊥PA，PA∩AB=A，

∴ PD⊥平面PAB，则为平面PAB 的一个法向量，．

∴cos＜＞==．由图可知，二面角A﹣PB﹣C为钝角，

∴二面角A﹣PB﹣C的余弦值为．

4.（菱形建系） [2014 新·课标全国卷Ⅰ ] 如图三棱柱 ABC - A1B1C1中，侧面 BB1C1C 为菱形， AB⊥B1 C.

(1)证明： AC＝ AB1；

(2)若 AC⊥ AB1，∠ CBB1＝60°， AB＝BC，求二面角 A -A1B1 - C1的余弦值．

4 解： (1)证明：连接 BC1，交 B1C 于点 O，连接 AO，因为侧面 BB1C1 C 为菱形，所以 B1C⊥ BC1，且 O 为 B1C 及 BC1的中点．

又AB⊥ B1C，所以 B1C⊥平面 ABO.

8

由于 AO? 平面 ABO ，故 B 1C ⊥AO. 又 B 1O ＝CO ，故 AC ＝AB 1 .

(2)因为 AC ⊥AB 1，且 O 为 B 1C 的中点，所以 AO ＝CO.

又因为 AB ＝BC ，所以△ BOA ≌ △BOC.故 OA ⊥OB ，从而 OA ， OB ，OB 1 两两垂

直．

以 O 为坐标原点， OB 的方向为 x 轴正方向， |OB|为单位长，建立如图所示的空间直角坐标系 O- xyz.

因为∠ CBB 1＝60°，所以△ CBB 1 为等边三角形，又

AB ＝ BC ，则 A 0 ， ， 3 ，

3

B(1， 0， 0)，B 1 ， 3

， 0 ，C ，－

3

， 0

.

0 3 0 3

→

3

3

→

， ，－ 3 ，

AB 1＝ ，

，－

，A 1 B 1＝AB ＝

3

3

1 0

3

→

3

，0 .

B 1

C 1＝BC ＝ － 1，－ 3

设 n ＝ (x ，y ，z)是平面 AA 1 1 的法向量，则

B

3 3

n ·AB ＝0，

3 y － 3 z ＝ 0，

1

所以可取 n ＝(1，

3， 3)．

→

即

3

1 1＝0，

n ·A B x － 3 z ＝0.

设 m 是平面 A 1

1 1 的法向量，

B C

→

则 m ·A 1B 1＝0，

同理可取 m ＝(1，－ 3， 3)．

→ 1＝0，

1

m ·B C

则 cos 〈 n ， m 〉＝ n ·m 1

|n||m|＝ 7.

1

所以结合图形知二面角 A -A1B1 - C1的余弦值为7.

5.（菱形建系）【 2015 高考新课标 1】如图，四边形 ABCD为菱形，∠ ABC=120 °，E，

F 是平面 ABCD 同一侧的两点， BE⊥平面 ABCD， DF⊥平面 ABCD，BE=2 DF，

AE⊥EC.

（Ⅰ）证明：平面 AEC⊥平面 AFC；

（Ⅱ）求直线 AE 与直线 CF 所成角的余弦值 .

5.，【答案】（Ⅰ ）见解析（Ⅱ ）

3

3

又∵AE⊥EC，∴EG= 3 ，EG⊥ AC，

在 Rt△ EBG中，可得 BE= 2 ，故 DF= 2 .

2

在Rt△ FDG 中，可得 FG= 6 .

2

在直角梯形 BDFE 中，由 BD=2 ， BE= 2 ， DF=2可得 EF=3 2 ，

22

∴ EG 2FG 2EF 2，∴EG⊥FG，

∵ AC∩ FG=G，∴ EG⊥平面 AFC，

10

∵ EG 面 AEC ，∴平面 AFC ⊥ 平面 AEC

??6分

.

uuur uuur

uuur

（ Ⅱ）如 ，以 G 坐 原点，分 以

GB ,GC 的方向 x ， y 正方向， | GB|

位 度，建立空 直角坐 系

G-xyz ，由（ Ⅰ ）可得 A （0，－ 3 ， 0）， E(1,0,

2 ) ， F （－ 1,0 ， 2

）， （ ， 3 ， ）， ∴ uuur = （ 1，

3 ， uuur

2 ）， CF = （ -1 ，

2

C 0 0 AE

2 ）

- 3 ，

.? 分

2

10

uuur uuur

uuur uuur

3 故 cos

AE ?CF

AE ,CF

uuur

uuur

.

| AE ||CF |

3

所以直 AE 与 CF 所成的角的余弦

3 . 分 ?? 12

3

6. （翻折） (2018 年 I 卷 )如图，四边形 ABCD 为正方形， E, F 分别为 AD , BC 的中点，以

DF 为折痕把 △ DFC 折起，使点 C 到达点 P 的位置，且 PF

BF .

（ 1）证明：平面 PEF

平面 ABFD ；

（ 2）求 DP 与平面 ABFD 所成角的正弦值 .

6. 解：（ 1）由已知可得， BF ⊥ PF ， BF ⊥ EF ，所以 BF ⊥平面 PEF .

又 BF 平面 ABFD ，所以平面 PEF ⊥平面 ABFD .

11

（2）作 PH ⊥EF ，垂足为 H .由（ 1）得， PH ⊥平面 ABFD .

uuur

uuur

以 H 为坐标原点， HF 的方向为 y 轴正方向， | BF | 为单位长，建立如图所示的空间直角

坐标系 H - xyz .

由（ 1）可得， DE ⊥ PE .又 DP =2 ， DE =1 ，所以 PE = 3 .又 PF =1 ，EF =2 ，故 PE ⊥PF .

可得 PH

3 3

, EH

.

2

2

则 H (0,0,0), P(0,0,

3

), D ( 1, 3 uuur (1, 3 , 3 ), uuur

3

) 为平面 ABFD 的

,0), DP HP (0,0,

2 2 2 2

2

法向量 .

uuur uuur 设 DP 与平面 ABFD 所成角为

HP DP

，则 sin | uuur uuur |

| HP | | DP |

3

4

3

.

34

所以 DP 与平面 ABFD 所成角的正弦值为

3 .

4

（翻折）（ 2016 年全国 II 高考）如图，菱形 ABCD 的对角线 AC 与 BD 交于点 O ，

7.

AB 5, AC

6 ，点 E, F 分别在 AD , CD 上， AE CF

5

， EF 交 BD 于点 H ．将

4

DEF 沿 EF 折到 D ' E F 位置， OD10 ． （Ⅰ）证明： D H 平面 ABCD ；

（Ⅱ）求二面角 B D A C 的正弦值．

7.【解析】⑴证明：∵

AE CF

5

，∴

AE CF

，

4

AD CD

∴ EF ∥ AC ．∵四边形 ABCD 为菱形，∴

12

AC BD ，

∴ EF BD ，∴ EF

DH ，∴ EF D H ．

∵ AC 6 ，∴ AO 3；又 AB 5， AO OB ，∴ OB 4 ， ∴ OH

AE

OD 1 ， ∴ DH D H 3 ， ∴ OD 2

OH 2

D ' H 2

， ∴

AO

D ' H OH ．又∵ OH I EF

H ，∴ D 'H

面 ABCD ．

⑵建立如图坐标系 H xyz ．

B 5，0，0 ，

C 1，3，0 ，

D ' 0，0，3 ， A 1， 3，0 ，

uuur

uuur 1 ，3，3

， ，

， AD '

，

AB 4 3 0

ur

设面 ABD ' 法向量 n 1

x ，y ，z ，

uuur

AC

0 ，6 ，0 ，

uur uuur

4x 3 y 0

x 3

n 1 AB 0

，取 y

ur

3

，

，

．

由 uur

uuuur

得

4 ，∴ n 1

4 5 n 1 AD

x

3 y 3z 0

z 5

uur

同理可得面 AD 'C 的法向量 n 2

3，0 ，1 ，

ur uur

∴ cos

n 1 n 2 9 5 7 5

，∴ sin

2 95 ．

ur uur

n 1 n 2 5 2 10

25

25

8. （动点问题）（ 2018 年 II 卷）如图，在三棱锥

P ABC 中， AB BC 2 2 ，

PA PB PC

AC 4 ， O 为 AC 的中点．

13

（ 1）证明：PO平面ABC；

（ 2）若点 M 在棱BC上，且二面角M PA C 为 30 ，求 PC 与平面PAM所成角的正弦值．解：（ 1）因为AP CP AC 4 ， O 为 AC 的中点，所以 OP AC ，且OP2 3 .

连结 OB .因为AB BC

2

AC ，所以△ABC为等腰直角三角形，2

且 OB AC ，OB 1

AC2. 2

由 OP2OB2PB 2知PO OB .

由 OP OB , OP AC 知PO平面 ABC .

uuur

O xyz .（2）如图，以O为坐标原点，OB的方向为x轴正方向，建立空间直角坐标系

uuur

由已知得 O(0,0,0), B(2,0,0), A(0, 2,0), C(0,2,0), P(0,0,23), AP (0,2,2 3), 取平面 uuur PAC 的法向量 OB(2,0,0) .

uuur

设 M (a,2 a,0)(0a2)，则 AM (a,4 a,0) .

设平面 PAM 的法向量为n(x, y, z) .

14

uuur uuur n 0 得 2y

2 3z

0 ，可取 n (

3( a

4), 3a, a) ，

由 AP n 0, AM

ax (4

a) y 0

所以 cos uuur

2 3( a 4)

.由已知得 | cos uuur

| 3 . OB, n

a 2 OB, n

2 3(a 4) 2 3a 2

2 所以

2 3 | a 4| a 2 =

3

.解得 a 4 （舍去）， a

4 . 2 3(a 4) 2 3a 2 2

3

所以 n

(

8

3 ,

4 3 ,

uuur (0,2, 2 3) ，所以 cos uuur

3 . 4

) .又 PC

PC, n

3

3

3

4

所以 PC 与平面 PAM 所成角的正弦值为

3 .

4

15