第七讲 摩擦角及其它
工程力学-摩擦

18
滚阻力偶与主动力偶(F,FS)相平衡
滚动 摩擦 ①滚阻力偶M随主动力偶(F , F S )的增大而增大; ② 0MMmax 有个平衡范围; ③ M max与滚子半径无关;
④滚动摩擦定律:Mmax dFN,d 为滚动摩擦系数。
19
滚动摩擦系数 d 的说明:
①有长度量纲,单位一般用mm,cm; ②与滚子和支承面的材料的硬度和温度有关。 滚阻力偶M的力偶臂正是d(滚阻系数),所以,d 具 有长度量纲。
平衡范围应是
Qmi nQQmax
15
例2 已知:b,d, fs , 不计凸轮与挺杆处摩擦,不计挺杆质量;
求: 挺杆不被卡住之a值.
解: 研究挺杆,设挺杆处于刚好卡住位置. Fx 0 FANFBN0
Fy 0 F AF BF0 MA0 F(ab 2)FBdFBb N0
F AfsF AN F BfsF BN
[例1] 已知: =30º,G =100N,f =0.2
求:①物体静止时,水平力Q的平衡范围; ②当水平力Q = 60N时,物体能否平衡?
(翻页请看动画)12
13
解:①先求使物体不致于上滑的Qmax 图(1)
由 FX0, Q m axcosGsinFm ax0 FY0, NQ m axsinGcos0
②计算:
翻
页
tgmFN maxfN Nf
请 看
动
画
7
8
四、自锁
①定义:当物体依靠接触面间的相互作用的摩擦 力 与正
压力(即全反力),自己把自己卡 紧,不会松开 (无论外力多大),这种现象称为自锁。
②自锁条件:
当m时,永远平衡(即自锁)
m
9
③自锁应用举例
第7章机械动力学
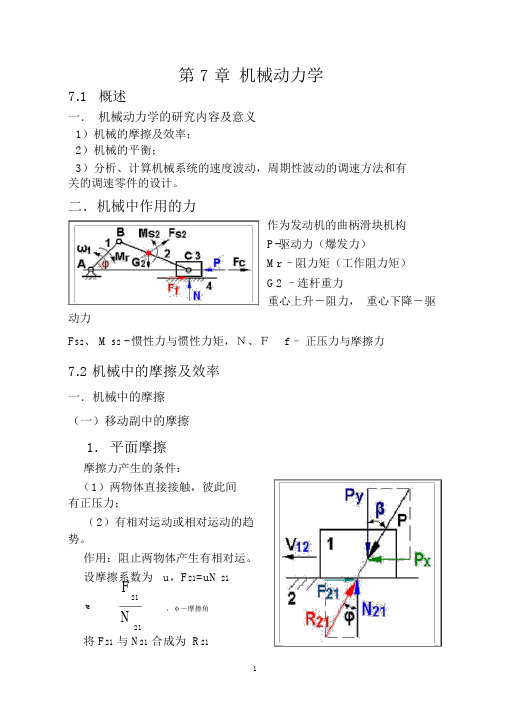
第 7 章机械动力学7.1概述一.机械动力学的研究内容及意义1)机械的摩擦及效率;2)机械的平衡;3)分析、计算机械系统的速度波动,周期性波动的调速方法和有关的调速零件的设计。
二.机械中作用的力作为发动机的曲柄滑块机构P-驱动力(爆发力)Mr –阻力矩(工作阻力矩)G2 –连杆重力重心上升-阻力,重心下降-驱动力F S2、 M S2 - 惯性力与惯性力矩,N、F f –正压力与摩擦力7.2 机械中的摩擦及效率一.机械中的摩擦(一)移动副中的摩擦1.平面摩擦摩擦力产生的条件:(1)两物体直接接触,彼此间有正压力;(2)有相对运动或相对运动的趋势。
作用:阻止两物体产生有相对运。
设摩擦系数为u,F21=uN 21F21tg,φ-摩擦角N21将 F21与 N21合成为 R21R21-总反力(全反力)P X P分解为 P和 P ,tgX Y P Y( P X P sin、 P Y P cos )F21P X,有F21tgY 方向平衡: Py=N 21,即:tg tg P Xtg讨论:①总反力 R21恒与相对速度V 12成 90° +φ②当β >φ, P X > F21,滑块作加速运动;当β =φ, P X = F21,动则恒动,静则恒静;当β <φ, P X < F21,原来运动,作减速运动,原来静止,永远静止,称自锁。
③ 自锁条件:β≤φβ=φ,条件自锁(静止);β<φ,无条件自锁。
2.斜面摩擦斜面机构如图,滑块置于升角α的斜面上,摩擦角为φ,作用于滑块上的铅垂力为Q,求滑块等速上升和下降时所需水平平衡力P 和 P’。
(1)求等速上升水平平衡力 PP-驱动力, Q-阻力PQ R 21 0 ,tg ()P,P Qtg () (1)Q( 2)求等速下降水平平衡力 P ’Q -驱动力, P ’-阻力P'Q R 21 0 ,tg () P ',P 'Qtg () (2)Q讨论:① 欲求下滑 (反行程) P ’,只需将式 ( 1)中 P →P ’,φ→ (-φ )② 下滑时,当α >φ, P ’为平衡力α <φ, P ’为负,成为驱动力的一部分,该条件下,若无 P ’,则无论 Q 多大,滑块不下滑,称自锁,自锁条件:α≤φ。
高中物理入门之六:全反力与摩擦角专题

高中物理入门之六:全反力与摩擦角专题(学习本节预计需要20分钟)1.全反力物体与支持面之间存在摩擦力的前提是存在正压力N,由于总是伴随着N出现,两个力的施力对象和受力对象相同,所以人们经常把两个力结合起来一起考虑,把这两个力的合力R称为支持面对物体的全反力,R与N的夹角称为全反角θ。
如图所示⑴当为静摩擦力时,我们知道静摩擦力是被动力,它的范围是,表示最大静摩擦力,⑵当为动摩擦力时,摩擦力与正压力存在关系,N是接触面的正压力,2.摩擦角当物体在支持面上滑动或即将滑动时,由全反力的知识,全反角是一个定值,仅与接触面的动摩擦因数有关,我们把此时的全反角称为摩擦角,用表示。
记住:摩擦角的引入,其实质是指明两物体在相对滑动或即将相对滑动时全反力的方向。
3.应用举例[例1] 一物块置于水平的地面上。
当用与水平方向成斜向上的力拉物块时,物块做匀速直线运动,当改用与水平方向成斜向下的力拉物块时,物块仍做匀速直线运动。
若和大小相等,求物块与地面的动摩擦因数?解析:当物块处于滑动状态时,全反角必然等于摩擦角,即全反力R的方向是确定的,与支持力的夹角θ=arc tanμ,对物块做受力分析,如图所示物块受到重力G、全反力R和拉力F三个力的作用,由几何知识易知,所以。
[例2]如图,斜劈A静止放置在水平面上,质量为m的物体B在外力和的作用下沿斜劈表面向下运动,当方向水平向右、方向沿斜劈的表面向下时,斜劈A受到地面的摩擦力方向向左,则下列说法中正确的是()A.若同时撤去和,物体B的加速度方向一定沿斜面向下B.若只撤去,在物体B仍向下运动的过程中,A所受地面摩擦力方向可能向右C.若只撤去,在物体B仍向下运动的过程中,A所受地面摩擦力大小、方向都不变D.无论撤去还是,在物体B仍向下运动的过程中,A所受地面摩擦力始终向左解析:引入全反力后,对B做受力分析,如图,B受到重力、外力、和A对B的全反力R,注意,R是A对B的支持力与滑动摩擦力的合力,摩擦角为。
哈尔滨工业大学理论力学第七版第4章 摩擦

F ϕ F
R1
Q
2
α
2
G
P
lj
F
F
N
m ax
ϕ
f
F
Rm
Q
α
G
P
lj
F
F
N
m ax
ϕ F
f
Rm
ϕ
—摩 角 擦
f
tgϕ = Fmax =
f
F
f
S
N
2、自锁现象
Q α
G
P
lj
F
F
N
m ax
F
N
ϕ
ϕ F
f
Rm
f
结论: 1.只要:α ≤
ϕ ,不论Q多大,必平衡 2.只 : >ϕ ,不 Q多 , 不 衡 要 α 论 小 必 平
第 四 摩
章 擦
一、概述 * 摩擦的利弊 弊 —— 发热、发光、磨损 利 —— 制动、传动、抛光
摩擦传动 车床三抓卡盘
*产生 摩擦的原因
摩擦
{
滑动摩擦 滚动摩擦
{ {
静滑动摩擦 动滑动摩擦 静滚动摩擦 动滚动摩擦
摩擦
{ 湿摩擦
干摩擦
§4-1
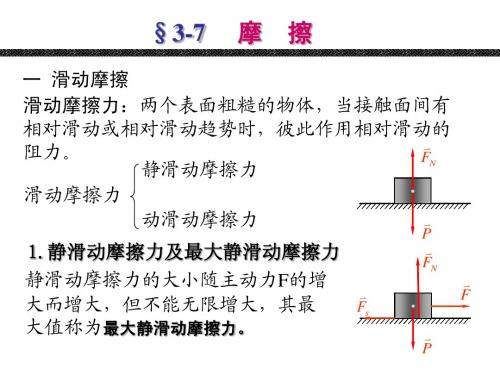
滑动摩擦
1、静滑动摩擦力及最大静滑动摩擦力 W F = 0, =0 F
FT
30
o
A
B P
正确答案是: 正确答案是:C
2、求平衡范围
图示系统仅在OA与小车接触的点 处存在摩 与小车接触的点A处存在摩 图示系统仅在 与小车接触的点 在保持系统平衡的前提下,逐步增加拉力F, 擦 , 在保持系统平衡的前提下 , 逐步增加拉力 , 则在此过程中, 处的法向约束力将 处的法向约束力将___________。 则在此过程中,A处的法向约束力将 。 (A)越来越大; )越来越大; (B)越来越小; )越来越小; (C)保持不变; )保持不变; (D)不能确定。 )不能确定。
3摩擦材料力学
§3-7 摩
擦
静滑动摩擦力的大小随主动力的改变而改变,但介于 零和最大值之间。
0 ≤ Fs ≤ Fmax
静摩擦定律:最大滑动摩擦力的大小和两物体间的 法向约束反力成正比。
Fmax = fs FN
2.动滑动摩擦力 2.动滑动摩擦力
fs-静摩擦因数
动滑动摩擦力:两个表面接触面间有相对滑动时, 彼此作用相对滑动的阻力。
(d)
′ ′ FNb − F a = Ff′c≤ fsFNc 1
′ FN
或 得
′ FN (b − fsc) ≤ F a 1
′ FN
F′ f
A
F1
B
≤
所以
Ff =
r r F= G R R
F≥ 1 rG(b − fsc) fs Ra
代入式(d)得
块与鼓轮表面间的摩擦 因 数 为 fs, 试 求 制 动 鼓 轮转动所必需的力F1。
A b a
G
§3-7
摩
擦
解: 1. 取鼓轮为研究对象,
受力分析如图。
O
列平衡方程
c
r
R O1
F1
C B
∑ M ( F ) = 0,
O1
Fr - Ff R = 0
(a)
A b a
FO1y FO1x
O1
解方程得
r r Ff = F = G R R (b)
x B
1.取支架为研究对象,受力 分析如图。 2.列平衡方程
FNB
∑F = 0,
x
− FNA + FNB = 0
∑F
3.联立求解。
FNA = FNB = 2F
x = 40 cm
Chapter7金属的摩擦与接触疲劳详解

粘着磨损过程示意图
3 磨损量的估算
粘着磨损量正比于法向载荷 F ,滑动
距离 L ,反比于软材料压缩屈服强度或硬
度
KFlt KFlt V 9 sc H KFlt V 9 sc
4 磨损表面特征 大小不等的结疤。
5 降低粘着磨损的措施: 磨损局部的变形 - 粘着 - 断裂过程 故:降低变形,减少粘着 (1) 选择合适的摩擦副材料 a、强、硬度高则不易粘着; b 、互溶性小的材料不易粘着:晶格类型不 同、晶格间距相差大、电化学性质相差大的材 料组成摩擦件,粘着倾向小; 例:金属-非金属摩擦副;化合物;多相金 属
尖锐的磨粒或材料脆性较高时损示意图
3、磨损量的估算 可证明,磨损量可以用下式表示:
F tg F tg V =K 3 sc H
可见: 正比于法向载荷,摩擦距离(硬度)-1。 同时与硬材料凸出部分尖端或磨粒的 形状有关。
4、磨损表面特征 犁沟、擦伤。
麻点剥落形成过程示意图 a)初始裂纹形成 b)初始裂纹扩展 c)二次裂纹形成 d)二次裂纹扩展 e)形成磨屑 f) 锯齿形表面
提高抗力措施:
(1) 提高机件表面的塑性变形抗力;
(2) 提高零件表面光洁度,使 F 降低,表面
折叠几率降低;
(3) 提高润滑油的粘度,降低油楔作用。
2、浅层剥落 ——裂纹起源于次表层的接触疲劳损伤 深度:0.2-0.4mm。 浅层剥落在次表层(最大切应力处): 0.786b处; 0.5b处; 实际多在0.5-0.7b处)。
5、降低磨粒磨损的措施
(1)影响因素
材料硬度高,磨损量小,耐磨性高;
但过高反而不利——韧度低
还与材料的韧性有关。
(2)降低磨粒磨损的措施 P145-147
《机械设计基础》第7章 蜗杆传动
tanγ= z1/q d1 = q m q是d1与m的比值,不一定是整数。 m一定时,q越小(或d1越小)导程角γ越大,传动效率 越高,但蜗杆的强度和刚度降低。 设计蜗杆传动,在刚度准许的情况下,要求传动效率高 时q选小值;要求强度和刚度大时q选大值。
蜗杆直径系数q
q = d1/m
P1----蜗杆传动输入功率,kW;ks----为散热系数,根据箱体周围通风 条件,一般取ks =10~17[w/(m2·℃)];自然通风良好地方取大值,反 之取小值; η----传动效率;A----散热面积m2。 t0----周围空气温 度℃ 通常取20℃; [t1]----许可的工作温度,通常取70~90℃。
齿圈与轮芯用铰制孔螺栓联接。由于装拆方便,常用尺寸较大或磨损后 需要更换蜗轮齿圈的场合.
浇铸式:(图7-10c) 该型式仅用于成批生产的蜗轮。齿圈最小厚度c=2m,但不小于10 mm
§7-4 蜗杆传动的强度 计算 蜗杆传动的受力分析
蜗轮旋转方向的判定
蜗轮旋转方向,按照蜗杆的螺旋线旋向和旋转方
蜗杆传动的特 点
§7-2 蜗杆传动的主要参数和几何尺 寸 概念(图7-6)
连心线:蜗杆轴线与蜗轮轴线的公垂线。 中间平面:圆柱蜗杆轴线和连心线构成的平面。 所以中间平面内蜗杆与蜗轮的啮合相当于渐开线 齿轮与齿条(直线)的啮合
规定:设计计算以中间平面参数及其几何尺寸关系为准。 主要参数
1.模数m和压力角α;2.传动比i,蜗杆头数z1和蜗 轮齿数z2 ; 3.蜗杆导程角γ; 4.蜗杆分度圆直径d1和蜗杆直径系数q ;5.中心距a。
5.中心距a。
标准蜗杆传动其中心距计算公式:
a=
d1+d2 2
= m (q+z2) 2
工程力学—第六章(II)-摩擦
FAmax f s FNA
FCmax f s FNC
由上述方程解得
b f s d - 2l
结论:抽屉顺利抽出的尺寸选择为b>fs(d-2l)。
第二节 摩 擦
例题3 制动器构造如图。已知各尺寸a,b,c,R, r,且制动轮与制动块之间的摩擦因数为fs,闸瓦 的的宽 自度 由不 端B计上。,若重制物动E力的F重1垂量直为地W作,用求在所A需B的杠最杆 小制动力F1min。
B
F r W
R
F ' F= r W
R
FN' FN
第二节 摩 擦
再建立制动杆AB的平衡方程
a
FAx
b
c
A FAy
F’FN’
D
M AF 0,
F1
FN' b - F' c - F1min a 0
B
FN
FN'
1 b
F1m in
a
F'
c
1 b
F1m
in
a
r R
W
c
第二节 摩 擦
当处于临界状态时
衡问题所得到的结果也不是一个定值,而是一个范围。
➢ 第一类平衡问题,即F F max,求约束力,与一般平衡
问题一样,摩擦力作为约束力,其方向可以假设.
➢ 第二类平衡问题,即F = F max,要求确定平衡或不平
衡条件,这时必须根据滑动趋势正确确定滑动摩擦力的 方向,而不能任意假设。
第二节 摩 擦
而梯不致滑倒,B处的静摩擦系数fsB至少应该多 大?已知θ=arctan3/4, fsA=1/3.
P1 A
P2 C θ B
求静摩擦因数问题解题要点: 假设物体处于临界平衡状态, 力系既要满足平衡条件,还 应满足物理条件:Fmax=f·FN
第四讲 摩擦角及其它
第四讲摩擦角及其它一、摩擦角1、全反力:接触面给物体的摩擦力与支持力的合力称全反力,一般用R表示,亦称接触反力。
2、摩擦角:全反力与支持力的最大夹角称摩擦角,一般用φm表示。
此时,要么物体已经滑动,必有:φm = arctgμ(μ为动摩擦因素),称动摩擦力角;要么物体达到最大运动趋势,必有:φms = arctgμs(μs为静摩擦因素),称静摩擦角。
通常处理为φm = φms。
3、引入全反力和摩擦角的意义:使分析处理物体受力时更方便、更简捷。
二、隔离法与整体法1、隔离法:当物体对象有两个或两个以上时,有必要各个击破,逐个讲每个个体隔离开来分析处理,称隔离法。
在处理各隔离方程之间的联系时,应注意相互作用力的大小和方向关系。
2、整体法:当各个体均处于平衡状态时,我们可以不顾个体的差异而讲多个对象看成一个整体进行分析处理,称整体法。
应用整体法时应注意“系统”、“内力”和“外力”的涵义。
三、应用1、物体放在水平面上,用与水平方向成30°的力拉物体时,物体匀速前进。
若此力大小不变,改为沿水平方向拉物体,物体仍能匀速前进,求物体与水平面之间的动摩擦因素μ。
解说:这是一个能显示摩擦角解题优越性的题目。
可以通过不同解法的比较让学生留下深刻印象。
法一,正交分解。
(学生分析受力→列方程→得结果。
)法二,用摩擦角解题。
2:如图20所示,一上表面粗糙的斜面体上放在光滑的水平地面上,斜面的倾角为θ。
另一质量为m的滑块恰好能沿斜面匀速下滑。
若用一推力F作用在滑块上,使之能沿斜面匀速上滑,且要求斜面体静止不动,就必须施加一个大小为P = 4mgsinθcosθ的水平推力作用于斜面体。
使满足题意的这个F的大小和方向。
解四、物体平衡的种类下面讨论物体在重力和支力作用下所处的各种平衡状态,图6表示放在凹面底端、凸面顶端和平面上的小球,它们所受的重力和支力等值反向,都处在平衡位置。
由于某种因素,小球稍稍偏离平衡位置,在凹面底部的小球重心升高,重力势能增大,重力mg和支力N不再保持平衡,合力指向原来的平衡位置,小球会恢复平衡,这种平衡叫做稳定平衡。
机械原理第七章机讲义械动力学
执行构件位置的函数 曲柄压力机、活塞式压缩机的工作 阻力
执行构件速度的函数 鼓风机、离心泵的工作阻力
时间的函数 揉面机、球磨机的工作阻力
作用在运动副中的力 约束反力(constrained force)—作用在运动副元素上的 力。对机构而言,约束反力是内力(internal force);对构件 而言,约束反力是外力(external force)。
实际工况
机械运转时,绝大多数机械系统主轴(main shaft)的速 度都是波动变化的。过大的速度波动会影响机器的正常工 作,增大运动副中的动负荷,加剧运动副的磨损,降低机器 的工作精度和传动效率,缩短机器的使用寿命,激发机器振 动,产生噪音等。
本章讨论的问题 ● 机构的摩擦(friction)与效率(efficiency) ● 机械的平衡(balancing of machinery) ● 机械的真实运动(actual motion)规律分析与速度波动调
驱动力类型举例
常数 重力FdC 位移的函数 弹簧力FdFd(s)、内燃机驱动力矩MdMd(s)
速度的函数 电动机驱动力矩Md Md()
阻力(resistance force)—力作用线与构件运动速度方向 夹角为钝角。与构件角速度方向相反的力矩称为阻力矩 (resistance moment)。
工作阻力类型举例
总反力R21
考Q虑 构R21件 P惯 0性力的重要性
水平驱动力 P Qtan()
n
R21 N21
1 v12
F21
P
Q 2
P
n
R21 Q
(一)移动副中的摩擦
斜面摩擦 2. 滑块等速下降
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四川省武胜中学高中物理竞赛培训教材 1 第七讲 摩擦角及其它 四川省武胜中学高中物理竞赛培训教材
2 1、“千斤顶”中的学问 【例1】在固定的斜面上放一物体,并对它施加一竖直向下的压力,物体与斜面间的摩擦因数为μ。求斜面倾角θ的最大值,使得当θ≤θm时,无论竖直向下的压力有多大,物体也四川省武胜中学高中物理竞赛培训教材 3 不会滑下。
分析:如图,物体受四个力,重力和压力的合力为G+F,静摩擦力Fs,斜面支持力FN。将G+F分解为F1和F2,根据平衡条件得 FN = F2=(G+F)cosθ Fs= F1=(G+F)sinθ 物体不会滑下的条件是Fs小于最大静摩擦力Fm,而Fm=μFN ,从而有 (G+F)sinθ≤(G+F)cosθ 化简得 θ≤arctanμ 所以只要θ≤arctanμ,无论F有多大,物体也不会滑下。 说明: “千斤顶”螺旋实际可以看作是tan<μ的弯曲斜面。
2、推力的极大值(自锁) 【例2】在机械设计中,常用到下面的力学装置,如图只要使连杆AB与滑块m所在平面法线的夹角θ小于某个值,那么无论连杆AB对滑块施加多大的作用力,都不可能使之滑动,且连杆AB对滑块施加的作用力越大,滑块就越稳定,工程力学上称为‘自锁’现象。则自锁时θ应满足什么条件?设滑块与所在平面间的动摩擦因数为μ。 分析:将连杆AB对滑块施加的推力F分解,且F远远大于mg,可以忽略。则滑块m 不产生滑动的条件为 Fsinθ<μFcosθ 化简得自锁的条件为 θ<arctanμ。
θ 四川省武胜中学高中物理竞赛培训教材
4 3、运动员的弯道技术 【例3】在田径比赛、摩托车赛、自行车赛等运动项目中,当通过弯道时,运动员必须倾斜与路面保持一定的角度θ才能顺利通过弯道,这就是运动员的弯道技术。路面的弯道半径越小,运动员的速度越快,运动员的倾斜角就越大。设在摩托车比赛中,摩托车与路面间的摩擦因数为μ,试求摩托车所能达到的最大倾角。 分析:运动员要稳定地平动,路面对摩托车的力必须通过整体的重心,所以静摩擦力F1与支持力F2的夹角等于运动员与路面的倾斜角度。而路面对摩托车整体的力F是F1和F2的合力,由图知 F1= F2tanθ=mg tanθ 对摩托车的最大静摩擦力为 Fm=μF2=μmg 则摩托车不倾倒的条件是 F1≤Fm 化简得 θ≤arctanμ 所以摩托车所能达到的最大倾角为θm= arctanμ。
4、拉力的极小值 【例4】在水平面上放有一质量为m的物体,物体与地面的动摩擦因数为μ,现用力F拉物体,使其匀速运动,怎样施加F才能最小。 分析:设拉力与水平面间的夹角为θ,将拉力F分解,并列出平衡方程,由动摩擦力公式得 Fcosθ=μ(mg-Fsinθ),化简为
)sin(1sincos2mgmgF (其中令1cos,11sin22)
当90时F有最小值: 12minmgF, 且θ = arctanμ。 5、破冰船中的道理 【例5】1999年,中国首次北极科学考察队乘坐我国自行研制的“雪龙”号科学考察船。“雪龙”号科学考察船不仅采用特殊的材料,而且船体的结构也满足一定的条件,以对付北极地区的冰块和冰层。它是靠本身的重力压碎周围的冰块,同时又将碎冰块挤向船底,如果碎冰块仍挤在冰层与船体之间,船体由于受到巨大的侧压力而可能解体。为此,船体与竖直方向之间必须有一倾角α。设船体与冰块之间的动摩擦因数为μ。试问使压碎的冰块能被挤压向船底,四川省武胜中学高中物理竞赛培训教材 5 α角应满足的条件。
分析:冰块受到三个力:冰层对冰块的水平向后的挤压力,船体对冰块的侧压力F,以及沿船体方向的摩擦力(冰块的重力和浮力可以忽略)。将F分解,如图 FN = F1=Fcosα Ff =μFN 能使压碎的冰块被挤压向船底必须满足的条件为 F2>Ff ,有 Fsinα>μ Fcosα 化简得 α>arctanμ
6、压延机原理 【例6】压延机由两轮构成,两轮的直径均为d=50mm,轮间的间隙为a=5mm,两轮按反方向转动,如图中箭头所示。已知烧红的铁板和铸铁轮之间的摩擦因数为μ=0.1,问能压延的铁板厚度b是多少?
分析:铁板的A、B两点和铸铁轮接触,接触点与转轴连线的夹角为α。在A点铁板受到FN1和Ff1两个力,在B点铁板受到FN2和Ff2
两个力,如图所示。要使铁板能压延铁板所受合力必须向右,则
α <θ=arctanμ 则铁板的最大厚度为 bm= a+2(r-rcos)=7.48mm 所以能压延的铁板厚度 b<7.48mm
【例7】物体放在水平面上,用与水平方向成30°的力拉物体时,物体匀速前进。若此力大小不变,改为沿水平方向拉物体,物体仍能匀速前进,求物体与水平面之间的动摩擦因素μ。 四川省武胜中学高中物理竞赛培训教材 6 答案:引进全反力R ,对物体两个平衡状态进行受力分析,再进行矢量平移,得到图18中的左图和中间图(注意:重力G是不变的,而全反力R的方向不变、F的大小不变),φm指摩擦角。 再将两图重叠成图的右图。由于灰色的三角形是一个顶角为30°的等腰三角形,其顶角的角平分线必垂直底边„„故有:φm = 15°。 最后,μ= tgφm=0.268。 【例8】(第三届全国预赛)如图2—1—7所示用力F推一放在水平地面上的木箱,质量为M,木箱与地面间摩擦因数为 问:当力F与竖直成夹角多大时,力F再大也无法推动木箱? [思路分析]本题属于物体平衡问题,一般方法是用平衡条件列方程求极值,但这里用摩擦角的概念分析,问题会更加简单. 解:选物体为研究对象,受力如图2-1-8所示,其受四个力作用而静止,将弹力N和摩擦力f合成作出全反力F .当物体将要发生滑动时,静摩擦角0。满足tg0=,由平衡条件知当0<<0
时,物体出现自琐现象,也就是说此时无论用多大的力都不会使物体推动,故角属于范围(0,0)。
一个接触面的平衡问题
【例9】一物体质量为m,置于倾角为的斜面上,物体与斜面间的动摩擦因数为,若要使物体沿斜面匀速向上滑动,求拉力的最小值。 解析:本题有两种解法,一种是根据平衡条件利用数学建模得到)(FF后再求极值,另一种是引入全反力(摩擦角)化四力平衡为三力平衡根据矢量三角形直观快速地求解。 解法一:(利用平衡条件求解)设拉力与斜 面夹角为θ,则由平衡条件可得: 0sin)sincos(cosmgFmgF 即有 )sin/(cos)cos(sinmgF 四川省武胜中学高中物理竞赛培训教材 7 令tg,则有 mgmgF21cossin)sin()cos(sin
解法二:(引入摩擦角)如图1所示,设1tg,则由平衡条件 和矢量三角形可得:当拉力F垂直于全反力方向时此时F的拉 力最小,即:mgmgF21sincos)cos(
【例10】结构均匀的梯子AB,靠在光滑竖直墙上,已知梯子长为L,重为G,与地面间的动摩擦因数为μ,如图所示, (1) 求梯子不滑动,梯子与水平地面夹角θ的最小值θ0; (2) 当θ=θ0时,一重为P的人沿梯子缓慢向上,他上到什么位置,梯子开始滑动? 分析:本题也有两种解法:解法一是根据物体的平衡条件求解,这 是常规解法;另一解法是分析出它临界条件θ0再引入摩擦角解。 解法一:(1)如图2所示,平衡条件可得:
0011cos2sinLGLNGNNfN
由上述3式可解得:2110tg (2)如图3所示,由平衡条件可得:
00011coscos2sinxPLGLNPGNNfN
四川省武胜中学高中物理竞赛培训教材 8 由上述3式可解得:2/Lx 解法二:(1)(引入摩擦角)如图4所示,1tg,由平衡 条件可得: )(sincos200GtgLLG
所以有 2110tg (2)如图5所示,将梯子和人的重力用其等效重力代替G, 当等效重力的重心还在梯子重心下面时梯子还不会滑倒,当 等效重力的重心还在梯子重心上面时梯子就会滑倒,所以当 人上到梯子一半即L/2时,梯子开始滑动。 一. 两个接触面的平衡问题 【例11】一架均匀梯子,一端放置在水平地面上,另一端靠在竖直的墙上,梯子与地面及梯子与墙的静摩擦系数分别为μ1、μ2,求梯子能平衡时与地面所成的最小夹角。 分析:此题同样有两种解法,为了节省篇幅,接下来只介绍引入摩擦角的解法。此题是多点摩擦的问题,而且又是多点同时滑动,所以系统达到临界平衡状态(极限平衡状态)时,即梯子与水平所成的夹角最小时,各处摩擦力均达到最大值。现把两端点的受力用全反力表示,则梯子就只受三个力,且三个力必共点。 解:如图6所示,111tg ,212tg,由平衡条件 和几何关系可得: EBDEAHDHAHDEDHACBCtg222
121212121221212
1
ctgctg
即梯子与地面所成的最小的角为 121121tg [想一想]为什么多点摩擦同时滑动的临界条件是多点的摩擦力同时达到最大值?
