运筹学考卷(河海)_2010-2011..
2010—2011学年度第一次月考试卷(范围:第1章—第3章)[1]
![2010—2011学年度第一次月考试卷(范围:第1章—第3章)[1]](https://img.taocdn.com/s3/m/67012389f01dc281e43af0b4.png)
2010—2011学年度第一次月考试卷(范围:第1章—第3章)[1]DA .甲成绩比乙成绩稳定B .乙成绩比甲成绩稳定C .甲、乙两成绩一样稳定D .不能比较两人成绩的稳定性6.在计算某一样本:12,16,-6,11,….(单位:℃)的方差时,小明按以下算式进行计算:()()()()[] +-+--+-+-=22222201120620162012151S ,则计算式中数字15和20分别表示样本中的………………………………………………………………………( )A .众数、中位数B .方差、标准差C .样本中数据的个数、平均数D .样本中数据的个数、中位数7.如图,已知四边形ABCD 是平行四边形,下列结论中不正确的是……………………( )A .当AB=BC 时,它是菱形B .当AC ⊥BD 时,它是菱形A CC .当∠ABC=90°时,它是矩形D .当AC=BD 时,它是正方形8.如图,将一张长为70cm 的矩形纸片ABCD 沿对称轴EF 折叠后得到如图所示的形状,若折叠后AB 与CD 的距离为60cm ,则原纸片的宽度为……………………………………( )A .20 cmB .15 cmC .10 cmD .30 cm二、填空题(本大题共有10小题,每小题4分,满分40分)9.珠穆朗玛峰高出海平面8848米,吐鲁番盆地低于海平面155米,它们的极差是 .10.化简:(1)=12 ;(2)=32 ;(3)=28.11.计算:(1)182= ;(2)2a ·8a (a≥0)= .12.已知一组数据: ,,,321x x x 的平均数是2,方差是3,则另一组数据:231-x ,232-x ,233-x ,…E F 60E F D C B A的平均数和方差分别是 .13.如图,在等腰梯形ABCD 中,AC ⊥BD ,AC =6cm ,则等腰梯形ABCD 的面积为 cm 2.14.观察下列各式:42132⨯=- ,53142⨯=-,64152⨯=-,…将你猜想到的规律用一个式子来表示: .15.毛毛的作业本上有以下4题:325=②3223=;③632a a =;④33431163116=⋅=,其中毛毛做错的题有 (填写序号).16.在四边形ABCD 中,点E ,F ,G ,H 分别是边AB ,BC ,CD ,DA 的中点,如果四边形EFGH 为菱形,那么四边形ABCD 是 (只要写出一种即可).17.实数a 在数轴上的位置如图所示,化简:()2|1|2a a --= .-1012aB A D18.从边长为a 的大正方形纸板中间挖去一个边长为b 的小正方形后,将其截成四个相同的 等腰梯形﹙如图①﹚,可以拼成一个平行四边形﹙如图②﹚.现有一平行四边形纸片ABCD ﹙如图③﹚,已知∠A =45°,AB =6,AD =4.若将该纸片按图②方式截成四个相同 的等腰梯形,然后按图①方式拼图,则得到的大正方形的面积为 .三、解答题(本大题共有8小题,共86分)19.(本题满分20分)计算或化简:(1)322⨯ (2)()212-(3)54515-+ (4)6313122⨯⎪⎪⎭⎫ ⎝⎛-20.(本题满分6分)先将(1)(1x x ---化简,然后自图② A 图③BD 图① b选一个合适的x 值,代入化简后的式子求值.21.(本题满分8分)如图,四边形ABCD 是菱形,CE ⊥AB 交AB 延长线于E ,CF ⊥AD 交AD 延长线于F ,请猜想,CE 和CF 的大小有什么关系?并证明你的猜想.22.(本题满分9分)一种千斤顶利用了四边形的不稳定性. 如图,其基本形状是一个菱形,中间通过螺杆连接,转动手柄可改变ADC ∠的大小(菱形的边长不变),从而改变千斤顶的高度(即A 、C 之间的距离).若AB=40cm ,当ADC ∠从60°变为120°时,千斤顶升高了2 1.414,3 1.732,结果保留整数)FC D A 手柄C D B A23.(本题满分9分)一次期中考试中,A、B、C、A B C D E 平均分标准差数学71 72 69 68 70 2英语88 82 94 85 76 85(1)求这5位同学在本次考试中数学成绩的平均分和英语成绩的标准差(要有过程....).(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分的计算公式是:标准分=(个人成绩-平均成绩)÷成绩标准差从标准分看,标准分大的考试成绩更好,请问A同学在本次考试中,数学与英语哪个学科考得更好!24.(本题满分10分)如图,在△ABC中,AB=AC,D为BC中点,四边形ABDE是平行四边形.求证:四边形ADCE 是矩形.25.(本题满分10分)将三角形纸片ABC (AB >AC )沿过点A 的直线折叠,使得AC 落在AB 边上,折痕为AD ,展平纸片,如图(1);再次折叠该三角形纸片,使得点A 与点D 重合,折痕为EF ,再次展平后连接DE 、DF ,如图(2),证明:四边形AEDF 是菱形.26.(本题满分14分)(1)如图1,在正方形ABCD 中,M 是BC边(不含端点B 、C )上任意一点,P是BC 延长线上一点,N 是∠DCP 的C D A(1) A B D C C D F AE平分线上一点.若∠AMN=90°,求证:AM=MN .下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明.证明:在边AB 上截取AE=MC ,连ME .正方形ABCD 中,∠B=∠BCD=90°,AB=BC .∴∠NMC=180°-∠AMN -∠AMB=180°-∠B -∠AMB=∠MAB=∠MAE .(下面请你完成余下的证明过程)(2)若将(1)中的“正方形ABCD ”改为“正三角形ABC ”(如图2),N 是∠ACP 的平分线上一点,则当∠AMN=60°时,结论AM=MN 是否还成立?请说明理由.M N P D C E B A 图1 N A(3)若将(1)中的“正方形ABCD”改为“正n边形ABCD…”,请你作出猜想:当∠AMN= °时,结论AM=MN仍然成立.(直接写出答案,不需要证明)参考答案一、选择题(本大题共有8小题,每小题3分,满分24分)题1 2 3 4 5 6 7 8号答A DB A BCD C案二、填空题(本大题共有10小题,每小题4分,满分40分)9.9003m 10.32、36、2 11.223、a 4 12.4和2713.18 14.1112+•-=-n n n (n 是自然数,且3≥n )等 15.①②③④ 16.矩形或正方形或等腰梯形等(符合对角线相等即可)17.1 18.2611+三、解答题(本大题共有8小题,共86分)19.(1)原式=8; (2)原式=223-; (3)原式=554; (4)原式=29.20.原式=x +1,x 取非正数即可.21.猜想:CE = CF证明:连接AC .∵AC 是菱形ABCD 的对角线∴AC 平分∠DAB又∵CE ⊥AB ,CF ⊥AD∴CE = CF .22.连结AC ,与BD 相交于点O四边形ABCD 是菱形∴AC ⊥BD ,∠ADB =∠CDB ,AC =2AO当∠ADC =60时,△ADC 是等边三角形∴AC =AD =AB =40当∠ADC =120时,∠ADO =60∴AC 3因此增加的高度为340≈29(cm )23.(1)()70706869727151=++++=x ()()()()()[]636857685858594858285885122222==-+-+-+-+-=S (2)A 同学数学标准分:()2227071=÷- A 同学英语标准分:()2168588=÷- ∵2122> ∴A 同学在本次考试中,数学学科考得更好!24.证明:∵四边形ABDE 是平行四边形,∴AE ∥BC ,AB=DE ,AE=BD .∵D 为BC 的中点,∴CD=BDC D ∥AE ,CD=AE∴四边形ADCE 是平行四边形.∵AB=AC∴AC=DE∴平行四边形ADCE 是矩形.25.证明:由第一次折叠可知:AD 为∠CAB 的平分线,∴∠1=∠2由第二次折叠可知:∠CAB =∠EDF ,从而,∠3=∠4∵AD 是△AED 和△AFD 的公共边,∴△AED ≌△AFD∴AE =AF ,DE =DF又由第二次折叠可知:AE =ED ,AF=DF∴AE =ED =DF =AF故四边形AEDF 是菱形.26.解:(1)∵AE=MC ,∴BE=BM, ∴∠BEM=∠EMB=45°, ∴∠AEM=135°,∵CN 平分∠DCP ,∴∠PCN=45°,∴∠AEM=∠MCN=135°在△AEM 和△MCN 中:∵,,=CMN,AEM MCN AE MC EAM ∠=∠=∠∠⎧⎪⎨⎪⎩∴△AEM ≌△MCN ,∴AM=MN(2)仍然成立.在边AB 上截取AE=MC ,连接ME ∵△ABC 是等边三角形,∴AB=BC ,∠B=∠ACB=60°,∴∠ACP=120°.∵AE=MC ,∴BE=BM∴∠BEM=∠EMB=60°∴∠AEM=120°.∵CN 平分∠ACP ,∴∠PCN=60°, ∴∠AEM=∠MCN=120°∵∠CMN=180°—∠AMN —∠AMB=180°—∠B —∠AMB=∠BAM∴△AEM ≌△MCN ,∴AM=MN(3)(2)180n-︒.n。
2010级运筹学试题B
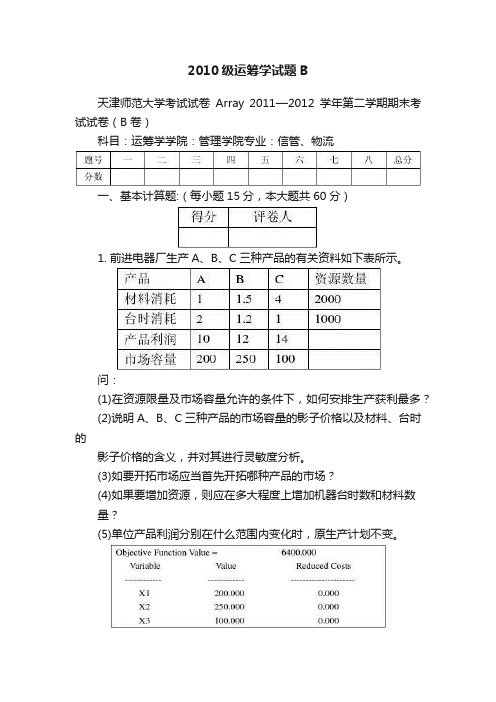
2010级运筹学试题B天津师范大学考试试卷Array 2011—2012学年第二学期期末考试试卷(B 卷)科目:运筹学学院:管理学院专业:信管、物流一、基本计算题:(每小题15分,本大题共60分)1. 前进电器厂生产A、B、C三种产品的有关资料如下表所示。
问:(1)在资源限量及市场容量允许的条件下,如何安排生产获利最多?(2)说明A、B、C三种产品的市场容量的影子价格以及材料、台时的影子价格的含义,并对其进行灵敏度分析。
(3)如要开拓市场应当首先开拓哪种产品的市场?(4)如果要增加资源,则应在多大程度上增加机器台时数和材料数量?(5)单位产品利润分别在什么范围内变化时,原生产计划不变。
2. 大西洋钢铁公司(Atlantic Steel Company)的采购部经理必须制订一个煤炭采购策略以运作12个炼钢炉,每个炼钢炉每天精确地需要5吨煤来运作。
公司每年运作360天。
采购部经理已经确定单位订购成本为80美元,持有成本为库存持有商品平均价值的20%。
采购部经理已签订了一份公司在未来一年内可以以每吨12美元的价格采购煤的合同。
a.求每次订购煤的最优订购批量;b.求最优订货策略下的库存相关总成本(不包括煤的成本);c.如果接收订购的煤所需的提前期为5天,则下订单时煤的现有库存量应为多少?3. 第一城市的第一美国银行(First American Bank of Rapid City)有一个室外取款机,它服务一个银行客户平均花费4分钟。
每小时有12个客户到达服务窗口。
银行的运营主管正在分析添加第2 台窗口的可能性,每年花费20000美元。
假定到达的车辆平均分到两个服务窗口。
业务主管估计在客户等待时间上减少1分钟那么银行每年的收入将增加2000美元。
请计算应该安装第2个服务窗口吗?4. 简和吉姆.史密斯将在星期五晚上7:00举行一个聚会,他们的两个孩子杰瑞和朱迪将帮助他们准备此次聚会。
史密斯夫妇将都在下午4:00从工作单位和学校回到家。
天津大学2011运筹学试题及答案

天津大学招收2011年硕士学位研究生入学考试试题及参考答案考试科目:运筹学基础 考试科目编号:832 一、填空题:(每空格2分,共16分)1、线性规划的解有唯一最优解、无穷多最优解、 无界解 和无可行解四种。
2、在求运费最少的调度运输问题中,如果某一非基变量的检验数为4,则说明 如果在该空格中增加一个运量运费将增加4 。
3、4X 1-2X 1X 1,X 256. 系为7. (2)8. 为0______;9. 极大化的线性规划问题为无界解时,则对偶问题_ 无解_____;10. 若整数规划的松驰问题的最优解不符合整数要求,假设X i =b i 不符合整数要求,INT (b i )是不超过b i 的最大整数,则构造两个约束条件:Xi ≥INT (b i )+1 和 Xi ≤INT (b i ) ,分别将其并入上述松驰问题中,形成两个分支,即两个后继问题。
11. 知下表是制订生产计划问题的一张LP 最优单纯形表(极大化问题,约束条件均为“≤”型不等式)其中对偶问题的最优解: Y =(4,0,9,0,0,0) (2)写出B -1=⎪⎪⎫ ⎛4011022)当C 2从4变成5时, σ4=-9/8 σ5=-1/4由于非基变量的检验数仍然都是小于0的,所以最优解不变。
3)当若b 2的量从12上升到15 X =9/8 29/8 1/4由于基变量的值仍然都是大于0的,所以最优解的基变量不会发生变化。
4)如果增加一种新的产品,则 P 6’=(11/8,7/8,-1/4)T σ6=3/8>0所以对最优解有影响,该种产品应该生产重新计算检验数所有的检验数都大于等于0,所以得到最优解3、某公司要把4个有关能源工程项目承包给4个互不相关的外商投标者,规定每个承包商只能且必须承包一个项目,试在总费用最小的条件下确定各个项目的承包者,总费用为多少?各承包商对工程的报价如表2所示:最优解为X1=185/33, X3=35/112)对偶问题最优解为Y=(1/22,1/11,68/33,0,0)T3)当b1=45时X= 45/11-11/90由于X2的值小于0,所以最优解将发生变化4Tσ5σσσV6. 考虑如下线性规划问题(20分)Max z=3x1+x2+4x3s.t. 6x1+3x2+5x3≤93x1+4x2+5x3≤8x 1,x2, x3≥0回答以下问题:1)求最优解;2)直接写出上述问题的对偶问题及其最优解;列的系数变为(3,2)T,问最优解是否有变化;3)若问题中x2由1变为2,是否影响最优解,如有影响,将新的解求出。
2011年4月高等教育自学考试运筹学基础试题及答案,笔记 (1)

2011年4月高等教育自学考试全国统一命题考试运筹学基础试题课程代码:02375一、单项选择题(本大题共15小题,每小题1分,共15分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.对某个企业的各项经济指标及其所涉及到的国内外市场经济形势的预测方法属于( A)A.微观经济预测B.C.科技预测D.2.一般而论,1-3年内的经济预测为( BA.长期预测(3~5)B.C.短期预测(<=1年)D.3.属于( B )A.指数平滑预测法B.回归模型预测法C.专家小组法D.特尔斐法4.下述各方法中,可用于不确定条件下决策标准的是( D )A.最大期望收益值B.最小期望损失值C.决策树D.最小最大遗憾值大小,大大,现实主义5.在库存管理中,“再订货时某项存货的存量水平”称为( A )A.再订货点B.前置时间C.安全库存量D.经济订货量6.线性规划的基本特点是模型的数学表达式是( D)A.变量的函数B.目标函数C.约束条件函数D.线性函数7.单纯形法求解线性规划问题时,若要求得基础解,应当令( B)A.基变量全为0B.非基变量全为0 就是将X N=0C.基向量全为0D.非基向量全为08.在线性规划中,设约束方程的个数为m,变量个数为n,m<n时,我们可以把变量分为基变量和非基变量两部分。
基变量的个数为( A ) 基变量的个数等于约束方程的个数A.m个B.n个基变量就是引入的那几个量C.n-m个D.0个9.EOQ模型用于解决管理中的( A )A.订货与库存问题B.环境条件不确定和风险问题C.具有对抗性竞争局势问题D.项目进度计划安排问题10.在网络计划技术中,以箭线代表活动(作业),以结点代表活动的开始和完成,这种图称之为( A )A.箭线式网络图B.结点式网络图C.最短路线图D.最大流量图11.网络图中,一定生产技术条件下,完成一项活动或一道工序所需时间,称为( A )A.作业时间B.最乐观时间C.最保守时间完成活动最长的时间D.最可能时间12.在一个网络中,如果图形是连通且不含圈的,则这种图形称之为( C)A.点B.线C.树D.最小枝叉树13.任意一个向量,如果它内部的各个元素均为非负数,且总和等于1,则该向量称之为( C)A.固定概率矩阵B.马尔柯夫向量C.概率向量D.概率矩阵14.在固定成本中,由所提供的生产能力所决定、不受短期管理控制支配的费用,称之为( D )A.总成本B.可变成本C.计划成本D.预付成本15.在盈亏平衡图中,变动费用线上的任何一点都表示对应于某一产量的( B)A.固定费用B.总生产费用C.半可变费用D.变动费用二、填空题(本大题共10小题,每小题1分,共10分)请在每小题的空格中填上正确答案。
2009~2010第一学期运筹学试卷(A)评分细则04

2009~2010第一学期《运筹学》试卷(A ) 评分细则一、单项选择题(每小题2分,共20分)1、A2、B3、D4、D5、C6、B7、D8、D9、B 10、A二、线性规划建模及对偶 (每小题10分,共10分)某产品要在某电视台作广告宣传,广告对象是妇女和老人,一次早上广告节目需要200元,估计有1000位妇女和1000位老人收看,一次中午的广告节目需280元,估计有1500位妇女和2000位老人收看。
一次晚上的广告节目需840元,估计有5000位妇女和4000位老人收看。
该企业广告节目要求每天至少有30000位家庭妇女和25000位老人收看,如何安排广告节目的配合比,使之达到上述要求,又能使广告费用费用最少? (1) 建立其线性规划模型(不需要求解); (2) 将其化为标准型;(3) 写出原规划的对偶模型。
(1)解:设早上广告次数为1x ,下午广告次数为2x ,晚上广告次数为3x , 则模型为:123123123123min z= 200+280+ 8401000+1500+5000 30000..1000+2000+400025000,,0x x x x x x s t x x x x x x ≥⎧⎪≥⎨⎪≥⎩ ………………………………………………………………………………………………4分 (2)解:原规划的标准型为:123121231123212312max(-z) = 200280 840001000+1500+5000 30000..1000+2000+400025000,,,,0x x x s s x x x s s t x x x s x x x s s ------=⎧⎪-=⎨⎪≥⎩………………………………………………………………………………………………3分 (3)解: 原规划的对偶模型为:12121212123max 30000250001000100020015002000280.50004000840,,0f y y y y y y st y y y y y =++≤⎧⎪+≤⎪⎨+≤⎪⎪≥⎩ ………………………………………………………………………………………………3分三、线性规划求解(二者只需选作其一,每小题10分,共10分) 请注明你选作的题目是第()小题1、已知线性规划(1)画出可行域; (2)画出等值线; (3)标出最值点;(4)利用图解法求出最优解和最优值。
2010级运筹学试题B

天津师范大学考试试卷Array 2011—2012学年第二学期期末考试试卷(B 卷)科目:运筹学学院:管理学院专业:信管、物流一、基本计算题:(每小题15分,本大题共60分)1. 前进电器厂生产A、B、C三种产品的有关资料如下表所示。
问:(1)在资源限量及市场容量允许的条件下,如何安排生产获利最多?(2)说明A、B、C三种产品的市场容量的影子价格以及材料、台时的影子价格的含义,并对其进行灵敏度分析。
(3)如要开拓市场应当首先开拓哪种产品的市场?(4)如果要增加资源,则应在多大程度上增加机器台时数和材料数量?(5)单位产品利润分别在什么范围内变化时,原生产计划不变。
2. 大西洋钢铁公司(Atlantic Steel Company)的采购部经理必须制订一个煤炭采购策略以运作12个炼钢炉,每个炼钢炉每天精确地需要5吨煤来运作。
公司每年运作360天。
采购部经理已经确定单位订购成本为80美元,持有成本为库存持有商品平均价值的20%。
采购部经理已签订了一份公司在未来一年内可以以每吨12美元的价格采购煤的合同。
a.求每次订购煤的最优订购批量;b.求最优订货策略下的库存相关总成本(不包括煤的成本);c.如果接收订购的煤所需的提前期为5天,则下订单时煤的现有库存量应为多少?3. 第一城市的第一美国银行(First American Bank of Rapid City)有一个室外取款机,它服务一个银行客户平均花费4分钟。
每小时有12个客户到达服务窗口。
银行的运营主管正在分析添加第2台窗口的可能性,每年花费20000美元。
假定到达的车辆平均分到两个服务窗口。
业务主管估计在客户等待时间上减少1分钟那么银行每年的收入将增加2000美元。
请计算应该安装第2个服务窗口吗?4. 简和吉姆.史密斯将在星期五晚上7:00举行一个聚会,他们的两个孩子杰瑞和朱迪将帮助他们准备此次聚会。
史密斯夫妇将都在下午4:00从工作单位和学校回到家。
2010交通《运筹学》试卷(A卷)参考答案及评分标准
2009级《运筹学》试卷(A 卷)参考答案及评分标准一.设A 、B 产品的产量为x 1,x 2,用于销售的C 产品的产量为x 3,需处理的C 产品的产量为x 4. 1.⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≤=--≤+≤+-++=-013000217003211002..273max 41343221214321x x x x x x x x x t s x x x x z 2.12341251262343717max 37221100231700..201300-=++-++=⎧⎪++=⎪⎪--=⎨⎪+=⎪⎪≥⎩z x x x x x x x x x x s t x x x x x x3.124121233431243min 10001700130023232721,,0,=+++≥⎧⎪++≥⎪⎪-+≥⎨⎪-≥-⎪⎪≥⎩w y y y y y y y y y y y y y y y 无约束4.在2中引入人工变量x 8,则有1234812512623483718max 37221100231700..2013000-=++--++=⎧⎪++=⎪⎪--+=⎨⎪+=⎪⎪≥⎩z x x x x Mx x x x x x x s t x x x x x x x 于是得到初始基可行解为:0(0,0,0,0,1100,1700,1300,0)=X ,则初始单纯形表为: 二.(1)本运输c j 3 72 -1 0 0 -M 0x 1 x 2 x 3 x 4 x 5 x 6 x 8 x 7 C B X B b 0 x 4 1100 1 2 1 0 0 0 0 x 5 1700 2 3 0 1 0 0 -M x 7 0 2 -1 -1 0 0 1 0 0 x 8 13001 0 0 0 1σj3 2M +7 -M +2 -M-1 0 0 0 0问题的线性规划模型为:⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧==≥=++=++=++=++=+++=+++=++++++++++++++=4,3,2,1;3,2,1,010141412151520.16141712206781115410min 342414332313322212312111343332312423222114131211343332312423222114131211j i x x x x x x x x x x x x x x x x x x x x x x x x x t s x x x x x x x x x x x x z ij(5分)(2)用最小元素法确定初始调运方案,如下表 (5分)(3)用位势法计算非基变量的检验数,结果如下表 (5分)(4)因为非基变量x 14检验数小于0,所以当前解不是最优解。
运筹学新疆班试题-2011
三、分析题(15 分) 某电子产品制造公司为某产品的改造制定了两种方案:一是采用充电电池的方案, 一是采用太阳能电池的方案。根据经验,充电电池方案成功的可能性为 0.8,太阳能电池 方案成功的可能性为 0.6。考虑到产品改造成功后,产品的质量和生产率均可提高,因此 又制定了两种生产方案:一是产量不变;一是产量增加。若改造失败则产量保持不变。 工厂决定该产品生产五年, 产品在今后五年内跌价的概率为 0.1, 保持原价的概率为 0.4, 涨价的概率为 0.5。分析如何安排生产获利最大。 单位:万元
2
状态 方案 跌价 0.1
1
原价 0.4
涨价 0.5
失败(原结构生产) 充电电池 产量不变 成功 0.8 产量增加 太阳能电 池成功 0.6 产量不变 产量增加
-100 -200 -400 -200 -450
0 90 100 0 -100
110 200 300 250 600
(1)画出决策树。 (2)计算各点的益损期望值。 (3)选择最优方案。 四、自设数据求解题(10 分) 炎炎夏日,身在乌鲁木齐的老王打算和朋友们去郊区游玩消夏,备选地点有天池, 南山牧场,青格达湖。老王主要考虑的因素有三个:费用、旅途条件和景色。 现聘请你担任专家,根据这三个评价指标,构造出关于三个旅游地的层次结构模型。 根据你的判断,对这三个旅游地就景色而言,给出相应的判断矩阵,要求天池的景色不 比其他两处差。
一、 建模: (15 分) 某物资要从三个产地 A1, A2, A3 运至三个销地 B1, B2, B3,单位运价由下表给出: B1 2 1 3 B2 5 6 2 B3 4 8 6
2011-2012-2运筹学试卷B
姓 学 号:
线
二、填空题(每小题 2 分,共 12 分)
1.对只包含 的线性规划问题,可以用图解法来求解。 2.求解不平衡的运输问题的基本思想是 。 3.称无圈的连通图为树,若图的顶点数为 n,则其边数为 。 4 . 当 满足 最 优解 , 且检 验 数 为零 的 变量 的 个数 大 于 基变 量 的个 数 时, 可 求 得 。 5. 在运输方案中出现退化现象,是指数字格的数目 。 6. 如果在用大 M 法求解线性规划问题时,如果最终表中的基变量中还含有人工变 量,这时原来的线性规划问题为 。 三、 (15 分)已知线性规划问题 max z=2x1+x2+5x3+6x4
七、 (12 分)求下图所示网络中的最大流,每条边上的序数表示(cij,fij)
广东工业大学试卷用纸,共
页,第
页
订
专
装
业:
2 x1 x 3 x 4 8 st 2 x1 2 x 2 x 3 2 x 4 12 x1, x 2, x 3, x 4 0
(1) 写出该线性规划问题的标准形式; (4 分) (2) 写出该线性规划问题的对偶问题,已知其对偶问题的最优解 y1*=4,y2*=1,求 出原问题的最优解,原问题的目标函数的最优值是多少?(9 分) (3)如果用单纯形法来求解原问题,那么它的最终单纯形表中松弛变量的检验数 是多少?(2 分) 四、 (5 分)试计算下面单纯形表中的参数 a~e。
学
院:
广东工业大学试卷用纸,共
页,第
页
cj CB 0 3 0 XB x1 x3 x6 cj-zj b 10 3 1
0 x1 a 0 0 0
-1 x2 5/2 -1/2 -5/2 b
天津大学2011运筹学试题及答案
天津大学2011运筹学试题及答案
天津大学招收2011年硕士学位研究生入学考试试题及参考答案
1 / 8
天津大学招收2011年硕士学位研究生入学考试试题及参考答案考试科目:运筹学基础考试科目编号:832
一、填空题:(每空格2分,共16分)
1、线性规划的解有唯一最优解、无穷多最优解、无界解和无可行解四种。
2、在求运费最少的调度运输问题中,如果某一非基变量的检验数为4,则说明如果在该空格中增加一个运量运费将增加4 。
3、
4X 1-2X 1X 1,X 256. 系为7. (2)8. 为0______;
9. 极大化的线性规划问题为无界解时,则对偶问题_ 无解_____;
10. 若整数规划的松驰问题的最优解不符合整数要求,假设X i =b
i 不符合整数要求,INT (b i )是不超
过b i 的最大整数,则构造两个约束条件:Xi ≥INT (b i )+1 和Xi ≤INT (b i ),分别
将其并入上述松驰问题中,形成两个分支,即两个后继问题。
11. 知下表是制订生产计划问题的一张LP 最优单纯形表(极大化问题,约束条件均为“≤”型不等式)其中。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1页 共10页
2010-2011学年第二学期《运筹学》期末试卷
(考试对象:商学院2009级各专业)
学院 专业班级 学号 姓名 成绩
(说明:请将正确答案写在题目后面的空白处)
一、 选择题(每题只有一个正确答案,每题3分,共24分)
1.现有如下四个线性规划模型:
①1212123230Maxzxxxxx ②0,3232212121xxxxxxMinz
③1212122323,0Maxzxxxxxx ④0,3232212121xxxxxxMaxz
其中属于标准型的模型有【 】
A. ①③ B. ①④ C. ③ D. ④
2. 下面的线性规划问题将取得【 】
Max 122zxx
12121232624,0xxxxxx
A. 唯一最优解 B. 多重最优解 C. 无界解 D. 无可行解
3. 某同学用隐枚举法求解如下0-1规划模型:
12
12
12
12
23121,01Maxzxxxxxxxx
或
按(0,0),(0,1),(1,0),(1,1)的顺序分别进行检查、判断,则该同
学最先确定的过滤条件是【 】
A. 0z B. 3z C. 2z D. 1z
4. 下列哪个方案能作为表上作业法求解时的初始方案【 】
第2页 共10页
A
销地
产地
一 二 三 四 五 六 产量
1
30 30
2 20 30 50
3
10 30 10 25 75
4
20 20
销量
20 40 30 10 20 25
B
销地
产地
一 二 三 四 产量
1
4 14 18
2
24 24
3
2 4 6
4
7 5 12
销量
6 14 35 5
C
销地
产地
一 二 三 四 产量
1
5 10 15
2
0 10 15 25
3
5 10
销量
5 15 15 10
D
销地
产地
一 二 三 四 产量
1 3 5 11
2 5 4 2 11
3 5 6 8
销量 5 9 9 7
5. 用分枝定界法计算到某一步后,保留了如下三个分枝:① B1 x1=6.2,
x2=5.1,z=28.3 ②B21 x1=2.2,x2=4.6,z=12.5;③B22 x1=3,x2=4,z=20;则可
得到新的上下界是【 】
A. 0≤z≤12.5 B. 0≤z≤28.3
C. 12.5≤z≤20 D. 20≤z≤28.3
第3页 共10页
6. 如下目标规划问题的解为【 】
Min z =2211dpdp
1211122212244,,,0,1,2iixxddxxddxxddi
A. 满意解(2,0) B.最优解(2,0)
C. 满意解(8/3,-4/3) D. 最优解(8/3,-4/3)
7.下面说法正确的是【 】
A.一个图若能一笔画出,则一定是欧拉图。
B.一连通图G的所有连通支撑子图中,G的支撑树一定是G中边数最少的
连通支撑子图。
C.有向图中的链一定是它的路。
D.任一连通图的最小支撑树是唯一的。
8.设有1,2,3,4四个零件需要在机床A、B上加工,每个零件都必须经
过先A而后B两道加工工序,每个零件在机床A、B上加工时间分别为(8,4)、
(6,7)、(3,7)、(5,8),试求最优加工顺序,使机床连续加工完所有的工件
加工总时间最少?【 】
A. (1,2,3,4) B. (2,3,1,4) C. (3,4,1,2) D. (3,4,2,1)
二、建模题(本题只建模,不求解,共32分)
1.(10分)某公司拟用集装箱托运甲、乙两种货物,现有船运和车运两种
方式,每箱的体积、重量、可获利润以及托运所受限制如下表所示, 问两种货
物各托运多少箱可获利润最大?试建立该问题的数学模型。
货物
体积每箱(m3) 重量每箱(百斤) 利润每箱(百元)
船运 车运 船运 车运 船运 车运
甲 7 5 6 2 25 20
乙 3 4 4 5 8 10
托运限制 45 25 20 13
第4页 共10页
2.(10分)某公司决定拿出100万元用于A、B、C三种新产品的研发。经
预测,研发A、B、C三种产品的投资利润率分别为8%,10%,15%。由于研发
新产品具有一定的风险,公司研究后制定了如下的目标:
第一:A和B两种产品至少共投资50万元;
第二:为分散投资风险,任何一种新产品的投资额不得超过总资金的35%;
第三:A、B两种产品的投资额比例应尽量与其利润率保持一致;
第四:希望总利润最大。
第5页 共10页
3.(12分)现有12吨钢材用于生产A、B、C两种产品,已知每生产1吨
A产品需要钢材4吨,每生产1吨B产品需要钢材2吨,每生产1吨C产品需
要钢材3吨。在市场上销售A产品每吨获利1万元,B产品每吨获利1.2万元,
C产品每吨获利1.5万元。问题:如何安排生产计划,使获得的利润最大?请建
立合理的动态规划模型。(注意:允许状态集合、状态转移方程和递推方程中的
收益函数请用题目中具体的数据表示)
第6页 共10页
三、 计算题(部分题目需要给出解题步骤,共44分)
1.(6分)用伏格尔法求下列运输问题的最优方案,请写出求解步骤。
销地
产地
1 2 3
产量
1 1 2 6 7
2 0 4 2 12
3 3 1 5 1
销量 10 10 10
第7页 共10页
2.(6分) 用单纯形法求某目标函数为极大的线性规划问题,已得如下单纯形
表:
cj
3 -1 -1 0 0 -M
CB XB b
x1 x2 x3 x4 x5 x6 i
0 x6 a -1 x2 3 -1 x3 1 c 0 0 1 -2 2
0 1 0 0 b 1
-2 0 1 0 0 0
jj
zc
d 0 0 0 -1 -M+1
其中,a,b,c,d都是未知数,原问题中要求0jx,问当a,b,c,d满
足什么条件时,下面各解成立。
(1) 是唯一最优解;
(2) 有无穷多最优解;
(3) 无可行解;
(4) 无界解。
3.(5分)试用匈牙利法求下列极大..化指派...问题的最优解。(要求写必要的解题
步骤)
151396
108811
3121210
109612
第8页 共10页
4.(5分)用Dijkstra算法求下图1V到4V的最短路。(要求写必要的解题步骤)
V2
V4
V3
2
8
1
5
3
5.(4分)下图是某建筑的平面图,要求在建筑有内部从每一个房间都能走到另
外的所有房间,问至少要在墙上开多少个门,并给出一个开门的方案。
八
一
二 三 四 五
七
六
第9页 共10页
6.(6分)现有一网络见下图,并提供一初始可行流,弧旁的数字(Cij,fij)分
别代表(容量,流量)。求网络的最大流,并写出最小截集与最小截量(计算过
程请直接在图上标号)
7.(4分) 根据下面的作业明细表绘制网络图。
工序
a b c d e f g
紧前工序
— — a,b a,b b c,d e,f
V1
V2
V3
V4
V5
(6,4)
(5,1)
(2,1)
(1,1)
(5,2)
(2,2)
(4,3)
第10页 共10页
8.(8分)求如下网络图的关键路线。事项的时间请直接标于图中,各时间
参数填入下表中。
工序 tij tES tFS tLF tLs TF
a
b
c
d
e
f
g
h
1 2 3 4 7 6
5
a 10 b e c f d g h
20 30 30 15 40
35
20
