桁架内力计算
桁架内力

桁架内力桁架内力是指桁架结构在受到外部力作用时所承受的内部力。
桁架结构是由多根互相连接的直线构成的一种空间结构形式,常见于建筑和机械工程中,用于支撑和分担结构的载荷。
了解桁架内力对于设计和分析桁架结构的稳定性和安全性非常重要。
以下是一些相关参考内容:1. 桁架结构和内力分析基本原理桁架结构的原理是将力沿桁架的元素进行传递和分担。
在受力分析中,通过应用平衡原理和静力学等基本原理,可以推导出桁架结构中各个桁架元素所受的内力。
这些内力包括张力、压力和剪力等。
了解这些基本原理对于理解桁架内力分析的方法和原则非常重要。
2. 桁架内力的计算方法桁架内力的计算可以通过静力平衡和弹性力学原理进行。
一般来说,可以根据桁架结构的几何形状和外部荷载,采用基本的力平衡原理和弹性力学公式,推导出各个桁架元素所受的内力。
计算方法包括节点法、截面法、力法和位移法等。
这些方法在不同场景和结构要求下应用于桁架结构的内力计算和分析。
3. 桁架内力的影响因素桁架内力的大小和分布受到多个因素的影响,包括结构的几何形状、荷载情况、边界条件和材料性能等。
通过对这些因素的研究和分析,可以更好地了解和预测桁架内力的变化规律。
例如,在分析桁架结构的受力性能时,需要考虑荷载的大小、方向和分布情况,以及桁架元素的尺寸和刚度等。
4. 桁架内力的应用案例桁架内力的计算和分析在实际工程中有广泛的应用。
例如,在建筑结构设计中,桁架结构常用于大跨度的屋顶、桥梁和支撑结构中。
通过分析桁架结构的内力,可以评估其受力性能和稳定性,并确保结构的安全性。
在机械工程中,桁架结构常用于起重机、吊车和机械臂等设备中,用于承载和分担重物。
通过分析桁架内力,可以评估结构的承载能力和运动性能。
总结来说,桁架内力是桁架结构在受到外部荷载作用时所承受的内部力。
了解桁架内力对于设计和分析桁架结构的稳定性和安全性非常重要。
通过应用平衡原理和弹性力学等基本原理,可以计算出桁架内力的大小和分布。
静定桁架的内力计算
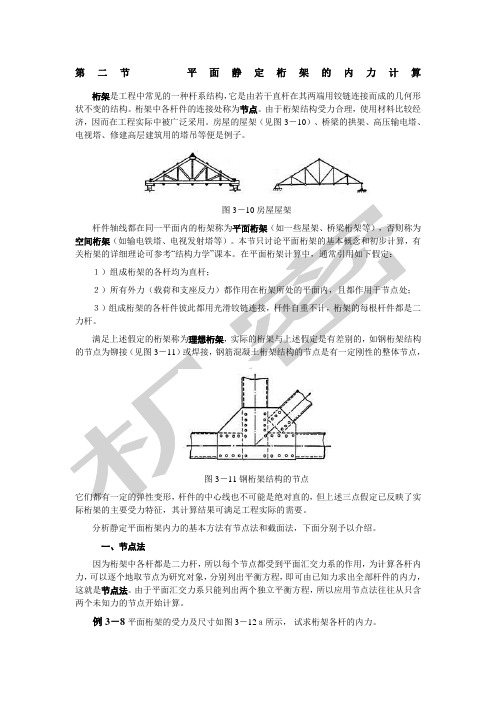
第二节平面静定桁架的内力计算桁架是工程中常见的一种杆系结构,它是由若干直杆在其两端用铰链连接而成的几何形状不变的结构。
桁架中各杆件的连接处称为节点。
由于桁架结构受力合理,使用材料比较经济,因而在工程实际中被广泛采用。
房屋的屋架(见图3-10)、桥梁的拱架、高压输电塔、电视塔、修建高层建筑用的塔吊等便是例子。
图3-10房屋屋架杆件轴线都在同一平面内的桁架称为平面桁架(如一些屋架、桥梁桁架等),否则称为空间桁架(如输电铁塔、电视发射塔等)。
本节只讨论平面桁架的基本概念和初步计算,有关桁架的详细理论可参考“结构力学”课本。
在平面桁架计算中,通常引用如下假定:1)组成桁架的各杆均为直杆;2)所有外力(载荷和支座反力)都作用在桁架所处的平面内,且都作用于节点处;3)组成桁架的各杆件彼此都用光滑铰链连接,杆件自重不计,桁架的每根杆件都是二力杆。
满足上述假定的桁架称为理想桁架,实际的桁架与上述假定是有差别的,如钢桁架结构的节点为铆接(见图3-11)或焊接,钢筋混凝土桁架结构的节点是有一定刚性的整体节点,图3-11 钢桁架结构的节点它们都有一定的弹性变形,杆件的中心线也不可能是绝对直的,但上述三点假定已反映了实际桁架的主要受力特征,其计算结果可满足工程实际的需要。
分析静定平面桁架内力的基本方法有节点法和截面法,下面分别予以介绍。
一、节点法因为桁架中各杆都是二力杆,所以每个节点都受到平面汇交力系的作用,为计算各杆内力,可以逐个地取节点为研究对象,分别列出平衡方程,即可由已知力求出全部杆件的内力,这就是节点法。
由于平面汇交力系只能列出两个独立平衡方程,所以应用节点法往往从只含两个未知力的节点开始计算。
例3-8 平面桁架的受力及尺寸如图3-12a所示,试求桁架各杆的内力。
图3-12 例3-8图解:(1)求桁架的支座反力以整体桁架为研究对象,桁架受主动力2F以及约束反力、、作用,列平衡方程并求解:,=0,2×-=0,=,+-2=0,=2-=(2)求各杆件的内力设各杆均承受拉力,若计算结果为负,表示杆实际受压力。
第6次 简单平面桁架的内力计算

a
a
a
a
B
C
D
FC
1.取整体为研究对象, 受力分析如图。
FAy
A
FAx
F
E FE
FB
a
a
a
a
C
D
B
FC
§2.9简单平面桁架的内力计算 例题 3-10
2.列平衡方程。
Fx 0, Fy 0, M AF 0,
FAx FE 0 FB FAy FC 0 FC a FE a FB 3a 0
§2.9简单平面桁架的内力计算
几个概念
平面桁架—— 所有杆件都在同一平面内的桁架。 节 点—— 桁架中杆件的铰链接头。 杆件内力—— 各杆件所承受的力。
§2.9简单平面桁架的内力计算
几个概念
无余杆桁架—— 如果从桁架中任意抽去一根杆件,则桁架 就会活动变形,即失去形状的固定性。
§2.9简单平面桁架的内力计算
FCA FCD FCE cos 45 0
FAy
A
FAx
F
E FE
FB
a
a
a
a
C
D
B
FC
Fy 0,
FC FCF FCE cos 45 0 解得
FCE 2 2 kN , FCD 2 kN
§2.9简单平面桁架的内力计算 例题 3-10
FDE
8.取节点D,受力分析如图。
A
FAx
Fx 0,
B
FBD FBE cos 45 0
Fy 0,
F
E FE
FB
a
a
a
a
C
桁架内力计算

21
一、节点法 (1)一般先研究整体,求支座约束力; (2)逐个取各节点为研究对象; (3)求杆件内力; (4)所选节点的未知力数目不大于2,由此 开始计算。
练习1
判断结构中的零杆
F F
F
FP
2015-3-5
15
结点法
基本概念 结点法 截面法 联合法 小结
۞
练习2
计算桁架各杆件内力
2F a
4×a
第一步:求支座反力 第二步:判断零杆和单杆,简化问题 第三步:逐次去结点,列平衡方程 第四步:自我检查
16
2015-3-5
结点法
基本概念 结点法 截面法 联合法 小结
目 ≤ 独立方程数(即2个);
小结
基本思路:尽可能简化问题,一般先求支座反力,
然后逐次列结点平衡方程。
2015-3-5 10
结点法
۞
例题1
如图所示为一施工托架计算简图,求图示 荷载作用下各杆轴力(单位:kN)。
基本概念 结点法 截面法 联合法 小结
8 A
1.5m
8
C 6 E8 G F
8
B
截面法
基本概念
۞ 例题2
求图示桁架25、34、35三杆内力(单位:kN)。 10 20
I 4
7 2m 8
结点法
10
3
a
截面法 联合法 小结
1
2
5 I8 m
6
解: 1)求支座反力。2)截面法,取分离体受力 分析,求内力。
简单桁架内力计算

3.4 静定平面桁架教学要求掌握静定平面桁架结构的受力特点和结构特点,熟练掌握桁架结构的内力计算方法——结点法、截面法、联合法3.4.1 桁架的特点和组成3.4.1.1 静定平面桁架桁架结构是指若干直杆在两端铰接组成的静定结构。
这种结构形式在桥梁和房屋建筑中应用较为广泛,如XX长江大桥、钢木屋架等。
实际的桁架结构形式和各杆件之间的联结以及所用的材料是多种多样的,实际受力情况复杂,要对它们进行精确的分析是困难的。
但根据对桁架的实际工作情况和对桁架进行结构实验的结果表明,由于大多数的常用桁架是由比较细长的杆件所组成,而且承受的荷载大多数都是通过其它杆件传到结点上,这就使得桁架结点的刚性对杆件内力的影响可以大大的减小,接近于铰的作用,结构中所有的杆件在荷载作用下,主要承受轴向力,而弯矩和剪力很小,可以忽略不计。
因此,为了简化计算,在取桁架的计算简图时,作如下三个方面的假定:(1)桁架的结点都是光滑的铰结点。
(2)各杆的轴线都是直线并通过铰的中心。
(3)荷载和支座反力都作用在铰结点上。
通常把符合上述假定条件的桁架称为理想桁架。
3.4.1.2 桁架的受力特点桁架的杆件只在两端受力。
因此,桁架中的所有杆件均为二力杆。
在杆的截面上只有轴力。
3.4.1.3 桁架的分类(1)简单桁架:由基础或一个基本铰接三角形开始,逐次增加二元体所组成的几何不变体。
(图3-14a)(2)联合桁架:由几个简单桁架联合组成的几何不变的铰接体系。
(图3-14b)(3)复杂桁架:不属于前两类的桁架。
(图3-14c)3.4.2 桁架内力计算的方法桁架结构的内力计算方法主要为:结点法、截面法、联合法结点法――适用于计算简单桁架。
截面法――适用于计算联合桁架、简单桁架中少数杆件的计算。
联合法――在解决一些复杂的桁架时,单独应用结点法或截面法往往不能够求解结构的内力,这时需要将这两种方法进行联合应用,从而进行解题。
解题的关键是从几何构造分析着手,利用结点单杆、截面单杆的特点,使问题可解。
理论力学(大学)课件6.3 平面简单桁架的内力计算

3、平面简单桁架的内力计算3、平面简单桁架的内力计算桁架一种由杆件彼此在两端用铰链连接而成的结构,它在受力后几何形状不变。
桁架结构的优点•结构强度大,稳定性和可靠性高,每根杆件只承受轴力,不承载弯矩和剪力。
•重量轻、耗材少、安装方便。
•分析、计算方便,更换部件容易。
•适用范围广、结构灵活多变。
•工程中被大量、广泛地使用。
本课程重点关注平面桁架问题。
节点桁架中杆件的铰链接头。
1. 各杆均为直杆,各杆轴线位于同一平面内;2. 杆件与杆件间均用光滑铰链连接;3. 载荷作用在节点上,且位于桁架几何平面内;4. 各杆件自重不计或平均分布在节点上。
桁架中每根杆件均为二力杆关于平面桁架的几点假设:理想桁架3、平面简单桁架的内力计算各种各样的平面桁架结构(静定桁架)基本三角形32(3)m n -=-平面静定桁架总杆数m 总结点数n >3>3(m =2n -3)32->nm 32-=n m 平面复杂(超静定)桁架32-<nm 非桁架(机构)3、平面简单桁架的内力计算计算桁架杆件内力的方法:(1) 节点法逐个地取节点为研究对象,由已知力求出全部未知的杆件内力。
例6 平面桁架的尺寸和支座如图所示,在结点D 处受一集中力F =10kN 的作用,试求桁架各杆件的内力。
解:(1)求支座约束力。
以整体为研究对象画受力图ååå===000By x M F F 04200=-=-+=Ay By Ay Bx F F F F F F kN5kN 50===Ay By Bx F F F (2)依次取一个结点为研究对象,计算各杆内力。
先取结点A ,假设各杆均受拉力,画出其受力图。
12平面汇交力系的平衡问题,列平衡方程:åå==00yx FF 030sin 030cos 112=°+=°+F F F F Ay kN66.8kN 1021=-=F F F 1为负值,代表杆1实际受压力;F 2为正值,代表杆2与假设一致,实际受拉力。
静力学-平面简单桁架的内力计算
3. 取左(右)部分分析, 列平面任意力系的平衡方程。
2. 截面法 求某几根杆件内力常用的方法 —平面任意力系问题
例: 求:1、2、3杆件内力
3. 取左(右)部分分析,假设 “拉”
C ①D
FAy
②
A
③
F FB 列平面任C意力①系的平F衡1方程。
B
FAy
② F2
FAx E
G
F1
F2
解:1. 求支座约束力
A
(2)
F
f f
A
如果作用于物块的全部主动力合力 F
的作用线落在摩擦角之外( ≥ f ),则
无论此合力多小,物块必滑动。
FRA
2. 自锁现象
(phenomena of self-locking)
FRA
FRA
0 f 物体静止平衡时,全约束力必在摩擦角内
Fmax FS
FN f
A
(1)
F
f f
(2)
A
FAx
③ E
F3
P1
MA0
FB
ME 0
F1
MB 0
FAy
Fy 0
F2
Fx 0
FAx
Fx 0
F3
2. 把桁架截开 不要截在节点处
赛 车 起 跑
为什么赛车运动员起跑前要将车轮与 地面摩擦生烟?
第四章 摩擦 Friction
摩擦(friction): 一种极其复杂的物理-力学现象。
涉及:
“滚动摩阻定律”
—滚动摩阻系数 ,长度量纲
r
P A
FS FN
Q
r
临界平衡 P
A
Mf
FS
FN
任务十桁架的内力计算
任务十桁架的内力计算一、填空题1.一次截取一个结点为研究对象,来计算杆件内力的方法称(结点法)。
2.桁架的特点是在结点荷载作用下,桁架各杆的内力只有(轴力 ),截面上应力分布是 ( 均匀 ) 的。
3.桁架类型有 ( 简单桁架 )、( 联合桁架 )、 ( 复杂桁架 )。
4.梁式桁架有哪些形式(平行弦桁架)、(三角形桁架)、(梯形桁架)、(抛物线形桁架)、(折线形桁架)等。
5.在特定荷载作用下,桁架中内力为零的杆件称为(零杆)。
6.三根杆汇交于一铰结点,其中两根杆共线,结点上无外荷载,另外一根不共线的杆为(零杆)。
7.桁架内力计算的方法(结点法)、(截面法)、(联合法)。
二、选择题1.下列结构内力只有轴力的是( C )。
A.梁B.刚架C.桁架D.拱2.悬式桁架在垂直向下的竖向荷载作用下,受力特点是( A )。
A.上弦杆受拉,下弦杆受压B.上弦杆受压,下弦杆受拉C.上弦杆受拉,下弦杆受弯3.梁式桁架在垂直向下的竖向荷载作用下,受力特点是( B )。
A.上弦杆受拉,下弦杆受压B.上弦杆受压,下弦杆受拉C.上弦杆受拉,下弦杆受弯三、简答题1.理想桁架假设是什么?答:①桁架的结点都是光滑的理想铰;②各杆的轴线都是直线,且在同一平面内,并通过铰的中心;③荷载和支座反力都作用于结点上,并位于桁架的平面内。
2.桁架零杆的判断规则有哪些?答:①不共线的两杆组成的结点上无荷载作用时,该两杆均为零杆。
②不共线的两杆组成的结点上有荷载作用时,若荷载与其中一杆共线,则另一4×2=8m a)l660KN4360KN 87260KN5杆必为零杆。
③三杆组成的结点上无荷载作用时,若其中有两杆共线,则另一杆必为零杆,且共线的两杆内力相等。
四、计算题1. 用结点法计算图示各杆的内力 1解:(1)先求反力,利用对称性得KNF y 902=(↑)KNF y 901=(↑)(2)依次用结点法求各杆轴力 先以结点1分析,受力如图示由∑=0yF 09030sin 13=+o N F 得 KN F N 18013-=(压) 由∑=0xF 030cos 1316=+o N N F F 得 KN F N 39016=(拉)由结点6可知 036=N F KN F F N N 3901667==(拉) 再以结点3分析,受力如图示由 ∑=0yF30cos 6030cos 037=--o N F得 KN F N 6037-=(压)由 ∑=0xF30sin 6030sin 133734=--+o N o N N F F F 得 KN F N 12034-=(压)再以结点7分析 由对称性知KN F F N N 605737-== KN F F N N 3907867==(拉)由 ∑=0yF30sin 23747=+o N N F F 得 KN F N 6047=(拉)一半结构内力解出,另一半亦知。
理论力学4.1、平面简单桁架的内力计算
F3 12.31(kN) F2 2.82(kN) F1 8.72(kN)
10
课堂练习题1 求图4.1-6a/b所示桁架结构中带数字 编号的各杆件内力。
I
F
I
11
课堂练习题2,图4.1-7a所示桁架结构中 Fp 10 KN 求JO杆、FK杆的内力
12
各图桁架中带有编号 的杆是否都是零力杆?
13
零杆作用:可以把处 于受压状态的细长杆 “割断”成“短粗杆 ”,避免其“突然变 形”
14
15
C
D
E FE
A
B
G FG H FH
F1
F4
F3
FAy F1
F3 F5 F2
F2
G
E
D
C
B
A
FAy
FBy
FBx
16
3m
C 1D
E
2
FE
A
3
B
G FG H FH
A
C
E
1
2
6
3
7H 45
J
B DF GF I
Fix
0
F2
F1
c os30
0
F2
8.66(kN)
研究对象:D节点(图c);
Fix Fiy
0 0
F5 F3
F2 8.66(kN) P 10(kN)
研究对象:C节点(图d)
Fix 0 F4 cos30 F1 cos30 0 F4 10(kN) 9
(刚化公理的应用)
6
平面简单桁架:以三角形框架为基础,每增加一个节点 就要增加两根杆,而且所有的杆件都在同一平面内;
四、平面桁架的内力计算
三、平面简单桁架的内力计算
2.平面简单桁架
以一个铰链三角形框架为基础,每增一个节点需增 加二根杆件,如此构成的无多余杆的平面桁架。
总杆数 m
总节点数 n
m 3 2(n 3)
m 2n 3
第三章 平面任意力系和平面平行力系
三、平面简单桁架的内力计算
m 2n 3 平面复杂(超静定)桁架:如果从桁架中抽去某几根杆 件,桁架不会活动变形。
a
C
D
F3
FC
Fx 0, F3 FAx F1 F2 cos 45 0 Fy 0, FAy FC F2 cos 45 0 M C F 0, F1 a FAy a 0
求解得 F1 2 kN F2 2 2 kN F3 2 kN
第三章 平面任意力系和平面平行力系
三、平面简单桁架的内力计算
n
FR Fi i 1
—— 力系的主矢
第三章 平面任意力系和平面平行力系
n
M O
M O (Fi )
i 1
—— 力系对简化中心的主矩
本章小结 3、平面任意力系向一点简化的结果分析 (1)主矢不等于零,即 FR’ ≠ 0
主矩 合成结果
说明
MO = 0
合力 FR’
此力为原力系的合力,合力的 作用线通过简化中心。
这就是桁架结构广泛应用的主要原因 同时应注意:实际桁架和理想桁架是有差别 的,对重要的建筑物上采用的桁架结构,还需 考虑节点刚性、非节点荷载和节点偏心等造成 的影响。
第三章 平面任意力系和平面平行力系
三、平面简单桁架的内力计算 (三) 计算平面简单桁架杆件内力的方法
1、节点法—— 应用汇交力系平衡方程,逐一地选取平面简
