八年级数学勾股定理的逆定理1(1)
合集下载
人教版八年级下册 17.2 勾股定理的逆定理 课件 (共15张PPT)
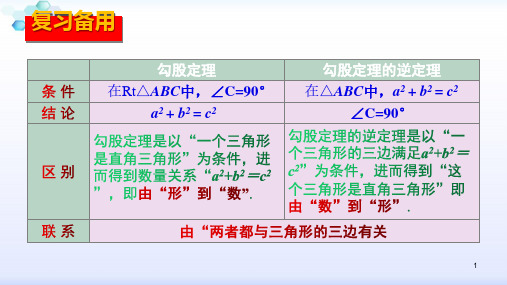
知识点一：勾股定理逆定理的实际应用
学以致用
1.我国南宋著名数学家秦九韶的著作《数书九章》里记载有
这样一道题目:“问有沙田块，有三斜，其中小斜五里，中斜
十二里，大斜十三里，欲知为田几何?”这道题讲的是:有一
块三角形沙田，三条边长分别为5里、12里13里，问这块沙
田面积有多大?题中的“里”是我国市制长度单位，1里＝
7
• 解:设AD=x,则CD=10-x.
• 在 RtABD 中，
•
DB2 AB2 AD2
在RtCDQ中，
DB2 CQ2 CD2
62 x2 82 (10 x)2
解得: x 3.6
AD长为6.4n mile
8
知识点二：勾股定理逆定理在几何中的应用
3.如图，在四边形ABCD中，AB=8，BC=6，AC=10，
①若∠C- ∠B= ∠A,则△ABC是直角三角形；
②若c2=b2-a2,则△ABC是直角三角形,且∠C=90°；
③若(c+a)(c-a)=b2,则△ABC是直角三角形;
④若∠A：∠B：∠C=5：2：3，则△ABC是直角三
角形.
以上命题中的假命题个数是（ A ）
A.1个
B.2个
C.3个
D.4个
4.已知a、b、c是△ABC三边的长，且满足关系式 c2 +a2 - b2 + c - a = 0 ，则△ABC的形状是
典例讲评
解:根据题意: PQ=16×1.5=24 PR=12×1.5=18 QR=30
∵242+182=302, 即 PQ2+PR2=QR2 ∴∠QPR=90°
由”远航“号沿东北方向航行可知,∠1=45°.所以∠2=45°,
人教版八年级下册数学 第17章《勾股定理》讲义 第6讲 勾股定理-逆定理(有答案)
人教版八年级下册数学第17章《勾股定理》讲义第6讲勾股定理－逆定理（有答案）第6讲 勾股定理－逆定理 第一部分 知识梳理知识点一：勾股定理的逆定理如果三角形三边长a ，b ，c 满足222a b c +=，那么这个三角形是直角三角形，其中c 为斜边 .①勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法，它通过“数转化为形”来确定三角形的可能形状，在运用这一定理时，可用两小边的平方和22a b +与较长边的平方2c 作比较，若它们相等时，以a ，b ，c 为三边的三角形是直角三角形；若222a b c +<，时，以a ，b ，c 为三边的三角形是钝角三角形；若222a b c +>，时，以a ，b ，c 为三边的三角形是锐角三角形；②定理中a ，b ，c 及222a b c +=只是一种表现形式，不可认为是唯一的，如若三角形三边长a ，b ，c 满足222a c b +=，那么以a ，b ，c 为三边的三角形是直角三角形，但是b 为斜边③勾股定理的逆定理在用问题描述时，不能说成：当斜边的平方等于两条直角边的平方和时，这个三角形是直角三角形知识点二：勾股数①能够构成直角三角形的三边长的三个正整数称为勾股数，即222a b c +=中，a ，b ，c 为正整数时，称a ，b ，c 为一组勾股数②记住常见的勾股数可以提高解题速度，如3,4,5；6,8,10；5,12,13；7,24,25等 ③用含字母的代数式表示n 组勾股数：221,2,1n n n -+（2,n ≥n 为正整数）；2221,22,221n n n n n ++++（n 为正整数）2222,2,m n mn m n -+（,m n >m ，n 为正整数）知识点三：勾股定理及其逆定理的应用勾股定理及其逆定理在解决一些实际问题或具体的几何问题中，是密不可分的一个整例4、已知:△ABC 的三边分别为m 2－n 2,2mn,m 2+n 2(m,n 为正整数,且m ＞n),判断△ABC 是否为直角三角形.例5、三边长为a ，b ，c 满足10a b +=，18ab =，8c =的三角形是什么形状？ 举一反三：1、以下列各组数为边长，能组成直角三角形的是（ ）A 、8，15，17B 、4，5，6C 、5，8，10D 、8，39，402、下列各组线段中的三个长度：①9、12、15；②7、24、25；③32、42、52；④3a、4a 、5a （a>0）；⑤m 2-n 2、2mn 、m 2+n 2（m 、n 为正整数，且m>n ）其中可以构成直角三角形的有（ ）A 、5组B 、4组C 、3组D 、2组3、现有两根木棒的长度分别为40厘米和50厘米，若要钉成一个直角三角形框架，那么所需木棒的长一定为（ ）A 、30厘米B 、40厘米C 、50厘米D 、以上都不对4、四边形ABCD 中，∠B=90°，AB=3，BC=4，CD=12，AD=13，求四边形ABCD 的面积。
八年级数学勾股定理的逆定理1(1)
合并心脏病临产产妇，在分娩期最好的体位是（）。A.平卧位B.仰卧位C.右侧卧位，上半身抬高D.左侧卧位，上半身抬高E.随意卧位 [多选]f列单位中，（）属于我国法定计量单位。A.小时(h)B.华氏度(℉)C.海里(nmile)D.公顷(hm2) [判断题]境外个人经常项目下非经营性结汇超过年度总额的，单笔等值5万美元以上的,应将结汇所得人民币资金直接划转至交易对方的境内人民币账户。A.正确B.错误 [单选]承诺人撤回承诺的通知()要约人。A.应当在承诺通知到达要约人之前或者与承诺通知同时到达B.可以后于承诺通知到达C.可以采取默示的方式送达D.可以后于承诺通知3日内到达 [填空题]曳引机采用刚性联轴器安装时同轴度应不大于（）mm。 [单选]“应收账款”科目所属明细科目如有贷方余额，应在资产负债表()项目中反映。A.预付款项B.预收款项C.应收账款D.应付账款 [单选,A1型题]属病因诊断的是（）.A.肺炎球菌性肺炎B.寒战、高热C.呼吸衰竭D.病变在右肺上叶E.肺实变 [单选]下列项目中，不属于会计核算的具体内容的是（）。A.有价证券的收付B.债权、债务的发生和结算C.资本的增减D.制定下年度管理费用开支计划 [单选]下列关于会计主体，说法不正确的是（）。A.会计主体是指会计信息所反映的特定单位B.会计主体也称为会计实体、会计个体C.会计主体不同于法律主体D.会计主体一定是法律主体 [单选,A2型题,A1/A2型题]多层螺旋CT与单层螺旋CT的主要区别是（）A.球管数目多B.计算机多C.探测器排数多D.准直器多E.滤线栅多 [单选]对（）的管理可以称为使需求与供给相适应的平衡性营销管理。A.不规则需求B.充足需求C.过度需求D.不健康需求 [单选]在航道整治工程中采用土工织物软体排：主要是利用了土工织物的（）作用。A.排水B.防水C.防护D.防渗 [单选]目前承担消防产品合格评定的评价机构是（）。A、公安部消防局B、各省、直辖市、自治区公安消防总队C、国家消防产品质量监督检验中心D、公安部消防产品合格评定中心 [配伍题,B1型题]一个昏迷病人被送到医院，医生对他进行处理，这种医患关系属于（）。</br>医生劝病人“你应该参加一些晨间锻炼”，这种医患关系属于（）。A.主动-被动型B.指导-合作型C.共同参与型D.强制-被动型E.指导-参与型 [单选,A2型题,A1/A2型题]最常用、最有效的热力灭菌法是（）A.煮沸法B.巴氏消毒法C.流通蒸汽灭菌法D.高压蒸汽灭菌法E.间歇灭菌法 [单选,A2型题,A1/A2型题]床单位进行紫外线灯照射消毒时，灯管应位于（）A.床旁2m处B.床面上2m处C.床旁1m处D.床面上1m处E.在房间内吸顶安装 [单选,A2型题,A1/A2型题]急性一氧化碳中毒者，从血液中HbCO含量测定来看，中度中毒应达到（）.A.20%～30%B.30%～40%C.50%～60%D.70%～80%E.80%～90% [多选]关于仲裁协议的效力，下列哪些选项是错误的？（）A.当事人对仲裁协议效力有争议的，既可以向法院申请认定，也可以向仲裁委员会申请认定B.作为合同内容的仲裁条款，在合同无效时，其效力不受影响C.仲裁裁决被法院撤销后，当事人可以依原仲裁协议重新申请仲裁D.仲裁裁决被法院 [单选]VCO电路中，通过改变回路电抗元件参数改变频率，此可变器件为（）。A.电感B.电容C.变容二极管 [单选]下列疾病与水痘为同一病因的是（）A.Kaposi水痘样疹B.传染性软疣C.手足口病D.带状疱疹E.花斑癣 [单选]某公司开发了一套教育软件，但刚一问世就出现了大量的盗版软件。在尚未进行软件著作权登记的情况下，该公司欲向盗版者追究法律责任。以下说法正确的是（）。A.未经登记的软件，不享有著作权B.未经登记的软件发生纠纷，法院不予受理C.只要符合起诉条件，法院应该受理该软件纠 [填空题]IT是InformationTechnology的简称，IIS是InternetInformationServer的简称，WWW是WorldWideWeb的简称，FTP是（）的简称。 [单选]某施工项目，工程合同价300万元，建设工期6个月。则开工前，建设单位到位资金不得少于（）万元。A．90B．100C．150D．300 [单选]变电所中的降压变压器，其高压侧的额定电压（）电网额定电压。A.高10%B.高5%C.相等 [单选,A1型题]紫绀可见于（）A.急性喉炎B.重症肌无力C.气胸D.先天性心脏病（右向左分流型）E.以上都是 [单选]下列路段中，不宜在雨期进行路基施工的是()。A．碎砾石路段B．路堑弃方路段C．膨胀土路段D．丘陵区砂类土路段 [填空题]氨是一种（）气体，有强烈的（）气味，沸点为（），自燃点（），与空气混合物爆炸极限（）。 [单选,共用题干题]患者女，60岁，典型心房扑动史3年，发作频繁，症状明显。该患首选的治疗是（）A.三尖瓣环峡部导管消融B.胺碘酮C.普罗帕酮D.索他洛尔E.房室结改良 [单选,A1型题]《医疗事故处理条例》规定，在诊疗护理工作中，属于医疗事故的是（）A.虽有诊疗护理错误，但未造成病员死亡、残疾、功能障碍B.因诊疗护理过失，直接造成病员死亡、残疾、组织器官损伤导致功能障碍C.由于病情和病员体质特殊而发生难以预料和防范的不良后果D.发生难以 [名词解释]市场营销者 [单选]对烧伤创面的处理，下列说法中哪个不正确（）A.宜先行烧伤创面简单清创B.肢体小面积Ⅱ度烧伤者，宜用包扎治疗C.创面清洁，局部外用抗生素，以防止细菌感染D.头部、颈部创面宜用暴露法E.全身多处烧伤可用包扎和暴露相结合的方法 [名词解释]乡村家庭和城市家庭功能的异同 [单选]丙烯塔回流泵全坏，操作调整中最应该注意（）。A、塔顶压力B、塔底液面C、回流罐液面D、塔底温度 [单选]对误服强酸所引起的急性腐蚀性胃炎，下列治疗哪项是错误的（）A.镁乳B.碳酸氢钠C.氢氧化铝凝胶D.牛奶E.蛋清 [单选]最易并发咯血的疾病是（）A.支气管扩张B.支气管内异物C.良性支气管瘤D.慢性支气管炎E.支气管哮喘 [单选]认为组织和组织成员的行为是复杂的、不断变化的，是一种固有的性质的观点所属的学派是（）。A.系统理论管理B.行为科学管理C.权变理论管理D.管理科学E.管理质量 [单选]3岁患儿在1小时前误吸浓盐酸少许，查体，意识清，上腹部压痛明显，唇及口腔有灼伤，心肺（-）应选用（）洗胃液。A.碳酸氢钠B.食醋C.液体石蜡D.果汁E.氢氧化铝凝胶 [单选]（）不是计算盘点差错率的指标。A.盘点品项误差率B.盘差损失率C.平均每件盘差品金额D.盘差次数比率 [单选]测深辨位时，测深仪所测得的水深应换算成相应的海图水深，其换算方法为（）。A．海图水深＝测深值＋吃水-潮高B．海图水深＝测深值＋吃水＋潮高C．海图水深＝测深值-吃水＋潮高D．海图水深＝测深值-吃水-潮高 [单选]不属于仓库的主要作业的是货品的（）A.入库作业B.在库管理C.包装作业D.出库作业
18.2(1)勾股定理逆定理(1)
C 准备好了吗? B D A
S四边形ABCD=36
练一练
1、已知 △ABC三角形的三边 分别为 a,b,c 且a = m - n ,b = 2mn, = m n c
2 2 2 2
(m > n,m,n是正整数)， △ABC是直角三角形 吗?说明理由
分析：先来判断a,b,c三边哪条最长， 可以代m,n为满足条件的特殊值来试， m=5,n=4.则a=9,b=40,c=41,c最大。 解： a b (m n ) (2mn) (m n ) c
问: (1) 上述解题过程,从哪一步开始出现错误?请写出该 步的代号＿＿＿ 3 a2- b2可能是0 (2) 错误原因是＿＿＿＿＿＿＿＿＿
直角三角形或等腰三角形 (3) 本题正确的结论是＿＿＿＿＿＿＿＿
当堂检测
必做题：习题18.2 第2题（1）（2）（3）（4） 第1题（3）（4） 第5题（自己据题目画出图形） 选做题： 第4题（写出推理过程） 拓展题： 第6题（判断并写出证明过程）
（逆定理） 勾股定理的逆命题
如果三角形的三边长a、b、c满足
2 a
+
2 b
=
2 c
那么这个三角形是直角三角形。
勾股定理
（互逆定理） 互逆命题
如果直角三角形两直角边分别为a，b， 斜边为c，那么 a2 + b2 = c2
中考链接
已知：如图，四边形ABCD 中，∠B＝900，AB＝3，BC＝4， CD ＝ 12 ， AD ＝ 13, 求 四 边 形 ABCD的面积?
B
a
C
B'
a
C'
∵ ∠ C’=900 ∴ A’B’2= a2+b2
∵ a2+b2=c2
S四边形ABCD=36
练一练
1、已知 △ABC三角形的三边 分别为 a,b,c 且a = m - n ,b = 2mn, = m n c
2 2 2 2
(m > n,m,n是正整数)， △ABC是直角三角形 吗?说明理由
分析：先来判断a,b,c三边哪条最长， 可以代m,n为满足条件的特殊值来试， m=5,n=4.则a=9,b=40,c=41,c最大。 解： a b (m n ) (2mn) (m n ) c
问: (1) 上述解题过程,从哪一步开始出现错误?请写出该 步的代号＿＿＿ 3 a2- b2可能是0 (2) 错误原因是＿＿＿＿＿＿＿＿＿
直角三角形或等腰三角形 (3) 本题正确的结论是＿＿＿＿＿＿＿＿
当堂检测
必做题：习题18.2 第2题（1）（2）（3）（4） 第1题（3）（4） 第5题（自己据题目画出图形） 选做题： 第4题（写出推理过程） 拓展题： 第6题（判断并写出证明过程）
（逆定理） 勾股定理的逆命题
如果三角形的三边长a、b、c满足
2 a
+
2 b
=
2 c
那么这个三角形是直角三角形。
勾股定理
（互逆定理） 互逆命题
如果直角三角形两直角边分别为a，b， 斜边为c，那么 a2 + b2 = c2
中考链接
已知：如图，四边形ABCD 中，∠B＝900，AB＝3，BC＝4， CD ＝ 12 ， AD ＝ 13, 求 四 边 形 ABCD的面积?
B
a
C
B'
a
C'
∵ ∠ C’=900 ∴ A’B’2= a2+b2
∵ a2+b2=c2
勾股定理的逆定理12勾股定理的逆定理1
1.“如果同旁内角互补，那么两条直线平行”的题设是
_____, 结论是 ，逆命题是_______.
2.“对顶角相等”的的题设是 结论是
，逆命题
是_______.
3. 已知：在△ABC中，∠A、∠B、∠C的对边分别是a、b、
c，分别为下列长度，判断该三角形是否是直角三角形？
（1）a=6，b=8，c=10； （2）a=5，b=12，c=13；
平方之间的大小关系. 你能发现什么规律？
量一量的结论 （1）：3、4、5 ； 直角 三角形 （2）：3、6、8； 钝角 三角形
（3）：6、8、10 ；直角 三角形
算一算的结论 大小关系：32 ? 42 __＝__ 52
_______3_2 _?_1_0_2 ___
探究一：动手实践.
（一）、画一画．画出边长分别是下列各组数的三角形（单位：厘米）.
（1）：3、4、5 ；（2）：3、6、8；（3）：6、8、10
（二）、量一量.用你的量角器分别测量一下小组内同学画出的三个三角形的
最大角的度数，并判断上述你们所画的三角形的形状：（按角分类）
（三）、算一算．请比较上述每个三角形的两条较短边的平方和与最长边的
第5题图
学习体会
1.本节课你又那些收获？ 2.预习时的疑难问题解决了吗？你还有那些疑惑？ 3.你认为本节还有哪些需要注意的地方？
当堂达标
（3）a=5，b=7，c=9； （4）a=8，b=15，c=17；
尝试应用
4.说出下列命题的逆命题．这些命题的逆命题成立吗? (1)两条直线平行，内错角相等． (2)如果两个实数相等，那么它们的平方相等． (3)如果两个实数相等，那么它们的绝对值相等． (4)全等三角形的对应角相等． 5.如图所示△ABC三边a,b,c为边向外作正方形， 若S1+S2=S3成立，则△ABC是什么三角形？为什么？
八年级数学勾股定理的逆定理1
原命题：猫有4只脚 逆命题：有4只脚的是猫
（正确）
（不正确）
（正确）
原命题：等边三角形的三边相等。
（不正确） 逆命题：三边相等的三角形是等边三角形。 （1）任何一个命题都有逆命题； （2）原命题正确，逆命题不一定正确；原命题不正 确，逆命题可能正确。 （3）原命题与逆命题的关系是题设和结论相互转换
写出下列命题的逆命题并判断它们是否成立:
（1）等腰三角形的两底角相等
原命题：如果一个三角形是等腰三角形，那么这个 三角形的两底角相等。
逆命题：如果一个三角形的两底角相等，那么这个 三角形是等腰三角形。
勾股定理: 若直角三角形的两直角边为a ,b , 斜边为 c ,则有
a2+ b2=c2。
逆定理:
2 2
B
)
A、锐角三角形 C、钝角三角形
B、直角三角形 D、等边三角形
已知a，b，c为△ABC的三边,且满 足 a2+b2+c2+338=10a+24b+26c. 试判断△ABC的形状.
训练：
1.如图，两个正方形的面积分别为64，49， 则AC=( ) 17 A
D 64 49
C
2.由四根木棒，长度分别为3，4，5，12， 13 若取其中三根木棒组呈三角形，有( ) 4 种取法，其中，能构成直角三角形的是 （ ）种取法。 2
2. 将直角三角形的三边的长度扩大同样的倍数, 则得到的三角形是 ( A )
A. 是直角三角形;
B. 可能是锐角三角形;
C. 可能是钝角三角形; D. 不可能是直角三角形.
中考链接
已知：如图，四边形 ABCD 中，∠B＝900，AB＝3，BC＝4， CD ＝ 12 ， AD ＝ 13, 求 四 边 形 ABCD的面积?