六方最密堆积的计算
最紧密堆积模型堆积密度
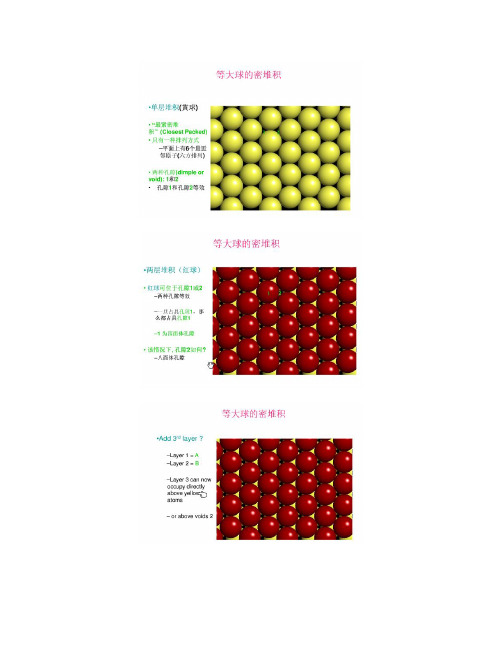
六方紧密堆积等大球体密置层堆积的两种基本型式之一。
其圆球的配位数为12,空间利用率为74.05%,晶胞内原子数为2,密置层按两层重复,即ABABAB……的方式重复堆积,其第三层的球心投影位置与第一层的重复,第四层与第二层重复,其余依此类推。
由于在这种堆积中可以划分出六方原始格子,故称为六方最密堆积。
其密置层平行于{0001}。
镁、锇、锌等的晶体结构即属此种堆积,故又称为镁型。
六方(最密)堆积空间利用率的证明晶胞参数a=b ,c=2/3 倍√6 倍a,α =β=90度γ=120度即一四棱柱,底面是以a为边长,一内角120度的菱形,高是c。
空间利用率74.05%,和立方面心最密的利用率一样。
证明 1 每个晶胞里有2个球,边长0.5a2 c是以a为边长的证四面体的高的2倍由此得出空间利用率74.05%实验5 14种布拉维格子和球体紧密堆积一、一、实验目的:加深对14种布拉维格子和球体紧密堆积原理的理解。
二、基本原理1. 布拉维格子只在单位平行六面体的八个角顶上分布有结点的空间格子,称为原始格子(Primitive lattice,符号P),在单位平行六面体的体中心还有一个结点时,则构成体心格子(Body-centered lattice,符号I)。
如果在某一对面的中心各有一个结点时,称为单面心格子(One-face-centered lattice),(001)面上有心的格子为底心格子或称C心格子(End-centered lattice, Base-centeredlattice or C-centered lattice,符号C),当(100)面或(010)面上有心时,分别称为A心格子(A-centered lattice,符号A)和B心格子(B-centered lattice,符号B)。
如果在所有三对面的中心都有结点时,称为面心格子或全面心格子(Face-centered lattice or All-face-centered lattice,符号F)。
六方最密堆积
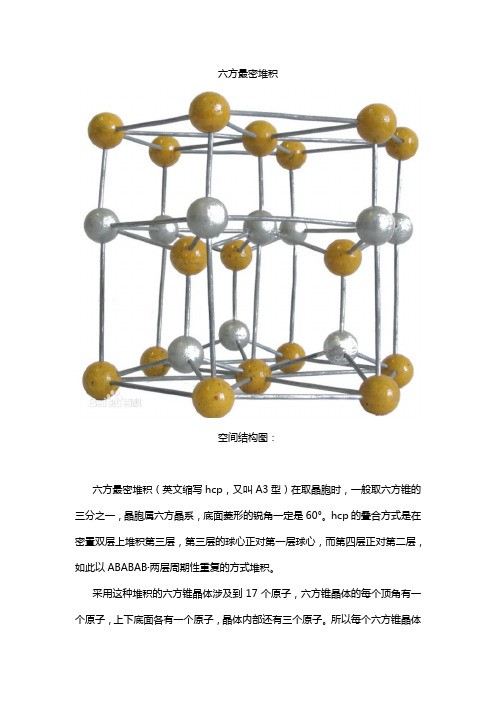
六方最密堆积
空间结构图:
六方最密堆积(英文缩写hcp,又叫A3型)在取晶胞时,一般取六方锥的三分之一,晶胞属六方晶系,底面菱形的锐角一定是60°。
hcp的叠合方式是在密置双层上堆积第三层,第三层的球心正对第一层球心,而第四层正对第二层,如此以ABABAB·两层周期性重复的方式堆积。
采用这种堆积的六方锥晶体涉及到17个原子,六方锥晶体的每个顶角有一个原子,上下底面各有一个原子,晶体内部还有三个原子。
所以每个六方锥晶体
内原子个数为:12*1/6+2*1/2+3=6,则晶胞的原子个数为六方锥晶体内原子个数的1/3,故晶胞的原子个数为6*1/3=2。
许多单质,尤其是金属单质为了获得较强的作用力,常采用最密堆积。
采用六方最密堆积的单质有:
铍、镁
钛、钴、锌、锆、锝、钌、镉、铪、铼、锇
钪、钇、镧、镨、钕、钷、钆、铽、镝、钬、铒、铥。
金属晶体四类晶胞空间利用率的计算知识讲解

金属晶体四类晶胞空间利用率的计算金属晶体四类晶胞空间利用率的计算高二化学·唐金圣在新课标人教版化学选修3《金属晶体》一节中,给出了金属晶体四种堆积方式的晶胞空间利用率。
空间利用率就是晶胞上占有的金属原子的体积与晶胞体积之比。
下面就金属晶体的四种堆积方式计算晶胞的空间利用率。
一、简单立方堆积:在简单立方堆积的晶胞中,晶胞边长a等于金属原子半径r的2倍,晶胞的体积V晶胞=(2r)3。
晶胞上占有1个金属原子,金属原子的体积V原子=4πr3/3 ,所以空间利用率V原子/V晶胞 = 4πr3/ (3×(2r)3)=52.33﹪。
二、体心立方堆积:在体心立方堆积的晶胞中,体对角线上的三个原子相切,体对角线长度等于原子半径的4倍。
假定晶胞边长为a ,则a2 + 2a2 = (4r)2, a=4 r/√3 ,晶胞体积V晶胞 =64r3/ 3√3 。
体心堆积的晶胞上占有的原子个数为2,原子占有的体积为V原子=2×(4πr3/3)。
晶胞的空间利用率等于V原子/V晶胞 =(2×4πr3×3√3)/(3×64r3)= 67.98﹪。
三、面心立方最密堆积在面心立方最密堆积的晶胞中,面对角线长度是原子半径的4倍。
假定晶胞边长为a,则a2 + a2 = (4r)2 ,a = 2√2r ,晶胞体积V晶胞=16√2r3。
面心立方堆积的晶胞上占有的原子数为4,原子占有的体积为V原子 = 4×(4πr3/3)。
晶胞的空间利用率等于V原子/V晶胞 =(4×4πr3)/(3×16√2r3)= 74.02﹪.四、六方最密堆积六方最密堆积的晶胞不再是立方结构。
晶胞上、下两个底面为紧密堆积的四个原子中心连成的菱形,边长a = 2r ,夹角分别为60°、120°,底面积s = 2r×2r×sin(60°) 。
金属晶体四类晶胞空间利用率的计算

金属晶体四类晶胞空间利用率的计算高二化学•唐金圣在新课标人教版化学选修 3《金属晶体》一节中,给出了金属晶体四种堆积方式的晶胞空间利用率。
空间利用率就是晶胞上占有的金属原子的体积与晶胞体积之比。
晶体的四种堆积方式计算晶胞的空间利用率。
一、简单立方堆积:在简单立方堆积的晶胞中,晶胞边长 a 等于金属原子半径r 的2倍,晶胞的体积 V 晶胞=(2r)3。
晶胞上占有1个金属原子,金属原子的体积 V 原子=4 n 「3/3 ,所以空间利用率 V 原3 3子/V 晶胞=4 n r / (3X (2r) ) =52.33 % 。
二、体心立方堆积:在体心立方堆积的晶胞中,体对角线上的三个原子相切,体对角线长度等于原子半径的4倍。
假定晶胞边长为a ,则a 2 + 2a 2 = (4r)2, a=4 r/ V 3 ,晶胞体积V 晶胞=64r 3/ 3V 3。
体心堆积的晶胞上占有的原子个数为 2,原子占有的体积为 V 原子=2 X( 4 n r 3/3 )。
晶胞 =(2X 4n r 3x 3V 3) / (3X 64r 3 ) = 67.98% 。
三、面心立方最密堆积在面心立方最密堆积的晶胞中,面对角线长度是原子半径的 则a 2 + a 2 = (4r)2 ,a = 2V 2r ,晶胞体积V 晶胞= 16V 2^。
面心立方堆积的晶胞上占有的原子数为4,原子占有的体积为 V 原子=4 X( 4 n r 3/3 )。
晶胞的空间利用率等于 V 原子N 晶胞= 的空间利用率等于 V 原子N 晶胞 4倍。
假定晶胞边长为a,(4X 4 n r3) /(3 X 16V2r3)= 74.02 % .四、六方最密堆积六方最密堆积的晶胞不再是立方结构。
晶胞上、下两个底面为紧密堆积的四个原子中心连成的菱形,边长a = 2r ,夹角分别为60° 120°,底面积s = 2r x 2r x sin( 60° )。
《六方最密堆积》课件

纳米技术
纳米技术是一种新兴的技术领域,它 涉及到纳米尺度上的材料、器件和系 统等,六方最密堆积在纳米技术中也 有着重要的应用。例如,在制造纳米 材料和纳米器件时,六方最密堆积可 以提高材料的结晶度和纯度,从而获 得更好的性能和稳定性。
稳定性
六方最密堆积的稳定性高于简单 立方堆积,因为它能更好地抵抗
外界压力和温度变化。
应用领域
简单立方堆积在某些塑料和合金 中有所应用,而六方最密堆积在 需要高强度和稳定性的材料中更
为常见。
与体心立方堆积的比较
原子排列
体心立方堆积的原子排列 较为紧密,但层间排列不 如六方最密堆积紧凑。
稳定性
六方最密堆积的稳定性略 高于体心立方堆积,因为 它具有更好的对称性和适 应性。
边形填充周围空间。
模型特点
该模型具有高度的对称性和规则性 ,展现出优美的几何形态。
模型应用
六方最密堆积的几何模型在材料科 学、晶体结构等领域有广泛应用。
空间填充方式
01
02
03
空间填充原理
六方最密堆积的空间填充 方式基于几何学原理,通 过合理排列大、小六边形 ,实现空间的高效利用。
填充规则
大六边形占据中心位置, 小六边形围绕大六边形紧 密排列,形成有序的结构 。
03
与其他堆积方式相比,六方最密堆积的空间利用率更高,这使
得它在材料科学等领域具有重要的应用价值。
03
六方最密堆积的应用
晶体结构
晶体结构是物质的基本排列方式,六方最密堆积在晶体结构 中有着广泛的应用。例如,在金属材料中,六方最密堆积是 一种常见的晶体结构,它可以提高材料的硬度和强度,从而 提高金属制品的耐磨性和耐腐蚀性。
常见晶体模型及晶胞计算
找铜型的晶胞
面心立方最密堆积的空间占有率 =74%
金属晶体的四种堆积模型对比
原子晶体
金刚石
该晶胞实际分摊到的碳原子数为 (4 + 6 ×1/2 + 8 ×1/8) = 8个。
小结:高考常见题型 (一) 晶胞中微粒个数的计算, 求化学式
(二) 确定配位数
(三) 晶体的密度及微粒间距离 的计算
(1)长方体(立方体):
N=N顶角×1/8 + N棱上×1/4 + N面上×1/2 + N体内
(2)非长方体(非立方体):
视具体情况分析。
分子晶体 干冰晶体结构 ——晶胞为面心立方体
8个CO2分子位于立方体顶点 6个CO2分子位于立方体面心 在每个CO2周围等距离且相距最近 的CO2共有 12 个。 在每个小立方体中平均分摊到的CO2 分子数为:(8×1/8 + 6×1/2) = 4 个
(2)晶胞的边长为acm,求NaCl晶 体的密度。
ρ=
M / NA×晶胞所含粒子数 晶胞的体积
=
58.5 / NA×4 a3
(3)若NaCl晶体的密度为ρg/cm3,则 NaCl晶体中Na+与 Na+间的最短距离是多少?
CsCl的晶体结构——晶胞为体心立方体
(1)每个Cs+( Cl-)周围等距
且紧邻的Cl- (Cs+)有 8 个, Cs+( Cl-)的配位数为 8 。
常见晶体模型及晶胞计算
晶胞 描述晶体结构的基本单元
晶胞一般是平行六面体,整块晶体可看作是数量巨大的 晶胞“无隙并置”而成。
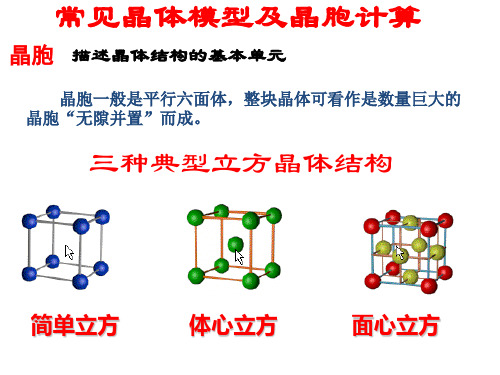
三种典型立方晶体结构
简单立方
体心立方
面心立方
晶胞中微粒的计算方法——均摊法
六方最密堆积中正八面体空隙和正四面体空隙
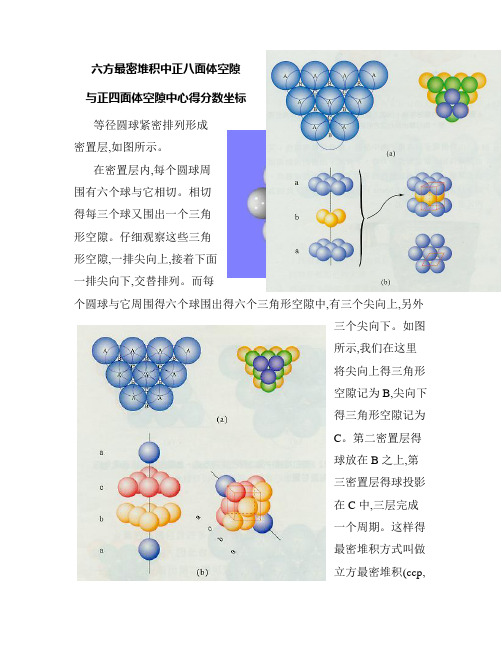
六方最密堆积中正八面体空隙与正四面体空隙中心得分数坐标等径圆球紧密排列形成密置层,如图所示。
在密置层内,每个圆球周围有六个球与它相切。
相切得每三个球又围出一个三角形空隙。
仔细观察这些三角形空隙,一排尖向上,接着下面一排尖向下,交替排列。
而每个圆球与它周围得六个球围出得六个三角形空隙中,有三个尖向上,另外三个尖向下。
如图所示,我们在这里将尖向上得三角形空隙记为B,尖向下得三角形空隙记为C。
第二密置层得球放在B之上,第三密置层得球投影在C中,三层完成一个周期。
这样得最密堆积方式叫做立方最密堆积(ccp,记为A1型),形成面心立方晶胞。
若第三密置层得球投影与第一密置层得球重合,两层完成一个周期。
这样得最密堆积方式叫做六方最密堆积(hcp,记为A3型),形成六方晶胞,如图所示。
在这两种堆积方式中,任何四个相切得球围成一个正四面体空隙;另外,相切得三个球如果与另一密置层相切得三个球空隙对应,它们六个球将围成一个正八面体空隙。
也就就是说,围成正八面体空隙得这六个球可以分为相邻得两层,每层得正三角形中心得连线垂直于正三角形所在得密置层,参瞧下图,黑色代表得不就是球而就是正八面体得中心。
在这两种最密堆积方式中,每个球与同一密置层得六个球相切,同时与上一层得三个球与下一层得三个球相切,即每个球与周围十二个球相切(配位数为12)。
中心这个球与周围得球围出八个正四面体空隙,平均分摊到每个正四面体空隙得就是八分之一个球。
这样,每个正四面体空隙分摊到得球数就是四个八分之一,即半个。
中心这个球周围还围出六个八面体空隙,它平均分摊到每个正八面体空隙得就是六分之一个球。
这样,每个正八面体空隙分摊到得球数就是六个六分之一,即一个。
总之,这两种最密堆积中,球数: 正八面体空隙数: 正四面体空隙数= 1:1:2 。
面心立方最密堆积(ccp, A1型)中正八面体空隙与正四面体空隙得问题比较简单、直观。
下面我们集中讨论六方最密堆积(hcp,A3型)中正八面体空隙与正四面体空隙中心得分数坐标。
金属晶体堆积模型及计算公式

面心立方 最密堆积
面心立方
74%
12
Cu、Ag、Au
金属晶体的两种最密堆积方式──镁型和铜型
镁型
铜型
镁型
12
6
3
54
铜型
12
6
3
54
12
6
3
54
12
6
3
54
12
6
3
54
12
6
3
54
下图是镁型紧密堆积的前视图
A
12
6
3
B
54
A
B A
第下四图层是再排铜A型,于型是紧形密堆积的前视图
A
成 ABC ABC 三层一个周 期。 得到面心立方堆积。
AC
CB
12
(1).简单立方堆积:
非最紧密堆积,每个晶胞含 1 个原子, 配位数是 6 个.
只有金属(Po)采取这种堆积方式
空间利用率的计算
(1)简单立方:在立方体顶点的微 粒为8个晶胞共享,
微粒数为:8×1/8 = 1
空间利用率: 4лr3/3 (2r)3
= 52.36%
(2)钾型 ----体心立方堆积:
V球=243π r3 (晶胞中有2个球)
V球 V晶胞100%=74.05%
铜型(面心立方紧密堆积)
7 1 9
6
5
8 2
3 4
12 10 11
这种堆积晶胞属于最密置层堆集,配位数
为 12 ,许多金属(如Cu、Ag、Au等)采取这
种堆积方式。
铜型
12
6
3
54
C
B
A
A
B
C
A
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
六方最密堆积的计算
???????????????????????????????????????????????????????
六方最密堆积空间利用率和密度的计算,需要弄清堆积方式、
晶胞切割方法、晶胞体积、晶胞中的原子数、原子的体积。
? 堆积方式为 ABAB-----(六方最密堆积)
一定要区别于ABCABC---(面心最密堆积)
??? 而学生感到困难的是六方最密堆积的晶胞体积,因为它
的晶胞是平行六面体,其余的金属晶体晶胞是正六面体!
六方最密堆积计算的关键------晶胞体积
至此,你再求晶体空间利用率和晶体密度,障碍是不是消
失了?
