第三章 弹性杆件横截面上的正应力分析
梁的正应力

D
d
FA
3q 4
kN
q
FB
梁的强度
FB
9q 4
kN
A
B
C
Mmax 0.5q
FA
2m
1m
WZ WZ
1q
q WZ 15.68kN / m
2
0.5
杆的强度
9q
9q 32
FNBD
A
4
1 d 2
4
q 1 d 2 22.3kN / m
16103 96.4 151.1.022MP1a08
B
M Byy IZ
12103 250
18.07MPa
96.4
1.02
例题 4.26 为了起吊重量为F=300kN的大型设备,采用一台150kN和一台
200kN的吊车,以及一根工字形轧制型钢作为辅助梁,组成临时的
附加悬挂系统,如图示。如果已知辅助梁的长度l=4m,型钢材料的
平面假设:
变形前杆件的横截面变形后仍
为平面。
中性层
中性轴:
中性层与横截面的交线称 为中性轴。
mn
o1
o2
m
n
中性轴
F
mn
mn
M
M
中性轴
z
m
n
y
o
o
dA
mn
dx
z
d
y
dx
y
F
yd d y
d
E y E
E
FN
dA
A
横截面上切应力分布规律

F Fsmax 2
F
max
3 2
Fs A
32 2 bh
3 F 4 bh
h
Mmax
FL 4
FL
b
max
M max WZ
4 1 bh
2
6
max max
d z
t
b
工字形截面梁由腹板和翼缘组成(中间的矩形部分称 为腹板;上下两矩形称为翼缘)。翼缘和腹板上均存在 着竖向切应力,而翼缘上还存在着与翼缘长边平行的 水平切应力。 经理论分析和计算表明:横截面上剪力的(95~97) %由腹板分担,而翼缘仅承担了剪力的(3~5)%, 并且翼缘上的切应力情况又比较复杂。为了满足实际 工程计算和设计的需要,仅分析腹板上的切应力。
Iz1 Iz a2A
例1 长为l的矩形截面悬臂梁,在自由端作用一集中力F,已知
b=120mm,h=180mm、l=2m,F=1.6kN,试求B截面上a、b
、c各点的正应力。
A
F
h6
a
B
z
C
b
h
l2
l2
h2
FL
c
b
a
M B ya IZ
1 FL h
2 bh
3
3
1.65MP(a拉 )
b 0
简易的矩形竹结构桥
钢管混凝土拱桥中的混凝土小横梁
建筑阳台挑梁受力分析与破坏问题
1.挑梁属于悬臂结构。 2.挑梁工作环境:常常处于室外,面对雨水、二氧化碳等的 直接侵蚀,荷载存在不确定性。 3. 破坏形式:出现裂缝后极有可能进一步扩大,严重的将危 及建筑物的安全。
建筑阳台挑梁受力分析与破坏问题
横截面上的应力

泊松比ν----在弹性变形范围内,横向线应 变与纵向线应变之间保持一定的比例关系,以
ν代表它们的比值之绝对值。
而横向线应变与纵向线应变正负号恒相反,故
例题6−4 图示一等直钢杆,材料的弹性模量E= 210GPa。试计算:(1) 每段的伸长;(2) 每段的 线应变;(3) 全杆总伸长。
p cos cos2
1
τα
pα
sin α
σ sin 2α 2
斜截面上的正应力和切应力分别为:
cos2
分析:
1
2
sin 2
正应力的最大值发生在α = 0的截面,即横截面上,其值为
σα0 σmax σ
当 α π 时对应的斜截面上,切应力取得最大值
解:(1)取节点A为脱离体,受力如图
Fy 0 Fx 0
FNAC
5 65 3
108.33kN
4
FNAB
65 3
86.67kN
B
(2)AB杆的横截面面积为AAB=300 3m mm2,AC杆为10号槽钢,由型钢 表(附表II,表3)查出横截面面积 为AAC =12.7cm2 =12.7×10-4m2。
§6−4 斜截面上的应力
研究目的:找出过一点哪一截面上应力达到最大 以作为强度计算的依据。
n-n截面的轴线方向的内力 F
nm
F
F F
F
斜截面面积
Aα
A cosα
F
斜截面上的应力pα为:
m
n
n α
Fα
n
n
σα
α
5.3拉压杆应力
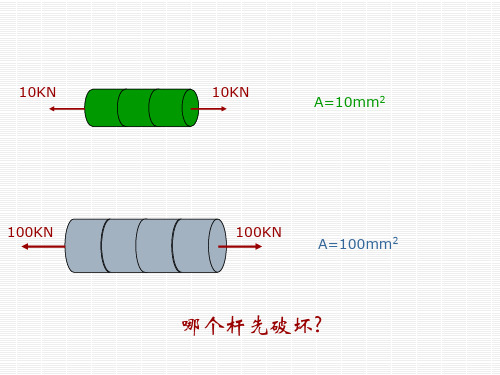
A=10mm 2A=100mm 210KN 10KN100KN 100KN哪个杆先破坏?§3应力.拉(压)杆内的应力应力的概念受力杆件某截面上一点的内力分布疏密程度,内力集度.F 1F nF 3F 2应力就是单位面积上的力?(工程构件,大多数情形下,内力并非均匀分布,集度的定义不仅准确而且重要,因为“破坏”或“失效”往往从内力集度最大处开始。
)F 1F 2ΔAD FΔF QyΔF QzΔF NdAdF A F NN A =D D =→D 0lim σdAdF A F QQ A =D D =→D 0lim τ垂直于截面的应力称为“正应力”位于截面内的应力称为“切应力”应力的国际单位为N/m 2 (帕斯卡)1N/m 2=1Pa1MPa=106Pa =1N/mm 21GPa=109PadAdF AF p A =D D =→D 0lim拉(压)杆横截面上的应力AdA dA F AAN σσσ===⎰⎰AF N=σ几何变形平面假设静力平衡dAdF A F NN A =D D =→D 0lim σdA dF N σ=横截面上各点只产生沿垂直于横截面方向的变形横截面上只有正应力两横截面之间的纵向纤维伸长都相等杆件的横截面在变形后仍保持为平面,且垂直于杆的轴线横截面上的正应力均匀分布σ——正应力F N ——轴力A ——横截面面积σ的符号与F N 轴力符号相同AF N=σ试计算图示杆件1-1、2-2、和3-3截面上的正应力.已知横截面面积A=2×103mm 220KN20KN40KN 40KN332211例题2.520kN40kNMPa1011-=-σ022=-σMPa2033=-σ图示支架,AB 杆为圆截面杆,d=30mm ,BC 杆为正方形截面杆,其边长a=60mm ,F=10KN ,试求AB 杆和BC 杆横截面上的正应力。
例题2.6F NABF NBCMPa A F ABNAB AB3.28==σMPa A F BCNBC BC8.4-==σFF NAB =030sin NBCNAB F F -=030cos CdAB Fa30试求图示结构AB 杆横截面上的正应力。
材料力学 杆件横截面上的应力2

y1
y y2
O 40 y1
zO z
M C y1 = 22MPa σ = Iz M y + σ B = B 2 = 40.50MPa Iz M C y2 − = −60.74MPa σC = − Iz M B y1 − σB = − = −14.67 MPa Iz
+ C
至此,该问题中最大拉应力位于B截面的上 至此,该问题中最大拉应力位于B 边缘,而最大压应力位于C 边缘,而最大压应力位于C截面的上边缘
2、梁横力弯曲矩形截面梁的切应力 2.1 矩形截面梁的切应力公式推导
b
儒拉夫斯基假设
h
1)截面上任意一点的切应力 τ 的方向 和该截面上的剪力F 的方向平行。 和该截面上的剪力FQ的方向平行。
z
2)切应力沿宽度均匀分布,即τ 的大小 切应力沿宽度均匀分布, 只与距离中性轴的距离有关。 只与距离中性轴的距离有关。
⑴ 截面关于中性轴对称
z
Mymax IZ σmax = WZ = IZ ymax M t c σ max = σ max = Wz
Wz ——截面的抗弯截面系数
t
⑵ 截面关于中性轴不对称
σ max
z
t
My max = Iz
σ max
c
My max = Iz
c
几种常见截面的 IZ 和 WZ
IZ WZ = ymax
* Sz = ∫ y1dA A 1
距中性轴为 y 处的横线以外部分横截面 对中性轴的静矩 静矩。 积A1对中性轴的静矩。
z y y1 x d
( M + dM ) * FN2 = Sz Iz
同理可得
y
M * FN1 = Sz Iz
材料力学——精选推荐

轴向拉压杆横截面上的应力:正应力:σ=N/A;应力单位N/m2,即Pa。
轴向拉压杆斜截面上的应力:总应力:pα=N/Aα=σcosα;正应力:σα=σcos2α;剪应力:τα= =(σsin2α)/2。
α:由横截面外法线转至斜截面外法线的转角,以逆时针转动为正;Aα:斜截面的面积;σα:拉应力为正,压应力为负;τα:以其对脱离体内一点产生顺时针转动为正,反之为负。
最大剪应力发生在α=±45°处的斜截面上。
轴向拉伸的变形:轴向变形△L=L’-L;ε=△L /L;横向变形:△a=a’-a;ε’=△a/a;虎克定律:应力不超过材料比例极限时,应力与应变成正比。
即:σ= Eε;△L= NL/ EA;EA为杆件的抗压(拉)刚度,表示杆件抵抗拉、压弹性变形的能力。
泊松比ν:应力不超过材料的比例极限时,ν=|ε’/ε|,ν是材料的弹性常数之一,无量纲。
变形能:杆件在外力作用下因变形而存储的能量。
轴向抗压杆的弹性变形能:U=N△L/2。
比能:单位体积存储的变形能。
u=σε/2。
单位:J/m3。
名义剪应力:假定剪应力沿剪切面均匀分布的。
则:τ=V/A V。
A V:剪切面面积。
纯剪切:单元体各个侧面上只有剪应力而无正应力称为纯剪切。
纯剪应力引起剪应变γ,即相互垂直的两线段间角度的改变。
单位为rad。
规定以单元体左下直角增大时,γ为正,反之为负。
剪应力互等定律:在互相垂直的两个平面上,垂直于两平面交线的剪应力,总是大小相等,且共同指向或背离这一交线。
τ=τ’。
剪切虎克定律:剪应力不超过材料的剪切比例极限时,剪应力τ与剪应变γ成正比,即τ=Gγ;G:剪切模量。
对各向同性材料,G=E/2(1+ν)。
扭转:杆两端受到一对力偶矩相等,转向相反,作用平面与杆件轴线相垂直的外力偶作用。
变形特征:杆件表面纵向线变成螺旋线,即杆件任意两横截面绕杆件轴线发生相对转动。
扭转角φ:杆件任意两横截面间相对转动的角度。
扭矩M T:受扭截面上的内力,是一个在截面平面内的的力偶,其力偶称为力偶矩。
材料力学基础
材料力学基础概念题1 •判断题:(以下结论对者画",错者画X)(1)只有肉眼看不到的变形才是小变形。
()(2)在静力学和材料力学中,内力概念的含义是相同的。
()(3)静力学中力的可传性原理和力的平移定理在材料力学中仍然普遍适用。
()(4)静力学中的加减平衡力系定理在材料力学中不能随意使用。
()(5)—般情况下,内力只是对质点而言,截面之间不存在内力。
()2 •选择题(1)下列说法正确的是:()A •材料力学主要研究各种材料的力学问题。
B •材料力学主要研究各种材料的力学性质。
C •材料力学主要研究各类杆件中力与材料的关系。
D .材料力学主要研究杆件受力后变形与破坏的规律。
(2)下列材料中,不属于各向同性材料的是()A・钢材B・塑料C 浇注很好的混凝土 D •木材(3)研究构件或其中一部分的平衡问题时,采用构件变形前的原始尺寸进行计算,这是因为采用了()A・基本假设 B • 均匀连续假设C 各向同性假设D • 小变形假设(4)下列说法正确的是:()A .应力分为三种,即正应力、负应力和切应力。
B .同一截面上,正应力与切应力必相互垂直。
C .同一截面上的正应力必定大小相等,方向相同。
D .同一截面上的切应力必相互平行。
(5)下列说法正确的是:()A •截面法是分析变形的基本方法。
B •截面法是分析内力的基本方法。
C •截面法是分析应力的基本方法。
D •截面法是分析内力与应力关系的基本方法。
(6)材料力学中的内力是指()A •构件内部的力。
B •构件内部各质点间固有的相互作用力。
C •构件内部一部分与另一部分之间的相互作用力。
D •在外力作用下,构件内部一部分与另一部分之间相互作用力的改变量。
(7)材料相同、横截面积相等的两根受轴向拉伸的等直杆,一根杆伸长量为另一根杆伸长量为0.1mm。
则下列结论中正确的是:()A •前者为大变形,后者为小变形。
B •两者都为大变形。
C .两者都为小变形。
【工程力学 课后习题及答案全解】第8章弹性杆件横截面上的正应力分析习题解
习题 8-9 图
8-10 图示直角三角形截面中,A、B 分别为斜边和直角边中点,y1z1、y2 z2 为两对互 相平行的直角坐标轴。试判断下列结论中,哪一个是正确的。
— 39 —
σa
=
−175Ea Es
= −175 70 200
= −61.25 MPa(压)
8-14 从圆木中锯成的矩形截面梁,受力及尺寸如图所示。试求下列两种情形下 h 与 b 的比值:
(1)横截面上的最大正应力尽可能小; (2)曲率半径尽可能大。 解:(1) σ = M z = M z = 6M z
正确答案是 A 。 解:若用右手系,y 轴坐标朝上为正,则由 h1 = b1 得
Sz
(I)
=
3 2
b1h12
>
0
,
Sz
(II)
=
−2b1h12
<
0
若考虑正负号,则应选 A;若考虑静矩的绝对值,则应选 B。
8-7 图示矩形中 y1、z1 与 y2、z2 为两对互相平行的坐标轴。试判断下列关系式中, 哪一个是正确的。
解:变形谐调:
FNs = FNa Es As Ea Aa FNs + FNa = FP
(1) (2)
⎧ ⎪⎪FNs ⎨ ⎪⎪⎩FNa
= =
Es As Es As + Ea Aa
Ea Aa Es As + Ea Aa
FP FP
(压)
(1)
σs
=
FNs As
第5章杆件横截面上的切应力
沿截面宽度方向均匀分布。
第5章
杆件横截面上的切应力分析
第5章
杆件横截面上的切应力分析
y
第5章
杆件横截面上的切应力分析
第5章
杆件横截面上的切应力分析
杆件横截面上的切应力分析
剪切虎克定律
当在弹性范围内加载时,剪 应力与剪应变成正比:
=G
这种线性关系称为剪切虎克定律。 G称为材料剪切弹性模量,单位:GPa。
第5章
杆件横截面上的切应力分析
§5-1 圆轴扭转时横截面上的切应力
第5章
杆件横截面上的切应力分析
平截面假设
圆轴扭转时,横截面保持 为平面,并且只在原地绕 轴线发生“刚性”转动。
第5章
杆件横截面上的切应力分析
第5章
杆件横截面上的切应力分析
第5章
杆件横截面上的切应力分析
第5章
杆件横截面上的切应力分析
已知:p=7.5kW,n=100r/min,最大切应力不得超过40MPa, 空心圆轴内外径之比a=0.5.二轴长度想相同。求:实心轴 的直径d1和空心轴的外直径D2,确定二轴的面积比。
第5章
杆件横截面上的切应力分析
第5章 杆件横截面上的正应力分析
§5-1 圆轴扭转时横截面上的切应力
§5-2 非圆截面扭转杆的切应力
§5-3 梁横截面上的切应力
第5章
杆件横截面上的切应力分析
切应力设作用在微元左、右面上的剪 应力为 ,这两个面上的剪应力 与其作用面的乘积,形成一对力, 二者组成一力偶
第5章
杆件横截面上的切应力分析
第5章
杆件横截面上的切应力分析
§5-3 梁横截面上的切应力
第5章
杆件横截面上的切应力分析
横力弯曲时的正应力计算公式
F
a/2
A
C
l/2 l/2
D
B
解: 分析:关键在于何为最佳,对于该题最佳就是两梁最大弯曲 应力同时达到最大。
主梁AB的最大弯矩
M maxAB
F (l a) 4
副梁CD的最大弯矩
M maxCD
Fa 4
由 即
M max AB M max CD
F Fa (l a) 4 4
得
4.纯弯曲的特点: 靠近凹入的一侧,纤维缩短,靠近凸出的一侧,纤维伸长; 由于纤维从凹入一侧的伸长或缩短到突出一侧的缩短或伸长 是连续变化的,故中间一定有一层,其纤维的长度不变,这 层纤维称为中性层。中性层与横截面的交线称为中性轴; 弯曲变形时,梁的横截面绕中性轴旋转。
中性层
中性轴
o
对称轴
z
目录
§6-3 非对称梁的纯弯曲
前面讨论的是梁上的弯曲力偶作用于纵向对称面内的情况; 下面讨论,当梁没有这样的纵向对称面时,或着虽然有纵向对称 面,但弯曲力偶并不作用于这一平面时的情况。
图6—7
如图(a)所示: Y、Z轴——横截面的形心主惯性轴
X轴——梁的轴线
My、Mz——对y轴、z轴的力偶矩
一.公式推导:
y
(6—1)
即:纵向纤维的线应变与它到中性层的距离成正比
(二) 物理关系 假设纵向纤维之间不存在相互挤压,那么当应力小于比 例极限时,可用单向拉伸时的虎克定律:
E E
y
物理意义:任意纵向纤维的正应力与它到中性层的距离成正 比,即:在横截面上的正应力沿截面高度按直线 曲率中心O 规律变化。
中性轴必然通过截面形心。 E 1 M EI z sin 0 0 (由于y 和z是形心主惯性轴,故Iyz=0)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章弹性杆横截面上的正应力分析——材料力学教案第三章弹性杆横截面上的正应力分析应用平衡原理可以确定静定问题中杆件横截面上的内力分量,但内力分量只是杆件横截面上连续分布内力的简化结果。
仅仅确定了内力分量并不能确定横截面上各点内力的大小。
这是因为,在一般情形下分布内力在各点的数值是不相等的,因此,只有当内力在横截面上的分布规律确定之后,才能由内力分量确定横截面上内力在各点的数值。
内力是不可见的,但变形却是可见的,而且二者之间通过材料的物性关系相联系。
因此,为了确定内力的分布规律,必须分析和研究杆件的变形,必须研究材料受力与变形之间的关系,即必须涉及变形协调与物性关系两个重要方面。
二者与平衡原理一起组成分析弹性体内力分布规律的基本方法。
§3-1 应力、应变及其关系考察图3-1中杆件横截面上的微小面积ΔA 。
假设分布内力在这一面积上的合力为ΔF R 则称ΔF R /ΔA 为这一微小面积上的平均应力。
当所取的面积趋于无穷小时,上述平均应力趋于一极限值。
这一极限值称为横截面上一点处的应力)。
这表明:应力实际上是分布内力在截面上某一点处的强弱程度,简称集度。
工程构件,大多数情形下,内力并非均匀分布,集度的定义不仅准确而且重要,因为“破坏”或“失效”往往从内力集度最大处开始。
1.正应力与切应力若将ΔF R 分解为x 、y 、z 三个方向上的分量ΔF Rx 、ΔF Qy 和ΔF Qz ,则根据应力定义,有A F A F A d d ΔΔNx Nx 0Δlim ==→σ (3-1) A F A F A y d d ΔΔQyQy 0Δlim ==→τ , A F A F A z d d ΔΔQz Qz 0Δlim ==→τ (3-2)式中,正应力σ垂直于横截面,称为正应力;τ位于横截面内,称为切应力。
应力单位为Pa ,工程上常用Mpa 。
2.正应变与切应变若围绕受力弹性体中的任意点截取一微元体(通常为六面体),一般情形下微元体的各个面上均有应力作用。
下面考察两种最简单的情形,分别如图3-2a 、b 所示。
不难发现,在正应力作用下,微元沿着正应力方向和垂直于正应力方向将产生伸长和缩短,这种变形称为线变形。
描写弹性体在各点处线变形程度的量,称为正应变或线应变,用x ε表示:dx du x =ε (3-3)图3-1式中,u 为微元受力后相距dx 的两截面沿正应力方向的相对位移。
x ε的下标表示应变方向。
约定:拉应变为正;压应变为负。
在切应力作用下,微元将发生剪切变形,剪切变形程度用微元直角的改变量度量。
微元直角改变量称为切应变,用γ表示。
在图3-2b 中, βαγ+=。
γ的单位为rad 。
3.线弹性材料的物性关系对于工程中常用材料制成的杆件,实验结果表明:若在弹性范围内加载(应力小于某一极限值),对于只承受单方向正应力或承受切应力的微元,正应力与正应变以及切应力与切应变之间存在着线性关系:x x E εσ= (3-4)γτG = (3-5)E 和G 与材料有关的常数:分别为弹性模量,和切变模量。
式(3-4)和(3-5)即为描述线弹性材料物性关系的方程,均可称为胡克定律。
所谓线弹性材料是指弹性范围内加载时应力-应变满足线性关系的材料。
§3-2杆件横截面上的正应力分析考察杆件横截面上只有轴力F N 、弯矩M y 和M z 作用的情形(为导出横截面上的正应力一般表达式,F N 、M y 和M z 的指向与相应坐标轴正向相同),如图3-3a 所示。
对应于这些内力分量,杆件横截面上将有什么应力?这种应力在截面上又是怎样分布的?不难看出,只有垂直于横截面的分布内力,经过简化才能得到上述内力分量。
这表明此时横截面上只有正应力而没有切应力,并且正应力不会是均匀分布的。
1. 平面假设与变形谐调方程在F Nx 、M y 、M z 的共同作用下,杆件上dx 微段的两截面将发生相对运动,产生位移。
假定杆横截面位移后依然保持平面。
这一假定称为平面假定。
设微段一侧截面不动,根据平面假定,另一侧截面将发生三种位移:在F Nx 作用下沿x 方向平行移动;在M y 和M z 作用下分别绕y 、z 轴转动。
如图3-3b 所示。
三种位移的结果,横截面上任意点(y 、z)的位移可以表示为z d y d du du y z N )()(θθ+-= (3-6)式中第1项由整个截面沿x 方向的位移所引起;第2、3两项分别由绕z 轴和y 铀的转动所引起,如图3-4a 和b 所示。
其中,y d θ和z d θ为dz 微段两截面分别绕y 轴和z 轴相对转过的角度。
方程(3-6)表明:在F Nx 、M y 、M z 作用下,各点的位移不能是任意的,只能从一个平面协调地移动到另一平面,故上述方程又称为变形协调方程。
2. 应变分布与应力分布对于直杆,微段上各处的纵向x 长度在变形前均为dx ,根据式(3-3)以及z y z z d dx d dx θρθρ==、,由方程(3-6)得到横截面上任意点(x ,y ,z )的正应变为yz N x z y dx du ρρεε+-== (3-7)(a) (b)图3-4其中,dxdu N N =ε——轴向荷载引起的应变; y y d dx θρ=——梁轴线在xz 坐标平面内弯曲时的曲率半径; zz d dx θρ=——梁轴线在xy 坐标平面内弯曲时的曲率半径; 对于确定的截面(x 坐标确定),N ε、y ρ、z ρ均为待定常数。
应用物理关系,根据弹性范围内的胡克定律,由式(3-4)、(3-7),得到横截面上任意点(y 、z )处的正应力为z E y EE y z N x ρρεσ+-= (3-8)上式表明:在轴力和弯矩作用下,杆件横截面上的正应力对于y 、z 都是线性分布,即在空间形成一应力平面。
3. 静力学平衡方程的应用——待定常数的确定作用在微元面积dA 上的内力x σdA(图3-5a)及其对y 、z 轴之矩(x σdA)z 、(x σdA)y 分别在整个横截面上积分,便组成三个内力分量x F N 、y M 、z M (图3-5b )。
即x A x F A N d =⎰σ (3-9)()y A x M z A =⎰d σ (3-10) ()z A xM y A -=⎰d σ (3-11)将方程(3-8)代入上述各式,经整理后得到x yy z z F ES ES EA N N 11=+ρρε- (3-12)y y y zyz y M EI EI ES =+ρρε11N - (3-13) z y yz z zz M EI EI ES =-+-ρρε11N (3-14) 其中,⎰⎰==A z A y A y S A z S d d ,, ⎰=AA A d ⎰⎰==Az A y A y I A z I d d 22,, ⎰=A yz yzdA I 分别为横截面对y 、z 轴的静矩(即截面一次矩);横截面面积;横截面对于Y 、z 轴的惯性矩(即截面二次轴矩)和惯性积。
对于给定的截面,这些量均为已知量。
于是由式(3-12)、(3-13)和(3-14)联立,即可确定式(3一8)中的待定常数N ε、y ρ和z ρ。
4. 正应力的一般表达式不难看出,求解上述联立方程过于繁琐。
但是,如果选择合适的坐标原点和坐标轴,则式(3-15)中的某些量将取零值。
注意到,在此之前,对于坐标系,只规定了坐标原点设在截面形心、x 轴与杆件的轴线重合。
根据本书附录A 中关于截面几何性质的分析,当坐标轴通过截面形心时,截面对这些坐标轴的静矩为零。
于是式(3-15)中的0==z y S S 。
若再将y 、z 取为形心主轴,则式(3-15)中的惯性积0=yz I ,且y I 、z I 皆为截面的形心主惯性矩。
在坐标原点与坐标轴这种特定的选择下,由式(3-12)~(3-14)直接得到EAF x N N =ε (3-16) y y yEI M =ρ1 (3-17)zz zEI M =ρ1 (3-18) 将它们代人方程(3-8),最后得到 yy z z x x I z M I y M A F +-=N σ (3-19) 这就是计算在F Nx 、M y 、M z 作用下,横截面上任意点处正应力的一般表达式。
式中,F Nx 、M y 、M z 可由截面法求得;A 为横截面面积;y I 、z I 分别为横截面对其形心主轴的惯性矩。
除了正应力公式,上述分析还得出关于计算杆件轴向变形和位移的公式(3-16)与dxdu N N =ε和曲率y ρ1和zρ1分别表示在xz 和xy 坐标平面内杆件轴线的弯曲变形程度。
上述各式中EA 称为杆的拉压刚度;y EI 和z EI 分别称为杆在xz 和xy 两个平面内的弯曲刚度。
§3-3正应力公式的应用实验结果表明,对于没有剪力作用的情形,正应力公式计算出的正应力值与实验值吻合得很好。
当横截面上除了轴力和弯矩外,尚有剪力(F Qy 或F Qz )存在时,横截面上除正应力外,还将有切应力存在,由此引起的切应变将使横截面在变形后不再保持平面。
因此,由平面假定导出的正应力表达式(3-19)算出的应力值将与实验值有一定的误差。
但是,对于细长的实心截面杆件,实验结果表明,这种误差是很小的,因而通常可以忽略不计。
因此,对于细长实心截面杆件,应力表达式(3-19)不仅可以用于无剪力作用情形,而且也可以用于有剪力存在的情形,这样便大大拓宽了式(3-19)的适用范围。
1. 轴向载荷作用下杆件横截面上的正应力当杆件承受沿轴线方向的荷载作用时,称为轴向拉压,其横截面上只有轴力F Nx 一个内力分量。
于是,由式(3-19),得到AF x x N =σ (3-20) 这时横截面上的应力分布如图(3-6)所示。
2. 平面弯曲正应力在内力分量M y 、F Qz 或M z 、F Qy 作用下,梁的轴线将在一个主轴平面(弯矩作用面,或者荷载作用面)内弯曲成一条平面曲线。
因此,梁的这种弯曲又称为平面弯曲。
这种情况下,式(3-19)将变为zz x I y M -=σ (3-21) 或 y y x I zM =σ (3-22)在两种平面弯曲情形下,横截面上的正应力分布如图3-7a 和b 所示。
图3-6不难看出,在两种情形下的最大正应力分别为zz x W M -=max σ (3-23)yy x W M =max σ (3-24) 其中, max z I W yy =, m a xy I W z z = (3-25) 分别称为横截面的对于z 轴和y 轴的弯曲截面系数。
表3一1中列出了几种常见截面的弯曲截面系数。
关于轧制的型钢的截面二次轴矩和弯曲截面系数等几何量可由本书附录B 型钢表中查得。
图3一7平面弯曲时梁横截面上的正应力分布(a)(b)3.斜弯曲的正应力当杆件的两个互相垂直的主轴平面内都有荷载作用(无纵向荷载)时,杆将在两个方向同时发生弯曲,这种弯曲称为斜弯曲或双向弯曲。
