典型光学系统部分例题
23球面反射境

放大率 折射球面
反射球面 l
nl’/n’l nl’2/n’l2
n’ —>-n
-l’/l -x’/f’=-f/x -(l’/l)2 -x’/x
g=u’/u
l/l’
l/l’ x/f’= f/x’
例题-共轴球面光学系统
例题1 一个玻璃球直径为40mm,折射率为1.5,一 束平行光入射到玻璃球上,其汇聚点在什么 位置?如果在玻璃球前25mm处放置一个高 为1mm的物体,试求解像的位置和大小.
折射球面 n’/l’ –n/l =(n’-n)/r
球面镜 1/l’ +/l =2/r A (2) 高斯公式
1 1 1 或 f ' f 1
l' l f '
l' l
(3) 牛顿公式
A
xx' f '2 或 xx' ff '
A’
C F(F’) O
-l’ -l
A’
C F(F’) O
-x’
-x
-f ’
3 放大率公式—球面反射镜成像关系
1 焦距—球面反射镜成像关系
(1) 光焦度
折射球面
球面镜 (2) 像方焦距
折射球面
球面镜 (3) 物方焦距
折射球面
球面镜
j=(n’-n)/r
j=-2n/r
f ’=n’/j
f’=r/2
f=-n/j
f=r/2
C F(F’) O
-f=-f ’
O F(F’) C
f=f ’
2 物像公式—球面反射镜成像关系
(1) 一般物像公式
例题-球面镜成像
例题1 一球面反射境,半径r=12cm,当物相距 球面镜顶点物距分别为-18cm,-2cm和 12cm时,求像的位置和垂轴放大率。
大学物理光学第一章答案
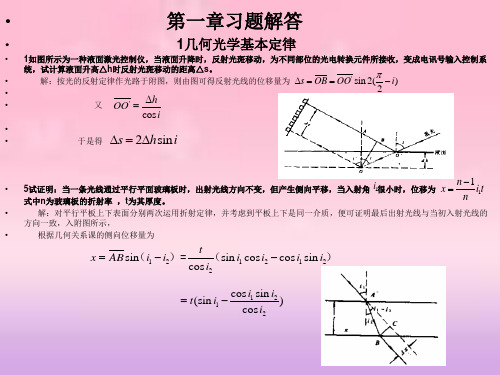
i1《1的条件下,取小角近似
于是有
sin i1 i1 ,cos i1 cos i2 1
x n 1 i1t n
•
12如图所示,在水中有两条平行线1和2,光线2射到水和平行平板玻璃的分界面上。
• •
(1)两光线射到空气中是否还平行? (2)如果光线1发生全反射,光线2能否进入空气? 解: 我们先推到一下光线经过几个平行界面的多层媒质时出射光线的方向。 因为界面都是平行的,所以光线在同一媒质中上界面的的折射角与下界面的入射角相等,如下图所示:
• • • • •
解得
S0 R
sin i sin u
S0 ' R
sin i ' sin u '
u u ' (i ' i)
又根据折射定律 进一步得到 由此可见,只在
n sin i n 'sin u
S0 n ' sin i ' R n sin u
以及角度关系
S0 '
f 如设该透镜在空气中和在水中的焦距分别为 f1 ,2 ,按上式有 f2 n 1 L f1 ( nL 1) n0 1.50 1 ( f1 10.0) f1 则 f2 3 1.50 1 4
4 f1 40cm
•
• •
• •
3用一曲率半径为20cm的球面玻璃和一平玻璃粘合成空气透镜,将其浸入水中(见图),设玻璃壁厚可忽略,水和空气的折射 率分别为4/3和1,求此透镜的焦距f。此透镜是会聚的还是发散的? 1 n 4 r 解:以 nL 1 ,0 3 , 20cm , r2 代入薄透镜焦距公式 f 1 n 1 1 ( L 1)( ) n0 r1 r2 算出该空气薄透镜(置于水中)的焦距为 f= - 80cm ,它是发散透镜。
工程光学14章例题分析

第一章1、已知真空中的光速c =3 m/s ,求光在水(n=1.333)、冕牌玻璃(n=1.51)、火石玻璃(n=1.65)、加拿大树胶(n=1.526)、金刚石(n=2.417)等介质中的光速。
解:则当光在水中,n=1.333时,v=2.25 m/s, 当光在冕牌玻璃中,n=1.51时,v=1.99 m/s, 当光在火石玻璃中,n =1.65时,v=1.82 m/s , 当光在加拿大树胶中,n=1.526时,v=1.97 m/s , 当光在金刚石中,n=2.417时,v=1.24 m/s 。
(例题)2、一物体经针孔相机在 屏上成一60mm 大小的像,若将屏拉远50mm ,则像的大小变为70mm,求屏到针孔的初始距离。
解:在同种均匀介质空间中光线直线传播,如果选定经过节点的光线则方向不变,令屏到针孔的初始距离为x ,则可以根据三角形相似得出:所以x=300mm即屏到针孔的初始距离为300mm 。
(例题)3、一厚度为200mm 的平行平板玻璃(设n=1.5),下面放一直径为1mm 的金属片。
若在玻璃板上盖一圆形纸片,要求在玻璃板上方任何方向上都看不到该金属片,问纸片最小直径应为多少?1mmI 1=90n 1 n 2 200mmLI 2x解:令纸片最小半径为x,则根据全反射原理,光束由玻璃射向空气中时满足入射角度大于或等于全反射临界角时均会发生全反射,而这里正是由于这个原因导致在玻璃板上方看不到金属片。
而全反射临界角求取方法为:(1)其中n2=1, n1=1.5,同时根据几何关系,利用平板厚度和纸片以及金属片的半径得到全反射临界角的计算方法为:(2)联立(1)式和(2)式可以求出纸片最小直径x=179.385mm,所以纸片最小直径为358.77mm。
4、光纤芯的折射率为n1、包层的折射率为n2,光纤所在介质的折射率为n0,求光纤的数值孔径(即n0sinI1,其中I1为光在光纤内能以全反射方式传播时在入射端面的最大入射角)。
光学第二章

例题1 例题1 一个折射率为1.6的玻璃哑铃,长为 20cm,两端的曲率半径为2cm.若在离哑 铃左端5cm处的轴上有一发光点,试求 像点的位置和性质
例题2 例题2 曲率半径为R,折射率为1.5的玻璃球, 在右半个球面上镀上铝膜,若平行光由 左→右传播,问最后象的位置与性质
§2-4 近轴物体经单球面成像的性质 一.近轴物体成理想像条件 1 轴外物点Q发出的所有光线到 像点Q’的光程都应相等:
例题1 例题1 如图,已知P′Q′为PQ的像,作图求物像方 焦点的位置及球面的曲率中心 例题2 例题2 如图,已知物体PQ,像方焦点的位置及 曲率中心,作图确定像的位置以及物方 焦点的位置
§2-5 共轴球面系统的基点与基面 理想光具组: 共轴球面系统+近轴条件 一.共轴球面系统的成像 方法1:逐次成像,依次计算,比较繁琐 方法2:简化处理,找一个等效光具组来 代替整个共轴光学系统,一次成像
n' n' f '= r= n'−n Φ
• 物方焦点F 主光轴上S′=∞的像点的共轭物点 S 物方焦距为:
n n f =− r =− n'−n Φ
• 两焦距的关系 说明:
f'
n' =− f n
• n与n′大于零,所以两焦点分居顶点两侧 • n≠n′,所以两焦点关于球面顶点不对称
• 高斯公式
f' S' f + S =1
任意光线经 过平面镜反 射后均相交 于一点
成像特点: 成像特点: • 反射光束仍为单心光束。平面镜反射成 理想像,为一理想光具组 • 成一与物等大且关于镜面对称的正立的 虚像 • 物方、象方在同一侧
二. 光在平面上的折射 1. 平面折射为非理想成像 不同入射角的光经过平面折射后不相 交于一点,光束的单心性被坏 !!!
工程光学-1-4章例题分析

工程光学-1-4章例题分析(总22页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第一章1、已知真空中的光速c =3 m/s ,求光在水(n=)、冕牌玻璃(n=)、火石玻璃(n=)、加拿大树胶(n=)、金刚石(n=)等介质中的光速。
解:则当光在水中,n=时,v= m/s, 当光在冕牌玻璃中,n=时,v= m/s, 当光在火石玻璃中,n =时,v= m/s , 当光在加拿大树胶中,n=时,v= m/s , 当光在金刚石中,n=时,v= m/s 。
(例题)2、一物体经针孔相机在 屏上成一60mm 大小的像,若将屏拉远50mm ,则像的大小变为70mm,求屏到针孔的初始距离。
解:在同种均匀介质空间中光线直线传播,如果选定经过节点的光线则方向不变,令屏到针孔的初始距离为x ,则可以根据三角形相似得出:所以x=300mm即屏到针孔的初始距离为300mm 。
(例题)3、一厚度为200mm 的平行平板玻璃(设n=),下面放一直径为1mm 的金属片。
若在玻璃板上盖一圆形纸片,要求在玻璃板上方任何方向上都看不到该金属片,问纸片最小直径应为多少解:令纸片最小半径为x, 则根据全反射原理,光束由玻璃射向空气中时满1mmI 1=90n 1 n 2 200mmLI 2x足入射角度大于或等于全反射临界角时均会发生全反射,而这里正是由于这个原因导致在玻璃板上方看不到金属片。
而全反射临界角求取方法为:(1)其中n2=1, n1=, 同时根据几何关系,利用平板厚度和纸片以及金属片的半径得到全反射临界角的计算方法为:(2)联立(1)式和(2)式可以求出纸片最小直径x=,所以纸片最小直径为。
4、光纤芯的折射率为n1、包层的折射率为n2,光纤所在介质的折射率为n,求光纤的数值孔径(即n0sinI1,其中I1为光在光纤内能以全反射方式传播时在入射端面的最大入射角)。
解:位于光纤入射端面,满足由空气入射到光纤芯中,应用折射定律则有:n0sinI1=n2sinI2(1)而当光束由光纤芯入射到包层的时候满足全反射,使得光束可以在光纤内传播,则有:(2)由(1)式和(2)式联立得到nsinI1 .(例题)5、一束平行细光束入射到一半径r=30mm、折射率n=的玻璃球上,求其会聚点的位置。
球面反射境

放大率 折射球面
反射球面 高斯 牛顿
b=y’/y
=dl’/dl
nl’/n’l nl’2/n’l2
n’ —>-n
-l’/l -x’/f’=-f/x -(l’/l)2 -x’/x
g=u’/u
l/l’
l/l’ x/f’= f/x’
例题-共轴球面光学系统
例题1 一个玻璃球直径为40mm,折射率为1.5,一 束平行光入射到玻璃球上,其汇聚点在什么 位置?如果在玻璃球前25mm处放置一个高 为1mm的物体,试求解像的位置和大小.
例题-球面镜成像
例题1 一球面反射境,半径r=12cm,当物相距 球面镜顶点物距分别为-18cm,-2cm和 12cm时,求像的位置和垂轴放大率。
折射球面 n’/l’ –n/l =(n’-n)/r
球面镜 1/l’ +/l =2/r A (2) 高斯公式
1 1 1 或 f ' f 1
l' l f '
l' l
(3) 牛顿公式
A
xx' f '2 或 xx' ff '
A’
C F(F’) O
-l’ -l
A’
C F(F’) O
-x’
-x
-f ’
3 放大率公式—球面反射镜成像关系
1 焦距—球面反射镜成像关系
(1) 光焦度
折射球面
球面镜 (2) 像方焦距
折射球面
球面镜 (3) 物方焦距
折射球面
球面镜
j=(n’-n)/r
j=-2n/r
f’=n’j
f’=r/2
f=-n/j
f=r/2
C F(F’) O
-f=-f ’
应用光学例题

近轴光学系统例1.一厚度为200mm的平行平板玻璃(n=1.5)下面放着一直径为1mm的金属片。
若在玻璃板上盖一圆形纸片,要求在玻璃板上方任何方向上都看不到该金属片,问纸片的最小直径为多少?例2.用费马定理证明光的折射定律和反射定律。
例3.如图有两个平面反射镜,M1、M2夹角为α,今在两反射镜之间有一光线以50°角入射,入射到M1的反射镜上,经M1、M2四次反射后,起反射光线与M1平行,求其夹角α。
例4.设计一个在空气中和某种玻璃之间的单个折射表面构成的光学系统,希望物在空气中离表面15.0cm。
实像在玻璃中,离表面45.0cm,放大率为2.0。
那么玻璃的折射率应为多少?表面的曲率半径为多少?例5.直径为100mm的球形玻璃缸,将半面镀银,内有一条鱼在镀银面前25mm处。
问缸外的观察者看到几条鱼?位置在何处?相对大小事多少?(水的折射率为4/3)例6.在一张报纸上放一个平凹透镜,通过镜面看报纸。
当平面朝着眼睛时,报纸的虚像在平面下13.3mm处。
当凸面朝着眼睛时,报纸的虚像在凸面下14.6mm处。
若透镜中央厚度为20mm。
求透镜的折射率和凸球面的曲率半径。
例7.一凹球面镜将一实物成一实像,物与像的距离为1m,物高为像高的4倍,求凹面镜的曲率半径。
例8.①一束平行光入射到一半径r=30mm,折射率n=1.5的玻璃球上,求其汇聚点的位置。
②如果在凸面上镀反射膜,其汇聚点应在何处?③如果凹面镀反射膜,则反射光束在玻璃中的汇聚点在何处?④反射光束经前表面折射后,汇聚点在何处?说明各汇聚点的虚实。
(2)(3)(4)例9.一直径为400mm,折射率为1.5的玻璃球中有两个小气泡,一个位于球心,另一个在1/2半径处。
沿两气泡连线方向在球两边观察,问看到的气泡在何处?如果在水中观察者看到的气泡又在何处?例10.位于空气中的等腰直角棱镜折射率n=1.54,问当光线在斜边上发生全反射时直角边1上入射光线的入射角I1应为多大?若棱镜折射率增大,I1增大还是减小?又问若棱镜放入水中,按图中光轴方向入射的光线是否会发生全反射。
物理光学高频考试例题
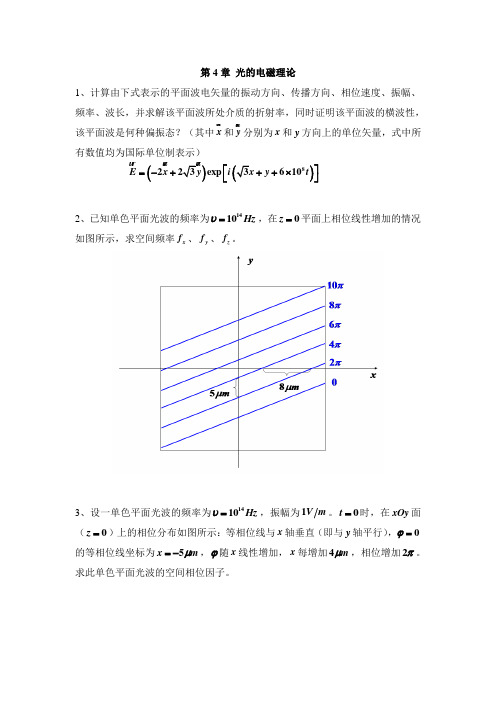
第4章 光的电磁理论1、计算由下式表示的平面波电矢量的振动方向、传播方向、相位速度、振幅、频率、波长,并求解该平面波所处介质的折射率,同时证明该平面波的横波性,该平面波是何种偏振态?(其中x 和y 分别为x 和y 方向上的单位矢量,式中所有数值均为国际单位制表示)())8223exp 610E x y i y t ⎡⎤=-+++⨯⎣⎦ 2、已知单色平面光波的频率为1410Hz υ=,在0z =平面上相位线性增加的情况如图所示,求空间频率x f 、y f 、z f 。
3、设一单色平面光波的频率为1410Hz υ=,振幅为1V m 。
0t =时,在xOy 面(0z =)上的相位分布如图所示:等相位线与x 轴垂直(即与y 轴平行),0ϕ=的等相位线坐标为5x m μ=-,ϕ随x 线性增加,x 每增加4m μ,相位增加2π。
求此单色平面光波的空间相位因子。
4、试确定下列各组光波表达式所代表的偏振态:(1)、()0si n x E E t k z ω=-,()0cos y E E t kz ω=- (2)、()0co s x E E t k z ω=-,()0cos 4y E E t kz ωπ=-+ (3)、()0si n x E E t kz ω=-,()0sin y E E t kz ω=--5、若要使自然光经过红宝石( 1.76n =)表面反射后成为完全偏振光,入射角应等于多少?求在此入射角的情况下,折射光的偏振度t P 。
6、如图所示,玻璃块周围介质(水)的折射率为1 1.33n =。
若光束射向玻璃块的入射角为45,问玻璃块的折射率至少应为多大才能使透入光束发生全反射。
7、如图所示,光束垂直入射到45直角棱镜的一个侧面,经斜面反射后从第二个侧面透出。
若入射光强为0I ,问从棱镜透出的光束的强度为多少?(设棱镜的折射率为1.52,棱镜周围为空气,并且不考虑棱镜的吸收)8、穆尼棱体能将偏振方向与入射面成45的线偏振光变成圆偏振光,如图所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 2、6倍双目望远镜系统中,物镜焦距为108mm,物 镜口径为30mm,目镜口径为20mm,如系统中没有 视场光阑,问该望远镜最大极限视场角等于多少? 渐晕系数KD=0.5时的视场角等于多少。
• 解:
• 望远镜系统的视放大率公式:
f `O f `e
f `e
f `O
108 6
f `物 D D D` 5 5 25 f `目 D`
则有 : h1 12.5
tgu1`
tgu1
h11
tg(5)
12.5
1 100
0.2125
tgu场
h2 h1 dtgu`1 12.5 100tgu`1 8.75
tgu`场 tgu场 h2场 u`场 5
• 4、200倍显微镜的目镜焦距为25mm,镜筒内径为20, 求显微镜的线视场,如果出瞳直径D`=1mm,显微物 镜的物像共轭距为195mm,求显微镜的数值孔径, 物镜的口径为多大?(均按薄透镜计算)
• 5、望远系统由焦距分别为100和20的两正透镜构成, 出瞳直径D`=5,由于目镜口径的限制,轴外边缘视场 渐晕系数KD=0.5,为了消除渐晕,需在中间像平面 上加场镜,问在不增加目镜口径的条件下,场镜焦距 为多大时,能消除渐晕。
18
• 极限视场角是刚好进入系统一条光线所对应的视场 角,如图所示。
C E O 1
f`=108
B`பைடு நூலகம்GD
O
F`O F
2
e
• 3、7倍望远镜系统,视场角为2ω=8°,目镜焦距为 25mm,出瞳直径为5mm,设无渐晕,求孔径光阑、 入瞳、出瞳位置,物镜和目镜的口径、视场光阑口 径。
• 解: • 根据视放大率公式可求得入瞳口径:
f`O=1
75 d
l`z
tgu`1 tgu1 h11
tgu`1 17.5 tg(4 ) 0.1699 175
h2 h1 dtgu`1 17.5 (175 25)(0.1699 ) 16.486 mm
De 2h2 33mm
• 通过计算主光线将出瞳位置确定下来:
• 4、解: • 目镜视放大率为:
目 250 / f `目 250 / 25 10
• 物镜的垂轴放大率为:
/ 目 200 /10 20 l`/ l 20 l` 20*l
又 l l` 195 l 9.286mm,l` 185.714mm
D D D` 75 35mm D`
• 无渐晕,边缘视场成像光束的中心光线应过孔径光 阑中心O1,从图中可见,边缘视场下边缘光线在目 镜上投射高最大,由它决定目镜的口径:
h1 17.5mm,1 4 u1
f `o f `e 7 25 175mm
习题
• 1、照相镜头焦距为f`=35mm,底片像幅尺寸为 24*36mm,求该相机的最大视场角,视场光阑位置。
• 解: • 像范围由底片框限制,底片框就是视场光阑,
位于镜头的焦平面。 • 由 y` f `tg • 可得 tg y`/ f `
y` 1 242 362 21.36(底片框对角线一半) 2
• 边缘视场被目镜切割,渐晕系数为0.5,只有上半部光进 行目镜,目镜的口径为:
D目 2 ( f1 f2 )tg 2 120 tg5 21
ω=5°
• 在不增加目镜口径的条件下,在目镜物方焦平面上加 一块场镜,使下边缘光线折射进入目镜,则无渐晕,这样 对下边缘光线进行光路计算就可以求出场镜焦距.
hz1 0, hz2 hz1 dtg() 200tg4 13.99
tgu`z tgu2 hz22 0.4895
l`z
hz 2 tgu`z
28.58mm
视场光阑孔径:
D 2 y`max 2 f `O tg 2*175*tg(4 ) 24.5mm
• 物镜的数值孔径: NA / 500 200/ 500 0.4 • 物镜的通光口径: D物 2(lu) 2*9.286 *0.4 7.429
•线视场:2ymax=20/β=20/20=1
• 5、解: • 无限远轴外点所成像高为:
y` f1`tg 100tg(5) 100tg5 8.75
