基于小波的自适应阈值算法
基于EMD和小波熵阈值算法的超声回波信号降噪
基于EMD和小波熵阈值算法的超声回波信号降噪作者：杜必强孙立江来源：《中国测试》2017年第01期摘要：超声检测信号中通常包含大量噪声，而其中材料晶界散射的噪声是一种相关噪声。
鉴于传统的方法难以将这种噪声和缺陷回波信号区分，提出一种EMD和小波熵阈值联合降噪的算法。
该算法首先对目标信号进行EMD分解，提取具有噪声特性的IMF分量进行小波分解，利用含噪系统熵增的特性，在分解各尺度层的细节部分选用小波熵自适应阈值降噪，然后将剩余分量和降噪处理后的信号进行重构。
仿真信号结果表明：该降噪方法（EMD-WET）输出信号的信噪比（SNR）为7.9 dB、均方根误差（RMSE）为18.1、相似系数（NCC）为0.92，优于传统的小波软、硬阈值方法。
对实测信号进行处理，该方法降低信号中的大部分噪声，更好地还原回波信号的波形。
关键词：超声检测；降噪；小波熵；经验模态分解文献标志码：A 文章编号：1674-5124（2017）01-0101-05收稿日期：2016-06-18；收到修改稿日期：2016-07-25基金项目：中央高校基本科研业务费项目（2014MS118）作者简介：杜必强（1974-），男，江西吉安市人，副教授，博士，研究方向为旋转机械故障诊断、机器人标定及无人飞行器。
引言在现场超声检测中，技术人员通常根据回波信号来判断被检测对象是否存在缺陷。
作为一种典型的非线性、非平稳信号，回波信号本身含有许多突变成分，包含大量的有用信息，但超声波在材料晶界散射引起的微结构噪声以及采集仪器的散射噪声都会使回波信号包含大量噪声，严重干扰有用信号特征的提取，影响检测结果。
因此，采用有效的信号处理方法抑制回波信号携带的各种噪声，提高信噪比，有利于下一步对缺陷回波信号的特征提取，模式识别。
近年来，对非线性、非平稳信号降噪的方法有：EMD阈值去噪、小波阈值去噪、EMD和小波阈值联合去噪等。
李秋锋等[1]采用EMD对粗晶材料超声检测信号进行了去噪方法研究，取得了一定的效果。
srad降噪原理
srad降噪原理SRAD（Self-Regularizing Adaptive Denoising）是一种图像降噪算法，基于局部自适应阈值和正则化方法。
其原理可以概括为以下几个步骤：1.小波变换：SRAD首先对图像进行小波变换，将图像转换到频域。
小波变换可以将图像的高频和低频信息分离开来，便于处理和分析。
2.局部自适应阈值：SRAD根据图像在局部区域内的特征确定自适应阈值。
在图像的低频分量中，噪声相对较少，因此可以选择较小的阈值来保留图像的细节信息；而在图像的高频分量中，噪声相对较多，需要选择较大的阈值来抑制噪声。
3.非线性滤波：SRAD使用非线性滤波方法对图像进行降噪。
对于每个小波系数，首先与自适应阈值进行比较。
如果小于阈值，则保留该系数；否则，将该系数置零。
这样可以抑制噪声，并保留图像的细节信息。
4.正则化：SRAD使用正则化方法对降噪后的图像进行处理。
正则化的目的是进一步平滑图像，并消除可能引入的伪影。
SRAD采用了平均滤波器对图像进行平滑处理，同时还考虑到了降噪后图像的梯度信息，以保持图像的边缘特征。
5.重建：SRAD最后对正则化后的图像进行逆小波变换，将图像恢复到空域。
这样就得到了降噪后的图像。
SRAD降噪算法的优点是可以自适应地选择阈值，并采用正则化方法对降噪后的图像进行平滑处理，以避免降噪过程中引入的伪影。
它能够同时抑制高频噪声和保留图像的细节信息，有效地降低图像的噪声。
然而，SRAD算法也有一些局限性。
首先，它对图像的局部特征较为敏感，可能在图像的细节部分引入伪影；其次，SRAD算法在处理均匀区域时可能会损失一些细节信息，因为它使用了平均滤波器进行正则化处理。
总之，SRAD降噪原理是基于局部自适应阈值和正则化方法的图像降噪算法。
它通过选择合适的阈值来抑制噪声，并采用正则化方法来平滑图像，从而实现对图像的降噪处理。
这种算法在图像处理领域具有一定的实用价值，可应用于图像去噪、图像增强等方面。
(整理)在众多基于小波变换的图像去噪方法中
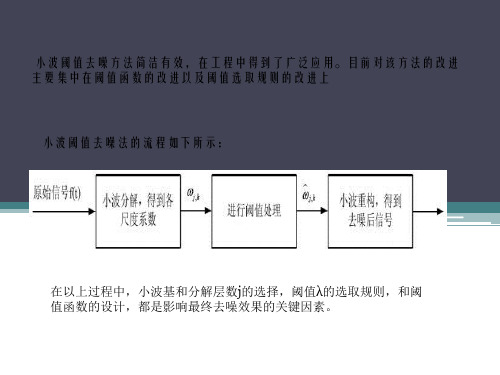
在众多基于小波变换的图像去噪方法中,运用最多的是小波阈值萎缩去噪法。
传统的硬阈值函数和软阈值函数去噪方法在实际中得到了广泛的应用,而且取得了较好的效果。
但是硬阈值函数的不连续性导致重构信号容易出现伪吉布斯现象;而软阈值函数虽然整体连续性好,但估计值与实际值之间总存在恒定的偏差,具有一定的局限性。
鉴于此,本文提出了一种基于小波多分辨率分析和最小均方误差准则的自适应阈值去噪算法。
该方法利用小波阈值去噪基本原理,在基于最小均方误差算法L M S和Stein无偏估计的前提下,引出了一个具有多阶连续导数的阈值函数,利用其对阈值进行迭代运算,得到最优阈值,从而得到更好的图像去噪效果。
最后,通过仿真实验结果可以看到,该方法去噪效果显著,与硬阈值、软阈值方法相比,信噪比提高较多,同时去噪后仍能较好地保留图像细节,是一种有效的图像去噪方法。
小波基函数选择可从以下3个方面考虑。
（1）复值与实值小波的选择复值小波作分析不仅可以得到幅度信息，也可以得到相位信息，所以复值小波适合于分析计算信号的正常特性。
而实值小波最好用来做峰值或者不连续性的检测。
（2）连续小波的有效支撑区域的选择连续小波基函数都在有效支撑区域之外快速衰减。
有效支撑区域越长，频率分辨率越好；有效支撑区域越短，时间分辨率越好。
（3）小波形状的选择如果进行时频分析，则要选择光滑的连续小波，因为时域越光滑的基函数，在频域的局部化特性越好。
如果进行信号检测，则应尽量选择与信号波形相近似的小波。
小波变换与傅里叶变换的比较小波分析是傅里叶分析思想方法的发展和延拓。
自产生以来，就一直与傅里叶分析密切相关。
它的存在性证明，小波基的构造以及结果分析都依赖于傅里叶分析，二者是相辅相成的。
两者相比较主要有以下不同：（1）傅里叶变换的实质是把能量有限信号tf分解到以jwte为正交基的空间上去；而小波变换的实质是把能量有限的信号tf分解到由小波函数所构成的空间上去。
两者的离散化形式都可以实现正交变换，都满足时频域的能量守恒定律。
自适应模糊小波阈值去噪算法在图像中的应用
ｉ ｒ ｎ ｓ ｈ ｏ ｗ【 Ｘ ） ｝
ｔ ｉ ｔ ｌ ｅ （ ’ 高 斯 噪声 图 片 ） ； ｋ ｌ ＝ ｍｅ ｄ ｉ ｆ ｌ ｔ ２ （ ｘ， ［ ３ ３ 】 ） ； ｓ ｕ ｂ ｐ ｌ ｏ ｔ （ ２ ２ ２ ） ； ｉ ｍｓ ｈ ｏ ｗ（ Ｉ ） ｔ ｉ ｔ ｌ ｅ （ ’ ３ ｘ ３ 模 板 中值 滤 波 ’ ） ； ｋ ２ ＝ ｍｅ ｄ ｉ ｆ ｌ ｔ ２ （ ｘ， 【 ５ ５ 】 ） ； ｓ ｕ ｂ ｐ ｌ ｏ ｔ （ ２ ２ ３ ） ， ｉ ｍｓ ｈ ｏ ｗ（ Ｉ ） ； ３ ４ 一 一 ｔ ｉ ｌ ｔ ｅ （ ’ ５ ｘ ５ 模板 中值 滤 波 。 ） ； ｋ ３ ＝ ｍｅ ｄ Ｉ ｉ ｌ ｔ ２ （ ｘ， ［ ７ ７ 】 ） ； ｓ ｕ ｂ ｐ ｌ ｏ ｔ （ ２ ２ ４ ） ； ｉ ｍｓ ｈ ｏ ｗ（ Ｉ ） ； ｔ ｉ ｌ ｔ ｅ （ ’ ７ ｘ ７ 模板 中值 滤 波 ’ ） ； ２ ２ 维纳 滤波法 对含 高斯 噪声 的图像 去噪仿 真
像。 首先对 图像 中 的噪声进 行检测 。 信 号经 过中值 滤波后 ， 信 号的 幅度将 会有 较高 的保 真度 ， 避 免 了引入量化 噪声 ， 有效地 滤 出了脉冲噪声 ， 还 可 以抑 制一部 分高斯 噪 声 。 （ ２ ） 对 预处 理后 的 图像进 行小 波变 换 ， 滤 除图像 中 的高斯 噪声 。 软 阈值 函数 ：
＾
＜
， ｎ
中图分 类号 ： Ｔ Ｐ ３ ９ １ ． ４ １
文献 标识码 ： Ａ
文 章编号 ： １ ０ ０ ９ — ９ １ ４ Ｘ（ ２ ０ １ ４ ） ０ ６ — ０ １ ７ ４ — ０ ２
１自适应 模糊 小波 阈值 去噪 （ １ ） 对含 噪 图像用 中值 滤波 法预 处理 基于 中值 滤波 算法 能够 很好地 消除脉 冲噪 声 ， 保证 图像 细节 及其 边缘 的
小波去噪阈值的确定和分解层数的确定
代价函数M:
01
常用代价函数：
02
数列中大于给定门限的系数的个数。即预先给定一门限值 ，并计数数列中绝对值大于 的元素的个数。
03
范数。
01
常用代价函数：
02
熵
常用代价函数：
能量对数
“最优树”的搜索方法：
二元树搜索方法：
[thr2,nkeep]=wdcbm(c,l,alpha2);%获得阈值
获取各个高频段的阈值，
阈值选取是根据Birge-Massart准则。
小波去噪阈值的几种方法
[thr,sorh,keepapp]=ddencmp('den','wv',x); xd2=wdencmp('gbl',c,l,wname,level,thr,'h',1);
02
小波包阈值去噪的过程
1 DecompositionFor a given wavelet, compute the wavelet packet decomposition of signal x at level N.（计算信号x在N层小波包分解的系数）2 Computation of the best treeFor a given entropy, compute the optimal wavelet packet tree. Of course, this step is optional. The graphical tools provide a Best Tree button for making this computation quick and easy.（以熵为准则，计算最佳树，当然这一步是可选择的。）3 Thresholding of wavelet packet coefficientsFor each packet (except for the approximation), select a threshold and apply thresholding to coefficients.（对于每一个小波包分解系数，选择阈值并应用于去噪）The graphical tools automatically provide an initial threshold based onbalancing the amount of compression and retained energy. This threshold is.（工具箱会根据压缩量和剩余能量提供一个初始化的阈值，不过仍需要不断测试来选择阈值优化去噪效果）a reasonable first approximation for most cases. However, in general youwill have to refine your threshold by trial and error so as to optimize theresults to fit your particular analysis and design criteria.
小波去噪阈值的确定和分解层数的确定
小波包阈值去噪的过程
4 Reconstruction Compute wavelet packet reconstruction based on the original approximation coefficients at level N and the modified coefficients.（根据计算后的小 波包系数重构原信号。）
1
0.5
0
-0.5
获得单个阈值，对所有的高频小波系数进行处理。
-1
-1.5
0
50
100
150
200
250
300
350
400
450
软阈值去噪 1.5
1
0.5
0
-0.5
-1
-1.5
0
50
100
150
200
250
300
350
400
450
小波去噪阈值的几种方法
1.5 1
小波包分解和重构去噪
[c,l]=wavedec(x,level,wname); ca3=appcoef(c,l,wname,3); cd3=detcoef(c,l,3); cd2=detcoef(c,l,2); cd1=detcoef(c,l,1); xd4=wrcoef('a',c,l,wname,level);
小波包阈值去噪的过程
1 Decomposition For a given wavelet, compute the wavelet packet decomposition of signal x at level N.（计算信号x在N层小波包分解的系数） 2 Computation of the best tree For a given entropy, compute the optimal wavelet packet tree. Of course, this step is optional. The graphical tools provide a Best Tree button for making this computation quick and easy.（以熵为准则，计算最佳树，当然 这一步是可选择的。） 3 Thresholding of wavelet packet coefficients For each packet (except for the approximation), select a threshold and apply thresholding to coefficients.（对于每一个小波包分解系数，选择阈值 并应用于去噪） The graphical tools automatically provide an initial threshold based on balancing the amount of compression and retained energy. This threshold is.（工具箱会根据压缩量和剩余能量提供一个初始化的阈值，不过仍需要不 断测试来选择阈值优化去噪效果） a reasonable first approximation for most cases. However, in general you will have to refine your threshold by trial and error so as to optimize the results to fit your particular analysis and design criteria.
基于小波变换的自适应QRS-T对消P波检测算法
ｓ ｔ ｆ ｃ ｏ ｙ ｒ ｓ ｌｓ ａ ｉ ａ ｔ ｒ ｅ ｕｔ ． ｓ
Ｋ ｅ ｒ ｓ ＥＣＧ ｉｎａ； ｙｗｏ ｄ ： ｓｇ ｌ Ｄｙａ ｉ ａ ｒｗａ ｅｅ ； ａｌｔａｇ ｒｔ ｍ ； ｗａ ｅｄ ｔ ｃｉｎ ｄ ｃＭ ｒ ｖ ｌｔ Ｍ ｌ ａ ｌｏ ｉｈ Ｐ— ｖ ｅ ｅ ｔｏ
（ ｏ ｅ ｌ ｔ ｎｃ ｎ ｎｉｅｒ ｇ Ｎ ｔ ｎｌ ｎｖ ｏ ｆ ｓ Ｔｃｎ ｌ ｙ Ｃ ａｇｈ １０ ３ Ｃ ｉａ Ｃ ｌｇ ｏＥｅ ｒ ｉ ａ ｄ ｇ ｅｉ ， ａ ｏ ａ Ｕ ｉ ｆ ｅ ｅ ｅｈ ｏ ｇ， ｈｎ ｓａ ０７ ， ｈ ） ｌｅ ｆ ｃｏ Ｅ ｎ ｎ ｉ ． Ｄｅ ｎ ｏ ４ ｎ
法经 ＭＩ — Ｉ Ｔ Ｂ Ｈ心 电数据库数据验证 ，取得 了满意 的结果 。
关键词 ：心 电信号 ：二进 Ｍａｒ小波 ；Ｍａｌｔ算法 ；Ｐ 检测 ｒ ｌ ａ 波
中图分类号： Ｎ １． ， ５０ Ｔ ９１ ３ Ｒ ４． １ ２ ４
文献标识码： Ａ
文章编号： ０ ９ ８６２０ ）８１６—４ １０— ９（０７０—８８ ５ ０
自适应小波阈值去噪方法
3. 2 自适应梯度优化算法及阈值方程 若观测数据向量为 y = [ y 0 , y1 , …, y N - 1 ] T , 则 :
y i = f i + ni ( i = 0 , 1 , …, N - 1)
其中 : f 为真实信号 ; n 为独立同分布高斯白噪声 。 首先 , 用离散小波变换将观测数据分解 , 得到 j 尺度 ( x , tj) = 的小波系数 u j , k , 这时再使用标准软门限方程 η
Adaptive Denoising by Sof t
thresholding with Wavelets
L IU Jing1 ,ZHAN G Daoming1 , TIAN Hua2 ,CU I Liancheng3
(1. College of Info rmation and Elect rical Engineering ,China University of Mining and Technology ,Xuzhou ,221008 ,China ; 2. Ningxia Coal Indust ry Group Co. L td. , Yinchuan ,751410 ,China ;3. Longkou Mining Group Co. L td. ,Longkou ,265700 ,China)
多媒体技术
刘 静等 : 自适应小波阈值去噪方法
自适应小波阈值去噪方法
刘 静1 ,张道明1 ,田 华2 ,崔连成3
( 1. 中国矿业大学 信息与电气工程学院 江苏 徐州 221008 ; 2. 神华宁夏煤业集团 宁夏 银川 751410 ;3. 龙口矿业集团有限公司 山东 龙口 265700)
1 2k + 1
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1 一种基于小波变化的自适应阈值算法研究 黄诚学1） 韩绍泽2） （武汉数字工程研究所军代室1） 武汉 430074） （武汉数字工程研究所2） 武汉 430074） 摘 要：雷达信号处理在整个雷达系统中一直都起着举足轻重的作用，同时也是雷达技术发展中最为活跃的部分。本文主要探讨小波变换在雷达视频压缩中的应用。针对雷达回波信号这些特点，提出了一种基于小波的自适应阈值方法进行雷达回波信号去噪处理，在保留雷达回波的前提下，降低了雷达数字视频的信息量，为雷达数字视频数据的编码打下了良好的基础。而在雷达图像处理中，嵌入式零树小波算法对雷达图像进行压缩取得了不错的效果。利用本文的信号去噪方法对雷达视频数据进行预处理后在实时性传输方面具有很高的应用价值和前景。 关键词：小波变换 雷达 信号处理 图像压缩
A Kind of Research on Self-adaptive Threshold Method Based on
Wavelet Transform Huang Chengxue1） Han Shaoze2） (Military Delegate Chamber in WuHan Digital Engineering Institute1）,WuHan 430074) (WuHan Digital Engineering Institute2）,WuHan 430074) Abstract：The application of wavelet transform in radar video data compressing is mainly discussed in this paper. This paper proposed an adaptive threshold method. The main idea of this method is to use the sub of adjacent threshold coefficient which is less than a parameter to determine the threshold value. The simulation results show that the self-adaptive threshold method mentioned in the paper can get satisfactory result for radar echo signal de-noising and the coding method of EZW can also get good results. The threshold method decreases the information of radar video and gets a good foundation for radar signal coding when we consider the radar echo as a precondition. The research on radar video data processing in this thesis is of significant application value and is prospective in signal actual time transmitting. Key Words: wavelet transform radar signal processing image compression
1. 雷达回波信号去噪 雷达回波信号是由雷达天线接收到有效目标反射回来的有用信号、空间其它物体反射回来的杂波信号、自然界噪声干扰以及机器工作时的热噪声等线性迭加形成的，雷达原始视频
信号()zt有两种可能性[1]：信号加噪声即()()()ztstet；只有噪声即()()ztet。
1.1小波分析用于信号消噪处理 由Mallat小波变换算法的分解和重构步骤，可以得到各级小波变换的逼近信号和细节信号。粗分辨逼近相对原始信号是越来越粗略和平滑，将原始信号的边缘的轮廓和噪声导致 2
的毛刺逐渐平滑掉，剩下的即为原始信号的主体部分；细节信息主要体现原始信号的边缘成分。由于小波变换的多分辨率特性，在合适的尺度下原来是非平稳的跳变信号会呈现出与噪声截然不同的特性[2]。 含噪的一维信号模型可表示为如下形式：
()()()skfkek，0,1,...,1kn
其中，()sk为含噪信号，()fk为有用信号，()ek为噪声信号。()ek通常表现为高频信号，而实际中()fk通常为低频信号。
图 1信号的三层小波分解 一维信号消噪的过程可分为如下3个步骤： （1）信号的小波分解。（如进行三层分解，分解过程如图1所示)，噪声信号多包含在具有较高频率的细节cD1、cD2和cD3中。（2）小波分解高频系数的硬阈值量化。（3）一维小波重构。根据小波分解的底层低频系数和各层高频系数进行一维小波重构。最关键的是如何选择阈值及如何进行阈值量化，在某种程度上，它关系到信号消噪的质量
1.2 阈值选取准则 对于被高斯白噪声污染的信号基本噪声模型，选择阈值的准则如下[3]： （1）无偏似然估计原理的自适应阈值选择。给定一个阈值，得到它的似然估计，再将非似然最小化，就可得到所选的阈值。 （2）固定阈值准则。利用固定形式的阈值，可取得较好的去噪特性。所产生的阈值为
2log(2)n n为待估计矢量的长度。
（3）混合准则。它是前两种阈值的综合，所选择的是最优预测变量阈值。 （4）极小极大准则。本准则采用固定阈值获得理想过程的极小极大特性。
1.3 基于小波的雷达信号自适应阈值算法 本文提出了一种基于正交小波变换和自适应阈值算法的噪声抑制方法。 通过正交小波变换将原始信号分解到若干不同频带上，采用分层阈值的方式对雷达视频信号进行处理。低频子带的缩放因子大，表示小波比较宽，度量的是信号轮廓；高频子带的缩放因子小，表示小波比较窄，度量的是信号的细节，所以低频子带就有较高的幅度值，从 3
而较低频率回波脉冲保留了的较详细的轮廓；而高频子带有相对较低的幅度值，只保留下回波脉冲的高频细节部分，根据以上特征，采取有效措施，滤除幅度较低的高频杂波和噪声。 自适应阈值算法的基本思想是由于信号对应的小波系数其幅值较大，但数目较少，而噪声对应的小波系数是一致分布的，个数较多，但幅值小。基于以上性质，可以假设初始阈值，将绝对值小于该阈值的小波系数置零，当该阈值一步一步增大时，刚开始的非零值个数会快速下降，即小于阈值的小波系数个数快速增加（主要是噪声信号），但当下降到某一点假设只剩下有用信号的情况下，当阈值进一步增大时，此时所得出的非零值个数会减少比较缓慢，曲线相对平坦。图2所示为某雷达信号经3级小波分解后的高频分量及低频分量的绝对值分布图。
图2 分量绝对值分布图 算法如下：先定义一个初始阈值，然后定义一个步长 ，从初始阈值开始 ，每加一次步长 ，将阈值不断更新 ，将绝对值比阈值小的小波系数值置0 ，得出非零值个数 ，当两邻近阈值所得出的非零值个数差小于某个自定义的参数（跟信号有关）时 ，就得出所要求的阈值 ，选取两阈值中较小的那个 。 该算法流程图如图3所示： 4
图3自适应阈值算法流程图 1.4自适应阈值算法的实验仿真与结果分析
分别用现有的阈值选取准则与自适应阈值选取对实际采集的某雷达信号进行处理，结果如图4所示。由图可以看出现有的4种阈值选取准则对实际的雷达回波信号是不适用的，大量的噪声仍然存在，对信号的压缩起的作用不大。而自适应阈值处理雷达信号效果还是比较不错的，大量的噪声信号重构后都去除了，从而可以提高信号压缩效率。 5
图4不同阈值准则效果图 应用阈值法对信号消噪的流程图如图5所示。实验所用数据为2006年8月于葫芦岛实际采集的雷达数据。
图5信号消噪流程图 经小波分解后得到的各级小波系数是信号在不同频带的体现。各级小波系数与频带的关系见图6。其中，V0、V1、V2、V3等代表各级低频子空间，W1、W2、W3等代表各级高频子空间，在尺度为1时，V0分解为V1与W1的直和即V0=V1W1，W1就是V1在V0中的正交补空间，改变尺度继续分割下去就有V0=V1W1= V2W2W1=…，可见，Wi就是对V0空间结构的细节补充，同时Vi就是在尺度i下对V0的基本特性的表征。
图6 频带的逐级剖分 6
对某雷达信号进行3层小波分解，其小波系数向量如图7所示为该信号的原始小波系数向量图。
(b) 图7 信号3级小波分解系数向量图 统计地分析图7各组小波系数得知，低频分量的幅度值较大，最大幅值为5.4978，仅占据了小波系数总数的1/8；高频分量、次高频分量和次低频分量的幅值超过90%集中在0~0.05之间，最大幅值分别为1.6497、1.3560、2.0358，占据了小波系数总数的7/8，而所含能量少。 自适应阈值方法涉及3个主要相关参数——T：初始阈值，t：步长，n：自定义参数。 表1不同n值重构信号中的非零值 小波基 低频子带n=150 高频子带n=75 低频子带n=100 高频子带n=50 低频子带n=50 高频子带n=25 Haar（Db1） 3564 1692 1332 Db2 4026 2696 2204 Db3 4304 3136 2772 Db4 4360 3298 2836 表1列出了某雷达信号在不同小波基下进行三级小波分解后重构信号中的非零值个数，其中低频子带n分别取150，100，50，原信号的非零值个数为8094。图8所示为低频子带n分别取150，100，50的haar小波变换仿真结果(t=0.1)。
（a）