北京市海淀区2017届高三上学期期末考试地理试题Word版含答案
2017届北京市海淀区高三上学期期末考试语文试题(word版)

2017届北京市海淀区高三上学期期末考试语文试题2017.1学校班级姓名成绩一、本大题共7小题,共22分。
阅读下面的材料,完成1—7题。
材料一:太空之家①我国成功发射入轨的天宫二号,是一个长10米、最大直径3米多、重约8吨的人造航天器。
天宫二号在离地球近400公里的近地轨道上运行,开展各种工作和实验;它既是一个真正的太空实验室,也是能供航天员居住的“太空之家”。
②高智能是天宫二号作为“太空之家”的一个突出特点。
天宫二号可以自主进行飞行轨道及姿态调整、运行状态的智能化诊断等工作。
科研人员整合了航天器十多个分系统的数据,把复杂、晦涩的专业数据浓缩成52组画面,为航天员执行任务提供了清晰、直观、舒适的显示界面。
③科幻电影中技术人员像插拔U盘一样快捷更换损坏部件的场景,将在天宫二号内真实上演。
天宫二号在供配电、热控、数据管理等系统方面采用了高集成化模块设计,打造出“插拔式”接口,航天员在几分钟内就能完成一次维修更换。
这是天宫二号作为“太空之家”的一个新亮点。
④两名航天员要在太空驻留..30天,为避免出现“粮草不足”问题,科研人员研制了在轨补给系统。
天宫二号在太空可以边飞行边“加油”,而不必像天宫一号那样,起飞前必须把“油箱”加满,携带一吨多的推进剂。
天宫二号起飞前只加了半箱“油”,节省的重量..产品和航天员的生活物资。
..用来携带更多的载荷⑤科研人员还对天宫二号的居住环境进行了精心设计,使其更宜居。
航天员生活在由神舟十一号和天宫二号组成的组合体中,吃饭、睡觉在神舟飞船内,工作、娱乐和锻炼..在天宫二号内,15立方米的空间被紧凑地隔成多个功能区。
工作区和生活区的噪音控制在50分贝以内:舱内空气温度控制在22—24摄氏度,相对湿度控制在45%—55%,这是人体感觉最舒适的温湿度。
⑥此外,科研人员在天宫一号基础上,对电子邮件传输、天地视频通话等系统进行了改进。
天宫二号增加了邮件下行能力;航天员能与地面视频互动,也能与家人私密通话。
北京市西城区2022届高三上学期期末质量检测地理试题 Word版含答案

北京市西城区2021 — 2022学年度第一学期期末试卷高三地理 2022.1第一部分(选择题共40分)下图为冰岛地裂缝景观,拍摄于北京时间2021年7月19日22时,拍摄地点大致位于北纬64º、西经21º四周。
读图,回答第1、2题。
1.拍摄时A.当地时间正值傍晚 B.北京该日昼短夜长C.接近我国大暑节气 D.地球运行至近日点2.图中地裂缝A.大体呈东西向延长 B.两侧岩石来自地核C.处于板块消亡边界 D.为地震形成的褶皱圆明园武陵春色景区取意于《桃花源记》中“忽逢桃花林,夹岸数百步,中无杂树,……复前行,……便得一山,山有小口,仿佛若有光。
”下图为该景区原建筑布局示意图。
读图,回答第3、4题。
3.图中四条路线中最符合原文意境的是A.甲B.乙 C.丙D.丁4.获得该景区最佳观赏效果,适宜①置身景观其中②选择远观全景③把握观赏角度④洞悉文化定位A.①②B.①④ C.②③ D.③④2021年10月19日,北京、天津、河北中南部等地消灭大雾。
下图为该日08时亚洲局部地区海平面等压线分布图(单位:百帕)。
读图,回答第5~7题。
5.北京消灭大雾的缘由有①受低压把握,盛行上升气流②等值线分布稀疏,风力较小③水汽和分散核多,易形成雾④受冷锋过境影响,污染加重A.①②B.①④ C.②③D.③④6.假如甲天气系统向西北移动,台湾岛将可能消灭22:00 2021-07-19A.持续大雾B.狂风暴雨 C.晴空万里 D.大风降温7.图中A.风向普遍为偏南风B.地形以高原和山地为主C.河流均处于丰水期D.包括三种季风气候类型图4为四地气候要素统计图。
读图,回答第8、9题。
8.四地中终年温存多雨的是A.甲B.乙 C.丙D.丁9.图中A.甲地受海陆热力性质差异影响B.乙地全年受西风和暖流的影响C.丙地常年受东北信风带的把握 D.丁地夏季受副热带高气压把握图5为北京市某校同学赴南美洲和南极洲考察路线图。
读图,回答第10~12题。
2017届北京市海淀区高三上学期期末考试历史试题Word版含答案

海淀区高三年级2016-2017学年第一学期期末练习历史2017.1第Ⅰ卷(选择题,共48分)一、选择题(32小题,每小题1.5分,共48分)1.1919年5月31日,《申报》刊登了一个社会团体的通电:“全省议会、教育会、商会、农会、工会暨全国公民均鉴北京政府反民好恶,任用内奸,视爱国行动为煽惑……共和国家主权在民,安能任其压制而不思抵抗?”由材料可知A.五四运动得到了各界的支持B.参加巴黎和会引起广泛不满C.五四运动取得了初步的胜利D.推翻北洋政府成为民众共识2.1924年11月,孙中山在一次谈话中说:“十三年来,民国绝无起色,党务并不进步,皆由尔等不肯奋斗之过……彼共产党成立未久,已有青年同志二百万人,可见其奋斗之成绩。
”这段话表明孙中山A.决定与中国共产党进行合作B.赞赏共产党人的革命精神C.责备国民党“右派”背叛革命D.依靠共产党发动北伐战争3.1926年至1927年我国南方出现了为数众多的农民报刊,其中尤以地方农民协会主办的农运报刊有影响力,如湖北、山东、湖南、四川等地都有关于农民运动的定期刊物。
这说明A. 农民已成为国民革命的领导力量B. 农民运动是国民革命的主要形式C. 国民革命重视对农民的政治宣传D. “工农武装割据”思想迅速传播4. 1933年,中共临时中央提出“短促突击”的战术,“御敌于国门之外”,让装备很差的红军同用现代武器装备的敌军打正规战、阵地战、堡垒战。
其结果是A.粉碎国民党对根据地的围剿B. 为武装斗争积累了成功的经验C.中央红军主力被迫进行长征D. 造成了军事上的“左”倾冒进5.按照一级标题,二级标题,三级标题的逻辑顺序,下表空格处应该填入的A.南昌起义B.土地革命战争时期 C.遵义会议D.抗日战争时期6.右下图为埃德加·斯诺1936年8月在豫旺堡(今宁夏同心县豫旺堡)拍摄的经典照片《抗战之声》。
对照片出现的历史背景解释准确的是A.中央红军完成战略转移B.抗日民族统一战线形成C.日本发动了卢沟桥事变D.红军主力改编为八路军7. 中国近代生产与旧式生产的增长及比重变化(货币单位:1936年币值亿元)由上表数据可得出的正确结论是①国民经济中传统部门和近代部门并存②近代企业生产增长缓慢,规模小③民国成立后政府压制近代经济的发展④传统的自然经济成分仍大量存在A.①②③B. ①③④C. ②③④D. ①②④8. 1937年9月,毛泽东发出指示:“要实行这样的方针,就要战略上有有力部队处于敌之侧翼,就要以创造根据地发动群众为主,就要分散兵力,而不是集中打仗为主。
北京市西城区2015届高三上学期期末考试地理试题 Word版含答案

北京西城区2014—2015学年度第一学期高三期末考试地理试题试卷满分100分考试时长120分钟一、选择题(40题,共40分)美国“猎户座”飞船于当地时间2014年12月5日07:05分,在佛罗里达州卡纳维拉尔角()发射成功,将承担火星探索重任。
火星大气压不足地球大气压的1%,自转轴与公转轨道面的夹角为。
据此回答第1~3题。
1.“猎户座”飞船发射时,世界时是A.4日12:05 B.4日20:05 C.5日12:05 D.5日20:052.“猎户座”飞船A.脱离了太阳系B.穿过木星轨道C.受太阳辐射影响 D.探测到火星生命3.与火星比,地球A.昼夜温差小B.表面温度低C.黄赤交角大D.太阳高度角大2014年11月APEC领导人峰会在北京举行,会址位于三面环山,背倚明长城的怀柔区雁栖渤畔。
读图1,回答第4—6题。
4.北京APEC峰会举办时,图中四地A.符拉迪沃斯托克出现极昼B.横滨角速度最快C.夏威夷正午太阳高度最大D.巴厘岛昼长夜短5.北京APEC峰会选址雁栖湖畔,主要考虑其①旅游资源丰富②基础设施先进③循环经济发达④生态环境优越A.①②B.①④C.②③D.③④6.图中四地均A.位于东半球B.处于地震带C.西临太平洋D.属同一大洲7.图2 (a)中A.地势南北高,中部低B.虎山比龙山气温低C.河流在春季出现凌汛D.以落叶阔叶林为主8.与甲村相比,乙村A.纬度更低且位于阳坡B.年降水量大且较为集中C.人口和用地规模较小D.易受滑坡或泥石流影响9.图2 (b)中,河谷所处的地质构造是①背斜②向斜③地垒④地堑A.①②B.①③C.②④D.③④10.拟在该区域建设太阳能发电站,最适宜的地点是图2(b)中A.①B.②C.③D.④图3为1974年、2014年青海湖示意图。
读图,回答第11~13题。
11.能够实时全面监测青海湖湖面变化的是A.全球定位系统B.遥感技术C.地理信息系统D.野外考察12.青海湖A.补给来源包括河流和降水B.直接参与了海陆间水循环C.周边地区水土流失很严重D.湖面面积因围湖造田减小13.沙岛形成的主要原因是A.湖水的搬运作用B.沙尘暴的强烈侵蚀C.滑坡岩体的风化D.沉积物的堆积作用图4 (a)为2014年10月10日郝佳与刘毅的微信实时界面图,图4(b)是郝佳手机的GPS 定位界面图,图示时间均为北京时间。
北京市海淀区2017届高三上学期期末考试数学(理)试题(全Word版,含答案)
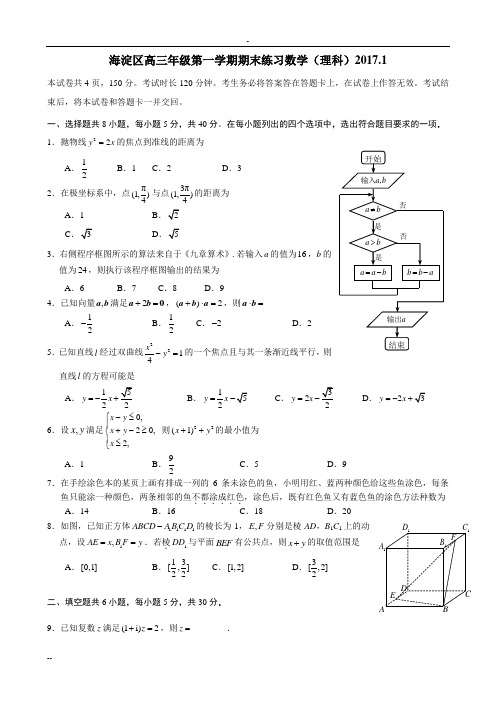
海淀区高三年级第一学期期末练习数学(理科)2017.1本试卷共4页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
一、选择题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项. 1.抛物线22y x =的焦点到准线的距离为A .12B .1C .2D .32.在极坐标系中,点π(1,)4与点3π(1,)4的距离为A .1B .2C .3D .53.右侧程序框图所示的算法来自于《九章算术》.若输入a 的值为16,b 的值为24,则执行该程序框图输出的结果为 A .6B .7C .8D .94.已知向量,a b 满足2+=0a b ,()2+⋅=a b a ,则⋅=a bA .12-B .12C .2-D .25.已知直线l 经过双曲线2214x y -=的一个焦点且与其一条渐近线平行,则直线l 的方程可能是A .1522y x =-+B .152y x =- C .322y x =- D .23y x =-+6.设,x y 满足0,20,2,x y x y x -≤⎧⎪+-≥⎨⎪≤⎩则22(1)x y ++的最小值为A .1B .92C .5D .97.在手绘涂色本的某页上画有排成一列的6条未涂色的鱼,小明用红、蓝两种颜色给这些鱼涂色,每条鱼只能涂一种颜色,两条相邻的鱼不.都.涂成红色....,涂色后,既有红色鱼又有蓝色鱼的涂色方法种数为 A .14 B .16 C .18 D .20 8.如图,已知正方体1111ABCD A B C D -的棱长为1,,E F 分别是棱AD ,B 1C 1上的动点,设1,AE x B F y ==.若棱.1DD 与平面BEF 有公共点,则x y +的取值范围是 A .[0,1]B .13[,]22C .[1,2]D .3[,2]2二、填空题共6小题,每小题5分,共30分. 9.已知复数z 满足(1i)2z +=,则z =________.ABCD1D 1A 1B 1C E F开始是否是否a a b=-b b a=-a输出结束,a b输入a b≠a b>10.在261()x x+的展开式中,常数项为________.(用数字作答)11.若一个几何体由正方体挖去一部分得到,其三视图如图所示,则该几何体的体积为________.12.已知圆C :2220x x y -+=,则圆心坐标为_____;若直线l 过点(1,0)-且与圆C 相切,则直线l 的方程为____13.已知函数2sin()y x ωϕ=+π(0,||)2ωϕ><.① 若(0)1f =,则ϕ=________;② 若x ∃∈R ,使(2)()4f x f x +-=成立,则ω的最小值是__. 14.已知函数||()e cos πx f x x -=+,给出下列命题:①()f x 的最大值为2;②()f x 在(10,10)-内的零点之和为0; ③()f x 的任何一个极大值都大于1. 其中所有正确命题的序号是________.三、解答题共6小题,共80分.解答应写出文字说明、演算步骤或证明过程. 15.(本小题满分13分)在∆ABC 中,2c a =,120B =,且∆ABC 面积为32. (Ⅰ)求b 的值; (Ⅱ)求tan A 的值.16.(本小题满分13分)诚信是立身之本,道德之基.某校学生会创设了“诚信水站”,既便于学生用水,又推进诚信教育,并用“周实际回收水费周投入成本”表示每周“水站诚信度”.为了便于数据分析,以四周为一....周期..,下表为该水站连续十二周(共三个周期)的诚信度数据统计:第一周 第二周 第三周 第四周 第一个周期95% 98% 92% 88% 第二个周期94% 94% 83% 80% 第三个周期85%92%95%96%(Ⅰ)计算表中十二周“水站诚信度”的平均数x ;(Ⅱ)分别从上表每个周期的4个数据中随机抽取1个数据,设随机变量X 表示取出的3个数据中“水站诚信度”超过91%的数据的个数,求随机变量X 的分布列和期望;(Ⅲ)已知学生会分别在第一个周期的第四周末和第二个周期的第四周末各举行了一次“以诚信为本”的主题教育活动.根据已有数据,说明两次主题教育活动的宣传效果,并根据已有数据陈述理由.17.(本小题满分14分)如图1,在梯形ABCD 中,//AB CD ,90ABC ∠=,224AB CD BC ===,O 是边AB 的中点.将三俯视图2左视图211主视图角形AOD 绕边OD 所在直线旋转到1A OD 位置,使得1120AOB ∠=,如图2.设m 为平面1A DC 与平面1A OB 的交线.(Ⅰ)判断直线DC 与直线m 的位置关系并证明; (Ⅱ)若直线m 上的点G 满足1OG A D ⊥,求出1A G 的长; (Ⅲ)求直线1A O 与平面1A BD 所成角的正弦值.18.(本小题满分13分)已知(0,2),(3,1)A B 是椭圆G :22221(0)x y a b a b+=>>上的两点.(Ⅰ)求椭圆G 的离心率;(Ⅱ)已知直线l 过点B ,且与椭圆G 交于另一点C (不同于点A ),若以BC 为直径的圆经过点A ,求直线l 的方程.19. (本小题满分14分)已知函数()ln 1af x x x=--. (Ⅰ)若曲线()y f x =存在斜率为1-的切线,求实数a 的取值范围;(Ⅱ)求()f x 的单调区间;(Ⅲ)设函数()ln x ag x x+=,求证:当10a -<<时,()g x 在(1,)+∞上存在极小值.20.(本小题满分13分)对于无穷数列{}n a ,{}n b ,若1212max{,,,}min{,,,}(1,2,3,)k k k b a a a a a a k =-=,则称{}n b 是{}n a 的“收缩数列”.其中,12max{,,,}k a a a ,12min{,,,}k a a a 分别表示12,,,k a a a 中的最大数和最小数.已知{}n a 为无穷数列,其前n 项和为n S ,数列{}n b 是{}n a 的“收缩数列”.(Ⅰ)若21n a n =+,求{}n b 的前n 项和; (Ⅱ)证明:{}n b 的“收缩数列”仍是{}n b ;(Ⅲ)若121(1)(1)22n n n n n n S S S a b +-+++=+(1,2,3,)n =,求所有满足该条件的{}n a .海淀区AOBCD1图ODCB2图1A高三年级第一学期期末练习数学(理科)答案及评分标准2017.1一、选择题(共8小题,每小题5分,共40分)1.B2.B3. C4.C5.A6. B7.D8.C 二、填空题(共6小题,每小题5分,共30分,9. 1i -10.15 11.16312.(1,0);3(1)3y x =+和3(1)3y x =-+13.π6,π214.①②③三、解答题(共6小题,共80分) 15.(本小题满分13分)解:(Ⅰ)由∆ABC 面积公式及题设得1sin 2S ac B ==1332222a a ⨯⨯=,解得1,2,a c ==由余弦定理及题设可得2222cos b a c ac B =+-114212()72=+-⨯⨯⨯-=,又0,7b b >∴=. (不写b>0不扣分) (Ⅱ)在∆ABC 中,由正弦定理sin sin a bA B =得:1321sin sin 2147a A B b ==⨯=, 又120B =,所以A 是锐角(或:因为12,a c =<=) 所以217557cos 1sin 19614A A =-==, 所以sin 213tan .cos 557A A A === 16. (本小题满分13分)解:(Ⅰ)十二周“水站诚信度”的平均数为x =95+98+92+88+94+94+83+80+85+92+95+96=91%12100⨯(Ⅱ)随机变量X 的可能取值为0,1,2,3三个周期“水站诚信度”超过91%分别有3次,2次,3次1212(0)44464P X ==⨯⨯=32112112314(1)44444444464P X ==⨯⨯+⨯⨯+⨯⨯=32132132330(2)44444444464P X ==⨯⨯+⨯⨯+⨯⨯=32318(3)44464P X ==⨯⨯=随机变量X的分布列为X0 1 2 3P 1327321532932171590123232323232EX=⨯+⨯+⨯+⨯=.(Ⅲ)本题为开放问题,答案不唯一,在此给出评价标准,并给出可能出现的答案情况,阅卷时按照标准酌情给分.给出明确结论,1分,结合已有数据,能够运用以下三个标准中的任何一个陈述得出该结论的理由,2分.标准1:会用主题活动前后的百分比变化进行阐述标准2:会用三个周期的诚信度平均数变化进行阐述标准3:会用主题活动前后诚信度变化趋势进行阐述可能出现的作答情况举例,及对应评分标准如下:情况一:结论:两次主题活动效果均好.(1分)理由:活动举办后,“水站诚信度”由88%→94%和80%→85%看出,后继一周都有提升.(2分)情况二:结论:两次主题活动效果都不好.(1分)理由:三个周期的“水站诚信度”平均数分别为93.25%,87.75%,92%(平均数的计算近似即可),活动进行后,后继计算周期的“水站诚信度”平均数和第一周期比较均有下降.(2分)情况三:结论:第一次主题活动效果好于第二次主题活动.(1分)理由:第一次主题活动举办的后继一周“水站诚信度”提升百分点(94%-88%=6%)高于第二次主题活动举办的后继一周“水站诚信度”提升百分点(85%-80%=5%).(2分)情况四:结论:第二次主题活动效果好于第一次主题活动.(1分)理由:第一次活动后“水站诚信度”虽有上升,但两周后又有下滑,第二次活动后,“水站诚信度”数据连续四周呈上升趋势. (2分)(答出变化)情况五:结论:两次主题活动累加效果好.(1分)理由:两次主题活动“水站诚信度”均有提高,且第二次主题活动后数据提升状态持续周期好.(2分)情况六:以“‘两次主题活动无法比较’作答,只有给出如下理由才给3分:“12个数据的标准差较大,尽管平均数差别不大,但比较仍无意义”.给出其他理由,则结论和理由均不得分(0分).说明:①情况一和情况二用极差或者方差作为得出结论的理由,只给结论分1分,不给理由分2分.②以下情况不得分.情况七:结论及理由“只涉及一次主题活动,理由中无法辩析是否为两次活动后数据比较之结果”的.例:结论:第二次主题活动效果好.理由:第二次主题活动后诚信度有提高.③其他答案情况,比照以上情况酌情给分,赋分原则是:遵循三个标准,能使用表中数据解释所得结论.17. (本小题满分14分)解:(Ⅰ)直线DC //m .证明:由题设可得//,CD OB 1CD AOB ⊄平面,1OB AOB ⊂平面, 所以//CD 平面1A OB .又因为CD ⊂平面1A DC ,平面1ADC 平面1A OB m =所以//CD m .法1:(Ⅱ)由已知224AB CD BC ===,O 是边AB 的中点,//AB CD ,所以//CD OB ,因为90ABC ∠=,所以四边形CDOB 是正方形, 所以在图1中DO AB ⊥,所以结合题设可得,在图2中有1DO OA ⊥,DO OB ⊥, 又因为1OA OB O =,所以1DO AOB ⊥平面. 在平面AOB 内作OM 垂直OB 于M ,则DO OM ⊥. 如图,建立空间直角坐标系O xyz -,则1(3,1,0),(0,2,0),(0,0,2)A B D -,所以1(3,1,2)A D =-.设(3,,0)G m ,则由1OG A D ⊥可得10A D OG ⋅=,即(3,1,2)(3,,0)30m m -⋅=-+=解得3m =.所以14AG =. (Ⅲ)设平面1A BD 的法向量(,,)x y z =n ,则110,0,A D A B ⎧⋅=⎪⎨⋅=⎪⎩n n 即320,330,x y z x y ⎧-++=⎪⎨-+=⎪⎩令1y =,则3,1x z ==, 所以(3,1,1)=n ,设直线1A O 与平面1A BD 所成角为θ,则sin θ=1115cos ,5A O n A O n A O n⋅<>==⋅.法2:(Ⅱ)由已知224AB CD BC ===,O 是边AB 的中点,//AB CD ,所以//CD OB ,因为90ABC ∠=,所以四边形CDOB 是正方形, 所以在图1中DO AB ⊥,所以结合题设可得,在图2中有1DO OA ⊥,DO OB ⊥, 又因为1OA OB O =,ODCBG1A zxy M所以1DO AOB ⊥平面. 又因为1OG AOB ⊂平面,所以DO OG ⊥. 若在直线m 上的点G 满足1OG A D ⊥,又1OD A D D =,所以1OG AOD ⊥平面, 所以1OG OA ⊥,因为11120,//AOB OB AG ∠=,所以160OAG ∠=, 因为12OA =,所以14A G =.(注:答案中标灰部分,实际上在前面表达的符号中已经显现出该条件,故没写不扣分) (Ⅲ)由(II )可知1OD OA OG 、、两两垂直,如图,建立空间直角坐标系O xyz -,则10,0,0),(2,0,0),(1,3,0),(0,0,2)O A B D -(, 所以11(2,0,2),(3,3,0,)A D A B =-=- 设平面1A BD 的法向量(,,)n x y z =,则110,0,n A D n A B ⎧⋅=⎪⎨⋅=⎪⎩即220,330,x z x y -+=⎧⎪⎨-+=⎪⎩令1x =,则3,1y z ==,所以(1,3,1)n =,设直线1A O 与平面1A BD 所成角为θ,则 sin θ=1115cos ,5AO n AO n AO n ⋅<>==⋅.18. (本小题满分13分) 解:(Ⅰ)由已知2,b =由点(3,1)B 在椭圆G 上可得29114a +=, 解得212,23a a ==.所以2228,22c a b c =-==, 所以椭圆G 的离心率是6.3c e a == (Ⅱ)法1:因为以BC 为直径的圆经过点A ,所以AB AC ⊥,O DCBG1A zxy由斜率公式和(0,2),(3,1)A B 可得13AB k =-,所以3Ac k =,设直线AC 的方程为32y x =+. 由2232,1124y x x y =+⎧⎪⎨+=⎪⎩得2790x x +=,由题设条件可得90,7A C x x ==-,所以913()77C -,-,所以直线BC 的方程为213y x =-. 法2:因为以BC 为直径的圆经过点A ,所以AB AC ⊥,由斜率公式和(0,2),(3,1)A B 可得13AB k =-,所以3Ac k =,设C C C x y (,) ,则23C Ac Cy k x -==,即32C C y x =+① 由点C 在椭圆上可得221124C C x y +=② 将①代入②得2790C C x x +=,因为点C 不同于点A ,所以97C x =-,所以913()77C -,-,所以直线BC 的方程为213y x =-. 法3:当直线l 过点B 且斜率不存在时,可得点(3,1)C -,不满足条件.设直线BC 的方程为1(3)y k x -=-,点C C C x y (,)由2213,1124y kx k x y =+-⎧⎪⎨+=⎪⎩可得222(31)6(13)3(13)120k x k k x k ++-+--=,显然0∆>,此方程两个根是点B C 和点的横坐标,所以223(13)12331C k x k --=+,即22(13)4,31C k x k --=+所以22361,31C k k y k --+=+因为以BC 为直径的圆经过点A , 所以AB AC ⊥,即0AB AC ⋅=. (此处用1AB AC k k ⋅=-亦可)2222963961(3,1)(,)3131k k k k AB AC k k -----⋅=-⋅=++2236128031k k k --=+,即(32)(31)0k k -+=,1221,,33k k ==-当213k =-时,即直线AB ,与已知点C 不同于点A 矛盾,所以12,3BC k k ==所以直线BC 的方程为213y x =-.19. (本小题满分14分) 解:(Ⅰ)由()ln 1af x x x =--得221'()(0)a x af x x x x x+=+=>.由已知曲线()y f x =存在斜率为1-的切线, 所以'()1f x =-存在大于零的实数根, 即20x x a ++=存在大于零的实数根, 因为2y x x a =++在0x >时单调递增, 所以实数a 的取值范围0∞(-,).(Ⅱ)由2'()x af x x+=,0x >,a ∈R 可得 当0a ≥时,'()0f x >,所以函数()f x 的增区间为(0,)+∞; 当0a <时,若(,)x a ∈-+∞,'()0f x >,若(0,)x a ∈-,'()0f x <, 所以此时函数()f x 的增区间为(,)a -+∞,减区间为(0,)a -.(Ⅲ)由()ln x a g x x+=及题设得22ln 1('()(ln )(ln )a x f x x g x x x --==), 由10a -<<可得01a <-<,由(Ⅱ)可知函数()f x 在(,)a -+∞上递增, 所以(1)10f a =--<,取e x =,显然e 1>,(e)lne 10e a af e=--=->, 所以存在0(1,e)x ∈满足0()0f x =,即存在0(1,e)x ∈满足0'()0g x =,所以(),'()g x g x 在区间(1,)+∞上的情况如下:x0(1,)x 0x 0(,)x +∞'()g x-0 +()g x极小所以当10a -<<时,()g x 在(1,)+∞上存在极小值. (本题所取的特殊值不唯一,注意到0(1)ax x->>),因此只需要0ln 1x ≥即可)20. (本小题满分13分)解:(Ⅰ)由21n a n =+可得{}n a 为递增数列, 所以12121max{,,,}min{,,,}21322n n n n b a a a a a a a a n n =-=-=+-=-,故{}n b 的前n 项和为22(1)2n n n n -⨯=-.- (Ⅱ)因为12121max{,,,}max{,,,}(1,2,3,)n n a a a a a a n +≤=,12121min{,,,}min{,,,}(1,2,3,)n n a a a a a a n +≥=,所以1211211212max{,,,}min{,,,}max{,,,}min{,,,}n n n n a a a a a a a a a a a a ++-≥-所以1(1,2,3,)n n b b n +≥=. 又因为1110b a a =-=, 所以12121max{,,,}min{,,,}n n n n b b b b b b b b b -=-=,所以{}n b 的“收缩数列”仍是{}n b .(Ⅲ)由121(1)(1)22n n n n n n S S S a b +-+++=+(1,2,3,)n =可得 当1n =时,11a a =;当2n =时,121223a a a b +=+,即221b a a =-,所以21a a ≥;当3n =时,123133263a a a a b ++=+,即3213132()()b a a a a =-+-(*), 若132a a a ≤<,则321b a a =-,所以由(*)可得32a a =,与32a a <矛盾;若312a a a <≤,则323b a a =-,所以由(*)可得32133()a a a a -=-,--所以3213a a a a --与同号,这与312a a a <≤矛盾; 若32a a ≥,则331b a a =-,由(*)可得32a a =. 猜想:满足121(1)(1)22n n n n n n S S S a b +-+++=+(1,2,3,)n =的数列{}n a 是: 1212,1,,1,n a n a a a a n =⎧=≥⎨>⎩.经验证,左式=121212(1)[12(1)]2n n n S S S na n a na a -+++=++++-=+, 右式=112112(1)(1)(1)(1)(1)()22222n n n n n n n n n n n a b a a a na a +-+--+=+-=+.下面证明其它数列都不满足(Ⅲ)的题设条件.法1:由上述3n ≤时的情况可知,3n ≤时,1212,1,,1,n a n a a a a n =⎧=≥⎨>⎩是成立的.假设k a 是首次不符合1212,1,,1,n a n a a a a n =⎧=≥⎨>⎩的项,则1231k k a a a a a -≤===≠,由题设条件可得2212(1)(1)222k k k k k k k k a a a b ----+=+(*), 若12k a a a ≤<,则由(*)式化简可得2k a a =与2k a a <矛盾; 若12k a a a <≤,则2k k b a a =-,所以由(*)可得21(1)()2k k k k a a a a --=- 所以21k k a a a a --与同号,这与12k a a a <≤矛盾; 所以2k a a ≥,则1k k b a a =-,所以由(*)化简可得2k a a =.这与假设2k a a ≠矛盾.所以不存在数列不满足1212,1,,1,n a n a a a a n =⎧=≥⎨>⎩的{}n a 符合题设条件.法2:当i n ≤时,11212max{,,,}min{,,,}i i i i a a a a a a a a b -≤-=,所以1121()ki k i a a b b b =-≤+++∑,(1,2,3,,)k n =即112()k k S ka b b b ≤++++,(1,2,3,,)k n =由1(1,2,3,)n n b b n +≥=可得(1,2,3,,)k n b b k n ≤=又10b =,所以可得1(1)k n S ka k b ≤+-(1,2,3,)k =, 所以12111(2)[02(1)]n n n n n S S S a a na b b b n b +++≤++++⨯++++-,--即121(1)(1)22n n n n n nS S S a b +-+++≤+ 所以121(1)(1)22n n n n n n S S S a b +-+++≤+等号成立的条件是1(1,2,3,,)i i n a a b b i n -===,所以,所有满足该条件的数列{}n a 为1212,1,,1,n a n a a a a n =⎧=≥⎨>⎩.(说明:各题的其他做法,可对着参考答案的评分标准相应给分)精品文档考试教学资料施工组织设计方案。
北京市丰台区2017届高三上学期期末考试地理试题 Word版无答案

注意事项:丰台区2016~2017 学年度第一学期期末练习高三地理2017.012.大会期间A.马拉喀什炎热干燥B.地球绕日公转速度逐渐变慢C.恰逢中国霜降节气D.北京日落时刻早于马拉喀什3.摩洛哥A.地处中纬度,西临大西洋东邻撒哈拉沙漠1. 答题前,考生务必先将答题卡上的学校、年级、班级、姓名、准考证号用黑色字迹签字笔填写清楚,并认真核对条形码上的准考证号、姓名,在答题卡的“条形码粘贴区”贴好条形码。
2. 本次考试所有答题均在答题卡上完成。
选择题必须使用2B 铅笔以正确填涂方式将各小题对应选项涂黑,如需改动,用橡皮擦除干净后再选涂其它选项。
非选择题必须使用标准黑色字迹签字笔书写,要求字体工整、字迹清楚。
3. 请严格按照答题卡上题号在相应答题区内作答,超出答题区域书写的答案无效,在试卷、草稿纸上答题无效。
4. 请保持答题卡卡面清洁,不要装订、不要折叠、不要破损。
第Ⅰ卷(选择题共45 分)一、选择题:本大题共30 小题,每小题1.5 分,共45 分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
(请把正确答案填涂在答题卡上)第 22 届联合国气候变化大会于 2016 年 11 月 7 日至 18 日在摩洛哥马拉喀什市举行。
读图1,回答第1~4 题。
1.大会于当地时间2016 年11 月7 日上午开幕,此时北京正值图1A.11 月6 日午时B.11 月6 日傍晚C.11 月7 日下午D.11 月7 日深夜B.平均人口密度由东、南向西、北逐渐递减 C.北部河流冬季水位高,南部多季节性河流 D.沿海海域广,寒暖流交汇而渔业资源丰富4.全球气候变暖对摩洛哥可能产生的影响是A.缩短河流结冰期B.酸雨危害加重C.淹没大部分国土D.山地雪线上升图 2 为我国某地区等高线地形图。
读图,回答第5~7 题。
图2 5.在图中乙处进行从崖顶到崖底的绳降比赛,需准备绳子最适宜的长度是A.185 米B.245 米C.325 米D.415 米6.图中A.甲村与丙山温差大约为3℃至6℃ B.①河段比②河段水位季节变化大 C.③地适宜安排极限运动员露营地D.④地为图示比赛照片的拍摄地点7.利用智能手机软件测算丙山平均坡度所采用的地理信息技术是A.RS B.GPS C.GPS、GIS D.RS、GIS2016 年 11 月 17 日中央气象台发布寒潮蓝色预警。
北京市石景山区2024届高三下学期一模试题 地理 Word版含答案
石景山区2024年高三统一练习地理本试卷共10页,100分。
考试时长90分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将答题卡交回。
第一部分本部分共15题,每题3分,共45分。
在每题列出的四个选项中,选出最符合题目要求的一项。
首艘国产大邮轮“爱达·魔都号”于2024年1月1日首航,开启上海-济州-长崎福冈-上海7天6晚的旅程(图1)。
据此完成1~2题。
图11.“爱达·魔都号”首航期间()A.地球公转过远日点B.全程约一千千米C.船上日出时间变早D.沿途可见常绿林2.“爱达·魔都号”首航的意义有()A.维护国家海洋权益B.为国产邮轮发展提供经验C.探索新型旅游模式D.奠定我国的海洋强国地位图2示意2023年12月我国东部部分城市气象站最低气温变化。
据此完成3~4题。
2023年12月部分气象站最低气温曲线(℃)图2建设用地是指建造建筑物、构筑物的土地。
图5为我国2018-2022年国有建设用地供应情况。
据此完成9~10题。
图59.甲土地利用类型最有可能是()A.交通用地B.住宅用地C.商服用地D.农业用地10.下列说法正确的是()A.国有建设用地供应总量持续增加B.2022年各种用地供应占比均增长C.工矿仓储用地面积较大,地价高D.基础设施是国家发展的重要支撑2023年9月17日,云南“普洱景迈山古茶林文化景观”申遗成功,成为全球首个茶主题世界文化遗产。
“普洱景迈山古茶林文化景观”包含5片规模宏大、保存完好的古茶林和分布其中的9个古村寨以及古茶林之间的3片分隔防护林。
图6为景迈山林下种植立体结构和景迈山土地垂直利用示意图。
据此完成11~12题。
图611.普洱景迈山古茶林文化景观()A.地处我国东南地区,少数民族数量较多B.防护林主要功能是防风固沙,保护环境C.林下古茶树可避免强日照,茶叶品质好D.古村寨海拔高,利于种茶、采茶和制茶12.促进古茶林文化保护与发展措施合理的是()A.禁止开发生态茶园B.山麓应退耕还林C.培育优良茶树品种D.大力开发旅游业非洲人口第一大国尼日利亚(图7)是“一带一路”倡议的积极支持者。
北京市海淀区2017届高三上学期期中数学试卷(理科)Word版含解析
2016-2017学年北京市海淀区高三(上)期中数学试卷(理科)一、选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.已知集合A={x|x>2},B={x|(x﹣1)(x﹣3)<0},则A∩B=()A.{x|x>1} B.{x|2<x<3}C.{x|1<x<3}D.{x|x>2或x<1}2.已知向量=(﹣1,2),=(2,﹣4).若与()A.垂直 B.不垂直也不平行C.平行且同向D.平行且反向3.函数y=2x+的最小值为()A.1 B.2 C.2D.44.已知命题p:∃c>0,方程x2﹣x+c=0 有解,则¬p为()A.∀c>0,方程x2﹣x+c=0无解B.∀c≤0,方程x2﹣x+c=0有解C.∃c>0,方程x2﹣x+c=0无解D.∃c<0,方程x2﹣x+c=0有解5.已知函数y=a x,y=x b,y=log c x的图象如图所示,则()A.a>b>c B.a>c>b C.c>a>b D.c>b>a6.设,是两个向量,则“|+|>|﹣|”是“•>0”的()A.充分而不必要条件 B.必要而不充分条件C.充分必要条件 D.既不充分也不必要条件7.已知函数f(x)=cos4x+sin2x,下列结论中错误的是()A.f(x)是偶函数B.函f(x)最小值为C.是函f(x)的一个周期D.函f(x)在(0,)内是减函数8.如图所示,A是函数f(x)=2x的图象上的动点,过点A作直线平行于x轴,交函数g(x)=2x+2的图象于点B,若函数f(x)=2x的图象上存在点C使得△ABC为等边三角形,则称A 为函数f(x)=2x上的好位置点.函数f(x)=2x上的好位置点的个数为()A.0 B.1 C.2 D.大于2二、填空题共6小题,每小题5分,共30分.9.已知数列{a n}的前n项和S n=3n+1,则a2+a3=.10.若角θ的终边过点P(3,﹣4),则sin(θ﹣π)=.11.已知正方形ABCD边长为1,E是线段CD的中点,则•=.12.去年某地的月平均气温y(℃)与月份x(月)近似地满足函数y=a+bsin(x+)(a,b为常数).若6月份的月平均气温约为22℃,12月份的月平均气温约为4℃,则该地8月份的月平均气温约为℃.13.设函数f(x)=(a>0,且a≠1).①若a=,则函数f(x)的值域为;②若f(x)在R上是增函数,则a的取值范围是.14.已知函数f(x)的定义域为R.∀a,b∈R,若此函数同时满足:①当a+b=0时,有f(a)+f(b)=0;②当a+b>0时,有f(a)+f(b)>0,则称函数f(x)为Ω函数.在下列函数中:①y=x+sinx;②y=3x﹣()x;③y=是Ω函数的为.(填出所有符合要求的函数序号)三、解答题共6小题,共80分.解答应写出文字说明、演算步骤或证明过程.15.已知数列{a n}是公差为2的等差数列,数列{b n满足b n﹣b n=a n,且b2=﹣18,b3=﹣24.+1(Ⅰ)求数列{a n}的通项公式;(Ⅱ)求b n取得最小值时n的值.16.已知函数f(x)=cos(2x﹣)﹣cos2x.(Ⅰ)求f()的值;(Ⅱ)求函数f(x)的最小正周期和单调递增区间.17.已知函数f(x)=x3﹣9x,函数g(x)=3x2+a.(Ⅰ)已知直线l是曲线y=f(x)在点(0,f(0))处的切线,且l与曲线y=g(x)相切,求a的值;(Ⅱ)若方程f(x)=g(x)有三个不同实数解,求实数a的取值范围.18.如图,△ABC是等边三角形,点D在边BC的延长线上,且BC=2CD,AD=.(Ⅰ)求CD的长;(Ⅱ)求sin∠BAD的值.19.已知函数f (x )=e x (x 2+ax +a ).(Ⅰ)求f (x )的单调区间;(Ⅱ)求证:当a ≥4时,函数f (x )存在最小值.20.已知数列{a n }是无穷数列,满足lga n +1=|lga n ﹣lga n ﹣1|(n=2,3,4,…).(Ⅰ)若a 1=2,a 2=3,求a 3,a 4,a 5的值;(Ⅱ)求证:“数列{a n }中存在a k (k ∈N *)使得lga k =0”是“数列{a n }中有无数多项是1”的充要条件;(Ⅲ)求证:在数列{a n }中∃a k (k ∈N *),使得1≤a k <2.2016-2017学年北京市海淀区高三(上)期中数学试卷(理科)参考答案与试题解析一、选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.已知集合A={x|x>2},B={x|(x﹣1)(x﹣3)<0},则A∩B=()A.{x|x>1} B.{x|2<x<3}C.{x|1<x<3}D.{x|x>2或x<1}【考点】交集及其运算.【分析】求出B中不等式的解集确定出B,找出A与B的交集即可.【解答】解:由B中不等式解得:1<x<3,即B={x|1<x<3},∵A={x|x>2},∴A∩B={x|2<x<3},故选:B.2.已知向量=(﹣1,2),=(2,﹣4).若与()A.垂直 B.不垂直也不平行C.平行且同向D.平行且反向【考点】平行向量与共线向量;数量积判断两个平面向量的垂直关系.【分析】直接利用向量关系,判断即可.【解答】解:向量=(﹣1,2),=(2,﹣4).=﹣2,所以两个向量共线,反向.故选:D.3.函数y=2x+的最小值为()A.1 B.2 C.2D.4【考点】基本不等式.【分析】直接利用基本不等式化简求解即可.【解答】解:函数y=2x+≥2=2,当且仅当x=时,等号成立.故选:C.4.已知命题p:∃c>0,方程x2﹣x+c=0 有解,则¬p为()A.∀c>0,方程x2﹣x+c=0无解B.∀c≤0,方程x2﹣x+c=0有解C.∃c>0,方程x2﹣x+c=0无解D.∃c<0,方程x2﹣x+c=0有解【考点】命题的否定.【分析】直接利用特称命题的否定是全称命题写出结果即可.【解答】解:因为特称命题的否定是全称命题,所以,命题p:∃c>0,方程x2﹣x+c=0 有解,则¬p为∀c>0,方程x2﹣x+c=0无解.故选:A.5.已知函数y=a x,y=x b,y=log c x的图象如图所示,则()A.a>b>c B.a>c>b C.c>a>b D.c>b>a【考点】指数函数的单调性与特殊点.【分析】根据指数函数、对数函数与幂函数的图象与性质,用特殊值即可判断a、b、c的大小.【解答】解:根据函数的图象知,函数y=a x是指数函数,且x=1时,y=a∈(1,2);函数y=x b是幂函数,且x=2时,y=2b∈(1,2),∴b∈(0,1);函数y=log c x是对数函数,且x=2时,y=log c2∈(0,1),∴c>2;综上,a、b、c的大小是c>a>b.故选:C.6.设,是两个向量,则“|+|>|﹣|”是“•>0”的()A.充分而不必要条件 B.必要而不充分条件C.充分必要条件 D.既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断.【分析】根据向量数量积的定义和性质结合充分条件和必要条件的定义进行判断即可.【解答】解:若|+|>|﹣|,则等价为|+|2>|﹣|2,即||2+||2+2•>||2+||2﹣2•,即4•>0,则•>0成立,反之,也成立,即“|+|>|﹣|”是“•>0”的充要条件,故选:C.7.已知函数f(x)=cos4x+sin2x,下列结论中错误的是()A.f(x)是偶函数B.函f(x)最小值为C.是函f(x)的一个周期D.函f(x)在(0,)内是减函数【考点】三角函数的周期性及其求法;三角函数的最值.【分析】根据奇偶性的定义,判断函数f(x)是偶函数;化简函数f(x),求出它的最小值为;化简f(x),求出它的最小正周期为;判断f(x)在x∈(0,)上无单调性.【解答】解:对于A,函数f(x)=cos4x+sin2x,其定义域为R,对任意的x∈R,有f(﹣x)=cos4(﹣x)+sin2(﹣x)=cos4x+sin2x=f(x),所以f(x)是偶函数,故A正确;对于B,f(x)=cos4x﹣cos2x+1=+,当cosx=时f(x)取得最小值,故B正确;对于C,f(x)=+=+=+=+=+,它的最小正周期为T==,故C正确;对于D,f(x)=cos4x+,当x∈(0,)时,4x∈(0,2π),f(x)先单调递减后单调递增,故D错误.故选:D.8.如图所示,A是函数f(x)=2x的图象上的动点,过点A作直线平行于x轴,交函数g(x)=2x+2的图象于点B,若函数f(x)=2x的图象上存在点C使得△ABC为等边三角形,则称A 为函数f(x)=2x上的好位置点.函数f(x)=2x上的好位置点的个数为()A.0 B.1 C.2 D.大于2【考点】函数的图象.【分析】根据题意,设出A、B、C的坐标,由线段AB∥x轴,△ABC是等边三角形,x=log2(m﹣)=log2m﹣1,求出m的值,计算出结果.【解答】解:根据题意,设A,B的纵坐标为m,则A(log2m,m),B(log2m﹣2,m),∴AB=log2m﹣log2m+2=2,设C(x,2x),∵△ABC是等边三角形,∴点C到直线AB的距离为,∴m﹣2x=,∴x=log2(m﹣),∴x=(log2m+log2m﹣2)=log2m﹣1,∴log2(m﹣)=log2m﹣1=log2,∴m﹣=,解得m=2,∴x=log2(m﹣)=log2,函数f(x)=2x上的好位置点的个数为1个,故选:B.二、填空题共6小题,每小题5分,共30分.9.已知数列{a n}的前n项和S n=3n+1,则a2+a3=24.【考点】数列的求和;数列递推式.【分析】直接利用数列的和,化简求解即可.【解答】解:数列{a n}的前n项和S n=3n+1,S1=31+1=4,S3=33+1=28,a2+a3=28﹣4=24.故答案为:24.10.若角θ的终边过点P(3,﹣4),则sin(θ﹣π)=.【考点】任意角的三角函数的定义.【分析】利用同角三角函数的基本关系、诱导公式,求得要求式子的值.【解答】解:∵角θ的终边过点P(3,﹣4),∴x=3,y=﹣4,r=|OP|=5,∴sinθ=﹣,则sin(θ﹣π)=﹣sinθ=,故答案为:.11.已知正方形ABCD边长为1,E是线段CD的中点,则•=.【考点】平面向量数量积的运算.【分析】由题意可得=0,AD=AB=1,再根据•=(+)•(﹣),计算求得结果.【解答】解:由题意可得=0,AD=AB=1,∴•=(+)•(﹣)=﹣﹣=1﹣0﹣=,故答案为:.12.去年某地的月平均气温y(℃)与月份x(月)近似地满足函数y=a+bsin(x+)(a,b为常数).若6月份的月平均气温约为22℃,12月份的月平均气温约为4℃,则该地8月份的月平均气温约为31℃.【考点】y=Asin(ωx+φ)中参数的物理意义.【分析】根据题意,把x、y的值代入函数解析式,列出方程求出函数y的解析式,再计算x=8时y的值即可.【解答】解:函数y=a+bsin(x+)(a,b为常数),当x=6时y=22;当x=12时y=4;即,化简得,解得a=13,b=﹣18;∴y=13﹣18sin(x+),当x=8时,y=13﹣18sin(×8+)=31.故答案为:31.13.设函数f(x)=(a>0,且a≠1).①若a=,则函数f(x)的值域为(﹣,﹣]∪(0,+∞);②若f(x)在R上是增函数,则a的取值范围是[2,+∞).【考点】分段函数的应用.【分析】(1)根据指数函数和对数函数的性质,分别求其值域,再求并集即可,(2)由题意可得a的不等式组,解不等式组可得.【解答】解:(1)当a=时,若x≤1,则f(x)=2x﹣,则其值域为(﹣,﹣],若x>1,f(x)=log x,则其值域为(0,+∞),综上所述函数f(x)的值域为(﹣,﹣]∪(0,+∞),(2)∵f(x)在R上是增函数,∴a>1,此时f(x)=2x﹣a的最大值为2﹣a,f(x)=log a x>0,∴2﹣a≤0,解得a≥2,故a的取值范围为[2,+∞),故答案为:(1):(﹣,﹣]∪(0,+∞),(2):[2,+∞)14.已知函数f(x)的定义域为R.∀a,b∈R,若此函数同时满足:①当a+b=0时,有f(a)+f(b)=0;②当a+b>0时,有f(a)+f(b)>0,则称函数f(x)为Ω函数.在下列函数中:①y=x+sinx;②y=3x﹣()x;③y=是Ω函数的为①②.(填出所有符合要求的函数序号)【考点】命题的真假判断与应用.【分析】容易判断函数①②为奇函数,且在定义域R上为增函数,可设y=f(x),容易得出这两函数满足Ω函数的两条,而函数③是奇函数,不是增函数,这样显然不能满足Ω函数的第②条,这样即可找出为Ω函数的函数序号.【解答】解:容易判断①②③都是奇函数;y′=1﹣cosx≥0,y′=ln3(3x+3﹣x)>0;∴①②都在定义域R上单调递增;③在定义域R上没有单调性;设y=f(x),从而对于函数①②:a+b=0时,a=﹣b,f(a)=f(﹣b)=﹣f(b);∴f(a)+f(b)=0;a+b>0时,a>﹣b;∴f(a)>f(﹣b)=﹣f(b);∴f(a)+f(b)>0;∴①②是Ω函数;对于函数③,a+b>0时,得到a>﹣b;∵f(x)不是增函数;∴得不到f(a)>f(﹣b),即得不出f(a)+f(b)>0.故答案为:①②.三、解答题共6小题,共80分.解答应写出文字说明、演算步骤或证明过程.15.已知数列{a n}是公差为2的等差数列,数列{b n满足b n﹣b n=a n,且b2=﹣18,b3=﹣24.+1(Ⅰ)求数列{a n}的通项公式;(Ⅱ)求b n取得最小值时n的值.【考点】数列递推式.【分析】(Ⅰ)由已知求得a2,结合公差求得首项,则数列{a n}的通项公式可求;﹣b n=a n,利用累加法求得b n,结合二次函数求得b n取(Ⅱ)把数列{a n}的通项公式代入b n+1得最小值时n的值.【解答】解:(Ⅰ)由题意知d=2,﹣b n=a n,且b2=﹣18,b3=﹣24,得a2=b3﹣b2=﹣6,再由b n+1则a1=a2﹣d=﹣6﹣2=﹣8,∴a n=﹣8+2(n﹣1)=2n﹣10;(Ⅱ)b n﹣b n=2n﹣10,+1∴b2﹣b1=2×1﹣10,b3﹣b2=2×2﹣10,…=2(n﹣1)﹣10(n≥2),b n﹣b n﹣1累加得:b n=b1+2[1+2+…+(n﹣1)]﹣10(n﹣1)=b2﹣a1+2[1+2+…+(n﹣1)]﹣10(n﹣1),=﹣10+=.∴当n=5或6时,b n取得最小值为b5=b6=﹣30.16.已知函数f(x)=cos(2x﹣)﹣cos2x.(Ⅰ)求f()的值;(Ⅱ)求函数f(x)的最小正周期和单调递增区间.【考点】三角函数的周期性及其求法;余弦函数的单调性.【分析】(Ⅰ)根据函数f(x)的解析式,计算f()的值即可;(Ⅱ)化函数f(x)为正弦型函数,即可求出它的最小正周期与单调递增区间.【解答】解:(Ⅰ)函数f(x)=cos(2x﹣)﹣cos2x,∴f()=cos(﹣)﹣cos=﹣(﹣)=1;(Ⅱ)函数f(x)=cos(2x﹣)﹣cos2x=cos2xcos+sin2xsin﹣cos2x=sin2x﹣cos2x=sin(2x﹣);∴函数f(x)的最小正周期为T==π;由y=sinx的单调递增区间是[2kπ﹣,2kπ+],(k∈Z);令2k π﹣≤2x ﹣≤2k π+,k ∈Z ,解得k π﹣≤x ≤k π+;∴函数f (x )的单调递增区间为[k π﹣,k π+],(k ∈Z ).17.已知函数f (x )=x 3﹣9x ,函数g (x )=3x 2+a .(Ⅰ)已知直线l 是曲线y=f (x )在点(0,f (0))处的切线,且l 与曲线y=g (x )相切,求a 的值;(Ⅱ)若方程f (x )=g (x )有三个不同实数解,求实数a 的取值范围.【考点】利用导数研究曲线上某点切线方程;根的存在性及根的个数判断.【分析】(Ⅰ)求出f (x )的导数和切线的斜率和方程,设l 与曲线y=g (x )相切于点(m ,n ),求出g (x )的导数,由切线的斜率可得方程,求得a 的值;(Ⅱ)记F (x )=f (x )﹣g (x )=x 3﹣9x ﹣3x 2﹣a ,求得导数和单调区间,极值,由题意可得方程f (x )=g (x )有三个不同实数解的等价条件为极小值小于0,极大值大于0,解不等式即可得到所求范围.【解答】解:(Ⅰ)函数f (x )=x 3﹣9x 的导数为f ′(x )=3x 2﹣9,f (0)=0,f ′(0)=﹣9,直线l 的方程为y=﹣9x ,设l 与曲线y=g (x )相切于点(m ,n ),g ′(x )=6x ,g ′(m )=6m=﹣9,解得m=﹣,g (m )=﹣9m ,即g (﹣)=+a=,解得a=; (Ⅱ)记F (x )=f (x )﹣g (x )=x 3﹣9x ﹣3x 2﹣a ,F ′(x )=3x 2﹣6x ﹣9,由F ′(x )=0,可得x=3或x=﹣1.当x <﹣1时,F ′(x )>0,F (x )递增;当﹣1<x <3时,F ′(x )<0,F (x )递减;当x >3时,F ′(x )>0,F (x )递增.可得x=﹣1时,F (x )取得极大值,且为5﹣a ,x=3时,F (x )取得极小值,且为﹣27﹣a ,因为当x →+∞,F (x )→+∞;x →﹣∞,F (x )→﹣∞.则方程f (x )=g (x )有三个不同实数解的等价条件为:5﹣a >0,﹣27﹣a <0,解得﹣27<a <5.18.如图,△ABC 是等边三角形,点D 在边BC 的延长线上,且BC=2CD ,AD=.(Ⅰ)求CD 的长;(Ⅱ)求sin ∠BAD 的值.【考点】余弦定理;正弦定理.【分析】(Ⅰ)由已知及等边三角形的性质可得AC=2CD,∠ACD=120°,由余弦定理即可解得CD的值.(Ⅱ)由(Ⅰ)可求BD=3CD=3,由正弦定理即可解得sin∠BAD的值.【解答】(本题满分为13分)解:(Ⅰ)∵△ABC是等边三角形,BC=2CD,∴AC=2CD,∠ACD=120°,∴在△ACD中,由余弦定理可得:AD2=AC2+CD2﹣2AC•CDcos∠ACD,可得:7=4CD2+CD2﹣4CD•CDcos120°,解得:CD=1.(Ⅱ)在△ABC中,BD=3CD=3,由正弦定理,可得:sin∠BAD==3×=.19.已知函数f(x)=e x(x2+ax+a).(Ⅰ)求f(x)的单调区间;(Ⅱ)求证:当a≥4时,函数f(x)存在最小值.【考点】利用导数研究函数的单调性.【分析】(Ⅰ)求出函数的导数,通过讨论a的范围,求出函数的单调区间即可;(Ⅱ)结合(Ⅰ)得到函数f(x)在x∈[﹣a,+∞)上f(x)≥f(﹣2),而x∈(﹣∞,﹣a)时,f(x)=e x[x(x+a)+a]>0,从而求出f(x)的最小值是f(﹣2);法二:根据函数的单调性求出f(x)的最小值是f(﹣2)即可.【解答】解:(Ⅰ)f′(x)=e x(x+2)(x+a),由f′(x)=0,解得:x=﹣2或x=﹣a,①﹣a=﹣2即a=2时,f′(x)=e x(x+2)2≥0恒成立,∴函数f(x)在R递增;综上,时,函数()在递增,<时,()在(﹣,﹣),(﹣a ,+∞)递增,在(﹣2,﹣a )递减,a >2时,f (x )在(﹣∞,﹣a ),(﹣2,+∞)递增,在(﹣a ,﹣2)递减;(Ⅱ)法一:由(Ⅰ)得:a ≥4时,函数f (x )在x ∈[﹣a ,+∞)上f (x )≥f (﹣2), 且f (﹣2)=e ﹣2(4﹣a )≤0,∵a ≥4,∴x ∈(﹣∞,﹣a )时,x (x +a )≥0,e x >0,x ∈(﹣∞,﹣a )时,f (x )=e x [x (x +a )+a ]>0,∴a ≥4时,函数f (x )存在最小值f (﹣2);法二:由(Ⅰ)得:a ≥4时,函数f (x )在x ∈[﹣a ,+∞)上f (x )≥f (﹣2), 且f (﹣2)=e ﹣2(4﹣a )≤0, x →﹣∞时,x 2+ax +a →+∞,∴f (x )>0,由(Ⅰ)可知,函数f (x )在(﹣∞,﹣a )递增,∴x ∈(﹣∞,﹣a )时,f (x )>0,∴a ≥4时,函数f (x )的最小值是f (﹣2).20.已知数列{a n }是无穷数列,满足lga n +1=|lga n ﹣lga n ﹣1|(n=2,3,4,…).(Ⅰ)若a 1=2,a 2=3,求a 3,a 4,a 5的值;(Ⅱ)求证:“数列{a n }中存在a k (k ∈N *)使得lga k =0”是“数列{a n }中有无数多项是1”的充要条件;(Ⅲ)求证:在数列{a n }中∃a k (k ∈N *),使得1≤a k <2.【考点】数列递推式.【分析】(Ⅰ)由a 1=2,a 2=3,结合lga n +1=|lga n ﹣lga n ﹣1|(n=2,3,4,…)可得a 3,a 4,a 5的值;(Ⅱ)分必要性和充分性证明,充分性利用反证法证明;(Ⅲ)利用反证法,假设数列{a n }中不存在a k (k ∈N *),使得1≤a k <2,则0<a k <1或a k ≥2(k=1,2,3,…).然后分类推出矛盾得答案.【解答】(Ⅰ)解:∵a 1=2,a 2=3,lga n +1=|lga n ﹣lga n ﹣1|(n=2,3,4,…),∴lga 3=|lg3﹣lg2|=,即;,即a 4=2;,即;(Ⅱ)证明:必要性、已知数列{a n }中有无数多项是1,则数列{a n }中存在a k (k ∈N *)使得lga k =0.∵数列{a n }中有无数多项是1,∴数列{a n }中存在a k (k ∈N *)使得a k =1,即数列{a n }中存在a k (k ∈N *)使得lga k =0.充分性:已知数列{a n }中存在a k (k ∈N *)使得lga k =0,则数列{a n }中有无数多项是1.假设数列{a n }中没有无数多项是1,不妨设是数列{a n }中为1的最后一项,则a m +1≠1,若a m +1>1,则由lga n +1=|lga n ﹣lga n ﹣1|(n=2,3,4,…),可得lga m +2=lga m +1, ∴lga m +3=|lga m +2﹣lga m +1|=0,则lga m +3=1,与假设矛盾;若0<a m +1<0,则由lga n +1=|lga n ﹣lga n ﹣1|(n=2,3,4,…),可得lga m +2=﹣lga m +1, ∴lga m +3=|lga m +2﹣lga m +1|=﹣2lga m +1,lga m +4=|lga m +3﹣lga m +2|=|﹣2lga m +1+lga m +1|=﹣lga m +1,lga m +5=|lga m +4﹣lga m +3|=|﹣lga m +1+2lga m +1|=﹣lga m +1,∴lga m +6=|lga m +5﹣lga m +4|=0,得lga m +6=1,与假设矛盾.综上,假设不成立,原命题正确;(Ⅲ)证明:假设数列{a n }中不存在a k (k ∈N *),使得1≤a k <2, 则0<a k <1或a k ≥2(k=1,2,3,…).由lga n +1=|lga n ﹣lga n ﹣1|(n=2,3,4,…),可得(n=1,2,3,…)*,且a n >0(n=1,2,3,…),∴当n ≥2时,a n ≥1,a n ≥2(n=3,4,5,…).若a 4=a 3≥2,则a 5=1,与a 5≥2矛盾;若a 4≠a 3≥2,设b m =max {a 2m +1,a 2m +2}(m=1,2,3,…),则b m ≥2.由(*)可得,,,∴,即(m=1,2,3,…), ∴,对于b 1,显然存在l 使得.∴,这与b m ≥2矛盾. ∴假设不成立,原命题正确.2016年11月17日。
河北省定州中学2017届高三(高补班)上学期周练(12.30)地理试题 Word版含答案
河北定州中学2016-2017学年第一学期高四地理周练试题(13)一、单项选择题下图中①一⑤为0°-66°34′N之间不同日期的昼长分布曲线。
读图完成下列问题。
1.曲线①→②→③变化的时段内,太阳直射点的移动情况是A.从北回归线向赤道移动B.从赤道向南回归线移动C.从南回归线向赤道移动D.从赤道向北回归线移动2.曲线⑤→④→③变化的时段内,下列说法正确的是A.北半球昼长夜短,且昼逐渐缩短B.北半球昼短夜长,且昼逐渐增长C.南半球昼长夜短,且夜逐渐缩短D.南半球昼短夜长,且夜逐渐增长下图为某区域等高线地形图,读图回答各题。
3.关于甲乙丙丁四地的判断,正确的是A.甲位于山脉北坡 B.乙地可能有河流流经C.丙地坡度最大 D.丁地位于高原4.对于图示地区自然环境的描述,准确的是A.该区域气候冬夏风向明显更替B.侵蚀作用对地形形成影响最大C.该区域内盐碱、台风灾害多发D.该区域主要分布亚热带常绿阔叶林上海是世界著名的六大“都市经济圈”之一,具有“东方明珠”的美誉。
在这片肥沃的三角洲上,环境人口容量很大。
读下图,5.陕西有“黄帝陵”,河南有“炎帝陵”;但具有“东方明珠”的上海周围却没有留下任何“炎黄足迹”,其原因是:()A.适逢冰期,冻害严重 B.间冰时期,洪灾频繁C.秦、淮以南,缺少食物 D.长江三角洲尚未形成6.近年来,长江三角洲的增长速度已大大放慢,甚至停止……,其原因不正确的叙述是:()A.南水北调,导致水流量减少,携带泥沙量也随之减少B.全球变暖,海平面升高,海浪侵蚀,海岸线退缩C.长江三峡水库截留了大部分来自上游的泥沙D.长江流域退耕还林和水土保持工作成绩显著“寒江雪柳日新晴,玉树琼花满目春”是吉林雾凇的真实写照。
读吉林市雾淞景点分布图和甲、乙、丙、丁四处表层水温统计表,回答下列各题。
7.该季节图示河段的水文特征是A.流量大,结冰期长 B.含沙量大,流速快C.处于丰水期,以地下水补给为主 D.流量稳定,无结冰8.该地区为著名雾凇观赏区的主要自然原因是①地形平坦②交通便利③水温与气温的温差大④夜间晴朗,气温低A.①② B.②③ C.③④ D.①③下图表示某地气温与降水量逐月分配情况。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
- 1 - 本卷共20小题,在每小题给出的四个选项中。只有一项是符合题目要求的。请将所选答案前的代表字母填写在答题纸上(每小题2分,多选、错选、精选,该小题均不得分)。 图1为2000年到2015年上海市人口数据.读图回答第1—3题.
1.图中数据表明,上海市 A.城镇化水平下降 B.工业化水平下降 C.城镇化速度放缓 D.农业总产值下降 2.上海市农村户籍人口减少的主要原因是 A_人口出生率下降 B.迁出人口数量增加 C.人口死亡率上升 D.区域产业结构调整 3.上海市 A.适度引导人口迁出会使人口合理容量提升 B。提升居民消费水平会导致环境承载力下降 C。提高地域开放程度会使人口合理容量提升 D.第三产业比重的上升导致环境承载力下降 我国南方部分城市为改变“雨季一来,城里看海”的状况,在城市低洼区域修建“生态草洼”和铺设渗渠提升雨水处理能力。据此,回答第4-5题: 4,上述措施 - 2 -
A.减缓了雨水渗漏速度 B.增加了地下水储存量 C.缩短了雨洪汇流时间 D.增加了地面的蒸发量 5,修建上述设施的主要目的是 A.储存淡水资源 B.缓解城市内涝 C. 推广环保技术 D.削弱热岛效虚 匮2琦2016年的348路公交车运菅蠖路示意图,阁3为l995年的348路套交车站脾。读图,回答6-8题。
6.目前348路公室车逾经的城市功能赋毫要是 A.住宅区 B.文化区 C.工业区 D.中心商务区 7.同前348路公盘车沿线 A.站点I附近人口数量昼夜差异大 B.站点3附近适合建大型批发市场 C.站点l4附近适合开发高端住宅区 D.站点l5周边高楼林立,建筑密集 8,与1995年相比,目前348蹄部分站名的变化,直接反映了图示地区 - 3 -
A.交通通达程度的提高 B.土地利用方式的变化 C.地域分化程度的降低 D.土地地租水平的提升 图4中甲、乙、丙三地属于不同的农业地域类型、读图回答9-10题。
9.与甲地相比,而地 A.劳动力充足,生产规模大 B.市场广阔,农产品商品率高 C.工业发达,机械化水平高 D.精耕细作,单位面积产量高 10.下列叙述正确昀是 A.甲地春旱,臣重,辫响冬小壹返青 B.乙地交通的改善,削弱了产品对本地市场的依赖 C.丙地光照充足,农作物一年一熟 D.三地自然条件的差异,决定其农业地域类型不同 读图5。回答第11、12题。 - 4 -
11.图中分别示意产业升级、产业转移、区域产业分工的序号是 A.①②③ B.①③② C.②③① D.③②① 12.②过程的产生主要是由于不同国家或地区间 A.工资水平差异 B.自然资源差异 C.科技水平差异 D.市场规模差异 圈6为1986年以前美国汽车工业分布图,图7为1986—2006年美国新建汽车企业分布图。读图,回答第13、14题。
13。图中 A. 1986年前汽车企业集中在东部沿海地区 B.1986年之后。汽车企业向中部平原集聚 C.2006年时,本国企业数量少于外国企业 D.二十年间汽车企业南东北部向南部扩散 - 5 -
14.新建的外国企业 A.扩大了美国汽车消费市场 B.改善了所在地区环境质量 C.促进企业之间的技术交流 D.加大了本地区的就业压力 2016年1 1月13日,由中资套司运营的巴基斯坦瓜迭尔港正式开航,与规划中的中巴铁路一起构成我国西北地区对外联系的新通遭。图8为瓜达尔港位置厦中巴辕路规划示意图。读圈,回答第15、16题。
L5.瓜达尔港 A.将成为东南亚重要的海上交通枢纽 B.易受飕风、海啸等气象灾害的影响 C.将成为沟通东亚与非洲的重要通道 D.将会极大促进新疆新鲜果蔬的出口 16.中巴铁路 A.经过的自然带比较单一 B.途经地区的地势起伏大 C.比公路运输灵活性更强 D.比海运运量大、运价低 虚拟水是指在生产产品和服务中所需要的水资源。地区之间的农产品蟹易是实现虚拟水资源调配的重要方式。图9为中国部分省区虚拟水净输入量统计图(单位:10亿吨)。读图,回答第17、18题。 - 6 -
17。固中 A.虚拟水净输入区多分布于干旱、半十旱区 B.虚拟水净输人区均位于我国东部经济地带 C.虚拟水净输出区地跨地势第二、i级阶梯 D.虚拟水净输出区多分布在西北及东北地区 18.图中的虚拟水资源调配 A.增加水资源输出地区的经济收入 B.能促进不同区域间水资源的均衡 C.有利于输出地区自然环境的改善 D.由水资源的空间分布差异所央定 图10中甲、乙为我国某地两种不同的生态农业生产模式。读囤,回答第19、20题。
19.比较两种生产模式 A.甲一产品附加值更高 B.乙一农产品种类更多
C.甲一受市场影响更大 D.乙一生产规模更大 - 7 -
20.图中两种生产模式均可 ①实现笫一、二、三产业有机结合 ②体现可持续发展中的公平性原则 ③带来经济、生态、社会综合效益 ④实现物质循环利用,减少废弃物 A.①③ B.①④ C.②③ D.③④
第Ⅱ卷 (综合题 共60分) 21,(10分)图11为2000年、2010年中国各省区人口老龄化程度分布圈。读图,完成下列问题。
(1)描述2000年到2010年我旧人口老龄化的变化特点。(4分) (2) 2000年到2010年川渝地区人口老龄化程度加重,请说明其原因并提出合理的应对措施。(6分)
22.(21分)读闭12、图13及文字资料,完成下列问题。 - 8 -
(1)概括巴西城市分布的特点,并说出其主要影响因素。(6分) 圣保罗人口超过2000万,是巴西最大的城市。圣保罗拥有钢铁、汽车、化学、农产品加工等众多工业部门,其工业产值占到了巴西全国工业总值的二分之一,是巴西最大的综合性工业中心。
(2)分析圣保罗成为巴西综合性工业中心的有利区位条件。(8分) 近年来,在巴西政府的戈力支持下,位于圣保罗东北方向80套里的小镇坡普新正逐步成为汇集焱多世界级航空企业的“巴西科技谷”,成为巴西经济新的增长点。 (3)筒述“巴西科技谷”的形成对圣保罗经济发展条件的影响。(4分) (4)目前圣保罗周边建立了多个卫星城,说明卫星城的建立给圣保罗带来的积极影响。(3分) - 9 -
23.(17分)图14为我国某区域示意图.凄网,完成下列问题。 (l)说出自祁连山至黑河不同区域适宜发展的主要农业部门 (3分) (2)图示区域为我国重要的农业区,说明该区域发展农业生产的水资源较丰富的原因.(4分) 为了推进该区域农业发展,当地政府大力推广滴灌技术,以替代大水漫灌为主的传统灌溉方式。 (3)简述该区域大力推广滴灌技术的主要日的。(4分) 在政府引导下,近年该地充分利用当地自然条件,建成了一批蔬幕种植、加工基地。蔬菜播种面积扩大至70万亩,建成万亩蔬菜多27个,鲜冷和深加工蔬菜大量出口到中亚各国。 (4)分析蔬菜种植、加工基地的建设对该地社会、经济的积极影响.(6分)
24.(12分)阅读图文资料,回答下列问题。 《徐霞客游记》是一部以日记体为主的地理著作,记述了撩霞客在旅行中的观察所得,对地理、水文、地质、植物等现象均作了详细记录,在地理学和文学上做出了卓有价值的贡献.:图15为徐霞客西行路线示意图。 - 10 -
(l)从徐霞客西行路线中选择一项世界遗产,说出该旅游资源的类型及突出的游览价值。(3分) 徐霞客在游历云南腾冲时,曾写到“采孔随地而出,其大如管,喷窍而上,作鼓沸状,滔滔有声,跃起地面者二三寸,其热如沸”。 (2)说出文中记述的地理景观,并说明腾冲地区该类地理景观丰富的原因:(3分) (3)“世界那么大,你该去看看”.请从徐霞客心行路线所经地区中选择目的地,为你所在的学校设计一条5日地理实践考察线路。要求:旅游主题明确,旅游活动安排合理,有地理特色。(6分) - 11 -
海淀区高三年级第一学期期末练习参考答案 地 理 第Ⅰ卷 (选择题 共40分) 本卷共20小题,在每小题给出的四个选项中,只有一项是符合题目要求的。请将所选答案前的代表字母填写在答题纸上(每小题2分,多选、错选、漏选,该小题均不得分)。 题号 1 2 3 4 5 6 7 8 9 10 答案 C D C B B A A B D B 题号 11 12 13 14 15 16 17 18 19 20 答案 A A D C C B C A D D 第Ⅱ卷 (综合题 共60分) 21.(10分) (1)(4分) 我国老龄化程度整体加重(1分);部分省区进入深度老龄化(1分);进入老龄化的省区增多(或进入老龄化的地区范围加大)(1分);老龄化省区由分散分布到集中连片(1分)。 (2)(6分) 原因:人口出生率下降(1分);医疗水平提高,人口寿命增长(1分);青壮年劳动力持续迁出(1分)。 应对措施:调整完善生育政策(放开二孩)(1分);完善社会福利制度(1分);政策引导,鼓励青年回乡创业(1分)。 22.(21分) (1)(6分) 分布特点:分布不均匀(1分);南部高原地区多于北部平原(1分);东南沿海多(1分)。 影响因素:气候、地形、海陆位置、河流、交通、开发历史。(答出其中3点得3分) (2)(8分) 拥有机场、港口、公路,交通便利;临近铁矿、油田,原料、燃料丰富;周边地区盛产咖啡、大豆、玉米,农业基础好;人口众多,劳动力充是;地处巴西东南部城市群,国内市场广阔(或临近港口,国际市场广阔)。(答出其中4点得8分)
