分子的对称性与点群
分子的对称操作与对称元素
3. 群的定义是广义的 群的乘法是广义的 群中元素的数目成为群的阶 子群:群众某些元素构成的群
G= {Eˆ , Cˆ2}
三、 分子点群
由分子中所有对称操作构成的群
分子点群的分类:5 类,16 个群
1. 无轴群 —无Cn轴或Sn轴的群,
如 C1,Ci,Cs群
H
H
Cl
F
Br
C
F
Br FClFra bibliotekClCl
H
C6H6 D6h
重叠式C2H6 D3h
3) Dnd群 Dn+nd
d :平分相邻两个C2轴之间的夹角
H C2
H
H
丙二烯
H
H
H
D2d 反式乙烷
D3d
D3d : 乙烷交错型
D4d :单质硫
俯视图
D5d : 交错型二茂铁
4. 高对称群 —含有二个以上高次轴Cn(n2) Td, Th, Oh, Ih
正四面体 正六面体 正八面体 正十二面体 正二十面体
Sn是虚轴. 对于Sn,若n等于奇数,则Cn和与之垂直的σ都 独立存在;若n等于偶数,则有Cn/2与Sn共轴,但Cn 和与之垂直的σ并不一定独立存在.
(1) 重叠型二茂铁具有 S5, 所以, C5和与之垂直 的σ也都独立存在;
(2) 甲烷具有S4,所以, 只有C2与S4共轴,但C4和与 之垂直的σ并不独立存在.
C2
O
{Eˆ,Cˆ2,ˆv,ˆv'}
C2v
H
H
C3
N H HH
{E ˆ,C ˆ3,C ˆ32, ˆv, ˆv', ˆv"} C3
v
O
Cl
Cl
O
乙烷的点群

乙烷的点群乙烷是一种简单的有机化合物,由两个碳原子和六个氢原子组成。
在化学中,乙烷的点群被用来描述它的对称性。
点群是一种对称性分类系统,根据物体在空间中的对称性操作,将物体分为不同的类别。
乙烷的点群是D3d,表示它具有四个旋转轴和三个反射面的对称性。
乙烷的点群是D3d,这意味着它具有四个旋转轴和三个反射面。
具体来说,乙烷有一个C3轴,它通过两个碳原子和两个氢原子的中心。
这个轴可以让乙烷分子绕着C3轴旋转120度,使得分子保持不变。
此外,乙烷还有三个反射面,它们分别通过两个碳原子和两个氢原子的中心,使得分子在镜面反射后保持不变。
乙烷的点群D3d还可以通过乙烷的分子轨道来解释。
分子轨道描述了乙烷中电子的分布情况。
乙烷的分子轨道主要分为σ轨道和π轨道。
σ轨道是通过原子之间的头叠加形成的,而π轨道是通过原子之间的侧叠加形成的。
在乙烷的点群D3d下,它的分子轨道分为两组,分别是a1g和e。
a1g是对称的轨道,e是非对称的轨道。
a1g轨道对应着乙烷分子中所有的σ键,而e轨道对应着乙烷分子中所有的π键。
这种分子轨道的对称性与乙烷的点群D3d是一致的。
乙烷的点群D3d还可以通过它的拉曼光谱来确定。
拉曼光谱是一种观察分子振动和转动的方法。
乙烷的点群D3d下,它的拉曼光谱显示了四个不同的拉曼活性模式,分别对应着乙烷分子中的不同振动和转动。
总的来说,乙烷的点群D3d描述了它的对称性和分子轨道的对称性。
通过研究乙烷的点群D3d,我们可以更好地理解乙烷的化学性质和行为。
此外,乙烷的点群D3d也是研究其他有机化合物对称性的基础。
通过对乙烷的点群D3d的研究,我们可以拓展对称性的应用领域,深入探索有机化学的奥秘。
总结一下,乙烷的点群D3d是描述乙烷对称性的分类系统。
它通过分析乙烷的旋转轴、反射面、分子轨道和拉曼光谱等性质,揭示了乙烷分子的对称性和化学行为。
乙烷的点群D3d对于有机化学的研究具有重要意义,是探索有机化学世界的关键之一。
萘分子点群

萘分子点群
萘是一种具有芳香性质的有机化合物,其分子式为C10H8。
它是一种白色晶体,在室温下呈固体状态。
萘的分子结构呈现出C2v点群对称性,这意味着它具有一个旋转轴和一个反演中心。
萘分子的旋转轴是垂直于分子平面的C2轴,通过旋转180度,可以使得分子保持不变。
这个旋转轴使得萘分子具有轴对称性,从而使得它在空间中有两个等效的旋转构型。
萘分子还具有一个反演中心,这是指当把分子沿着中心反演,所有原子的位置都可以重合。
这个反演中心使得萘分子具有平面反演对称性,并使得它在空间中具有两个等效的平面反演构型。
由于C2v对称性,萘分子的一些物理和化学性质也受到影响。
例如,萘分子具有两个等效的苯环,这使得它在化学反应中表现出苯的特性。
此外,由于反演对称性,萘分子的光学活性为零,即它不会旋光。
萘分子具有C2v点群对称性,这使得它在空间中具有两个等效的旋转构型和平面反演构型。
这种对称性不仅影响着萘分子的外部形态,还对其物理和化学性质产生影响。
通过深入理解萘分子的点群对称性,我们可以更好地理解和解释其在化学反应中的行为。
分子对称性和群论初步

Cn轴产生n个旋转操作的周期均为n。
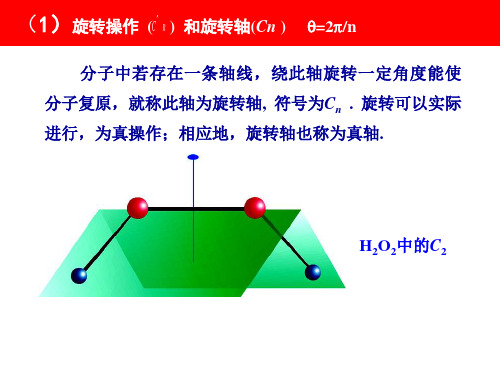
(2)对称轴 (Cn )和旋转操作 (Cn )
对称元素: 旋转轴C2 对称操作: 旋转
H2O中的C2
H2O2中的C2
NH3中的C3轴
SF6中的C4轴
Fe(C5H5)2中的C5轴
C6H6中的C6轴
N2中的C∞轴
(3)对称面 s 和反映操作 s
对称面
相当于一个镜面,把分子图形分成两个完全相等的对称 部分,两部分之间互为镜中映象;对称面所相应的对称 操作是镜面的一个反映,在对称面的反映操作下,分子 图形相等的两部分互相交换位置,相同性质的点(同类 原子)彼此置换。显然,反映操作的周期为2,即:
ˆ ˆ =E s
操作定义
Cn旋转轴能生成n个旋转操作,记为:
2 ˆ ˆ n, Cn , C
…
, ˆn=E ˆ C Cn
n 1 n
ˆk 若取逆时针方向的旋转为正操作,表示为 C n,则顺 k ˆ 时 针 旋 转 为 逆 操 作 , 表 示 为C n ,不难理 (nk )。 ˆk ˆ 解C n =C n
操作的周期
S8
2.5 假轴向群 Sn群
Sn:有一个 n重象转轴,须考虑 n的奇偶性。 n为偶数时, 群中有n个元素,n为奇数时,Sn不独立存在。 只有S4是独立的点群。例如:1,3,5,7-四甲基环辛四烯, 有一个S4映转轴,没有其它独立对称元素。
S2 S4
2.6 六方群
1). Td群
若一个四面体骨架的分子,存在4个C3轴,3个C2轴,同时每 个C2轴还处在两个互相垂直的平面sd的交线上,这两个平面还 平分另外2个C2轴(共有6个这样的平面)则该分子属Td对称性。 对称操作为{E,3C2,8C3,6S4,6sd}共有24阶。 四 面 体 CH4 、 CCl4 对 称 性 属 Td 群 , 一 些 含 氧 酸 根 SO42- 、 PO43-等亦是。在CH4分子中,每个C-H键方向存在1个C3轴,2 个氢原子连线中点与中心C原子间是C2轴,还有6个sd平面。
第六节分子对称性

ˆi n
Eˆ ˆi
( n为偶数) (n为奇数)
二氟二氯乙烷 C2H2F2Cl2
i
: i、
E
2个操作。
一个分子若有 i 时,除 i 上的原子,其他原 子必定成对出现。
平面正方形PtCl42-
具有对称中心
四面体SiF4
不具有对称中心
5.象转轴(Sn)和旋转反映操作( S n )
第二类是反演、反映等,属虚操作(非 真操作),在想象中实现。
二、分子点群
1.群
按一定的运算规则,相互联系的一些元素的集合。
其中的元素可以是操作、矩阵、算符或数字等。
构成群的条件:
(1)封 闭 性 A ˆ : G,B ˆ若 G,则 A ˆB ˆC ˆG; (2)结 合A ˆ律 (B ˆC ˆ: )(A ˆB ˆ)C ˆ; (3)有 单 位 E: 元 A ˆE ˆ 素 E ˆA ˆA ˆ; (4)逆 操A ˆ作 A ˆ: A ˆA ˆ E ˆ
旋转与反映的乘积是n个反映
(4) 偶次旋转轴和与它垂直的镜面的组合
一个偶次轴与一个垂直于它的镜面组合,必定在 交点上出现一个对称中心;一个偶次轴与对称中心 组合,必有一垂直于该轴的镜面;对称中心与一镜 面组合,必有一垂直于该镜面的偶次轴。
小结
第一类是简单旋转操作,为实操作,其 特点是能具体,可直接实现。
a v
ˆ
b v
Cˆ
1 3
Cˆ
2 3
Eˆ
3. 分子的点群
分子点群有二层解释含义:
(1)对称操作都是点操作,操作时分子中 至少有一点不动。
(2)分子中全部对称元素至少通过一个公 共点,若不交于一点,分子就不能维持有限性 质。
分子的对称性和群论初步

H3BO3分
子
C3h C31, C32 , C33 E, h , S31, S35
属6阶群 S31 hC31,S32 C32,S33 h S34 C31,S35 hC32,S36 E
Cnh Cnk (k 1,n 1), E, h , hCnl (l 1,l 1)
非全同:不能通过平移或转动等第一类对称操 作使两个图形叠合。
2.旋光异构体:一对等同而非全同的分子构成 的一对对映体。
3.手性分子:没有第二类对称元素的分子。
R(右,顺时针方向转)和 S(左,逆时针旋转) 外消旋体:等量的R和S异构体混合物一定无旋光
性方向相反
4.对称性和旋光性的关系
✓ 若分子具有反轴Ι(先旋转360°/n,再反演)的对 称性,一定无旋光性;若分子不具有反轴的对称性, 则可能出现旋光性。
元的数目有限的群称为有限群,数目无限的群 称为无限群。
点群:一个有限分子的对称操作群 ☞“点”的含义 ✔这些对称操作都是点操作,操作时分子中至少
有一个点不动。 ✔分子的对称元素至少通过一个公共点。
2.2 群的乘法表
※顺序
乘法表由行和列组成,在行坐标x和列坐标y的 交点上找到的元是yx,即先操作x,后操作y。每一 行和每一列都是元的重新排列。
C6轴: C6轴包括C2 和C3 的全部对称操作。
1.3 反演操作和对称中心 i
反演操作: 将分子的各点移到对称中心连线的延长线上,
且两边的距离相等。若分子能恢复原状,即反演操 作。
✔对称因素:对称中心 i ✔特点:延长线,等距
除位于对称中心的原子外,其余均成对出现
若对称中心位置在原点 (0,0,0)处,反演操作i的表 示矩阵为:
✓ 一重反轴=对称中心,二重反轴=镜面,独立的反 轴只有I4 。则具有这三种对称操作的无旋光性, 不具有这3种对称元素的分子都可能有旋光性。
第三章 分子的对称性
逆元素
I--- I C3+---C3– v1--- v1 v2---v2 v3 ---v3
封闭性
结合律 v1(v2 v3) = v1 C3+ = v2
(v1v2)v3 = C3+ v3 = v2
3.5 群的表示
矩阵乘法 矩阵 方阵 对角元素
分子的所有对称操作----点群
如果每一种对称操作可以用一个矩阵(方阵)表示, 矩 阵集合满足群的要求,矩阵乘法表与对称操作乘法表
相似, 矩阵集合---群的一个表示
恒等操作I
矩阵
C2v: I C2 v v
特征标: 对角元素和 9
特征标3
特征标 1
特征标 -1
单位矩阵
I 矩阵, C2 矩阵, v 矩阵, v 矩阵 满足群的要求, 是C2v 点群的一个表示
集合G 构成群
1 –1, 乘法
1X1=1, 1X(-1)= -1 (-1)X1= -1, (-1)X(-1)=1 封闭性 恒等元素1 逆元素 1---1, -1--- -1,
群的乘法表 I A I A
I
I
IA
AA
I
I
A
?
A AI
A A
交叉线上元素 = 行元素 X 列元素
已知,I,A,B构成群, I 为恒等元素, 写出群的乘法表
3) 如果对称中心上无任何原子, 则同类原子是成双出现的.
例如: 苯中C, H
NH3 有无对称中心, 为什么? C2H3Cl有无对称中心, 为什么?
(b) 旋转轴Cp
绕轴旋转3600/p, 等价构型 水分子----绕轴旋转1800, 等价构型 C2轴 C3轴 360/2=180
BF3, 旋转1200, 等价构型 360/3=120
点对称操作群点群课件
二、 点对称操作群(点群)
1 群的定义、群阶 2 主要点群 3 分子点群的确定
3.2.1 群的定义、群阶
我们称元素的某个集合形成一个群,群有着严 格的定义:“封闭性、结合律成立、存在恒等元素、 存在逆元素”。群中元素的个数,称作群阶。
例如:NH3分子: 含有6个群元,E、C31,C32,
v(1), v(2), v(3),可以写成 2C3,3v,E,所以NH3分子是6
通过主轴且平分相邻两个两次轴(xy平面内)夹
角的平面叫分角对称面, d;
σv
C4
i C2
C2
σh C2
E C2
4 恒等操作E
一个分子在操作后,其取向与原来的恒等不变, 即分子中的每个原子都回到了原来的位置,我们称 此操作为恒等操作,记做E。
总的说来,对于分子的对称性,即点对称性, 一共有旋转、反映、反演、旋转-反映和恒等5种 点操作,以及对应于上述操作的旋转轴、反映面、 对称中心和旋转-反映轴4种对称元素。 旋转——第一类对称操作,或实际操作; 反映、反演、旋转-反映只能在想象中实现,称 作第二类对称操作或虚操作;
Cs群
乙醇 邻氯吡啶
4. Cnv点群
C2
O H
H σv
σv
含有一个Cn轴和n个通过Cn轴的对称面。如:
H2O 分子具有一个C2轴和两个包含该轴的互相垂直
的对称面,故属于C2v点群。又如:NH3属于C3v点
群,XeOF4属于C4v点群,CO,HCl属于C∞v点群。
H2O C2v
与水分子类似的V型分子,如SO2、NO2、ClO2、 H2S, 船式环已烷(图IV)、N2H4(图V)等均属C2v点群。
这个配合物具有D3对称性, 有三个垂直于C3轴的C2 轴, 在Δ−对映异构体中, 对于每个C2轴, 两个鳌环呈 现相反的手性螺旋. 总体来看, 含有C2轴的光学活 性配合物比含有C3轴的光学活性配合物要多得多. 可以先考察配合物中C2或C3轴的存在情况, 进而以 Λ或Δ来描述它们的绝对构型.
分子的对称性-图
面数
面的边数 会聚顶点 的棱数 棱数 顶点数 双面数 点数
4
3
8
3
6
4
12
5
20
3
3
6 4 7032 Td
4
12 6 10928 Oh
3
12 8 90 Oh
3
30 20 11634 Ih
5
30 12 13812 Ih
T表示四面体群,O表示八面体群,它包括正八面体和立方体; I表 示二十面体群,包括正五角十二面体和正三角二十面体。
只有镜面 COFCl
亚硝酸酐 N2O3
B6H10
21
确定分子点群的流程简图
分子
线形分子:
C , Dh Td , Th , Oh , I h ...
C1 , Ci , Cs
有多条高阶轴分子(正四面体、正八面体…)
只有镜面或对称中心,或无对称性的分子:
只有S2n(n为正整数)分子:
S4 , S6 , S8 ,...
7
D4d :单质硫
俯视图
侧视图
图S 1.3.7 若干属于Dnd点群的分子
8
D5d : 交错型二茂铁
俯视图
图S 1.3.7 若干属于Dnd点群的分子
9
(3)立方群:包括Td、Th、Oh、Ih 等 这类点群的共同特点是有多条高次(大于二次)旋转轴相交。
Td 群:属于该群的分子,对称性与正四面体完全相同。
CH4
P4 (白磷)
10
在Td群中,你可以找到一个四面体结构。打开P4分子,对照以下讲解自己进行操作:
从正四面体的每两条相对的棱中点有一条 S4穿过,6 条棱对应着3条S4。每个S4可作出S41 、S42 、S43 三个 对称操作,共有9个对称操作。 但每条S4必然也是 C2, S42与C2对称操作等价,所以将3个S42划归C2, 穿过正四面体每条棱并 将四面体分为两半的是 一个σd , 共有6个σd 。
分子的对称性
(1)封闭性:指A和B若为同一群G中的对称操作,则 AB=C C也是群G中的一个对称操作。 (2)主操作:在每个群G中必有一个主操作E,它与 群中任何一个操作相乘给出 AE=EA=A (3)逆操作:群G中的每一个操作A均存在逆操作A-1, A-1也是该群中的一个操作。逆操作是按原操作途径 退回去的操作。 AA-1=A-1A=E (4)结合律:对称操作的乘法符合下面的结合律(括 号中的2个对称操作表示先进行相乘)。 A(BC)=(AB)C
现以二氯乙烯分子为例,说明C2h点群。 H CI
CI
Ⅰ.C2旋转轴
H
Ⅱ.σh对称面 Ⅲ.C2h点群
该分子是一个平面分子。C=C键中点存在垂直于 分子平面的C2旋转轴(Ⅰ),分子所在平面即为水平对 称面 σh(Ⅱ),C=C键中点还是分子的对称中心i。所 以C2h点群(Ⅲ)的对称操作有四个:{E,C2,σh,i}, 若分子中有偶次旋转轴及垂直于该轴的水平平面, 就会产生一个对称中心。反式丁二烯等均属 C2h点群。
旋转操作是将分子绕通过其中心的轴旋转一 定的角度使分子复原的操作,旋转所依据的 对称元素为旋转轴。n次旋转轴的记号为C n . 使物体复原的最小旋转角( 0度除外)称为 基转角(α)称为基转角 α,对C n轴的基转 角α= 3600/n。旋转角度按逆时针方向计算。 和C n轴相应的基本旋转操作为Cn1,它 为绕轴转 3600/n的操作。分子中若有多个旋 转轴,轴次最高的轴一般叫主轴。
C2v
图IV. 船式环已烷
图V. N2H4
C2v
NH3分子(图VII)是C3v点群典型例子。C3轴穿过 N原子和三角锥的底心,三个垂面各包括一个N-H 键。其它三角锥型分子PCl3、PF3、PSCl3、CH3Cl、 CHCl3等,均属C3v点群。P4S3(图Ⅷ)亦属C3v点群。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
分子的对称性与点群
摘要:分子也像日常生活中见到的物体一样,具有各种各样的对称性。
分子的对称性是分子的很重要的几何性质,它是合理解释许多化学问题的简明而重要的基础。
例如,往往从对称性入手,我们就能获得有关分子中电子结构的一些有用的定性结论,并从光谱推断有关分子的结构。
关键词:对称性点群对称操作
一.对称操作与点群
如果分子的图形相应于某一几何元素(点、线、面)完成某种操作后,所有原子在空间的排布与操作前的排布不可区分,则称此分子具有某种对称性。
一般将能使分子构型复原的操作,称为对称操作,对称操作所据以进行的几何元素称为对称元素。
描述分子的对称性时,常用到“点群”的概念。
所谓点群,就是指能使一个分子的图象复原的全部点操作的集合。
而全部对称元素的集合构成对称元素系。
每个点群具有一个持定的符号。
一个分子的对称性是高还是低,就可通过比较它们所属的点群得到说明。
二.分子中的对称元素和对称操作
2.1 恒等元及恒等操所谓点群,就是指能使一个分子的图象复原的全部点操作的集合。
作
分别用E、 E^表示。
这是一个什么也没有做的动作,保持分子不动,是任何分子都具有的对称元素与对称操作。
2.2旋转轴和旋转操作
分别用C n、C^n表示。
如果一个分子沿着某一轴旋转角度α能使分子复原,则该分子具有轴C n,α是使分子复原所旋转的最小角度,若一个分子中存在着几个旋转轴,则轴次高的为主轴(放在竖直位置),其余的为副轴。
分子沿顺时针方向绕某轴旋转角度α,α=360°/n (n=360°/α(n=1,2,3……)能使其构型成为等价构型或复原,即分子的新取向与原取向能重合,就称此操作为旋转操作,并称此分子具有 n 次对称轴。
n是使分子完全复原所旋转的次数,即为旋转轴的轴次,对应于次轴的对称操作有n个。
C n n=E﹙上标n表示操作的次数,下同﹚。
如NH3 (见图 1)旋转 2π/3 等价于旋转 2π (复原),
基转角α=360°/n C3 - 三重轴;再如平面 BF3 分子,
具有一个 C3 轴和三个 C2 轴,倘若分子中有一个以上
的旋转轴,则轴次最高的为主轴。
图1
2.3 对称面与反映操作
分别用σ、σ^表示。
对称面也称为镜面,它将分子分为两个互为镜像的部分。
对称面所对应的操作是反映,它使分子中互为镜像的两个部分交换位置而使分子复原。
σ^ⁿ=E^﹙n为偶数﹚,σ^2n=E^﹙n为奇数﹚。
对称面又分为:σh面﹙垂直于主轴的对称面﹚、σv面﹙包含主轴的对称面﹚与σd面﹙包含主轴并平分垂直于主轴的两个C2轴的夹角的平面﹚,σd是σv 面的特殊类型。
例如,水分子有两个对称面,一个面是分子平面,它包含有 3 个原子;另一个面垂直上述分子平面,并且平分 H- O- H 键角(见图 2)
图2
2.4 对称中心及反演操作
分别用i及i^表示。
选取分子的中心为笛卡尔坐标的原点,将分子中的任何一点﹙x,y,z﹚移到另一点﹙-x,-y,-z﹚后分子能复原的操作称为反演,进行反演时所依据的中心点称为对称中心i。
i^n= E^﹙n为偶数﹚, i^2n=E^﹙n为奇数﹚。
C- C 键的中点便是对称中心,如果从一个 Cl 原子至中心连一直线,则在其延长线的相等距离处会遇到第二个 Cl 原子。
对于两个 H 原子也存在同样的关系。
例如 C2H4Cl2(见图 3)
图3
2.5 旋映轴和旋转反映操作
可用S n及S^n表示。
若分子绕某轴旋转 2π/n,再用垂直此轴的平面进行反映操作,得到分子的等价构型,将该轴与平面组合所得的对称元素称为旋映轴,以 Sn 表示。
S n n=E﹙n为偶数﹚,S n2n=E﹙n为奇数﹚。
在 CH4分子中,存在着 S4轴,绕垂直轴 z 轴旋转 2π/4。
在经 xy 平面反映,则使分子的取向与原来的相重合。
例如 CH4(见图4)
图4
三.对称群
3.1 对称群的定义
群是元素的集合G(元素是广义的,可以是矩阵、向量、操作等),在中G定义一种运算法则(通常称为乘法),如能满足封闭性、乘法的结合律、包含恒等元素与逆元等条件,
则称集合G为一个群。
对称操作的集合满足群的定义,可构成一个对称操作群。
对称群中的恒等元是不动E。
如NH3分子中有一个C3轴和三个包含C3轴的对称面σv,共有六个对称操作, G: {E, C13, C23, σv, σv', σv''},符合群
的四个条件,组成C3v群。
组成群的群元素的数目称为群阶,群阶越高,对称性越高。
任意一个分子的对称操作集合都可构成一个群,同时分子中所有对称元素至少交于一点,或者说分子中至少有一点在所有对称操作下保持不动,例如在对称操作时NH3中N原子始终保持不动,因而称这类群为点群。
3.2 点群的分类
常见的分子点群有:
Cn 群:分子中只有一个 Cn 轴,共有n 个操作。
如H2O2分子属C2群。
Cnv群:分子中有一个Cn轴,且有n个包含Cn轴的σv面,共有2n个操作。
如H2S分子属C2v群。
Cnh群:分子中有一个Cn轴,且有垂直于Cn的σh 面, 2n有个操作。
n为偶数时必有C1h=Cs。
没有其他
对称元素的平面型分子群均属均属Cs群
如分子
Dn群:分子中有一个Cn轴,另有n个垂直于Cn 轴的C2轴,该点群共有2n个操作。
如既非交叉又非重叠的CH3CH3分子属D3群。
Dnh群: Dn在基础上,另有一个垂直于Cn轴的σh 面,共有4n个操作(n个C2和σh作用自然地产生n个σv, Cn与σh也可产生n个独立操作, n为偶数时还有 i)。
如C6H6分子属D6h 群。
Dnd群:在Dn基础上,有n个σd面,该点群共有 4n个操作。
如交叉型CH3CH3分子属D3d群。
Sn群:有一个Sn轴,当n为偶数时,群中有n个操作, n为奇数时,即为Cnh群。
S2轴相当于一个i,
因此S2群亦为群Ci。
如CHClBrCHClBr属S2群。
Td 群:具有正四面体构型的分子,如 CH4、 CCl4、 SiH4
等均属Td,它有4个C3轴(指向正四面体顶点), 3个C2轴亦为S4轴(4个顶点两两相连成六条线,连接相对连线的中点即为3个C2轴)以及6个
σd面,共有24个操作。
Oh 群 : 具有正八面体构型的分子 , SF6、
[Fe(CN)6]4-、 [Co(NH3)6]3+、 [Cr(CN)6]3-等均属于群。
有4个C3轴(也是S6)(两个相对面中心的连线,八个面相应的有4个C3), 3个C4 (也是S4,六个相对顶点的连线是3个C4),6
个C2轴(12个相对棱中点的连线而成6 个C2)3个σh (与C4相垂直)和6个σd面以及对称中心。
共有48个操作。
分子所属点群的确定
为了使确定分子所属的点群不出差错,按照以下步骤进行。
1分子几何构型是否是直线型?
2是直线型,是否有对称中心i?如果对称中心属于D∞h点群。
无对称中心属于C∞v点群。
3不是直线型,是否有多个Cn(n>3)轴,如果有多个C n 轴,就属于T d或0h点群。
4若无多个C n轴,是否有C n?
5若无多个C n轴,是否有σ?如果有属于C S点群,没有σ,是否有i?如果有属于C i点群,没有属于C I点群。
6有C n轴,,是否有n个垂直于C n的C2轴?如果有,是否有σh?如果有则属于D nh点群,没有σh,是否有n个σd?如果有则属于D nd,,如果没有则属于D n点群。
7如果没有n个垂直于C n的C2轴?是否有σh?如果有则属于C nh点群。
8如果没有σh?是否有n个σv?如果有则属于C nv点群,如果没有则属于C n轴或属于S n点群。
分子点群类型和分子所属点群的确定用下表来表示,并得出结论。
参考文献:
[1] 周公度 . 结构和物性 [M]. 北京:高等教育出版社,1993.184 ~185.
[2]东北师范大学、华东师范大学、西北师范大学合编.结构化学[M].北京:高等教育出版社,2003.121~122.
[3]刘国璞,白光美,廖松生. 大学化学[M]. 北京:清华大学出版社,1985:415- 421.
[4]杜少华. 分子极性判断二法[J]. 中学理科教学,1999:(9):41- 48.
[5]周端政. 辞海[M]. 上海:上海辞书出版社,1979:431.
[6]卢嘉锡.化学键的本质[M]. 上海:上海科技出版社,1996:36.
如有侵权请联系告知删除,感谢你们的配合!。
