(完整)第十六章分式知识点和典型例习题,推荐文档.docx
人教版八年级数学第十六章分式知识点总结

第十六章 分式知识点及典型例子一、分式的定义:如果A 、B 表示两个整式,且B 中含有未知数,那么式子BA 叫做分式。
二、在分式中,如果________,则分式AB 有意义;如果________,则分式A B无意义;如果________且_________不为零时,则分式A B的值为零;如果__________,则分式0A B > 如果____________,则分式0A B <; 例1.下列各式aπ,11x +,15x+y ,22a b a b --,-3x 2,0•中,是分式的有( )个。
例2.下列分式,当x 取何值时有意义。
(1)2132x x ++; (2)2323x x +-。
例3. 当x________时,分式2134x x +-的值为正数,当x________时,分式2134x x +-的值为负数 例4.当x______时,分式2134x x +-无意义。
当x_______时,分式2212x x x -+-的值为零。
当x_________时,分式2361x x -+的值为负数。
三、分式的基本性质:分式的分子与分母同乘或除以一个不等于0的整式,分式的值不变,用字母表示为_________________________________.分式的分子、分母和分式本身的符号改变其中任何____个,分式的值不变.四、约分:把分式的分子与分母的公因式约去,这样的分式变形叫做分式的约分,约分的理论依据是分式的___________________。
约分的方法:分式的分子与分母同除以他们的公因式,如果分式的分子、分母都是单项式,就直接约去分子、分母的__________;如果分式的分子或分母是多项式,就先__________,再判断公因式进行约分。
最简分式:分子与分母没有____________的分式,叫做最简分式。
(注意约分一定要彻底)五、通分:利用分式的基本性质把几个异分母的分式化为_________的分式,这样的分式变形叫做分式的通分。
第十六章分式全章总结
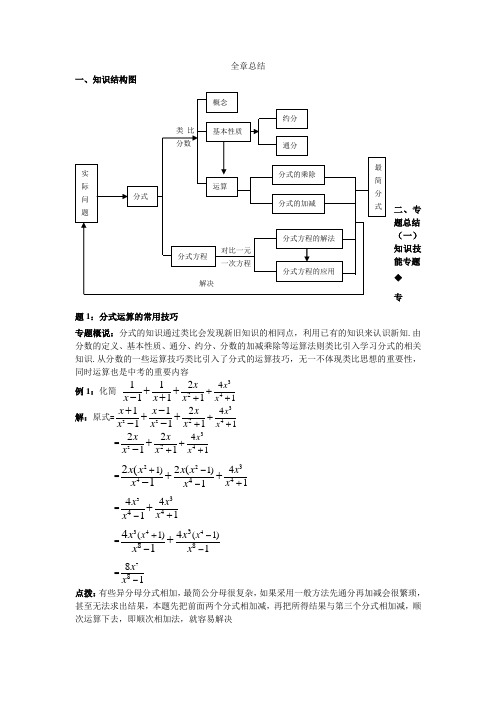
全章总结一、知识结构图二、专题总结 (一)知识技能专题 ◆专题1:分式运算的常用技巧专题概说:分式的知识通过类比会发现新旧知识的相同点,利用已有的知识来认识新知.由分数的定义、基本性质、通分、约分、分数的加减乘除等运算法则类比引入学习分式的相关知识.从分数的一些运算技巧类比引入了分式的运算技巧,无一不体现类比思想的重要性,同时运算也是中考的重要内容例1:化简 34241211111x x x x x x +++++-+解:原式=2234241211111x x x x x x x x ++++-++--=2342412121x x x x x x ++++- =2243441)1)412(12(1x x x x x x x x +--+++- =33444141x x x x -++ =344388(1)(1)4141x x x x x x +---+ =7881x x - 点拨:有些异分母分式相加,最简公分母很复杂,如果采用一般方法先通分再加减会很繁琐,甚至无法求出结果,本题先把前面两个分式相加减,再把所得结果与第三个分式相加减,顺次运算下去,即顺次相加法,就容易解决例2:计算:1111+(1)(1)(2)(2)(3)(2009)(2010)a a a a a a a a ++++++++++…解:原式=1111----12320101111+122009a a a a a a a a ++++++++++())))((…( =1111----12320101111+122009a a a a a a a a ++++++++++… =120101a a +—=2010(2010)a a +=220102010a a+ 点拨:对于分子相同,分母是相邻两个连续整数的积的分式相加减,这样的分式无法进行通分,因此,可以用公式:111(1)1n n n n =-++,这样可以抵消一些项,即巧用裂项法;要注意裂项法计算时可能会出现公式:1111(()n n k k n n k=-++)●专题1的即时练习1.计算:2411241-111x x x x ++++++ 2.计算:1271651231222++++++++x x x x x x◆专题2:与增根有关的问题专题概说:分式方程我们通常转化为已经学习过的整式方程来解决.在去分母时,方程两边同时乘以所有分母的最简公分母.这种转化可能是等价转化,也就是说转化前的分式方程的解与转化后的整式方程的解完全一致;也可能是非等价转化,即在将分式方程转化为整式方程的过程中,x 的的取值范围发生了变化,这时整式方程的解不一定是原分式方程的解,这种解题过程中增加的根称为分式方程的增根. 例3:a 为何值时,关于x 的方程223242ax x x x +=--+会产生增根? 解: 在方程两边同时乘以(2)(2)x x +-,得2(2)3(2)x ax x ++=-整理,得(1)10a x -=- 如果方程有增根,则x=2或-2当x=2时,(1)210a -⨯=-,解得4a =- 当x=-2时,(1)(2)10a -⨯-=-,解得6a = 所以,当46a =-或时,原方程会产生增根点拨:分式方程的增根是使最简公分母为零的根,但增根一定是由分式方程得到的整式方程的根。
新人教版八年级数学下册第十六章分式知识点总结

第十六章 分式知识点及典型例子一、分式的定义:如果A 、B 表示两个整式,并且B 中含有字母,那么式子B A 叫做分式。
例1.下列各式a π,11x +,15x+y ,22a b a b--,-3x 2,0•中,是分式的有( )个。
二、 分式有意义的条件是分母不为零;【B ≠0】分式没有意义的条件是分母等于零;【B=0】分式值为零的条件分子为零且分母不为零。
【B ≠0且A=0 即子零母不零】例2.下列分式,当x 取何值时有意义。
(1)2132x x ++; (2)2323x x +-。
例3.下列各式中,无论x 取何值,分式都有意义的是( )。
A .121x +B .21x x +C .231x x +D .2221x x + 例4.当x______时,分式2134x x +-无意义。
当x_______时,分式2212x x x -+-的值为零。
例5.已知1x -1y =3,求5352x xy y x xy y+---的值。
三、分式的基本性质:分式的分子与分母同乘或除以一个不等于0的整式,分式的值不变。
(0≠C )四、分式的通分和约分:关键先是分解因式。
例6.不改变分式的值,使分式115101139x y x y -+的各项系数化为整数,分子、分母应乘以(• )。
例7.不改变分式2323523x x x x -+-+-的值,使分子、分母最高次项的系数为正数,则是(• )。
例8.分式434y x a +,2411x x --,22x xy y x y-++,2222a ab ab b +-中是最简分式的有( )。
例9.约分:(1)22699x x x ++-; (2)2232m m m m-+- 例10.通分:(1)26x ab ,29y a bc ; (2)2121a a a -++,261a - 例11.已知x 2+3x+1=0,求x 2+21x 的值. C B C A B A ⋅⋅=C B C A B A ÷÷=例12.已知x+1x =3,求2421x x x ++的值. 五、分式的运算:分式乘法法则:分式乘分式,用分子的积作为积的分子,分母的积作为分母。
分式分类总结

矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。
如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。
㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。
(2 列出开发利用方案编制所依据的主要基础性资料的名称。
如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。
对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。
二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。
2、国内近、远期的需求量及主要销向预测。
㈡产品价格分析
1、国内矿产品价格现状。
2、矿产品价格稳定性及变化趋势。
三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。
2、矿区矿产资源概况。
3、该设计与矿区总体开发的关系。
㈡该设计项目的资源概况
1、矿床地质及构造特征。
2、矿床开采技术条件及水文地质条件。
分式知识点整理

用心教育个性化辅导讲义第十六章 分式知识点整理 1.分式的定义:如果A 、B 表示两个整式,并且B 中含有字母,那么式子B A 叫做分式。
例1.下列各式a π,11x +,15x+y ,22a b a b --,-3x 2,0•中,是分式的有( )个。
分式有意义的条件是分母不为零,分式值为零的条件分子为零且分母不为零。
例2.下列分式,当x 取何值时有意义。
(1)2132x x ++; (2)2323x x +- 变式练习:已知2-=x 时,分式ax b x +-无意义,4=x 时,分式的值为零,则____=+b a 。
例3.下列各式中,无论x 取何值,分式都有意义的是( )。
A .121x + B .21x x + C .231x x + D .2221x x + 例4.当x______时,分式2134x x +-无意义。
当x_______时,分式2212x x x -+-的值为零。
2.分式的基本性质:分式的分子与分母同乘或除以一个不等于0的整式,分式的值不变。
(0≠C )例5.不改变分式的值,使分式115101139x y x y -+的各项系数化为整数,分子、分母应乘以(• )。
例6.不改变分式2323523x x x x -+-+-的值,使分子、分母最高次项的系数为正数,则是(• )。
3.分式的通分和约分:关键先是分解因式例7.分式434y x a +,2411x x --,22x xy y x y-++,2222a ab ab b +-中是最简分式的有( )。
例8.约分:(1)22699x x x ++-; (2)2232m m m m-+- A A C B B C •=•A A C B B C ÷=÷例9.通分:(1)26x ab ,29y a bc ; (2)2121a a a -++,261a - 例10.已知x 2+3x+1=0,求x 2+21x 的值. 例11.已知x+1x=3,求2421x x x ++的值.4.分式的运算:分式乘法法则:分式乘分式,用分子的积作为积的分子,分母的积作为分母。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十六章分式知识点和典型例习题【知识网络】【思想方法】1.转化思想转化是一种重要的数学思想方法,应用非常广泛,运用转化思想能把复杂的问题转化为简单问题,把生疏的问题转化为熟悉问题,本章很多地方都体现了转化思想,如,分式除法、分式乘法;分式加减运算的基本思想:异分母的分式加减法、同分母的分式加减法;解分式方程的基本思想:把分式方程转化为整式方程,从而得到分式方程的解等.2.建模思想本章常用的数学方法有:分解因式、通分、约分、去分母等,在运用数学知识解决实际问题时,首先要构建一个简单的数学模型,通过数学模型去解决实际问题,经历“实际问题———分式方程模型———求解———解释解的合理性”的数学化过程,体会分式方程的模型思想,对培养通过数学建模思想解决实际问题具有重要意义.3.类比法本章突出了类比的方法,从分数的基本性质、约分、通分及分数的运算法则类比引出了分式的基本性质、约分、通分及分式的运算法则,从分数的一些运算技巧类比引出了分式的一些运算技巧,无一不体现了类比思想的重要性,分式方程解法及应用也可以类比一元一次方程.第一讲分式的运算【知识要点】 1. 分式的概念以及基本性质;2.与分式运算有关的运算法则3.分式的化简求值 ( 通分与约分 )4.幂的运算法则【主要公式】 1. 同分母加减法则:b c b c a0a a a2. 异分母加减法则 :b d bc da bc daa 0, c 0 ;a c ac ac ac3. 分式的乘法与除法b d bd bc bd bd:?ac,d a?aca c a c4.同底数幂的加减运算法则 : 实际是合并同类项5. 同底数幂的乘法与除法m n=am+n mn m-n; a●a; a÷a =a6.积的乘方与幂的乘方:(ab)m= a m b n, (a m)n=a mn7. 负指数幂 :a-p =1p a0=1a8.乘法公式与因式分解: 平方差与完全平方式(a+b)(a-b)= a 2- b 2 ;(a±b) 2= a 2±2ab+b2(一)、分式定义及有关题型题型一:考查分式的定义b , x2y 21【例 1】下列代数式中:x ,1x y,a,xy ,是分式的有:.2a b x y x y题型二:考查分式有意义的条件【例 2】当x有何值时,下列分式有意义( 1)x 4(2)3x( 3)x2( 4)6 x( 5)1x 4x2221| x | 3x1x题型三:考查分式的值为0 的条件【例 3】当x取何值时,下列分式的值为0.( 1)x 1(2) | x | 2(3) x22x 3x 3x24x2 5 x6题型四:考查分式的值为正、负的条件【例 4】( 1)当x为何值时,分式4为正;8x( 2)当x为何值时,分式35x为负;(x1)2( 3)当x为何值时,分式x2为非负数 .x3练习:1.当 x 取何值时,下列分式有意义:( 1)1(2)3 x( 3)16 | x | 311( x 1) 21x2.当 x 为何值时,下列分式的值为零:( 1) 5 | x1 |(2)25 x 2x 426x5x3.解下列不等式( 1) | x | 2(2)x 53 0x 1x 2 2x(二)分式的基本性质及有关题型A A M A M 1.分式的基本性质:B B MB Ma a a a 2.分式的变号法则:bbbb【例 4】已知: x12 ,求 x 21 的值 .xx 2【例 5】若 | x y1 | ( 2x 3)20 ,求1 的值 .4x 2 y练习:1.不改变分式的值,把下列分式的分子、分母的系数化为整数 .( 1) 0.03x 0.2y0.4a 3 b(2) 1 50.08x 0.5y1ab4102.已知: x1 3 ,求 x 2的值 .xx 2x 4 13.已知:11 3 ,求 2a 3ab2b的值 .abb ab a 4.若 a22a b26b 100 ,求 2ab的值 .3a 5b5.如果 1x2 ,试化简| x2 | x 1 | x | .2 x | x 1|x题型一:化分数系数、小数系数为整数系数【例 1】不改变分式的值,把分子、分母的系数化为整数.(三)分式的运算1 x2 y (2) 0.2a0.03b1.确定最简公分母的方法:( 1) 2 31 x 1 y0.04a b①最简公分母的系数,取各分母系数的最小公倍数;3 4②最简公分母的字母因式取各分母所有字母的最高次幂.题型二:分数的系数变号2.确定最大公因式的方法:①最大公因式的系数取分子、分母系数的最大公约数;【例 2】不改变分式的值,把下列分式的分子、分母的首项的符号变为正号.②取分子、分母相同的字母因式的最低次幂.( 1) x y( 2)a ( 3)a题型一:通分x ybba题型三:化简求值题【例 1】将下列各式分别通分 .【例 3】已知:1 1 5 ,求2x 3xy 2y 的值 .cbaa bxy x 2xyy( 1) 2ab ,3a 2c ,5b 2 c;( 2) a b,2b 2a ;提示:整体代入,①x y3xy ,②转化出1 1( 3) 1 x2 ;( 4) a 2,1x y .x2,1 2x x2 ,x 2xx 22 a题型二:约分【例 2】约分:( 1) 16 x 2y ;( 3) n2m 2 ;(3) x2x 2 .20xy 3m nx 2 x 6题型三:分式的混合运算【例 3】计算:( 1) ( a2b)3( c 2 )2(bc) 4;( 2) ( 3a3) 3 (x2y 2) (yx) 2;c abax yy x( 3)m 2nnn 2m ; ( 4) a21a 1 ;n m m n ma ( 5) 1 1 2 x4x 3 8 x 71 x 21 x4;1 x 1 x1 x8( 6)111;(x 1)( x1) (x 1)( x3) ( x3)( x 5)( 7) (x 2 44 x 1) ( x22x )x 24x2x 1题型四:化简求值题【例 4】先化简后求值( 1)已知: x1 ,求分子 1x 284 [(x 2 4 1) ( 1 1)] 的值;4x 2 x( 2)已知:xy z ,求 xy 2 yz 3xz 的值;234x2y2z2( 3)已知:231 021 1a,试求 (aa2)(aa ) 的值 .a题型五:求待定字母的值【例 5】若13x M N ,试求 M , N 的值 .x 2 1x 1x 1练习:1.计算( 1)2a 5a 1 2a 3 ; ( 2) a 2bb 2 2ab ;2(a 1)2(a 1)2(a 1)a b a ( 3)ab ca 2b3cb2c;( 4) ab2b 2 ;a b cb c ac a b a b4ab 4ab ) ;( 6)11 2 ;( 5) (a b )( a b1 x1 x 2a b a b1 x( 7)121.( x 2)( x3)( x 1)( x 3)( x 1)(x2)2.先化简后求值( 1)a1a24 1,其中 a 满足 a 2a 0 .a2 a 22a 1a 21( 2)已知 x : y 2 : 3 ,求 (x 2y 2) [( xy ) (xy )3 ] x 的值 .xyxy 23.已知:5 x 4AB ,试求 A 、 B 的值 .(x 1)( 2x 1) x12x14.当 a 为何整数时,代数式399a805的值是整数,并求出这个整数值 .a 2(四)、整数指数幂与科学记数法题型一:运用整数指数幂计算【例 1】计算:( 1) (a2 ) 3(bc 1)3 ( 2) (3x 3 y 2 z1 )2 (5xy 2 z3 ) 2( 3) [ (a b) 3(ab) 5 ] 2 ( 4) [( x y) 3 (xy) 2 ]2 (x y) 6(a b)2(ab) 4题型二:化简求值题【例 2】已知 xx15 ,求( 1) x 2x 2 的值;( 2)求 x 4x 4的值 .题型三:科学记数法的计算【例 3】计算:(1)(3103)(8.2102)2;( 2)(4 103)2(21023.【例 2】解下列方程)练习:( 1)x4x 44;(2) x 7 x 9 x 10 x 6 x 1x x 6 x 8x 9x 51.计算:( 1)(11)(1)2 | 1 |(1 3 )0(0.25)200742008提示:(1)换元法,设x y ;(2)裂项法,x711. 3553x1x6x6(2)(313n2)2(m2n)3【例 3】解下列方程组m(2ab 2 ) 2(a 2 b) 2111(1)(3)x y2 (3a3 b2 )(ab 3 )2111( 2)y z3(4) [4( x y)2( x y)2]2111(3) 2z x4 [2( x y)1(x y)]2.已知 x25x10 ,求( 1) x x 1,( 2) x2x 2的值 .题型三:求待定字母的值第二讲分式方程【例 4】若关于x的分式方程21m有增根,求 m 的值.x3x3【知识要点】 1.分式方程的概念以及解法;【例 5】若分式方程2x a1的解是正数,求a 的取值范围.x22. 分式方程产生增根的原因2a 3. 分式方程的应用题提示:0且 x 2 , a 2 且 a 4 .x3【主要方法】 1. 分式方程主要是看分母是否有外未知数;题型四:解含有字母系数的方程2.解分式方程的关健是化分式方程为整式方程; 方程两边同乘以最简公分母 .3.解分式方程的应用题关健是准确地找出等量关系, 恰当地设末知数 .【例 6】解关于x的方程(一)分式方程题型分析x a c(c d0)题型一:用常规方法解分式方程b x d【例 1】解下列分式方程提示:(1) a,b,c, d 是已知数;( 2) c d0 .( 1)13;( 2)210 ;(3)x 14 1 ;( 4)5 x x 5题型五:列分式方程解应用题x1x x3x x 1x21x 3 4 x练习:提示易出错的几个问题:①分子不添括号;②漏乘整数项;③约去相同因式至使漏根;④忘记1.解下列方程:验根 .( 1)x 12 x0 ;( 2)x24;题型二:特殊方法解分式方程x 1 1 2 x x3x3( 3)2x232 2 ;(4)7 31 7 x 2xxx 2x x x 2x 21( 5) 5x 4 2x 5 1(6) 11 112x 4 3x 2 2x 1 x 5 x 2 x 4( 7)x x 9 x 1 x 8x2x7x1 x62.解关于 x 的方程:( 1)11 2 (b 2a) ;( 2) 1 a1 b(a b) .ax ba xb x3.如果解关于 x 的方程k 2x会产生增根,求 k 的值 .x 2x24.当 k 为何值时,关于x 的方程x3k1 的解为非负数 .x2 (x 1)( x 2)5.已知关于 x 的分式方程2a1 a 无解,试求 a 的值 .x1(二)分式方程的特殊解法解分式方程,主要是把分式方程转化为整式方程, 通常的方法是去分母,并且要检验,但对一些特殊的分式方程,可根据其特征,采取灵活的方法求解,现举例如下:一、交叉相乘法例 1.解方程:1x 3x 2二、化归法例 2.解方程:121 x 21 x三、左边通分法例 3:解方程:x8 1 x 8 x7 7四、分子对等法例 4.解方程:1a 1b (a b)axbx五、观察比较法例 5.解方程:4 x5 x 2 172 4 x45x六、分离常数法例 6.解方程:x 1 x 8 x 2 x 7x2 x9 x3 x 8七、分组通分法例 7.解方程:1 1 1 1x2 x5 x3 x4(三)分式方程求待定字母值的方法例 1.若分式方程x 1m 无解,求 m 的值。
