细长压杆的临界压力得推导ppt课件
合集下载
压杆稳定(工程力学课件)
压杆稳定的概念
桁架结构
在轴向压力作用下，
短粗压杆 只要满足杆受压时的强度
条件，就能正常工作
细长压杆
破坏形式呈现出与强度问题 截然不同的现象
FN [ ]
A
压杆失稳
细长压杆:
临界压力或临界力ห้องสมุดไป่ตู้Fcr
F Fcr F Fcr
稳定的平衡 不稳定的平衡
压杆失稳
在轴向压力 F 由小逐渐增大 的过程中，压杆由稳定的平衡 转变为不稳定平衡，这种现象 称为压杆失稳。
首先判断压杆的失稳方向
(1)两端约束 1
(2)截面形状
Fcr （2 El）I2
Iz
hb3 12
140 803 12
597.3104
mm4
Iy
bh3 12
80 1403 12
1829.3104
mm4
Fcr1
2 EImin
(l)2
2 10 103 MPa 597.3104 (1 3103 mm)2
mm4
65 435 N 65.44 kN
（N、mm、MPa）
【例 1】 细长压杆，两端为球形铰支，
矩形横截面, E 10 GPa ，求其临界力。
Fcr （2 El）I2
长度影响
【例 2】细长压杆，上端约束为球形铰支，
下端约束在 xOz平面内可视为两端铰支，
Fcr （2 El）I2
在 xOy 平面内可视为一端铰支、一端固定
M
Wz
[ ]
81.67
πD4 i I 64 D 40mm
A πD2 4 4
l 1 3103 75
i
40
查表： 0.54
81.67
桁架结构
在轴向压力作用下，
短粗压杆 只要满足杆受压时的强度
条件，就能正常工作
细长压杆
破坏形式呈现出与强度问题 截然不同的现象
FN [ ]
A
压杆失稳
细长压杆:
临界压力或临界力ห้องสมุดไป่ตู้Fcr
F Fcr F Fcr
稳定的平衡 不稳定的平衡
压杆失稳
在轴向压力 F 由小逐渐增大 的过程中，压杆由稳定的平衡 转变为不稳定平衡，这种现象 称为压杆失稳。
首先判断压杆的失稳方向
(1)两端约束 1
(2)截面形状
Fcr （2 El）I2
Iz
hb3 12
140 803 12
597.3104
mm4
Iy
bh3 12
80 1403 12
1829.3104
mm4
Fcr1
2 EImin
(l)2
2 10 103 MPa 597.3104 (1 3103 mm)2
mm4
65 435 N 65.44 kN
（N、mm、MPa）
【例 1】 细长压杆，两端为球形铰支，
矩形横截面, E 10 GPa ，求其临界力。
Fcr （2 El）I2
长度影响
【例 2】细长压杆，上端约束为球形铰支，
下端约束在 xOz平面内可视为两端铰支，
Fcr （2 El）I2
在 xOy 平面内可视为一端铰支、一端固定
M
Wz
[ ]
81.67
πD4 i I 64 D 40mm
A πD2 4 4
l 1 3103 75
i
40
查表： 0.54
81.67
材料力学课件第9章 压杆稳定
BC ≈ 0.7l
FACcr =
( 2 × 0.3l )
π 2 EI
2
=
( 0.6l )
2
π 2 EI
2
, FBCcr =
( 0.7l )
π 2 EI
2
综合得： 综合得：
Fcr =
( 0.7l )
π 2 EI
（9.4） ）
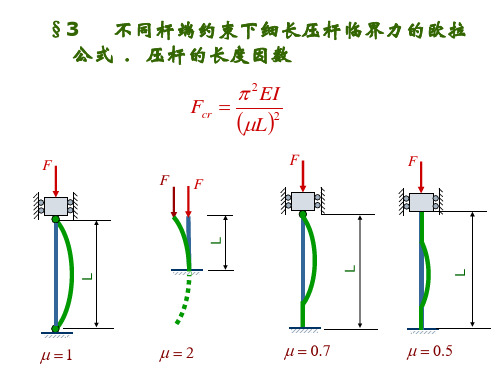
三、欧拉公式的普遍表达式 π 2 EI 1、公式： 、公式： Fcr = 2 ( µl ) 2、常见约束压杆的长度系数： 、常见约束压杆的长度系数： •两端铰支： 两端铰支： µ=1 两端铰支 •一端固定，一端自由： 一端固定， µ=2 一端固定 一端自由： •两端固定： 两端固定： µ=0.5 两端固定 •一端固定，一端铰支： 一端固定， µ≈0.7 一端固定 一端铰支：
FACcr = FBDcr =
π 2 EI
2
l 2× 4 l 2
=
π 2 EI
l 2
2
, FCDcr =
π 2 EI
l 2
2
综合得： 综合得： Fcr =
π 2 EI
2
（9.3） ）
3、一端固定，一端铰支： 、一端固定，一端铰支：
µl
λ > λ1
d=25mm杆为大柔度杆。 杆为大柔度杆。 杆为大柔度杆 由欧拉公式试算结果正确。 由欧拉公式试算结果正确。 5、活塞直径确定为 、活塞直径确定为25mm。 。
§9— 5 提高压杆稳定性的措施 一、影响因素 •压杆截面形状、长度、约束条 压杆截面形状、 压杆截面形状 长度、 件和材料的性质。 件和材料的性质。 二、提高压杆稳定性的措施 1、选择合理的截面形状： 、选择合理的截面形状：
7章8章九章10章11章12章课件 (19)
y k 2 y k 2 M 0 F
F
M (x)
y Asin kx B cos kx M0 F
y kAcos kx kBsin kx
x 将x=0,y=0, y 0 代入上述二式得
y
A0
B M0
y
M0 F
(1
cos kx)
y
kM0 F
sin
kx
X=L
sin kL 0
k
L
F
y 0
2.两杆下端固定上端自由，以z为中性轴弯曲失稳。Fcr 2Fra bibliotekIzd 4
64
2
z
Fcr 2
2
2EI
L2
2E d 4
2
64
2L2
3Ed 4
128L2
两根直径为d的圆杆,上下两端分别与刚性板固结,如图 示.试分析在总压力作用下,压杆可能失稳的几种形式,并 求出最小的临界荷载.(设满足欧拉公式的使用条件)
Fcr
0.62 12 15.4N
两杆均为细长杆的杆系如图示，若杆件在ABC面内 因失稳而引起破坏，试求载荷F为最大值时的θ角（设 0＜θ＜π／2）。设AB杆和BC杆材料截面相同。
1.节点B的平衡
B
FAB
F
B
FBC F
FAB F cos FBC F sin
2.两杆分别达到临界力时F可达最大值
A
l
tg FBC
FAB
F BC cr
F AB cr
ctg2
C
FcrAB
2EI LAB 2
2EI
L cos
2
FcBr C
2EI LBC 2
arctg ctg2
细长压杆的临界压力欧拉公式
(l)2
(2)
Fc r正 Fc r圆
π2EI正
( l)2
π2 EI圆
I正 I圆
a4
12 πd 4
( l)2
64
πd 2 4
2
12 πd 4
64
π 3
例2：图示两桁架中各杆的材料和截面均相同，设 F1和F2 分别为这两个
桁架稳定的最大载荷，则
(A) F1 = F2；
π2EI
( l )2
称为长度因数，l 称为相当长度
π2EI (0.5l ) 2
0.5
Fc r
π2EI (0.7l ) 2
0.7
Fc r
~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~~~~~~~~~~
π2EI (2l ) 2
2
Fc r
π2EI l2
1
Fc r
例1：圆截面的细长压杆，材料、杆长和杆端约束保持不变，若将压杆的
直径缩小一半，则其临界力为原压杆的多少倍？若将压杆的横截面改变为面
积相同的正方形截面，则其临界力为原压杆的多少倍？
解：(1)
Fc r
π2EI
(l)2
π2E πd 4 64
第一讲 基本概念与欧拉公式
一：压杆稳定的概念
钢板尺：一端固 定 一端自由
Fcr ：临界压力
二：细长压杆的临界压力
一、两端铰支细长压杆的临界压力
M (x) F w
EI w M (x) F w
(2)
Fc r正 Fc r圆
π2EI正
( l)2
π2 EI圆
I正 I圆
a4
12 πd 4
( l)2
64
πd 2 4
2
12 πd 4
64
π 3
例2：图示两桁架中各杆的材料和截面均相同，设 F1和F2 分别为这两个
桁架稳定的最大载荷，则
(A) F1 = F2；
π2EI
( l )2
称为长度因数，l 称为相当长度
π2EI (0.5l ) 2
0.5
Fc r
π2EI (0.7l ) 2
0.7
Fc r
~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~~~~~~~~~~
π2EI (2l ) 2
2
Fc r
π2EI l2
1
Fc r
例1：圆截面的细长压杆，材料、杆长和杆端约束保持不变，若将压杆的
直径缩小一半，则其临界力为原压杆的多少倍？若将压杆的横截面改变为面
积相同的正方形截面，则其临界力为原压杆的多少倍？
解：(1)
Fc r
π2EI
(l)2
π2E πd 4 64
第一讲 基本概念与欧拉公式
一：压杆稳定的概念
钢板尺：一端固 定 一端自由
Fcr ：临界压力
二：细长压杆的临界压力
一、两端铰支细长压杆的临界压力
M (x) F w
EI w M (x) F w
压杆的稳定性PPT课件
l 2
l 表示把压杆折算成两端铰支的长度，称为相当长度。
称为长度系数，它反映了杆端不同支座情况对临界压力
的影响。
第28页/共68页
支座情况 两端铰支
一端固定 一端自由
一端固定 一端铰支
两端固定
压杆简图
临界压力 公式
2EI
l2
1.0
2EI
2l 2
2
2EI
0.7l 2
0.7
第29页/共68页
约小100倍！杆件先发生失稳现象！
F
第30页/共68页
8.3 压杆的临界应力、经验公式
1 临界应力
压杆处于临界状态时，近似认为压杆横截面上的轴向 正应力临界压力Fcr 与压杆的横截面面积A之比，该正应
力称为临界应力，以 cr 表示。
即
cr
Fcr A
2EI l2 A
式中，I i2 ,
A
i为截面的惯性半径，是一个与截面形状和尺寸
第13页/共68页
载 荷 更 大 的 状 态
第14页/共68页
压杆的平衡稳定性
F Fcr
临界力
F Fcr
F Fcr
微小横 向力Q
微小横 向力Q
上界
下界
稳定平衡
临界状态
不稳定平衡
稳定的直线平
微弯平衡状态
衡状态
第15页/共68页
压杆的平衡稳定性 F
F FFcr F F F Fcr
当 P Pcr 当 P Pcr
第19页/共68页
8.2 压杆的稳定性分析、欧拉公式
1 两端铰支细长杆的临界压力
如图所示细长等直杆
当压杆在压力F作用下处于临界状态时，杆件发生“微弯” 变形，x截面处的弯矩
l 表示把压杆折算成两端铰支的长度，称为相当长度。
称为长度系数，它反映了杆端不同支座情况对临界压力
的影响。
第28页/共68页
支座情况 两端铰支
一端固定 一端自由
一端固定 一端铰支
两端固定
压杆简图
临界压力 公式
2EI
l2
1.0
2EI
2l 2
2
2EI
0.7l 2
0.7
第29页/共68页
约小100倍！杆件先发生失稳现象！
F
第30页/共68页
8.3 压杆的临界应力、经验公式
1 临界应力
压杆处于临界状态时，近似认为压杆横截面上的轴向 正应力临界压力Fcr 与压杆的横截面面积A之比，该正应
力称为临界应力，以 cr 表示。
即
cr
Fcr A
2EI l2 A
式中，I i2 ,
A
i为截面的惯性半径，是一个与截面形状和尺寸
第13页/共68页
载 荷 更 大 的 状 态
第14页/共68页
压杆的平衡稳定性
F Fcr
临界力
F Fcr
F Fcr
微小横 向力Q
微小横 向力Q
上界
下界
稳定平衡
临界状态
不稳定平衡
稳定的直线平
微弯平衡状态
衡状态
第15页/共68页
压杆的平衡稳定性 F
F FFcr F F F Fcr
当 P Pcr 当 P Pcr
第19页/共68页
8.2 压杆的稳定性分析、欧拉公式
1 两端铰支细长杆的临界压力
如图所示细长等直杆
当压杆在压力F作用下处于临界状态时，杆件发生“微弯” 变形，x截面处的弯矩
材料力学压杆稳定PPT课件
6
工程背景 (Engineering background)
crane truck
7
问题的提出
p pcr
p pcr
p pcr
求载荷pcr是稳定问题的实质!!! 对象—压杆
方法—静力学方法
基本问题—
求pcr； 讨论支承对临界力的影响；
8
压杆稳定条件
2 细长压杆的欧拉临界压力
横向干扰力产生初始变形, P
1983年10月4日，北京的一幢正在施工的高层建筑 的高54.2m、长17.25m、总重565.4kN大型脚手架屈 曲坍塌，5人死亡、7人受伤 。
1907年北美魁北克圣劳伦斯河上大铁桥施工中,珩架下 弦受压杆屈曲,就如少一杆,成变形体而坍塌.
1925年苏联莫兹尔桥试运行时，因压杆失稳而破坏。
1940年美国塔科马桥,一场大风,因侧向压杆失稳而破 坏。
解：压杆在xoy平面内，
z
l
iz
1210012.21 17 .32
压杆在xoz平面内，
y
l1
iz
1200086 .6 11 .55
1
2E p
2205109
200106
101
maxmax{y,z}121.21
18
iz
b 23
17 .32 mm
iy
a 23
1ห้องสมุดไป่ตู้ .55 mm
所以，压杆为细长杆。
Pcr2E2 A33.06kN
3
液压缸顶杆
hydraulic pressure post rod
4
Scaffold frame
脚手架中的压杆
工程背景 (Engineering background)
材料力学课件 第十章压杆稳定
sinkL0
kn P
L EI
临界力 Pcr 是微弯下的最小压力，故，只能取n=1 ；且 杆将绕惯性矩最小的轴弯曲。
Pcr
2
EImin L2
14
Pcr
2
EImin L2
二、此公式的应用条件：
两端铰支压杆临界力的欧拉公式
1.理想压杆； 2.线弹性范围内； 3.两端为球铰支座。
三、其它支承情况下，压杆临界力的欧拉公式
29
我国钢结构柱子曲线
二、 受压构件的稳定公式
利用最大强度准则确定出轴心受压构件的临界应力 cr ，引入抗力分项系数 R ，则轴心受压构件的稳定计算公式如下：
N cr cr f y f A R R fy
f ：钢材的强度设计值
（10.24）
30
例6
如图所示，两端简支，长度l 5m 的压杆由两根槽钢组成，若限定两个槽钢腹板
Iy [73.3 (51.8)2 21.95]2 2176.5cm4
33
若失稳将仍会在 xoy平面内，有
imin iz
Iz A
1732.4 6.28cm 43.9
max
l imin
500 79.6 6.28
查表得2 0.733
此时3 与3 已经很接近，按两个 16a 槽钢计算压杆的许可压力，有
20
[例3] 求下列细长压杆的临界力。
y y
x
z
z
h
L1
L2
解：①绕
y 轴，两端铰支：
=1.0，
I
y
b3h 12
,
②绕 z 轴，左端固定，右端铰支：
b
Pcry
2EI L22
y
=0.7，
工程力学精品课程压杆稳定.ppt
第 10 章
压杆稳定
Stability of columns
一。稳定性概念
细长杆件承受轴向压缩载荷作用时，会表现出与强度失效性质全然不同的失效现象， 即将会由于平衡的不稳定性而发生失效，这种失效称为稳定性失效，简称失稳，又称为 屈曲失效。
内燃机配气机构中的挺杆
磨床液压装置的活塞杆
细长压杆随受力的改变，平衡的稳定性会发生改变，由稳定平衡转为不稳定平衡的 临界值称为压杆的临界压力或临界力；它是压杆保持稳定的直线平衡的最大值，或是 压杆保持微曲平衡的最小值。
b
经验公式: cr a b
其中，a，b是由杆件材料决定的常数
2）小柔度杆的临界应力
小柔度杆或短杆： λ < λ2 此时压杆属强度问题，临界应力就是屈服极限或强度极限，即
cr s
或
b
3） 临界应力总图
σ σcr=σs
σs σp
σcr=a-bλ σcr=π2E/λ2
O
λ2
λ1
可以明显地看出，短杆的临界应力与柔度λ无关，而中、长杆的临界应力则随柔度 λ的增加而减小。
例10-4图示钢结构，承受载荷F作用，试校核斜撑杆的稳定性。已知载荷F＝12kN，其
外径D＝45mm，内径d=36 mm，稳定安全系数nst=2.5。斜撑杆材料是Q235钢，弹性模 量E=210 GPa， σp=200 MPa， σs=235 MPa，
1m A
1m B
F 解：(a) 受力分析。以梁AC为研究对象，由静力
1.减小压杆的支承长度；因为临界应力与杆长平方成反比，因此可以显著地提高压杆承 载能力。 2. 改变压杆两端的约束；使长度系数减小，相应地减小柔度，从而增大临界应力。 3. 选择合理的截面形状；可以在不增加截面面积的情况下，增加横截面的惯性矩I， 从而减小压杆柔度，起到提高压杆稳定性的作用。图10.10是起重臂合理截面。
压杆稳定
Stability of columns
一。稳定性概念
细长杆件承受轴向压缩载荷作用时，会表现出与强度失效性质全然不同的失效现象， 即将会由于平衡的不稳定性而发生失效，这种失效称为稳定性失效，简称失稳，又称为 屈曲失效。
内燃机配气机构中的挺杆
磨床液压装置的活塞杆
细长压杆随受力的改变，平衡的稳定性会发生改变，由稳定平衡转为不稳定平衡的 临界值称为压杆的临界压力或临界力；它是压杆保持稳定的直线平衡的最大值，或是 压杆保持微曲平衡的最小值。
b
经验公式: cr a b
其中，a，b是由杆件材料决定的常数
2）小柔度杆的临界应力
小柔度杆或短杆： λ < λ2 此时压杆属强度问题，临界应力就是屈服极限或强度极限，即
cr s
或
b
3） 临界应力总图
σ σcr=σs
σs σp
σcr=a-bλ σcr=π2E/λ2
O
λ2
λ1
可以明显地看出，短杆的临界应力与柔度λ无关，而中、长杆的临界应力则随柔度 λ的增加而减小。
例10-4图示钢结构，承受载荷F作用，试校核斜撑杆的稳定性。已知载荷F＝12kN，其
外径D＝45mm，内径d=36 mm，稳定安全系数nst=2.5。斜撑杆材料是Q235钢，弹性模 量E=210 GPa， σp=200 MPa， σs=235 MPa，
1m A
1m B
F 解：(a) 受力分析。以梁AC为研究对象，由静力
1.减小压杆的支承长度；因为临界应力与杆长平方成反比，因此可以显著地提高压杆承 载能力。 2. 改变压杆两端的约束；使长度系数减小，相应地减小柔度，从而增大临界应力。 3. 选择合理的截面形状；可以在不增加截面面积的情况下，增加横截面的惯性矩I， 从而减小压杆柔度，起到提高压杆稳定性的作用。图10.10是起重臂合理截面。
材料力学第九章-压杆稳定
Iy Iz
按照 Iy计算临界压力。
工程力学
例 按照 Iy计算临界压力。
F b z
h l
π 2 EI π 2 200 10 3 48 10 4 Fcr N 2 2 ( l ) (2 2500 )
37860N 37.86kN
若
y
h b 60mm
bh3 60 4 Iy Iz mm 108 10 4 mm 12 12
工程力学
三、其它支承情况下细长压杆的临界力 不同约束形式 压杆的临界力，可 以用类似的方法求 解微分方程导出。 但在已经导出 两端铰支压杆的临 界压力公式之后， 便可以用比较简单 的方法，得到其他 约束条件下的临界 力。
l
F
F
一端固定，一端自由， 长为l 的的压杆的挠曲线 和两端铰支，长为2l的 压杆的挠曲线的上半部 分相同。则临界压力:
工程力学
二、稳定性问题的分类 1.压杆的稳定性。2.板壳的稳定性。 本课程只讨论压杆的稳定性。
三、压杆的稳定与失稳 1．压杆的稳定性： 压杆维持其原有直线平衡状态的能力
2．压杆的失稳： 压杆丧失其原有直线平衡状态，不能稳定地工作。
工程力学
四、压杆失稳的原因 1)杆轴线本身不直(有初曲率)； 2)加载偏心； 3)压杆的材质不均匀；
4)外界干扰力。 五、失稳现象的特点 1.多样性。（如扭转、弯曲失稳，板、壳、柱） 2.整体性。构件失稳引起受力重新分配。整体失效、 整体分析。 3.破坏的突然性。应力在弹性范围，类似脆性破坏。
工程力学
• 1907年加拿大
魁北克大桥在 剪彩前突然坍 塌，600米长， 19000吨重的大
桥和86名建桥
3、中柔度杆的经验公式 对于 < p的压杆，其临界应力大于材料的比例极限，欧拉 公式已经不适用。
按照 Iy计算临界压力。
工程力学
例 按照 Iy计算临界压力。
F b z
h l
π 2 EI π 2 200 10 3 48 10 4 Fcr N 2 2 ( l ) (2 2500 )
37860N 37.86kN
若
y
h b 60mm
bh3 60 4 Iy Iz mm 108 10 4 mm 12 12
工程力学
三、其它支承情况下细长压杆的临界力 不同约束形式 压杆的临界力，可 以用类似的方法求 解微分方程导出。 但在已经导出 两端铰支压杆的临 界压力公式之后， 便可以用比较简单 的方法，得到其他 约束条件下的临界 力。
l
F
F
一端固定，一端自由， 长为l 的的压杆的挠曲线 和两端铰支，长为2l的 压杆的挠曲线的上半部 分相同。则临界压力:
工程力学
二、稳定性问题的分类 1.压杆的稳定性。2.板壳的稳定性。 本课程只讨论压杆的稳定性。
三、压杆的稳定与失稳 1．压杆的稳定性： 压杆维持其原有直线平衡状态的能力
2．压杆的失稳： 压杆丧失其原有直线平衡状态，不能稳定地工作。
工程力学
四、压杆失稳的原因 1)杆轴线本身不直(有初曲率)； 2)加载偏心； 3)压杆的材质不均匀；
4)外界干扰力。 五、失稳现象的特点 1.多样性。（如扭转、弯曲失稳，板、壳、柱） 2.整体性。构件失稳引起受力重新分配。整体失效、 整体分析。 3.破坏的突然性。应力在弹性范围，类似脆性破坏。
工程力学
• 1907年加拿大
魁北克大桥在 剪彩前突然坍 塌，600米长， 19000吨重的大
桥和86名建桥
3、中柔度杆的经验公式 对于 < p的压杆，其临界应力大于材料的比例极限，欧拉 公式已经不适用。
【材料力学课件】压杆的临界应力
15-3 压杆的临界应力如上节所述，欧拉公式只有在弹性范围内才是适用的。
为了判断压杆失稳时是否处于弹性范围，以及超出弹性范围后临界力的计算问题，必须引入临界应力及柔度的概念。
压杆在临界力作用下，其在直线平衡位置时横截面上的应力称为临界应力，用表示。
压杆在弹性范围内失稳时，则临界应力为：（15-3）式中称为柔度，为截面的惯性半径，即,（15-4）式中Ｉ为截面的最小形心主轴惯性矩，Ａ为截面面积。
柔度又称为压杆的长细比。
它全面的反映了压杆长度、约束条件、截面尺寸和形状对临界力的影响。
柔度在稳定计算中是个非常重要的量，根据所处的范围，可以把压杆分为三类：1.细长杆（）当临界应力小于或等于材料的比例极限时，即压杆发生弹性失稳。
若令（15-5）则时，压杆发生弹性失稳。
这类压杆又称为大柔度杆。
对于不同的材料，因弹性模量Ｅ和比例极限各不相同，的数值亦不相同。
例如A3钢，，，用式（15-5）可算得。
2. 中长杆（）这类杆又称中柔度杆。
这类压杆失稳时，横截面上的应力已超过比例极限，故属于弹塑性稳定问题。
对于中长杆，一般采用经验公式计算其临界应力，如直线公式：（15-6）式中a 、b 为与材料性能有关的常数。
当时，其相应的柔度为中长杆柔度的下限，据式（15-6）不难求得：例如Ａ3钢，，，，代入上式算得。
3. 粗短杆（）这类杆又称为小柔度杆。
这类压杆将发生强度失效，而不是失稳。
故上述三类压杆临界应力与的关系，画出曲线如图15-7为压杆的临界应力图。
不同的工程设计中，式计算临界应力，如抛物线公式（和也是和材料有关的常数）等，请读者注意查阅相关 的设计规范。
和值钢优质碳钢两处用螺栓夹紧。
已知,, ,材料的弹性模量,，A3钢的属于弹性稳定问题。
在x-y平面内:A3钢的，属于弹塑性稳定问题。
由表15-1查得:，故此杆的临界载荷为。