多元统计分析报告对应分析报告
统计学_多元统计分析报告

南京财经大学统计学系
本章内容
第一节 主成分分析
一、基本思想 二、数学模型 三、模型的求解
四、主成分的性质
五、基本步骤与应用实例
第二节 因子分析
一、基本思想
二、数学模型
三、因子载荷矩阵的统计含义 四、因子的求解
五、因子得分
六、基本步骤与应用实例
第三节 聚类分析
一、基本思想
二、统计量
主成分的性质
性质1:第k个主成分yk的系数向量是第k个特征 根λk所对应的标准化特征向量Uk。 性质2:第k个主成分的方差为第k个特征根λk, 且任意两个主成分都是不相关的,也就是主成 分y1,y2,…,yp的样本协方差矩阵是对角矩阵。
主成分的性质
性质3:样本主成分的总方差等于原变量样本的 总方差。 性质4:第k个样本主成分与第j个变量样本之间 的相关系数为:
r( yk , x j ) r( yk , zx j ) k ukj
该相关系数又称为因子载荷量。 主成分据矩阵进行 标准化变换 (2)求标准化数据矩阵的相关系数 矩阵R (3)求R的特征根及相应的特征向 量和贡献率等 (4)确定主成分的个数 (5)解释主成分的实际意义和作用
x
21
x22
......
x
2
p
...... ...... ...... ......
x
n1
xn2
......
xnp
绝对距离: dij xik x jk
欧氏距离:
dij
在实际工作中,在不损失较多信息的情况下, 通常选取前几个主成分来进行分析,达到简化 数据结构的目的。
多元统计实验报告二

实验报告2班级学号姓名开课学院商学院任课教师马艳梅成绩实验报告:实验2.1(1)选用Employee data.sav 文件中的变量,Analyze 中选择Compare Means再选择One---Sample T Test。
将salary作为Test因变量,test值分别取34000、35000、34419、24000,作均值检Test 取34000实验结果如下图所示:Test取35000时,实验结果如下图所示:Test 取34419时,实验结果如下图所示:Test 取24000时,实验结果如下图所示:可知,p=0.000<0.05,故原假设不成立。
说明样本salary均值与假设的24000有显著性差别。
(2)仍选用Employee data.sav 文件中的变量,先作10%的随机抽样,然后将salary作为Test因变量,test值取34419,作均值检验。
首先做随机抽样:data 选项中选择select cases,再选random sample of cases,单击sample,approximately 10%,点击确定。
运行完成后,发现原始数据序号前面有些被划掉。
再进行均值检验过程:Analyze 中选择Compare Means再选择One---Sample T Test。
将salary作为Test因变量,test值取34419,所得实验数据结果如下图所示:可知,P=0.284>0.05,故接受原假设。
说明随机抽样的样本均值salary与假设的34419没有显著性差异。
实验2.2 熟悉Independent--Samples T Test 功能Analyze 选择Compare Means选择Independent--Samples T test,选用Employee data.sav 文件中的变量,将Current Salary作为Test Variables, gender作Grouping Variable,作两样本比较T检验,选择define groups,两个group分别定义为0、1实验结果如下:实验2.3熟悉Paired--Samples T Test 功能录入数据Analyze 选择Compare Means再选择Paired--Samples T test,Paired-variables里面将before 与after 选入其中,单击ok实验结果如下图所示:可以看出,P>0.05,说明消费者购买前与购买后的物品购买意愿均值没有显著性差异。
应用多元统计分析教学课件08对应分析

6
一、什么是对应分析
(3)在进行数据处理时,为了将数量级相差很大的变量 进行比较,需要对变量进行标准化处理,然而这种只 按照变量列进行的标准化处理对于变量和样品是非对 等的,这给寻找型因子分析和型因子分析的联系带 来—定的困难。
启发得到的。 2 统计量的计算公式是
应用多元统计分析
第八章 对应分析
1
第八章 对应分析
由上一章分析我们知道,因子分析方法是用少数公共因子去提 取研究对象的绝大部分信息,这种做法既减少了因子的数目, 又把握住了研究对象的相互关系。在因子分析中,根据研究 对象的不同,分为型和型。若研究变量之间的相互关系则采 用型因子分析;若研究样品间的相互关系则采用型因子分析。 但无论型还是型因子分析,都不能很好地揭示变量和样品间 的双重关系。但在某些实际问题中,既要研究变量之间的关 系,还需要研究样品之间的关系。不仅如此,人们往往还希 望能够在同一个直角坐标系内直观地同时表达变量和样品之 间的相互关系。为实现这一目的就需要进行对应分析。
F ( 1u1, 2 u2 ,
1u11
,
m um )
1u21
1u p1
2 u12 2 u22
2 u p2
m u1m
m u2m
m
u
pm
9
二、对应分析的基本思想
这样,利用关系式 Zui vi 也很容易地写出样品点协差阵 B 对应的因子载荷阵(记为 G ):
G ( 1 v1, 2 v2 ,
5
一、什么是对应分析
(1)型因子分析和型因子分析是分开进行的。 当研究的对象是变量时,通常作型因子分析, 当研究的对象是样品时,则采用型因子分析, 而且把型和型看成两种分离的概念,无法使型 和型因子分析同时进行,这样将型和型割裂开 后就会损失很多有用的信息,而且还不能揭示 变量与样品之间的相关信息。
多元统计学分析报告
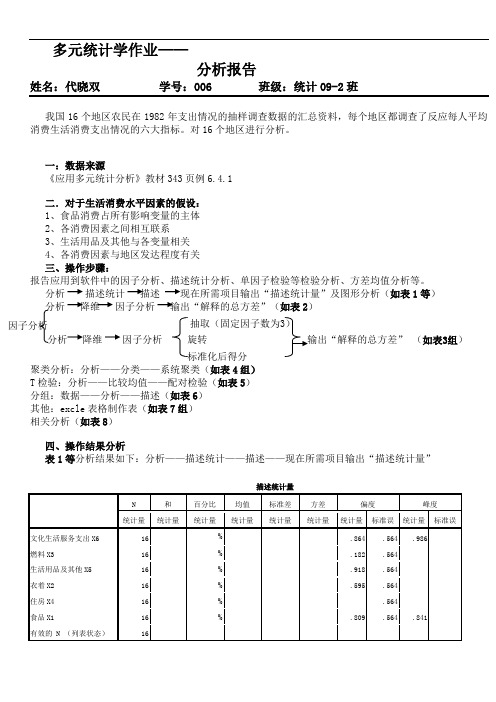
多元统计学作业——分析报告姓名:代晓双 学号:006 班级:统计09-2班我国16个地区农民在1982年支出情况的抽样调查数据的汇总资料,每个地区都调查了反应每人平均消费生活消费支出情况的六大指标。
对16个地区进行分析。
一:数据来源《应用多元统计分析》教材343页例6.4.1二.对于生活消费水平因素的假设: 1、食品消费占所有影响变量的主体 2、各消费因素之间相互联系 3、生活用品及其他与各变量相关 4、各消费因素与地区发达程度有关 三、操作步骤:报告应用到软件中的因子分析、描述统计分析、单因子检验等检验分析、方差均值分析等。
分析描述统计 描述 如表1等) 分析 降维 因子分析 输出“解释的总方差”(如表2)抽取(固定因子数为分析 降维 因子分析 旋转 (如表3组)标准化后得分聚类分析:分析——分类——系统聚类(如表4组) T 检验:分析——比较均值——配对检验(如表5) 分组:数据——分析——描述(如表6) 其他:excle 表格制作表(如表7组) 相关分析(如表8)四、操作结果分析表1等分析结果如下:分析——描述统计——描述——现在所需项目输出“描述统计量” 因子分析由上表分析如下4点:1、由和可以知道食品消费的数量是最大的,为,起主体作用,文化生活服务支出相对数量较小,为。
且由百分比可以知道食品占多部分高达%,生活用品及其他占%,住房占%,燃料占%,衣着占%,文化生活服务支出占%。
2、由方差可以知道食品的方差最大是文化生活服务支出方差最小是,从而可以知道食品消费的落差大,不稳定。
而文化生活服务支出落差较小,相对较稳定。
3、由偏度值>0表示为右偏,偏度值<0表示为左偏,由以上可以知道,平均消费生活消费支出情况的六大指标均为右偏。
4、由峰度值>0表示为在均值以上,偏度值<0表示为在均值以下,由以上可以知道,燃料、生活用由上图说明:在任何地区食品所占比例都是比较大的,文化生活服务支出各地区差距不大,综合来看,上海、北京、江苏各指标相对较高,说明这些地区相对较发达。
多元统计分析聚类分析,判别分析,对应分析 ppt课件

总计 .135 .934 .999 .045
第三部分是对列联表行与列个状态有关信息 的概括(概述行点只截取了部分数据)。其 中,质量部分分别指列联表中行与列的边缘 概率。维中的得分是各维度的分值,指行列 各状态在二维图中的坐标值。如语文坐标为 (-0.00,-0.143)。惯量是每一行(列)与 其重心的加权距离的平方,可以看出 I=J=0.01,即行剖面的总惯量等与列剖面的 总惯量。贡献部分是指行(列)的每一状态 对每一维度(公共因子)特征值的贡献及每 一维度对行(列)各个状态的特征值等贡献。 如第一维度中,外语对应的数值最大,为 0.975,说明外语这一状态对第一维度的贡 献最大。
多元统计分析聚类分析,判别分析,对应分析
操作步骤
(1)打开SPSS文件,在表格下方有两个选项,分别是数据试图和变量视 图,点击变量视图选项,在前三行分别输入“学号”、“科目”、“成 绩”,其中学号与科目的值项需要做如下设置:在弹出的值标签对话框 里,在值这一项里输入“1”,标签输入“1”,再点击“添加”按钮, 依次添加到40为止,在科目的值标签对话框内,在值这一项中输入“1”, 标签输入“语文”,点击“添加”按钮,再依次添加“2”对应标签为 “数学”,“3”对应标签为“外语”,“4”对应标签为“体育”,综 上分别完成对1号至40号学号以及4项科目进行数字的赋值。 然后点击数据视图进行数据输入,数据输入按照成绩单输入,如:第一 行第一列输入“1”,第二列输入“1”,第三列输入“82”,第二行第 一列输入“2”,第二列输入“1”,第三列输入“81”,以此类推,共
2 -.143 -.427 .065 -.013
概述列点a
惯量 .002 .003 .005 .000 .010
点对维惯量
1
对应分析实验报告

对应分析实验报告一、引言对应分析是一种常用的数据分析方法,用于研究两个或多个变量之间的关系。
在这个实验中,我们将通过对一组数据进行对应分析来探究变量之间的关系和相关性。
二、实验设计1. 数据收集首先,我们需要收集一组相关的数据。
这些数据可以是任何类型的变量,例如销售额、用户数量、广告投入等。
确保数据的准确性和完整性对于得出可靠的结论非常重要。
2. 数据预处理在进行对应分析之前,我们需要对数据进行预处理。
这包括清洗数据、填补缺失值、处理异常值等。
确保数据的质量可以减少对应分析过程中的误差和偏差。
3. 对应分析对应分析的目标是找到两个或多个变量之间的相关性。
在这个实验中,我们将使用对应分析方法来确定变量之间的关系。
我们可以使用相关系数、散点图等方法来进行对应分析。
三、实验步骤以下是进行对应分析实验的步骤:步骤1:收集数据首先,我们需要收集一组相关的数据。
这些数据可以是任何类型的变量,例如销售额、用户数量、广告投入等。
确保数据的准确性和完整性非常重要。
步骤2:数据预处理在进行对应分析之前,我们需要对数据进行预处理。
这包括清洗数据、填补缺失值、处理异常值等。
确保数据的质量可以减少对应分析过程中的误差和偏差。
步骤3:对应分析对应分析的目标是找到两个或多个变量之间的相关性。
在这个实验中,我们将使用对应分析方法来确定变量之间的关系。
我们可以使用相关系数、散点图等方法来进行对应分析。
步骤4:结果解释根据对应分析的结果,我们可以得出结论并解释变量之间的关系。
我们可以使用数据可视化工具,如折线图、柱状图等来展示结果。
确保结果的解释准确清晰,便于读者理解。
四、实验结果根据对应分析的结果,我们得出以下结论:•变量A和变量B之间存在强相关性,相关系数为0.8。
•变量C和变量D之间存在负相关性,相关系数为-0.6。
五、讨论和结论在这个实验中,我们使用对应分析方法来研究变量之间的相关性。
通过对数据进行预处理和对应分析,我们得出了变量之间的相关性和相关系数。
多元统计分析—判别分析实验报告
Unweighted Cases
N
Percent
Valid Excluded
Total
Missing or out-of-range group codes At least one missing discriminating variable Both missing or out-of-range group codes and at least one missing discriminating variable Total
组别
Function
1
2
1
-2.647
2
9.444
3
-6.797
1.013 -.259 -.754
实用文档
表5是标准化的判别函数,表示为: Y1=-17.046X1+14.757X2-1.306X3+6.381X4+1.332X5+4.315X6
Y2=-7.677X1+9.870X2-0.531X3-0.666X4+0.710X5+1.833X6 表6为结构矩阵,即判别载荷,表四是反映判别函数在各组的重心 表7是非标准化的判别函数,表示为: Y1=-78.896-1.950X1+1.748X2-0.930X3+0.825X4+0.102X5+1.662X6
3 .001
14.106 -3.393
.834
18 ungrouped
2 .000
2 1.000
31.237
1 .000
295.309 14.502
2.120
19 ungrouped
3 .310
2 1.000
应用多元统计分析实验报告
多元统计分析实验报告学院名称理学院专业班级应用统计学14-2学生姓名张艳雪学号201411081051工资、受教育年限、初始工资和工作经验资料如下表所示: 设职工总体的以上变量服从多元正态分布,根据样本资料利用 SPSS 软件求出均注 1:最大似然估计公式为: μˆ = X = ∑ ∑ (X i - X )(X i - X )' ; ˆ第一章 多元正态分布1.1 从某企业全部职工中随机抽取一容量为 6 的样本,该样本中个职工的目前值向量和协方差矩阵的最大似然估计。
1 n n i =1 X i , Σ = 1 nn i =1一.SPSS 操作步骤:第一步:利用 spss 建立数据集第二步:分析--描述统计--描述 计算样本均值向量 第三步:分析--相关--双变量计算样本协方差阵与样本相关系数二.输出结果:⎪ μ= 37125 ⎪ 152.50⎪ ⎛ 352068000 12500 -110677500 102000 ⎫= -110677500 - 86250 2192793750 691125 ⎪16695.1⎪⎭ ∑ X i,∑ (X i - X )(X i - X )'ˆ三.实验结果分析:样本均值为样本的协方差∑⎪⎪如此就可以按照极大似然估计方程:1 nΣ =n i =1得出均值向量与协方差向量的最大似然估计结果。
μ=X=1nn i=1ˆ第三章聚类分析3.1下表是15个上市公司2001年的一些主要财务指标,使用系统聚类法和K-均值法利用SPSS软件分别对这些公司进行聚类,并对结果进行比较分析。
公司编号净资产收益率每股净利润总资产周转率资产负债率流动负债比率每股净资产净利润增长率总资产增长率111.090.210.0596.9870.53 1.86-44.0481.99211.960.590.7451.7890.73 4.957.0216.11300.030.03181.99100-2.98103.3321.18411.580.130.1746.0792.18 1.14 6.55-56.325-6.19-0.090.0343.382.24 1.52-1713.5-3.366100.470.4868.486 4.7-11.560.85710.490.110.3582.9899.87 1.02100.2330.32811.12-1.690.12132.14100-0.66-4454.39-62.759 3.410.040.267.8698.51 1.25-11.25-11.4310 1.160.010.5443.7100 1.03-87.18-7.411130.220.160.487.3694.880.53729.41-9.97128.190.220.3830.31100 2.73-12.31-2.771395.79-5.20.5252.3499.34-5.42-9816.52-46.821416.550.350.9372.3184.05 2.14115.95123.4115-24.18-1.160.7956.2697.8 4.81-533.89-27.74一、实验原理:1.系统聚类的基本思想是:首先,每个样品(或变量)先聚成一类,然后,选择距离公式计算类与类之间的距离,把距离相近的样品(或变量)先聚成类,距离相远的后聚成类,该过程一直进行下去,每个样品(或变量)总能聚到合适的类中,最后,所有的样品(或变量)聚成一类。
多元统计分析报告
多元统计分析课程设计主成分分析法在我国居民生活质量状况综合评价中的应用姓名:专业班级:学院:数学与系统科学学院学号:指导教师:山东科技大学2014年6月24日目录摘要 (1)1.问题及背景 (2)1.1背景提出 (2)2主成分分析概念与方法 (2)3主成分分析法在我国居民生活质量状况综合评价中的应用 (4)3.1原始数据 (4)3.2数据标准化 (5)3.3相关系数矩阵 (6)3.4特征方程及主成分确定 (6)3.5各特征值的单位特征向量 (6)3.6主成分值以及综合分值 (7)3.7各主成分上的得分 (8)3.8综合因子得分 (9)3. 9评价结果和排序 (9)4.聚类分析 (10)5 建议 (10)摘要改革开放以来,我国各地区间的经济发展速度有着明显差别,而人民的生活质量也因此产生了不同,本文用主成分分析法、聚类分析法,选取职工人均工资1()X ,人均居住面积2()X ,城市人口用水普及量3()X ,城市煤气普及量4()X ,人均拥有道路面积5()X ,人均绿地公共面积6()X ,批发零售贸易商品销售总额7()X ,旅游外汇收入8()X 8个指标,以综合因子的贡献率确定主成分和权重, 计算出主成分分值值以及综合分值,对全国31个省市居民的生活质量进行了简单的分析,得到以下结论:根据31个省市的综合分值可以将居民生活质量状况按照降序进行以下排序:上海、广东、北京、江苏、浙江、福建、天津、山东、重庆、辽宁、湖北、安徽、 湖 南、江西、山西、河北、陕西、四川、新疆、广西、青海、河南、云南、贵州、内蒙古、 宁夏、黑龙江、吉林、海南、甘肃、西藏。
关键词主成分分析法、聚类分析法、居民生活质量状况、综合评价使用软件:SPSS 17.0 Matlab 7.01.问题及背景1.1背景提出随着生产水平的的不断提高,我国居民生活水平不断提高,生活质量也在不断改进。
但是,受各地区生产力发展水平不平衡的影响,我国各地区居民生活质量也表现为不平衡。
spss对应分析实验报告
spss对应分析实验报告SPSS对应分析实验报告引言:对应分析是一种常用的统计分析方法,它可以帮助研究者确定两个或多个变量之间的关系。
在本次实验中,我们使用SPSS软件对一组数据进行了对应分析,并得出了一些有意义的结论。
实验设计:我们的实验设计是基于一个假设:消费者的年龄与其购买的产品类型之间存在关联。
为了验证这个假设,我们收集了一组消费者的数据,包括他们的年龄和购买的产品类型。
我们使用SPSS软件进行了对应分析,并得出了以下结果。
数据收集和处理:我们随机选择了200名消费者作为研究对象,并询问了他们的年龄和购买的产品类型。
在数据收集后,我们将数据输入SPSS软件进行处理。
首先,我们创建了两个变量:年龄和产品类型。
然后,我们使用对应分析功能进行了计算。
结果分析:通过对应分析,我们得到了一些有意义的结果。
首先,我们发现年龄与产品类型之间确实存在关联。
具体而言,我们观察到年龄较小的消费者更倾向于购买儿童玩具,而年龄较大的消费者更倾向于购买家居用品。
这一结果与我们的假设相符合。
进一步分析还显示了其他有趣的关联。
例如,我们发现中年消费者更倾向于购买电子产品,而青年消费者更倾向于购买时尚服装。
这些结果为我们进一步了解消费者行为提供了有价值的信息。
讨论和结论:我们的实验结果表明,消费者的年龄与其购买的产品类型之间存在关联。
这一发现对于市场营销和产品定位具有重要意义。
通过了解不同年龄段消费者的购买偏好,企业可以更好地制定市场策略和推广计划,以满足消费者的需求。
然而,我们也需要注意到对应分析只能显示变量之间的关联,并不能确定因果关系。
因此,在实际应用中,我们需要结合其他方法和数据,以更全面地了解消费者行为和市场趋势。
总结:本次实验使用SPSS软件进行了对应分析,研究了消费者的年龄与其购买的产品类型之间的关联。
通过对数据的处理和分析,我们得出了一些有意义的结果,并对市场营销和产品定位提供了一定的指导。
然而,我们也要意识到对应分析只是统计分析的一种方法,需要结合其他数据和方法进行综合分析。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
学生实验报告
学院:统计学院
课程名称:多元统计分析
专业班级:统计123班
姓名:叶常青
学号:0124253
学生实验报告
一、实验目的及要求:
目的熟悉和掌握对应分析的原理和上机操作方法
容及要求本次操作就父母与孩子的受教育程度的关系进行对应分析,分别对父亲与孩子和母亲与孩子的受教育程度做对应分析,最后再对输出结果进行详细的分析。
二、仪器用具:
三、实验方法与步骤:
打开GSS93 subset .sav数据,对变量Degree与变量padeg和madeg进行对应分析,依次选择分析→降维…进入对应分析对话框,进行进行如下设置,便可输出想要的数据的:
四、实验结果与数据处理:
按照上述方法和步骤得出以下输出结果.
对父亲受教育程度与孩子受教育程度的关系进行分析如下:
表1
表2
1 .400 .160 .846 .846 .025 .256
2 .164 .027 .142 .988 .026
3
.047 .002 .012 1.00
4
.006 .000 .000 1.00
总计. 228.
193
.000a 1.00
1.00
a. 16 自由度,
表3
第二部分摘要给出了惯量,卡方值以及每一维度所解释的总惯量的百分比信息。
总惯量为0.,卡方值为228.193 ,有关系式228.193=0.*1205,由此可以清楚的看到总惯量和卡方的关系。
Sig.是假设卡方值为0成立的概率,它的值几乎为0说明列联表之间有较强的相关性。
表注表明的自由度为(5-1)*(5-1)=16。
惯量部分是四个公共因子分别解释总惯量的百分比。
表4
表5
LT High School .808 .487 .387 .218 .253 .467 High School .140 .392 .453 .383 .374 .353 Junior College .005 .017 .027 .039 .030 .
Bachelor . .068 . .228 .182 .100 Graduate .016 . .040 .131 .162 .
有效边际 1.000 1.000 1.000 1.000 1.000
第三部分的结果是在对应分析中点击Statistics按钮,进入Statistics对话框,选中Row profiles和Column profiles 交友程序运行所得到的。
表6
Graduat
e
. 1. .749 .040 .211 .202 .838 .134 .971
有效总计
1.00
0 . 1.00
1.00
a. 对称标准化表7
Graduat
e
.082 .874 .395 . .157 .078 .875 . .949
有效总计
1.00
0 . 1.00
1.00
a. 对称标准化
第四部分是概述行点和概述列点,是对列联表行与列各状态有关信息的概括. 其中质量是行与列的边缘概率,也就是PI与PJ。
惯量是每一行(列)与其重心的加权距离平方,可以看到II=IJ=0.。
由概述行点表可知变量degree的状态Less than HS和Bachelor在第一维度中贡献较大分别为0.399和0.406。
状态Less than HS对第二维度贡献最大为0.416。
概述列表可知变量padeg的状态LT High School在第一维度贡献最大为0.432。
状态High School对第二维度贡献最大为0.559。
第五部分是degree各状态和paged各状态同时在一二维表上的投影. 由图可以看到父亲初中的教育程度、高中的教育程度与孩子的教育程度有较强的关联性。
表1
对应表 Mother's Highest Degree
R's Highest Degree Less than HS
High school
Junior college
Bac helor
Gra duate
有效边际
LT High School 169 286 25 37 23 540 High School 40 374 41 56 644 Junior College 2 13 6 15 5 41 Bachelor 3 33 11 34 15 96 Graduate
2 8 1 10
8 29 有效边际
216
714
84
229
107
135
第一部分是对应表,对应表是由原始数据按degree 与padeg 分类的列连表,可以看到总有效观测值为1350,而不是原始数据1500。
说明有效的观测数据有1350个,这是因为原始数据中有150个数据缺失。
表2
第二部分是摘要表。
第二部分摘要给出了惯量,卡方值以及每一维度所解释的总惯量的百分比信息。
总惯量为0.,卡方值为228.193 ,有关系式228.193=0.*1205,由此可以清楚的看到总惯量和卡方的关系。
Sig.是假设卡方值为0成立的概率,它的值几乎为0说明列联表之间有较强的相关性。
表注表明的自由度为(5-1)*(5-1)=16。
惯量部分是四个公共因子分别解释总惯量的百分比。
.
LT High School
.400 -.744 .143 . .546 .052 .986 .014
1.00
High School
.477 .371 -.339 . .162 .350 .755 .243 .998
Junior College
.030 .941 .807 .016 . . .683 . .877
Bachelo r
. .992 .733 . .173 .244 .817 .172 .989
Graduat e
.
1.00
4 1.28
5 .018 . .227 .479 .303 .781
有效总计
1.00
.
1.00
1.000
a. 对称标准化
第三部分是概述行点和概述列点,是对列联表行与列各状态有关信息的概括.由贡献部分可以看出LT High School这一状态对第一维度的贡献最大.在表的最后维度部分对各状态特征值的贡献部分,看到除了Graduate外,其余各最高学历的特征值的分布大部分集中在第一维度上,说明第一维度反映了最高学历各状态大部分的差异.
把母亲受教育程度和子女受教育程度的各状态投影到同一二维图上,如上图所示。
由图可以看到母亲受高中的教育程度和子女受初中,高中的教育程度有较强的关联性。
五、讨论与结论
通过对应分析可以大致了解父母亲受教育程度与孩子受教育程度的关系,并且实现了对应分析理论知识与实际操作的结合,此次试验的难点在于对输出数据的具体分析思维。
由以上所有分析我们可以大胆推断子女受教育程度与父母双方受教育程度有着密切的联系,父母受教育程度很大的限制着子女的受教育水平。
