下城区2016学年第一学期小学质量检测卷(数学)
2016-2017年浙江省杭州市下城区九年级上学期期中数学试卷及参考答案

2016-2017学年浙江省杭州市下城区九年级(上)期中数学试卷一、选择题(每小题3分,共30分)1.(3分)如果将抛物线y=x2+2向下平移1个单位,那么所得新抛物线的表达式是()A.y=(x﹣1)2+2 B.y=(x+1)2+2 C.y=x2+1 D.y=x2+32.(3分)一个盒子装有除颜色外其它均相同的2个红球和3个白球,现从中任取2个球,则取到的是一个红球、一个白球的概率为()A.B.C.D.3.(3分)有下列四个命题:①直径是弦;②经过三个点一定可以作圆;③平分弦的直径垂直弦;④相等的圆周角所对的弧相等.其中正确的有()A.4个 B.3个 C.2个 D.1个4.(3分)如图,是一个圆曲隧道的截面,若路面AB宽为10米,净高CD为7米,则此隧道圆的半径OA是()A.5 B.C.D.75.(3分)如图,矩形ABCD的外接圆O与水平地面有唯一交点A,圆O的半径为4,且=2.若在没有滑动的情况下,将圆O向右滚动,使得O点向右移动了98π,则此时该圆与地面交点在()上.A.B.C.D.6.(3分)坐标平面上,某二次函数图形的顶点为(2,﹣1),此函数图形与x 轴相交于P、Q两点,且PQ=6.若此函数图形通过(1,a)、(3,b)、(﹣1,c)、(﹣3,d)四点,则a、b、c、d之值何者为正?()A.a B.b C.c D.d7.(3分)如图,坐标平面上,二次函数y=﹣x2+4x﹣k的图形与x轴交于A、B 两点,与y轴交于C点,其顶点为D,且k>0.若△ABC与△ABD的面积比为1:4,则k值为何?()A.1 B.C.D.8.(3分)已知函数y=ax2﹣2ax﹣1(a是常数,a≠0),下列结论正确的是()A.当a=1时,函数图象过点(﹣1,1)B.当a=﹣2时,函数图象与x轴没有交点C.若a>0,则当x≥1时,y随x的增大而减小D.若a<0,则当x≤1时,y随x的增大而增大9.(3分)如图△ABC中,∠ACB=90°,AC+BC=8,分别以AB、AC、BC为半径作半圆,若记图中阴影部分的面积为y,AC为x,则下列y关于x的图象中正确的是()A.B.C.D.10.(3分)如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0②4a+2b+c>0③4ac﹣b2<8a④<a<⑤b>c.其中含所有正确结论的选项是()A.①③B.①③④C.②④⑤D.①③④⑤二、填空题(每小题4分,共24分)11.(4分)如图,在3×3的方格中,A、B、C、D、E、F分别位于格点上,从C、D、E、F四点中任取一点,与点A、B为顶点作三角形,则所作三角形为等腰三角形的概率是.12.(4分)如图,半圆O是一个量角器,△AOB为一纸片,AB交半圆于点D,OB交半圆于点C,若点C、D、A在量角器上对应读数分别为45°,70°,150°,则∠AOB的度数为;∠A的度数为.13.(4分)已知:如图,在△ABC中,∠CAB=70°,将△ABC绕点A按逆时针方向旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′的度数为.14.(4分)如图,在平面直角坐标系中,⊙P的圆心坐标是(4,a)(a>4),半径为4,函数y=x的图象被⊙P截得的弦AB的长为4,则a的值是.15.(4分)已知二次函数y=(x﹣h)2+1(h为常数),在自变量x的值满足1≤x≤3的情况下,与其对应的函数值y的最小值为5,则h的值为.16.(4分)在平面直角坐标系中,点O为原点,平行于x轴的直线与抛物线L:y=ax2相交于A,B两点(点B在第一象限),点C在AB的延长线上.(1)已知a=1,点B的纵坐标为2.如图1,向右平移抛物线L使该抛物线过点B,与AB的延长线交于点C,AC的长为.(2)如图2,若BC=AB,过O,B,C三点的抛物线L3,顶点为P,开口向下,对应函数的二次项系数为a3,=.三、解答题(本大题共7小题,共66分.解答应写出必要的文字说明、证明过程或演算步骤)17.(6分)已知二次函数y=x2﹣4x+c.(1)若该图象过点(4,5),求c的值并求图象的顶点坐标;(2)若二次函数y=x2﹣4x+c的图象与坐标轴有2个交点,求字母c的值.18.(8分)(1)尺规作图:作△ABC的外接圆⊙O.(保留作图痕迹,不写画法)(2)若∠A=45°,⊙O的半径为1,求BC的长.(3)求所作的⊙O中弧BC和弦BC围成的区域面积.19.(8分)为了解学生的艺术特长发展情况,某校音乐决定围绕在“舞蹈、乐器、声乐、戏曲、其他活动”项目中,你最喜欢哪一项活动(每人只限一项)的问题,在全校范围内随机抽取部分学生进行问卷调查,并将调查结果绘制如下两幅不完整的统计图.请你根据统计图解答下列问题:(1)在这次调查中,一共抽查了名学生,其中喜欢“舞蹈”活动项目的人数占抽查总人数的百分比为.扇形统计图中喜欢“戏曲”部分扇形的圆心角为度.(2)请你补全条形统计图.(3)若在“舞蹈、乐器、声乐、戏曲”项目中任选两项成立课外兴趣小组,请用列表或画树状图的方法求恰好选中“舞蹈、声乐”这两项的概率.20.(10分)如图,需在一面墙上绘制几个相同的抛物线型图案.按照图中的直角坐标系,最左边的抛物线可以用y=ax2+bx(a≠0)表示.已知抛物线上B,C 两点到地面的距离均为m,到墙边OA的距离分别为m,m.(1)求该拋物线的函数关系式,并求图案最高点到地面的距离;(2)若该墙的长度为10m,则最多可以连续绘制几个这样的拋物线型图案?21.(10分)已知一次函数y 1=x+b 的图象与二次函数y2=a(x2+bx+3)(a≠0,a,b 为常数)的图象交于A、B 两点,且点A 的坐标为(0,3)(1)求出a,b 的值;(2)求出点B 的坐标,并直接写出当y1≥y2时x 的取值范围;(3)设s=y1+y2,t=y1﹣y2,若n≤x≤m 时,s 随着x 的增大而增大,且t 也随着x 的增大而增大,求n 的最小值和m 的最大值.22.(12分)如图,AB是⊙O的直径,C是的中点,CE⊥AB于点E,BD交CE 于点F.(1)求证:CF=BF;(2)若CD=6,AC=8,求⊙O的半径及CE的长.23.(12分)在平面直角坐标系中,抛物线y=﹣x2+x+4的图象与x轴交于B,C两点(B在C的左侧),与y轴交于点A.(1)求出点A,B,C的坐标.(2)在抛物线上有一动点P,抛物线的对称轴上有另一动点Q,若以B,C,P,Q为顶点的四边形是平行四边形,直接写出点P的坐标.(3)向右平移抛物线,使平移后的抛物线恰好经过△ABC的外心,求出平移后的抛物线的解析式.2016-2017学年浙江省杭州市下城区九年级(上)期中数学试卷参考答案与试题解析一、选择题(每小题3分,共30分)1.(3分)如果将抛物线y=x2+2向下平移1个单位,那么所得新抛物线的表达式是()A.y=(x﹣1)2+2 B.y=(x+1)2+2 C.y=x2+1 D.y=x2+3【解答】解:∵抛物线y=x2+2向下平移1个单位,∴抛物线的解析式为y=x2+2﹣1,即y=x2+1.故选:C.2.(3分)一个盒子装有除颜色外其它均相同的2个红球和3个白球,现从中任取2个球,则取到的是一个红球、一个白球的概率为()A.B.C.D.【解答】解:画树状图得:∵共有20种等可能的结果,取到的是一个红球、一个白球的有12种情况,∴取到的是一个红球、一个白球的概率为:=.故选:C.3.(3分)有下列四个命题:①直径是弦;②经过三个点一定可以作圆;③平分弦的直径垂直弦;④相等的圆周角所对的弧相等.其中正确的有()A.4个 B.3个 C.2个 D.1个【解答】解:①直径是弦,说法正确;②经过不在同一直线上的三点可以作圆,原说法错误;③平分弦的直径垂直弦,这条弦应强调不是直径,故错误;④在同圆或等圆中,相等的圆周角所对的弧相等,原说法没有加条件限制,故错误;综上可得只有①正确.故选:D.4.(3分)如图,是一个圆曲隧道的截面,若路面AB宽为10米,净高CD为7米,则此隧道圆的半径OA是()A.5 B.C.D.7【解答】解:∵OD⊥AB,∴AD=DB=AB=×10=5m,在Rt△OAD中,设半径OA=R,OD=CD﹣R=7﹣R,∴OA2=OD2+AD2,即R2=(7﹣R)2+52,解得R=,∴此隧道圆的半径OA是m.故选:B.5.(3分)如图,矩形ABCD的外接圆O与水平地面有唯一交点A,圆O的半径为4,且=2.若在没有滑动的情况下,将圆O向右滚动,使得O点向右移动了98π,则此时该圆与地面交点在()上.A.B.C.D.【解答】解:∵圆O半径为4,∴圆的周长为:2π×r=8π,∵将圆O向右滚动,使得O点向右移动了98π,∴98π÷8π=12…2π,即圆滚动12周后,又向右滚动了2π,∵矩形ABCD的外接圆O与水平地面相切于A点,=2,∴=×8π=π<2π,+=×8π=4π>2π,∴此时与地面相切;∴此时该圆与地面交点在上,故选:B.6.(3分)坐标平面上,某二次函数图形的顶点为(2,﹣1),此函数图形与x 轴相交于P、Q两点,且PQ=6.若此函数图形通过(1,a)、(3,b)、(﹣1,c)、(﹣3,d)四点,则a、b、c、d之值何者为正?()A.a B.b C.c D.d【解答】解:∵二次函数图形的顶点为(2,﹣1),∴对称轴为x=2,∵×PQ=×6=3,∴图形与x轴的交点为(2﹣3,0)=(﹣1,0),和(2+3,0)=(5,0),已知图形通过(2,﹣1)、(﹣1,0)、(5,0)三点,如图,由图形可知:a=b<0,c=0,d>0.故选:D.7.(3分)如图,坐标平面上,二次函数y=﹣x2+4x﹣k的图形与x轴交于A、B 两点,与y轴交于C点,其顶点为D,且k>0.若△ABC与△ABD的面积比为1:4,则k值为何?()A.1 B.C.D.【解答】解:∵y=﹣x2+4x﹣k=﹣(x﹣2)2+4﹣k,∴顶点D(2,4﹣k),C(0,﹣k),∴OC=k,∵△ABC的面积=AB•OC=AB•k,△ABD的面积=AB(4﹣k),△ABC与△ABD 的面积比为1:4,∴k=(4﹣k),解得:k=.故选:D.8.(3分)已知函数y=ax2﹣2ax﹣1(a是常数,a≠0),下列结论正确的是()A.当a=1时,函数图象过点(﹣1,1)B.当a=﹣2时,函数图象与x轴没有交点C.若a>0,则当x≥1时,y随x的增大而减小D.若a<0,则当x≤1时,y随x的增大而增大【解答】解:A、∵当a=1,x=﹣1时,y=1+2﹣1=2,∴函数图象不经过点(﹣1,1),故错误;B、当a=﹣2时,∵△=42﹣4×(﹣2)×(﹣1)=8>0,∴函数图象与x轴有两个交点,故错误;C、∵抛物线的对称轴为直线x=﹣=1,∴若a>0,则当x≥1时,y随x的增大而增大,故错误;D、∵抛物线的对称轴为直线x=﹣=1,∴若a<0,则当x≤1时,y随x的增大而增大,故正确;故选:D.9.(3分)如图△ABC中,∠ACB=90°,AC+BC=8,分别以AB、AC、BC为半径作半圆,若记图中阴影部分的面积为y,AC为x,则下列y关于x的图象中正确的是()A.B.C.D.【解答】解:∵AC+BC=8,AC=x,∴BC=8﹣x.又∵在△ABC中,∠ACB=90°,∴AB=.=π×()2+π×()2﹣π×()2+x(8﹣x)=x2+4x,∴S阴影即y=﹣x2+4x(0<x<8).则该函数图象是开口向下的抛物线,且自变量的取值范围是0<x<8.故选:A.10.(3分)如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0②4a+2b+c>0③4ac﹣b2<8a④<a<⑤b>c.其中含所有正确结论的选项是()A.①③B.①③④C.②④⑤D.①③④⑤【解答】解:①∵函数开口方向向上,∴a>0;∵对称轴在y轴右侧∴ab异号,∵抛物线与y轴交点在y轴负半轴,∴c<0,∴abc>0,故①正确;②∵图象与x轴交于点A(﹣1,0),对称轴为直线x=1,∴图象与x轴的另一个交点为(3,0),∴当x=2时,y<0,∴4a+2b+c<0,故②错误;③∵图象与x轴交于点A(﹣1,0),∴当x=﹣1时,y=(﹣1)2a+b×(﹣1)+c=0,∴a﹣b+c=0,即a=b﹣c,c=b﹣a,∵对称轴为直线x=1∴=1,即b=﹣2a,∴c=b﹣a=(﹣2a)﹣a=﹣3a,∴4ac﹣b2=4•a•(﹣3a)﹣(﹣2a)2=﹣16a2<0∵8a>0∴4ac﹣b2<8a故③正确④∵图象与y轴的交点B在(0,﹣2)和(0,﹣1)之间,∴﹣2<c<﹣1∴﹣2<﹣3a<﹣1,∴>a>;故④正确⑤∵a>0,∴b﹣c>0,即b>c;故⑤正确;故选:D.二、填空题(每小题4分,共24分)11.(4分)如图,在3×3的方格中,A、B、C、D、E、F分别位于格点上,从C、D、E、F四点中任取一点,与点A、B为顶点作三角形,则所作三角形为等腰三角形的概率是.【解答】解:根据从C、D、E、F四个点中任意取一点,一共有4种可能,选取D、C、F时,所作三角形是等腰三角形,故P(所作三角形是等腰三角形)=;故答案为:.12.(4分)如图,半圆O是一个量角器,△AOB为一纸片,AB交半圆于点D,OB交半圆于点C,若点C、D、A在量角器上对应读数分别为45°,70°,150°,则∠AOB的度数为105°;∠A的度数为50°.【解答】解:∵点C、D、A在量角器上对应读数分别为45°,70°,150°,∴∠AOB=∠MOA﹣∠MOC=150°﹣45°=105°,连接OD,则OA=OD,∵∠AOD=150°﹣70°=80°,∴∠A=(180°﹣80°)=50°.故答案为:105°,50°.13.(4分)已知:如图,在△ABC中,∠CAB=70°,将△ABC绕点A按逆时针方向旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′的度数为40°.【解答】解:∵CC′∥AB,∴∠C′CA=∠CAB=70°.∵由旋转的性质可知;AC=AC′,∴∠ACC′=∠AC′C=70°.∴∠CAC′=180°﹣70°﹣70°=40°.∴∠BAB′=40°.故答案为;40°.14.(4分)如图,在平面直角坐标系中,⊙P的圆心坐标是(4,a)(a>4),半径为4,函数y=x的图象被⊙P截得的弦AB的长为4,则a的值是4+2.【解答】解:作PC⊥x轴于C,交AB于D,作PE⊥AB于E,连结PB,如图,∵⊙P的圆心坐标是(4,a),∴OC=4,PC=a,把x=4代入y=x得y=4,∴D点坐标为(4,4),∴CD=4,∴△OCD为等腰直角三角形,∴△PED也为等腰直角三角形,∵PE⊥AB,∴AE=BE=AB=×4=2,在Rt△PBE中,PB=4,∴PE==2,∴PD=PE=2,∴a=4+2.故答案为:4+2.15.(4分)已知二次函数y=(x﹣h)2+1(h为常数),在自变量x的值满足1≤x≤3的情况下,与其对应的函数值y的最小值为5,则h的值为﹣1或5.【解答】解:∵当x>h时,y随x的增大而增大,当x<h时,y随x的增大而减小,∴①若h<1≤x≤3,x=1时,y取得最小值5,可得:(1﹣h)2+1=5,解得:h=﹣1或h=3(舍);②若1≤x≤3<h,当x=3时,y取得最小值5,可得:(3﹣h)2+1=5,解得:h=5或h=1(舍).综上,h的值为﹣1或5,故答案为﹣1或5.16.(4分)在平面直角坐标系中,点O为原点,平行于x轴的直线与抛物线L:y=ax2相交于A,B两点(点B在第一象限),点C在AB的延长线上.(1)已知a=1,点B的纵坐标为2.如图1,向右平移抛物线L使该抛物线过点B,与AB的延长线交于点C,AC的长为4.(2)如图2,若BC=AB,过O,B,C三点的抛物线L3,顶点为P,开口向下,对应函数的二次项系数为a3,=﹣.【解答】解:(1)当a=1时,抛物线L的解析式为:y=x2,当y=2时,2=x2,∴x=±,∵B在第一象限,∴A(﹣,2),B(,2),∴AB=2,∵向右平移抛物线L使该抛物线过点B,∴AB=BC=2,∴AC=4;(2)如图2,设抛物线L3与x轴的交点为G,其对称轴与x轴交于Q,过B作BK⊥x轴于K,设OK=t,则AB=BC=2t,∴B(t,at2),根据抛物线的对称性得:OQ=2t,OG=2OQ=4t,∴O(0,0),G(4t,0),设抛物线L3的解析式为:y=a3(x﹣0)(x﹣4t),y=a3x(x﹣4t),∵该抛物线过点B(t,at2),∴at2=a3t(t﹣4t),∵t≠0,∴a=﹣3a3,∴=﹣,故答案为:(1)4;(2)﹣.三、解答题(本大题共7小题,共66分.解答应写出必要的文字说明、证明过程或演算步骤)17.(6分)已知二次函数y=x2﹣4x+c.(1)若该图象过点(4,5),求c的值并求图象的顶点坐标;(2)若二次函数y=x2﹣4x+c的图象与坐标轴有2个交点,求字母c的值.【解答】解:(1)把(4,5)代入y=x2﹣4x+c,∴5=16﹣16+c,∴c=5,∴y=x2﹣4x+5=(x﹣2)2+1∴顶点坐标(2,1)(2)当抛物线与x轴只有一个交点时,∴△=0,∴16﹣4c=0,∴c=4,当抛物线与x轴、y轴的交点重合时,此时抛物线必过(0,0),∴c=0,综上所述,c=4或018.(8分)(1)尺规作图:作△ABC的外接圆⊙O.(保留作图痕迹,不写画法)(2)若∠A=45°,⊙O的半径为1,求BC的长.(3)求所作的⊙O中弧BC和弦BC围成的区域面积.【解答】解:(1)如图,⊙O为所作;(2)连结OB,OC,∵∠A=45∴∠BOC=2∠A=90°又∵OB=OC=1,∴△OBC是等腰直角三角形,∴BC=OB=;=S扇形BOC﹣S△BOC=﹣×1×1=.(3)S弓形BC19.(8分)为了解学生的艺术特长发展情况,某校音乐决定围绕在“舞蹈、乐器、声乐、戏曲、其他活动”项目中,你最喜欢哪一项活动(每人只限一项)的问题,在全校范围内随机抽取部分学生进行问卷调查,并将调查结果绘制如下两幅不完整的统计图.请你根据统计图解答下列问题:(1)在这次调查中,一共抽查了50名学生,其中喜欢“舞蹈”活动项目的人数占抽查总人数的百分比为24%.扇形统计图中喜欢“戏曲”部分扇形的圆心角为28.8度.(2)请你补全条形统计图.(3)若在“舞蹈、乐器、声乐、戏曲”项目中任选两项成立课外兴趣小组,请用列表或画树状图的方法求恰好选中“舞蹈、声乐”这两项的概率.【解答】解:(1)一共抽查学生数为:8÷16%=50,“舞蹈”活动项目的人数占抽查总人数的百分比为:×100%=24%;∵喜欢戏曲的人数:50﹣12﹣16﹣8﹣10=50﹣46=4人,∴扇形统计图中喜欢“戏曲”部分扇形的圆心角为:×360°=28.8°,故答案为:50,24%,28.8.(2)补全统计图如图:(3)画树状图如下:∵共有12种等可能结果,其中恰好选中“舞蹈、声乐”这两项活动的有2种结果,故恰好选中“舞蹈、声乐”两项活动的概率是:=.20.(10分)如图,需在一面墙上绘制几个相同的抛物线型图案.按照图中的直角坐标系,最左边的抛物线可以用y=ax2+bx(a≠0)表示.已知抛物线上B,C 两点到地面的距离均为m,到墙边OA的距离分别为m,m.(1)求该拋物线的函数关系式,并求图案最高点到地面的距离;(2)若该墙的长度为10m,则最多可以连续绘制几个这样的拋物线型图案?【解答】解:(1)根据题意得:B(,),C(,),把B,C代入y=ax2+bx得,解得:,∴拋物线的函数关系式为y=﹣x2+2x;∴图案最高点到地面的距离==1;(2)令y=0,即﹣x2+2x=0,∴x1=0,x2=2,∴10÷2=5,∴最多可以连续绘制5个这样的拋物线型图案.21.(10分)已知一次函数y1=x+b 的图象与二次函数y2=a(x2+bx+3)(a≠0,a,b 为常数)的图象交于A、B 两点,且点A 的坐标为(0,3)(1)求出a,b 的值;(2)求出点B 的坐标,并直接写出当y1≥y2时x 的取值范围;(3)设s=y1+y2,t=y1﹣y2,若n≤x≤m 时,s 随着x 的增大而增大,且t 也随着x 的增大而增大,求n 的最小值和m 的最大值.【解答】解:(1)把A(0,3)代入y1=x+b中得:b=3,∴y1=x+3,y2=a(x2+3x+3),把A(0,3)代入y2=a(x2+3x+3)中得:3a=3,a=1,∴a=1,b=3;(2)由题意得:,解得:,∴B(﹣2,1),如图所示,当y1≥y2时x 的取值范围是:﹣2≤x≤0;(3)s=y1+y2=x+3+x2+3x+3=x2+4x+6=(x+2)2+2,∵抛物线开口向上,∴当x≥﹣2时,s 随着x 的增大而增大,t=y1﹣y2=x+3﹣(x2+3x+3)=﹣x2﹣2x=﹣(x+1)2+1,∵抛物线开口向下,∴当x≤﹣1时,t随着x 的增大而增大,∴当﹣2≤x≤﹣1时,s 随着x 的增大而增大,且t 也随着x 的增大而增大,∵n≤x≤m,s 随着x 的增大而增大,且t 也随着x 的增大而增大,∴n 的最小值﹣2,m 的最大值﹣1.22.(12分)如图,AB是⊙O的直径,C是的中点,CE⊥AB于点E,BD交CE 于点F.(1)求证:CF=BF;(2)若CD=6,AC=8,求⊙O的半径及CE的长.【解答】(1)证明:∵AB是⊙O的直径,∴∠ACB=90°,∴∠A=90°﹣∠ABC.∵CE⊥AB,∴∠CEB=90°,∴∠ECB=90°﹣∠ABC,∴∠ECB=∠A.(2分)又∵C是的中点,∴=,∴∠DBC=∠A,∴∠ECB=∠DBC,∴CF=BF;(2)解:∵=,∴BC=CD=6,∵∠ACB=90°,∴AB===10,∴⊙O的半径为5,=AB•CE=BC•AC,∵S△ABC∴CE===.23.(12分)在平面直角坐标系中,抛物线y=﹣x2+x+4的图象与x轴交于B,C两点(B在C的左侧),与y轴交于点A.(1)求出点A,B,C的坐标.(2)在抛物线上有一动点P,抛物线的对称轴上有另一动点Q,若以B,C,P,Q为顶点的四边形是平行四边形,直接写出点P的坐标.(3)向右平移抛物线,使平移后的抛物线恰好经过△ABC的外心,求出平移后的抛物线的解析式.【解答】解:(1)当x=0时,y=4,∴与y轴交点A(0,4),当y=0时,﹣x2+x+4=0,解得:x=﹣2或8,∴B(﹣2,0),C(8,0);(2)y=﹣x2+x+4=﹣(x﹣3)2+,当P在x轴的上方时,即为抛物线的顶点P(3,)时,可以构成平行四边形BPCQ,如图1,当P在x轴的下方时,∵BC=2+8=10,若四边形BPCQ为平行四边形,则BC∥PQ,BC=PQ=10,有两种情况:①当P在抛物线对称轴的左侧时,如图2,∴点P的横坐标为﹣7,当x=﹣7时,y=﹣×(﹣7)2+×(﹣7)+4=﹣,此时P(﹣7,﹣);②当P在抛物线对称轴的右侧时,如图3,∴点P的横坐标为13,当x=13时,y=﹣×132+×13+4=﹣,此时P(13,﹣);综上所述,点P的坐标为P(3,)或(﹣7,﹣)或(13,﹣);(3)如图3,∵A(0,4)、B(﹣2,0)、C(8,0)∴OA=4,OB=2,OC=8,∴=,,∴,∵∠AOB=∠AOC=90°,∴△AOB∽△COA,∴∠BAO=∠ACO,∵∠ACO+∠OAC=90°,∴∠BAO+∠OAC=90°,∴∠BAC=90°,∴△ABC是直角三角形,∴△ABC的外心就是斜边AB的中点E,∵BC=10,∴BC的中点E的坐标为(3,0),即平移后的解析式经过E(3,0),∴相当于把原抛物线向右平移5个单位,∴平移后的解析式为:y=﹣(x﹣3﹣5)2+=﹣+4x﹣.赠送初中数学几何模型【模型五】垂直弦模型:图形特征:运用举例:1.已知A、B、C、D是⊙O上的四个点.(1)如图1,若∠ADC=∠BCD=90°,AD=CD,求证AC⊥BD;(2)如图2,若AC⊥BD,垂足为E,AB=2,DC=4,求⊙O的半径.O DAB CEAOD CB2.如图,已知四边形ABCD内接于⊙O,对角线AC⊥BD于P,设⊙O的半径是2。
2016年春新人教版小学数学二年级下册第一单元试卷
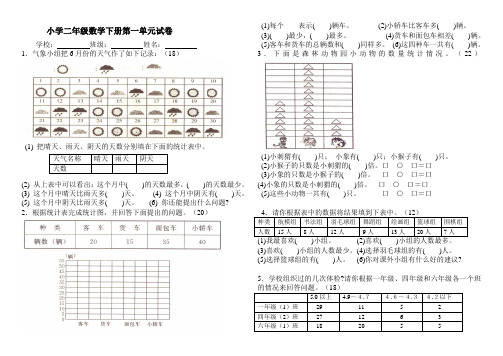
小学二年级数学下册第一单元试卷学校:班级:姓名:1.气象小组把6月份的天气作了如下记录:(18)(1) 把晴天、雨天、阴天的天数分别填在下面的统计表中。
(2) 从上表中可以看出:这个月中( )的天数最多,( )的天数最少。
(3) 这个月中晴天比雨天多( )天。
(4) 这个月中阴天有( )天。
(5) 这个月中阴天比雨天多( )天。
(6) 你还能提出什么问题? 2.根据统计表完成统计图,并回答下面提出的问题。
(20)(1)每个表示( )辆车。
(2)小轿车比客车多( )辆。
(3)( )最少,( )最多。
(4)货车和面包车相差( )辆。
(5)客车和货车的总辆数和( )同样多。
(6)这四种车一共有( )辆。
3.下面是森林动物园小动物的数量统计情况。
(22)(1)小刺猬有( )只;小象有( )只;小猴子有( )只。
(2)小猴子的只数是小刺猬的( )倍。
口○口=口(3)小象的只数是小猴子的( )倍。
口○口=口(4)小象的只数是小刺猬的( )倍。
口○口=口(5)这些小动物一共有( )只。
口○口=口4.请你根据表中的数据将结果填到下表中。
(12)种类航模组书法组羽毛球组舞蹈组绘画组篮球组围棋组人数15人8人12人9人13人20人7人(1)我最喜欢( )小组。
(2)喜欢( )小组的人数最多。
(3)喜欢( )小组的人数最少。
(4)选择羽毛球组的有( )人。
(5)选择篮球组的有( )人。
(6)你对课外小组有什么好的建议?5.学校组织过的几次体检?请你根据一年级、四年级和六年级各一个班的情况来回答问题。
(18)5.0以上 4.9~4.74.6~4.34.2以下一年级(1)班29 11 5 2四年级(2)班27 12 6 3六年级(1)班18 20 5 5天气名称晴天雨天阴天天数(1)一年级5.0以上有( )人。
(2)六年级5.0以上有( )人。
(3)四年级4.2以下有( )人。
(4)六年级( )的人数最多。
(5)5.0的视力是正常的,低于5.0的一年级的有( )人;六年级的有( )人。
2016年小学毕业生综合能力数学测试

2016年小学毕业生综合能力数学测试一、填一填(每题2分,共30分)1、把一根2m长的木料锯成同样长的5段,每段是这根木料总长的(),每锯一段用的时间是全部时间的()。
2、如果x与y互为倒数,且6xa y,那么,a=()。
3、一堆煤,第一天运出20%,第二天运出剩下的14,这堆煤比原来少了()。
4、如果甲数是乙数的32,乙数是丙数的34,那么甲数比丙数多()。
5、一个分数分子和分母的和是72,约分后得57,原分数是()。
6、有一个电子钟,每走18分钟亮一次灯,每到整点时响一次铃,中午12时正,电子钟响铃又亮灯,问下一次既响铃又亮灯的时间是()。
7、如右图,一只蚂蚁从长方体的一个顶点A沿着长方体的棱爬到另一个顶点B。
请你找一找,最短路线一共有()条。
8、甲、乙两数的平均数是100,甲:乙=1:9,则甲数=()。
9、一个等腰直角三角形,腰长3厘米,如果以腰为轴旋转一周,占空间()立方厘米。
10、一个质数的平方与一个奇数的和等于115,那么这两个数的积等于()。
11、用一架天平称3次,最多能从()个乒乓球中找出仅有的一个因质量较轻而不合格的乒乓球。
12、观察按下列规律排列的等式:9×0+1=01,9×1+2=11,9×2+3=21,9×3+4=31,9×4+=41,⋯按以上格式成立的规律,第11个等式是()。
13、14和35是很有趣的两个数,这两数的积恰好是这两数的和的10倍:14×35=490,14+35=49.满足这个条件的非0自然数还有()。
(请写出两组)14、六年级一班体育测试,跳绳成绩是“优”的有20人,跑步成绩是“优”的有16人,这两项成绩都是“优”的有6人,两项成绩都不是“优”的有2人。
全班有()人。
15、蔬菜超市有一批土豆,如果每千克卖1.2元,就会亏40元;如果每千克卖1.5元,就能赚80元。
为了尽快卖出,老板决定降价出售,结果赚的40元钱,每千克土豆是以()元出售的。
2016年人教版小学三年级数学下册第一单元试题
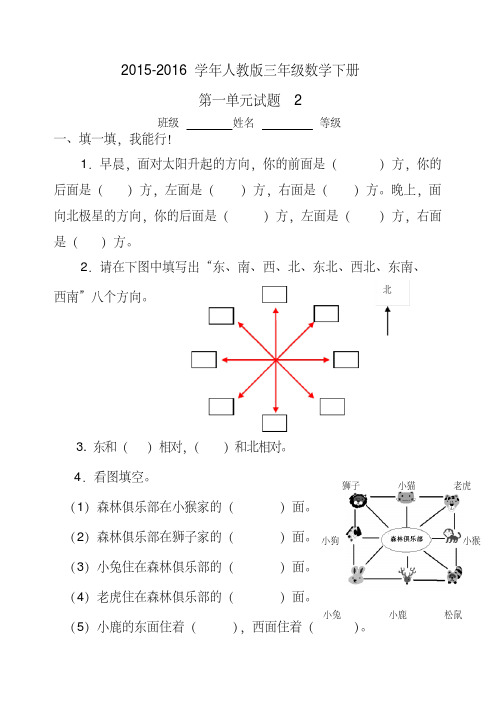
西南”八个方向。
北
3. 东和( )相对,( )和北相对。
4.看图填空。 (1)森林俱乐部在小猴家的(
狮子
小猫
)面。
(2)森林俱乐部在狮子家的( (3)小兔住在森林俱乐部的(
)面。 小狗 )面。
(4)老虎住在森林俱乐部的(
)面。
(5)小鹿的东面住着(
小兔
小鹿
),西面住着(
)。
老虎 小猴
松鼠
(6)小狗住在狮子的(
)面,住在小兔的(
二、对号入座。(选一选)
1. 丽丽面向西面骑车,她的后面是( )。
)面。
A.东面 B. 西面 C. 南面 D. 北面
2. 晴朗的夜晚,我们可以利用( )来辨别方向。
A.星星 B. 月亮 C. 北极星 D. 太阳
3. 图书馆在邮局的北面,少年宫在邮局的南面,少年宫在图书馆的
( )。 A .东面 B. 西面 C. 南面 D. 北面
小华从家出发,向(
再向(
)方向(
走了(
)米。
七、我也来当设计师。
)方向(
)米到(
);
)米到达博物院,一共用(
)分钟,
某市要建设一座现代化的实验小学,你能为他们设计一张图纸吗?
设计要求:
( 1)必须要有天文台、教学楼、科技楼、游泳池。
( 2)其他建筑和设施可由同学们自由发挥想像,进行设计。
4. 王阿姨从超市往东走到家,超市在他家的( )
A.东面 B. 西面 C. 南面 D. 北面
5. 小明座位的西南方向是张强的座位,那么小明在张强的 ( ) 方向。
A.东南
B.
西北
C
.东北
三、我有一双小巧手。
2016春新人教版数学三年级下册第一次月考试卷

小学数学三年级下册第一次质量检测 一、填空。
(每空1分,共22分) 一、地图一般是按上( )下( ),左( )右( )绘制的。
二、把腕表平放在桌面上,用数字12正对着北方,正对着南方的数字是( );数字 3正对着( )方。
3、316÷8的商是( )位数,708÷7的商是( )位数。
4、李清家在学校的东南面,那么学校在李清家的( )方向。
五、□59÷6,若是商是三位数,□里最小能够填( ),若是商是两位数,□里最大能够填( )。
六、通常所说的八个方向是( )、( )、( )、( )、 ( )、( )、( )、( )。
7、验算有余数除法时,要把( )和( )相乘,再加上( )。
二、、判定题。
(每空1分,共5分) 一、在丛林中能够利用树叶的疏密来识别方向。
( ) 二、早晨面对太阳时,你的右面是北方,你的后面是西方。
( ) 3、0除以任何不是0的数都得0。
( ) 4、被除数末尾有两个零,那么商的末尾至少有一个零。
( ) 五、三位数除以一名数,商是必然是三位数。
( ) 三、选择题。
(每题1分,共5分) 一、一个数的4倍是824,那个数是( )。
二、一个三位数除以6,余数最大是( )。
A .7 B .4 C .5 3、张丽面向南站立,当她向后转以后,她的右面是( ),后面是( )。
A.东B.西C.南D.北4、一个三位数除以3的商仍是一个三位数,那么被除数的百位不可能是( )。
学校______________ 班级______________ 姓名______________学号_____________ ---------------------------------密-------------------------封----------------------线---------------------------------C. 4四、计算(30分)一、直接写出得数。
2016江苏省小学数学学业水平测试卷

江苏省小学数学学业水平测试卷姓名:准考证号:说明:1.答题前,请将你的姓名和准考证号认真填涂在试卷和答题卡上。
2.本卷分为“选择题”“填空题”和“解答题”三部分,共6页。
3.选择题的答案用铅笔填涂在答题卡上,填空题和解答题的答案写在答题卡上。
4.考试时间为70分钟,请合理安排答题时间。
5.考试结束后,请将试卷和答题卡交回。
一、选择题(共12小题,在每小题给出的四个选项中,只有一项是正确的,请将正确选项前的字母填涂在答题卡相应的位置。
) 1 ,计算下面的式子时,要选算“100-31"的是( )oA.1OO-31X3B.100- (31+3)C.3X 100-31D. 100—31+32.下面涂色部分不能用;表示的是( )。
4.学校有一块正方形草坪,正好能够容纳100个小朋友做广播体操,这块草坪的面积大约是 ( )oA.150平方分米B.150平方米C.1500平方分米D.1500平方米5.一根彩带,做蝴蝶结用去12分米,做彩花用去6分米,正好用完。
这根彩带原来有多长?下面列式正确的是( )。
B. 12-6C. 12X6D. 12 + 6A. 124-66.学校举行广播操表演,每行有12人,一共有16行(如右图)。
小明通过竖式计算知道一共有192人参加表演。
每行12人____________ 入_________A.第①根长B. 第②根长C. 一样长 D ,无法判定哪根长8.小强在计算96 ・ 8时, 把“8”抄成了“2”,并计算出了结果。
他要想得到正确的结果, 应该再()oA.加6B.C.除以4D.乘4竖式中箭头所指的可以用下面图()框中的点来表示。
9,下面的图形中,)通过平移能和右面的小房图完全重合。
纸片展开,得到的是( )o11 ,在口34:9,要使商是两位数,口里最大填( )oA. 1B. 7C. 8D. 912.将长方形沿一条直线剪开,不可能得到图形()。
• • •二、填空题(共5小题,请将答案写在答题卡相应的位置。
2016春三年级数学下学期期中检测卷新人教版
2016春三年级数学下学期期中检测卷(新人教版)2016年春季学期官渡区小学期中教学质量检测卷三年级数学满分100分,考试时间100分题号一二三四五六总分得分一、填空(每空1分,共20分)。
1、645÷5的商是()位数,最高位在()位。
2、把456平均分成8份,每份是()。
3、暖袋每个23元,李师傅买了40个,要付()元。
4、估算82×19时,可以把82看成(),把19看成(),所以82×19≈()。
5、()32÷6,要使商是三位数,括里最小填(),要使商是两位数,括里最大填()。
6、计算12×60时,可以先算()×(),得(),再在乘得的得数末尾添上()个0.7、在○里填上“>”“<”或“=”。
56÷6○56÷345×24○24×440×12○0÷12400÷2○800÷4160×2○16×20104÷8○104×88、三(1)班的同学排队坐缆车,每辆缆车限坐4人,笑笑排在第16位,她应坐第()辆缆车:淘气排在第34位,他应坐第()辆缆车。
二、判断题(6分)1、0×6,0×0,0÷6,0+6四个算式的结果都是0。
()2、960÷2÷3=960÷(2×3)。
()3、被除数的末尾有0,商的末尾一定有0.()4、面对早晨的太阳,你的右手边是南方。
()5、估算的结果都比实际计算的结果大。
()6、一个数除以8,有余数,那么余数最大是7。
()三、选择题(10分)1、在除法算式中,0不能作()。
A.被除数B.除数C.商2、一个数被6除,商是28,余数是5,这个数是()。
A.92B.121C.1733、除数是一位数的除法,应从被除数的()除起。
A.个位B.十位C.百位D.高位4、太阳()是东升西落。
2016-2017学年度第二学期六年级数学期末质量检测试题
2016-2017学年度第二学期六年级数学期末质量检测试题2016-2017学年第二学期,六年级数学期末质量检测卷3.钟表在下午3点半时,时针和分针所成的角度是90度。
()2.甲乙两桶水,甲用去四分之一,乙用去一半,剩下的水一样多。
甲乙原来水的比是4:3.()一、填空题。
1.地球上陆地面积约为1亿4千8百9十9万5千平方千米,写作()平方千米。
省略万位后面的尾数约为()万平方千米。
2.分数单位为1/7的最大真分数是()。
至少再加上()个分数单位,就变成了最小的质数。
3.3时15分=()时50分。
1平方米=()公顷。
4.7千克比()少1/2千克;20吨增加()%后是25吨。
5.一根圆柱形木料长4米,把它锯成3段,表面积增加了12平方分米。
这根木料的体积是()。
如果将它锯成6段,需要()分钟。
6.在a÷b=5……3中,将a、b同时扩大10倍,商是(),余数是()。
7.用5厘米的线段表示实际距离3000千米,这幅地图的比例尺是()。
在这幅地图上量得甲、乙两地相距4厘米,甲、乙两地实际相距()。
8.5/4:5/6的比值是()。
写成最简整数比是()。
9.已知A=2×3×5,B=3×3×5.那么A和B的最大公约数是(),最小公倍数是()。
10.一个周长为46厘米的长方形,如果长和宽都增加10厘米,那么面积增加()平方厘米。
11.一只长方体油箱的容量为27升,里面高为6厘米,底面积为()平方厘米。
12.如下左图,一长方形被一条直线分成两个长方形,这两个长方形的宽的比为1∶3.若阴影三角形面积为1平方厘米,则原长方形面积为()平方厘米。
二、判断。
1.工作总量一定,工作效率和工作时间成反比例。
(×)2.圆锥的侧面展开后是一个等腰三角形。
(×)5.一个长方体,它的长、宽、高都扩大2倍,它的体积扩大6倍。
(√)三、选择题。
1.一列分数的前5个是1/2、2/5、3/10、4/17、5/26.根据这5个分数的规律可知,第8个分数是(C)。
