成都七中育才学校2019届八(下)第十二周周测《第12周周测》试卷(含答案)
成都七中育才学校2019届八年级数学下册《第8周周练》试卷【名校学案+详细解答】

成都七中育才学校2019届八年级数学下册第8周周练班级_________姓名________学号________A卷(100分)一.选择题(每小题3分,共30分)1.下面四个汽车标志图案中是中心对称图形的是()A.B.C.D.2.已知a>b,下列各式中,错误的是()A.a﹣3>b﹣3 B.5﹣a>5﹣b C.﹣a<﹣b D.a﹣b>03.化简÷的结果是()A.m B. C.m﹣1 D.4.把不等式组的解集表示在数轴上,正确的是()A.B.C.D.5.下列因式分解正确的是()A.x3﹣x=x(x2﹣1)B.﹣a2+6a﹣9=﹣(a﹣3)2C.x2+y2=(x+y)2 D.a3﹣2a2+a=a(a+1)(a﹣1)6.在平面直角坐标系中,将点B(﹣3,2)向左平移5个单位长度,再向上平移3个单位长度后与点A(x,y)重合,则点A的坐标是()A.(2,5) B.(﹣8,5) C.(﹣8,﹣1) D.(2,﹣1)7.如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△A B′C′的位置,使得CC′∥AB,则∠BAB′的度数是()A.70° B.35° C.40° D.50°8.关于y的方程的解正确的是()A.y=﹣2 B.y=2 C.y=﹣2或y=2 D.方程无解9.如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为DC的中点,DG⊥AE,垂足为G.若AE=4,则DG的长为()A. B.C.1 D.10.为迎接2014年巴西世界杯开幕,某校举办了以欢乐世界杯为主题趣味颠足球比赛:各班代表队所有成员按指定规则同时颠球,成功颠球300个所用时最短的代表队即获胜.预赛中某班的参赛团队每分钟共颠球X个进入决赛,决赛中该团队每分钟颠球的成功率提高为预赛的1.2倍,结果提前了2分钟完成比赛,根据题意,下面所列方程中,正确的是()A .=2 B .﹣=2 C .= D .=题号 1 2 3 4 5 6 7 8 9 10答案二.填空题(每小题4分,共20分)11.已知2x﹣y=,xy=2,则2x2y﹣xy2= .12.分解因式:x3﹣4x2+4x= .13.已知x2+y2+z2+2x﹣4y﹣6z+14=0,则x﹣y+z= .14.若+=,那么a= ,b= .15.如图,△AOB中,∠AOB=90°,AO=3,BO=6,△AOB绕顶点O逆时针旋转到△A′OB′处,此时线段A′B′与BO的交点E为BO的中点,则线段B′E的长度为.三.解答题16.(每小题6分,共12分)(1)解不等式组,并求其整数解:(2)已知实数x,y满足|x+y﹣1|+|xy+3|=0,求代数式xy3+x3y+2x2y2的值.17.(6分)解方程:﹣=1.18.(10分)先化简,再求值÷(m﹣1+),其中m=.19.(10分)2014年5月28日,成都新二环迎来改造通车一周年的日子.在二环路的绿化工程中,甲、乙两个绿化施队承担了某路段的绿化工程任务,甲队单独做要40天完成,若乙队先做30天后,甲、乙两队合作再做20天恰好完成任务,请问:乙队单独做需要多少天能完成任务?20.(12分)如图,四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.(1)求证:四边形BDFC是平行四边形;(2)若△BCD是等腰三角形,求四边形BDFC的面积.(12分)B卷一. 填空题(每小题3分,共9分)21.若关于x的方程﹣1=的解为负数,则k的取值范围是.23.已知x2﹣5x+1=0,则的值是.23.如图,直线y=﹣x+m与y=x+5的交点的横坐标为﹣2,则关于x的不等式﹣x+m>x+5>0的整数解为.24.(11分)如图1,等腰直角三角形ABC 中,∠ACB=90°,CB=CA ,直线ED 经过点C ,过A 作AD ⊥ED 于D ,过B 作BE ⊥ED 于E .(1)求证:△BEC ≌△CDA .(2)已知直线l 1:y =34x +4与y 轴交于A 点,将直线l 1绕着A 点顺时针旋转45°至l 2,如图2,求l 2的函数解析式.(3)如图3,长方形ABCO ,O 为坐标原点,B 的坐标为(8,6),A 、C 分别在坐标轴上,P 是线段BC 上动点,已知点D 在第一象限,且是直线y =2x ﹣6上的一点,若△APD 是不以A 为直角顶点的等腰直角三角形,请直接写出点D 的坐标.。
成都七中育才学校初2019届八年级下期第4周周测数学试题(附答案)

成都七中育才学校初2019届八年级下期第4周周测数学试题班级_______姓名________学号________A 卷(100分)一.选择题(每题3分,共30分)1.在下面的汽车标志图形中,是中心对称但不是轴对称有( ) A .2 个 B .3个 C .4个 D .5个2.下列各式从左到右的变形中,是因式分解的为( ) A 、bx ax b a x -=-)(B 、222)1)(1(1y x x y x ++-=+-C 、)1)(1(12-+=-x x xD 、c b a x c bx ax ++=++)(3.如图,△ODC 是由△OAB 绕点O 顺时针旋转31°后得到的图形,若点D 恰好落在AB 上,且AOC ∠的度数为100°,则DOB ∠的度数为( )A.36°B.38°C.34°D.40° 4. 将a 2b ﹣ab 2提公因式后,另一个因式是( )A .a+bB .a+2bC .a ﹣bD .a ﹣2b5.如图,在等边△ABC 中,点O 在AC 上,且AO=3,CO=6,点P 是AB 上一动点,连接OP ,将线段OP 绕点O 逆时针旋转60°得到线段OD .要使点D 恰好落在BC 上,则AP 的长是( ) A.4 B.5 C.6 D.86.如图,函数x y 2=和4+=ax y 的图象相交于点A (m ,3),则不等式x 2<4+ax 的解集为( )A.32x > B.3x > C.3x < D. 23<x 7. 如图,已知在△ABC 中,CD 是AB 边上的高线,BE 平分∠ABC,交CD 于E,BC=5,DE=2,则△BCE 的面积等于( ) A.5 B.7 C.10 D.3 8.若1124n n aa -+-的公因式是M,则M 等于 ( )A.1n a -B.2n aC.12n a -D.12n a + 9.若0<a ,则不等式a x a <的解集是( )A .1<xB .1>xC .1->xD .1-<x第3题二.填空题(每小题4分,共20分) 12. 已知312=-y x ,2=xy ,则222x y xy -= 13.在平面直角坐标系中,以坐标原点为中心,把点A(4,5)逆时针旋转90°,得到的点A 1的坐标为 14.矩形纸片ABCD 中,AB =3cm ,BC =4cm ,现将纸片折叠压平,使A 与C 重合,设折痕为EF ,则重叠部分△AEF 的面积等于__________.15.如图,在□ABCD 中,AD=2,AB=4,°=∠30A ,以点A 为圆心,AD 的长为半径画弧交AB 于点E ,则阴影部分面积是 (结果保留π) 三.解答题(50分)16.分解因式(每小题4分,共16分)(1)3222245954a b c a bc a b c +- (2) 324322693x y z x y z x y -+-(3) 2(1)(1)x a x a -+- (4) 433()()()a b a a b b b a -+-+-17.(8分)已知关于x,y 的方程组212x y x y m +=⎧⎨-=⎩的解都小于1.第14题第15题⑴ 求m 的取值范围 .⑵ 化简:13-++m m18.(6分) 如图,在平面直角坐标系中,Rt △ABC 的三个顶点分别是A (-3,2),B (0,4),C (0,2).(1)将△ABC 以点C 为旋转中心旋转180°,画出旋转后对应的△A 1B 1C ;平移△ABC ,若点A 的对应点A 2的坐标为 (0,-4),画出平移后对应的△A 2B 2C 2;(2)在x 轴上有一点P ,使得PA+PB 的值最小,请直接写出点P 的坐标为 .20.(10分) 如图(1),已知△ABC 是等腰直角三角形,∠BAC=90°,点D 是BC 的中点.作正方形DEFG ,使点A 、C 分别在DG 和DE 上,连接AE 、BG .(1)试猜想线段BG 和AE 的关系(位置关系及数量关系),请直接写出你得到的结论: (2)将正方形DEFG 绕点D 逆时针方向旋转一角度a 后(0°<a <90°),如图(2),通过观察或测量等方法判断(1)中的结论是否仍然成立?如果成立,请予以证明;如果不成立,请说明理由; (3)若BC=DE=m ,正方形DEFG 绕点D 逆时针方向旋转角度a (0°<a <360°)过程中,当AE 为最大值时,求AF 的值.B 卷(20分)一.填空题(每小题4分,共12分)21. 如图,在平面直角坐标系中,点A 的坐标为(0,3),△OAB 沿x 轴向右平移后得到B A O '''∆,点A 的对应点在直线x y 43=上一点,则点B 与其对应点B '的距离是22. 已知关于x 的不等式组0320x a x ->⎧⎨->⎩的整数解共有6个,则a 的取值范围是____________二.解答题(8分)24.如图,直线1l 与坐标轴分别交于点A 、B,经过原点的直线2l 与AB 交于点C ,与过点A 且平行于y 轴的直线交于点D ,已知点C (3,154),且OA=8.在直线AB 上取点P ,过点P 作y 轴的平行线,与CD 交于点Q, 以PQ 为边向右作正方形PQEF.设点P 的横坐标为t. (1)求直线1l 的解析式;(2)当点P 在线段AC 上时,用t 表示正方形PQEF 与△ACD 重叠部分(阴影部分)的面积; (3)设点M 坐标为(4,92),在点P 的运动过程中,当点M 在正方形PQEF 内部时,请直接写出t 的取值范围.。
七年级下数学第十二周周练习含答案

七年级下期数学第十二周周练习姓名: 班级: 学号:A 卷(共100分))一、选择题:(每小题3分,共30分)) 1. 下列运算正确的是( )A .3362x x x = B .224(2)4x x -=- C .326()x x = D .55x x x ÷= 2. 以下列各组长度的线段为边,能构成三角形的是( )A .6cm 、8cm 、15cmB .7cm 、5cm 、12cmC .4cm 、6cm 、5cmD .8cm 、4cm 、4cm3. 如图,已知AB CD ∥,35A ∠= ,75C ∠=,那么M ∠=( )A .35B .40C .45D .754. 如图,已知12∠=∠,要证ABC ADC △≌△,还要从下列条件中选一个,错误的选法是( )A .ACD ACB ∠=∠ B .B D ∠=∠C .BC DC =D .AB AD =5. 如图,已知ABC △的六个元素,则甲、乙、丙三个三角形中和ABC △全等的图形是( )A .甲和乙B .乙和丙C .只有乙D .只有丙6. 在直角三角形中,下列条件:①两直角边对应相等;②两锐角对应相等;③一锐角和它的对边对应相等;④一锐角和斜边对应相等;⑤斜边和一直角边对应相等。
其中能判定两个三角形全等的条件共有( ) A .1个 B .2个 C .3个 D .4个7. 如图,ABC △中,AB AC =,AD BC ⊥,垂足为D ,E 是AD 上任一点,则有全等三角形( )A BC a cbcacaa甲 乙 丙505872505050A B D CM(第3题图) A B C D 1 2(第4题图)AB DC E (第7题图) (第8题图)A .1对B .2对C .3对D .4对8. 如图所示是55⨯的正方形网格,以点D 、E 为两个顶点作位置不同的格点三角形,使所作的格点三角形与ABC △全等,这样的格点三角形最多可以画出( ) A .2个 B .4个 C .6个 D .8个9. 如图,从下面四个条件:①BC B C '=;②A C AC '=;③AC A BC B ''∠=∠;④AB AB ''=中,任取三个为条件可以判定ABC A B C '''△≌△,正确的取法有( )种 A .1 B .2 C .3D .410.如图,在ABC △中,BD 、CE 分别是AC 、AB 边上的中线,分别延长BD 、CE 到F 、G ,使得DF BD =,EG CE =,则下列结论:①GA AF =;②GA BC ∥;③AF BC ∥;④G 、A 、F 在一条直线上;⑤四边形GBCF 的面积是ABC △的3倍,其中正确的个数是( ) A .2个 B .3个 C .4个 D .5个二、填空题:(每小题4分,共20分)11.已知m 为正整数,且948162mm⨯⨯=,则m = 。
成都市第七中学初中数学八年级下期中经典练习题(含答案)
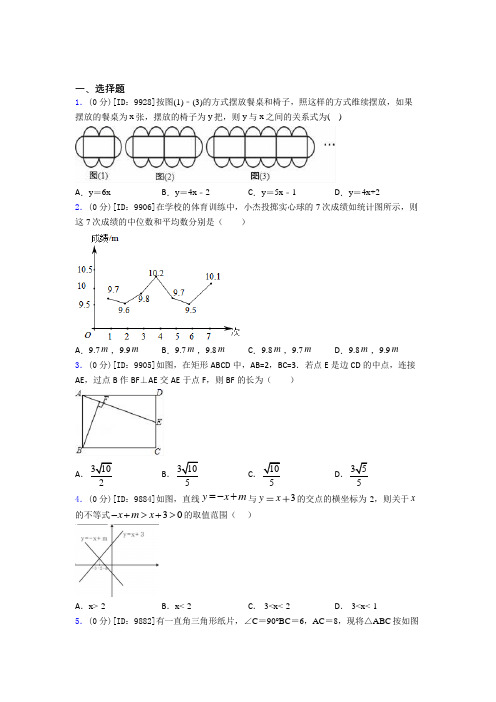
一、选择题1.(0分)[ID :9928]按图(1)﹣(3)的方式摆放餐桌和椅子,照这样的方式维续摆放,如果摆放的餐桌为x 张,摆放的椅子为y 把,则y 与x 之间的关系式为( )A .y =6xB .y =4x ﹣2C .y =5x ﹣1D .y =4x+22.(0分)[ID :9906]在学校的体育训练中,小杰投掷实心球的7次成绩如统计图所示,则这7次成绩的中位数和平均数分别是( )A .9.7m ,9.9mB .9.7m ,9.8mC .9.8m ,9.7mD .9.8m ,9.9m3.(0分)[ID :9905]如图,在矩形ABCD 中,AB=2,BC=3.若点E 是边CD 的中点,连接AE ,过点B 作BF ⊥AE 交AE 于点F ,则BF 的长为( )A .3102B .3105C .105D .3554.(0分)[ID :9884]如图,直线y x m =-+与3yx 的交点的横坐标为-2,则关于x的不等式30x m x -+>+>的取值范围( )A .x>-2B .x<-2C .-3<x<-2D .-3<x<-15.(0分)[ID :9882]有一直角三角形纸片,∠C =90°BC =6,AC =8,现将△ABC 按如图那样折叠,使点A与点B重合,折痕为DE,则CE的长为( )A.27B.74C.72D.46.(0分)[ID:9878]如图,在平行四边形ABCD中,AC、BD相交于点O,下列结论:①OA =OC;②∠BAD=∠BCD;③AC⊥BD;④∠BAD+∠ABC=180°中,正确的个数有()A.1个 B.2个 C.3个 D.4个7.(0分)[ID:9870]函数y=11xx+-中,自变量x的取值范围是()A.x>-1B.x>-1且x≠1C.x≥一1D.x≥-1且x≠1 8.(0分)[ID:9868]若一次函数y=(k-3)x-k的图象经过第二、三、四象限,则k的取值范围是()A.k<3B.k<0C.k>3D.0<k<39.(0分)[ID:9854]如图,已知圆柱底面的周长为4dm,圆柱的高为2dm,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为()A.42dm B.22dm C.25dm D.45dm10.(0分)[ID:9850]如图,在菱形ABCD中,AB=5,对角线AC=6.若过点A作AE⊥BC,垂足为E,则AE的长为( )A.4B.2.4C.4.8D.511.(0分)[ID:9926]如图是自动测温仪记录的图象,它反映了齐齐哈尔市的春季某天气温T如何随时间t的变化而变化,下列从图象中得到的信息正确的是( )A.0点时气温达到最低B.最低气温是零下4℃C.0点到14点之间气温持续上升D.最高气温是8℃12.(0分)[ID:9839]为了研究特殊四边形,李老师制作了这样一个教具(如图1):用钉子将四根木条钉成一个平行四边形框架ABCD,并在A与C、B与D两点之间分别用一根橡皮筋拉直固定,课上,李老师右手拿住木条BC,用左手向右推动框架至AB⊥BC(如图2)观察所得到的四边形,下列判断正确的是()A.∠BCA=45°B.AC=BDC.BD的长度变小D.AC⊥BD13.(0分)[ID:9910]小明搬来一架 3.5 米长的木梯,准备把拉花挂在 2.8 米高的墙上,则梯脚与墙脚的距离为( )A.2.7 米B.2.5 米C.2.1 米D.1.5 米⊥于,D E是AC的中点.若14.(0分)[ID:9885]如图,ABC中,CD AB==则CD的长等于()6,5,AD DEA.5B.6C.8D.1015.(0分)[ID:9869]如图,菱形ABCD的对角线AC,BD相交于点O,E,F分别是EF=,BD=4,则菱形ABCD的周长为()AB,BC边上的中点,连接EF.若3A.4B.6C.47D.28二、填空题16.(0分)[ID :10017]计算:2(21)+=__________.17.(0分)[ID :10009]如图,E 、F 分别是平行四边形ABCD 的边AB 、CD 上的点,AF 与DE 相交于点P,BF 与CE 相交于点Q,若215APD S cm ∆=,225BQC S cm ∆=,则阴影部分的面积为__________2cm .18.(0分)[ID :9998]一组数据4、5、a 、6、8的平均数5x =,则方差2s =________.19.(0分)[ID :9983]△ABC 中,AB =13cm ,BC =10cm ,BC 边上的中线AD =12cm .则AC =______cm .20.(0分)[ID :9978]在矩形ABCD 中,对角线AC 、BD 交于点O ,AB =1,∠AOB =60°,则AD =________.21.(0分)[ID :9976]如图,在ABC ∆中,D 、E 分别为AB 、AC 的中点,点F 在DE 上,且AF CF ⊥,若3AC =,5BC =,则DF =__________.22.(0分)[ID :9967]如图,矩形纸片ABCD 中,已知AD =8,折叠纸片使AB 边与对角线AC 重合,点B 落在点F 处,折痕为AE ,且EF =3,则AB 的长为____.23.(0分)[ID :9944]2a =3b =,用含,a b 0.54,结果为________.24.(0分)[ID :9939]在平面直角坐标系中,(1,0)(4,0)(0,3),A B C -、、若以A B C D 、、、为顶点的四边形是平行四边形,则D 点坐标是________________.25.(0分)[ID :9965]如图,矩形ABCD 的对角线AC 和BD 相交于点O ,过点O 的直线分别交AD 和BC 于点E 、F ,AB=2,BC=4,则图中阴影部分的面积为_______.三、解答题26.(0分)[ID :10132]如图,在菱形ABCD 中,对角线AC 、BD 相交于点O ,过点D 作对角线BD 的垂线交BA 的延长线于点E(1)证明:四边形ACDE 是平行四边形;(2)若AC=8,BD=6,求△ADE 的周长.27.(0分)[ID :10128]如图,已知AC 是矩形ABCD 的对角线,AC 的垂直平分线EF 分别交BC 、AD 于点E 和F ,EF 交AC 于点O .(1)求证:四边形AECF 是菱形;(2)若AB =6,AD =8,求四边形AECF 的周长.28.(0分)[ID :10112]计算:16(23)(23)273--. 29.(0分)[ID :10061](1)用>=<、、填空 32 21②23 3252 2365 5220182017 20172016(2)观察.上式,请用含1)1,(,1n n n n -+≥的式子,把你发现的规律表示出来,并证明结论的正确性.30.(0分)[ID :10035]“五一”节假期间, 小亮一家到某度假村度假.小亮和他妈妈坐公交车先出发,他爸爸自驾车沿着相同的道路后出发,他爸爸到达度假村后,发现忘了东西在家里,于是立即返回家里取,取到东西后又马上驾车前往度假村,如图是他们离家的距离()s km 与小亮离家的时间()t h 的关系图,请根据图回答下列问题:(1)小亮和妈妈坐公交车的速度为 /km h ;爸爸自驾的速度为 /km h (2)小亮从家到度假村期间,他离家的距离()s km 与离家的时间()t h 的关系式为 ;小亮从家到度假村的路途中,当他与他爸爸相遇时,离家的距离是 km (3)当小亮和妈妈与他爸爸第2次相遇后,一直到全家会和为止,t 为多少时小亮和妈妈与爸爸相距10km ?【参考答案】2016-2017年度第*次考试试卷 参考答案**科目模拟测试一、选择题1.D2.B3.B4.C5.B6.C7.D8.D9.A10.C11.D12.B13.C14.C15.C二、填空题16.3+2【解析】【分析】【详解】解:故答案为:3+217.40【解析】【分析】作出辅助线因为△ADF与△DEF同底等高所以面积相等所以阴影图形的面积可解【详解】如图连接EF∵△ADF与△DEF同底等高∴S=S即S−S=S−S即S=S=15cm同理可得S=S18.4【解析】【分析】首先根据其平均数为5求得a的值然后再根据方差的计算方法计算即可【详解】解:根据题意得(4+5+a+6+8)=5×5解得a=2则这组数据为45268的平均数为5所以这组数据的方差为s19.13【解析】【分析】在△ABD中根据勾股定理的逆定理即可判断AD⊥BC然后根据线段的垂直平分线的性质即可得到AC=AB从而求解【详解】∵AD是中线AB=13BC=10∴∵52+122 =132即BD220.【解析】【分析】【详解】解:∵四边形ABCD是矩形∴AC=2OABD=2BOAC=BD∴OB=O A∵∴是等边三角形故答案为【点睛】本题考查矩形的对角线相等21.1【解析】【分析】根据三角形中位线定理求出DE根据直角三角形的性质求出EF计算即可【详解】解:∵DE分别为ABAC的中点∴DE=BC=25∵AF⊥CFE为AC的中点∴EF=AC=15∴DF=DE﹣E22.6【解析】【分析】先根据矩形的特点求出BC的长再由翻折变换的性质得出△CEF是直角三角形利用勾股定理即可求出CF的长再在△ABC中利用勾股定理即可求出AB的长【详解】解:∵四边形ABCD是矩形AD=23.【解析】【分析】将化简后代入ab即可【详解】解:∵∴故答案为:【点睛】本题考查了二次根式的乘除法法则的应用解题的关键是将化简变形本题属于中等题型24.(-53)(53)(3−3)【解析】【分析】作出图形分ABBCAC为对角线三种情况进行求解【详解】如图所示①AC为对角线时AB=5∴点D的坐标为(-53)②BC为对角线时AB=5∴点D的坐标为(5325.4【解析】【分析】根据矩形的性质可得阴影部分的面积等于矩形面积的一半即可求得结果【详解】由图可知阴影部分的面积故答案为:4考点:本题考查的是矩形的性质点评:解答本题的关键是根据矩形的性质得到△DOE三、解答题26.27.28.29.30.2016-2017年度第*次考试试卷参考解析【参考解析】**科目模拟测试一、选择题1.D解析:D【解析】【分析】观察可得,第一张餐桌上可以摆放6把椅子,进一步观察发现:多一张餐桌,多放4把椅子.第x张餐桌共有6+4(x-1)=4x+2,由此即可解答.【详解】有1张桌子时有6把椅子,有2张桌子时有10把椅子,10=6+4×1,有3张桌子时有14把椅子,14=6+4×2,∵多一张餐桌,多放4把椅子,∴第x张餐桌共有6+4(x-1)=4x+2.∴y与x之间的关系式为:y=4x+2.【点睛】本题考查了图形的变化类问题,注意结合图形进行观察,发现数字之间的运算规律,利用规律即可求得y 与x 之间的关系式.2.B解析:B【解析】【分析】将这7个数据从小到大排序后处在第4位的数是中位数,利用算术平均数的计算公式进行计算即可.【详解】把这7个数据从小到大排列处于第4位的数是9.7m ,因此中位数是9.7m ,平均数为:(9.59.69.79.79.810.110.2)79.8++++++÷=m ,故选:B .【点睛】考查中位数、算术平均数的计算方法,将一组数据从小到大排列后处在中间位置的一个数或两个数的平均数就是这组数据的中位数,平均数则是反映一组数据的集中水平.3.B解析:B【解析】【分析】根据S △ABE =12S 矩形ABCD =3=12•AE•BF ,先求出AE ,再求出BF 即可. 【详解】如图,连接BE .∵四边形ABCD 是矩形,∴AB=CD=2,BC=AD=3,∠D=90°,在Rt △ADE 中,22AD DE +2231+10, ∵S △ABE =12S 矩形ABCD =3=12•AE•BF , ∴BF=310. 故选:B .本题考查矩形的性质、勾股定理、三角形的面积公式等知识,解题的关键是灵活运用所学知识解决问题,学会用面积法解决有关线段问题,属于中考常考题型.4.C解析:C【解析】【分析】【详解】解:∵直线y x m =-+与3y x 的交点的横坐标为﹣2,∴关于x 的不等式3x m x -+>+的解集为x <﹣2,∵y=x+3=0时,x=﹣3,∴x+3>0的解集是x >﹣3,∴3x m x -+>+>0的解集是﹣3<x <﹣2,故选C .【点睛】本题考查一次函数与一元一次不等式.5.B解析:B【解析】【分析】已知,∠C=90°BC=6,AC=8,由勾股定理求AB ,根据翻折不变性,可知△DAE ≌△DBE ,从而得到BD=AD ,BE=AE ,设CE=x ,则AE=8-x ,在Rt △CBE 中,由勾股定理列方程求解.【详解】∵△CBE ≌△DBE ,∴BD=BC=6,DE=CE ,在RT △ACB 中,AC=8,BC=6,∴.∴AD=AB-BD=10-6=4.根据翻折不变性得△EDA ≌△EDB∴EA=EB∴在Rt △BCE 中,设CE=x ,则BE=AE=8-x ,∴BE 2=BC 2+CE 2,∴(8-x )2=62+x 2,解得x=74. 故选B .【点睛】此题考查了翻折变换的问题,找到翻折后图形中的直角三角形,利用勾股定理来解答,解答过程中要充分利用翻折不变性.6.C解析:C【解析】试题分析:根据平行四边形的性质依次分析各选项即可作出判断.∵平行四边形ABCD∴OA=OC,∠BAD=∠BCD,∠BAD+∠ABC=180°,但无法得到AC⊥BD故选C.考点:平行四边形的性质点评:平行四边形的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.7.D解析:D【解析】根据题意得:1010 xx+≥⎧⎨-≠⎩,解得:x≥-1且x≠1.故选D.8.D解析:D【解析】【分析】由一次函数图象经过第二、三、四象限,利用一次函数图象与系数的关系,即可得出关于k的一元一次不等式组,解之即可得出结论.【详解】∵一次函数y=(k-3)x-k的图象经过第二、三、四象限,∴{k−3<0−k<0,解得:0<k<3,故选:D.【点睛】本题考查了一次函数图象与系数的关系,牢记“k<0,b<0⇔y=kx+b的图象在二、三、四象限”是解题的关键.9.A解析:A【解析】【分析】要求丝线的长,需将圆柱的侧面展开,进而根据“两点之间线段最短”得出结果,在求线段长时,根据勾股定理计算即可.【详解】解:如图,把圆柱的侧面展开,得到矩形,则这圈金属丝的周长最小为2AC 的长度,圆柱底面的周长为4dm ,圆柱高为2dm ,2AB dm ,2BC BC dm , 22222448AC , 22AC dm ,∴这圈金属丝的周长最小为242ACdm . 故选:A .【点睛】本题考查了平面展开-最短路径问题,圆柱的侧面展开图是一个矩形,此矩形的长等于圆柱底面周长,高等于圆柱的高,本题就是把圆柱的侧面展开成矩形,“化曲面为平面”,用勾股定理解决.10.C解析:C【解析】【分析】连接BD ,根据菱形的性质可得AC ⊥BD ,AO=12AC ,然后根据勾股定理计算出BO 长,再算出菱形的面积,然后再根据面积公式BC•AE=12AC•BD 可得答案. 【详解】连接BD ,交AC 于O 点,∵四边形ABCD 是菱形,∴AB =BC =CD =AD =5,∴1,22AC BD AO AC BD BO ⊥==,, ∴90AOB ∠=,∵AC=6,∴AO=3,∴4 BO==,∴DB=8,∴菱形ABCD的面积是116824 22AC DB⨯⋅=⨯⨯=,∴BC⋅AE=24,245AE=,故选C.11.D解析:D【解析】【分析】根据气温T如何随时间t的变化而变化图像直接可解答此题.【详解】A.根据图像4时气温最低,故A错误;B.最低气温为零下3℃,故B错误;C.0点到14点之间气温先下降后上升,故C错误;D描述正确.【点睛】本题考查了学生看图像获取信息的能力,掌握看图像得到有用信息是解决此题的关键. 12.B解析:B【解析】【分析】根据矩形的性质即可判断;【详解】解:∵四边形ABCD是平行四边形,又∵AB⊥BC,∴∠ABC=90°,∴四边形ABCD是矩形,∴AC=BD.故选B.【点睛】本题考查平行四边形的性质.矩形的判定和性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.13.C解析:C【解析】【分析】仔细分析题意得:梯子、地面、墙刚好形成一直角三角形,梯高为斜边,利用勾股定理解此直角三角形即可.【详解】=2.1(米).故选C .【点睛】本题考查了勾股定理的应用.善于提取题目的信息是解题以及学好数学的关键.14.C解析:C【解析】【分析】先根据直角三角形的性质求出AC 的长,再根据勾股定理即可得出结论.【详解】解:∵ABC 中,CD AB ⊥于D ,∴∠ADC =90°,则ADC 为直角三角形,∵E 是AC 的中点,DE =5,∴AC =2DE =10,在Rt ADC 中,AD =6,AC =10,∴8CD =, 故选:C .【点睛】本题考查的是直角三角形斜边上的中线,熟知在直角三角形中,斜边上的中线等于斜边的一半是解答此题的关键. 15.C解析:C【解析】【分析】首先利用三角形的中位线定理得出AC ,进一步利用菱形的性质和勾股定理求得边长,得出周长即可.【详解】解:∵E ,F 分别是AB ,BC 边上的中点,∴∵四边形ABCD 是菱形,∴AC ⊥BD ,OA=12OB=12BD=2,∴,∴菱形ABCD 的周长为.故选C.二、填空题16.3+2【解析】【分析】【详解】解:故答案为:3+2解析:3+22【解析】【分析】【详解】(2+1)=(2)+22+1=3+22.解:222故答案为:3+22.17.40【解析】【分析】作出辅助线因为△ADF与△DEF同底等高所以面积相等所以阴影图形的面积可解【详解】如图连接EF∵△ADF与△DEF同底等高∴S=S 即S−S=S−S即S=S=15cm同理可得S=S解析:40【解析】【分析】作出辅助线,因为△ADF与△DEF同底等高,所以面积相等,所以阴影图形的面积可解.【详解】如图,连接EF∵△ADF与△DEF同底等高,=S DEF∴SADF−S DPF =S DEF−S DPF,即SADF即S APD =S EPF =15cm2,同理可得S BQC =S EFQ =25cm2,∴阴影部分的面积为S EPF +S EFQ =15+25=40cm2.故答案为40.【点睛】此题考查平行四边形的性质,解题关键在于进行等量代换.18.4【解析】【分析】首先根据其平均数为5求得a的值然后再根据方差的计算方法计算即可【详解】解:根据题意得(4+5+a+6+8)=5×5解得a=2则这组数据为45268的平均数为5所以这组数据的方差为s解析:4【解析】【分析】首先根据其平均数为5求得a的值,然后再根据方差的计算方法计算即可.【详解】解:根据题意得(4+5+a+6+8)=5×5,解得a=2,则这组数据为4,5,2,6,8的平均数为5,所以这组数据的方差为s2= 15[(4-5)2+(5-5)2+(2-5)2+(6-5)2+(8-5)2]=4.故答案为:4【点睛】本题考查方差的定义、意义、计算公式,方差反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.19.13【解析】【分析】在△ABD中根据勾股定理的逆定理即可判断AD⊥BC然后根据线段的垂直平分线的性质即可得到AC=AB从而求解【详解】∵AD是中线AB=13BC=10∴∵52+122=132即BD2解析:13【解析】【分析】在△ABD中,根据勾股定理的逆定理即可判断AD⊥BC,然后根据线段的垂直平分线的性质,即可得到AC=AB,从而求解.【详解】∵AD是中线,AB=13,BC=10,∴152BD BC==.∵52+122=132,即BD2+AD2=AB2,∴△ABD是直角三角形,则AD⊥BC,又∵BD=CD,∴AC=AB=13.故答案为13.【点睛】本题考查的知识点是勾股定理的逆定理与线段的垂直平分线的性质,解题关键是利用勾股定理的逆定理证得AD ⊥BC .20.【解析】【分析】【详解】解:∵四边形ABCD 是矩形∴AC=2OABD=2BOAC=BD ∴OB=OA ∵∴是等边三角形故答案为【点睛】本题考查矩形的对角线相等 解析:3 【解析】【分析】【详解】解:∵四边形ABCD 是矩形,∴AC=2OA ,BD=2BO ,AC=BD ,∴OB=OA ,∵60∠=,AOB ∴OAB 是等边三角形,1OB AB ∴==22BD OB ==223AD BD AB =-=故答案为3.【点睛】本题考查矩形的对角线相等.21.1【解析】【分析】根据三角形中位线定理求出DE 根据直角三角形的性质求出EF 计算即可【详解】解:∵DE 分别为ABAC 的中点∴DE=BC =25∵AF⊥CFE 为AC 的中点∴EF=AC =15∴DF=DE ﹣E解析:1【解析】【分析】根据三角形中位线定理求出DE ,根据直角三角形的性质求出EF ,计算即可.【详解】解:∵D 、E 分别为AB 、AC 的中点,∴DE =12BC =2.5, ∵AF ⊥CF ,E 为AC 的中点, ∴EF =12AC =1.5, ∴DF =DE ﹣EF =1,故答案为:1.【点睛】本题考查的是三角形中位线定理、直角三角形的性质,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.22.6【解析】【分析】先根据矩形的特点求出BC的长再由翻折变换的性质得出△CEF是直角三角形利用勾股定理即可求出CF的长再在△ABC中利用勾股定理即可求出AB的长【详解】解:∵四边形ABCD是矩形AD=解析:6【解析】【分析】先根据矩形的特点求出BC的长,再由翻折变换的性质得出△CEF是直角三角形,利用勾股定理即可求出CF的长,再在△ABC中利用勾股定理即可求出AB的长.【详解】解:∵四边形ABCD是矩形,AD=8,∴BC=8,∵△AEF是△AEB翻折而成,∴BE=EF=3,AB=AF,△CEF是直角三角形,∴CE=8-3=5,在Rt△CEF中,4CF===设AB=x,在Rt△ABC中,AC2=AB2+BC2,即(x+4)2=x2+82,解得x=6,则AB=6.故答案为:6.【点睛】本题考查了翻折变换及勾股定理,熟知折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解答此题的关键.23.【解析】【分析】将化简后代入ab即可【详解】解:∵∴故答案为:【点睛】本题考查了二次根式的乘除法法则的应用解题的关键是将化简变形本题属于中等题型解析:3 10 ab【解析】【分析】化简后,代入a,b即可.【详解】====∵2a=,3b=,∴3 0540 .1=ab故答案为:310 ab.【点睛】本题考查了二次根式的乘除法法则的应用,解题的关键是将0.54化简变形,本题属于中等题型.24.(-53)(53)(3−3)【解析】【分析】作出图形分ABBCAC为对角线三种情况进行求解【详解】如图所示①AC为对角线时AB=5∴点D的坐标为(-53)②BC为对角线时AB=5∴点D的坐标为(53解析:(-5,3)、(5,3)、(3,−3)【解析】【分析】作出图形,分AB、BC、AC为对角线三种情况进行求解.【详解】如图所示,①AC为对角线时,AB=5,∴点D的坐标为(-5,3),②BC为对角线时,AB=5,∴点D的坐标为(5,3),③AB为对角线时,C平移至A的方式为向左平移1个单位,向下平移3个单位,∴点B 向左平移1个单位,向下平移3个单位得到点D的坐标为(3,−3),综上所述,点D的坐标是(-5,3)、(5,3)、(3,−3).故答案为:(-5,3)、(5,3)、(3,−3).【点睛】本题考查了坐标与图形的性质,平行四边形的判定,根据题意作出图形,注意要分情况进行讨论.25.4【解析】【分析】根据矩形的性质可得阴影部分的面积等于矩形面积的一半即可求得结果【详解】由图可知阴影部分的面积故答案为:4考点:本题考查的是矩形的性质点评:解答本题的关键是根据矩形的性质得到△DOE 解析:4【解析】【分析】根据矩形的性质可得阴影部分的面积等于矩形面积的一半,即可求得结果.【详解】由图可知,阴影部分的面积1424 2=⨯⨯=故答案为:4考点:本题考查的是矩形的性质点评:解答本题的关键是根据矩形的性质得到△DOE的面积等于△BOF的面积,从而可以判断阴影部分的面积等于矩形面积的一半.三、解答题26.(1)证明见解析;(2)18.【解析】【分析】【详解】解:(1)∵四边形ABCD是菱形,∴AB∥CD,AC⊥BD,∴AE∥CD,∠AOB=90°,∵DE⊥BD,即∠EDB=90°,∴∠AOB=∠EDB,∴DE∥AC,∴四边形ACDE是平行四边形;(2)解:∵四边形ABCD是菱形,AC=8,BD=6,∴AO=4,DO=3,AD=CD=5,∵四边形ACDE是平行四边形,∴AE=CD=5,DE=AC=8,∴△ADE的周长为AD+AE+DE=5+5+8=18.27.(1)见解析;(2)25【解析】【分析】(1)根据四边相等的四边形是菱形即可判断;(2)设AE=EC为x,利用勾股定理解答即可.【详解】(1)证明:∵四边形ABCD是矩形∴AD∥BC,∴∠DAC=∠ACB,∵EF垂直平分AC,∴AF=FC,AE=EC,∴∠FAC=∠FCA,∴∠FCA=∠ACB,∵∠FCA+∠CFE=90°,∠ACB+∠CEF=90°,∴∠CFE=∠CEF,∴CE=CF,∴AF=FC=CE=AE,∴四边形AECF是菱形.(2)设AE=EC为x,则BE=(8-x)在Rt△ABE中,AE2=AB2+BE2,即x2=62+(8-x)2,解得:x=254,所以四边形AECF的周长=254×4=25.【点睛】考查矩形的性质、线段的垂直平分线的性质、菱形的判定和性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题.28.1【解析】【分析】先利用平方差公式计算,然后把二次根式化为最简二次根式后合并即可.【详解】解:原式=43--=1【点睛】本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后合并同类二次根式即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.29.(1)<,<,<,<,<;(2<【解析】【分析】(1)首先用1除以每个数,求出商是多少;再比较出它们商的大小;然后根据商越大,则原来的数就越小,判断出它们的大小关系即可;(2)根据(1<【详解】=解:(1)=1>11;2==∵>∴22=2=>+22<2==2>22==>故答案为:<;<;<;<;<;(2<证明:因为22n =+ (24n =②②-①得(222n -=-因为1n ≥<n <所以(220->200n >>∴>【点睛】此题主要考查了实数大小的比较,二次根式的性质,以及不等式的性质,解答此题的关键是要明确:被除数一定时,商越大,则除数越小. 30.(1)20,60;(2)()2003s t t =≤≤,30或45;(3)198t =或236t =时,小亮和妈妈与爸爸相距10km【解析】【分析】(1)根据函数图象可以分别求得小亮和妈妈坐公交车的速度和爸爸自驾的速度; (2)根据题意可以求得相应的函数解析式;(3)根据函数图象和各段对应的函数解析式可以解答本题.【详解】解:(1)由图可得,小亮和妈妈坐公交车的速度为:60÷3=20km/h ,爸爸自驾的速度为:60×(2-1)=60km/h ,故答案为:20,60;(2)∵小亮和妈妈坐公交车的速度为20km/h ,∴小亮从家到度假村期间,他离家的距离s (km )与离家的时间(h )的关系式为:s=20t ,当1≤t≤2时,设小亮爸爸离家的距离s (km )与离家的时间(h )的关系式为:s=kt+b ,则0260k b k b +=⎧⎨+=⎩,得6060k b =⎧⎨=-⎩, 即当1≤t≤2时,小亮爸爸离家的距离s (km )与离家的时间(h )的关系式为:s=60t-60, 当2≤t≤3时,设小亮爸爸离家的距离s (km )与离家的时间(h )的关系式为:s=ct+d ,则 30260c d c d +=⎧⎨+=⎩,得60180c d =-⎧⎨=⎩, 即当2≤t≤3时,小亮爸爸离家的距离s (km )与离家的时间(h )的关系式为:s=-60t+180,令20t=60t-60,得t=1.5,此时,s=20×1.5=30, 20t=-60t+180,得t=2.25,此时s=20×2.25=45,故答案为:()2003s t t =≤≤,30或45;(3)解:由题意:第2次相遇时,小明离家45km ,离家的时间(h )为45÷20=94h , ①当爸爸在回家途中当94≤t≤3时,20t-(-60t+180)=10,解得,198t =, 即小明离家198h ,小亮和妈妈与爸爸相距10km ②当爸爸再次返回,3≤t≤4时,设小亮爸爸离家的距离s (km )与离家的时间(h )的关系式为:s=et+f ,则30460e f e f +=⎧⎨+=⎩,得60180e f =⎧⎨=-⎩, ∴当3≤t≤4时,小亮爸爸离家的距离s (km )与离家的时间(h )的关系式为: s=60t-180,令60-(60t-180)=10,得236t =, 即小明离家236h ,小亮和妈妈与爸爸相距10km , 综上:198t =或236t =时,小亮和妈妈与爸爸相距10km . 【点睛】本题考查函数图象以及常量与变量、函数关系式,利用函数图象获取正确信息是解题关键.。
成都七中育才学校 2019届八年级数学下册 《第17周 周周测》试卷【名校学案】

成都七中育才学校 2019届八年级数学下册 《第17周 周周测》试卷班级: 姓名: 学号:A 卷(100分) 一.选择题 (每小题3分,共30分)1.下列各式中从左到右的变形属于分解因式的是( )A.2(1)a a b a ab a +-=+-B.22(1)2a a a a --=-- C.2249(23)(23)a b a b a b -+=-++ D.121(2)x x x+=+ 2.在数轴上表示不等式360x --≥的解集,正确的是( ) A.B.C.D.3.如果把分式yx y+中的x 和y 的值都扩大到原来两倍,那么分式的值( ) A.扩大4倍 B.不变 C.缩小2倍 D.以上都不对4.()2()y x y x ---的因式分解的结果是( )A.()()1x y x y ---B.()()y x x y --C.()() 1y x y x ---D.()() 1y x y x --+5.某多边形的内角和是其外角和的3倍,则此多边形的边数是( ) A.8 B.7 C.6 D.56.下列运算正确的是( )A.y x y y x y --=--B.3232=++y x y xC.y x y x y x -=--22D.1112122-+=+--x x x x x 7.不等式114x x >-的非负整数解的个数是( ) A.1 B.2 C.3 D.无数个8.直线y kx b =+与坐标轴的两交点分别为()20A ,和()03B -,,则不等式30kx b ++≤ 的解为( ) A.0x ≤ B.0x ≥ C.2x ≥ D.2x ≤9.如图,四边形ABCD 是矩形,四边形AEFG 是正方形,点E 、G 分别在AB ,AD 上,连接FC ,过点E 做EH ∥FC 交BC 于点H.若∠BCF=30°,CD=4,CF=6,则正方形AEFG 的周长为( )A.1B.2C.3D.410.如图,在△ABC 中,BD 、CE 是△ABC 的中线,BD 与CE 相交于点O ,点F 、G 分别是BO 、CO 的中点,连接AO . 若AO=6cm ,BC=8cm ,则四边形DEFG 的周长是( )A.14cmB.18cmC.24cmD.28cm二. 填空题(每小题3分,共15分) 11. 化简211m m m m -÷-的结果是 . 12. 当x = 时,分式211x x -+的值为0. 13.若三角形的三条中位线长分别为2cm ,3cm ,4cm ,则原三角形的周长为 . 14.已知直线a x y 2+-=和32+-=a x y 的交点在第二象限,则a 的范围是 .15.若一个平行四边形一个内角的平分线把一条边分成2厘米和3厘米的两条线段,则该平 行四边形的周长是_________厘米. 三. 解答题(共55分)16.(每小题5分,共20分)(1)分解因式: 22)1(4)1(m m m --- (2)解分式方程:22513x x x x-+-= 0 (3)解不等式组()6152432112323x x x x +>+⎧⎪⎨-≥-⎪⎩ 并求出该不等式组整数解之和.17. (8分)先化简,再求值:)111(11222+---÷-+-m m m m m m ,其中3=m .18. (8分)已知关于x 、y 的方程组⎩⎨⎧=++=-a y x a y x 523的解满足0>>y x ,求a a --2的值.19.(9分)如果关于x 的方程22124x m x x +=--的解也是不等式组()122238xx x x -⎧>-⎪⎨⎪-≤-⎩的一个解,求m 的范围.20.(10分)如图,在ABCD □中,M 、N 分别是AD 、BC 的中点,90AND ∠=o ,连接CM 交DN 于点O 。
成都七中育才学校 2019届八年级数学下册 《第16周周练》试卷

成都七中育才学校 2019届八年级数学下册 《第16周周练》试卷A 卷(共100分)第Ⅰ卷(选择题,共30分)一、选择题(每小题3分,共30分,每小题均有四个选项,其中只有一项符合题目要求)1.下面四个汽车标志图案中是中心对称图形的是( )A. B. C. D.2.已知b a >,下列各式中,错误的是( )A.33->-b aB.b a ->-55C.b a -<-D.0>-b a3.如图,点A 、B 、C 、D 、O 都在方格纸的格点上,若△COD 是由△AOB 绕点O 按逆时针方向旋转而得,则旋转的角度为( )A.30°B.45°C.90°D.135°4.如图,△ABC 中,AC=AD=BD ,∠DAC=40°,则∠B 的度数是( )A.35°B.30°C.25°D.20°5.化简211m m mm -÷-的结果是( ) A.m B.m 1 C.m-1 D.11-m 6.把不等式组⎪⎩⎪⎨⎧≥->+123063x x 的解集表示在数轴上,正确的是( ) A. B. C. D.7.下列因式分解正确的是( )A.22)3(96--=-+-a a aB.)1(23-=-x x x xC.222)(y x y x +=+D.1)1(2222++=+-a a a8.关于y 的方程244222-+=-++y y y 的解正确的是( ) A.2-=y B.2=y C.2-=y 或2=y D.方程无解9.一个多边形的内角和是900°,则这个多边形的边数是( )A.4B.5C.6D.710.如图,四边形ABCD 是矩形,四边形AEFG 是正方形,点E 、G 分别在AB ,AD 上,连接FC ,过点E 做EH ∥FC 交BC 于点H.若∠BCF=30°,CD=4,CF=6,则正方形AEFG 的周长为( )A.1B.2C.3D.4第II 卷(非选择题,共70分)二、填空题(每小题4分,共16分)11.要使分式21-x 有意义,则x 的取值范围为 12.如图所示,在Rt △ABC 中,∠C=90°,BA 的垂直平分线交BC 于E ,垂足为D ,连接AE ,若AE 平分∠CAB ,则∠B 的度数为13.函数)0(≠+=k b kx y 的图象如图所示,则不等式0<+b kx 的解集为14.如图所示,△ABC 中,AH ⊥BC 于点H ,点E 、D 、F 分别是AB 、BC 、AC 的中点,HF=10cm,则ED 的长度是 cm.三、解答题(本大题共6个小题,共54分,解答过程写在答题卡上)15.(每小题5分,共15分)(1)分解因式:)2(9)2(42---y y x (2)解不等式3722x x -≤-,并求出它的正整数解. (3)计算:111122----÷-a a a a a a 16.(本小题满分6分)如图,每个小方格都是边长为1个单位长度的小正方形,△ABC 的是三个顶点都在格点上(1)将△ABC 向右平移3个单位长度,画出平移后对应的△111C B A 。
四川省成都市成都市第七中学初中学校2023-2024学年八年级下学期期中数学试题(解析版)
成都七中初中学校2024-2024学年下2025届期中质量检测数 学(满分150分,120分钟完成)A 卷(满分100分)一、选择题(每小题4分,共32分)1. 以下是回收、绿色包装、节水、低碳四个标志,其中是中心对称图形的是( )A. B. C. D.【答案】B【解析】【分析】根据中心对称图形的概念,中心对称图形是图形沿对称中心旋转180度后与原图重合.【详解】解:A 、不是中心对称图形,不符合题意;B 、是中心对称图形,符合题意;C 、不是中心对称图形,不符合题意;D 、不是中心对称图形,不符合题意;故选:B .【点睛】本题考查了中心对称图形,解题的关键是根据中心对称图形的概念,中心对称图形是图形沿对称中心旋转180度后与原图重合.2. 下列等式从左边到右边的变形,属于因式分解的是( )A. B. C. D. 【答案】C【解析】【分析】根据因式分解是把一个多项式化为几个整式的积的形式,可得答案.【详解】A 、,原结果有误,故此选项不符合题意;B 、是整式的乘法,不是因式分解,故此选项不符合题意;C 、把一个多项式化为几个整式的积的形式,故此选项符合题意;()ax ay a a x y ++=+()()2224x x x -+=-()22693m m m -+=-()()2211x y x y x y -+=+-+()1ax ay a a x y ++=++()()2224x x x -+=-()22693m m m -+=-D 、没把一个多项式化为几个整式积的形式,不是因式分解,故此选项不符合题意;故选:C .【点睛】此题考查因式分解的意义,解题关键在于因式分解是把一个多项式转化成几个整式积的形式.3. 若,则下列结论不正确的是( )A. B. C. D. 【答案】D【解析】【分析】根据不等式的性质逐项判断即得答案.【详解】解:A 、若,则,所以本选项变形正确,不符合题意;B 、若,则,所以本选项变形正确,不符合题意;C 、若,则,所以本选项变形正确,不符合题意;D 、若,则,所以本选项变形错误,符合题意.故选:D .【点睛】本题考查了不等式的性质,属于基础题型,熟记不等式的性质是解题的关键.4. 在数轴上表示不等式组的解集,正确的是( )A.B.C.D.【答案】B【解析】【分析】根据一元一次不等式解集在数轴上的表示方法进行判断即可.【详解】解:x ≥﹣2在数轴上表示时用实心点,而x <3则用空心点,的()()2211x y x y x y -+=+-+x y <22x y<22x y -<-22x y <22x y -<-x y <22x y <x y <22x y -<-x y <22x y <x y <22x y ->-23x x ≥-⎧⎨<⎩因此选项B 中的表示方法符合题意,故选B .【点睛】本题主要考查了在数轴上表示不等式的解集,解题的关键在于能够熟练掌握在数轴上表示等式的解集.5. 在平面直角坐标系中,点关于原点对称的点的坐标是( )A. B. C. D. 【答案】D【解析】【分析】本题考查了求关于原点对称的点的坐标,关于原点对称的两点,其横、纵坐标均互为相反数,据此即可求解.【详解】解:∵关于原点对称的两点,其横、纵坐标均互为相反数,∴关于原点对称的点的坐标是 故选:D .6. 三条公路将A ,B ,C 三个村庄连成一个如图的三角形区域,如果在这个区域内修建一个集贸市场,要使集贸市场到三条公路的距离相等,那么这个集贸市场应建的位置是( )A. 三条高线的交点B. 三条中线的交点C. 三条角平分线的交点D. 三边垂直平分线的交点【答案】C【解析】【分析】本题主要考查了角平分线上的点到角的两边的距离相等的性质.根据角平分线上的点到角的两边的距离相等解答即可.【详解】解:在这个区域内修建一个集贸市场,要使集贸市场到三条公路的距离相等,根据角平分线的性质,集贸市场应建在、、的角平分线的交点处.故选:C .7. 若二次三项式可分解为,则的值为( )A. 1B. 2C. -2D. -1()3,2()2,3--()3,2()3,2-()3,2--()3,2()3,2--A ∠B ∠C ∠26x mx +-()()32x x -+m【答案】D【解析】【分析】先根据多项式乘以多项式法则进行计算,再根据已知条件得出答案即可.【详解】解:(x ﹣3)(x +2)=x 2+2x ﹣3x ﹣6=x 2﹣x ﹣6,∵二次三项式x 2+mx ﹣6可分解为(x ﹣3)(x +2),∴m =﹣1,故选:D .【点睛】本题考查了多项式乘以多项式法则和分解因式,注意:分解因式的方法有:提取公因式法,公式法,十字相乘法,分组分解法等.8. 直线与直线在同一平面直角坐标系中的位置关系如图所示,则关于的不等式的解集为()A. B. C. D. 【答案】A【解析】【分析】结合函数图象,写出直线在直线上方所对应的自变量的范围即可.【详解】解∶直线与直线的交点的横坐标为2,当时,,关于的不等式的解集为.故选:A .【点睛】本题考查了一次函数与一元一次不等式,熟练掌握图象法解不等式,是解题的关键.二、填空题(每小题4分,共20分)111:l y k x =222:l y k x b =+x 12k x k x b >+2x >2x <3x >3x <1l 2l 111:l y k x =222:l y k x b =+∴2x >12y y >∴x 12k x k x b >+2x >9. 分解因式: _______________.【答案】【解析】【分析】先提取公因数m ,然后再运用平方差公式因式分解即可;灵活运用提取公因式法和公式法因式分解成为解答本题的关键.【详解】解:.故答案为.10. 次知识竞赛中共20道题,对于每一道题,答对了得10分,答错了或不答扣5分,选手至少要答对________道题,其得分才不低于95分.【答案】13【解析】【分析】可设答对x 道题,则答错或不答的题目就有(20-x )道,再根据得分才会不少于95分,列出不等式,解出x 的取值即可.【详解】解:设答对x 道,则答错或不答的题目就有(20-x )道.即10x -5(20-x )≥95去括号:10x -100+5x ≥95∴15x ≥195x ≥13因此选手至少要答对13道.故答案为:13.【点睛】本题考查的是一元一次不等式的运用,解此类题目时常常要设出未知数再根据题意列出不等式解题即可.11. 如图,一块长方形草坪的长为5米,宽为3米,在草坪中间,有一条处处为宽的弯曲小路,则这块草地的面积为_____.【答案】【解析】【分析】本题考查了平移的实际应用,有理数的运算,根据草地的面积长方形草坪的面积弯曲小路的面积即可求解.34m m -=()()22m m m +-()()()324422m m m m m m m -=-=+-()()22m m m +-1m 2m 12=-【详解】解:这块草地的面积为:,故答案为:.12. 如图,在△中,,的平分线交于,若,,则为_____.【答案】【解析】【分析】本题考查了角平分线性质定理:角平分线上的点到角两边的距离相等,作,根据求出,然后根据角平分线的性质定理即可求解.【详解】解:作,如图所示:则,∵,,∴∴∵平分,∴故答案为:.的533112⨯-⨯=2m 12ABC 90C ∠=︒A ∠BC D 222cm ABD S = 10cm AB =CD cm 225DE AB ⊥12ABD S AB DE =⨯⨯ DE DE AB ⊥12ABD S AB DE =⨯⨯ 222cm ABD S = 10cm AB =122102DE =⨯⨯22cm 5DE =AD CAB ∠90ACD AED ∠=∠=︒22cm 5CD DE ==22513. 如图,在中,,分别以点A 和点C为圆心,大于的长为半径画弧,两弧相交于点M ,N ,作直线,交于点D ,连接,则的度数为________.【答案】##度【解析】【分析】本题主要考查了三角形内角和定理,等边对等角,线段垂直平分线的性质和尺规作图,先由三角形内角和为180度求出,由作图方法可知垂直平分,则,可得,则.【详解】解:∵在中,,∴,由作图方法可知垂直平分,∴,∴,∴,故答案为:.三、解答题(共48分)14. 因式分解:(1)(2)【答案】(1)(2)【解析】【分析】本题考查因式分解,熟练掌握提取公因式法和公式法是解题的关键.(1)先提取公因式y ,再利用完全平方公式因式分解即可;(2)利用平方差公式和完全平方公式进行因式分解即可.ABC 7030B C ∠=︒∠=︒,12AC MN BC AD BAD ∠50︒5080BAC ∠=︒MN AC AD CD =30DAC C ∠=∠=︒50BAD BAC DAC =-=︒∠∠∠ABC 7030B C ∠=︒∠=︒,18080BAC C B ∠=︒-∠-∠=︒MN AC AD CD =30DAC C ∠=∠=︒50BAD BAC DAC =-=︒∠∠∠50︒2232x y xy y -+()22214y y +-()2-y x y ()()2211y y +-【小问1详解】解:==;【小问2详解】解:==.15. 解不等式(组)(1)(2)【答案】(1)(2)【解析】【分析】本题考查的是解一元一次不等式(组),正确的计算是解题关键.(1)去括号、移项、合并同类项即可求解;(2)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集.【小问1详解】解:,,【小问2详解】解:解①得:;解②得:;∴原不等式组的解集为:16. 如图,在平面直角坐标系中,每个小方格都是边长为1个单位的正方形,的顶点均在格点上,2232x y xy y -+()222y x xy y-+()2-y x y ()22214y y +-()()221221y y y y ++-+()()2211y y +-()()51332x x -≤--()512125131x x x x +⎧-≤⎪⎨⎪-<+⎩①②2x ≥-32x -≤<55336x x -≤-+24x -≤2x ≥-3x ≥-2x <32x -≤<ABC ∆点B 的坐标为(1,0).(1)画出向左平移4个单位所得的;(2)画出将绕点B 按顺时针旋转90°所得的(点A 、C 分别对应点A 2、C 2);(3)线段 的长度为 .【答案】(1)见解析(2)见解析(3【解析】【分析】(1)根据平移变换的性质分别作出A ,B ,C 的对应点A 1,B 1,C 1即可.(2)根据旋转变换的性质分别作出A ,C 的对应点A 2,C 2即可.(3)利用勾股定理求解即可.【小问1详解】ABC ∆111A B C ∆ABC ∆222A B C ∆12B C如图,即为所求.【小问2详解】如图,即为所求.小问3详解】线段,.【点睛】本题考查旋转变换,解题的关键是熟练掌握旋转变换的性质,正确作出图形.17. 如图,在平面直角坐标系中,,直线交轴于,过点A 作交轴于点D .(1)求直线和直线的关系式;(2)点M 在直线上,且与的面积相等,求点M 的坐标.【答案】(1)直线的解析式为:;直线的解析式为: 【111A B C ∆222A B C ∆12B C =(3,0),(1,4)A B -BC x ()4,0AD BC ∥y BC AD AD ABM ABO AD 443y x =--BC 41633y x =-+(2)或【解析】【分析】本题考查了一次函数的解析式求解、平行线间的距离处处相等等知识点,掌握待定系数法是解题关键.(1)设直线的解析式为:,将两点代入即可求解;设直线的解析式为:,将点代入即可求解;(2)求出直线的解析式,过点作的平行线,则点M 是直线与直线的交点,据此即可求解;【小问1详解】解:设直线的解析式为:,则,解得:,∴直线的解析式为:,∵∴设直线的解析式为:,则,解得:∴直线的解析式为:,【小问2详解】解:如图所示:过点作的平行线,1212,77⎛⎫-- ⎪⎝⎭3012,77⎛⎫- ⎪⎝⎭BC y kx b =+,B C AD 43y x b '=-+A AB O AB l AD l BC y kx b =+440k b k b +=⎧⎨+=⎩16343b k ⎧=⎪⎪⎨⎪=-⎪⎩BC 41633y x =-+AD BC∥AD 43y x b '=-+()4033b =-⨯+'-4b '=-AD 443y x =--O AB l设直线的解析式为:,则,解得:,∴直线的解析式为:,则直线的解析式为:,∵点M 在直线上,且与的面积相等,∴点M 是直线与直线的交点则,解得:∴点关于点的对称点为:综上所述:点M 的坐标为或18. (1)如图1,在四边形中,,,连接,探究线段,,之间的数量关系.小芳同学探究此问题的思路是:过点D 作,交延长线于点E ,从而得出结论:,请用上述方法证明:;(2)如图2,在四边形中,,,若,,求AB y mx n =+304m n m n -+=⎧⎨+=⎩13m n =⎧⎨=⎩AB 3y x =+l y x =AD ABM ABO AD l 443y x y x =⎧⎪⎨=--⎪⎩127127x y ⎧=-⎪⎪⎨⎪=-⎪⎩1212,77M ⎛⎫-- ⎪⎝⎭1212,77M ⎛⎫-- ⎪⎝⎭()3,0A -3012,77M ⎛'⎫- ⎪⎝⎭1212,77⎛⎫-- ⎪⎝⎭3012,77⎛⎫- ⎪⎝⎭ACBD 90ACB ADB ∠=∠=︒AD BD =CD AC BC CD DE CD ⊥CA AC BC +=AC BC +=ACDB 90ACB ADB ∠=∠=︒AD BD =3AC =5BC =CD的长;(3)如图3,在中,,,点D 为外一点,且,点P ,Q 分别为的中点,连接,求的长.【答案】(1)见解析;(2;(3)【解析】【分析】(1)证得是等腰直角三角形即可求证;(2)作,证即可求解;(3)连接作,结合(1)得证明过程可得,推出,即可求解;【详解】(1)证明:由题意得:∴∵∴∵∴∴∴是等腰直角三角形∴(2)解:作,如图所示:ABC 90ACB ∠=︒6AC BC ==ABC 63CD AD ==,AB AD ,PQ PQ PQ =AED BCD ≌△△CDE DF CD ⊥DAC DBF ≌CP CQ 、,PM PQ ⊥AQP CMP V V ≌AQ CQ +=90,90CDE ADC ADE ADB ADC BDC ∠=∠+∠=︒∠=∠+∠=︒ADE BDC∠=∠90AED DCE BCD DCE ∠+∠=∠+∠=︒AED BCD∠=∠AD BD=AED BCD≌△△,DE CD AE BC==CDE AC BC AC AE CE +=+==DF CD ⊥由题意得:∴∵,∴∵∴∴∴是等腰直角三角形∵,,∴,∴(3)解:连接作,如图所示:∵,,点P 为的中点,∴∵点Q 为的中点,∴由(1)可得:∴∴是等腰直角三角形∴90,90CDF ADC ADF ADB ADF BDF ∠=∠+∠=︒∠=∠+∠=︒ADC BDF∠=∠90DAC AOC DBF BOD ∠+∠=∠+∠=︒AOC BOD∠=∠DAC DBF∠=∠AD BD=DAC DBF≌,FD CD AC BF==CDF 3AC =5BC =3BF AC ==2CF BC BF =-=CD ==CP CQ 、,PM PQ ⊥90ACB ∠=︒AC BC =AB ,90PA PC APC =∠=︒6AC CD ==,AD 90AQC ∠=︒AQP CMPV V ≌,AQ CM QP MP==QPMAQ CQ CM CQ QM +=+==∵∴∴解得:【点睛】本题考查了全等三角形的常见模型—旋转模型,涉及了等腰直角三角形的判定与性质、勾股定理等知识点,正确作出辅助线,学会举一反三是解题关键.B 卷(共50分)一、选择题(每小题4分,共20分)19. 已知,,那么_______.【答案】【解析】【分析】本题考查了求代数式的值,将变形为,再代入值进行计算即可,采用整体代入的思想是解此题的关键.【详解】解:,,,故答案为:.20. 如图,在△ABC 中,AB =AC ,BD 平分∠ABC ,交AC 于点D .若BD =BC ,则∠A =________度.【答案】36【解析】【详解】分析:题中相等的边较多,且都是在同一个三角形中,因为求“角”的度数,将“等边”转化为有关的“等角”,充分运用“等边对等角”这一性质,再联系三角形内角和为180°求解此题.13,622AQ AD CD ===CQ ==32=PQ =3m n +=2mn =22m n mn +=622m n mn +()mn m n +3m n += 2mn =()22236m n mn mn m n ∴+=+=⨯=6详解:∵BD=BC , ∴∠C=∠BDC ,∵AB=AC , ∴∠ABC=∠C ,∵BD 平分∠ABC , ∴∠ABD=∠CBD , 又∵∠BDC=∠A+∠ABD ,∴∠C=∠BDC=2∠A , 又∵∠A+∠ABC+∠C=180°, ∴∠A+2∠C=180°把∠C=2∠A 代入等式,得∠A+2×2∠A=180°,解得∠A=36°.点睛:本题反复运用了“等边对等角”,将已知的等边转化为有关角的关系,并联系三角形的内角和及三角形一个外角等于与它不相邻的两个内角的和的性质求解有关角的度数问题.21. 关于x 的不等式组恰好有3个整数解,则a 的取值范围是______.【答案】【解析】【分析】先求出不等式组的解集,根据不等式组恰好有3个整数解,列式求解即可.【详解】解:,由①,得:,由②,得:,∵不等式组恰好有3个整数解,∴不等式组的解集为:,整数解为:,∴,∴;故答案为:.【点睛】本题考查根据不等式组的解集求参数的取值范围.正确的求出不等式组的解集,是解题的关键.22. 已知点位于第二象限,并且,,均为整数,则满足条件的点的个数有_________个.【答案】110【解析】【分析】根据第二象限内的点的横坐标小于零,纵坐标大于零,可得不等式,根据解不等式,即可得出答案.【详解】解:由点在第二象限,得,,6302x x a -<⎧⎨≤⎩1012a ≤<6302x x a -<⎧⎨≤⎩①②2x >2a x ≤22a x <≤3,4,5562a ≤<1012a ≤<1012a ≤<(),P ab 223a b >-a b P (,)P a b a<00b >又因为,,解得:,,,,均为整数,;当时,,则取不到整数,有0种情况;当时,,则,有2种情况;当时,,则,有4种情况;当时,,则,有6种情况;当时,,则,有8种情况;当时,,则,有10种情况;当时,,则,有12种情况;当时,,则,有14种情况;当时,,则,有16种情况;当时,,则,有18种情况;当时,,则,有20种情况;故共有:,则满足条件的点的个数有110,故答案为:110.223a b >-2230b ∴-<1112b <0b > 10112b <<a b 1,2,3,4,5,6,7,8,9,10,11b ∴=11b =10a -<<10b =30a -<<2,1a =--9b =50a -<<4,3,2,1a =----8b =70a -<<6,5,4,3,2,1a =------7b =90a -<<8,7,6,5,4,3,2,1a =--------6b =110a -<<10,98,7,6,5,4,3,2,1a =----------5b =130a -<<12,11,10,98,7,6,5,4,3,2,1a =------------4b =150a -<<14,13,12,11,10,98,7,6,5,4,3,2,1a =--------------3b =170a -<<16,15,14,13,12,11,10,98,7,6,5,4,3,2,1a =----------------2b =190a -<<18,17,16,15,14,13,12,11,10,98,7,6,5,4,3,2,1a =------------------1b =210a -<<20,19,18,17,16,15,14,13,12,11,10,98,7,6,5,4,3,2,1a =--------------------02468101214161820110++++++++++=P【点睛】此题考查了解一元一次不等式,以及点的坐标,解题的关键是熟练掌握不等式的解法.23. 如图,在矩形中,,点E 为上一点,且,点F 为边上一动点,连接,过点A 作于点G ,连接,则最小值为______,连接,将绕点E 顺时针旋转,得到,在点F 运动的过程中,的最小值为_______.【答案】①. ## ②. ##【解析】【分析】如图所示,取中点O ,连接,则由直角三角形的性质可得,再由矩形的性质和勾股定理得到,再由,可得当三点共线,且点G 在线段上时,有最小值,最小值为;如图所示,将线段绕点E 顺时针旋转得到,连接,证明,得到;求出,,进而推出,则H 在上时,有最小值,最小值为.【详解】解:如图所示,取中点O ,连接,∵,∴,∵点O 为中点,∴,∵四边形是矩形,∴,∴,∵,的ABCD 46AB BC ==,BC 2BE =AD BF AG BF ⊥CG CG EG EG 45︒EHCH 2-2-+2-2-+AB OG OC ,122OG OB AB ===OC ==CG OC OG ≤-O C G 、、OC CG 2-OE 45︒ME MH MC ,()SAS OEG MEH ≌2MH OG ==45OEB ∠=︒ME OE ==90MEC ∠=︒CM ==CM CH 2-AB OG OC ,AG BF ⊥90AGB ∠=︒AB 122OG OB AB ===ABCD 90ABC ∠=︒OC ==CG OC OG ≤-∴当三点共线,且点G 在线段上时,有最小值,最小值为;如图所示,将线段绕点E 顺时针旋转得到,连接,由旋转的性质可得,∴,∴,∴;∵,∴,,∴,∴,∵,∴同理可得当M 、H 、C 三点共线,且点H 在上时,有最小值,最小值为,故答案为:;.【点睛】本题主要考查了矩形的性质,全等三角形的性质与判定,旋转的性质,勾股定理,直角三角形的性质,等腰直角三角形的性质等等,正确作出辅助线构造全等三角形和直角三角形是解题的关键.二、解答题(共30分)24. 为保护环境,我市某公交公司计划购买型和型两种环保节能公交车共10辆.若购买型公交车1辆,型公交车2辆,共需400万元;若购买型公交车3辆,型公交车2辆,共需600万元.(1)求购买型和型公交车每辆各需多少万元.(2)经测算,在两种公交车均购买的前提下,该公司购买公交车的总费用不得超过1150万元,则该公司有哪几种购车方案?(3)在(2)的条件下,哪种购车方案总费用最少?最少总费用是多少万元?【答案】(1)购买型公交车每辆需100万元,购买型公交车每辆需150万元O C G 、、OC CG 2OE 45︒ME MH MC ,45EO EM EG EH OEM GEH ====︒,,∠∠OEG MEH =∠∠()SAS OEG MEH ≌2MH OG ==290OB BE OBE ===︒,∠45OEB ∠=︒ME OE ===BEM 90∠=︒90MEC ∠=︒4CE BC BE =-=CM ==CM CH 2-22-A B A B A B A B A B(2)三种购车方案:购买型公交车7辆,购买型公交车3辆;购买型公交车8辆,购买型公交车2辆;购买型公交车9辆,购买型公交车1辆(3)购买型公交车9辆,购买型公交车1辆总费用最少,最少总费用是1050万元【解析】【分析】(1)设购买型公交车每辆需万元,购买型公交车每辆需万元,根据题意列二元一次方程组并求解即可;(2)设购买型公交车辆,则购买型公交车辆,根据题意“总费用不得超过1150万元”可得,求解并讨论即可;(3)分别求出各种购车方案总费用,即可作出判断.【小问1详解】解:设购买型公交车每辆需万元,购买型公交车每辆需万元,根据题意,可得,解得,所以,购买型公交车每辆需100万元,购买型公交车每辆需150万元;【小问2详解】在两种公交车均购买的前提下,可设购买型公交车辆,则购买型公交车辆,则有,解得,又且m 为整数,所以,8,9,则,2,1,所以,可有三种方案:购买型公交车7辆,购买型公交车3辆;购买型公交车8辆,购买型公交车2辆;购买型公交车9辆,购买型公交车1辆;【小问3详解】方案①:购买型公交车7辆,购买型公交车3辆,总费用万元;方案②:购买型公交车8辆,购买型公交车2辆,A B A B A B A B A x B y A m B (10)m -100150(10)1150m m +-≤A x B y 240032600x y x y +=⎧⎨+=⎩100150x y =⎧⎨=⎩A B A m B (10)m -100150(10)1150m m +-≤7m ≥10m <7m =(10)3m -=A B A B A B A B 100715031150⨯+⨯=A B总费用万元;方案③:购买型公交车9辆,购买型公交车1辆,总费用万元.所以,购买型公交车9辆,购买型公交车1辆总费用最少,最少总费用是1050万元.【点睛】本题主要考查了二元一次方程组以及一元一次不等式的应用,理解题意,弄清数量关系是解题关键.25. 如图,点P 为正方形的边上的一个动点,连接,点D 与点E 关于直线对称,连接,射线与射线交于点,连接.(1)当时,求的度数;(2)i )点P 在运动过程中,的度数是否发生变化?如果不变,请求出它的度数,如果改变,请说明理由;ii )求证:;(3)若P 从点C 运动到点B 时,求点F 运动路径的长度.【答案】(1)(2)i )不变化,且为;ii )证明见详解(3)【解析】【分析】(1)先根据正方形的性质得到,再根据等腰三角形的性质及三角形内角和定理求得,即可求解;(2)i :设,则,再根据等腰三角形的性质及三角形内角和定理求得,最后由三角形内角和得;ii :过点A 作于点M ,过点C 作于点N ,先证明“一线三等角”,100815021100⨯+⨯=A B 100915011050⨯+⨯=A B ABCD BC AP AP AE EB AP F CF 65DAF ∠=︒AFE ∠AFE ∠BE =AB =45︒45︒32π25PAB ∠=︒70E ABE ∠=∠=︒BAP x ∠=902BAE x ∠=︒-45E ABE x ∠=∠=︒+45AFE ∠=︒AM BF ⊥CN BF ⊥AMB BNC ≌△△再根据全等三角形的性质及勾股定理即可求证;(3)连接,取中点为点O ,连接,,证明出,继而可得点F 在以点O 为圆心,为半径的弧上运动,即路径为,再由弧长公式即可求解.【小问1详解】解:点D 与点E 关于直线对称,,,∵四边形为正方形,∴,,∴,,,,;【小问2详解】i 解:不变化,,设,,线段与关于直线对称,,,,,;ii 证明:如图2,过点A 作于点M ,过点C 作于点N ,∴,AC AC OF OB 90AFC ∠=︒OF BCAP 65DAP EAP ∴∠=∠=︒AD AE =ABCD 90DAB ∠=︒AB AD =906525PAB ∠=︒-︒=︒652540BAE ∴∠=︒-︒=︒AB AE =18040702E ABE ︒-︒∴∠=∠==︒180706545AFE ∴∠=︒-︒-︒=︒45AFE ∠=︒BAP x ∠=90DAP x ∴∠=︒- AE AD AP 90DAP EAP x ∴∠=∠=︒-902BAE x ∴∠=︒-AB AE = ()180902452x E ABE x ︒-︒-∴∠=∠==︒+180(90)(45)45AFE x x ∴∠=︒-︒--︒+=︒AM BF ⊥CN BF ⊥90AMB N ∠=∠=︒四边形是正方形,∴,∴,∴,∴,∴,∵,∴为等腰直角三角形,∴,∴,∴,∴,∵,∴同(1)可得,∵,∴,设,则,,∴;【小问3详解】ABCD ,90BC AB ABC =∠=︒139023∠+∠=︒=∠+∠12∠=∠AMB BNC ≌△△,AM BN BM CN ==45,90AFE AMF Ð=°Ð=°AMF AM MF =MF BN =BM NF =CN NF =90N ∠=︒CF =,AB AE AM BE =⊥BM M E =BM ME CN NF x ====CF =2BE x=BE =解:如图3,连接,取中点为点O ,连接,,由ii 得,而,∴,∵O 为中点,∴,∴点F 在以点O 为圆心,为半径的弧上运动,∵点P 从点C 运动到点B 时,∴点F 运动路径为,∵四边形为正方形,∴,,∵,∴同上可得,∴点P 从点C 运动到点B 时,点F运动路径长度为.【点睛】本题是四边形综合题,考查了正方形的性质,等腰三角形的性质,三角形内角和定理,轴对称的性质,全等三角形的判定和性质,弧长公式,正确添加辅助线,灵活运用这些性质解决问题是本题的关键.26. 如图,在平面直角坐标系中,直线与轴交于点,直线与轴交于AC AC OF OB 45CFN ∠=︒45AFE ∠=︒90AFC ∠=︒AC OF OA OC ==OF BCABCD OC OB =90COB ∠=︒AB =3OB BC ==90331802ππ⨯=17:424l y x =-+y A 23:64l y x =-y点,与直线交于点.(1)求点C 的坐标及的长;(2)直线分别交直线,于点,,直线与直线,交于点,,若,求的值;(3)在(2)的条件下,将△沿射线的方向以每秒个单位的长度匀速平移,设移动时间为秒.在△移动的过程中,点到直线,的距离相等,请求出此时点的坐标.【答案】(1), (2)(3)或【解析】【分析】(1)根据解析式分别求出两点的坐标即可;(2)由题意得,进一步可得,,即可求解;(3)由题意得,可知点在直线上运动;根据题意可推出点在的角平分线上,结合进而可得,据此即可求解;【小问1详解】解:,令,则;∴B 1l C AC ()0x m m =<1l 2l M N 4y =-MN 2l E F 98ME EF =m NEF BC 5t ()0t >NEF E 1l 2l E 486,55C ⎛⎫⎪⎝⎭10AC =6-26259125,A C 73,4,,6244M m m N m m ⎛⎫⎛⎫-+- ⎪ ⎪⎝⎭⎝⎭(),4E m -8,43F ⎛⎫- ⎪⎝⎭()64,43E t t -+-+E 3142y x =+E ACB ∠2e l ∥DC DE =17:424l y x =-+0x =4y =()0,4A由得:∴【小问2详解】解:∵直线分别交直线,于点,,∴∵直线与直线,交于点,,∴令,解得:∴∴∵,∴,解得:【小问3详解】解:由(2)得: 由可知:当△沿射线的方向以每秒个单位的长度匀速平移,秒后,,7424364y x y x ⎧=-+⎪⎪⎨⎪=-⎪⎩48565x y ⎧=⎪⎪⎨⎪=⎪⎩486,55C ⎛⎫ ⎪⎝⎭10AC ==()0x m m =<1l 2l M N 73,4,,6244M m m N m m ⎛⎫⎛⎫-+- ⎪ ⎪⎝⎭⎝⎭4y =-MN 2l E F (),4E m -3644x -=-83x =8,43F ⎛⎫- ⎪⎝⎭()778448,24243ME m m EF m =-+--=-+=-98ME EF =88378924m m -+=-6m =-()6,4E --23:64l y x =-NEF BC 5t ()64,43E t t -+-+∵故点在直线:上运动易知:∵点到直线,的距离相等,∴点在角平分线上∴∵∴∴∴由得:∴解得:或的()31436442t t -+=⨯-++E e 3142y x =+2e l ∥E 1l 2l E ACB ∠ACE BCE∠=∠2e l ∥DCE BCE∠=∠DCE DEC∠=∠DC DE=31427424y x y x ⎧=+⎪⎪⎨⎪=-+⎪⎩842515150x y ⎧=⎪⎪⎨⎪=⎪⎩151,842550D ⎛⎫ ⎪⎝⎭=2625t =9125【点睛】本题考查了一次函数与几何综合问题,涉及了一次函数的解析式求解、角平分线的判定定理、勾股定理等知识点,综合性较强.。
成都七中育才学校 2019 届下期入学测试初三语文试卷
七中育才初2019届语文2月入学检测命题: A:曹源 B:李琳懿审题:李琳懿试卷说明:全卷分A卷和B卷,A卷满分100分,B 卷满分50分;完成时间120分钟。
A卷分第I卷和第II卷,第I卷为选择题,第II卷为其它类型的题。
A卷(共100分)第|卷(选择题共24分)一、基础知识(每小题3分,共12分)1.下列字词中注音无误的一项是()A. 干瘪.(biě)俄顷.(qǐn)拾掇.(duo)蹑.手蹑脚(niè)B.胆怯.(qiè)睥睨.(nì)踌.(chòu)躇摩肩接踵.(zhǒng)C.国殇.(shāng)犀.利(xī)咀嚼.(jué)衣衫褴褛.( lǔ )D.瘦削.(xuē)旌.(jīng)旗脚镣.(liào)气喘吁.吁(yū)2.下列句子中书写正确的一项是()A.我要看那滚滚的波涛,我要听那鞺鞺鞳鞳的咆哓,我要飘流到那没有阴谋、没有污秽、没有自私自利的没有人的小岛上去呀!B.我是你簇新的理想,刚从神话的蛛网里挣脱;我是你雪被下古莲的胚芽;我是你挂着眼泪的笑蜗;我是新刷出的雪白的起跑线;是绯红的黎明正在喷勃。
C.孟实苦干了十年,有点积蓄不假,可是,他辛辛苦苦把个要关张的福聚德拾掇得名噪京师,就落了这名声,就太冤枉人了。
D.因有脚撩行步甚有限制,时而贮立睥睨,目中含有怒火。
3.下列句子中加点成语使用恰当的一项是()A.在西南地区遭遇了60年不遇的特大旱灾之际,小明一家人又是捐钱,又是捐物,真可谓取义成仁....。
B.掌握自然规律以前,人们往往认为沙漠里有魔鬼在作怪;但是掌握了科学知识以后,人们便可以把这种哗众取宠....的现象解释清楚。
C. 放学回到家,小明早已疲惫不堪,饥肠辘辘的他看到桌子上的面包,便囫囵吞枣地吃起来。
D.这时是阴天离下雨不远了,老人家按捺不住地拿起画笔,想象着淅淅沥沥的景象,渐渐地,纸上便出现了一个人拖泥带水的画面。
4.下列语句中没有语病的一项是()A. 从中国的简帛、埃及的莎草纸、欧洲的羊皮卷到今天的电子墨水屏,让人类的阅读载体不断演进,但人们对阅读的热爱,对精神世界的守望却从未改变。
成都七中育才学校初2019届八年级下期第7周周测数学试题(附答案)
成都七中育才学校初2019届八年级下期第7周周测数学试题班级____ ;姓名________ _ ;学号____A 组(100分)一、选择题(30分)1、在线段、等边三角形、平行四边形、圆中,是中心对称图形又是轴对称图形的有( ). A .1个 B.2个 C.3个 D.4个 2、函数y =)A .2x ≥-B .2x >-C .2x <-D .2x ≤-3 、分式28,9,12z yx xy z x x z y -+-的最简公分母是( ) A . 72xyz 2B . 108xyz C. 72xyz D. 96xyz 24、用分组分解法将x y xy x 332-+-分解因式,下列的分组方式中不恰当的是( ) A .)3()3(2xy y x x -+- B.)33()(2x y xy x -+- C. )33()(2y x xy x --- D.y x xy x 3)3(2+-- 5、 如果把分式yx x 23y2-中的x,y 都扩大3倍,那么分式的值( )A. 扩大3倍B. 不变C. 缩小3倍D. 扩大2倍 6、 若分式222)(+-x x 的值为0,则x 的值为( )A .2 B. -2 C .2或-2 D .2或37、把不等式组的解在数轴上表示出来,正确的是( )8、化简aba b a +-222的结果为( )A.a b a 2- B.a b a - C.a b a + D.ba ba +- 2010x x -≥⎧⎨+<⎩9 、 如果0<<b a ,那么不等式b ax <的解是( ) A 、a b x <B 、a b x >C 、a b x -<D 、ab x -> 10、如图,在正方形ABCD 中,E 为DC 边上的点,连结BE ,将△BCE 绕点C 顺时针方向旋转900得到△DCF ,连结EF ,若∠BEC=600,则∠EFD 的度数为( )A 、100B 、150C 、200D 、250 题号 1 2 3 4 5 6 7 8 9 10 答案二 填空(16分)11、当m ___________时,不等式8)2(<-x m 的解集为mx ->28。
成都七中育才学校2019届八年级数学下册 《第14周周练》试卷(含答案)
成都七中育才学校 2019届八年级数学下册 《第14周周练》试卷班级 学号 姓名A 卷(100分)一、选择题:(每小题3分,共30分)1.关于x 的一元二次方程()()0412222=-+-+-m x m x m 的一个根是0,则 m 的值是( )A. 2B. —2C. 2或者—2D.122.下列多项式中,能用完全平方公式分解因式的是( ) A .x 2﹣x +1 B .1﹣2xy +x 2y 2 C .m 2﹣2m ﹣1 D .3.分式的值为0,则x 的值是( ) A .x=±2 B .x ≠2 C .x=2 D .x=﹣24.直线与直线y 2=2x 在同一平面直角坐标系中的图象如图所示,则不等式y 1≤y 2的解集为( )A .x ≤﹣1B .x ≥﹣1C .x ≤﹣2D .x ≥﹣25.如图,△ABC 的周长为36cm ,DE 垂直平分边AC ,交BC 边于点E ,交AC 边于点D ,连接AE ,若AD=cm ,则△ABE 的周长是( )A .22cmB .20 cmC .21cmD .15cm6.如图,在四边形ABCD 中,对角线AC ,BD 交于点O ,下列选项不能得到四边形ABCD 是平行四边形的是( )A.AC=BD,OA=OC B.OB=OD,OA=OCC.AD=BC,AD∥BC D.△ABC≌△CDA7.下列各式变形正确的是()A.B.C.D.8.如图,点A、B、C、D都在方格纸的格点上,若△AOB绕点O按逆时针方向旋转到△COD的位置,则旋转的角度为()A.30°B.45°C.90°D.135°9.若二次三项式x2﹣mx﹣6可分解为(x﹣3)(x+n),则m的值为()A.﹣1 B.1 C.﹣2 D.210.已知:如图所示,在四边形ABCD中,E、F、G、H分别是AB、CD、AC、BD的中点,则关于四边形EGFH判断错误的是()A.可能是正方形B.一定是平行四边形C.可能是菱形D.可能是梯形题号 1 2 3 4 5 6 7 8 9 10 答案二、填空题:(每小题4分,共l6分)11.分解因式:a2y﹣4y=.12.如图,AD∥BC,∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P,作PE⊥AB于点E.若PE=2cm,则两平行线AD与BC间的距离为cm.13.若一个多边形的内角和是外角和的3倍,则该多边形是边形(填该多边形的边数).14.平行四边形ABCD的对角线AC、BD相交于点O,若平行四边形ABCD的面积为12,则△AOB的面积为.三、解答题:(本大题共5个大题,共54分)15.(每小题6分)(1)解不等式组:543(1)12125x xx x+<+⎧⎪--⎨≥⎪⎩(2)解方程:.16.当时,求的值.17.(8分)如图,在边长为1的小正方形组成的网格中,△ABC的顶点均在格点上,请按要求完成下列各题:(1)以直线BC为对称轴作△ABC的轴对称图形,得到△A1BC,再将△A1BC绕着点B逆时针旋转90°,得到△A2BC1,请依此画出△A1BC、△A2BC1;(2)求线段BC旋转到BC1过程中所扫过的面积(计算结果用π表示).18.(10分)对x,y定义一种新运算T,规定:T(x,y)=(其中a、b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)==b.(1)已知T(1,﹣1)=﹣2,T(4,2)=1.①求a,b的值;②若关于m的不等式组恰有4个整数解,求实数p的取值范围;(2)若T(x,y)=T(y,x)对任意实数x,y都成立(这里T(x,y)和T(y,x)均有意义),则a,b应满足怎样的关系式?19.(8分)某漆器厂接到制作480件漆器的订单,为了尽快完成任务,该厂实际每天制作的件数比原来每天多50%,结果提前10天完成任务.原来每天制作多少件?20.(10分)如图1,图2,正方形ABCD的边长为1,P是对角线BD上一动点,连接AP、CP,过P 作PN⊥AP交射线CD与点N.(1)求证:AP=CP.(2)①若点N在边CD上,如图1,判断△APN的形状,并说明理由;②若点N在边CD的延长线上,如图2,①中的结论还成立吗?(不需要证明).(3)若N为边CD的中点,求BP的长.一、填空题:(每小题4分,共12分)21.如图,折叠长方形的一边AD,使点D落在BC边上的F点处,若AB=8cm,BC=10cm,则EC长为.22.已知关于x、y的方程组的解满足x>0,y>0,实数a的取值范围是.23.在△ABC中,AB=AC,AB的垂直平分线与AC所在的直线相交所得的锐角为46°,则底角∠B的大小为.二、解答题:(8分)24.已知正方形ABCD,点F是射线DC上一动点(不与C、D重合).连接AF并延长交直线BC于点E,交BD于H,连接CH,过点C作CG⊥HC交AE于点G.(1)若点F在边CD上,如图1①证明:∠DAH=∠DCH②猜想△GFC的形状并说明理由.(2)取DF 中点M,连MG.若MG=2.5,正方形边长为4,求BE的长.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
成都七中育才学校2019届八(下)第十二周周测 班级_________姓名______________学号_____
A 卷(100分)
一.选择题(每小题3分,共30分)
1. 不等式x+3>0的解集在数轴上表示正确的是( )
2.下列电视台的台标,是中心对称图形的是( )
A .
B .
C .
D . 3.在21=0x x +、()211x x x +=+、20ax bx c -+=、2x x =中一元二次方程有( )个 A.1 B.2 C.3
D.4 4.()2()y x y x ---的因式分解的结果是( )
A.()()1x y x y ---
B.()()y x x y --
C.()() 1y x y x ---
D.()() 1y x y x --+
5.某多边形的内角和是其外角和的3倍,则此多边形的边数是( )
A.8
B.7
C.6
D.5
6.下列运算正确的是( )
A.y x y y x y --=--
B.3232=++y x y x
C.y x y x y x -=--22
D.1112122-+=+--x x x x x 7.关于x 的方程()27310m m x x ----=是一元二次方程,则m 的值为( )
A.3m =
B.3m =-
C.3m =±
D.3m ≠±
8.在四边形ABCD 中,AC BD =,EFGH 分别为AB 、BC 、CD 、DA 的中点,则四边形EFGH 的形状为( )
A.平行四边形
B.菱形
C.矩形
D.正方形
9.如图在矩形ABCD 中,对角线AC 、BD 交于点O ,OE BD ⊥交AB 于E ,若30ABD ∠=︒,6DE =,则矩形ABCD 的周长为( )
A.39+
B.339+
C.6318+
D.2318+
10.如图,已知正方形ABCD 的边长为2,以C 为圆心将线段BC 顺时针旋转60°至CP ,连接BP 、PD ,则PD 的长是( )
A.23-
B.743-
C.32-
D.843-
温馨提示:请将选择题答案填在以下表格中
题号
1 2 3 4 5 6 7 8 9 10 答案
3-03A . 3-03B . 3-03C .
3-03D .
二.填空题(每小题4分,共20分)
11. 若三角形的三条中位线长分别为2cm ,3cm ,4cm ,则原三角形的周长为 .
12. 如果分式23273
x x --的值为0,则x 的值应为 . 13. 已知直线a x y 2+-=和32+-=a x y 的交点在第二象限,则a 的范围
是 .
14.一个多边形的内角和是720°,那么这个多边形的对角线的条数
是 .
15.如图,正方形ABCD 中,25DAF ∠=︒,AF 交BD 于点E ,
那么BEC ∠等于_________.
三.解答题
16. (每题5分)因式分解:⑴ 1)2)(4(+++x x ⑵ 322318153ab b a b a +--
(3)解方程:
11122x x x -=+--
17.(8分)先化简,再求值:1
2)113(
2--÷--+x x x x x x ,其中23=x
18.(8分) 如图,矩形ABCD 中,AB =8,AD =6,点E 、F 分别在边CD 、AB 上.(12分)
(1)若DE =BF ,求证:四边形AFCE 是平行四边形;
(2)若四边形AFCE 是菱形,求菱形AFCE 的周长.
19.(9分) 如果关于x 的方程22124x m x x +=--的解也是不等式组()122238x x x x -⎧>-⎪⎨⎪-≤-⎩
的一个解,求m 的范围.
20.(10分) 如图,P 为正方形ABCD 的边BC 上一动点(P 不与B 、C 重合),连接AP ,过点B 作BQ AP ⊥交CD 于点Q ,将BQC ∆沿BQ 所在的直线对折得到'BQC ∆,延长'QC 交BA 的延长线于点M .
(1)试探究AP 与BQ 的数量关系,并证明你的结论;
(2)当3AB =,2BP PC =,求QM 的长;
(3)当BP m =,PC n =时,求AM 的长.
B 卷
一.填空题(每小题4分,共12分,请写出主要过程,否则不得分)
21. 幼儿园把新购进的一批玩具分给小朋友,若每人3件,那么还剩59件;若每人5件,那么最后一个小朋友分到玩具,但不足6件,这批玩具共有______件
22.如果要使关于x 的方程
3123-=+--x m m x x 有唯一解,那么m 的取值范围__________.
23.如图直线l 经过正方形ABCD 的顶点A ,分别过此正方形的
顶点B 、D 作l BE ⊥于点E 、l DF ⊥于点F 。
以正方形对角
线的交点O 为端点,引两条相互垂直的射线分别与AD 、CD 交
于G 、H 两点,若2=EF ,2
1=
∆ABE S ,则线段GH 长度的最小值是___________.
二.解答题(8分)
24. 如图,已知一次函数633+=x y 的图象分别交x 轴、y 轴于A 、B 两点,点P 从点A 出发沿AO 方向以每秒3个单位长度的速度向点O 匀速运动,同时点Q 从点B 出发沿BA 方向以每秒2个单位长度向点A 匀速运动,当其中一点到达终点时,另一点也停止运动,设运动时间为t 秒,过点Q 作y QC ⊥轴,连接PQ 、PC .
(1)点A 的从标为 ,点B 的坐标为 ,=AB ;
(2)四边形APCQ 能够成为菱形吗?如果能,求出相应的t 值;如果不能,说明理由.
(3)若点)2,0(D ,点N 在x 轴上,直线AB 上是否存在点M ,使以M 、N 、B 、D 为顶点的四边形是平行四边形?若存在,请直接写出M 点的坐标;若不存在,请说明理由.。
