2019年浙江三位一体招生考试6所高校真题
2019年6月浙江省学业水平真题考试卷word版附答案

2019年6月浙江省普通高中学业水平考试选择题部分一、选择题(本题共18小题,每小题2分,共36分。
每小题列出的四个备选项中只有一个是符合题目要求的,不选、多选、错选均不得分) 1.在国际单位制中,速度单位的符号是A .m/sB .mC .kgD .s2.电容器的符号是3.如图所示,真空玻璃管内的鸡毛、铜钱由静止开始自由下落。
能表示铜钱在自由下落过程中速度随时间变化的图象是4.万有引力定律的表达式是A .F =Gm 1m 2r 2B .F =Gm 1m 2rC .F =kq 1q 2r 2D .F =kq 1q 2r5.如图所示,花样跳伞运动员在跳伞降落过程中手拉手做成一个环状造型。
如果把构成环状造型的运动员看作一个整体,则此整体在竖直降落过程中 A .只受重力B .只受空气阻力C .受重力和空气阻力D .所受合力一定为零6.如图所示,以甲为头雁的人字形雁阵以相同的速度整齐滑翔。
则A .选地面为参考系,甲是静止的B .选地面为参考系,乙是静止的A B C D第3题图第5题图第6题图 第7题图A B C DC .选甲为参考系,乙是运动的D .选乙为参考系,甲是静止的7.如图所示,把A 、B 两个弹簧测力计连接在一起,B 的一端固定,用手拉测力计A 。
则关于A 对B 的作用力F AB 与B 对A 的作用力F BA 的说法正确的是 A .F AB 大小大于F BA 大小 B .F AB 大小等于F BA 大小 C .F AB 先于F BA 产生D .F AB 后于F BA 产生8.如图所示为水平桌面上的一条弯曲轨道。
钢球进入轨道的M 端沿轨道做曲线运动,它从出口N 端离开轨道后的运动轨迹是 A .aB .bC .cD .d9.如图所示,为了观察桌面的微小形变,在一张大桌子上放两个平面镜M 和N ,让一束光依次被这两面镜子反射,最后射到墙上,形成一个光点。
实验中,用力按压两镜之间的桌面,观察到的现象是 A .桌面明显向下凹陷 B .N 镜明显向右倾斜 C .M 镜明显向左倾斜D .光点位置明显变化10.如图所示是某幼儿园的一部直道滑梯,其滑道倾角为θ。
杭州师范大学钱江学院2019年三位一体综合评价招生.pdf
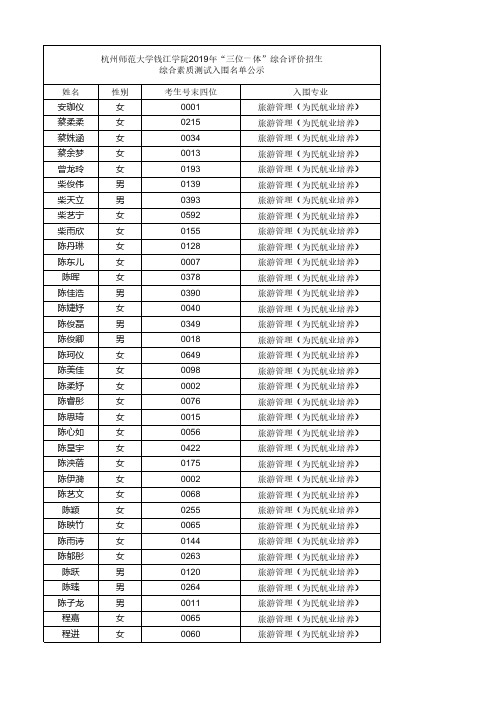
入围专业 旅游管理(为民航业培养) 旅游管理(为民航业培养) 旅游管理(为民航业培养) 旅游管理(为民航业培养) 旅游管理(为民航业培养) 旅游管理(为民航业培养) 旅游管理(为民航业培养) 旅游管理(为民航业培养) 旅游管理(为民航业培养) 旅游管理(为民航业培养) 旅游管理(为民航业培养) 旅游管理(为民航业培养) 旅游管理(为民航业培养) 旅游管理(为民航业培养) 旅游管理(为民航业培养) 旅游管理(为民航业培养) 旅游管理(为民航业培养) 旅游管理(为民航业培养) 旅游管理(为民航业培养) 旅游管理(为民航业培养) 旅游管理(为民航业培养) 旅游管理(为民航业培养) 旅游管理(为民航业培养) 旅游管理(为民航业培养) 旅游管理(为民航业培养) 旅游管理(为民航业培养) 旅游管理(为民航业培养) 旅游管理(为民航业培养) 旅游管理(为民航业培养) 旅游管理(为民航业培养) 旅游管理(为民航业培养) 旅游管理(为民航业培养) 旅游管理(为民航业培养) 旅游管理(为民航业培养) 旅游管理(为民航业培养) 旅游管理(为民航业培养) 旅游管理(为民航业培养) 旅游管理(为民航业培养)
姓名 安珈仪 蔡柔柔 蔡姝涵 蔡余梦 曾龙玲 柴俊伟 柴天立 柴艺宁 柴雨欣 陈丹琳 陈东儿
陈晖 陈佳浩 陈婕妤 陈俊磊 陈俊卿 陈珂仪 陈美佳 陈柔妤 陈睿彤 陈思琦 陈心如 陈星宇 陈泱蓓 陈伊漪 陈艺文
陈颖 陈映竹 陈雨诗 陈郁彤
陈跃 陈臻 陈子龙 程嘉 程进
杭州师范大学钱江学院2019年“三位一体”综合评价招生 综合素质测试入围名单公示
姓名 潘卓佳 彭佳怡 钱江涛 钱琦炜 钱昕怡 钱意恺
钱臻 邱静 裘哲培 饶婷 任笑笑 茹异程 阮幸子 商如萍 邵慧 邵慧 邵佳慧 邵杏子 邵萱 佘思怡 沈含笑 沈凯婷 沈璐滢 沈律 沈梦凡 沈诗源 沈宣妤 沈一如 沈昱 沈子怡 沈梓仁 盛佳芸 施涵予 施晓霞 施雅丹 史逸翀 宋施旖 宋唯一
2019年高考真题——英语(浙江卷) Word版含解析

科目:英语试卷名称2019年普通高等学校招生全国统一考试·浙江6月卷知识点28社会生活(2019·浙江6月卷·A) 话题:助人为乐——寻找军功章的主人词数:342难度:★★Zachariah Fike has an unusual hobby.He finds old military (军队的)medals for sale in antique stores and on t h e Internet.But unlike most collectors,Zac tracks down the medals’ rightful owners,and returns them.His effort to reunite families with lost medals began with a Christmas gift from his mother,a Purple Heart with t h e name Corrado A.G.Piccoli,found in an antique shop.Zac knows the meaning of a Purple Heart—he earned one himself in a war as a soldier.So when his mother gave him the medal,he knew right away what he had to do.Through the Internet,Zac tracked down Corrado’s sister Adeline Rockko.But when he finally reached her,the woman flooded him with questions: “Who are you?What antique shop?” However,when she hung up,she regretted the way she had handled the call.So she called Zac back and apologized.Soon she drove to meet Zacin Watertown,N.Y.“At that point,I knew she meant business,” Zac says.“To drive eight hours to come to see me.”The Piccolis grew up the children of Italian immigrants in Watertown.Corrado,a translator for the Army during WWⅡ,was killed in action in Europe.Before hearing from Zac,Adeline hadn’t realized the medal was missing.Like many military medals,the one Z a c’s mother had found was a family treasure.“This medal was very precious to my parents.Only on special occasions (场合) would they take it out and let us hold it in our hands,” Adeline says.As a child,Adeline couldn’t understand why the medal was so significant.“But as I grew older,” Adeline says, “and missed my brother more and more,I realized that was the only thing we had left.” Corrado Piccoli’s Purple H e a r t medal now hangs at the Italian American Civic Association in Watertown.Zac recently returned another lost medal to a family in Alabama.Since he first reunited Corrado’s medal,Zac s a y s h i s record is now 5 for 5.【文章大意】本文是一篇记叙文。
2019年复旦大学三位一体招生部分试题回忆(数学)问卷6.11

2019年复旦大学三位一体招生部分试题回忆(数学)问卷6.11work Information Technology Company.2020YEAR2复旦大学三位一体招生数学试题1.使得方程32360x x x a +++=有重根的a 取值情况有 ( )种 A.1 B.2 C.3 D.不存在2.记()0.00120.010.12xxxf x =-⨯-+,则()0f x <区间长为 ( ) A.小于0.5 B.大于0.5但小于1 C.大于1但有限 D.无限大3.解析几何的建立意味着 ( ) A.平行公设得到证明 B.代数与几何的结合 C.非欧几何的建立 D.以上均不正确4.记1xy xy y=-,则(2)0x x =的所有根的和为 。
5.两个四位数20XY 、YX 16的积为17817888,则X +Y = 。
6.若ab -1能被2017整除,则称b 是a 的逆。
在集合E ={1,2,3……2016}中,逆是其自身的元素个数为 ( ) A.1 B.2 C.4 D.不存在7.方程5432540x x x ax bx c +-+++=有三根1231,2,3x x x ===-。
则其余两根为( )A.不相等两实根B.共轭复根C.两相等实根D.相等复根 8.|x +3|=2|x -2+yi |,,x y R ∈该方程表示轨迹为 。
9.A (-1,0),B (3,0),P 在224236x xy y x +++=上,则三角形P AB 面积最大值为 ( ) A.6 B.7 C.8 D.10 10.222260x x xy y y -++--=上的点到y 轴最小值为 。
11.已知lg2=0.30103,lg5=0.69897,55lg(110)10--->-。
数列满足010,58n n a a a +==+,则2016cos(lg )a π∈ ( )A.[-1, -12] B.(12-,0) C.[0,12) D.[12,1] 12.方程1281940x x+--=的根x ∈ ( ) A.(-2, -1] B.(-1,0) C.[0,1) D.[1,2)13.已知,//,BF BC BD BC BA BF BD ⊥=+则2BC BD =是ABC ∆为等腰三角形的( )A.充分不必要条件B.充要条件C.必要不充分条件D.既不充分也不必要条件 14.参数方程为cos sin {x y θθθθ==的曲线与x 轴非负半轴的交点横坐标由小到大排列为12,,,na a a ⋯,则12ka k +∞-=∑( )A.121π- B.141π- C.1121π+- D.1141π+-15.2()3sin 4sin cos f x x x x =+最小值为 。
2019年浙江省三位一体招生考试必读——个人陈述写作要点

浙江省三位一体招生考试——个人陈述写作要点总起:个人陈述是面试官了解学生的唯一途径,也是向学校展现自己特点特长的最佳途径。
我之前也看过很多份考杭电的学生的个人陈述,大部分考生的文章往往是简单罗列参加过的活动以及所获奖项,而忽略了对自身个性及能力的详细描述,而后者恰恰是高校最希望学生能展示的“素质”,它是奖状和分数单无法体现的。
因此,一份生动的自荐信至关重要。
此外,面试中所有与个人经历相关的问题都来自于自荐信,对其中每一处细节的精心准备也是决定面试成败的关键。
事实上许多考官的整个面试过程就是由面试者个人经历中的某一条展开。
从这个方面来说,学生可以通过合理规划自荐信的重点来扬长避短,引导面试话题。
接下来我会教大家怎么写出一份比较好的个人陈述第一部分:制作三要素表格按照事件-细节-收获的思路原则:事无巨细,不分好坏目的:系统的整理高中生活全貌第二部分:制作完成之后,按照事情的重要程度重新排列。
排列的要求是从最合适写进个人陈述或用于面试降序排列。
表格在面试前是可以不断更新的。
第三部分:个人陈述的组成部分:那么我将它分为以下三个层次:1.认识自己:简单介绍自己,陈述个人特点2.肯定自己:写出个人特长;以及个人经历中最有感受(成长)的事(成果)申请入学的理由,为什么选这所学校,避免对大学的描述3.发展自己:进入高校的努力方向(即成才目标,理想成为什么样的人才(与专业选择挂钩))设想(如何成为这样的人才,但要避免假大空)第四部分:个人成熟写作中的一些基本原则1.文章要有真情实感和自己真实想法,而不是照抄,模仿百度上的范文2.语言叙述力求自然流畅,内容力求充实,避免官腔十足,如同入党申请书一样3.个人陈述中要保持结论(特点特长)-原因(事件)这么一个总分的文章架构.每个结论都需要有充分详实的事例来支持,避免结论多,论据少,下定义式的文章,这会给面试官留下王婆卖瓜的坏印象4.尽量避免对自己模式化的叙述。
比如热爱学习,喜欢读书。
2019高考浙江卷英语真题、答题卡、答案(16开、免排版、可编辑)

绝密★启用前2019年普通高等学校招生全国统一考试英语(浙江卷)选择题部分第一部分听力(共两节,满分30分)做题时,先将答案标在试卷上。
录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
例:How much is the shirt?A. £19.15.B. £9.18.C. £9.15.答案是C。
1.Where does this conversation take place?A. In a classroom.B. In a hospital.C.In a museum.2.What does Jack want to do?A. Take fitness classes.B. Buy a pair of gym shoes.C. Change his work schedule.3.What are the speakers talking about?A. What to drink.B. Where to meet.C. When to leave.4.What is the relationship between the speakers?A. Colleges.B. Classmates.C. Strangers.5.Why is Emily mentioned in the conversation?A. She might want a ticket.B. She is looking for the man.C. She has an extra ticket.第二节(共15小题,每小题1.5分,满分22.5分)听下面5段对话或独白。
2019年普通高等学校招生全国统一考试浙江
2019年普通高等学校招生全国统一考试·浙江卷 学校:___________姓名:___________班级:___________考号:___________1.已知全集{}1,0,1,2,3U =-,集合{}0,1,2A =,{}1,0,1B =-,则U A B =I ð( ) A .{}1-B .{}0,1C .{}1,2,3-D .{}1,0,1,3-2.渐近线方程为0x y ±=的双曲线的离心率是( )A .2B .1C D .23.若实数x,y 满足约束条件{x −3y +4≥03x −y −4≤0x +y ≥0,则z =3x +2y 的最大值是( )A .−1B .1C .10D .124.祖暅是我国南北朝时代的伟大科学家,他提出的“幂势既同,则积不容异”称为祖暅原理,利用该原理可以得到柱体的体积公式V Sh =柱体,其中S 是柱体的底面积,h 是柱体的高.若某柱体的三视图如图所示(单位:cm ),则该柱体的体积(单位:cm 3)是( )A .158B .162C .182D .324 5.若0,0a b >>,则“4a b +≤”是 “4ab ≤”的( )A .充分不必要条件B .必要不充分条件6.在同一直角坐标系中,函数11,log (02a x y y x a a ⎛⎫==+> ⎪⎝⎭且1)a ≠的图象可能是( ) A . B .C .D .7.设0<a <1,则随机变量X 的分布列是则当a 在(0,1)内增大时( )A .()D X 增大B .()D X 减小C .()D X 先增大后减小 D .()D X 先减小后增大8.设三棱锥V ABC -的底面是正三角形,侧棱长均相等,P 是棱VA 上的点(不含端点),记直线PB 与直线AC 所成角为α,直线PB 与平面ABC 所成角为β,二面角P AC B --的平面角为γ,则( )A .,βγαγ<<B .,βαβγ<<C .,βαγα<<D .,αβγβ<<9.已知,a b ∈R ,函数32,0()11(1),032x x f x x a x ax x <⎧⎪=⎨-++≥⎪⎩,若函数()y f x ax b =--恰有三个零点,则( )A .1,0a b <-<B .1,0a b <->C .1,0a b >-<D .1,0a b >->10.设,a b ∈R ,数列{}n a 中,211,n n a a a a b +==+,N n *∈ ,则( )A .当101,102b a =>B .当101,104b a => C .当102,10b a =->D .当104,10b a =-> 11.复数11iz =+(i 为虚数单位),则||z =________. 12.已知圆C 的圆心坐标是(0,)m ,半径长是r .若直线230x y -+=与圆相切于点(2,1)A --,则m =_____,r =______.13.在二项式9)x 的展开式中,常数项是________;系数为有理数的项的个数是_______.14.在ABC V 中,90ABC ∠=︒,4AB =,3BC =,点D 在线段AC 上,若45BDC ∠=︒,则BD =____;cos ABD ∠=________.15.已知椭圆22195x y +=的左焦点为F ,点P 在椭圆上且在x 轴的上方,若线段PF 的中点在以原点O 为圆心,OF 为半径的圆上,则直线PF 的斜率是_______.16.已知a R ∈,函数3()f x ax x =-,若存在t R ∈,使得2|(2)()|3f t f t +-≤,则实数a 的最大值是____.17.已知正方形ABCD 的边长为1,当每个(1,2,3,4,5,6)i i λ=取遍±1时,123456AB BC CD DA AC BD λλλλλλ+++++u u u v u u u v u u u v u u u v u u u v u u u v 的最小值是________;最大值是_______.18.设函数()sin ,f x x x =∈R .(1)已知[0,2),θ∈π函数()f x θ+是偶函数,求θ的值;(2)求函数22[()][()]124y f x f x ππ=+++ 的值域. 19.如图,已知三棱柱111ABC A B C -,平面11A AC C ⊥平面ABC ,90ABC ∠=︒,1130,,,BAC A A AC AC E F ∠=︒==分别是11,AC A B 的中点.(1)证明:EF BC ⊥;(2)求直线EF 与平面1A BC 所成角的余弦值.20.设等差数列{}n a 的前n 项和为n S ,34a =,43a S =,数列{}n b 满足:对每12,,,n n n n n n n S b S b S b *++∈+++N 成等比数列.(1)求数列{},{}n n a b 的通项公式;(2)记,n C n *=∈N证明:12+.n C C C n *++<∈N L 21.如图,已知点(10)F ,为抛物线22(0)y px p =>的焦点,过点F 的直线交抛物线于,A B 两点,点C 在抛物线上,使得ABC V 的重心G 在x 轴上,直线AC 交x 轴于点Q ,且Q 在点F 右侧.记,AFG CQG △△的面积为12,S S .(1)求p 的值及抛物线的准线方程;(2)求12S S 的最小值及此时点G 的坐标. 22.已知实数0a ≠,设函数()=ln 0.f x a x x >(1)当34a =-时,求函数()f x 的单调区间;(2)对任意21[,)e x ∈+∞均有()f x ≤ 求a 的取值范围. 注:e 2.71828...=为自然对数的底数.参考答案1.A【解析】【分析】本题根据交集、补集的定义可得.容易题,注重了基础知识、基本计算能力的考查.【详解】={1,3}U C A -,则(){1}U C A B =-I【点睛】易于理解集补集的概念、交集概念有误.2.C【解析】【分析】本题根据双曲线的渐近线方程可求得a b =,进一步可得离心率.容易题,注重了双曲线基础知识、基本计算能力的考查.【详解】根据渐近线方程为x ±y =0的双曲线,可得a b =,所以c =则该双曲线的离心率为 e c a==, 故选C .【点睛】理解概念,准确计算,是解答此类问题的基本要求.部分考生易出现理解性错误.3.C【解析】【分析】本题是简单线性规划问题的基本题型,根据“画、移、解”等步骤可得解.题目难度不大题,注重了基础知识、基本技能的考查.【详解】在平面直角坐标系内画出题中的不等式组表示的平面区域为以(-1,1),(1,-1),(2,2)为顶点的三角形区域(包含边界),由图易得当目标函数z =3x +2y 经过平面区域的点(2,2)时,z =3x +2y 取最大值z max =3×2+2×2=10.【点睛】解答此类问题,要求作图要准确,观察要仔细.往往由于由于作图欠准确而影响答案的准确程度,也有可能在解方程组的过程中出错.4.B【解析】【分析】先由三视图还原出原几何体,再进行计算【详解】由三视图得该棱柱的高为6,底面可以看作是由两个直角梯形组合而成的,其中一个上底为4,下底为6,高为3,另一个的上底为2,下底为6,高为3,则该棱柱的体积为264633616222++⎛⎫⨯+⨯⨯= ⎪⎝⎭. 故选B..【点睛】本题首先根据三视图,还原得到几何体——棱柱,根据题目给定的数据,计算几何体的体积,常规题目.难度不大,注重了基础知识、视图用图能力、基本计算能力的考查.易错点有二,一是不能正确还原几何体;二是计算体积有误.为避免出错,应注重多观察、细心计算 5.A【解析】【分析】本题根据基本不等式,结合选项,判断得出充分性成立,利用“特殊值法”,通过特取,a b的值,推出矛盾,确定必要性不成立.题目有一定难度,注重重要知识、基础知识、逻辑推理能力的考查.【详解】当0, 0a >b >时,a b +≥,则当4a b +≤时,有4a b ≤+≤,解得4ab ≤,充分性成立;当=1, =4a b 时,满足4ab ≤,但此时=5>4a+b ,必要性不成立,综上所述,“4a b +≤”是“4ab ≤”的充分不必要条件.【点睛】易出现的错误有,一是基本不等式掌握不熟,导致判断失误;二是不能灵活的应用“赋值法”,通过特取,a b 的值,从假设情况下推出合理结果或矛盾结果.6.D【解析】【分析】本题通过讨论a 的不同取值情况,分别讨论本题指数函数、对数函数的图象和,结合选项,判断得出正确结论.题目不难,注重重要知识、基础知识、逻辑推理能力的考查.【详解】当01a <<时,函数x y a =过定点(0,1)且单调递减,则函数1x y a=过定点(0,1)且单调递增,函数1log 2a y x ⎛⎫=+ ⎪⎝⎭过定点1(,0)2且单调递减,D 选项符合;当1a >时,函数x y a =过定点(0,1)且单调递增,则函数1x y a =过定点(0,1)且单调递减,函数1log 2a y x ⎛⎫=+ ⎪⎝⎭过定点1(,02)且单调递增,各选项均不符合.综上,选D.【点睛】易出现的错误有,一是指数函数、对数函数的图象和性质掌握不熟,导致判断失误;二是不能通过讨论a 的不同取值范围,认识函数的单调性.7.D【解析】【分析】利用方差公式结合二次函数的单调性可得结论;【详解】 解:1111()013333a E X a +=⨯+⨯+⨯=, 222111111()()()(1)333333a a a D X a +++=⨯+-⨯+-⨯ 2222212211[(1)(21)(2)](1)()279926a a a a a a =++-+-=-+=-+ 01a <<Q ,()D X ∴先减小后增大故选:D .【点睛】本题考查方差的求法,利用二次函数是关键,考查推理能力与计算能力,属于中档题. 8.B【解析】【分析】本题以三棱锥为载体,综合考查异面直线所成的角、直线与平面所成的角、二面角的概念,以及各种角的计算.解答的基本方法是通过明确各种角,应用三角函数知识求解,而后比较大小.而充分利用图形特征,则可事倍功半.【详解】方法1:如图G 为AC 中点,V 在底面ABC 的投影为O ,则P 在底面投影D 在线段AO 上,过D 作DE 垂直AE ,易得//PE VG ,过P 作//PF AC 交VG 于F ,过D 作//DH AC ,交BG 于H ,则,,BPF PBD PED α=∠β=∠γ=∠,则cos cos PF EG DH BD PB PB PB PB α===<=β,即αβ>,tan tan PD PD ED BDγ=>=β,即y >β,综上所述,答案为B.方法2:由最小角定理βα<,记V AB C --的平面角为γ'(显然γ'=γ)由最大角定理β<γ'=γ,故选B.方法3:(特殊位置)取V ABC -为正四面体,P 为VA 中点,易得cos sin sin α=⇒α=β=γ=B. 【点睛】常规解法下易出现的错误有,不能正确作图得出各种角.未能想到利用“特殊位置法”,寻求简便解法. 9.C 【解析】 【分析】当0x <时,()(1)y f x ax b x ax b a x b =--=--=--最多一个零点;当0x …时,32321111()(1)(1)3232y f x ax b x a x ax ax b x a x b =--=-++--=-+-,利用导数研究函数的单调性,根据单调性画函数草图,根据草图可得. 【详解】当0x <时,()(1)0y f x ax b x ax b a x b =--=--=--=,得1bx a=-;()y f x ax b =--最多一个零点; 当0x …时,32321111()(1)(1)3232y f x ax b x a x ax ax b x a x b =--=-++--=-+-, 2(1)y x a x =+-',当10a +„,即1a -„时,0y '…,()y f x ax b =--在[0,)+∞上递增,()y f x ax b =--最多一个零点.不合题意;当10a +>,即1a >-时,令0y '>得[1x a ∈+,)+∞,函数递增,令0y '<得[0x ∈,1)a +,函数递减;函数最多有2个零点;根据题意函数()y f x ax b =--恰有3个零点⇔函数()y f x ax b =--在(,0)-∞上有一个零点,在[0,)+∞上有2个零点, 如图:∴01b a <-且3211(1)(1)(1)032b a a a b ->⎧⎪⎨+-++-<⎪⎩, 解得0b <,10a ->,310(116,)b a a >>-+∴>-. 故选C .【点睛】遇到此类问题,不少考生会一筹莫展.由于方程中涉及,a b 两个参数,故按“一元化”想法,逐步分类讨论,这一过程中有可能分类不全面、不彻底. 10.A 【解析】 【分析】对于B ,令214x λ-+=0,得λ12=,取112a =,得到当b 14=时,a 10<10;对于C ,令x 2﹣λ﹣2=0,得λ=2或λ=﹣1,取a 1=2,得到当b =﹣2时,a 10<10;对于D ,令x 2﹣λ﹣4=0,得λ=1a =,得到当b =﹣4时,a 10<10;对于A ,221122a a =+≥,223113()224a a =++≥,4224319117()14216216a a a =+++≥+=>,当n ≥4时,1n n a a +=a n 12na +>11322+=,由此推导出104aa >(32)6,从而a 1072964>>10. 【详解】对于B ,令214x λ-+=0,得λ12=,取112a =,∴2111022n a a ==L ,,<, ∴当b 14=时,a 10<10,故B 错误;对于C ,令x 2﹣λ﹣2=0,得λ=2或λ=﹣1, 取a 1=2,∴a 2=2,…,a n =2<10, ∴当b =﹣2时,a 10<10,故C 错误; 对于D ,令x 2﹣λ﹣4=0,得λ=取1a =,∴2a =,…,n a =10, ∴当b =﹣4时,a 10<10,故D 错误; 对于A ,221122a a =+≥,223113()224a a =++≥, 4224319117()14216216a a a =+++≥+=>,a n +1﹣a n >0,{a n }递增,当n ≥4时,1n na a +=a n 12na +>11322+=, ∴5445109323232a a a a aa ⎧⎪⎪⎪⎪⎪⎪⋅⎨⎪⋅⎪⋅⎪⎪⎪⎪⎩>>>,∴104a a >(32)6,∴a 1072964>>10.故A 正确. 故选A . 【点睛】遇到此类问题,不少考生会一筹莫展.利用函数方程思想,通过研究函数的不动点,进一步讨论a 的可能取值,利用“排除法”求解.11 【解析】 【分析】本题先计算z ,而后求其模.或直接利用模的性质计算. 容易题,注重基础知识、运算求解能力的考查. 【详解】1|||1|2z i ===+. 【点睛】本题考查了复数模的运算,属于简单题.12.2m =- r =【解析】 【分析】本题主要考查圆的方程、直线与圆的位置关系.首先通过确定直线AC 的斜率,进一步得到其方程,将(0,)m 代入后求得m ,计算得解. 【详解】 可知11:1(2)22AC k AC y x =-⇒+=-+,把(0,)m 代入得2m =-,此时||r AC ===【点睛】解答直线与圆的位置关系问题,往往要借助于数与形的结合,特别是要注意应用圆的几何性质.13. 5 【解析】 【分析】本题主要考查二项式定理、二项展开式的通项公式、二项式系数,属于常规题目.从写出二项展开式的通项入手,根据要求,考察x 的幂指数,使问题得解.【详解】9)x 的通项为919(0,1,29)rr r r T C x r -+==L可得常数项为0919T C ==因系数为有理数,1,3,5,7,9r =,有246810T , T , T , T , T 共5个项 【点睛】此类问题解法比较明确,首要的是要准确记忆通项公式,特别是“幂指数”不能记混,其次,计算要细心,确保结果正确.14 10【解析】 【分析】本题主要考查解三角形问题,即正弦定理、三角恒等变换、数形结合思想及函数方程思想.在BDC ∆、ABD ∆中应用正弦定理,由cos cos()ABD BDC BAC ∠=∠-∠建立方程,进而得解. 【详解】在ABD ∆中,正弦定理有:sin sin AB BD ADB BAC =∠∠,而34,4AB ADB π=∠=,5AC ,34sin ,cos 55BC AB BAC BAC AC AC ∠==∠==,所以BD =cos cos()coscos sinsin 4410ABD BDC BAC BAC BAC ππ∠=∠-∠=∠+∠=【点睛】解答解三角形问题,要注意充分利用图形特征.15【解析】【分析】结合图形可以发现,利用三角形中位线定理,将线段长度用坐标表示成圆的方程,与椭圆方程联立可进一步求解.利用焦半径及三角形中位线定理,则更为简洁.【详解】方法1:由题意可知||=|2OF OM|=c=,由中位线定理可得12||4PF OM==,设(,)P x y可得22(2)16x y-+=,联立方程221 95x y+=可解得321,22x x=-=(舍),点P在椭圆上且在x轴的上方,求得3,22P⎛-⎝⎭,所以212PFk==方法2:焦半径公式应用解析1:由题意可知|2OF|=|OM|=c=,由中位线定理可得12||4PF OM==,即342p pa ex x-=⇒=-求得32P ⎛- ⎝⎭,所以212PF k ==【点睛】本题主要考查椭圆的标准方程、椭圆的几何性质、直线与圆的位置关系,利用数形结合思想,是解答解析几何问题的重要途径. 16.max 43a = 【解析】 【分析】本题主要考查含参绝对值不等式、函数方程思想及数形结合思想,属于能力型考题.从研究()2(2)()23642f t f t a t t +-=++-入手,令2364[1,)m t t =++∈+∞,从而使问题加以转化,通过绘制函数图象,观察得解. 【详解】使得()222(2)()2(2)(2)2234{}2]6f t f t a t t t t a t t +-=•[++++-=++-,使得令2364[1,)m t t =++∈+∞,则原不等式转化为存在11,|1|3m am ≥-≤,由折线函数,如图只需11133a -≤-≤,即2433a ≤≤,即a 的最大值是43【点睛】对于函数不等式问题,需充分利用转化与化归思想、数形结合思想. 17.0【解析】 【分析】本题主要考查平面向量的应用,题目难度较大.从引入“基向量”入手,简化模的表现形式,利用转化与化归思想将问题逐步简化. 【详解】正方形ABCD 的边长为1,可得AB AD AC +=u u u r u u u r u u u r ,BD AD AB =-u u u r u u u r u u u r,AB u u u r •AD =u u u r0,()()12345613562456AB BC CD DA AC BD AB ADλ+λ+λ+λ+λ+λ=λ-λ+λ-λ+λ-λ+λ+λu u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v要使123456AB BC CD DA AC BD λ+λ+λ+λ+λ+λu u u v u u u v u u u v u u u v u u u v u u u v的最小,只需要135562460λ-λ+λ-λ=λ-λ+λ+λ=,此时只需要取1234561,1,1,1,1,1λ=λ=-λ=λ=λ=λ=此时123456min0AB BC CD DA AC BDλ+λ+λ+λ+λ+λ=u u u v u u u v u u u v u u u v u u u v u u u v()()2212345613562456AB BC CD DA AC BD AB ADλλλλλλλλλλλλλλ+++++=-+-+-++()()2213562456λλλλλλλλ=-+-+-++()()2213562456λλλλλλλλ≤++-++++()()22565622λλλλ=+-+++()()()225656565684λλλλλλλλ=+-+++-++()225682λλ=++12=+1220=+=等号成立当且仅当1356,,λ-λλ-λ均非负或者均非正,并且2456,,λ-λλ+λ均非负或者均非正.比如1234561,1,,1,1,11λλλ=-λλ=-=λ===则123456maxAB BC CD DA AC BDλ+λ+λ+λ+λ+λ==u u u v u u u v u u u v u u u v u u u v u u u v 点睛:对于此题需充分利用转化与化归思想,从“基向量”入手,最后求不等式最值,是一道向量和不等式的综合题. 【点睛】对于平面向量的应用问题,需充分利用转化与化归思想、数形结合思想.18.(1)3,22ππ;(2)122⎡-+⎢⎣⎦. 【解析】 【分析】(1)由函数的解析式结合偶函数的性质即可确定θ的值;(2)首先整理函数的解析式为()sin y a x b ωϕ=++的形式,然后确定其值域即可. 【详解】(1)由题意结合函数的解析式可得:()()sin f x x θθ+=+, 函数为偶函数,则当0x =时,()02k k Z πθπ+=+∈,即()2k k Z πθπ=+∈,结合[)0,2θ∈π可取0,1k =,相应的θ值为3,22ππ.(2)由函数的解析式可得:22sin sin 124y x x ππ⎛⎫⎛⎫=+++ ⎪ ⎪⎝⎭⎝⎭1cos 21cos 26222x x ππ⎛⎫⎛⎫-+-+ ⎪ ⎪⎝⎭⎝⎭=+ 11cos 2cos 2226x x ππ⎡⎤⎛⎫⎛⎫=-+++ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦1112sin 2sin 222x x x ⎫=---⎪⎪⎝⎭131cos 2sin 2222x x ⎛⎫=-- ⎪ ⎪⎝⎭1226x π⎛⎫=+- ⎪⎝⎭.据此可得函数的值域为:122⎡-+⎢⎣⎦.【点睛】本题主要考查由三角函数的奇偶性确定参数值,三角函数值域的求解,三角函数式的整理变形等知识,意在考查学生的转化能力和计算求解能力. 19.(1)证明见解析;(2)35. 【解析】 【分析】(1)由题意首先证得线面垂直,然后利用线面垂直的定义即可证得线线垂直;(2)建立空间直角坐标系,分别求得直线的方向向量和平面的法向量,然后结合线面角的正弦值和同角三角函数基本关系可得线面角的余弦值. 【详解】(1)如图所示,连结11,A E B E ,等边1AAC △中,AE EC =,则1A E AC ⊥, 平面ABC ⊥平面11A ACC ,且平面ABC ∩平面11A ACC AC =, 由面面垂直的性质定理可得:1A E ⊥平面ABC ,故1A E BC ⊥,由三棱柱的性质可知11A B AB ∥,而AB BC ⊥,故11A B BC ⊥,且1111A B A E A =I , 由线面垂直的判定定理可得:BC ⊥平面11A B E , 结合EF ⊆平面11A B E ,故EF BC ⊥.(2)在底面ABC 内作EH ⊥AC ,以点E 为坐标原点,EH ,EC ,1EA 方向分别为x ,y ,z 轴正方向建立空间直角坐标系E xyz -.设1EH =,则AE EC ==11AA CA ==3BC AB ==,据此可得:()()()130,,,0,0,3,2A B A C ⎛⎫⎪ ⎪⎝⎭,由11AB A B =u u u r u u u u r 可得点1B的坐标为132B ⎛⎫⎪⎝⎭,利用中点坐标公式可得:34F ⎛⎫⎪⎝⎭,由于()0,0,0E , 故直线EF的方向向量为:34EF ⎛⎫= ⎪⎝⎭u u u r 设平面1A BC 的法向量为(),,m x y z =u r,则:()()133,,,330222233,,,02222m A B x y z x y z m BC x y z x y u u u v v u u u v v ⎧⎛⎫⋅=⋅-=+-=⎪ ⎪ ⎪⎪⎝⎭⎨⎛⎫⎪⋅=⋅-=-+= ⎪⎪ ⎪⎝⎭⎩, 据此可得平面1A BC的一个法向量为()m =u r,34EF ⎛⎫= ⎪⎝⎭u u u r此时4cos ,5EF m EF m EF m⋅===⨯u u u r u ru u u r u r u u u r u r ,设直线EF 与平面1A BC 所成角为θ,则43sin cos ,,cos 55EF m θθ===u u u r u r .【点睛】本题考查了立体几何中的线线垂直的判定和线面角的求解问题,意在考查学生的空间想象能力和逻辑推理能力;解答本题关键在于能利用直线与直线、直线与平面、平面与平面关系的相互转化,通过严密推理,同时对于立体几何中角的计算问题,往往可以利用空间向量法,通过求解平面的法向量,利用向量的夹角公式求解. 20.(1)()21n a n =-,()1n b n n =+;(2)证明见解析. 【解析】 【分析】(1)首先求得数列{}n a 的首项和公差确定数列{}n a 的通项公式,然后结合三项成等比数列的充分必要条件整理计算即可确定数列{}n b 的通项公式;(2)结合(1)的结果对数列{}n c 的通项公式进行放缩,然后利用不等式的性质和裂项求和的方法即可证得题中的不等式. 【详解】(1)由题意可得:1112432332a d a d a d +=⎧⎪⎨⨯+=+⎪⎩,解得:102a d =⎧⎨=⎩, 则数列{}n a 的通项公式为22n a n =- . 其前n 项和()()02212n n n S nn +-⨯==-.则()()()()1,1,12n n n n n b n n b n n b -++++++成等比数列,即:()()()()21112n n n n n b n n b n n b ++=-+⨯+++⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦,据此有:()()()()()()()()2222121112121n n n n nn n n n b b n n n n n n b n n b b ++++=-++++++-+,故()()()()()22112121(1)(1)(1)(2)n n n n n n b n n n n n n n n n +--++==++++--+. (2)结合(1)中的通项公式可得:2n C ==<=<=,则)122022n C C C +++<+++=L L 【点睛】本题主要考查数列通项公式的求解,,裂项求和的方法,数列中用放缩法证明不等式的方法等知识,意在考查学生的转化能力和计算求解能力. 21.(1)1,1x =-;(2)1+()2,0G . 【解析】 【分析】(1)由焦点坐标确定p 的值和准线方程即可;(2)设出直线方程,联立直线方程和抛物线方程,结合韦达定理求得面积的表达式,最后结合均值不等式的结论即可求得12S S 的最小值和点G 的坐标. 【详解】 (1)由题意可得12p=,则2,24p p ==,抛物线方程为24y x =,准线方程为1x =-. (2)设()()1122,,,A x y B x y ,设直线AB 的方程为()1,0y k x k =->,与抛物线方程24y x =联立可得:()2222240k x k x k -++=,故:2222242,1k x x x x +=+=,()12121242,4y y k x x y y k+=+-==-⨯=-,设点C 的坐标为()33,C x y ,由重心坐标公式可得:1233G x x x x ++=321423x k ⎛⎫++ ⎝=⎪⎭,1233G y y y y ++=3143y k =⎛⎫+ ⎪⎝⎭,令0G y =可得:34y k =-,则233244y x k==.即222144123382G k x k k ⎛⎫⎛⎫+++ ⎪ ⎪⎝⎭⎝=⎭=,由斜率公式可得:131322311313444AC y y y y k y y x x y y --===-+-,直线AC 的方程为:()33134y y x x y y -=-+,令0y =可得:()()231331331334444Q y y y y y y y y yx x -+-+=+=+=-,故()11112218121323118223G F y S x x y y k k ⎡⎤⎛⎫⎛⎫+-⨯=⨯- ⎪=⨯-⨯ ⎪⎢⎥⎝⎭⎝=⨯⎭⎣⎦, 且()()32213311822423Q G y y y S x x y k ⎛⎫+ ⎪⎝⎭⎡⎤=⨯-⨯-=---⎢⎥⎣⎦, 由于34y k=-,代入上式可得:12222833y S k k k ⎛⎫=-- ⎪⎝⎭,由12124,4y y y y k +==-可得1144y y k -=,则12144y k y =-,则()()()2211122121112281233222284433y y S y S y y k k k y k -==⎛⎫-+--⎛⎫⨯- ⎭⎪⎝⎭⎪⎝()212142488168y y =--++-21≥=.当且仅当21214888yy -=-,即218y =+1y =. 此时12144y k y ==-,281223G x k ⎛⎫+= ⎪⎝⎭=,则点G 的坐标为()2,0G . 【点睛】直线与抛物线的位置关系和直线与椭圆、双曲线的位置关系类似,一般要用到根与系数的关系,本题主要考查了抛物线准线方程的求解,直线与抛物线的位置关系,三角形重心公式的应用,基本不等式求最值的方法等知识,意在考查学生的转化能力和计算求解能力. 22.(1)()f x 的单调递增区间是()3,+∞,单调递减区间是()0,3;(2)04a <≤. 【解析】 【分析】(1)首先求得导函数的解析式,然后结合函数的解析式确定函数的单调区间即可.(2)由题意首先由函数在特殊点的函数值得到a 的取值范围,然后证明所得的范围满足题意即可. 【详解】 (1)当34a =-时,()3ln 4f x x =-()0,∞+,且: ()3433'4x x f x x -+=-== 因此函数()f x 的单调递增区间是()3,+∞,单调递减区间是()0,3. (2)由1(1)2f a ≤,得04a <≤,当04a <≤时,()2fx a ≤,等价于22ln 0x a a --≥,令1t a=,则t ≥, 设()22lng t t x =,t ≥,则2()2ln g t t x =--, (i )当1,7x ⎡⎫∈+∞⎪⎢⎣⎭≤则()2ln g xg x =…,记1()ln ,7p x x x =≥, 则1()p x x '=-==列表讨论:()(1)0,()2()0p x p g t g p x ∴=∴=厖?(ii )当211,7x e ⎡⎫∈⎪⎢⎣⎭时,()g t g ≥=,令211()(1),,7q x x x x e ⎡⎤=++∈⎢⎥⎣⎦, 则()10q x'=>, 故()q x 在211,7e ⎡⎤⎢⎥⎣⎦上单调递增,1()7q x q ⎛⎫∴≤ ⎪⎝⎭,由(i )得11(1)077q p p ⎛⎫⎛⎫=<= ⎪ ⎪⎝⎭⎝⎭,()0,()0q x g t g ∴<∴≥=>,由(i )(ii )知对任意21,,),()0x t g t e ⎡⎫∈+∞∈+∞≥⎪⎢⎣⎭,即对任意21,x e ⎡⎫∈+∞⎪⎢⎣⎭,均有()2f x a≤,综上所述,所求的a 的取值范围是0,4⎛ ⎝⎦. 【点睛】导数是研究函数的单调性、极值(最值)最有效的工具,而函数是高中数学中重要的知识点,对导数的应用的考查主要从以下几个角度进行:(1)考查导数的几何意义,往往与解析几何、微积分相联系.(2)利用导数求函数的单调区间,判断单调性;已知单调性,求参数.(3)利用导数求函数的最值(极值),解决生活中的优化问题.(4)考查数形结合思想的应用.。
2019年高考真题——理综(浙江卷)word解析共18页
2019年普通高等学校招生全国统一考试(浙江卷)理科综合能力测试一、选择题(本题17小题。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1.下列关于高等动植物连续分裂细胞的细胞周期的叙述,正确的是A.用蛋白质合成抑制剂处理G1期细胞,不影响其进入S期B.S期细胞的染色体数目已增加一倍C.G2其细胞的细胞核DNA含量已增加一倍D.用秋水仙素处理细胞群体,M期细胞的比例会减少2.某哺乳动物神经细胞内外的K+和Na+浓度见下表。
下列属于主动转运的是A.K+经钾离子通道排出细胞B.K+与有关载体蛋白结合排出细胞C.Na+经钠离子通道排出细胞D.Na+与有关载体蛋白结合排出细胞3.某生物基因表达过程如图所示。
下列叙述与该图相符的是A.在RNA聚合酶作用下DNA双螺旋解开B.DNA-RNA杂交区域中A应与T配对C.mRNA翻译只能得到一条肽链D.该过程发生在真核细胞中4.下列关于出生率的叙述,正确的是A.若某一种群年初时的个体数为100,年末时为110,其中新生个体数为20,死亡个体数为10,则该种群的年出生率为10%B.若某动物的婚配制为一雌一雄,生殖期个体的雌雄比例越接近1:1,则出生率越高C.若通过调控环境条件,使某动物的性成熟推迟,则出生率会更高D.若比较三种年龄结构类型的种群,则稳定型的出生率最高5.光照、赤霉素和赤霉素合成抑制剂对某种植物茎伸长影响的实验结果如图所示。
下列叙述正确的是A.茎伸长受抑制均由赤霉素合成抑制剂引起B.赤霉素是影响茎伸长的主要因素之一C.植物茎伸长与光照时间无关D.该植物是赤霉素缺失突变体6.实验小鼠皮肤细胞培养(非克隆培养)的基本过程如图所示。
下列叙述错误的是A.甲过程需要对实验小鼠进行消毒B.乙过程对皮肤组织可用胰蛋白酶消化C.丙过程得到的细胞大多具有异倍体核型D.丁过程得到的细胞具有异质性7.下列说法不正确的是A.多孔碳可用氢氧燃料电池的电极材料B.pH计不能用于酸碱中和滴定终点的判断ks5uC.科学家发现一种新细菌的DNA链中有砷(As)元素,该As元素最有可能取代了普通DNA 链中的P元素D.CH3CH—CH2和CO2反应生成可降解聚合物[ O—CHCH2—O—C ]n,该反应符合绿O CH3 O化学的原则8.下列说法正确的是A.实验室从海带提取单质碘的方法是:取样灼烧溶解过滤萃取B.用乙醇和浓H2SO4制备乙烯时,可用水浴加热控制反应的温度C.氯离子存在时,铝表面的氧化膜易被破坏,因此含盐腌制品不宜直接放在铝制容器中D .将(NH 4)2SO 4、CuSO 4溶液分别加入蛋白质溶液,都出现沉淀,表明二者均可使蛋白质变性9.短周期元素X 、Y 、Z 、W 、Q 在元素周期表的位置如表所示,其中X 元素的原子内层电子数是最外层电子数的一半,则下列说法正确的是10.下列说法正确的是 A .按系统命名法,化合物 的名称是2,3,5,5-四甲基-4,4-二乙基己烷B .等物质的量的苯和苯甲酸完全燃烧消耗氧气的量不相等CD . 的高聚物,其单体是甲醛和苯酚 11浅。
2019年6月全国各地高考试题浙江省卷英语试题及参考答案
2019年普通高等学校招生全国统一考试(浙江卷)英语选择题部分第一部分听力(共两节,满分30分)做题时,先将答案标在试卷上。
录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
例:How much is the shirt?A. £19.15.B. £9.18.C. £9.15.答案是C。
1. Where does this conversation take place?A. In a classroom.B. In a hospital.C. In a museum.2. What does Jack want to do?A. Take fitness classes.B. Buy a pair of gym shoes.C. Change his work schedule.3. What are the speakers talking about?A. What to drink.B. Where to meet.C. When to leave.4. What is the relationship between the speakers?A. Colleagues.B. Classmates.C. Strangers.5. Why is Emily mentioned in the conversation?A. She might want a ticket.B. She is looking for the man.C. She has an extra ticket.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
2019年高考地理真题试卷(浙江卷)(6月卷)含详解
2019年6月浙江省普通高中学业水平考试地理试卷一,选择题(本大题共25小题,每小题2分,共50分。
每小题列出的四个备选项中只有一个是符合题目要求的,不选,多选,错选均不得分)1.最新研究表明,自2005年以来南极上空臭氧层空洞有逐渐缩小趋势,其原因可能是A.全球气候持续变暖B.植被覆盖率提高C.矿物燃料使用减少D.氟利昂排放减少2.可燃冰又称“天然气水合物”,按自然属性属于A.气候资源B.矿产资源C.土地资源D.生物资源3.夏至日前后,俄罗斯圣彼得堡(60°N)会出现夜晚不黑现象,这是因为大气对太阳辐射具有A.折射作用B.反射作用C.吸收作用D.散射作用2019年6月,呼(呼和浩特)—张(张家口)高铁顺利完工。
完成下面小题。
4.白云鄂博兴起的主要区位因素是A.矿产B.政治C.河流D.气候5.“呼—张”高铁的通车,将直接促进沿线地区A.风能开发B.铁矿石输出C.旅游业发展D.水资源利用石化工业是长三角地区重要产业之一。
完成下面小题。
6.长三角地区重点发展石化工业的优势条件是A.水能丰富B.接近市场C.地价低廉D.劳动力丰富7.从生产协作关系看,长三角石化工业园区能吸引的相关产业是A.造船工业B.合成橡胶C.电子装配D.精密机械我国南方某山区产业以耕作业和矿产开采为主,上世纪七十年代,该地“红色荒漠”面积有所扩大。
完成下面小题。
8.“红色荒漠”面积扩大导致该地()A.生物种类增多B.河流含沙量减少C.地下径流减少D.降水量明显增大9.从可持续发展角度考虑,该地适宜A.推广立体农业B.鼓励发展放牧业C.增加粮食种植D.加大矿产开发力度黄土高原沟壑纵横,黄土地貌广布。
完成下面小题。
10.在黄土高原上分布着梁,峁,土石山等地形单元,体现了自然地理环境的A.纬度地带分异规律B.垂直分异规律C.干湿度地带分异规律D.地方性分异规律11.黄土高原东部主要的自然带是A.亚热带常绿阔叶林带B.温带荒漠带C.亚热带常绿硬叶林带D.温带落叶阔叶林带2019年5月31日中俄黑龙江公路大桥顺利合龙,该大桥的开通结束了黑河与布拉戈维申斯克之间年内某时段不能运送货物的历史。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
浙江三位一体招生考试6所高校真题六所高校:杭州电子科技大学浙江工商大学浙江理工大学杭州师范大学浙江大学城市学院浙江树人大学浙江省三位一体考试属于高考,题目属于保密内容,本真题根据考生口述整理而成,如觉得有用,请下载予以支持,更多资料请从本文库好下载。
一、杭州电子科技大学杭州电子科技大学笔试题目(口述整理,仅供参考)笔试题目共180道,前40道题记1分,中间100道计2分,最后40道计3分,共360分。
考试内容涉及法律问题、时事政治、文学常识、信息技术、逻辑推理,另外还有英语、物理、数学等方面的问题。
美国总统特朗普主张美国从TTP中退出,TTP是什么意思?(跨太平洋伙伴协议)CPI的缩写代表什么意思?目前拉动国内经济增长的依旧是什么?标有1-17号的17张牌,顺时针摆着,数到2017时是哪一张?逻辑规律。
“己所不欲,勿施于人”是谁的名言?乌镇、凤凰古城等四个城市中,哪个是浙江省的?杭州电子科技大学官方网址的域名是什么?恒山、衡山、华山和黄山,哪个不是五岳里面的?“十年树木,百年树人”是谁的名言?黄河为什么没有支流汇入?荒诞戏剧()的作者是谁?“焚书坑儒”的目的是什么?中国第一部现代白话文小说是哪一部?狂人日记孔乙己故乡阿Q正传杏花什么时候开?hot spring是什么意思?温泉(水温在华氏98度以上)蓝天是怎么形成的?什么原理?诗歌中的意象诺贝尔物理学奖的内容下面是真命题的是:如果1+1=2,则血是黑的;如果1+1=3,则血是黑。
一个人花8块钱买了一只鸡,9块钱卖掉了,然后他觉得不划算,花10块钱又买回来了,11块钱卖给另外一个人,问他赚了多少钱?都江堰的作用是?IT指的是什么?一个圆形图案里有一个正方形/五边形/N边形(原题更具体),哪种情况下圆的剩余面积比较大?1/6,1/3,1,4,下一个数字是?(20)32位的电脑系统,最大能兼容的内存是?劳动工作者的英文是?blue/white/……历史上“金屋藏娇”的皇帝是?哪一位是从美国籍转为中国籍的科学家?杨振宁给出一个概念或形容的话,描述的是?GDP/CPI/……二、浙江工商大学浙江工商大学面试主要以无领导小组讨论的方式进行,按不同的测试类别分组进行,面试分为几个部分:3分钟自我介绍+个人对材料的看法;30分钟自由讨论并选出代表进行阐述;4分钟代表总结。
【无领导小组讨论的流程和步骤请关注本文库号】浙江工商大学面试题目(以下考题根据考生口述整理,仅供参考)1.两页纸材料,关于当公共自行车碰见共享单车,你怎么看?给出考生关于公共自行车的优势、共享单车的发展前景,以及专家对两者之间的不同看法等三段材料,让考生整合思路后进行个人阐述,最后派小组代表发言。
考生分享:有的考生说,“本来自己是认为两者可以共存互补的,但小组讨论得出的结论是倾向于发展共享单车,最后的代表发言我们就选择针对共享单车的优势以及改进方式去分析。
”有的考生则说,整组看法基本一致,认为可以因地制宜,在大学城多置些共享单车,在居民区多置些公共自行车,互相取长补短。
2.两页纸材料,你认为中国诗词大会,是吹响了文化号角还是一场娱乐盛宴?大多数考生认为文化性与娱乐性应该相互融合,这种娱乐是为了更好地传承中国传统文化,是披着娱乐外衣推动文化发展。
也有不少考生侧重文化或娱乐某一方面给出了看法。
那么,到底什么样的考生是考官最喜欢的?不少考官表示,今天参加面试考生很有想法,敢想敢说有新意,并且能在关注时事的基础上去思考,值得表扬。
浙商大经济学院的一位老师表示,这次考题出得很接地气,也很契合年轻人的思维;考生素质比较高,主动性也很强,既能很好地表达自己的观点又能积极参与到讨论中。
三、浙江理工大学浙江理工大学面试题目(以下考题根据考生口述整理,仅供参考)你是怎么看待大众创业,万众创新的?对于人工智能的看法?关于绿水青山即是金山银山的有啥看法?二元户籍制度问题据了解,浙理工第一次邀请校友作为考官,浙理工创业导师、校友代表尚贞涛作为本次理学院考生的面试官,他表示,不仅仅注重考生的知识面,更加注重考生的能力面。
“我们侧重于考生能力方面的表现,学生走向社会,自我再学习的时候需要的沟通、协调、组织能力的考察。
特别是人文专业,要在实战中学习,要适应能力强,要看重性格和周围的人相处程度。
”尚贞涛说,考生总体水平较好,许多高中学生的接触面和知识面较广,但是还是缺少一些历练,可以在之后的学习和工作中根据需求再进行锻炼。
万事利丝绸科技有限公司董事长马廷方认为,考生给人的第一感觉要真实。
不是通过培训班培训出来靠死背的学生,比如自我介绍要真实地介绍你自己包括你自己的特点;第二是遇事冷静。
在紧张之后能够迅速冷静下来,能够冷静的分析问题处理问题;第三是需要有一个比较广的知识面。
知识面广不广,在问题的回答上能够体现出来。
还有不少考官表示,三位一体招生模式主要是当面交流沟通比较多,每个人都喜欢相对来说亲和力好一点的,比较积极主动的,性格外向的,真诚的考生。
但是很多考生不善于表达,说话声音小,甚至有些人临场应变能力不是很高,很紧张,“回答问题一共两分钟的时间,你拆信封就要一分钟,这就说明你太紧张了。
”“其实临场的沟通都是有技巧的,包括后面的无领导小组中的沟通应答,涉及到团队的协作,有些人自己说得很多,有些人很清楚现在几点了他会提醒别人,有些人会让基本没有发过言的同学去回答,把他们很好的组织起来,明显看到能力的差距。
”四、杭州师范大学杭州师范大学分专业进行专业报名和测试电子商务专业笔试题有100道,专业相关性很强,比如电子商务和阿里巴巴的相关问题,此外,还有时事政治、逻辑所谓推理、数学题等,试题范围很广。
艺术教育和电子商务专业的考生参加了笔试,试卷内容都是跟专业相关的,比如艺术教育专业考到了很多艺术知识,比如音乐、美术等问题。
“每个专业安排各自专业相关的笔试内容,是想筛选出更适合这个专业的人才。
”杭州师范大学教务处副处长、招生办副主任翁灵丽说,自2011年起,学校就分专业报名和测试,各个环节都从专业的角度出发,这与2017年新高考改革更侧重于专业不谋而合。
杭师大2017年计划招生373人,网上报名人数2542人,初审通过的有2318 人。
今年,新增了特殊教育专业,计划招生40人。
据介绍,杭师大三位一体面试是根据各专业特性安排的,有个人面试,有全体面试,还分大组小组进行讨论。
小学教育、艺术教育、特殊教育等师范类专业均有特长和才艺展示环节,成绩占比较高。
报考电子商务的宁波考生小黄说,面试环节不是特别难,指定材料讨论部分稍微有点难度。
“考官让我们阅读一段材料,然后给出一个问题:成功的因素最重要的和最不重要的分别是哪些,让我们自己选择,然后进行阐述。
”杭师大各专业参与面试的考评专家有近两百位,校外专家比例超过了40%,比如很多都是杭师大校友的中小学校长、幼儿园园长等;护理学专业的面试官是杭州各大医院护理部主任;电子商务专业的面试官则是阿里巴巴人力资源部的高管;体育教育专业面试官25位全是校外专家。
翁灵丽表示,为保证面试工作更高效、更科学,更公正,考评专家的组成非常多元。
杭师大的每个考场均采用了计算机打分系统。
杭州师范大学面试题目(以下考题根据考生口述整理,仅供参考)成功的因素最重要的和最不重要的分别是哪些,让考生选择,然后进行阐述。
比如心态、比如优越的家庭条件等。
五、浙江大学城市学院浙大城院2017年计划招生人数是60人,网上报名人数为671人,参加笔试的有404人,获得面试资格的考生有261人。
2017学校新增了笔试,相比仅通过书面材料审核筛掉一批“不达线”的考生,笔试能弥补一点劣势,多样的考题更能全面地考察学生的综合素质。
2017城院“三位一体”招生中有两个新专业很抢眼:一个是中外合办的工业设计专业,一个是会展经济与管理专业。
这两个专业都下属于去年新成立的“浙江大学城市学院怀卡托大学联合学院”,这是第一所杭州市高等教育中外合作办学机构。
浙江大学城市学院测试题目(以下考题根据考生口述整理,仅供参考)笔试题目结合四句古诗,问哪一句是描写春天的?杭州哪一年举办亚运会?十二届全国人大五次会议表决通过哪部法律?半程马拉松的长度是多少?中国第一部现代白话文小说是哪一部?面试题目面试环节,5名考官对7名考生,小组讨论。
面试环节,分为以下部分:1.抽签,轮流朗读英语文章,每人两分钟。
2.分发一份资料,根据材料与问题,小组7人进行无领导小组讨论,先是个人陈述,讨论后下结论。
材料是关于共享经济、共享单车、城市公共自行车等内容。
1.在你的生活中,有哪些是涉及共享经济的?2. 对比城市公共自行车与共享单车,你觉得各有什么优缺点?为什么?3. 针对当下的现状,请分别从骑行者、企业和政府管理部门的角度提出合理化建议?六、浙江树人大学2017年浙江树人大学学校迎来了3371名考生进行三位一体招生的笔试。
2017三位一体计划招生数是80人,入围人数有400人。
浙江树人大学测试题目(以下考题根据考生口述整理,仅供参考)笔试题目笔试共200道选择题,每题0.5分,在一个半小时内完成。
内容不仅涵盖了各个科目,也有不少“超纲”内容,考察面很广,有些题目令考生们出乎意料:贾斯汀·比伯(Justin Bieber)是哪个国家的人?牡丹亭的作者是谁?步辇图的作者是谁?获得了被成为建筑学里的奥斯卡奖的人,是谁?获得诺贝尔文学奖的鲍勃·迪伦是哪国人?Application的英文读音是?一个二进制的题目:0+0=0,1+1=10,那么10+11=?我没有兄弟姐妹,他爸是我爸的儿子,他是谁?一个人从降落伞下来,他的动能、机械能是怎么变化的?用英语文章描述了一个关于英国的故事,最后问以下哪个国家曾是英国的殖民地?用英语文章描述了一个神话故事,最后问这是什么故事?据说应该是神农尝百草。
一个人卖了2张卡,一张亏了20%,一张赚了20%,最后他赚了或亏了多少?三个人打比赛,甲打了6场,乙打了4场,丙打了3场,问他们一共打了多少场?吃第一个包子时觉得很满足,吃第二个包子时没那么满足了,这是什么效应?△浙江树人的大学三位一体招生测试现场面试题目经过笔试,436人过关斩将,进入了今天的面试。
每人面对6个考官,面试不到10分钟。
1.进行自我陈述,如果有才艺的话在现场进行展示。
2.给出材料,上面有两个问题需要考生回答。
其中有一个版本是:1.谈谈你对小鲜肉和网红的看法。
2,有人认为科技使人越来越远,有人认为科技使人越来越近,你怎么看?有另一个版本是:1.模拟了一个场景:一男子进入动物园里老虎的散养场内,被多只老虎撕咬,最后幸被救出,但不久后因伤身亡。
你怎么看?2.室友在打游戏,声音过大影响他人休息,作为寝室长你会怎么做?。
