3+卡诺图化简法
卡诺图简单逻辑化简与五变量卡诺图化简

卡诺图简单逻辑化简与五变量卡诺图化简⼀、格雷码编码规则画卡诺图的时候需要先将所有变量可能以格雷码的形式排列在⽅格两侧,所有变量有2^n个,虽然我们常⽤的变量为四个及以下,可以熟记格雷码,但为了学习还是有必要了解格雷码的编码规则。
格雷码的基本特点就是任意两个相邻的代码只有⼀位⼆进制数不同,这样在数字电路中变化时每次就只有⼀位发⽣变化,提⾼了电路的稳定性。
规则:⾃然⼆进制数到格雷码:保留⼆进制码的最⾼位作为格雷码的最⾼位,⽽次⾼位格雷码为⼆进制码的⾼位与次⾼位相异或,⽽格雷码其余各位与次⾼位的求法相类似。
格雷码到⾃然⼆进制数:保留格雷码的最⾼位作为⾃然⼆进制码的最⾼位,⽽次⾼位⾃然⼆进制码为⾼位⾃然⼆进制码与次⾼位格雷码相异或,⽽⾃然⼆进制码的其余各位与次⾼位⾃然⼆进制码的求法相类似。
以⼀个四位⼆进制数来举例,⼆进制(abcd),依据规则转换为格雷码就是【a, (a^b), (b^c), (c^d)】,依据规则继续转化⼆进制的话就是【a, (a^a^b), (a^a^b^b^c), (a^a^b^b^c^c^d)】,化简之后仍然可以得到(abcd)。
⼆、卡诺图简单逻辑化简逻辑化简的实际⽬标是尽可能地减少表达式中包含的项数以及各项包含的变量数。
此图即为基本卡诺图的形式,如何画就不在赘述,两侧变量依据格雷码形式,⽬的就是画卡诺圈将⾥⾯的1全都包括在内,卡诺圈尽量⼤,卡诺圈的数量尽量少。
(a)卡诺图上处在相邻、相对、相重位置的⼩⽅格所代表的最⼩项为相邻最⼩项。
(b)两个⼩⽅格相邻, 或处于某⾏(列)两端时,所代表的最⼩项可以合并,合并后可消去⼀个变量。
(c) 四个⼩⽅格组成⼀个⼤⽅格、或组成⼀⾏(列)、或处于相邻两⾏(列)的两端、或处于四⾓时,所的表的最⼩项可以合并,合并后可消去两个变量。
(d) ⼋个⼩⽅格组成⼀个⼤⽅格、或组成相邻的两⾏(列)、或处于两个边⾏(列)时,所代表的最⼩项可以合并,合并后可消去三个变量。
逻辑函数的卡诺图法化简

精品课件
26
输入变量ABC取值为001、010、100时,
逻辑函数Y有确定的值,根据题意,有任一命令(正 转、反转和停止)时为1,否则为0。
反变 函换 数为
CD BD
CD
AB
00 01 11 10
Y AB AC BD CD AB
00 1
0
1
1
01 1
0
0
1
11 0
0
0
0
10 0
0
1
1
AC
精品课件
13
4、卡诺图的性质
(1)任何两个(21个)标1的相邻最小项,可以合并为一项, 并消去一个变量(消去互为反变量的因子,保留公因子)。
AB C
但是,若 F= ABCD+ABC+BC+ABC ,显然,该函数式
难于找到相邻项。
精品课件
1
2.4.2 逻辑函数的标准式——最小项表达 式
问题的提出:逻辑函数 F= ABC+ABC ,之所以易于看出它们 的乘积项是逻辑相邻项,是因为它们的每一个乘积项中都包 含了所有的变量。而F= ABCD+ABC+BC+ABC,每个乘积项没有 包含所有的变量,所以逻辑相邻关系不直观。于是引入了最 小项的概念。
15
AB CD
00 01 11 10
00 0
1
1
0
01 1 0 0 1
11 1
0
0
1 AD
10 0 1 1 0
BD
AB CD
00 01 11 10
00 1
0
0
1
01 0
1
1
0
11 0
《逻辑函数的卡诺图化简法》习题及参考答案
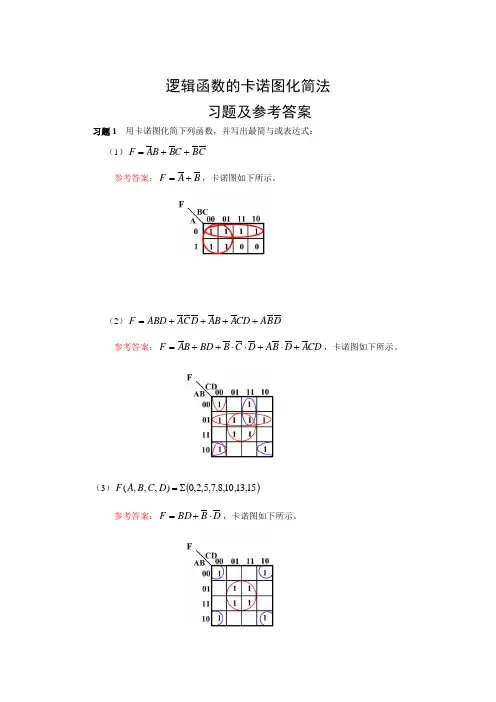
逻辑函数的卡诺图化简法 习题及参考答案习题1 用卡诺图化简下列函数,并写出最简与或表达式: (1)C B C B B A F ++=参考答案:B A F +=,卡诺图如下所示。
(2)D B A CD A B A D C A ABD F ++++=参考答案:CD A D B A D C B BD B A F +⋅+⋅⋅++=,卡诺图如下所示。
(3)()15,13,10,8,7,5,2,0),,,(∑=D C B A F参考答案:D B BD F ⋅+=,卡诺图如下所示。
习题2 用卡诺图化简下列具有约束条件为AB +AC = 0的函数,并写出最简与或表达式:(1)C A B A F +=参考答案:C A B F ⋅+=,卡诺图如下所示。
(2)D C B A D B A BD A C B A F +++=参考答案:D A C B F ++=,卡诺图如下所示。
习题3 根据如下真值表,写出逻辑函数。
化简此函数,并画出逻辑图。
A B C F 1 F 2 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 10 1 1 0 0 1 0 10 0 0 1 0 1 1 1参考答案:C B A AC C B ABC C B A C B A C B A F ++=+++⋅=1BC AC AB ABC C AB C B A BC A F ++=+++=2逻辑图如下所示:习题4 某逻辑电路有三个输入A 、B 、C ,当输入相同时,输出为1,否则输出为0,列出此逻辑事件的真值表,写出逻辑表达式。
参考答案:真值表如下图所示 逻辑表达式为ABC C B A F +⋅⋅=。
逻辑函数的卡诺图化简法

逻辑函数的卡诺图化简法逻辑函数的卡诺图化简法由前面的学习得知,利用代数法可以使逻辑函数变成较简单的形式。
但要求熟练掌握逻辑代数的基本定律,而且需要一些技巧,特别是经化简后得到的逻辑表达式是否是最简式较难确定。
运用卡诺图法可以较简便的方法得到最简表达式。
但首先需要了解最小项的概念。
一、最小项的定义及其性质1.最小项的基本概念由A、B、C三个逻辑变量构成的许多乘积项中有八个被称为A、B、C的最小项的乘积项,它们的特点是1. 每项都只有三个因子2. 每个变量都是它的一个因子3. 每一变量或以原变量(A、B、C)的形式出现,或以反(非)变量(A、B、C)的形式出现,各出现一次一般情况下,对n个变量来说,最小项共有2n个,如n =3时,最小项有23=8个2.最小项的性质为了分析最小项的性质,以下列出3个变量的所有最小项的真值表。
由此可见,最小项具有下列性质:(1)对于任意一个最小项,只有一组变量取值使得它的值为1,而在变量取其他各组值时,这个最小项的值都是0。
(2)不同的最小项,使它的值为1的那一组变量取值也不同。
(3)对于变量的任一组取值,任意两个最小项的乘积为0。
(4)对于变量的任一组取值,全体最小项之和为1。
3.最小项的编号最小项通常用mi表示,下标i即最小项编号,用十进制数表示。
以ABC为例,因为它和011相对应,所以就称ABC是和变量取值011相对应的最小项,而011相当于十进制中的3,所以把ABC记为m3按此原则,3个变量的最小项二、逻辑函数的最小项表达式利用逻辑代数的基本公式,可以把任一个逻辑函数化成一种典型的表达式,这种典型的表达式是一组最小项之和,称为最小项表达式。
下面举例说明把逻辑表达式展开为最小项表达式的方法。
例如,要将化成最小项表达式,这时可利用的基本运算关系,将逻辑函数中的每一项都化成包含所有变量A、B、C的项,然后再用最小项下标编号来代表最小项,即又如,要将化成最小项表达式,可经下列几步:(1)多次利用摩根定律去掉非号,直至最后得到一个只在单个变量上有非号的表达式;(2)利用分配律除去括号,直至得到一个与或表达式;(3)在以上第5个等式中,有一项AB不是最小项(缺少变量C),可用乘此项,正如第6个等式所示。
卡诺图化简逻辑函数

卡诺图化简逻辑函数的方法和理论依据摘要:从最小项的定义和性质入手,简述卡诺图化简逻辑函数的理论依据以及化简是否达到最简形式的判定标准。
通过举例来解释利用卡诺图化简少变量逻辑函数的一般方法,以及卡诺图在数字电子技术中其他应用。
另外介绍一种多变量逻辑函数的卡诺图解法。
关键词:卡诺图;最小项;逻辑函数化简;多变量0 引言在逻辑电路的分析和设计中,经常会遇到逻辑函数的化简问题。
如果利用常规的公式法化简,除需要掌握大量的基本公式外,还需要能够灵活、交替地运用各种方法,方可求得最简结果,而且有时不易判断是否已简化到最简形式,技巧性较强,对使用者的要求较高。
当所需化简的逻辑函数输入变量较少时(一般不大于4个),利用科诺图化简法可以更简单、直接的得到逻辑函数的最简表达式。
因此逻辑函数的卡诺图化简法在实际分析、设计电路时有很广泛的应用。
1 最小项定义及其性质1.1最小项的定义设有n个逻辑变量,由它们组成具有n个变量的“与”项中,每个变量以原变量或者反变量的形式出现一次且仅出现一次,则称这个与项为最小项。
对于n个变量来说,可有2n个最小项。
任何一个逻辑函数均可表示成惟一的一组最小项之和,称它为标准的与或表达式,也称为最小项表达式。
对于任意一个最小项,只有一组变量取值使它的值为1,而变量的其他取值都使该最小项为0。
事实上,真值表的每一行对应着一个最小项。
表(1)中列出了最小项取值为1时,各输入变量的取值。
我们约定:将最小项为l时各输入变量的取值视为二进制,其对应的十进制i作为最小项的编号,并把该最小项记作m i。
如A、B、C三个变量有2n =8个最小项,如表(1)所示。
图(1)1.2最小项的性质最小项具有以下三个性质:(1)全体最小项之和为1;(2)任意两个最小项之积为0;(3)若两个最小项之间只有一个变量不同,即在一个最小项中是原变量,在另一个最小项中是反变量,其余各变量均相同,则称这两个最小项是相邻项。
两个相邻的最小项之和可以合并成一个与项,并消去一个因子。
卡诺图化简
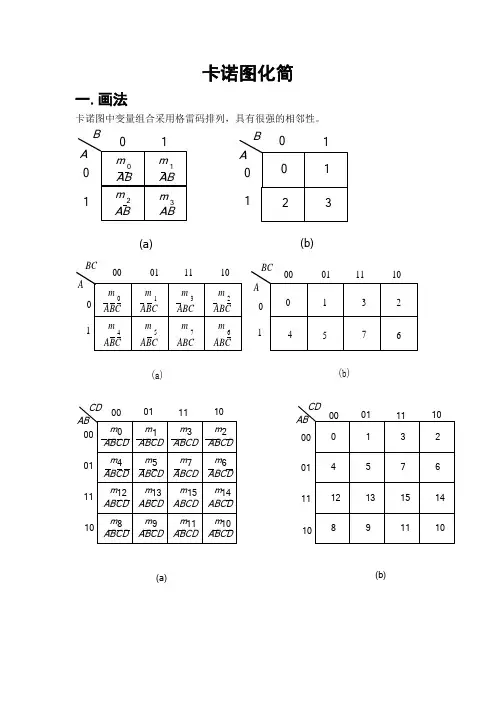
卡诺图化简一.画法卡诺图中变量组合采用格雷码排列,具有很强的相邻性。
0110m AB m AB1m 03m AB AB2(a)0132B (b)B A0101A0m ABC m ABC 1m 3m ABC ABC 265m ABC74ABCm m m ABCABC 0(a)(b)132457610011100BC A01BC A 1001110001m 0ABCD ABCD m 1ABCD m 3m ABCD 2m 567m m ABCD ABCD m ABCD 4ABCD ABCD m m 13ABCDABCD 1412m 15m ABCDABCDABCDm ABCD8m 1011m 9m ABCD 0132765413141512981110ABCD0000010*******10(a)(b)ABCD 0000010111111010二.步骤1.逻辑函数化为最小项表达式;写出最小项之和的形式、标准与或式2.根据变量的个数画出相应的卡诺图。
3.画卡诺圈并检查;填卡诺图(Y中包含的最小项填1),画包围圈(2n个相邻方格组,n=1,2,…4.将各卡诺圈合并为与项;各包围圈合并为一个与项(消去形式不同的变量,保留形式相同的变量5.将所有与项相加写出最简与或表达式合并后的各与项相加即为化简的逻辑函数三.注意:1.卡诺圈的面积要尽可能大,这样消去的变量就多,可保证与项中变量最少。
2.卡诺圈的个数要尽可能少,每个卡诺圈合并后代表一个与项,这样可保证与项最少。
3.每个卡诺圈内方格数为2n(n=0,1,2…),根据“去异留同”的原理将这2n个相邻的最小项结合,可以消去n个共有并且互补的变量而合并为一项。
4. 卡诺图中所有取值为1的方格均要被圈过,不能漏下。
5.取值为1的同一方格可被不同卡诺圈重复包围,但新增卡诺圈要有新方格。
6. 相邻方格包括上下相邻、左右相邻、四角相邻(注意对角不相邻)。
综上所述,画卡诺圈时应遵循先画大圈后画小圈的顺序,同时要保证圈内方格数为2n且不能漏下任何1方格。
卡诺图化简所应用的逻辑代数原理与方法
卡诺图化简所应用的逻辑代数原理与方法kamaugh map Simplification of the applicationof principles and methods of algebraic logic【摘要】逻辑代数卡诺图化简是数字电子技术的一个重要内容,本文讨论了卡诺图化简逻辑代数的化简原理以及基本方法。
卡诺图利用了格雷码的循环相接性质进行化简,采用画卡诺圈进行逻辑合并。
【关键词】逻辑代数;卡诺图;化简【Abstract】Simplifying logic function by kamaugh map is an important content of digital electronic technique. This paper explores the principle and basic methods of Simplifying logic function by kamaugh map.K-map use the cycle phase nature of the Gray code to simplifying logic function and use carnot cycle to merge logic.【Key Word】Logic Function;Karnaugh Map;Simplifying引言在ASIC设计和基于PLD的设计中,最小化都是一个重要的步骤。
多余的门和门输入端需要更多的面积,从而增加了成本。
但是在杂乱的代数符号中找出可结合的项是困难的。
卡诺图是逻辑函数真值表的图形表示,是一种更适于人工操作的最小化方法,其出发点是对真值表进行图形等效,它是通过一种直观形象、易于操作的方式来实现逻辑代数化简。
一、卡诺图化简的相关概念1、最小和:逻辑函数F的最小和是F的一个“积之和”表达式,F的其它“积之和”表达式不会比最小和最小和式中的乘积项更少。
描述卡诺图化简函数的三个原则
描述卡诺图化简函数的三个原则
卡诺图化简函数的三个原则:
1、只能对个相邻方格实施包围,包围圈越大,式子越简。
2、小方格可以重复包围,但每一包围必须含有一个未被包围过的方格,否则多余。
3、包围“1”格得原函数,包围“0”格得反函数,经二次求反后分别可用“与非”逻辑和“或非”逻辑实现。
卡诺图化简法是化简真值函数的方法之一,它具有几何直观性这一明显的特点,在变元较少的情况下比较方便,且能得到最简结果。
此法由卡诺于1953年提出,其具体步骤如下:
1.构造卡诺框;
2.在卡诺框上做出所给真值函数f的卡诺图;
3.用卡诺图化简真值函数,首先把相邻的1字块两两合成矩形得到一维块;把2个相邻的1字块合成矩形得到二维块;把2个相邻的1字块合成矩形得到三维块等,合成的各种维块统称f的合块;
4.把f的卡诺图中全部1字块做成若干个合块,这样一组合块就称为f的一个覆盖组,f 的一切覆盖组中所含块数最小的组即是f的最小覆盖组;
5.在最小覆盖组中,合块维数总和最大的组的对应式是f的最简式。
卡诺图化简法
卡诺图化简法
的项填到卡诺图中
表2.6.7 Y的卡诺图
例2.6.7 用卡诺图表示下面 的逻辑函数
CD AB 00 01 11 10
Y A' B'C' D A' BD' ACD AB'
00
1
A 01 1
1
解:其卡诺图如表 2.6.7所示
11
1
A
10 1 1 1 1
2.6.2 卡诺图化简法
从上面卡诺图可以看出
任意两个相邻的最小项 在图上是相邻的,并且图中 最左列的最小项与左右列相 应最小项也是相邻的(如m0 和m2, m9和m10 )。位于最上 面和最下面的相应最小项也 是相邻的( m0和m9 , m2和 m10),所以四变量的最小项 有四个相邻最小项。可以证 明n变量的卡诺图中的最小项 有n个相邻最小项
Y ( A, B,C) A AC BC ABC 解: Y的卡诺图如表2.6.9所示
表2.6.9 Y的卡诺图
BC
A 00 01 11 10
1
011 11
111 11
2.6.2 卡诺图化简法 练习:画出下列函数的卡诺图
Y1 AB B BCD
Y2 ( A, B,C, D) m(0,1,2,3,4,6,7,8,9,11,15)
2.6.2 卡诺图化简法 下面表2.6.1 是二变量的卡诺图
表2.5.10 二变量
十进 制数
A
B
mi
0 0 0 AB(m0)
1 0 1 AB(m1) 2 1 0 AB(m2 )
3 1 1 AB(m3)
表2.6.1 二变量的卡诺图
B A0
1
0 m0
m1
1 m2 m3
