理论力学习题答案第三章
理论力学习题答案

第三章 空间力系
一、是非题判断题
3.1.1对一空间任意力系,若其力多边形自行封闭,则该力系的主矢为零。 (∨)
平面力系中,若其力多边形自行闭合,则力系平衡。(×)
3.1.2只要是空间力系就可以列出6 个独立的平衡方程。 (×)
2.3.4悬臂式吊车的结构简图如图所示,由DE、AC二杆组成,A、B、C为铰链连接。已知P1=5kN,P2=1kN,不计杆重,试求杆AC杆所受的力和B点的支反力。
(答案:FBx=3.33kN,FBy=0.25kN,FAC=6.65kN)
2.3.5由AC和CD构成的组合粱通过铰链C连接,它的支承和受力如图所示,已知均布载荷强度q=10kN/m,力偶矩M=40kN.m,不计梁重,求支座A、B、D的约束反力和铰链C处所受的力。
3.1.3若由三个力偶组成的空间力偶系平衡,则三个力偶矩矢首尾相连必构成自行封闭的三角形。(∨)
3.1.4空间汇交力系平衡的充分和必要条件是力系的合力为零;空间力偶系平衡的充分和必要条件是力偶系的合力偶矩为零。(∨)
二、填空题
3.2.1若一空间力系中各力的作用线平行于某一固定平面,则此力系有5个独立的平衡方程。
3.3.3如图所示,三圆盘A、B、C的半径分别为15cm、10cm、5cm,三根轴OA、OB、OC在同一平面内,∠AOB为直角,三个圆盘上分别受三个力偶作用,求使物体平衡所需的力F和α角。
3.3.4某传动轴由A、B两轴承支承。圆柱直齿轮的节圆直径d=17.3cm,压力角 =20º,在法兰盘上作用一力偶矩为M=1030N.m的力偶,如轮轴的自重和摩擦不计,求传动轴匀速转动时A、B两轴承的约束反力。(答案:FAx=4.2kN,FAz=1.54kN,FBz=7.7kN,FBz.=2.79kN)
理论力学思考题习题答案

第一章 质点力学矿山升降机作加速度运动时,其变加速度可用下式表示:⎪⎭⎫ ⎝⎛-=T t c a 2sin1π 式中c 及T 为常数,试求运动开始t 秒后升降机的速度及其所走过的路程。
已知升降机的初速度为零。
解 :由题可知,变加速度表示为⎪⎭⎫ ⎝⎛-=T t c a 2sin1π 由加速度的微分形式我们可知dtdv a =代入得 dt T t c dv ⎪⎭⎫ ⎝⎛-=2sin 1π 对等式两边同时积分dt T t c dv t v⎰⎰⎪⎭⎫⎝⎛-=002sin 1π 可得 :D T t c T ct v ++=2cos 2ππ(D 为常数)代入初始条件:0=t 时,0=v , 故c T D π2-=即⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+=12cos 2T t T t c v ππ 又因为dtds v =所以 =ds dt T t T t c ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+12cos 2ππ 对等式两边同时积分,可得:⎥⎦⎤⎢⎣⎡⎪⎭⎫⎝⎛-+=t T t T T t c s 2sin 22212πππ 直线FM 在一给定的椭圆平面内以匀角速ω绕其焦点F 转动。
求此直线与椭圆的焦点M 的速度。
已知以焦点为坐标原点的椭圆的极坐标方程为()θcos 112e e a r +-=式中a 为椭圆的半长轴,e 为偏心率,常数。
解:以焦点F 为坐标原点题1.8.1图则M 点坐标 ⎩⎨⎧==θθsin cos r y r x 对y x ,两式分别求导⎪⎩⎪⎨⎧+=-=θθθθθθcos sin sin cos r r yr r x 故()()22222cos sin sin cos θθθθθθ r r r r y xv ++-=+=222ωr r+= 如图所示的椭圆的极坐标表示法为()θcos 112e e a r +-=对r 求导可得(利用ωθ= ) 又因为()()221cos 111ea e e a r -+-=θ即 ()rer e a --=21cos θ所以()()2222222221211cos 1sin e r e ar r ea --+--=-=θθ故有 ()2222224222sin 1ωθωr e a r e v +-=()2224221e a r e -=ω()()]1211[2222222e r e ar r e a --+--22ωr +()()⎥⎦⎤⎢⎣⎡--+-⋅-=2222222221121e e ar r r e e a r ω()r r a b r -=2222ω即 ()r a r br v -=2ω(其中()b a e b ,1222-=为椭圆的半短轴)质点作平面运动,其速率保持为常数。
理论力学3分析力学基础课后答案
代入拉格朗日方程,得
则 3-3
[
]
质量为 m 的质点悬在 1 线上,线的另 1 端绕在 1 半径为 R 的固定圆柱体上,如图
250
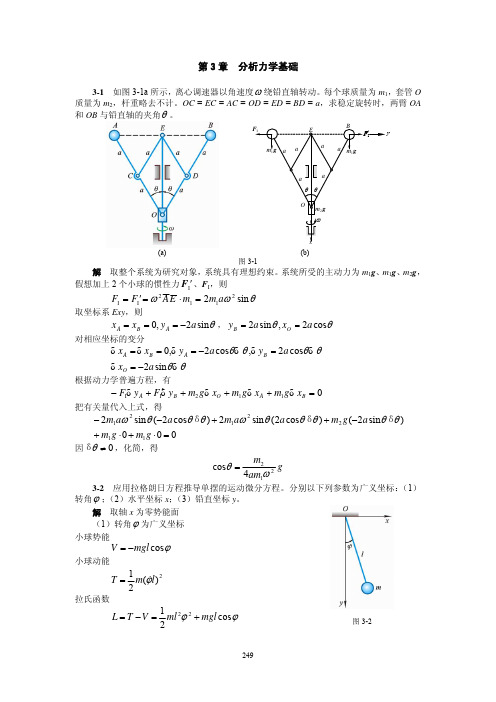
3-3 所示。设在平衡位置时,线的下垂部分长度为 l,且不计线的 质量。求此摆的运动微分方程。 解 取 θ 为广义坐标,设小球的静平衡位置为其零势能点。 系统势能
V = mg [(l + R sin θ ) − (l + θR ) cosθ ]
A
A x
& & x
θ
C
θ
FN
ϕ
θ −ϕ
l & ϕ 2 y
θ
& & x
θ
x′ B
C mg B
(c)
l && ϕ 2 y
(a)
& (见图 3-7b) & 、ϕ 解 2 自由度,给广义坐标 x, ϕ ,则广义速度为 x
(b) 图 3-7
l & & − cos(θ − ϕ )ϕ vCx = x 2 l & sin(θ − ϕ ) vCy = ϕ 2
x A = x B = 0, y A = −2a sin θ , y B = 2a sin θ , xO = 2a cosθ
对相应坐标的变分
δ x A = δ x B = 0,δ y A = −2a cosθδ θ ,δ y B = 2a cosθδ θ δ xO = −2a sin θδ θ
根据动力学普遍方程,有
系统动能
势能
m 2 m 2 l2 2 m 1 m 2 & 2 = (x & + ϕ & − lx &ϕ & cos(θ − ϕ )) + l 2ϕ &2 (vCx + vCy ) + ⋅ l 2ϕ 2 2 12 2 4 24 m 2 m 2 2 m & + lϕ & − lx &ϕ & cos(θ − ϕ ) = x 2 6 2 l V = − mgx sin θ − mg cos ϕ (设初始 A 处势能为零) 2 T= ∂L m & cos(θ − ϕ ) & − lϕ = mx & ∂x 2 d ∂L m m && cos(θ − ϕ ) − lϕ & sin(θ − ϕ )ϕ & & − lϕ ( ) = m& x & dt ∂x 2 2
理论力学习题及答案(全)

第一章静力学基础一、是非题1.力有两种作用效果,即力可以使物体的运动状态发生变化,也可以使物体发生变形。
()2.在理论力学中只研究力的外效应。
()3.两端用光滑铰链连接的构件是二力构件。
()4.作用在一个刚体上的任意两个力成平衡的必要与充分条件是:两个力的作用线相同,大小相等,方向相反。
()5.作用于刚体的力可沿其作用线移动而不改变其对刚体的运动效应。
()6.三力平衡定理指出:三力汇交于一点,则这三个力必然互相平衡。
()7.平面汇交力系平衡时,力多边形各力应首尾相接,但在作图时力的顺序可以不同。
()8.约束力的方向总是与约束所能阻止的被约束物体的运动方向一致的。
()二、选择题1.若作用在A点的两个大小不等的力F1和F2,沿同一直线但方向相反。
则其合力可以表示为。
①F1-F2;②F2-F1;③F1+F2;2.作用在一个刚体上的两个力F A、F B,满足F A=-F B的条件,则该二力可能是。
①作用力和反作用力或一对平衡的力;②一对平衡的力或一个力偶。
③一对平衡的力或一个力和一个力偶;④作用力和反作用力或一个力偶。
3.三力平衡定理是。
①共面不平行的三个力互相平衡必汇交于一点;②共面三力若平衡,必汇交于一点;③三力汇交于一点,则这三个力必互相平衡。
4.已知F1、F2、F3、F4为作用于刚体上的平面共点力系,其力矢关系如图所示为平行四边形,由此。
①力系可合成为一个力偶;②力系可合成为一个力;③力系简化为一个力和一个力偶;④力系的合力为零,力系平衡。
5.在下述原理、法则、定理中,只适用于刚体的有。
①二力平衡原理;②力的平行四边形法则;③加减平衡力系原理;④力的可传性原理;⑤作用与反作用定理。
三、填空题1.二力平衡和作用反作用定律中的两个力,都是等值、反向、共线的,所不同的是。
2.已知力F沿直线AB作用,其中一个分力的作用与AB成30°角,若欲使另一个分力的大小在所有分力中为最小,则此二分力间的夹角为度。
理力答案_第三章

3-1. 下述物体的约束属于何种约束?试写出约束方程。
(1) 如图(a )所示。
绳长l ,两端固定于A 、B 点,AB =a ,圆环M 可在绳上任意滑动,但不许达到天花板AB 上方,亦不可离开绳。
假设任何时刻绳索都绷紧。
(2) 放在水平地面上的物块M 。
(图b ) (3) 轮沿斜面纯滚动。
(图c )(4) 摇摆木马放在水平面上,且与水平面间无滑动。
(图d ) (5) 曲柄连杆机构的连杆AB 。
(图e )答:(1)由于A M B M l +=,代入AM BM = 得l =, 几何约束。
(2) 由于物块只能沿水平面运动,故 y=0, 几何约束。
(3)因为轮子做纯滚动,故轮心位移 O x r θ=,θ 为任一半径转角,两边对时间求导得 O x r θ=,运动约束。
(4) 因为轮子做纯滚动,故轮心位移 O x R ϕ=,φ 为任一半径转角,两边对时间求导得 O x R ϕ=,运动约束。
(5) 由于2222()B A A AB x x y l =-+=,代入A x 得)222BAx yl +=, 几何约束。
3-2在筒内放两个相同的球A和B,各重P,筒D重W,放在光滑的地面上,试画出:(1)球A及B,(2)球A和B一起,(3)筒D的受力图。
解:受力图如下:(1)球A及球B2(2)球A和球B一起(3)筒DCN1其中,14tanN N Pθ==,2cosN Pθ=,32N P=,52N W P=+,θ为A、B重心连线与竖直方向夹角。
3-3 构架ABC在O铰处连接一滑轮B,且在滑轮B上吊一重物W.。
试画:(1)弯杆AB,(2)弯杆BC,(3)滑轮B,(4)弯杆AB、BC作为整体的受力图。
解:弯杆AB,BC均为二力杆,受力分别沿AB,BC连线,如图1,2所示。
图3为滑轮B的受力图,图4为弯杆AB、BC作为整体的受力图。
图3 图43-4 若将图中的载荷P作用于铰链C处。
(1)试分别画出左、右两拱及销C的受力图;(2)若销钉C属于AC,分别画出左、右两拱的受力图;(3)若销钉C属于BC,分别画出左、右两拱的受力图。
理论力学习题答案

第一章静力学公理和物体的受力分析一、是非判断题1.1.1 在任何情况下,体内任意两点距离保持不变的物体称为刚体。
( ∨ ) 1.1.2 物体在两个力作用下平衡的必要与充分条件是这两个力大小相等、方向相反,沿同一直线。
( × )1.1.3 加减平衡力系公理不但适用于刚体,而且也适用于变形体。
( × ) 1.1.4 力的可传性只适用于刚体,不适用于变形体。
( ∨ ) 1.1.5 两点受力的构件都是二力杆。
( × ) 1.1.6只要作用于刚体上的三个力汇交于一点,该刚体一定平衡。
( × ) 1.1.7力的平行四边形法则只适用于刚体。
( × ) 1.1.8 凡矢量都可以应用平行四边形法则合成。
( ∨ ) 1.1.9 只要物体平衡,都能应用加减平衡力系公理。
( × ) 1.1.10 凡是平衡力系,它的作用效果都等于零。
( × ) 1.1.11 合力总是比分力大。
( × ) 1.1.12只要两个力大小相等,方向相同,则它们对物体的作用效果相同。
( × ) 1.1.13若物体相对于地面保持静止或匀速直线运动状态,则物体处于平衡。
( ∨ ) 1.1.14当软绳受两个等值反向的压力时,可以平衡。
( × ) 1.1.15静力学公理中,二力平衡公理和加减平衡力系公理适用于刚体。
( ∨ ) 1.1.16静力学公理中,作用力与反作用力公理和力的平行四边形公理适用于任何物体。
( ∨ ) 1.1.17 凡是两端用铰链连接的直杆都是二力杆。
( × ) 1.1.18 如图所示三铰拱,受力F ,F1作用,其中F作用于铰C的销子上,则AC、BC构件都不是二力构件。
( × )二、填空题1.2.1 力对物体的作用效应一般分为 外 效应和 内 效应。
1.2.2 对非自由体的运动所预加的限制条件称为 约束 ;约束力的方向总是与约束所能阻止的物体的运动趋势的方向 相反 ;约束力由 主动 力引起,且随 主动 力的改变而改变。
理论力学习题答案
静力学第一章习题答案1-3 试画出图示各结构中构件AB 的受力图1-4 试画出两结构中构件ABCD 的受力图1-5 试画出图a 和b 所示刚体系整体合格构件的受力图1-5a 1-5b1- 8在四连杆机构的ABCD 的铰链B 和C 上分别作用有力F 1和F 2,机构在图示位置平衡。
试求二力F 1和F 2之间的关系。
解:杆AB ,BC ,CD 为二力杆,受力方向分别沿着各杆端点连线的方向。
解法1(解析法)假设各杆受压,分别选取销钉B 和C 为研究对象,受力如图所示:由共点力系平衡方程,对B 点有:对C 点有:解以上二个方程可得:22163.1362F F F ==F 2F BC F ABB45oyxF BCF CDC 60oF 130oxy解法2(几何法)分别选取销钉B 和C 为研究对象,根据汇交力系平衡条件,作用在B 和C 点上的力对B 2BC F F =对C 点由几何关系可知: 0130cos F F BC =解以上两式可得:2163.1F F =静力学第二章习题答案2-3 在图示结构中,二曲杆重不计,曲杆AB 上作用有主动力偶M 。
试求A 和C 点处的约束力。
解:BC 为二力杆(受力如图所示),故曲杆AB 在B 点处受到约束力的方向沿BC 两点连线的方向。
曲杆AB 受到主动力偶M 的作用,A 点和B 点处的约束力必须构成一个力偶才能使曲杆AB 保持平衡。
AB 受力如图所示,由力偶系作用下刚体的平衡方程有(设力偶逆时针为正):其中:31tan =θ。
对BC 杆有:aM F F F A B C 354.0=== A ,C 两点约束力的方向如图所示。
2-4解:机构中AB 杆为二力杆,点A,B 出的约束力方向即可确定。
由力偶系作用下刚体的平衡条件,点O,C 处的约束力方向也可确定,各杆的受力如图所示。
对BC 杆有: 0=∑MF CD F AB030sin 20=-⋅⋅M C B F B对AB 杆有: A B F F = 对OA 杆有: 0=∑M01=⋅-A O F M A求解以上三式可得:m N M ⋅=31, N F F F C O AB 5===,方向如图所示。
理论力学课后习题答案整合
(a-1)第1篇 工程静力学基 础第1章 受力分析概述1-1 图a 、b 所示,Ox 1y 1与Ox 2y 2分别为正交与斜交坐标系。
试将同一力F 分别对两坐标系进行分解和投影,并比较分力与力的投影。
习题1-1图解:(a )图(c ):11 s i n c o s j i F ααF F +=分力:11 cos i F αF x = , 11 s i n j F αF y = 投影:αcos 1F F x = , αs i n 1F F y =讨论:ϕ= 90°时,投影与分力的模相等;分力是矢量,投影是代数量。
(b )图(d ):分力:22)cot sin cos (i F ϕααF F x -= ,22sin sin j F ϕαF y = 投影:αcos 2F F x = ,)cos(2αϕ-=F F y讨论:ϕ≠90°时,投影与分量的模不等。
(c )22x(d )C(a-2)DR(a-3)(b-1)1-2试画出图a和b两种情形下各物体的受力图,并进行比较。
DR习题1-2图比较:图(a-1)与图(b-1)不同,因两者之F R D值大小也不同。
1-3试画出图示各物体的受力图。
习题1-3图B或(a-2)B(a-1) (b-1) F(c-1) 或(b-2)1-4图a 所示为三角架结构。
荷载F 1作用在铰B 上。
杆AB 不计自重,杆BC 自重为W 。
试画出b 、c 、d 所示的隔离体的受力图,并加以讨论。
习题1-4图(e-1)1(f-1)(e-3)'A(f-2)1O(f-3) F AF BF AF(a)1-5 图示刚性构件ABC 由销钉A 和拉杆D 支撑,在构件C 点作用有一水平力F 。
试问如果将力F 沿其作用线移至D 或E (如图示),是否会改为销钉A 的受力状况。
解:由受力图1-5a ,1-5b 和1-5c 分析可知,F 从C 移至E ,A 端受力不变,这是因为力F 在自身刚体ABC 上滑移;而F 从C 移至D ,则A 与ABC为不同的刚体。
力学第三章标准答案
力学第三章答案————————————————————————————————作者:————————————————————————————————日期:3.5.1 质量为2kg 的质点的运动学方程为j t t i t r ˆ)133(ˆ)16(22+++-=ρ(单位:米,秒), 求证质点受恒力而运动,并求力的方向大小。
解:∵j idt r d a ˆ6ˆ12/22+==ρρ, j i a m F ˆ12ˆ24+==ρρ为一与时间无关的恒矢量,∴质点受恒力而运动。
F=(242+122)1/2=125N ,力与x 轴之间夹角为:'34265.0/︒===arctg F arctgF x y α3.5.2 质量为m 的质点在o-xy 平面内运动,质点的运动学方程为:j t b i t a r ˆsin ˆcos ωω+=ρ,a,b,ω为正常数,证明作用于质点的合力总指向原点。
证明:∵r j t b it a dt r d a ρρρ2222)ˆsin ˆcos (/ωωωω-=+-== r m a m F ρρρ2ω-==, ∴作用于质点的合力总指向原点。
3.5.3 在脱粒机中往往装有振动鱼鳞筛,一方面由筛孔漏出谷粒,一方面逐出秸杆,筛面微微倾斜,是为了从较低的一边将秸杆逐出,因角度很小,可近似看作水平,筛面与谷粒发生相对运动才可能将谷粒筛出,若谷粒与筛面静摩擦系数为0.4,问筛沿水平方向的加速度至少多大才能使谷物和筛面发生相对运动?解:以地为参考系,设谷物的质量为m ,所受到的最大静摩擦力为 mg f oμ=,谷物能获得的最大加速度为2/92.38.94.0/s m g m f a o =⨯===μ ∴筛面水平方向的加速度至少等于3.92米/秒2,才能使谷物与筛面发生相对运动。
μ1 μ23.5.3 题图 3.5.4题图3.5.4 桌面上叠放着两块木板,质量各为m 1 ,m 2,如图所示,m 2和桌面间的摩擦系数为μ2,m 1和m 2间的摩擦系数为μ1,问沿水平方向用多大的力才能把下面的木板抽出来。
理论力学习题(3)
第三章 思考题3.1 刚体一般是由n (n 是一个很大的数目)个质点组成,为什么刚体的独立变量却不是3n 而是6或者更少?答:若组成刚体的每个质点都是自由质点,则质点的自由度为3n ,但刚体在运动中形状不变,各质点间的距离保持不变。
组成刚体的质点不是完全自由的,因而刚体的自由度大大少于3n 。
事实上,对于自由刚体,确定其位置只要确定其中任意不共线的3点的位置就行了,确定3点的位置需要9个变量,考虑到3点之间3个距离不变,9个变量之间有3个约束方程,所以独立变量共有6个。
若刚体不是自由的,还受到其它约束,独立变量的个数还可能少于6个。
3.2 何谓物体的重心?它和质心是不是总是重合在一起的?答:物体各部分所受重力的合力作用点叫做物体的重心。
在一般情况下,物体各部分所受重力的方向是平行的,那么,重心就是平行力系的中心,且无论物体方位如何,其重心在物体内的位置不变。
当物体中各部分重力加速度相同时,物体的重心和质心重合,若物体各部分重力加速度不同,重心可能与质心不重合,由于物体的大小比地球小得多,物体各部分重力加速度的差异实际上观察不到,所以可以认为重心和质心是重合的,但重心和质心是两个完全不同的概念,质心只与物体的质量分布有关,完全由物体本身性质决定,而与重力是否存在无关。
因此,质心的概念比重心具有更重要的意义。
3.3 试讨论图形的几何中心、质心和重心重合在一起的条件。
答:当物体质量均匀分布,物体各部分重力加速度都相同时,物体的几何中心、质心和重心三者重合。
3.4 简化中心改变时,主矢和主矩是不是也要随着改变?如果要改变,会不会影响刚体的运动?答:简化中心改变时,主矢不变,主矩改变。
这种主矩的改变,不会影响刚体的运动。
因为力系对任意简化中心的主矩和主矢都是和原力系等效的,它们对刚体运动产生的效果是等效的。
3.5 已知一均匀棒,当它绕其一端并垂直于棒的轴转动时,转动惯量为231ml ,m为棒的质量,l 为棒长。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章思考题解答3.1 答:确定一质点在空间中得位置需要3个独立变量,只要确定了不共线三点的位置刚体的位置也就确定了,故须九个独立变量,但刚体不变形,此三点中人二点的连线长度不变,即有三个约束方程,所以确定刚体的一般运动不需3n 个独立变量,有6个独立变量就够了.若刚体作定点转动,只要定出任一点相对定点的运动刚体的运动就确定了,只需3个独立变量;确定作平面平行运动刚体的代表平面在空间中的方位需一个独立变量,确定任一点在平面上的位置需二个独立变量,共需三个独立变量;知道了定轴转动刚体绕转动轴的转角,刚体的位置也就定了,只需一个独立变量;刚体的平动可用一个点的运动代表其运动,故需三个独立变量。
3.2 答物体上各质点所受重力的合力作用点即为物体的重心。
当物体的大小远小于地球的线度时物体上各质点所在点的重力加速度都相等,且方向彼此平行即重力场为均匀场,此时质心与重心重合。
事实上但物体的线度很大时各质点所在处g 的大小是严格相等,且各质点的重力都指向地心,不是彼此平行的,重心与质心不和。
3.3答 当物体为均质时,几何中心与质心重合;当物体的大小远小于地球的线度时,质心与重心重合;当物体为均质且大小远小于地球的线度时,三者都重合。
3.4 答 主矢F 是力系各力的矢量和,他完全取决于力系中各力的大小和方向,故主矢不随简化中心的位置而改变,故而也称之为力系的主矢;简化中心的位置不同,各力对简化中心的位矢i r 也就不同则各力对简化中心的力矩也就不同,故主矩随简化中心的位置而变,被称之为力系对简化中心的主矩。
分别取O 和O '为简化中心,第i 个力i F 对O 和O '的位矢分别为i r 和i r ',则i r =i r '+O O ',故()()iii ii i O F O O r F r M ⨯'-'=⨯'=∑∑'()∑∑⨯'-⨯'=ii ii i F O O F r ∑⨯'+=ii o F O O M即o o M M ≠'主矢不变,表明刚体的平动效应不变,主矩随简化中心的位置改变,表明力系的作用对刚体上不同点有不同的转动效应,但不改变整个刚体的转动规律或者说不影响刚体绕质心的转动。
设O 和O '对质心C 的位矢分别为C r 和C r ',则C r '=C r +O O ',把O 点的主矢∑=ii F F ,主矩oM移到C 点得力系对重心的主矩∑⨯+=ii C o C F r M M把O '为简化中心得到的主矢∑=ii F F 和主矩o 'M移到C 点可得∑⨯+'=ii C oC F r M M ()∑⨯'-'+=ii C o F O O r M ∑⨯+=ii C o F r M简化中心的改变引起主矩的改变并不影响刚体的运动。
事实上,简化中心的选取不过人为的手段,不会影响力系的物理效应。
3.5 答 不等。
如题3-5图示,l题3-5图dx lm dm =绕Oz 轴的转动惯量 22243424131487⎪⎭⎫ ⎝⎛+≠==⎰-l m ml ml dx l m x I l l z这表明平行轴中没有一条是过质心的,则平行轴定理2md I I c +=是不适应的3.6不能,如3-5题。
但平行轴定理修改后可用于不过质心的二平行轴。
如题3-6图所示,Bl题3-6图均质棒上B A ,二点到质心的距离分别为A x 和B x 由平行轴定理得:2A c A mx I I +=2B c B mx I I +=则()22B A B A x x m I I -=-,此式即可用于不过质心的二平行轴。
如上题用此式即可求得:22224872431m l l l m m l I z =⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛+= 3.7 答 任一瞬时,作平面平行运动的刚体上或与刚体固连且与刚体一起运动的延拓平面总有也仅有一点的瞬时速度为零(转动瞬心)从运动学观点看由(3.7.1)式()0r r ωv ωv v -⨯+='⨯+=A A r知选此点的基点较好,这样选基点,整个刚体仅绕此点作瞬时转动从(3.7.4)式2A ωr r d d ωa a '-'⨯+=t可知,求加速度时选加速度为零的点为基点较方便,但实际问题中,加速度瞬心往往不如速度瞬心好找。
从动力学角度考虑,选质心为基点较好,因质心的运动可由质心运动定理解决;而且质点系相对质心的动量矩定理于对固定点的动量矩定理具有相同的形式,亦即刚体绕过质心与平面垂直的轴的转动可用刚体绕定轴转动的定律去解决。
因刚体上不同点有不同的速度和加速度,基点选取的不同,则(3.7.1)和(3.7.4)式中A A a v ,不同,即A v 和A a 与基点有关;又任一点相对基点的位矢r '于基点的选取有关。
故任一点绕基点转动速度r ω'⨯,相对基点的切线加速度r d d ω'⨯t和相对基点的向心加速度2ωr -与基点选取有关;角速度ω为刚体各点所共有与基点选取无关,故td d ω也与基点选取无关;基点选取的不同是人为的方法,它不影响刚体上任一点的运动,故任一点的速度a v ,与基点的选取无关。
这也正是基点选取任意性的实质所在。
3.8 答 转动瞬心在无穷远处,标志着此瞬时刚体上各点的速度彼此平行且大小相等,意味着刚体在此瞬时的角速度等于零,刚体作瞬时平动3.9 答 转动瞬心的瞬时速度为零,瞬时加速度并不为零,否则为瞬时平动瞬心参考系是非惯性系,应用动量矩定理是必须计入惯性力系对瞬心的力矩。
而惯性力系向瞬心简化的结果,惯性力系的主矩一般不为零(向质心简化的结果惯性力系的主矩为零),故相对瞬心与相对定点或者质心的动量矩定理有不同的形式;另外,转动瞬心在空间中及刚体上的位置都在不停的改变,(质心在刚体上的位置是固定的),故对瞬心的写出的动量矩定理在不同时刻是对刚体上不同点的动力学方程,即瞬心参考系具有不定性;再者,瞬心的运动没有像质心一点定理那样的原理可直接应用。
故解决实际问题一般不对瞬心应用动量矩定理写其动力学方程。
3.10 答 因圆柱体沿斜面滚下时,圆柱体与斜面之间的反作用力不做功,只有重力作功,故机械能守恒且守恒定律中不含反作用,故不能求出此力。
此过程中由于圆柱体只滚动不滑动,摩擦力做功为零,故不列入摩擦力的功,也正是摩擦力不做功才保证了机械能守恒;若圆柱体即滚且滑的向下运动,摩擦力做功不为零免责必须列入摩擦力的功。
机械能不守恒,必须用动能定理求解。
在纯滚动过程中不列入摩擦力的功并不是没有摩擦力,事实上,正是摩擦力与重力沿下滑方向的分离组成力偶使圆柱体转动且摩擦阻力阻止了柱体与斜面的相对滑动,才使圆柱体沿斜面滚动而不滑动;如果斜面不能提供足够的摩擦力,则圆柱体会连滚带滑的向下运动;如果斜面绝对光滑,即斜面对圆柱体不提供摩擦力,则圆柱体在重力作用下沿斜面只滑动不滚动。
答 圆柱体沿斜面无滑动滚动,如课本195页例[2]示,θ a xc =,当柱体一定时,相对质心的转动惯量越大则θ 越小,故与转动惯量有关。
当圆柱体沿斜面既滚动又滑动地向下运动时,如课本图3.7.7有f mg xm -=αsin 这里f 是滑动摩擦力,αμμcos mg n f ==,μ是滑动摩擦系数,(注意,无滑动时,静摩擦力f 并不一定达到极限值,nf μ'≠,μ'是静摩擦系数)、所以()αμαcos sin -=g xc 与转动惯量无关。
又有转动定律得fa I =θ即 αμθcos Iamg = 由S a xc +=θ得圆柱与斜面的相对滑动加速度 ()αμαμαcos cos sin 2g Ima g S --= 与转动惯量有关 3.11 答3.12 答 刚体绕定点转动时,()t ωω=的大小、方向时刻改变,任意时刻ω所在的方位即为瞬时转轴,r ω⨯dtd 表示由于ω大小和方向的改变引起的刚体上某但绕瞬时轴的转动速度,故称转动加速度。
()v ωr ωω⨯=⨯⨯是由于刚体上某点绕瞬时轴转动引起速度方向改变产生的加速度,它恒垂直指向瞬时转轴,此方向轨迹的曲率中心或定点,故称向轴加速度而不称向心加速度。
第三章习题3.2解 如题3.2.1图所示,图题1.3.2均质棒分别受到光滑墙的弹力1N ,光滑棱角的弹力2N ,及重力G 。
由于棒处于平衡状态,所以沿y 方向的合力矩为零。
即0cos 2=-=∑G N Fyθ①0cos 22cos 2=-=∑θθlG d N M z 由①②式得: ld =θ3cos所以 31arccos ⎪⎭⎫ ⎝⎛=l d θ 3.3解 如题3.3.1图所示。
图题1.3.32AB 棒受到重力i G ag ρ=1。
棒受到的重力i G bg ρ=2。
设均质棒的线密度为ρ。
由题意可知,整个均质棒沿z 轴方向的合力矩为零。
()BHBF G OD G Mz--⋅=∑21sin θ=0sin cos 2sin 2=⎪⎭⎫ ⎝⎛--θθρθρa b gb a gaaba b 2tan 22+=θ 3.4解 如题3.4.1图。
图题1.3.4Ox 轴竖直向下,相同的球A 、B 、C 互切,B 、C 切于D 点。
设球的重力大小为G ,半径为r ,则对A 、B 、C 三个球构成的系统来说,在x 轴方向的合力应为零。
即:0cos 23=-=∑αT G Fx①对于C 球,它相对于过D 点与z 轴平行的轴的合力矩等于零。
即:()0sin sin =--=∑βαβGr Tr MD②由式得: αβtan 3tan = 3.5解 如题3.5.1图。
1图题1.3.5梯子受到地面和墙的弹力分别为1N ,2N ,受地面和墙的摩擦力分别为1f ,2f 。
梯子和人的重力分别为1G ,2G 且123G G =。
设梯长为l ,与地面夹角为θ。
由于梯子处于平衡,所以012=-=∑f N F x①02112=--+=∑G G N f Fy②且梯子沿过A 点平行于z 轴的合力矩为零。
即:sin cos cos 2cos 2212=--+=∑θθθθl N l f lG l G M i ③又因梯子是一个刚体。
当一端滑动时,另一端也滑动,所以当梯与地面的倾角达到最小时,1121N f =④ 2231N f =⑤ 由①②③④⑤得:2441tan =θ所以 ⎪⎭⎫ ⎝⎛=-2441tan 1θ 3.6解 (a )取二原子的连线为x 轴,而y 轴与z 轴通过质心。
O 为质心,则Ox ,Oy ,Oz 轴即为中心惯量主轴。
y1m 2m C hax ∙1m 图题1.3.6设1m 、2m 的坐标为()()0,0,,0,0,21ll ,因为O 为质心(如题3.6.2图)故 02211=+l m l m ① 且 l l l =-12 ② 由①②得21122121,m m lm l m m l m l +=+-= 所以中心惯量主轴:()0221=+=∑i i i z y m I()22121222l m m m m x z m I i i i +=+=∑()22121223l m m m m y x m I i i i +=+=∑(b )如题3.6.3图所示, 图题3.6.3该原子由A 、B 、D 三个原子构成。
