金尚年版理论力学第二版答案5章
高等教育出版社_金尚年_马永利编著的理论力学课后习题答案
高等教育出版社，金尚年，马永利编著的理论力学课后习题答案第一章1.2afG — sin0)；殳上运动的质点的微写出约束在铅直平面内的光滑摆线afl - COS0)分方程，并证明该质点在平衡位置附近作振动时，振动周期与振幅无关.解：设s为质点沿摆线运动时的路程，取0=0时，s=0H ( x = a(0-sine) * ly = —a(l — COS0)ds - J (dx)2 + (dy)2 二J((i9 — COS0 亠de)2+(sirL9 de)2 = 2asin|2a sin舟dO = 4 a (L co 马ee As=2acos^59 + 2asin?9 = acos| 9^ + 2a sin? 9x轴的夹角，取逆时针为正，tan (p即切线斜率设（P为质点所在摆线位置处切线方向与dy cos 0 -1 tan <p =—=———〒dx sin 01聶siin<p = -cosI受力分析得:ms = —mg sin （p = mg cos-0 •・B・r a贝U2a sin二6 + a cos二6' = geos-，此即为质点的运动微分方程。
S = =（S = 4a）-（S 二4a） + —（s = 4a） =4a—周期性变化的函数，周期T=2TT产P e 该质点在平衡位置附近作振动时，振动周期与振幅无关，为2讥启.1.3证明：设一质量为m的小球做任一角度日0的单摆运动运动微分方程为m（2 + 2「日）=F gmrO = mg sin £给式两边同时乘以d9 r日d£=gsind8对上式两边关于6积分得护jgcog + c利用初始条件日=日0时日=0故c = -gcos£0由可解得0 =-{2& • J c 0 s-c 0 8o上式可化为-岸•J cos。
-cosgd日=dt两边同时积分可得 评J ； J co £o 页迅咼.1卑匸萼严进-步化简可得t 辟 J 站n r由于上面算的过程只占整个周期的1/4故由 s in 2/sin ¥=s z 两边分别对6 3微分可得cos % =s 碍C 。
高等教育出版社_金尚年_马永利编著的理论力学课后习题答案
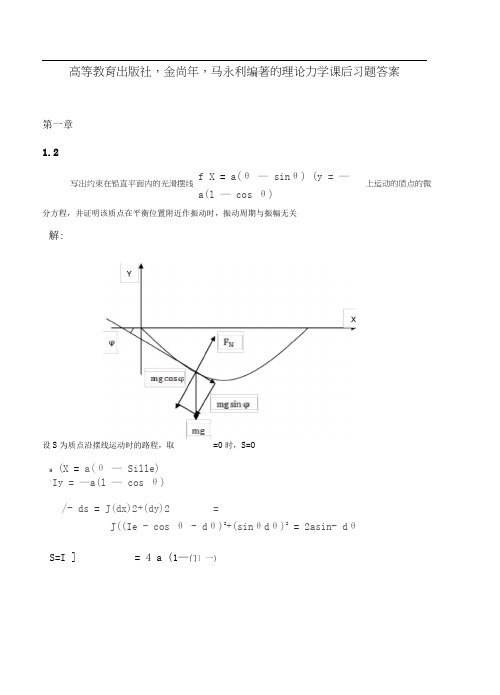
高等教育出版社，金尚年，马永利编著的理论力学课后习题答案第一章1.2f X = a(θ — sinθ) (y = —a(l — cos θ)分方程，并证明该质点在平衡位置附近作振动时，振动周期与振幅无关解:设S 为质点沿摆线运动时的路程，取=0时，S=OH (X = a(θ — Sille) ,Iy = —a(l — cos θ) /- ds = J(dx)2+(dy)2=J((Ie - cos θ - dθ)2+(sinθdθ)2= 2asin- dθS=I ]= 4 a (1—门〕一)写出约束在铅直平面内的光滑摆线上运动的质点的微S = 2acosθ-θ + 2asiιι-θ = a cos - θ2+ 2a Sin-θ2 2 2 2 2设:为质点所在摆线位置处切线方向与 X 轴的夹角，取逆时针为正，L 二弔即切线斜率dy COS θ -1tan φ = — = ——dx sιnθ受力分析得:InS = —mg sin φ = mg cos yΩ .. Ω . - Ω 则1 ' : . 一，此即为质点的运动微分方程。
2 2 t52S =鲁(S — 4a)Λ (S - 4a) + ~(β — 4a) = 01.3证明：设一质量为m 的小球做任一角度Λ的单摆运动运动微分方程为m(L ∙2L )=F ,mr J - mg Sin给 式两边同时乘以LdV-gsind^ 对上式两边关于T 积分得1L 2=gcos*c2利用初始条件V - J 0时V - 0故c = -g COS 71由 可解得 日=-* JC o S - c o So上式可化为-\：丰∙Jcos 日-CoS 日0 日=Zdt・s - 4a —周期性变化的函数，周期T = 2π该质点在平衡位置附近作振动时，振动周期与振幅无关，为进一步化简可得sin 2? —sin 22°由于上面算的过程只占整个周期的1/4故由 Sin /sin - = Sin2 2两边分别对二「微分可得COSEdV - Sin -cos ：:d ：:2 2COSAJIYin 学sin^Sin -cos tP故dr -2 ------- 2 d ‘ I I-Si n 2 电 Si n2 CP \ 2 由于Or VvO 故对应的0 <2—CoSe ∕J 1 —s in 2电 S in 2 申2 2d 「Sin cos : 2故T =4l 2-- d其中 K 2=sin 2玉Y g J 1—K 2sin 2 半2通过进一步计算可得T 仔1 [1 (1* (jκ-(1 3 5 (2n」)*「•]Vg 22江42^4><6汇…Tne 二 Sin 2 2 两边同时积分可得701故T =2.2^0 ■Sin Si n —2 21.5M 为地球的质量；可知，地球表面的重力加速度 g , X 为取地心到无限远的广义坐标,【I ：二 Ill- 「，②联立①，②可得:岂 仃；,M 为地球的质量；③解:如图，在半径是R 的时候，由万有引力公式, 对表面的一点的万有引力为PMm* 一 ,①R a当半径增加,R2=R+jl ,此时总质量不变，仍为M,此时表面的重力加速度1可求:由④得:对⑥式进行通分、整理后得：AGM ΔR 3+2ΔRR8 =R 7 CR+ΔR)2A2ΔR R 2AR⑧则当半径改变J N 时，表面的重力加速度的变化为:A2ΔRR2AR =S —。
理论力学 第二版 (金尚年 马永利 著) 高等教育出版社 课后答案 1-4章答案
G F
课
w.
θ
cos − − cos
kh
运动方程为 ̇ 2 Fr 0 ̈ − r mr ̈ 2r ̇ F ̇ mr 由径向方程 ̇ ̈ r 2 r 方程的解为 r Ae t Be −t 带入初始条件
da
x
R2 z2 r2
课
2.9 体系的动能为
后
̇ sin cos 0 ̈ sin 2 2mr 2 ̇ mr 2
网
−
∂L ∂
ww
w.
kh
da
w.
co
m
5
d ∂L − ∂L ̇ dt ∂ ∂ 2 ̈ ̇ 0 ̇ mr 2mrr 2.11 体系的动能为 T 势能为 V mgz mg R 2p 该体系只有一个自由度，取R为广义坐标，拉各朗日函数为 ̇2 2 ̇ 2 R22 R L m R R − mg R 2 2p p2 相应的拉各朗日方程为 d ∂L − ∂L ̇ dt ∂R ∂R ̇2 mg ̈ 1 R 2 2m R mR R − mR 2 2 2p p p2 ̇ 0，R ̈ 0则 对于平衡点R g R 2p 2 m R ̇ 2 R2 ̇2 z ̇ 2 2 ̇2 2 m R ̇ 2 R22 R R 2 p2
课
后
答 案
网
Chap3
7
ww
w.
kh
da
w.
co
m
3.1 tanh
L r2
dr
a r2
2mE
L r2
−
L r2
dr
2ma−L 2 r2
E
金尚年版理论力学第二版答案
v E v E = 0 er R
v v 和均匀磁场 B = B 0 k
v &v v v & & v = R e r + R ϕ eϕ + z e z
qE && & & mR − mRϕ 2 − 0 − qB0 Rϕ = 0 R 化简得： d qB & (mR2ϕ + 0 R2 ) = 0 2 dt d & dt (mz) = 0
4R 2 & 2 m &2 mg 2 2 &2 ( R + R θ + 2 R )− R L = T −V = 2 a a 代入完整保守体系的拉格朗日方程，并化简得
4 R 2 && 8 R & 2 2 gR 1 + R + 2 R − R θ& 2 + = 0 2 a a a && && R θ + 2θ R = 0
M R o'
m 2 & & T = ( r + r 2ϕ 2 ) 2
由几何关系：
∴
V =0
θ ωt
o
x
r = cos θ , ϕ = θ + ω t 2R m L = T −V = ( − 2 R sin θ ⋅ θ& ) 2 + (θ& + ω ) 2 ⋅ ( 2 R cos θ ) 2 2 = 2 mR 2 ⋅ (θ& 2 + 2ω θ& cos 2 θ + ω 2 cos 2 θ )
α
2.7 用拉格朗日方程写出习题1.21的运动微分方程 解：建立柱坐标系，取R，ϕ 为广义坐标
高等教育出版社,金尚年,马永利编著的理论力学课后习题答案
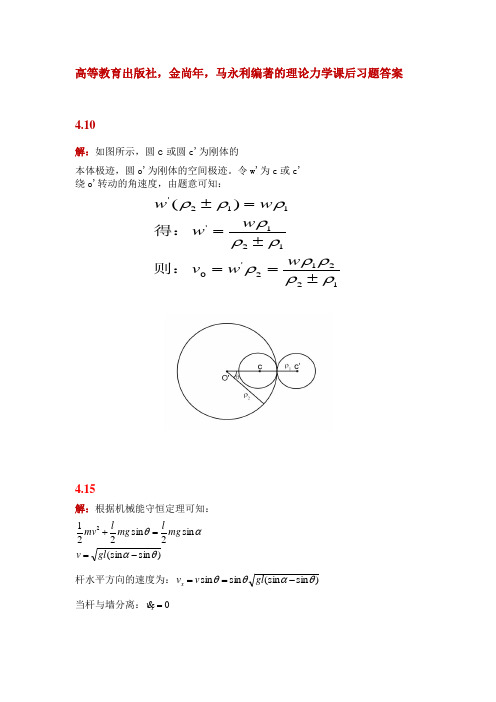
高等教育出版社，金尚年，马永利编著的理论力学课后习题答案 4.10解：如图所示，圆c 或圆c'为刚体的本体极迹，圆o'为刚体的空间极迹。
令w'为c 或c' 绕o'转动的角速度，由题意可知：12212'0121'112')(ρρρρρρρρρρρ±==±==±w w v w w w w 则：得：4.15解：根据机械能守恒定理可知：)sin (sin sin 2sin 2212θααθ-==+gl v mg lmg l mv 杆水平方向的速度为：)sin (sin sin sin θαθθ-==gl v v x当杆与墙分离：0=x v即：0)sin (sin cos )sin (sin cos sin 21=-+--=θαθθαθθgl gl gl v dt d x得：θαsin 23sin = 即：)sin 32arcsin(αθ=4.19如图，该体系中只有一个自由度，取任意位置时棒中点与O 连线与竖直线的夹角θ为广义坐标。
其中设棒的质量为m ，圆周的半径为r ，则棒长为r 3。
另取O 点为重力势能零点。
则对棒θθcos 21212r mg I L o += ，()2221331⎪⎭⎫⎝⎛+=r m r m I o 为棒对O 点的转动惯量。
代入0=∂∂-∂∂θθL L dt d ，得0sin 214522=+θθmgr mr 用θθ=sin 代替，得方程为052=+θθrgrg52=ω，而对于单摆，lg =ω 所以对比得25r l =即等值单摆摆长为25r l =4.20解：如图：设球的半径为R ,设经过时间t 后，会达到如图所示状态，所有参量如图所示。
对其运用牛顿力学方法，有mgRI FR mgma a m F μαμ====''=252mR I =tatv t a v v αω=='=-110同时有对于纯滚动，有 ugtRgt v m m gtv v 25110=='-=ωμμ解上述方程，得代入会得所以有4.23求均匀圆锥体底面圆周上一点的惯量椭球方程。
理论力学(金尚年-XXX编著)课后习题答案详解
理论力学(金尚年-XXX编著)课后习题答案详解高等教育出版社的《理论力学课后题答案》一书中，第一章包含了以下三个问题的解答：1.2 题目要求写出在铅直平面内的光滑摆线，并分方程。
解答中使用了微积分和力学原理，得出了运动微分方程。
最后证明了质点在平衡位置附近作振动时，振动周期与振幅无关。
1.3 题目要求证明单摆运动的振动周期与摆长无关。
解答中使用了微积分和力学原理，得出了运动微分方程。
最后通过进一步计算，得出了单摆运动的振动周期公式。
1.5 题目要求使用拉格朗日方程计算质点的运动。
解答中使用了拉格朗日方程，并通过进一步计算得出了质点的运动轨迹。
如图，在半径为R时，地球表面的重力加速度可以由万有引力公式求得：g=\frac{GM}{R^2}$$其中M为地球的质量。
根据广义相对论，地球表面的重力加速度还可以表示为：g=\frac{GM}{R^2}\left(1-\frac{2GM}{c^2R}\right)$$其中c为光速。
当半径增加到R+ΔR时，总质量仍为M，根据XXX展开，可以得到：frac{1}{(R+\Delta R)^2}=\frac{1}{R^2}-\frac{2\DeltaR}{R^3}+\mathcal{O}(\Delta R^2)$$代入上式可得：g'=\frac{GM}{R^2}\left(1-\frac{2GM}{c^2R}\right)\left(1+\frac{2\Delta R}{R}\right)$$ 化简后得：g'=g-\frac{2g\Delta R}{R}$$因此，当半径改变时，表面的重力加速度的变化为：Delta g=-\frac{2g\Delta R}{R}$$2.在平面极坐标系下，设质点的加速度的切向分量和法向分量都是常数，即$a_t=k_1$，$a_n=k_2$（其中$k_1$和$k_2$为常数）。
根据牛顿第二定律，可以得到质点的运动方程：r\ddot{\theta}+2\dot{r}\dot{\theta}=k_2$$ddot{r}-r\dot{\theta}^2=k_1$$其中$r$为极径，$\theta$为极角。
理论力学第五章习题答案
& = ak sin kt y
得
积分得 s = 4a (1 − cos
kt ) 2
5.3
根据下列点在极坐标系中的轨迹方程
试写出点的直角坐标轨迹方程
式中 p
e 均为正的常数
1
ρ=
p 1 + e cos ϕ p 1 − e cos ϕ p 1 − cos ϕ
e <1
2
ρ=
e >1
3 解
ρ=
直角坐标与极坐标有以下关系:
与 前 题 相 比 仅
e 差 一 符 号
→ (1 − e 2 ) x 2 + y 2 − 2 pex − p 2 = 0
3
ρ=பைடு நூலகம்
p 1 − cos ϕ
与 前 题 相 比
只 要 令 前 题 中 e =1 即 可
→ y 2 − 2 px − p 2 = 0
5.4 加速度 解
试以直角坐标及其导数表示 x = a ( kt − sin kt ) 切向加速度 法向加速度以及轨迹的曲率半径
sin γ = Rω / v
则由式 (**) 得 ρ = v / Rω = R / sin γ
2
2
2
5.8
如图所示
飞机 P 在任一时刻的经度为 ψ (t )
纬度为 λ (t )
高度为 h(t )
其在
地心坐标系中的球坐标运动方程为
r = R + h(t )
其中 R 是地球半径
θ = π / 2 − λ (t )
5.1 解
试写出点的柱坐标与球坐标之间的关系式 质点柱坐标系为 ρ
ϕ
z 球坐标为 r θ
ϕ
两者的 ϕ 坐标是相同的
理论力学课后答案第五章
第五章思考题5、1虚功原理中的“虚功”二字作何解释？用虚功原理理解平衡问题,有何优点与缺点？ 5、2 为什么在拉格朗日方程中,a θ不包含约束反作用力？又广义坐标与广义力的含义如何？我们根据什么关系由一个量的量纲定出另一个量的量纲?5、3广义动量a p 与广义速度a q &就是不就是只相差一个乘数m ？为什么a p 比a q &更富有意义？5、4既然aq T &∂∂就是广义动量,那么根据动量定理,⎪⎪⎭⎫ ⎝⎛∂∂αq T dt d &就是否应等于广义力a θ？为什么在拉格朗日方程()14.3.5式中多出了a q T ∂∂项？您能说出它的物理意义与所代表的物理量不？5、5为什么在拉格朗日方程只适用于完整系？如为不完整系,能否由式()13.3.5得出式()14.3.5？5、6平衡位置附近的小振动的性质,由什么来决定？为什么22s 个常数只有2s 个就是独立的？5、7什么叫简正坐标？怎样去找？它的数目与力学体系的自由度之间有何关系又每一简正坐标将作怎样的运动？5、8多自由度力学体系如果还有阻尼力,那么它们在平衡位置附近的运动与无阻尼时有何不同？能否列出它们的微分方程？5、9 dL 与L d 有何区别？a q L ∂∂与aq L ∂∂有何区别？ 5、10哈密顿正则方程能适用于不完整系不？为什么？能适用于非保守系不？为什么？ 5、11哈密顿函数在什么情况下就是整数？在什么情况下就是总能量？试祥加讨论,有无就是总能量而不为常数的情况？5、12何谓泊松括号与泊松定理？泊松定理在实际上的功用如何？5、13哈密顿原理就是用什么方法运动规律的？为什么变分符号δ可置于积分号内也可移到积分号外？又全变分符号∆能否这样？5、14正则变换的目的及功用何在？又正则变换的关键何在？5、15哈密顿-雅可比理论的目的何在？试简述次理论解题时所应用的步骤、5、16正则方程()15.5.5与()10.10.5及()11.10.5之间关系如何？我们能否用一正则变换由前者得出后者？5、17在研究机械运动的力学中,刘维定理能否发挥作用？何故？5、18分析力学学完后,请把本章中的方程与原理与牛顿运动定律相比较,并加以评价、第五章思考题解答5、1 答:作、用于质点上的力在任意虚位移中做的功即为虚功,而虚位移就是假想的、符合约束的、无限小的、即时位置变更,故虚功也就是假想的、符合约束的、无限小的、且与过程无关的功,它与真实的功完全就是两回事、从∑⋅=ii i r F W ρρδδ可知:虚功与选用的坐标系无关,这正就是虚功与过程无关的反映;虚功对各虚位移中的功就是线性迭加,虚功对应于虚位移的一次变分、在虚功的计算中应注意:在任意虚过程中假定隔离保持不变,这就是虚位移无限小性的结果、虚功原理给出受约束质点系的平衡条件,比静力学给出的刚体平衡条件有更普遍的意义;再者,考虑到非惯性系中惯性力的虚功,利用虚功原理还可解决动力学问题,这就是刚体力学的平衡条件无法比拟的;另外,利用虚功原理解理想约束下的质点系的平衡问题时,由于约束反力自动消去,可简便地球的平衡条件;最后又有广义坐标与广义力的引入得到广义虚位移原理,使之在非纯力学体系也能应用,增加了其普适性及使用过程中的灵活性、由于虚功方程中不含约束反力、故不能求出约束反力,这就是虚功原理的缺点、但利用虚功原理并不就是不能求出约束反力,一般如下两种方法:当刚体受到的主动力为已知时,解除某约束或某一方向的约束代之以约束反力;再者,利用拉格朗日方程未定乘数法,景观比较麻烦,但能同时求出平衡条件与约束反力、5.2 答 因拉格朗日方程就是从虚功原理推出的,而徐公原理只适用于具有理想约束的力学体系虚功方程中不含约束反力,故拉格朗日方程也只适用于具有理想约束下的力学体系,αθ不含约束力;再者拉格朗日方程就是从力学体系动能改变的观点讨论体系的运动,而约束反作用力不能改变体系的动能,故αθ不含约束反作用力,最后,几何约束下的力学体系其广义坐标数等于体系的自由度数,而几何约束限制力学体系的自由运动,使其自由度减小,这表明约束反作用力不对应有独立的广义坐标,故αθ不含约束反作用力、这里讨论的就是完整系的拉格朗日方程,对受有几何约束的力学体系既非完整系,则必须借助拉格朗日未定乘数法对拉格朗日方程进行修正、广义坐标市确定质点或质点系完整的独立坐标,它不一定就是长度,可以就是角度或其她物理量,如面积、体积、电极化强度、磁化强度等、显然广义坐标不一定就是长度的量纲、在完整约束下,广义坐标数等于力学体系的自由度数;广义力明威力实际上不一定有力的量纲可以就是力也可以就是力矩或其她物理量,如压强、场强等等,广义力还可以理解为;若让广义力对应的广义坐标作单位值的改变,且其余广义坐标不变,则广义力的数值等于外力的功由W q r F s i ni i δδθδααα==⋅∑∑==11ρρ知,ααδθq 有功的量纲,据此关系已知其中一个量的量纲则可得到另一个量的量纲、若αq 就是长度,则αθ一定就是力,若αθ就是力矩,则αq 一定就是角度,若αq 就是体积,则αθ一定就是压强等、5.3 答 αp 与αq &不一定只相差一个常数m ,这要由问题的性质、坐标系的选取形式及广义坐标的选用而定。
理论力学课后习题部分答案
B
A FAC FBA
P
(l)
(l1)
(l2)
(l3)
图 1-1
1-2 画出下列每个标注字符的物体的受力图。题图中未画重力的各物体的自重不计，所 有接触处均为光滑接触。
(a)
B
FN1
C
FN 2
P2 P1
FAy
A
FAx
(a2)
(b)
FN1
A
P1
FN
(b2)
C
FN′
P2
(a1)
B
FN1
FN 2
FN
P1
F Ay
FCy
FAx (f2)
C FC′x
FC′y F2
FBy
FBx B (f3)
FAy A FAx
FB
C B
(g)
FAy
FAx A
D FT C FCx
(g2)
FB
B
F1
FB′ B
FAy
A
FAx
(h)
(h1)
P (g1)
FC′y
FT
C
FC′x
P (g3)
D
FCy
FB
F2
C FCx
B
(h2)
A FAx
FAy
FCy
D FAy
A
FAx
(k3)
6
FB
F1
FB′
B B
FD D
(l) FD′ D
A FA
(l1) F2
C
FC (l2)
F1
D
F2
B
A
E
FE
FA
(l3) 或
F1
FB′
(完整版)高等教育出版社_金尚年_马永利编著的理论力学课后习题答案
高等教育出版社，金尚年，马永利编著的理论力学课后习题答案第一章1.2写出约束在铅直平面内的光滑摆线上运动的质点的微分方程，并证明该质点在平衡位置附近作振动时，振动周期与振幅无关.解：设s为质点沿摆线运动时的路程，取=0时，s=0 S== 4 a (1) XY设为质点所在摆线位置处切线方向与x 轴的夹角，取逆时针为正，即切线斜率=受力分析得：则，此即为质点的运动微分方程。
该质点在平衡位置附近作振动时，振动周期与振幅无关，为.1.3证明：设一质量为m 的小球做任一角度0θ的单摆运动运动微分方程为θθθF r r m =+)2( θθsin mg mr = ①给①式两边同时乘以d θ θθθθd g d r sin = 对上式两边关于θ积分得 c g r +=θθcos 212 ② 利用初始条件0θθ=时0=θ 故0cos θg c -= ③ 由②③可解得 0cos cos 2-θθθ-•=lg 上式可化为dt d lg=⨯-•θθθ0cos cos 2-两边同时积分可得θθθθθθθθd g l d g l t ⎰⎰---=--=020222002sin 12sin 10012cos cos 12进一步化简可得θθθθd g l t ⎰-=0002222sin sin 121 由于上面算的过程只占整个周期的1/4故⎰-==0222sin 2sin 124T θθθθd g l t由ϕθθsin 2sin /2sin 0=两边分别对θϕ微分可得ϕϕθθθd d cos 2sin 2cos 0=ϕθθ202sin 2sin 12cos-=故ϕϕθϕθθd d 202sin 2sin 1cos 2sin2-= 由于00θθ≤≤故对应的20πϕ≤≤故ϕϕθϕθϕθθθθπθd g l d g l T ⎰⎰-=-=202022cos 2sinsin 2sin 1/cos 2sin42sin2sin 2故⎰-=2022sin 14πϕϕK d g l T 其中2sin022θ=K 通过进一步计算可得glπ2T =])2642)12(531()4231()21(1[224222 +⨯⨯⨯⨯-⨯⨯⨯⨯++⨯⨯++n K n n K K1.5zp点yx解：如图，在半径是R的时候，由万有引力公式，对表面的一点的万有引力为, ①M为地球的质量；可知，地球表面的重力加速度g , x为取地心到无限远的广义坐标，，②联立①，②可得：,M为地球的质量；③当半径增加,R2=R+,此时总质量不变，仍为M,此时表面的重力加速度可求：④Be ө e tөy由④得：⑤则，半径变化后的g 的变化为⑥对⑥式进行通分、整理后得：⑦对⑦式整理，略去二阶量，同时远小于R ，得⑧则当半径改变 时，表面的重力加速度的变化为：。
理论力学课后习题答案解析第5章点的复合运动分析)
第5章 点的复合运动分析5－1 曲柄OA 在图示瞬时以ω0绕轴O 转动，并带动直角曲杆O 1BC 在图示平面内运动。
若d 为已知，试求曲杆O 1BC 的角速度。
解：1、运动分析：动点：A ，动系：曲杆O 1BC ，牵连运动：定轴转动，相对运动：直线，绝对运动：圆周运动。
2、速度分析：r e a v v v +=0a 2ωl v =；0e a 2ωl v v ==1e1ωω==AO v BCO （顺时针）5－2 图示曲柄滑杆机构中、滑杆上有圆弧滑道，其半径cm 10=R ，圆心O 1在导杆BC 上。
曲柄长cm 10=OA ，以匀角速rad/s 4πω=绕O 轴转动。
当机构在图示位置时，曲柄与水平线交角 30=φ。
求此时滑杆CB 的速度。
解：1、运动分析：动点：A ，动系：BC ，牵连运动：平移，相对运动：圆周运动，绝对运动：圆周运动。
2、速度分析：r e a v v v += πω401a =⋅=A O v cm/s ； 12640a e ====πv v v BC cm/s5－3 图示刨床的加速机构由两平行轴O 和O 1、曲柄OA 和滑道摇杆O 1B 组成。
曲柄OA 的末端与滑块铰接，滑块可沿摇杆O 1B 上的滑道滑动。
已知曲柄OA 长r 并以等角速度ω转动，两轴间的距离是OO 1 = d 。
试求滑块滑道中的相对运动方程，以及摇杆的转动方程。
解：分析几何关系：A 点坐标 d t r x +=ωϕcos cos 1 （1） t r x ωϕsin sin 1= （2） （1）、（2）两式求平方，相加，再开方，得： 1．相对运动方程trd r d t r d t rd t r x ωωωωcos 2sin cos 2cos 22222221++=+++=将（1）、（2）式相除，得： 2．摇杆转动方程： dt r tr +=ωωϕcos sin tandt r t r +=ωωϕcos sin arctan5－4 曲柄摇杆机构如图所示。
理论力学(金尚年)5-8章答案
1 mR ̇ 1 cos 1 r ̇ 2 cos 2 2 R ̇ 1 sin 1 r ̇ 2 sin 2 2 2
1 I 2̇2 ̇ 2 1 mR 2 ̇2 ̇ ̇ 1 r 2 2Rr 1 2 2 2 2 ̇2 ̇2 ̇ ̇ 6. 75 1 0. 5 2 1. 5 1 2 − MgR cos 1 mR r − mgR cos 1 r cos 2 V 1 MgR 2 mgR 2 r 2 1 1 2 2 1 M mgR 2 mgr 2 1 2 2 1 45 2 5 2 1 2 2 0
Chapter 5
5.3 在以圆心为坐标原点的圆环参照系看来 i ′ − R sin2t j′ r ′ R cos2t v ′ −2R sin2t i ′ 2R cos2t j′ 以C点为坐标原点的惯性系中圆心的坐标和速度为 r c R cost i R sint j v c −R sint i R cost j 又 i sint j i ′ cost j ′ − sint i cost j 则质点位置在惯性系看来为 r rc r′ 2R cost i 其速度和加速度为 −2R sint dr i dt i a −2 2 R cost 5.6 在初始条件下，质点受力为 0 − 20 2 mdi F 3 t 8 m 2 di F 3 c 8 m 2 di F 3 − 4 m 2 di F 3 d相对于距O点C处 由于此时受力垂直于运动方向，此时质点相当于以速度 4 3 4 r c 3 di做圆周运动。假设之后质点一直以该点为圆心做匀速圆周运动，在任意 时刻，质点位于 r处，则质点受力为 0 −4m 2 r − rA F t m 2 F r v c F r − rc 8 md 2 3 r − rc | | r − rc −3m 2 注意到| r − rc | r − rc − 4 m 2 d F 3 r − rc | | 因此此时体系依然满足匀速圆周运动条件。在非惯性系中 4 de ′ r 4 di 3 r 3
高等教育出版社,金尚年,马永利编著的理论力学课后习题答案解析
高等教育出版社，金尚年，马永利编著的理论力学课后习题答案第一章1.2写出约束在铅直平面内的光滑摆线上运动的质点的微分方程，并证明该质点在平衡位置附近作振动时，振动周期与振幅无关. 解：设s为质点沿摆线运动时的路程，取=0时，s=0S== 4 a (1)设为质点所在摆线位置处切线方向与x 轴的夹角，取逆时针为正，即切线斜率=受力分析得：则，此即为质点的运动微分方程。
该质点在平衡位置附近作振动时，振动周期与振幅无关，为.1.3证明：设一质量为m 的小球做任一角度0θ的单摆运动运动微分方程为θθθF r r m =+)2( θθsin mg mr = ①给①式两边同时乘以d θ θθθθd g d r s i n = 对上式两边关于θ 积分得 c g r +=θθc o s 212 ②利用初始条件0θθ=时0=θ 故0cos θg c -= ③ 由②③可解得 0c o s c o s 2-θθθ-∙=lg 上式可化为dt d lg=⨯-∙θθθ0cos cos 2-两边同时积分可得θθθθθθθθd g l d g l t ⎰⎰---=--=020222002sin 12sin 10012cos cos 12进一步化简可得θθθθd g l t ⎰-=0002222sin sin 121 由于上面算的过程只占整个周期的1/4故⎰-==0222sin 2sin 124T θθθθd g l t由ϕθθsin 2sin /2sin 0=两边分别对θϕ微分可得ϕϕθθθd d cos 2sin 2cos 0=ϕθθ202sin 2sin 12cos-=故ϕϕθϕθθd d 202sin 2sin 1cos 2sin2-= 由于00θθ≤≤故对应的20πϕ≤≤故ϕϕθϕθϕθθθθπθd g l d g l T ⎰⎰-=-=202022cos 2sinsin 2sin 1/cos 2sin42sin2sin 2故⎰-=2022sin 14πϕϕK d g l T 其中2sin022θ=K 通过进一步计算可得glπ2T =])2642)12(531()4231()21(1[224222 +⨯⨯⨯⨯-⨯⨯⨯⨯++⨯⨯++n K n n K K1.5解：如图，在半径是R 的时候，由万有引力公式， 对表面的一点的万有引力为, ①M 为地球的质量；可知，地球表面的重力加速度 g , x 为取地心到无限远的广义坐标，，②联立①， ②可得：,M 为地球的质量；③当半径增加 ,R2=R+ ,此时总质量不变，仍为M,此时表面的重力加速度 可求：④由④得：⑤则，半径变化后的g 的变化为⑥对⑥式进行通分、整理后得：⑦对⑦式整理，略去二阶量，同时远小于R ，得⑧则当半径改变 时，表面的重力加速度的变化为：。
理论力学参考答案第5章
理论力学参考答案第5章第5章摩擦· ·47· 47·第5章摩擦一、是非题正确的在括号内打“√”、错误的打“×” 1静滑动摩擦力与最大静滑动摩擦力是相等的。
× 2最大静摩擦力的方向总是与相对滑动趋势的方向相反。
√ 3摩擦定律中的正压力即法向约束反力是指接触面处物体的重力。
× 4当物体静止在支撑面上时支撑面全约束反力与法线间的偏角不小于摩擦角。
× 5斜面自锁的条件是斜面的倾角小于斜面间的摩擦角。
√ 二、填空题1当物体处于平衡时静滑动摩擦力增大是有一定限度的它只能在0≤Fs≤Fsmax范围内变化而动摩擦力应该是不改变的。
2静滑动摩擦力等于最大静滑动摩擦力时物体的平衡状态称为临界平衡状态。
3对于作用于物体上的主动力若其合力的作用线在摩擦角以内则不论这个力有多大物体一定保持平衡这种现象称为自锁现象。
4当摩擦力达到最大值时支撑面全约束反力与法线间的夹角为摩擦角。
5重量为G的均质细杆AB与墙面的摩擦系数为0.6f如图5.12所示则摩擦力为0。
6物块B重2kNP物块A重5kNQ在B上作用一水平力F如图5.13所示。
当系A之绳与水平成30角B与水平面间的静滑动摩擦系数s102f.物块A与B之间的静滑动摩擦系数s2025f.要将物块B拉出时所需水平力F的最小值为2.37kN。
A CB G A B F 图5.12 图5.13 ·48·理论力学·48·三、选择题1如图5.14所示重量为P的物块静止在倾角为的斜面上已知摩擦系数为sfsF为摩擦力则sF的表达式为B 临界时sF的表达式为 A 。
A sscosFfP B ssinFP C sscosFfP D ssinFP NF P sF 图5.14 2重量为G的物块放置在粗糙的水平面上物块与水平面间的静摩擦系数为sf今在物块上作用水平推力P 后物块仍处于静止状态如图5.15所示那么水平面的全约束反力大小为C 。
理论力学（第2版）习题答案
各章习题(计算题)部分答案第1章 略 第2章2-1 R 3284kN F .=，R cos()2063,.=︒F i ，R cos()1163,.=︒F j 2-2 3162kN T .=，30β=︒ 2-3 482.α=︒，R 496kN x F .= 2-4 11866N 50N x y F .F ==，2230N 40N x y F F ==-， 330N 60N x y F F ==， 44566N 566N x y F .F .==， 2-5 R 0F =2-6(a) 707kN 354kN 354kN Ax Ay B F .F .F .===，，(b) 05kN 5kN Ax Ay B F F F ===，，(c) 933kN 433kN 612kN Ax Ay B F .F .F .===，，(垂直于支撑面，指向简支梁) 2-7 min 15kN F =，N 25kN F =2-8 0866kN 05kN 1kN Ax Ay BD F .F .T ===，， 2-9 N N 1732kN 3464kN 15m A C F .F .AC .===，， 2-10 03436kN AB AC F F .==，2-11 BC F =，Ax F =，Ay F G = 2-12 N 65EF G F =+2-13 N N C D F F =2-14 231N 1155N 231N 845N AB AE BC BD F F .F F .====，，，2-15 (a) 33PF P F B Ay =-=，(b) P F F B A 32== (A F ，B F 方向相反，组成一力偶) (c) 0==B A F F2-16 1F，AB F，OA F =，7kN BC F =- 2-17 1905N 1905N 1905N 1905N Ax Ay Cx Cy F F F F =-===-，，， 2-18 3571N 3571N 3571N 3571N Ax Ay Cx Cy F F F F ==-=-=，，，·312··312·2-19 24kN m M =⋅，1155kN A B F F .== 第3章3-1 2400N Ax F =，1200N Ay F =，8485N BC F .= 3-2 R 0F'=，260N m O M =⋅ 3-3 (a) R F'qa =，221qa M O = (b) R12F'ql =，21ql q M O = 3-4(a) Ax F =，40kN Ay F =，120kN m A M =⋅，N C F = (b) 0=AxF ，25kN Ay F .=-，15kN By F =，D 25kN y F .=3-5 当60α=︒时，min 4AB PrF L= 3-6 0=Ax F ，qa F Ay2=，2qa M A =3-7 (a)2400N Ax F =，1000N Ay F =-，2400N Dx F =-，2000N Dy F = (b)2400N Ax F =-，1000N Ay F =-，2400N Dx F =，2000N Dy F =3-8 Ax F =，Ay F =，Bx F =，By F =3-9 rPLF Ax 2-=，P F Ay =，r PL F Bx 2=，P F By =，r PL F D 2=，P F C 2=3-10 R 32E F qa =-，qa F BD 22= 3-11 23kN Ax Cx F F .=-=-，1kN Ay Cy F F == 3-12 3PF AC -=，0=EF F ，32P F BD -= 3-13 2F F BC=，2F F DE = 第4章4-1 T 20kN F =，104kN OA F .=-，139kN OB F .=- 4-2 254kN m x M .=⋅，146kN m y M .=⋅，0=z M 4-3 0)(=P z M4-4 θαsin sin )(Pa M AB =P 4-5 3C A B WT T T ===4-6 1kN T =，0=Ax F ，750N Ay F =-，500N Az F =-，433N Bx F =，500N BZ F = 4-7 F F F -==61，F F =3，0542===F F F·313··313·4-8 321M a cM a b M +=，a M F Ay 3=，a M F Az 2=，0=Dx F ，a M F Dy 3-=，aM F Dz 2-= 4-9 4kN Ax F =，146kN Az F .=-，79kN Bx F .=，29kN Bz F .=-4-10 5kN Ox F =-，4kN Oy F =-，8kN Oz F =，32kN m Ox M =⋅，30kN m Oy M =-⋅，20kN m Oz M =⋅4-11 (a ) 10412kN N F .=，20213kN N F .=，30375kN N F .= 4-12 )(22221221r r r r x C --=，0=C y4-13 (a ) 589mm C x .=-，0=C y (b ) 797mm C x .=，349mm C y .= 4-14 )(22221221r r r r x C --=，0=C y4-15 0Ax F =，121(P )2Ay F P =-+，21P 2Az P F =+，0Cx F =，0Cy F =，22Cz P F =第5章5-1 min F =，s arctan f α= 5-2 )()m m sin +cos -P F αϕθϕ=，m θϕ=5-3 (1) A 先滑动，(2) A 、B 一起滑动 5-4 能保持平衡，S 201N F = 5-5 223.0=f5-6 3πarcsin 43πff α=+5-7 1s sin cos P F f αα=-，2s sin cos PF f αα=+，故21F F >5-8 min 845kN Q .= 5-9 435N P .=5-10 θ≤9926.︒5-11 120cm x >5-12 s 2(sin cos )Q R f L αα⋅+≤P ≤s 2(sin cos )Q Rf L αα⋅-5-13 min 1475N P .=5-14 4961N m .⋅≤C M ≤7039N m .⋅ 5-15 11cm b <5-16s s sin cos cos sin f Q f αααα-+≤P ≤s s sin cos cos sin f Q f αααα+- 5-17 arc ϕ=·314··314·5-18 500N P = 5-19 s f ≥15.0 5-20 75mm b .< 第6章6-1 (cos sin )x v lk kt kt =-，(cos sin )y v lk kt kt =-+； )sin (cos 2kt kt lk a x +-=，)sin (cos 2kt kt lk a y --= 6-2 (1) 0=s ；v R ω=；0a τ=，2n a R ω=(2) R s 23=；12v R ω=；2a ωτ=，2n 14a R ω= (3) R s =；0v =；2a R ωτ=-，n 0a =6-3 直角坐标法：t R x ω2cos =，t R y ω2sin =；2sin2x v R t ωω=-，2cos2y v R t ωω=； t R a x ωω2cos 42-=，t R a y ωω2sin 42-=自然坐标法：t R s ω2=；2v R ω=；0a τ=，2n 4a R ω= 6-4 ()sin M x l b t ω=+，()cos M y l b t ω=-；22221()()M M x y l b l b +=+-6.52222()1()x a y b l l-+=+6-6 22)sin (cos h t r l t r x B +-+=ωω，h y B -=6-7v =322xb u a -= 6-8 )cos sin arctan(00tr h tr ωωθ-=6-9 当0s t =时，157cm s M v ./=；0M a τ=，n2617cm s M a ./=当2s t =时，0M v =；2123cm s M a ./τ=-，n0M a =6-10 C x =C y =2C avv l=6-11 t e R t e y ωω222cos sin -+=；[cos v e t ωω=6-12 02cos4m x .t =；0566m s v ./=-；22263m s a ./=-6-13 0arctan rad v tbϕ=；02220rad s bv /b v t ω=+6-14 225t =ϕ；120m s v /=；236000m s n a /= 6-15 8rad s /ω=；2384rad s ./ε=-6-16 转轴O 的位置位于正方形的中心；1rad s /ω=，21rad s /ε=6-17 12C v r ω=；n 214C a r ω=，12C a r ετ=·315··315·6-18 12m s M v ./=；n 272m s M a ./=，206m s M a ./τ= 6-19 0377m s C v ./=6-20 2225000rad s /dεπ=；25922m s a ./= 6-21 32rad .ϕ=6-22 12mm h =6-23 02=ω，222r lb ωε-=6-24 02m s AB v ./=，2005m s AB a ./=；02m s C v ./=，n 20267m s C a ./=，2005m s C a ./τ=6-25 2012ωr a =，方向沿1AO ；2024ωr a =，指向轮心第7章7-1 x'vt =，cos()a kt y'ϕ=+，轨迹方程为cos()ky'a x'vϕ=+ 7-2 2cos M v R ωϕ=，方向水平向左 7-3 (a )2309rad s ./ω=； (b )2182rad s ./ω=7-4 (1)34OC v b ω=，34C lv v b=；(2)234K v a b = 7-5 当0ϕ︒=时，0v =；当30ϕ=︒时，100cm s v /=，向右；当90ϕ︒=时，200cm s v /=，向右7-6 126m s BC v ./=；2274m s BC a ./= 7-7 10cm s CD v /=；2346cm s CD a ./= 7-8 a a =7-9 3v ω=，方向向上7-10 1.732rad /s ω=，28.66rad /s ε=- 7-11 0.173m /s v =，20.05m /s a = 7-12 0.173m /s M v =，20.35m/s M a =7-13 πcos 15sin BC nr v αβ=7-14 23CD r v ω=；29310ωr a C D =7-15 a 3465mm s v ./=；21400mm s CD a /=第8章8-1 122v v r ω-=，122O v v v +=8-2 156cm s C v ./=,17cm s D v /=·316··316·8-3 877cm s C v ./=8-4 375rad s OB ./ω=，I 6rad s /ω=8-5 600mm s A v /=，200mm s B v /=，s C v /=；4rad s 3ABC /ω=，05rad s BD ./ω= 8-6 2rad s AB /ω=，2578rad s AB ./ε=-；667rad s BC ./ω=-，21926rad s BC ./ε=8-7 2()C A Rv a R r r=-，2Bx C a a τ=，2(2)()C By R r v a R r r -=- 8-8 2022ωr a B =，20211ωε=B O 8-9 032C v r ω=，20123ωr a C =8-10 01.15v l ω=8-11 16186rad s O C ./ω=，127817rad s O C ./ε=-8-12 s CD v /=，22m s 3CD a /= 8-13 n 2400cm s B a /=，21705cm s B a ./τ=-，21705cm s C a ./=-8-14 34e OC v v OB b ω==，OC ε=；12E v v =，E a = 8-15 21960mm s B a /=，298rad s AB ./ε=8-160C v ω，方向向左；rR B O 01ωω=，逆时针转向8-17 22()C Rv a R r =-，B a =8-18 n 202B a a ω=，2002)B a a ετ=-8-19 330ωω=B ；209)349(10ω+-=B a 8-20 2m s B v /=，2828m s C v ./=，28m s B a /=，21131m s C a ./= 第9章9-1 rgf=max ω 9-2 min 67r min n /=9-3 1v =9-4 0cos cos sin v x b kt kt k α=+，0sin sin vy kt kα=9-5 0cos x v t α=，201sin 2y v t gt α=+·317··317·9-6 0(1e )kt v s k-=- 9-7 202s t .=，707m s .= 9-8 172N F .=9-9 )(22g a amL F AC +=ω，)(22g a a mL F BC -=ω9-10 max 584kN F .=，min 536kN F .=9-11 g f f a ααααsin cos cos sin -+=，N cos sin W F f αα=- 9-12 )cos 1(200t m F t x ωωυ-+=第10章10-1 (a ) 12p mL ω=，方向水平向右；(b ) p mR ω=，方向水平向右；(c ) p me ω=，方向垂直于OC 的连线；(d ) C p mv =，方向水平向右10-2 30N x F =10-3 11221022a gP P P P F -++= 10-4 11r 12m v v v m m =++10-5 0(sin cos )v t g f'αα=-10-6 12(54)2l p m m ω=+，方向与曲柄垂直且向上 10-7 t m m l m x m m kx ωωsin 1211+=++10-8 2R s =10-9 (1) 3123123(22)cos ,2()C P L P P P L tx P P P ω+++=++ (2) 12123(2)sin ;2()C P P L t y P P P ω+=++2321max 222ωL gP P P F Ox ++=10-10 椭圆 2224l y x =+10-11 (1) 2sin G Wx l t P W Gω+=++ (2) 2m a x 2x G W F l g ω+=10-12 向右移377cm . 10-13 33(sin )cos ox R F m g m a r θθ=+，1233()(sin )sin oy RF m g m g a m g m a rθθ=+-++ 10-14 21212)(m m gm m f b m a ++-=·318··318·10-15 17cm A s =，向左移动；9cm B s =，向右移动 10-16 2max12(2)2ox r F F G G gω=++10-17 24(cos sin )3Ox mR F ωϕεϕπ=-+，24(sin cos )3Oy mR F mg ωϕεϕπ=+- 第11章11-1 (a ) ω2031ml L =，(b ) ω2021mR L =，(a ) ω2023mR L =11-2 208m s a ./=，2862kN T F .=，4626kN Oy F .=11-3 (1) ωωω22231ml mR Ml L O ---=，(2) ωω2231ml Ml L O --=11-4 θω22sin )312(l M m L O +=11-5 480r min n /=11-6 022ωωmr J ma J z z ++=11-7 0N 0Pr F fgt ω= 11-8 211212122()()R M R M'm m R R ε-=+11-9 )()(2212J i J gPR R PR Mi a ++-=11-10 t P P gkl)3(3cos210+=δϕ11-11 gR RW g J R W M a 2101sin +-=α，1T 1sin W F W a g α=+ 11-12 g J r m r m r m r m O++-=2222111122ε11-13 g R m r R m r R m a )()()(2222121ρ++++=，)()()(22221212ρρ+++-=R m r R m g m m Rr F11-14 v =T 13F mg =11-15 θsin 74g a =，θsin 71mg F -= 11-16 g a C 355.0=11-17 3)(2121m m gm m f F a ++-=·319··319·11-18 gr M R m r m R fm r m a 2222121ρ++-=，T 11A F m g m a =-，2T 2B m RF fm g a r=+11-19 2N 22sin 12D QL F a Lα=+，αcos g a Cx =，22212sin 12L a g a a Cy +=α 11-20 N 3633N B F .=11-21 P F F x O x O 516.021==，P F y O 434.11=，P F y O 164.12=第12章12-1 )cos 1(0ϕ+=mgr W AB ，)sin (cos 0θϕ-=mgr W AC 12-2 129904J F W .=，10500J f W =- 12-3 12206J W .=-，23206J W .=，031=W 12-4 (a) 2216T ml ω=，(b) 2234T mR ω=，(c) 2214T mR ω=，(d) 234C T mv =，12-5 10J W =重，503J W .=重12-6 θω222sin 61ml T = 12-7 21s s hf += 12-8 2122)cos (sin 2m m f gr m M r++-=ααϕϕω12-9 v=12-10 A v =12-11 A v =12-12 v =11/sin M R W a g W Wα-=+12-13 C v =45C a g =12-14 98N F .= 12-15 θωsin 3632121l g m m m m ++=，θεcos 23632121lgm m m m ++=12-16 C v =321321843)43(m m m gm m m F +++=12-17 (1) 2211)3()sin (2Rm m gR m M +-=αε， (2) R m m gR m M m F Ox )3(2)2sin cos 6(2121++=αα； ααsin )3()sin 3(21212⋅+++=Rm m gR m M m g m F Oy·320··320·12-18 v =m khmg a 34-=，41s 36F kh mg =+ 第13章13-1 αsin 32g a =13-2 g a 32=，T 3WF =13-3 Q P Pg a 322+=，QP PQF 32+=13-4 g P T a 3cos 2α=，N sin F P T α=-，s 1cos 3F T α= 13-5 22233cos sin 3()sin 2b a g b a ϕϕωϕ-=-13-6 445N ADF .=，54N BE F =13-7 2222(sin )cos sin J mr mr M ϕϕϕϕϕ++= 13-8 2222143)2(43ωr m gr m m M -+=，2143ωr m F Ox -=，4)2()(22121ωr m m g m m F Oy +-+= 13-9 0β=︒时，2329N Ax F =-，1382N Bx F =，1962N Ay By F F .==180β=︒时，12238N Ax F .=，592N Bx F =-，1962N Ay By F F .==13-10 2023ωmr F Ax -=，mgr F Ay =,20221ωmr F Bx =，mgr F By =13-11 g a a C x C 1712==，mg F 175= 13-12 l g 791=ε，lg 732-=ε，0=Ox F ，mg F Oy 72=第14章14-1 ctg 2P /Q /ϕ= 14-2 (3ctg 2)Ax F /P θ=14-3 A F P /=14-4 ctg Q P θ= 14-5 450N Q P /==14-6 12F F l =／2(cos )a ϕ14-7 05kN 21kN m Ax Ay A F F m ===⋅，，14-8 1866kN P .=14-9 2()F lx a k b=+14-10 2(kN)Ax F =， 3.804(kN)Ay F =，24(kN m)A M =-⋅，18.588(kN)B F =。
高等教育出版社,金尚年,马永利编著的理论力学课后习题答案
高等教育出版社，金尚年，马永利编著的理论力学课后习题答案第一章1.2写出约束在铅直平面内的光滑摆线上运动的质点的微分方程，并证明该质点在平衡位置附近作振动时，振动周期与振幅无关.解：设s为质点沿摆线运动时的路程，取=0时，s=0 S== 4 a (1) XY设为质点所在摆线位置处切线方向与x 轴的夹角，取逆时针为正，即切线斜率=受力分析得：则，此即为质点的运动微分方程。
该质点在平衡位置附近作振动时，振动周期与振幅无关，为.1.3证明：设一质量为m 的小球做任一角度0θ的单摆运动运动微分方程为θθθF r r m =+)2( θθsin mg mr = ①给①式两边同时乘以d θ θθθθd g d r sin = 对上式两边关于θ积分得 c g r +=θθcos 212 ② 利用初始条件0θθ=时0=θ 故0cos θg c -= ③ 由②③可解得 0cos cos 2-θθθ-•=lg 上式可化为dt d lg=⨯-•θθθ0cos cos 2-两边同时积分可得θθθθθθθθd g l d g l t ⎰⎰---=--=020222002sin 12sin 10012cos cos 12进一步化简可得θθθθd g l t ⎰-=0002222sin sin 121 由于上面算的过程只占整个周期的1/4故⎰-==0222sin 2sin 124T θθθθd g l t由ϕθθsin 2sin /2sin 0=两边分别对θϕ微分可得ϕϕθθθd d cos 2sin 2cos 0=ϕθθ202sin 2sin 12cos-=故ϕϕθϕθθd d 202sin 2sin 1cos 2sin2-= 由于00θθ≤≤故对应的20πϕ≤≤故ϕϕθϕθϕθθθθπθd g l d g l T ⎰⎰-=-=202022cos 2sinsin 2sin 1/cos 2sin42sin2sin 2故⎰-=2022sin 14πϕϕK d g l T 其中2sin022θ=K 通过进一步计算可得glπ2T =])2642)12(531()4231()21(1[224222 +⨯⨯⨯⨯-⨯⨯⨯⨯++⨯⨯++n K n n K K1.5zp点yx解：如图，在半径是R的时候，由万有引力公式，对表面的一点的万有引力为, ①M为地球的质量；可知，地球表面的重力加速度g , x为取地心到无限远的广义坐标，，②联立①，②可得：,M为地球的质量；③当半径增加,R2=R+,此时总质量不变，仍为M,此时表面的重力加速度可求：④Be ө e tөy由④得：⑤则，半径变化后的g 的变化为⑥对⑥式进行通分、整理后得：⑦对⑦式整理，略去二阶量，同时远小于R ，得⑧则当半径改变 时，表面的重力加速度的变化为：。
理论力学(金尚年-马永利编著)课后习题答案详解
高等教育出版社，金尚年，马永利编著理论力学课后习题答案第一章1.2写出约束在铅直平面内的光滑摆线上运动的质点的微分方程，并证明该质点在平衡位置附近作振动时，振动周期与振幅无关.解：设s为质点沿摆线运动时的路程，取=0时，s=0XYF Nmg sinφmgmg cosφφS== 4 a (1)设为质点所在摆线位置处切线方向与x 轴的夹角，取逆时针为正，即切线斜率=受力分析得：则，此即为质点的运动微分方程。
该质点在平衡位置附近作振动时，振动周期与振幅无关，为.1.3证明：设一质量为m 的小球做任一角度0θ的单摆运动运动微分方程为θθθF r r m =+)2( θθsin mg mr = ①给①式两边同时乘以d θ θθθθd g d r sin = 对上式两边关于θ积分得 c g r +=θθcos 212 ② 利用初始条件0θθ=时0=θ 故0cos θg c -= ③ 由②③可解得 0cos cos 2-θθθ-•=lg 上式可化为dt d lg=⨯-•θθθ0cos cos 2-两边同时积分可得θθθθθθθθd g l d g l t ⎰⎰---=--=020222002sin 12sin 10012cos cos 12进一步化简可得θθθθd g l t ⎰-=0002222sin sin 121 由于上面算的过程只占整个周期的1/4故⎰-==0222sin 2sin 124T θθθθd g l t由ϕθθsin 2sin /2sin 0=两边分别对θϕ微分可得ϕϕθθθd d cos 2sin 2cos 0=ϕθθ202sin 2sin 12cos-=故ϕϕθϕθθd d 202sin 2sin 1cos 2sin2-= 由于00θθ≤≤故对应的20πϕ≤≤故ϕϕθϕθϕθθθθπθd g l d g l T ⎰⎰-=-=202022cos 2sinsin 2sin 1/cos 2sin42sin2sin 2故⎰-=2022sin 14πϕϕK d g l T 其中2sin022θ=K 通过进一步计算可得glπ2T =])2642)12(531()4231()21(1[224222 +⨯⨯⨯⨯-⨯⨯⨯⨯++⨯⨯++n K n n K K1.5zp点yx解：如图，在半径是R的时候，由万有引力公式，对表面的一点的万有引力为, ①M为地球的质量；可知，地球表面的重力加速度 g , x为取地心到无限远的广义坐标，，②联立①，②可得：,M为地球的质量；③当半径增加 ,R2=R+ ,此时总质量不变，仍为M,此时表面的重力加速度可求：④e өe tөy由④得：⑤则，半径变化后的g 的变化为⑥对⑥式进行通分、整理后得：⑦对⑦式整理，略去二阶量，同时远小于R ，得⑧则当半径改变 时，表面的重力加速度的变化为：。