工程热力学习题 第十一章 辐射换热
传热学辐射传热课后习题及答案.doc

Q.2第八章黑体辐射基本定律8-1、一电炉的电功率为1KW,炉丝温度为847°C,直径为Immo 电炉的效率为0.96。
试确 定所需炉丝.的最短长度。
<273 + 847丫 〃 八* 前------------ jvdL = 0.96 x 10解:5.67x1 1°° 7 得 L=3.61m8-5、在一空间飞行物的外壳上有一块向阳的漫射面板。
板背面可以认为是绝热的,向阳面 得到的太阳投入辐射GT300W 〃疟。
该表面的光谱发射率为:时£(") = 0.5; 人>2彻时£(人)二°・2。
试确定当该板表而温度处于稳态时的温度值。
为简化计算,设太 阳的辐射能均集中在0〜2即刀之内。
解:由 UOOJ 得 T=463K8-6、人工黑体腔上的辐射小孔是一个直径为20mm 的圆,辐射力场=3.72 x " W /帚。
一个辐射热流计置于该黑体小孔的正前方l=0.5m,处,该热流计吸收热量的面积为 1.6'10一5 "己问该热流计所得到的黑体投入辐射是多少?L. =^ = 1.185xlO 5W/m 2 解: 人 AO = T = 6.4x10-5rL h .A = 312W所得投入辐射能量为37.2X6.4X10-5 = 2.38x IO” w8-15、已知材料AB 的光谱发射率林久)与波K 的关系如附图所示,试估计这两种材料的发射 那£随温度变化的特性,并说明理由。
解:A 随稳定的降低而降低;B 随温度的降低而•升高。
理由:温度升高,热辐射中的短波比例增加。
8-16、一•选择性吸收表面的光谱吸收比随人变化的特性如附图所示,试计算当太阳投入辐射 为G=8()0W//H 2时,该表面单位面积上所吸收的太阳能量及对太阳辐射的总吸收比。
1-4QF -------------- + % -----------o o解:二°・9氏(()~|.4)+ °・2丹(].4~8)查表代入数据得 a = 0.7 x 86.0792% = 0.80268-23、已知一表面的光谱吸收比与波长关系如附图所示,在某一瞬间,测得表面温度为lOOOKo投入辐射G/按波长分布的情形示于附图b。
工程热力学课后作业答案(第十一章)第五版 .

11-1空气压缩致冷装置致冷系数为2.5,致冷量为84600kJ/h ,压缩机吸入空气的压力为0.1MPa ,温度为-10℃,空气进入膨胀机的温度为20℃,试求:压缩机出口压力;致冷剂的质量流量;压缩机的功率;循环的净功率。
解:压缩机出口压力1)12(1/)1(-=-k k p p ε 故:))1/(()11(12-+=k k p p ε=0.325 MPa 2134p p p p = T3=20+273=293K k k p p T T /)1()34(34-==209K 致冷量:)41(2T T c q p -==1.01×(263-209)=54.5kJ/kg 致冷剂的质量流量==2q Q m 0.43kg/s k k p p T T /)1()12(12-==368K 压缩功:w1=c p (T2-T1)=106 kJ/kg压缩功率:P1=mw1=45.6kW膨胀功:w2= c p (T3-T4)=84.8 kJ/kg膨胀功率:P2=mw2=36.5kW循环的净功率:P=P1-P2=9.1 KW11-2空气压缩致冷装置,吸入的空气p1=0.1MPa ,t1=27℃,绝热压缩到p2=0.4MPa ,经冷却后温度降为32℃,试计算:每千克空气的致冷量;致冷机消耗的净功;致冷系数。
解:已知T3=32+273=305Kk k p p T T /)1()12(12-==446K k k p p T T /)1()34(34-==205K 致冷量:)41(2T T c q p -==1.01×(300-205)=96kJ/kg致冷机消耗的净功: W=c p (T2-T1)-c p (T3-T4)=46.5kJ/kg 致冷系数:==wq 2ε 2.06 11-3蒸气压缩致冷循环,采用氟利昂R134a 作为工质,压缩机进口状态为干饱和蒸气,蒸发温度为-20℃,冷凝器出口为饱和液体,冷凝温度为40℃,致冷工质定熵压缩终了时焓值为430kJ/kg ,致冷剂质量流量为100kg/h 。
热辐射、换热器习题课

=> q1,2 = 1.52 E 4 (W/m 2 )
E b1 − J 1 表面1的净热交换量为:q1 = = q1,2 1 − ε1
Eb 2 − J 2 表面2的净热交换量为:q2 = = − q1,2 1− ε2
ε1
ε2
两板面的有效辐射分别为:
J1 = Eb1- 1 − ε1
ε1
• q1, 1.95 E 4 (W/m ) 2=
θ 是投射到 dA 2的射线和 dA 2的法线的夹角;
r是射线源至 dA 2的距离。
因此, A 1中心对 A 2、 A 3、 A 4 所张的立体角分别为 A 2 cos 30 o ω1-2= = 3.46 E − 4 ( sr) 2 0.5
A 3 cos 0 o ω1-3= = 4 E − 4 ( sr) 0.5 2
解:(1)题目已知A1表面为漫射表面,因此各个方向上 辐射强度I是相同的,即:
Iθ 1=Iθ 2=...=Iθ n
而法线方向,有E n=I n,因此I 2=I3=I 4=I n=3500W/(m 2 • sr)
(2) 求立体角,立体角的定义式: dA cos θ dΩ= 2 2 , r 其中 dΩ是射线投射到面积 dA 2所张开的立体角;
热辐射部分习题课
2007-06-18
p216/11.有一漫射微面积F1=1cm2 , 其法向的定向辐射力 En = 3500W /(m 2 • sr)。在离开A1中心为0.5m的圆周上布 置有微面积A 2、A 3、A 4,其面积亦均为1cm2 , 相对位置如 图8-12所示,试计算(1)A 2、A 3、A 4 表面所接受到的辐 射强度;(2)A1的中心对A 2、A 3、A 4 表面所张的立体角; (3)A1朝A 2、A 3、A 4 表面所发射的辐射能。
传热学辐射传热课后习题及答案.doc

Q.2第八章黑体辐射基本定律8-1、一电炉的电功率为1KW,炉丝温度为847°C,直径为Immo 电炉的效率为0.96。
试确 定所需炉丝.的最短长度。
<273 + 847丫 〃 八* 前------------ jvdL = 0.96 x 10解:5.67x1 1°° 7 得 L=3.61m8-5、在一空间飞行物的外壳上有一块向阳的漫射面板。
板背面可以认为是绝热的,向阳面 得到的太阳投入辐射GT300W 〃疟。
该表面的光谱发射率为:时£(") = 0.5; 人>2彻时£(人)二°・2。
试确定当该板表而温度处于稳态时的温度值。
为简化计算,设太 阳的辐射能均集中在0〜2即刀之内。
解:由 UOOJ 得 T=463K8-6、人工黑体腔上的辐射小孔是一个直径为20mm 的圆,辐射力场=3.72 x " W /帚。
一个辐射热流计置于该黑体小孔的正前方l=0.5m,处,该热流计吸收热量的面积为 1.6'10一5 "己问该热流计所得到的黑体投入辐射是多少?L. =^ = 1.185xlO 5W/m 2 解: 人 AO = T = 6.4x10-5rL h .A = 312W所得投入辐射能量为37.2X6.4X10-5 = 2.38x IO” w8-15、已知材料AB 的光谱发射率林久)与波K 的关系如附图所示,试估计这两种材料的发射 那£随温度变化的特性,并说明理由。
解:A 随稳定的降低而降低;B 随温度的降低而•升高。
理由:温度升高,热辐射中的短波比例增加。
8-16、一•选择性吸收表面的光谱吸收比随人变化的特性如附图所示,试计算当太阳投入辐射 为G=8()0W//H 2时,该表面单位面积上所吸收的太阳能量及对太阳辐射的总吸收比。
1-4QF -------------- + % -----------o o解:二°・9氏(()~|.4)+ °・2丹(].4~8)查表代入数据得 a = 0.7 x 86.0792% = 0.80268-23、已知一表面的光谱吸收比与波长关系如附图所示,在某一瞬间,测得表面温度为lOOOKo投入辐射G/按波长分布的情形示于附图b。
《传热学辐射换热》PPT课件

对于凹面:
Fii 0
31
(3) 完整性
对于有n个外表组成的封闭系统,据能量守恒可得:
Q i Q i 1 Q i 2 Q i i Q i N
Q i1Q i2 Q ii Q iN 1
Q i Q i
Q i
Q i
N
F ij F i1 F i2 F ii F iN 1
即
G G
所吸收的波长为的投射辐射,w/m2 波长为的投射辐射,w/m2
1G G 10
E d ,T1 ,T2 b,T2
E d 0 ,T2 b,T2
?
黑体
1
E d 0 ,T1 b,T2 T24
?
24
基尔霍夫定律 〔吸收率与辐射率之间的关系〕
1859年,Kirchhoff 用热力学方法答复了这个问题,从而提出了 Kirchhoff 定律。最简单的推导是用两块无限大平物体,参数分别为Eb, T1 以 及E, , T2,那么当系统处于热平衡时,有
QEAJA 1
因为: E Eb 所以有:QEb1AJAE1bJ
A
外表辐射 热阻
35
5.1 辐射换热热阻
〔2〕空间辐射热阻
Eb Eb
J JJ1 J1
J2 J2
1 1 A A
11 A1F12 A1F12
物体外表1辐射到外表2的辐射能为
Q 12J1A 1F 12
物体外表2辐射到外表1的辐射能为
Q 21 J2A 2F 21
右图是根据上式描绘的黑体单色辐 射力随波长和温度的关系。
m与T 的关系由Wien偏移定律给
出 m T 2 .8 9 6 1 0 3m K
到达最大单色辐射力时的波长
辐射习题
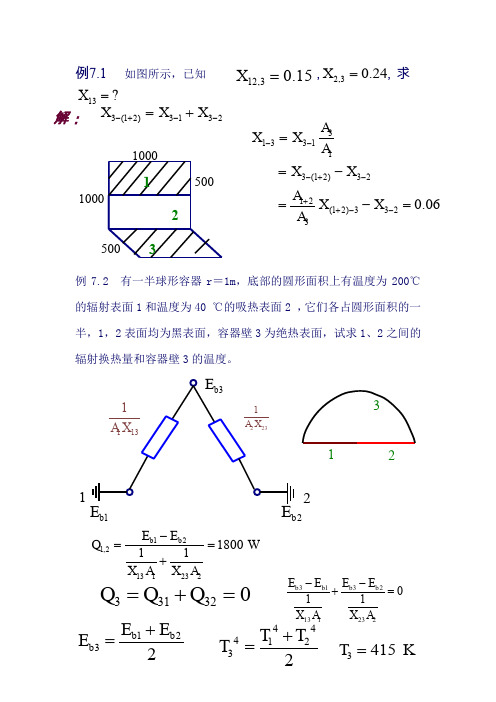
例7.1 如图所示,已知 , ,求例7.2 有一半球形容器r =1m ,底部的圆形面积上有温度为200℃的辐射表面1和温度为40 ℃的吸热表面2 ,它们各占圆形面积的一半,1,2表面均为黑表面,容器壁3为绝热表面,试求1、2之间的辐射换热量和容器壁3的温度。
123100010005005003121131A X 2231A X 121b E 2b E 3b E 12,30.15X =2,30.24X =3(12)3132X X X -+--=+解: 13?X =3133113(12)3212(12)33230.06A X X A X X A X X A ---+-++--==-=-=331320Q Q Q =+=121,2131232180011b b E E Q WX A X A -==+3132131232011b b b b E E E E X A X A --+=4441232T T T +=3415T K=1232b b b E E E +=例7.3 有一圆柱形一端开口的空腔体,其直径和高度均为100mm ,表面温度t 1=327℃,发射率 =0.75,此空腔放置在大房间中,房间表面温度t 2=27℃,试计算通过空腔体开口的辐射热损失。
1 1b E 1J 2211A X 21111A εε-2b E ε例7.4 有一圆柱状容器,直径为0.1m ,高也为0.1m ,上下圆面积之间的角系数 , 若下底面A1温度为T 1=500K ,发射率=0.9,侧面A2绝热,顶面A3敞口,该容器放置在大房间中,房间的绝对温度为300K ,求容器通过A3面向外辐射的热损失。
A 2 A 1A 3130.17X =1ε例7.5 一个外径为d1的圆管,置于另一个内径为d2的圆管中,如果两个球的温度分别为T1和T2,且T1 > T2 ,两管的表面发射率分别为ε1和ε 2 ,试求:(1)角系数X12、X21和X22各为多少;(2)画出辐射换热网络图;(3)写出辐射换热计算式。
《工程热力学》(第四版)习题提示及答案11章习题提示与答案
习题提示与答案第十一章 水蒸气及蒸汽动力循环11-1 试根据水蒸气的h -s 图,求出下述已知条件下各状态的其他状态参数p 、v 、t 、h 、s 及x (或过热蒸汽的过热度D =t -t s )。
已知:(1) p =0.5 MPa 、t =500 ℃;(2) p =0.3 MPa 、h =2 550 kJ/kg ;(3) t =180 ℃、s =6.0 kJ/(kg ·K);(4) p =0.01 MPa 、x =0.90;(5) t =400 ℃、D =150 ℃。
提示:水蒸气h -s 图上,两个独立的状态参数可确定一个状态;饱和区内,p 、T 两个参数直接相关。
答案:h =3 500 kJ/kg ,s =8.08 kJ/(kg·k),x =1,=v 0.72 m 3/kg, =D 448 ℃;(1)s =6.54 kJ/(kg·k),x =0.921,t =134 ℃,57.0=v m 3/kg ;(2)h =2 534 kJ/kg, x =0.865,=v 0.168 m 3/kg ;(3)h =2 534 kJ/kg ,s =7.4 kJ/(kg·k),t =46 ℃;(4)h =3 200 kJ/kg ,s =6.68 kJ/(kg·k),x =1,p =3.97 MPa 。
11-2 根据水蒸气表,说明下述已知条件下各状态的其他状态参数t 、v 、h 及s 。
已知: (1) p =0.3 MPa 、t =300 ℃;(2) p =0.5 MPa 、t =155 ℃;(3) p =0.3 MPa 、x =0.92。
提示:参照习题11-1的提示;湿饱和蒸汽的状态与其干度有关。
答案:(1)kg m 16081.03=v ,kg kJ 2.4299=h ,K kJ 8540.6⋅=s ;(2)kg m 525093001.03=v ,kJ 525.656=h ,K kJ 5886.1⋅=s ;(3)v /kg m 48557.03=;h =2 552.372 kJ/kg ;s =6.567 3 kJ/( kg·k)11-3 某锅炉每小时生产10 t 水蒸气,蒸汽的压力为1 MPa 、温度为350 ℃,锅炉给水的压力为1 MPa 、温度为40 ℃。
《传热学》习题课(辐射换热)
第八章 热辐射基本定律及物体的 辐射特性—复习题
• 6. 什么叫光谱吸收比?在不同光源的照耀 下,物体常呈现不同的颜色,如何解释? 答:光谱吸收比:物体对某一特定波长的辐 射能所吸收的百分数。 是因为物体的光谱吸收具有选择性,而造成 的。如果只反射了一种波长的可见光,而几 乎全部吸收了其他可见光,它就呈现被反射 的这种辐射线的颜色。
第九章 辐射换热的计算—复习题
• 6. 对于温度已知的多表面系统,试总结求解 每一表面净辐射换热量的基本步骤。 答:温度已知时,发射率、辐射能可求出。 可采用网络法或数值方法求解。 但首先应计算出每个面的辐射能Ebi发射率εi, 解系数Xi,j。然后再计算各表面的有效辐射Ji, 最后由 Ebi J i 确定每个表面的净辐射换热 i 1 i 量。
《传热学》习题课(辐射换热)
课件制作:尹华杰
第八章 热辐射基本定律及物体的 辐射特性—复习题
• 1. 什么叫黑体?在热辐射理论中为什么要引 入这一概念? 答:黑体:吸收比等于1的物体。 因吸收比等于1,反射比和透射比等于零,黑 体的辐射能力最大。引入这一概念可使物体 辐射的研究简化,方便充分地研究物体辐射 的各种性质、规律。在研究了黑体辐射的基 础上,处理其他物体辐射时,与黑体相比较, 找出其与黑体辐射的偏离,然后确定修正系 数。把黑体的研究结果运用于实际。
dAc H=1m 传感器 θ θ dA
x1
热试件
d dA cos dL
第八章 热辐射基本定律及物体的 辐射特性—习题
dAc 直上下时 : d0 dA 2 L cos 0 dAdAc L 1 dAc cos 1 斜方向时 : d dA L cos cos 2 1 x1 1 x12 d dA
热辐射、换热器习题课
因为两个面相互间角系数为1,投入辐射为
对板1的投入辐射:G1=J 2=4.26 E 3 (W/m 2 ) 对板2的投入辐射:G 2=J1=1.95 E 4 (W/m 2 )
板一的反射辐射:ρ1G1=0.2*4.26 E 3 = 852(W/m 2 )
两个面之间辐射热交换为: q=J1-J 2=1.52 E 4 (W/m 2 )
2
J 2 = Eb 2 +
1− ε2
ε2
2 4.26 3 (W/m ) • q1, = E 2
两板的投入辐射:
G 2=J1
G1=J 2
p254.26用热电偶来测量管内流动着的空气的温 度,如图9-39。热电偶读得温度t1=400℃, 管壁测得温度t2=350℃,热电偶头部和管壁 的发射率分别为0.8和0.7。从气流到热电偶头 部的对流表面传热系数为35W/(m2K).试计算由 于热电偶头部和管壁之间辐射换热而引起的测 温误差,此时气流的真实温度是多少?讨论测 温误差和换热系数的关系,测温误差和热电偶 头部发射率的关系。
Q1-3=3500*0.5*cos 0o *4E-4=1.4E-4 (W)
Q1-4=3500*0.5*cos 45o *4E-4=9.9E-5 (W)
P252 .11 某采暖房间采用立式悬挂辐射采暖板, 试求
此采暖板和房间各表面间的角系数,房间和采暖板的 尺寸见图9-38。
解题要领:利用角系数的分解性、对称性。
p252 /12. 两块平行放置的平板的表面发射率为0.8,温
度分别为t1=527℃及t2=27 ℃,板间距远小于板的宽度与 高度。试计算:
(1)板1的本身辐射; (2)板2对1的投入辐射; (3)板1的反射辐射; (4)板1的有效辐射; (5)板2的有效辐射; (6)板1-2间的辐射换热量
传热学第十一章
传热学第⼗⼀章第⼗⼀章质交换第⼀节质交换及其基本定律⼀、浓度与扩散通量1. 浓度质量浓度:容积V m 3中组分i 的质量,kg 。
kg /m 3V m ii =ρ(11-1)摩尔浓度: mol/m 3或kmol/m 3。
Vn c ii =(11-2)理想混合⽓体T R p M T R p ii i i i m *==ρ(11-3) TR pc i i m =(11-4)式中,R m 为摩尔⽓体常数,R m =8.314 J/(mol ?K);R i 为⽓体常数,J/(mol ?K);*i M 为组分i 的摩尔质量,kg/mol 。
在“⼯程热⼒学”中讲混合⽓体性质时提及的质量成分g i 、摩尔成分x i 与质量浓度ρi 、摩尔浓度c i 的换算关系是ρρi i i m m g ==;c c n n x i i i ==式中m —— 混合物的总质量,kg ;n —— 混合物的总摩尔数,mol ;ρ —— 混合物的密度,kg/m 3;c —— 混合物的总摩尔浓度,mol/m 3。
⼆、扩散通量图11-1 组分A 、B 的相互扩散图11-2 等摩尔逆向扩散随着取⽤的浓度单位不同,扩散通量可表⽰为质扩散通量M [kg/(m 2?s)]和摩尔扩散通量N [kmol/(m 2?s)]等。
⼆、斐克定律扩散基本定律——斐克(A.E.Fick )定律,其表达式为:yD M ??-=AABA ρ kg/( m 2?s)(11-5) yc D N ??-=AABA kmol/( m 2?s)(11-6)传递通量= - 扩散率?传递的推动⼒式中负号表⽰传递的⽅向与传递特征量增加的⽅向相反。
对于理想混合⽓体斐克定律还可以表达为y p T R D M ??-=A A AB A (11-7)ypT R D N ??-=A m AB A (11-8)V c N N A A A+=' V c y p T R D N A Am AB A +??-='(11-9) V c yp T R D N B Bm BA B +??-='(11-10) B AN N '-=' p =p A + p B = 常数yp yp ??-=??B A (11-11)D AB = D BA = D (11-12)yc c D y p p T R D N ?-=?-=2,A 1,A 2,A 1,A m A (11-13)yD y p p T R D M ?-=?-=2,A 1,A 2,A 1,A A A ρ三、斯蒂芬定律图11-3 ⽔⾯蒸汽向空⽓中扩散0=+-=+='TR p v y d p d T R D v M M B B BB B B Bρ(11-15)dydp p D v BB =(11-16a )p = p A + p B = 常数ypy p d d d d B A -= dydp p p D AA --=ν(11-16b )TR p v dy p d T R D v M M A A AA AA A +-=+='ρ(11-17)yp T R p p p Dy p T R D M d d d d A A A A A A A---='yp p p p T R D M d d AA A A --=' (11-18)这就是斯蒂芬(J.Stefan )定律的微分表达式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
工程热力学与传热学
第十一章辐射换热习题
1. 何谓黑体,灰体?引入黑体,灰体的概念对热辐射理论及辐射换热计算有何意义?
2. 何谓发射率(黑度),吸收比?写出其定义式。
3. 何谓辐射力,辐射强度,有效辐射?
4. 何谓光谱辐射力?写出它与辐射力之间的关系式。
5. 何谓漫发射表面?漫发射表面的辐射力与辐射强度有何关系?
6. 简述普朗特定律,维恩位移定律的主要内容。
7. 请写出斯沁藩-玻耳兹曼定律的表达式。
8. 简述基尔霍夫定律的主要内容,写出表达式,说明其适用条件。
9. 有人说:“颜色愈黑的物体发射率愈大”。正确吗?为什么?
10. 太阳能集热器表面一般涂黑色,以加强对太阳辐射的吸收,是否可以将暖气片表面涂成黑色来
增加其辐射散热量?
11. 何谓角系数?角系数是物理量还是几何量?
12. 何谓角系数的相对性,完整性和可加性?试用表达式加以说明。
13. 绘出3个灰体表面组成的封闭空腔的辐射换热网络,并说明什么是表面辐射热阻,空间辐射热
阻?
14. 简述遮热板的原理。
15. 何谓大气“温室效应” ?为什么减少CCh的排放就可以降低温室效应?
16. 发射率分别为0.3和0.5的两个大平行平板,其温度分别维持在800 °C和370C,在它们之间
放 置一个两面发射率均为0.05的辐射遮热板。试计算:
(1) 没有辐射遮热板时,单位面积的辐射换热量是多少?
(2) 有辐射遮热板时,单位面积的辐射换热量是多少?
(3) 辐射遮热板的温度。
习题课
有效辐射的计算
17. 两块平行放置的平板表面发射率均为0.6,其板间距远小于板的宽度和高度,且两表面温度分
别为圮427 °C, t2=27 °C。
试计算:(1)板1的自身辐射;(2)对板1的投入辐射;
(3)板1的反射辐射;(4)板1的有效辐射;
(5)板2的有效辐射;(6)板1, 2间的辐射换热量。
18. 两块平行放置的钢板之间的距离与其长和宽相比,可以忽略不计,己知它们的温度和发射率分
别为tL427 °C, &二27 °C,八二八二0.8。试计算两块钢板相对表面处的(1)自身辐射;(2)有
效 辐射;(3)投入辐射;(4)净辐射换热量。
遮热板的计算
19. 辐射率分别为0.3和0.5的两个大平行平板,其温度分别维持在800 °C和37(TC,在它们之
间 放一个两面发射率均为0. 05的辐射遮热板。试计算:
(1) 没有辐射遮热板时,单位面积的辐射换热量是多少?
(2) 有辐射遮热板时,单位面积的辐射换热量是多少?
(3) 辐射遮热板的温度。
20. 试证明:在两个平行平板之间加上n块遮热板后,辐射换热量将减少到无遮热板时的一匚。
72 + 1
设各板均为漫灰表面,且发射率相同。
多个灰体间的辐射换热
21. 液氧贮存容器为双壁镀银的夹层结构,外壁内表面温度为twL20°C,内壁表面温度为tw2=-
183 °C,镀银壁的发射率为£=0.02,试计算由于辐射换热每单位面积容器壁的散热量。
22. 一根直径d=50mm,长度为1=8 m的钢管,被放置于横截面为0.2X0. 2虻的砖槽道内。若钢管
温度和发射率分别为J=250 °C, £ i=0. 79,砖槽壁面温度和发射率分别为t2=27 °C, £ 2=0. 93,
试 计算该钢管的辐射热损失。
23. 两块尺寸为1x2m,间距为Im的平行平板置于壁温t3=27 °C的大厂房内。平板背面不参与换
热。 己知两板的温度和发射率分别为:私=827 °C, t2=327 °C。j=0.2, £2=0.5。试计算:
(1)每个板的净辐射散热量;(2)厂房壁所得到的辐射热量。
I. 答:1—10基本概念(略)。
II. 答:角系数是几何量。只取决于两个物体表面的几何形状,大小和相对位置。
12. 答:(1)角系数的相对性:&X],2 =人2乂2,1;
(2) 完整性:支Xw = X,』+Xb+... + X,"(3):可加
性:
1=1
X[,(2+3)= & X],2 + Aj B 9 即:X[,(2+3)= X[,2 + X[, B
13. 答:辐射换热网络图:
热阻包括表面辐射热阻,空间辐射热组
14.答:遮热板的主要作用是削弱换热。在整个辐射换热中净辐射换热量为Oo
即遮热板即不向
原系统放出热量,也不从中吸收热量,只是在热流通路中增大了原系统的热阻,
使换热表面之间的
辐射换热受到阻
碍。
(1)没有加遮热板时,两块平板间的辐射换热网络图:
©1. 2
J1 ] J
2 Eb2
AX〕2
Ae
2
(2)加遮热板时,辐射换热网络图:
E5 1 —
Aex AX
J3,1 —马,_ $3=3" 1 1 —弓 Eb2
15.答:温室效应是利用玻璃对阳光的吸收较少,而对红外线吸收较多的特性,
使大部分太阳能穿
过玻璃进入室内,而阻止室内物体发射的辐射能透过玻璃散到室外,达到保温的目
的。
16.解:依题意:
'1,2 = I X|,3 =
X32
=
I
Ehl = 5.67x10-8 x(800 + 273)4 = 75146W
/m2
E
b2
=0■&4 =5.67x10—8x(370+273)4 =9691W/〃2
网络中的热阻
为:
壬=他=2.333,上= -L = _Ul,
£
\ °3 、1,2 、1,3
、3.2
1-& 1一0.05 〔A 1 — £-> 1 —
0.5 1
——-= ---- =19, --- = --- = 1
0.05 £. 0.5
(1)无辐射遮热板时:
75146-9691 = 151Q5MZ/m2
1,2
2.333 + 1 + 1
(2)有辐射遮热板时:
75146-9691
加 2 = 2.333+由9+19 + 1 + 广151。
・
5
叼冰
(3)辐射遮热板的温度:
依能量平衡,列出下列方程式:
75146-9691
75146-孩3
2.333+1 + 19 2.333 + 1 + 19 + 19
+ 1 + 1
解之:
Eh3 =aT^ =41411 W/m
2
因此:
7; = 924 K = 651 °C
17. 解:(1)板1的自身辐射Ei=8186W/m2; (2)对板1的投入辐射Gi=J2=4218W/m2;
(3)板 1 的反射辐射 PlGi=Ji-Ei=1687W/m2; (4)板 1 的有效辐射 Ji=9855W/m2;
(5)板2的有效辐射J2=4218W/m2; (6)板1, 2间的辐射换热量qi2=5638W/m2o
18. 解:(1)自身辐射 Ei=18579.4kW/m2, E2=367.42kW/m2; (2)有效辐射 Ji=19430.15kW/m2,
J2=4253.45kW/m2; (3)投入辐射 Gi=4253.45kW/m2, G2=19430.15kW/m2; (4)净辐射换热量
qi2=15176.7kW/m2o
19. 解:板的温度是:T3=867Ko
20. 解(1)没有遮热板时,单位面积的辐射换热量:qi2=15105W/m2; (2)有遮热板时,单位面积 的
辐射换热量:qi32=1510.5W/m2; (3)辐射遮热板的温度:T3=924KO
21. 证明(略)。
22. 解:单位面积容器壁的散热量:qi2=4.18W/m2o
23. 解:钢管的辐射热损失:Q=3.712kW。
24. 解:(1)每个板的净辐射散热量:Qi=32.34kW,Q2=1.822kW; (2)厂房壁所得到的辐射热量:
Q3=34.16kWo
25. 解:若设大房间为重辐射面,温度较高表面的净辐射散热为:Qi=23.06kW。
