第二十五章概率初步复习课件
合集下载
期末第25章概率初步复习课件.ppt

解:(1)如图 D52,画树状图,得:
图 D52 ∴一共有 12 种等可能的结果,两球编号之和为奇数有 5 种 情况. ∴P(甲胜)=152.
(2)∵P(乙胜)=172,
∴P(甲胜)≠P(乙胜). ∴这个游戏规则对甲、乙双方不公平. 将红盒子中装有编号分别为 1,2,3,5 的四个红球,改 为 1,2,3,4 的四个红球即可.
某校为庆祝国庆节举办游园活动,小军来到摸球兑奖活 动场地,李老师对小军说:“这里有 A,B 两个盒子,里面都 装有一些乒乓球,你只能选择其中一只盒子中摸球.”获奖规
则如下:在 A 盒中有白色乒乓球 4 个,红色乒乓球 2 个,一人 只能摸一次且一次摸出一个球,若为红球则可获得玩具熊一个,
否则不得奖;在 B 盒中有白色乒乓球 2 个,红色乒乓球 2 个, 一人只能摸一次且一次摸出两个球,若两球均为红球则可获得 玩具熊一个,否则不得奖.
况,当事件要经过两步完成时用列表法,当事件 要经过三步以上完成时用树形图法。
2.概率的意义
一般地,如果在一次试验中,有n种可能的结果, 并且它们发生的可能性都相等,事件A包含其中的m种
m
结果,那么事件A发生的概率P(A)= n .
[注意] 事件A发生的概率的取值范围 0 ≤P(A)≤ 1 ,当A为必然事件时,P(A)= 1 ;当A
m 3、在什么条件下适用P(A)= n 得到事件的概率?
一般地,如果在一次试验中,有n种可能的 结果,并 且它们发生的可能性都相等,事件A包含其中m种结果, 那么事件A发 生的概率为:
P(A)
A包含的基本事件的个数 基本事件的总数
m n
4、如何用列举法求概率? 当事件要经过一步完成时列举出所有可能 情
判断事件类型的流程
第二十五章概率初步(复习课)
黑白相间地排列共有8种
P(黑白相间排列)=8/24=1/3
能力提高
1、你能说出几个与必然事件、随机事件、不可能事件 相联系的成语吗?
如:必然事件:种瓜得瓜,种豆得豆,黑白分明。 随机事件:海市蜃楼,守株待兔。
不可能事件:画饼充饥,拔苗助长。
2、在一个不透明的口袋中装有除颜色外其余都相同的 1个红球,2个黄球,如果先后两从袋中各摸出1个球。 求下列情况中两次都摸到黄球的概率是多少? (1)第一次摸出的球要放回; (2)第一次摸出的球不再放回。
一般地,在大量重复进行同一试验时,事件A
发生的频率m/n稳定在某个常数p的附近,那么这
个常数就叫做事件A的概率,
记作:P(A)=P.且0≤P(A)≤1
3、如何用列举法求概率?
1.当事件完成由一个步骤(因素)决定时, 用直接列举法列出所有可能情况。
2.当事件完成由两个步骤(因素)决定时, 用列表法,列举出所有可能情况。
(1)用树形图表示出所有可能的寻宝情况; (2)求在寻宝游戏中胜出的概率.
练习5
小明拿着一个罐子来找小刚做游戏,罐子里有四个
一样大小的玻璃球,两个黑色,两个白色.小明说: “使劲摇晃罐子,使罐子中的示).就算甲方 赢,否则就算乙方赢.”他问小刚要当甲方还是乙方, 请你帮小刚出主意,并说明理由.
答案:P(奇数)=
2 3
3.用列表法求事件的概率
例3、某中学九年级有6个班,要从中选出2个班代表学校参加某 项活动,1班必须参加,另外再从2至6班选出一个班.4班有 学生建议用如下的方法:从装有编号为1,2,3的三个白球的 袋子中摸出一个球,再从装有编号为1,2,3的三个红球的袋 子中摸出一个球(两袋中球的大小、形状与质量完全一样), 摸出的两个球上的数字和是几,就选几班。 你认为这种方法公平吗?请说明理由.
第25章概率初步(复习课)

答:我认为这个游戏公平。因为
P(扎在黑色区域)=P(扎在白色区域) = 1/2.
练习2
(抢答题)如图所示,如果小明将镖随
意投中正方形木板,那么镖落在阴影部
分的概率为( C ).
A.1 B.1 C.1 D.1
6
8
9
12
• 2.计算简单随机事件的概率
例4 根据你的经验,分别写出下列事件发生的机会:
A.在一个不透明的袋中装有红球3个、白球2个、黑球
黄柳燕
练习7
(抢答题)乘火车从A站出发,沿途 经过3个车站方可到达B站,那么在A、 B两站之间需要安排 20 种不同的 车票.
5.能构成三角形吗?
四条线段的长度分别是2cm, 3cm,4cm,5cm,从中取三条能 构成三角形的概率是 ______
• (2)数形结合思想 例2 如图所示的图案中,黑白两色的直角三 角形都全等.将它作为一个游戏盘,游戏规 则是:按一定距离向盘中投镖一次,扎在黑 色区域为甲胜,扎在白色区域为乙胜.你认 为这个游戏公平吗?为什么?
第二十五章概率初步
复习与小结
一、知识回顾:
随机事件
随
事
必然事件
机
件
不可能事件
事
件 的
事
概率的定义
概件
率的
概 率
怎样得到随机 事件的概率
0<P<1
P=1
P=0
概率 频率
的概 稳率 定是 值频
率
用列举法求概率
用频率估计概率
随机事件 概率
用列举法求概率 用频率估计概率
直 列树
概
模
接 表形
列 法图
举
法
率 与 频 率
1中个取,出每一种个球球除,颜取色到外红其球余的都机相会同是,摇1匀后;随机地从袋 2
P(扎在黑色区域)=P(扎在白色区域) = 1/2.
练习2
(抢答题)如图所示,如果小明将镖随
意投中正方形木板,那么镖落在阴影部
分的概率为( C ).
A.1 B.1 C.1 D.1
6
8
9
12
• 2.计算简单随机事件的概率
例4 根据你的经验,分别写出下列事件发生的机会:
A.在一个不透明的袋中装有红球3个、白球2个、黑球
黄柳燕
练习7
(抢答题)乘火车从A站出发,沿途 经过3个车站方可到达B站,那么在A、 B两站之间需要安排 20 种不同的 车票.
5.能构成三角形吗?
四条线段的长度分别是2cm, 3cm,4cm,5cm,从中取三条能 构成三角形的概率是 ______
• (2)数形结合思想 例2 如图所示的图案中,黑白两色的直角三 角形都全等.将它作为一个游戏盘,游戏规 则是:按一定距离向盘中投镖一次,扎在黑 色区域为甲胜,扎在白色区域为乙胜.你认 为这个游戏公平吗?为什么?
第二十五章概率初步
复习与小结
一、知识回顾:
随机事件
随
事
必然事件
机
件
不可能事件
事
件 的
事
概率的定义
概件
率的
概 率
怎样得到随机 事件的概率
0<P<1
P=1
P=0
概率 频率
的概 稳率 定是 值频
率
用列举法求概率
用频率估计概率
随机事件 概率
用列举法求概率 用频率估计概率
直 列树
概
模
接 表形
列 法图
举
法
率 与 频 率
1中个取,出每一种个球球除,颜取色到外红其球余的都机相会同是,摇1匀后;随机地从袋 2
(最新整理)(完整版)第25章概率初步(复习课)

17
• 2.计算简单随机事件的概率
例4 根据你的经验,分别写出下列事件发生的机会:
A.在一个不透明的袋中装有红球3个、白球2个、黑球
1中个取,出每一种个球球除,颜取色到外红其球余的都机相会同是,摇1 匀后;随机地从袋 2
B.掷一枚普通正方形骰子,出现的点数为7的机会
是0 ;
1
C.掷两枚普通硬币,出现两个正面的机会是 4 .
经过某十字路口的汽车,它可能继续直行,也可能左转或右 转,如果这三种可能性大小相同,同向而行的三辆汽车都经过 这个十字路口时,求下列事件的概率:
(1)三辆车全部继续直行(2)两辆车右转,一辆车左转
(20321)/7/2至6 少有两辆车左转
24
能力提高
1、你能说出几个与必然事件、随机事件、不可能 事件相联系的成语吗?
中m种结果,那么事件A发 生的概率为:
P (A )A 包 含 基 的 本 基 事 本 件 事 的 件 总 的 数 个 数 m n
4、如何用列举法求概率? 当事件要经过一步完成时列举出所有可能 情
况,当事件要经过两步完成时用列表法,当事件 要经过三步以上完成时用树形图法。
2021/7/26
10
3、如何用列举法求概率?
所以
0≤
m
n
≤1,
可知频率
m
n
会稳
定到常数p 附近,且满足0≤ p ≤1.
于是可得 0≤P(A) ≤1.
显然,必然事件的概率是 1,不 可能事件的概率是 0 .
2021/7/26
9
3、在什么条件下适用P(A)=m 得到事件
的概率?
n
一般地,如果在一次试验中,有n种可能的 结
果,并且它们发生的可能性都相等,事件A包含其
概率初步复习PPT课件

次数叫 频数 ,某个事件出现的次数
与试验总次数的比,叫做这个事件出
现的 频率 ,一个事件在多次试验中发
生的可能性叫做这个事件发生
概率 的
。
高速磁悬浮交通技术
2、事件发生的概率与事件发生的频 率有什么联系?
一般地,在大量重复进行同一 试验时,事件A发生的频率m/n稳定
在某个常数 p 的附近,那么这个
第二十五章概率初步
复习与小结
高速磁悬浮交通技术
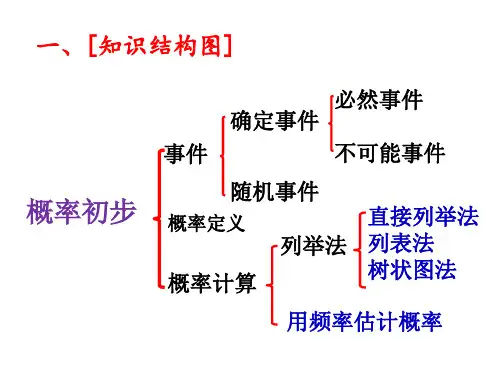
一、[知识网络]
事件
必然事件 确定事件
不可能事件
随机事件
概率初步
概率计算
直接列举法
列举法 列表法 树状图法
用频率估计概率
高速磁悬浮交通技术
随机事件 概率
概率定义 用列举法求概率 用频率估计概率
直 列树
概
模
接 表形
率
拟
列 法图
举
法
与 频 率
试 验
法
的
异
3.当事件要经过三步以上完成时 ,用树形图法,列举所有可能情况。
高速磁悬浮交通技术
4、用频率估计概率的一般做法
当试验的所有可能结果不是有限个, 或各种可能结果发生的可能性不相等时, 常常是通过统计频率来估计概率,即在同 样条件下,用大量重复试验所得到的随机 事件发生的频率的稳定值来估计这个事
件发生的概率。
(3)对于某些随机事件也可以不通过重复试验, 而只通过一次试验中可能出现的结果的分析 来计算概率。例如:掷两枚硬币,求两枚硬 币正面向上的高概速率磁。悬浮交通技术
因为在 n 次试验中,随机事件
A发生的频数 m 次 0≤m≤n ,
所以
0≤mn
≤1,
可知频率
