数学高二(上)沪教版(等比数列(一))教师版
沪教版高二数学上册

沪教版高二数学上册
本站不提供该课本链接,目录如下:第7章数列与数学归纳法一数列7.1数列7.2等差数列7.3等比数列二数学归纳法7.4数学归纳法7.5数学归纳法的应用7.6归纳-猜想-论证三数列的极限7.7数列的极限7.8无穷等比数列各项的和第8章平面向量的坐标表示8.1向量的坐标表示及其运算8.2向量的数量积8.3平面向量的分解定理8.4向量的应用第9章矩阵和行列式初步一矩阵9.1矩阵的概念9.2矩阵的运算二行列式9.3二阶行列式9.4三阶行列式第10章算法初步10.1算法的概念10.2程序框图。
沪教版(上海)高二数学上册7.1数列课件

(5)1,1,1,1,1,….
3.
项的序数
项
1, 2, 3, 4, …, n,…
ห้องสมุดไป่ตู้a1 , a2 , a3 , a4 , , an , ,
a1 f (1), a2 f (2), a3 f (3), a4 f (4), , an f (n)
与421是否为该数列中的项?若是应为第几项?
1.数列的定义
2数列的项与序数,通项公式
3.数列是定义在正整数集或其子集上函数
7.1 数 列(1)
“一尺之棰”每日剩下的部分
1 1 1
1
1
, , , , ⋯
2 4 8 16 32
中国数学家祖冲之在前人的基础上,经过刻苦钻
研,反复演算,将圆周率推算至小数点后7位数
(即3.1415926与3.1415927之间),并得出了
圆周率分数情势的近似值。
的不足近似值:
3, 3.1,3.14, 3.141, 3.1415,
(3) , , ,
2 4 8 16
例3.视察下列数列的构成规律,写出数列的一个通项公式
1 1 1 1
(1) − , , − , , ⋯
2 4 8 16
(2)9,99,999,9999, ⋯
3 2 5 3 7
(3) , , , , , ⋯
2 3 12 10 30
(4)2,0,2,0,2,0, ⋯
例4.已知无穷数列1×2,2×3,3×4,……,n(n+1),……判断420
的第一项,(也称首项)排在第二位称为这个数列的第二项,…,
排在第n位的数称为第n项.
沪教版高二上册数学等比数列的前N项和教案二级第一学期

7.3(3)等比数列的前n项和(1)一、教学内容分析《数列》是高中数学的重要内容之一.学习了数列的概念、等差数列的通项公式和前n 项的求和公式、等比数列的通项公式等知识内容后,为过渡到本节的学习起着铺垫作用.研究等比数列前n项和的公式完整了数列体系,又为进一步学习数列求和、数列的极限等内容打下基础,有承前启后的作用.数列是函数的延续,它实质上是可以看作为一种特殊的函数,函数思想同样在本节渗透.等比数列求和在产品的规格设计、储蓄、分期付款的有关计算中有着广泛的实际应用.学习数列需要观察、分析、猜想及综合运用其它知识解决数列中的一些问题,有利于学生数学能力的提高,是培养提高学生思维能力的好题材.二、教学目标设计1.进一步理解等比数列的前n项和公式的推导方法;2.掌握等比数列的前n项和公式及其初步应用;3.初步形成观察问题、灵活运用基本概念分析问题解决问题的能力;4.进一步树立理论联系实际的观点.三、教学重点及难点重点:等比数列的前n项和公式及其初步应用.难点:等比数列的前n项和公式的推导.四、教学用具准备实物投影仪五、教学流程设计六、教学过程设计1、引入(1) 印度国王西拉谟与国际象棋发明家的故事.相传国王要奖励国际象棋发明者,问他有什么要求,发明者说:“请在棋盘上的64格中的第1格放入1粒麦粒,第2格放入2粒麦粒,第3格放入4粒麦粒,第4格放入8粒麦粒,依此类推,每一个格子放的麦粒数都是前一个格子里放的麦粒数的2倍,直到放完64个格子为止.”国王立即答应了.问国王将会给发明者多少粒麦粒?[说明] 以小故事切入,具有趣味性,利用了学生的好奇心,也有利于知识的迁移,明确知识的现实应用.(2)建立数学模型.求麦粒的数目,实际上是什么数学问题呢?实际是计算1+2+4+8+…+632(=64S )的值,即求以1为首项、以2为公比的等比数列的前64项的和.(2) 求解数学模型.观察上式的特点,启发学生找到解决问题的方法.与等差数列类比.在推导等差数列的前n 项和时,充分利用了公差,即21a a d =+,31412,3,a a d a a d =+=+ …,1(1)n a a n d =+-;另外又可以写为1n n a a d -=-,22n n a a d -=-,…,1(1)n a a n d =--,这才有了逆序相加法.那么,对于等比数列是否也可以充分利用公比呢?方法一:每一项乘以2后都得到它的后一项.64S =1+2+4+8+…+632,264S =2+4+8+…+632+642,两式右边有62项相同.相减,得64642 1.S =-方法二:逆向思考,提取2,就得到前一项.64S =1+2+4+8+…+6362212(1242)=+++++=1+263S =636412(2)S +-解得,64642 1.S =-据查每千克小麦约10万粒,64S 约111.8410⨯吨.2004年世界粮食总产量为92.2510⨯吨,因此64S 相当于当今世界82年的粮食总产量. [说明] 解决问题的关键是意识到631242++++的模型就是前63个格子里麦粒数目的和,即等比数列前64项的和.(4)反思抽象.以上解决了一个特殊等比数列前几项的和,那么对于一般的等比数列,我们可以提出什么问题呢?并加以解决.[说明] 问题由学生提出,训练学生发现问题、提出问题的能力.一般地,设等比数列{}n a 的公比为q ,则211231111.n n n S a a a a a a q a q a q -=++++=++++(5)解决问题.从特殊问题推广到一般问题,是否可以继续使用解决特殊问题的方法呢?试一试.[说明] 板书时,可以利用前面的特殊化例子,将2改为q 即可,一方面可以节约时间和板书空间,另一方面让学生体会特殊性与一般性的关系.方法一:211111n n S a a q a q a q -=++++, 23111111n n n qS qa a q a q a q a q -=+++++相减,得11n n n S qS a a q -=-,即1(1)(1)nn q S a q -=-当1q ≠时,1(1).1n n a q S q-=- 当1q =时,12n a a a ===,则1.n S na =方法二:2122111111111()n n n S a a q a q a q a q a a q a q a q --=++++=+++++=111()n n n a qS a q S a -+=+- 即,1(1)n n q S a qa -=- 当1q ≠时,1.1nn a qa S q-=-当1q =时,12n a a a ===,则1.n S na =(方法一和方法二完全是特殊化问题的翻版,可以让学生直接回答,进一步理解公式的推导方法和过程.)(6)讨论探究.同学们还有其它的解法吗?[说明] 引起学生求胜心,激发积极性.启发引导学生自行完成.由等比数列的定义,得32121nn a a a q a a a -====,运用比例的性质, 23121n n a a a q a a a -+++=+++,即1n n nS aq S a -=-当1q ≠时,1.1nn a qa S q-=-当1q =时,12n a a a ===,则1.n S na =2、概念分析(1)对问题结构的观察分析,不同的视角获得不同的解题方法.要勤思考.(2)方法一称为错位相减法.这是一种重要的解题方法,不仅仅在解决数列问题时有重要应用,而且在类似问题(如:函数)中也将发挥它的作用.我们既重视公式的应用,也要重视公式的推导方法.(重结论,也重过程.)(3)使用等比数列的前n 项和公式,必须注意到公比是否等于1,1q =与1q ≠的公式形式是不一样的.(4)在1q ≠时,求和公式将根据已知条件有不同的选择.1(1)1n n a q S q -=-,1.1n n a qa S q-=- (5)求和公式中有5个量1,,,,n n a q n a S ,结合等比数列的通项公式,分析得到:若已知其中的3个量,则可以求得其它的2个量,即所谓的“知三求二”.3.例题例1.求下列等比数列的各项的和: (1)11111,,,,24816; (2)127,9,3,,.243- 选题目的:直接应用公式,选择公式,熟练公式.答案:(1)3116;(2)4921.243 例2.已知公比为12的等比数列的前5项和为318,求这个数列的1a 及5.a选题目的:逆向应用公式. 答案:12a =,51.8a =例3.已知等比数列11,,1,93,求使得n S 大于100的最小的n 的值.选题目的:综合应用公式.答案:使得n S 大于100的最小的n 的值为7.例4.设数列{}n a 的前n 项和为3nn S a =+.当常数a 满足什么条件时,{}n a 才是等比数列? 选题目的:沟通n a 与n S 的关系,灵活应用公式. 答案:1a =- 4、练习P27—练习7.3(4)—1,2,3 5、小结先由学生进行小结,再由教师进行小结.本节课从一个实例出发,探索了等比数列的前n 项和公式.错位相减法是我们的重要收获.不仅重视探索得到的结论,更应重视探究的过程,重视思维方法(还有两种推导方法).应用求和公式时一定要首先判断等比数列的公比是否等于1,再选择公式.本节课渗透的数学思想方法有方程思想、等价转化. 6、作业P9—10,P11—7,8 七、教学建议与说明(1)根据学生认知心理特点,采用从特殊到一般的方式推进教学.(2)具体实例是浅层次要求,使学生有概括印象,从而推广到一般情形.让学生自己推广,提出问题,培养学生思维能力.(3)重点是公式的推导,这是培养学生思维深刻性、灵活性、严密性的良好素材,要充分利用这一时机.(4)公式推导中,以启发性强的设问层层推进,让学生尝试探索,提供学生自主学习的时间和空间,创设宽松的、开放式的环境,可以小组讨论等,点燃学生思维火花,培养学生的创新意识和胆量. 八、教学反思现实课堂教学中必然会有教师备课中预想不到的问题出现,恰如其分地处理能反映教师的机智,更表现了尊重学生、以学生发展为本的理念.比如就有学生在求解64S =1+2+4+8+…+632时注意到了数字的特殊性,灵活解决1+64S =1+1+2+4+8+…+632=2+2+4+8+…+632=4+4+8+…+632=…=264,则64S =632-1. 简单明了.若将公比2改为3,则该方法就不能发挥作用,真正体现了具体问题具体分析,解决特殊性的方法不见得适用于一般性.抓住时机进一步理解特殊与一般的关系.由等比数列的定义,运用比例的性质探索求和的方法学生不容易想到,需要教师启发引导,“回到定义去!”,并及时进行数学文化渗透:这是两千多年前欧几里德的《几何原本》中提供的方法.解决问题的方法多样化,但都紧紧围绕等比数列的定义,所谓“一题多解,多解归一”,强调解决问题的突破点和实质,并强调错位相减法的重要性:在解决特殊数列求和中的价值体现.。
沪教版(上海)高二数学上册7.1数列_课件

为 a ,这里n是 n
正整数 .
3.数列的通项公式
如果数列的第n项an与 n 之间的关系可以用一个函数式an=f(n) 来表示,那么这个公式叫做这个数列的通项公式.
4.数列与函数的关系
(1)数列与函数的内在联系
从映射、函数的观点看,数列可以看作是一个定义域为 正整数集N+(或它的有限子集)的函数an=f(n),即当自变量按照从小到大的
整理得 a2n-2nan-2=0,
∴an=n± n2+2. 又 0<x<1,故 0<2an<1,于是 an<0,
∴an=n- n2+2(n∈N+).
(2)aan+n 1=n+1n--
n+12+2 n2+2
=
n+ n+1+
n2n++212+2<1.
∵an<0,∴an+1>an, ∴数列{an}是递增数列.
数列
1 . 如 果 f(x) = x2 - 1 , x∈{1,2,3,4,5} . 则 f(x) 的 值 域 为 {0,3,8,15,24}.
2.将前5个正整数的倒数排成一列 1,12,13,14,15 .
3.函数f(x)=2x+1,x∈{1,2,3,4,5}的图象上共有 5 个点,它 们是(1,3),(2,5),(3,7),(4,9.),(5,11)
4.若本例条件换为 f(x)=log2x-lo2g2x(0<x<1),且数列 {an}满足 f(2an)=2n(n∈N+).
(1)求数列{an}的通项公式; (2)判断数列{an}的增减性. 【解析】 (1)∵f(x)=log2x-lo2g2x, 又∵f(2an)=2n, ∴log22an-log222an=2n, 即 an-a2n=2n.
(2)∵bn=11·2+21·3+31·4+…+n·n1+1 =1-12+12-13+13-14+…+1n-n+1 1 =1-n+1 1=n+n 1, ∴b1=12,b2=23,b3=34,b4=45,b10=1110.
高二上册数学教案7.1等比数列的前n项和沪教版
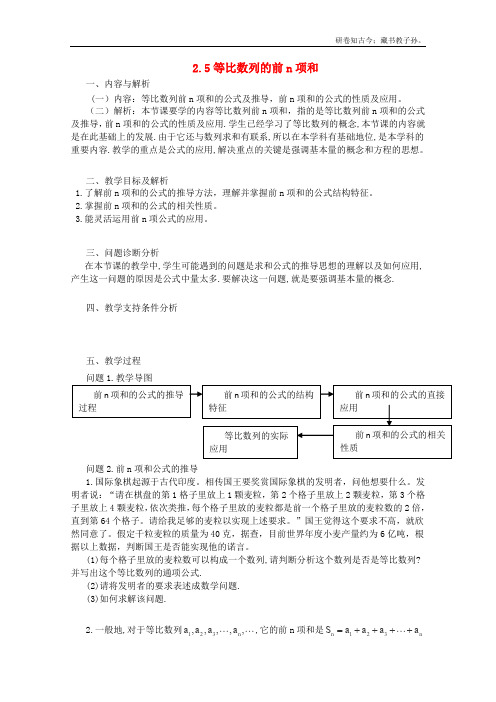
2.5等比数列的前n 项和一、内容与解析(一)内容:等比数列前n 项和的公式及推导,前n 项和的公式的性质及应用。
(二)解析:本节课要学的内容等比数列前n 项和,指的是等比数列前n 项和的公式及推导,前n 项和的公式的性质及应用.学生已经学习了等比数列的概念,本节课的内容就是在此基础上的发展.由于它还与数列求和有联系,所以在本学科有基础地位,是本学科的重要内容.教学的重点是公式的应用,解决重点的关键是强调基本量的概念和方程的思想。
二、教学目标及解析1.了解前n 项和的公式的推导方法,理解并掌握前n 项和的公式结构特征。
2.掌握前n 项和的公式的相关性质。
3.能灵活运用前n 项公式的应用。
三、问题诊断分析在本节课的教学中,学生可能遇到的问题是求和公式的推导思想的理解以及如何应用,产生这一问题的原因是公式中量太多.要解决这一问题,就是要强调基本量的概念.四、教学支持条件分析五、教学过程问题1.教学导图问题2.前n 项和公式的推导1.国际象棋起源于古代印度。
相传国王要奖赏国际象棋的发明者,问他想要什么。
发明者说:“请在棋盘的第1格子里放上1颗麦粒,第2个格子里放上2颗麦粒,第3个格子里放上4颗麦粒,依次类推,每个格子里放的麦粒都是前一个格子里放的麦粒数的2倍,直到第64个格子。
请给我足够的麦粒以实现上述要求。
”国王觉得这个要求不高,就欣然同意了。
假定千粒麦粒的质量为40克,据查,目前世界年度小麦产量约为6亿吨,根据以上数据,判断国王是否能实现他的诺言。
(1)每个格子里放的麦粒数可以构成一个数列,请判断分析这个数列是否是等比数列?并写出这个等比数列的通项公式.(2)请将发明者的要求表述成数学问题.(3)如何求解该问题.2.一般地,对于等比数列123,,,,,n a a a a ,它的前n 项和是123n n S a a a a =++++(1)利用它的通项公式,你能转化成什么式子呢?(2)观察等式右边的任意相邻两项,你发现了什么?(3)根据你的发现,你能构造一个新的等式,使得这两个等式有很多相同的项吗?(4)你可以采取什么样的运算,使得这些相同项消失呢?试试看,你得到了什么?(5)在上述运算过程中,你发现什么不妥吗?请改进.(6)综合上述的过程,请总结一下等比数列的前n 项和的公式及推导方法。
沪教版高二上册数学无穷等比数列的各项和教案二级第一学期

7.8(1)无穷等比数列的各项和(1)一、教学内容分析本小节的重点是无穷等比数列的各项和公式及简单应用.教材在前面已经介绍了等比数列的前n项和与极限的概念,利用极限不难将“等比数列的有限求和”转化为“等比数列的无限项求和”.教材这样处理,既符合学生的认知规律,又让学生深刻体会从有限认识无限、从已知认识未知、从近似认识精确的极限思想,能充分调动学生的求知欲望,开扩学生思路,激发学习数学的兴趣.本小节的难点是正确理解无穷等比数列的各项和的定义.突破难点的关键是创设问题情景,利用对问题的分析,得出定义,推导出无穷等比数列的的各项和的公式,激发学生学习知识的兴趣,引导学生进行思维创新,在不断探索中发现问题、解决问题.二、教学目标设计1.理解无穷等比数列的各项和的定义;2.掌握无穷等比数列的各项和的公式,会应用公式求无穷等比数列的各项和;3.理解无限个数的和与有限个数的和在意义上的区别;4.通过在利用无穷等比数列的各项和的公式解决一些简单的实际问题过程中,形成和提高数学的应用意识.三、教学重点及难点教学重点:无穷等比数列的各项和的公式的推导及其应用.教学难点:正确理解无穷等比数列的各项和的定义.四、教学用具准备实物投影仪五、教学流程设计六、教学过程设计一、复习引入 思考下列问题:1、0.9•和1哪个数大?为什么?2、由于空气的阻力,因此某一类钟的钟摆每摆动一次的弧的长度都是其上一次摆动弧的长度的95%.假设其第一次摆动弧的长度为40cm ,求它在停止前所有摆动的弧的长度和.对于问题1,先让学生进行讨论,然后展示他们的结果. 引导学生回答以下问题:(1)如果你认为0.91•<,那么0.9•比1小多少?(2)如果你认为0.91•<,那么你能否找到一个实数a ,使得0.91a •<<成立? 换一个角度来看,事实上()100.90.9990.90.090.0009n -•=⋅⋅⋅⋅⋅⋅=++⋅⋅⋅+⋅⋅⋅+⋅⋅⋅678个而()100.90.090.0009n -⋅⋅⋅⋅⋅⋅⋅⋅⋅678个,,,,是首项为0.9,公比为110的无穷等比数列,它的前n 项和为 ()1010.911010.90.090.00091110110n n n n S -⎡⎤⎛⎫-⎢⎥ ⎪⎝⎭⎢⎥⎛⎫⎣⎦=++⋅⋅⋅+⋅⋅⋅==- ⎪⎝⎭-678个.于是可以把0.9•看作n S 当n →∞时的极限,从而110.91111010n nn n n n n lim S lim lim lim •→∞→∞→∞→∞⎡⎤⎛⎫⎛⎫==-=-=⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦.对于问题2,同样进行分析.对比以上两个问题,它们有何共同特征? 二、讲授新课1、无穷等比数列的各项和的公式的推导提问:在问题1的讨论中,我们将0.9•看成首项为0.9、公比为0.1的无穷等比数列的前n 项和的极限.请同学们思考,是否无穷等比数列的前n 项和的极限都存在?如果它的极限存在,那么极限等于什么?指出:当无穷等比数列的公比q 满足||1q <时,其前n 项和的极限才存在. 当0||1q <<时,无穷等比数列前n 项和的极限如下:∵ 111(1)111n n n a q a aS q q q q-==-⋅---(||1q <) ∴ 11(1)(1)11n n n n n n n a q alim S limlim lim q qq →∞→∞→∞→∞-==⋅--- 11(1)11n n n a alim lim q q q→∞→∞=-=--. ∵ 0||1q <<,∴0nn lim q →∞=.∴ 11n n a lim S q→∞=-. 让学生尝试从上述推导过程中归纳出无穷等比数列的各项和的公式.强调:只有当无穷等比数列的公比q 满足0||1q <<时,其前n 项和的极限才存在. 2、无穷等比数列的各项和的定义提问:通过刚才的讨论,你能否给无穷等比数列各项和下一个定义?请用数学语言来描述一下.我们把||1q <的无穷等比数列的前n 项的和n S 当n →∞时的极限叫做无穷等比数列的各项和,并用符号S 表示.11a S q=-(||1q <). 强调:只有当无穷等比数列的公比q 满足0||1q <<时,其前n 项和的极限才存在. 3、无穷等比数列各项和的应用 例1 化下列循环小数为分数: (1)0.29••; (2)3.431••.分析:设法将循环小数化成等比数列的前n 项和,然后求极限.解:(1)()2100.290.290.00290.00029n -••=++⋅⋅⋅+⋅⋅⋅+⋅⋅⋅678个等式右边是首项为0.29,公比是0.01的无穷等比数列的各项的和,所以0.29290.2910.0199••==-.(2)3.431 3.40.0310.000310.0000031••=++++⋅⋅⋅,等式右边是3.4加上一个首项为0.031,公比是0.01的无穷等比数列的各项的和,所以0.0314314273.431 3.43310.0110990990••=+=++=-.师生共同总结得出: 循环小数化为分数的法则:1. 纯循环小数化分数:将一个循环节的数作分子,分母是99……9,其中9的个数是循环节数字的个数.2. 混循环小数化分数:将一个循环节连同不循环部分的数减去不循环部分所得的差作分子,分母是99…900…0,其中9的个数与一个循环节的个数相同,0的个数和不循环部分的数字个数相同. 练习:471,2P例2(补充) 求下列循环小数的和. 0.290.00290.000029••••••+++⋅⋅⋅分析:把每一个循环小数化为分数,然后再求和.解:同例1可求得,290.2999••=,290.00299900••=,290.000029990000••=,…∴ 原式=292929999900990000+++⋅⋅⋅ 上式表示首项为2999,公比为1100的无穷等比数列的各项和.∴ 原式=29290099198011100=-. 练习:求下列循环小数的和:0.30.030.003•••+++⋅⋅⋅.答案:1027例 3 如图,正方形ABCD 的边长为1,联结这个正方形各边的中点得到一个小正方形A 1B 1C 1D 1;又联结这个小正方形各边的中点得到一个更小正方形A 2B 2C 2D 2;如此无限继续下去.求所有这些正方形周长的和与面积的和.分析:关键是求出第n 个正方形 的边长与前一个正方形的边长的关系.解:由题意得第1个正方形的边长11a =,第n 个 正方形的边长n n n a A B ==12n a -==,2n ≥.即所有正方形的边长组成的数列为111,,,,2242n -⎛⋅⋅⋅⋅⋅⋅ ⎝⎭,于是所有正方形的周长组成的数列为B 1C 1A DABC14,,4,2n-⎛⋅⋅⋅⋅⋅⋅⋅⎝⎭,这是首项为4、公比为2的无穷等比数列,故所有的正方形的周长之和l为8l==+所有正方形的面积组成的数列为111111,,,,,,2482n-⋅⋅⋅⋅⋅⋅,这是首项为1、公项为12的无穷等比数列,故所有的正方形的面积之和S为12112S==-.练习:473P.补充练习:(可以和作业的思考题(2)联系讲解)在边长为1的正方形ABCD中,取AD、BC中点1A、1B,得矩形11ABB A;取11A B、DC中点2A、2B,得一小矩形212A B CB;再取1A D、22A B中点33A B、,得一小矩形1233A AB A;如此无限继续下去,求所有这些矩形的面积之和.所有面积组成首项为12,公比为12的无穷等比数列,所有这些矩形面积之和为1.事实上,从作图的过程可知,让作图无限下去,这些矩形面积之和正好是边长为1的正方形的面积.三、课堂小结1. 无穷等比数列的各项和的公式:S=qa-11(1<q);2.无穷等比数列各项的和,是一个极限值,并且这个极限是可以达到的;3.无穷等比数列的各项和存在是有条件的,即公比q满足01q<<;4.要学会从特殊问题的解决过程中体会一般化问题的解决方法.四、课后作业4211、书面作业:21.1,2,3,5P A ;22.1,2P B2、思考题:(1)正项等比数列的首项为1,前n 项和为n S ,求1nn n S limS →∞-.(2)早在公元前四世纪我国的公孙龙就有“一尺之捶,日取其半,万事不竭”的提法,(1)请写出此数列并求其各项的和;(2)可把此数列与哪个图形的面积联系起来,使此数列各项的和等于其面积和. 参看小结前的补充练习. 七、教学设计说明1.本节课的关键是让学生体会到:无穷多个数相加时,加法法则不再适用.求无穷多个数的和实际上是求一个极限(并且这个极限可以达到).一个无穷等比数列的各项和存在的关键是该数列的前n 项和的极限存在.所以,在新课引入时,利用课本的问题2让学生充分的讨论.得出无穷等比数列的各项和的概念,并推导出无穷等比数列的各项和的公式.2.本节课的设计意图在于用问题驱动学生学习,让学生在解决问题的过程中体会无穷的思想,真正理解为什么要用极限来定义一个无穷等比数列的各项和.当学生对无穷等比数列的各项和的概念理解后,应用也就水到渠成了.。
沪教版(上海)数学高二上册-7.8 无穷等比数列各项的和 课件
3
4n1
1 9
n
。
即,“雪花曲线”的面积是原来等边三角形的
8 5
倍。
三、课堂小结
1、无穷等比数列的各项和的定义:
我们把 q 1 的无穷等比数列前n项的和 Sn,当n
时的极限叫做无穷等比数列各项的和,并用S表示,
即S=
1
a1 q
(
q
1)
2、无穷等比数列各项的和几种等价表示形式.
四、作业 配套校本作业:7.8 节
每个小等边三角形的面积是
1
2
,增加的面积是
9
3
4
1 9
2
。
第三步以后,边数变成3×42,向外作了3×42个小等边三角形;
每个小等边三角形的面积是1 9源自3,增加的面积是3
42
1 9
3
。
依次类推,第n步以后,边数变成3×4n-1,向外作了3×4n-1个小等边三角
形;每个小等边三角形的面积是 1 n,增加的面积是
A
D1
D2
C3
D C2
A1
D3
B3
C1
A2
A3
B B1
B2 C
4、拓展探究:科克雪花曲线(分形图案)
边长为1的正三角形
无限变化下去
经过n次
(1)写出边数变化的递推公式;
N1 Nn
+1
3
4Nn
(n
N*)
(2)写出每条边长度变化的递推公式;
T1 1
Tn +1
1 3
Tn
(n
N*)
(3)写出周长变化的递推公式;
强调:(0< q 1)
2、巩固实践
沪教版高二上数学知识点
沪教版高二上数学知识点一、数列与数列极限1. 等差数列与等差数列的常用性质等差数列是指数列中的任意两项之差都相等的数列。
其常用性质有:a) 第n项公式:$a_n = a_1 + (n-1)d$,其中$a_1$为首项,$d$为公差,$n$为项数。
b) 前n项和公式:$S_n = \frac{n}{2}(a_1+a_n)$,其中$S_n$表示前n项和。
2. 等比数列与等比数列的常用性质等比数列是指数列中的任意两项之比都相等的数列。
其常用性质有:a) 第n项公式:$a_n = a_1 \cdot q^{n-1}$,其中$a_1$为首项,$q$为公比,$n$为项数。
b) 前n项和公式:$S_n = \frac{a_1(1-q^n)}{1-q}$,其中$S_n$表示前n项和。
二、函数与导数1. 基本初等函数基本初等函数是指由常数函数、幂函数、指数函数、对数函数、三角函数和反三角函数构成的函数。
a) 常数函数:$y = c$,其中$c$为常数。
b) 幂函数:$y = x^a$,其中$a$为常数,$x$为自变量。
c) 指数函数:$y = a^x$,其中$a > 0$且$a \neq 1$,$x$为自变量。
d) 对数函数:$y = \log_a{x}$,其中$a > 0$且$a \neq 1$,$x$为自变量。
e) 三角函数和反三角函数:包括正弦函数、余弦函数、正切函数等以及它们的反函数。
2. 导数与导数的应用a) 导数定义:函数$f(x)$在$x$点的导数为$f'(x) = \lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x}$。
b) 导数的计算:利用导数的四则运算法则和链式法则等进行计算。
c) 导数的应用:包括函数的极值、最值、曲线的切线方程以及函数图象和导函数之间的关系。
三、平面向量1. 平面向量的表示与运算a) 平面向量的表示:平面向量用带箭头的有序数对表示,如$\vec{AB}$表示从点$A$到点$B$的向量。
高中数学高二第一学期7.8无穷等比数列各项的和_教案2-沪教版
无穷等比数列各项的和【教学目标】1.理解无穷等比数列的各项和的定义;2.掌握无穷等比数列的各项和的公式,会应用公式求无穷等比数列的各项和;3.理解无限个数的和与有限个数的和在意义上的区别;4.通过在利用无穷等比数列的各项和的公式解决一些简单的实际问题过程中,形成和提高数学的应用意识。
【教学重难点】1.无穷等比数列的各项和的公式的推导及其应用。
2.正确理解无穷等比数列的各项和的定义。
【教学过程】一、复习引入思考下列问题:1.0.9•和1哪个数大?为什么?2.由于空气的阻力,因此某一类钟的钟摆每摆动一次的弧的长度都是其上一次摆动弧的长度的95%。
假设其第一次摆动弧的长度为40cm ,求它在停止前所有摆动的弧的长度和。
对于问题1,先让学生进行讨论,然后展示他们的结果。
引导学生回答以下问题:(1)如果你认为0.91•<,那么0.9•比1小多少?(2)如果你认为0.91•<,那么你能否找到一个实数a ,使得0.91a •<<成立?换一个角度来看,事实上: ()100.90.9990.90.090.0009n -•=⋅⋅⋅⋅⋅⋅=++⋅⋅⋅+⋅⋅⋅+⋅⋅⋅个;而()100.90.090.0009n -⋅⋅⋅⋅⋅⋅⋅⋅⋅个,,,,是首项为0.9,公比为110的无穷等比数列,它的前n 项和为: ()1010.911010.90.090.00091110110n n n n S -⎡⎤⎛⎫-⎢⎥ ⎪⎝⎭⎢⎥⎛⎫⎣⎦=++⋅⋅⋅+⋅⋅⋅==- ⎪⎝⎭-个。
于是可以把0.9•看作n S 当n →∞时的极限,从而:110.91111010n n n n n n n lim S lim lim lim •→∞→∞→∞→∞⎡⎤⎛⎫⎛⎫==-=-=⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦。
对于问题2,同样进行分析。
对比以上两个问题,它们有何共同特征?二、讲授新课1.无穷等比数列的各项和的公式的推导。
提问:在问题1的讨论中,我们将0.9•看成首项为0.9、公比为0.1的无穷等比数列的前n 项和的极限。
沪教版高中数学高二上册第七章无穷等比数列各项的和课件
an
[分析]
记
lim
n
an1
lim
n
an
A,则 A
1 2
A 3,故 A
6
巩固练习
9、若数列 lim lim an
满足an1
1 2 an
1, a1 3,且
n
a n 存在,求
n
an
无穷等比数列各项和的概念
无穷等比数列各项和的概念
1、若数列的通项公式为
,则该数列各项的和为:
(1)无穷等比数列各项的和有哪些表达方式?
题? (3)欣赏唐朝李白的诗:《黄鹤楼送孟浩然之广陵》
5、化下列循环小数为分数:(1)
;
无穷等比数列各项和的应用
2 4 8 由于空气的阻力,因此某一类钟的钟摆每摆动一次的弧的长度都是其上一次摆动弧的长度的95%.
,, 1 2n
(1)无穷等比数列各项的和有哪些表达方式?
,
合作讨论一:取得的所有木棒长的和是多少? 1、若数列的通项公式为
,则该数列各项的和为:
无穷等比数列各项和的概念
无穷等比数列各项和的概念
无穷等比数列各项和的概念
无穷等比数列各项和的概念
(1)口述等比数列的通项公式
,前项和的公式
发现二: q 满足:0 q 1 3、求数列
各项的和.
无穷等比数列各项和的概念
当且仅当公比
时,
无穷等比数列各项和的应用
由于空气的阻力,因此某一类钟的钟摆每摆动一次的弧的长度都是其上一次摆动弧的长度的95%.
无穷等比数列各项和的概念
证明: 无穷等比数列 a 前 n 项和的极限存在。 合作讨论五:猜想(※)还有其它证法吗?(小组讨论,交流成果)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
年 级:高二 辅导科目: 数学 课时数:3 课 题 等比数列
教学目的 1、 掌握等比数列的定义,会求等比中项; 2、 掌握等比数列的通项公式,前n项和的求和公式;
教学内容 【知识点回顾】
1.定义:qaann1(常数q为公比))(Nn (注意隐含条件:0,0naq)
2.通项公式:11nnqaa 推广: mnmnqaa 3.等比中项:如果在a与b间插入一个数G,使bGa,,成等比数列,那么G叫做a与b的等比中项,abG.)0(ab.
4.前n项和公式:11(1)(1)(1,0)1nnnaqSaqqqq且 (易错点:不分类讨论) 注意:应用前n项和公式时,一定要区分11qq与的两种不同情况,必要的时候要分类讨论. 5.等比数列na的一些常用性质 (1)对于任意正整数srqp,,,,如果srqp,则有srqpaaaa;如果qrp2,则有2qrpaaa (2)对于任意正整数,1n有112nnnaaa (3)对于任意非零实数b,数列nba是等比数列,则数列na是等比数列 (4)已知数列nb是等比数列,则nnba也是等比数列。 ⑸下标成等差数列的项构成等比数列 ⑹连续若干项的和也构成等比数列. 6.证明数列为等比数列的方法:
(1)定义法:若为等比数列数列nnnaNnqaa)(1
(2)等比中项法:若为等比数列数列且nnnnnnnaaaaNnaaa)0(21221 (3)通项法:若为等比数列数列的常数均是不为nnnaN,nqccqa)0,( (4)前n项和法:若为等比数列数列且为常数nnnaqq,qAAAqS)1,0,( 7.解决等比数列有关问题的常见思维方法 (1)方程的思想(“知三求二”问题) (2)分类的思想
①运用等比数列的求和公式时,需要对11qq和讨论
②为递增数列等比数列时或naqaqa,10,01,011 ()1(111qqaaannn) 为递减数列等比数列时或naqaqa,10,01,011
【基础训练】 1、在各项都为正数的等比数列{an}中,首项a1=3 ,前三项和为21,则a3+ a4+ a5= ( C ) ( A ) 33 ( B ) 72 ( C ) 84 ( D )189
2、已知等比数列{}na中,33a,10384a,则该数列的通项公式na 332n
3、命题甲:211(),2,22xxx成等比数列,命题乙:lg,lg(1),lg(3)xxx成等差数列,则甲是乙的 必要不充分 条件。(填“充分不必要”、“必要不充分”、“充要”或“既不充分也不必要”) 4、若干个能唯一确定一个数列的量称为该数列的“基本量”.设{an}是公比为q的无穷等比数列,下列{an}的四组量中,一定能成为该数列“基本量”的是 第 ①④ 组.(写出所有符合要求的组号) ①S1与S2; ②a2与S3; ③a1与an; ④q与an. 其中n为大于1的整数, Sn为{an}的前n项和. 5、有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点。已知最底层正方体的棱长为2,且该塔形的表面积(含最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是( C ) (A) 4; (B) 5; (C) 6; (D) 7.
6、设数列{}na的前n项和为nS(N*n),关于数列na有下列三个命题:
(1)若{}na既是等差数列又是等比数列,则1(N*)nnaan; (2)若2RnSanbnab、,则{}na是等差数列; (3)若11nnS,则{}na是等比数列. 这些命题中,真命题的序号是 ⑴⑵⑶ . 【例题讲练】 题型Ⅰ 等比数列中基本量的计算
例1、数列na为等比数列,求下列各值,
(1)已知.,2118367463naaaaan求 (2) .,15367382qaaaa求公比已知 (3) .),21(15,218aSq求已知 思维分析:运用等比数列的基本公式和基本性质”知三求二”问题 解(1)21,36,18)(63636374qaaaaqqaqaaa 9212)21(3232,36)1(833333333363nqaaaqaqaaaannnn
(2)
,03615,,1536273738273两根是方程xxaaaaaaaa
222414,3,1212,3447373qqqqaaaa或或或
(3)1)21()21()21(1521)15(21])2(1[11818aaaS 变式1.设一个等比数列的首项为a(a>0),公比为q(q>0),其前n项和为80,而其中最大的一项为54,又其前2n项和是6560,求a和q. 思维分析:运算等比数列的求和公式及整体代换思想和分类讨论思想,
解:若q=1,则na=80,∴2na=160矛盾,1q
于是)3(541,081)1()2()2(65601)1()1(801)1(11211nnnnnqaaqqqqqaqqa又得 3,2548111)3)(1(81qaqaqaqn及得代入 变式2.设等比数列na的前n项和为Sn,若S3+S6=2S9,求数列的公比q. 答案:243q 变式3.已知等比数列{an}中,a1+a2+a3=7,a1a2a3=8,求an. 剖析:利用等比数列的基本量a1,q,根据条件求出a1和q. 解:设{an}的公比为q,由题意知
,8,721112111qaqaaqaqaa
解得2,11qa或.21,41qa∴an=2n-1或an=23-n. 评述:转化成基本量解方程是解决数列问题的基本方法. 例2.已知等比数列na的公比为,q前n项和为nS,且396,,SSS成等差数列.
⑴ 求3q的值; ⑵ 求证:285,,aaa成等差数列. (答案: 3q=12) 题型Ⅱ 等比数列的判定和证明 例3、数列}{na的前n项和记为Sn,已知).3,2,1(2,111nSnnaann 证明:(Ⅰ)数列}{nSn是等比数列; (Ⅱ).41nnaS 证明:(Ⅰ)∵,2,111nnnnnSnnaSSa ∴ ),()2(1nnnSSnSn 整理得 ,)1(21nnSnnS
所以 .211nSnSnn 故}{nSn是以2为公比 的等比数列. (Ⅱ)由(Ⅰ)知).2(14111nnSnSnn 于是 ).2(41)1(411nanSnSnnn 又 ,3312Sa 故 ,4212aaS 因此对于任意正整数 ,1n 都有.41nnaS 评注:换元法体会肤浅,函数观点应用不当均会造成失误. 例4、已知数列na,Sn是它的前n项和,且1),(2411aNnaSnn
(1)设)(21Nnaabnnn,求证:数列nb是等比数列
(2)设nnnac2,,求证:数列nc是等差数列 思维分析:证明数列是等差数列还是等比数列.应紧扣定义式;而数列的前n项和Sn已知可求an
解:(1) 12121142,4244nnnnnnnnSaSaSSaa
2144nnnaaa即nnnnnnnnnbbaabaaaa22),2(2211112而,
由此可得nb是等比数列 且首项112123,2,32nnbqaab公比
(2)43223222,2111111nnnnnnnnnnnnnbaaccbc 可知nc是首项43,21211dac公差的等差数列,4143ncn 变式1:数列nnba,的通项公式分别是,23,2nbannn它们公共项由小到大排列的数列是nc, ①写出nc的前5项 ②证明nc是等比数列 思维分析:容易证明nc是等比数列,由定义式,只需找出nc中任意相邻两项关系即可. 解(1) nc的前5项为:8、32、128、512、2048 (2)设1)12(3)23(222,232,1ppapccbammmnnpm而 中在又中不在bnappabammmnm221,2)24(3)23(424,
是等比数列故项中的项即是nnnnnmccccca,4,112
变式2.已知数列{an}为等差数列,公差d≠0,{an}的部分项组成下列数列:a1k,a2k,…,ank,恰为等比数列,其中k1=1,k2=5,k3=17,求k1+k2+k3+…+kn. 剖析:运用等差(比)数列的定义分别求得ank,然后列方程求得kn.
解:设{an}的首项为a1,∵a1k、a2k、a3k成等比数列,∴(a1+4d)2=a1(a1+16d).
得a1=2d,q=12kkaa=3. ∵ank=a1+(kn-1)d,又ank=a1·3n-1, ∴kn=2·3n-1-1. ∴k1+k2+…+kn=2(1+3+…+3n-1)-n
=2×3131n-n=3n-n-1. 评述:运用等差(比)数列的定义转化为关于kn的方程是解题的关键,转化时要注意:ank是等差数列中的第kn
项,而又是等比数列中的第n项(双重身份). 变式3.设各项均为正数的数列{an}和{bn}满足5na,5nb,51na成等比数列,lgbn,lgan+1,lgbn+1成等差数列,且a1=1,b1=2,a2=3,求通项an、bn. 剖析:由等比中项、等差中项的性质得an+1=1nnbb递推出an=nnbb1(n≥2).
解:∵5na,5nb,51na成等比数列, ∴(5nb)2=5na·51na,即2bn=an+an+1. ① 又∵lgbn,lgan+1,lgbn+1成等差数列, ∴2lgan+1=lgbn+lgbn+1,即an+12=bn·bn+1. ② 由②及ai>0,bj>0(i、j∈N*)可得
an+1=1nnbb. ③
∴an=nnbb1(n≥2). ④
