库仑定律中k值
真空中库仑定律的表达式

真空中库仑定律的表达式库仑定律是描述电荷间相互作用的基本定律,它在真空中的表达式为:F = k * |q1 * q2| / r^2其中,F表示电荷间的相互作用力,k为库仑常数,q1和q2分别为两个电荷的大小,r为两个电荷间的距离。
库仑定律是物理学中的重要定律之一,它揭示了电荷之间相互作用的规律。
根据库仑定律,当两个电荷大小相同时,它们之间的相互作用力与它们之间的距离的平方成反比。
这意味着,当两个电荷之间的距离越远,它们之间的相互作用力越小;当两个电荷之间的距离越近,它们之间的相互作用力越大。
库仑定律的表达式中,k为库仑常数,它是一个与电介质有关的物理常数。
根据国际单位制,库仑常数的数值约为9 × 10^9 N·m^2/C^2。
这个常数的存在保证了库仑定律的普适性,即使是真空中也适用。
库仑定律的表达式中,|q1 * q2|表示两个电荷的乘积。
如果两个电荷的正负性相同(即同性电荷),它们的乘积为正,表示它们之间的相互作用力是吸引力;如果两个电荷的正负性相反(即异性电荷),它们的乘积为负,表示它们之间的相互作用力是斥力。
库仑定律的表达式中,r表示两个电荷之间的距离。
这个距离越小,相互作用力越大;距离越大,相互作用力越小。
这是因为电荷间的相互作用通过电场传递,电场的强度随距离的增大而减小。
库仑定律在物理学的许多领域都有重要应用。
例如,在静电学中,库仑定律被用来描述电荷之间的相互作用力,从而解释电荷的吸引和斥力现象。
在电动力学中,库仑定律被用来计算带电粒子在电场中的受力情况。
在电磁学中,库仑定律是电场的基本定律之一,它与高斯定律共同构成了电场理论的基础。
除了在物理学中的应用,库仑定律在日常生活中也有许多实际应用。
例如,电荷之间的相互作用力导致了静电粘附现象,使得我们可以使用静电贴、静电吸尘器等设备来清除灰尘。
电荷之间的相互作用力还导致了闪电的产生,给人们的生活带来了许多危害,但同时也使得我们能够利用闪电来进行电力的传输。
谈谈库仑定律中的比例常量
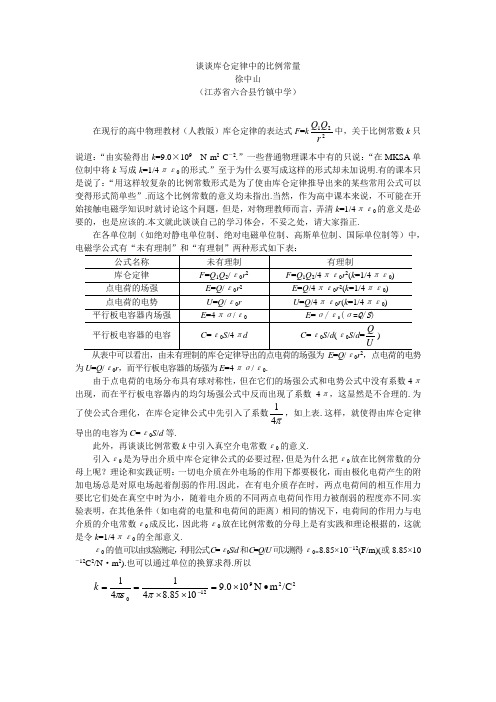
谈谈库仑定律中的比例常量徐中山(江苏省六合县竹镇中学)在现行的高中物理教材(人教版)库仑定律的表达式F =k221r Q Q 中,关于比例常数k 只说道:“由实验得出k =9.0×109 N·m 2·C -2.”一些普通物理课本中有的只说:“在MKSA 单位制中将k 写成k =1/4πε0的形式.”至于为什么要写成这样的形式却未加说明.有的课本只是说了:“用这样较复杂的比例常数形式是为了使由库仑定律推导出来的某些常用公式可以变得形式简单些”.而这个比例常数的意义均未指出.当然,作为高中课本来说,不可能在开始接触电磁学知识时就讨论这个问题,但是,对物理教师而言,弄清k =1/4πε0的意义是必要的,也是应该的.本文就此谈谈自己的学习体会,不妥之处,请大家指正.在各单位制(如绝对静电单位制、绝对电磁单位制、高斯单位制、国际单位制等)中,0为U =Q /ε0r ,而平行板电容器的场强为E =4πσ/ε0.由于点电荷的电场分布具有球对称性,但在它们的场强公式和电势公式中没有系数4π出现,而在平行板电容器内的均匀场强公式中反而出现了系数4π,这显然是不合理的.为了使公式合理化,在库仑定律公式中先引入了系数π41,如上表.这样,就使得由库仑定律导出的电容为C =ε0S /d 等.此外,再谈谈比例常数k 中引入真空介电常数ε0的意义.引入ε0是为导出介质中库仑定律公式的必要过程,但是为什么把ε0放在比例常数的分母上呢?理论和实践证明:一切电介质在外电场的作用下都要极化,而由极化电荷产生的附加电场总是对原电场起着削弱的作用.因此,在有电介质存在时,两点电荷间的相互作用力要比它们处在真空中时为小,随着电介质的不同两点电荷间作用力被削弱的程度亦不同.实验表明,在其他条件(如电荷的电量和电荷间的距离)相同的情况下,电荷间的作用力与电介质的介电常数ε0成反比,因此将ε0放在比例常数的分母上是有实践和理论根据的,这就是令k =1/4πε0的全部意义.ε0的值可以由实验测定,利用公式C =ε0S /d 和C =Q /U 可以测得ε0=8.85×10-12(F/m)(或8.85×10-12C 2/N ·m 2).也可以通过单位的换算求得.所以229120/C m N 100.91085.84141∙⨯=⨯⨯==-ππεk。
两点电荷之间的力公式k

两点电荷之间的力公式k引言电荷之间的相互作用力是电磁学中的一个基本概念。
当两个电荷之间存在静电作用时,它们之间将会产生电场,并且这个电场会对另一电荷施加一个电场力。
库仑定律是描述两个点电荷之间相互作用力的一个重要公式,其中的比例常数被称为库仑常数,通常用k表示。
本文将会详细介绍两点电荷之间的力公式k以及其物理意义。
库仑定律在真空或介电常数为1的介质中,两个点电荷之间的相互作用力可以用库仑定律来描述。
库仑定律表达为:$$ F = k \\cdot \\frac{q_1 \\cdot q_2} {r^2} $$其中,F为两点电荷之间的作用力,k为库仑常数,q1和q2分别为两个电荷的量,r为它们之间的距离。
库仑常数库仑常数在真空中的数值约为$8.9875 \\times 10^9 N m^2/C^2$,在国际单位制中,库伦常数的数值是固定的。
它是用来描述两个点电荷之间相互作用的比例常数,表征了电荷之间相互作用力的强度。
库仑常数的大小决定了电荷之间力的大小。
作用力方向根据库仑定律,两个点电荷之间的作用力的方向与电荷的属性有关。
如果两个电荷同号,它们之间的作用力是斥力,方向相反;如果两个电荷异号,它们之间的作用力是引力,方向相同。
这一规律是根据电场的性质所得出的。
物理意义库仑常数k的存在,使得我们可以量化电荷之间的相互作用力。
通过库仑定律,我们可以计算出两个点电荷之间的作用力大小。
这个公式在电学领域中的应用非常广泛,例如在静电场和电偶极子的研究中起着关键作用。
库仑常数的存在,使得我们能够通过数学的方式研究电荷之间的相互作用规律。
结论两点电荷之间的力公式k是描述电荷之间相互作用的关键公式之一。
通过库仑定律,我们可以计算出电荷之间的作用力大小,并探讨电荷之间的相互作用规律。
库仑常数k的存在使得我们能够量化电荷之间的作用力,从而更深入地了解电磁学领域中的基本概念。
电子间作用力公式k是什么

电子间作用力公式k是什么在物理学中,当两个带电粒子靠近时,它们之间会产生电子间作用力。
这种作用力是由它们之间的电荷引力和斥力相互作用形成的。
在描述这种相互作用时,我们通常使用一个很重要的参数,即Coulomb定律中的电子间作用力常数k。
那么这个作用力常数k具体是什么呢?首先,我们需要明白Coulomb定律是描述两个电荷之间的相互作用的物理定律。
它的数学表达式为:$$ F = \\frac{k \\cdot |q1 \\cdot q2|}{r^2} $$其中,F是两个电荷之间的作用力,k是电子间作用力常数,q1和q2分别是这两个电荷的量,r是它们之间的距离。
在这个公式中,电子间作用力常数k扮演着至关重要的角色。
这个常数的大小取决于所处的介质以及选定的单位制。
在真空中,k的值等于8.9875×109N m²/C²,常常被称为库仑常数。
在空气中,由于介质的相对电容率不同,k的值会有所变化。
因此,在实际计算中,我们需要根据具体情况来选择不同的k 值。
电子间作用力常数k的大小实际上反映了电荷之间相互作用的强度。
当k较小时,表示电荷之间的相互作用比较弱,而当k较大时,表示电荷之间的相互作用比较强。
因此,了解电子间作用力公式中k的具体意义和数值对于解决许多物理问题非常重要。
总结来说,电子间作用力公式的关键参数k是电子间作用力常数,它反映了电荷之间相互作用的强度。
k的具体取值会受到介质和单位制的影响,因此在实际计算中需要根据具体情况来选取适当的数值。
对于研究电磁力学和其他相关领域的学者和工程师来说,深入理解和熟练运用k值是解决复杂问题的关键所在。
库仑定律k的表达式

库仑定律k的表达式库仑定律中的k呀,那可是个相当有趣的存在呢。
咱们先来说说库仑定律是干嘛的吧。
就好比两个人之间有一种看不见摸不着的“力量”在互相拉扯或者推开,这在电荷之间也是一样的。
库仑定律就是描述两个静止点电荷之间相互作用力的规律。
这就像两个小伙伴,他们之间的关系有亲有疏,电荷之间的这种相互作用也有大有小呢。
那这个k呢,就像是一个隐藏在背后的“小管家”。
它决定着电荷之间相互作用力到底是个啥样的强度。
你看啊,要是没有这个k,就像一场游戏没有规则一样,我们就完全不知道电荷之间是怎么个互动法了。
这个k的表达式啊,在国际单位制里它的值是个常数,大概是9×10⁹N·m²/C²。
这数字看起来有点莫名其妙对吧?其实就把它想象成一个特殊的“魔法数字”,这个数字一旦确定了,整个库仑定律就像一台精密的机器开始运转起来了。
咱们来打个比方啊。
假设电荷是一群小蚂蚁,它们有的带正电,有的带负电。
正电的蚂蚁和负电的蚂蚁之间就像磁铁的南北极一样,有着一种吸引力。
而这个k呢,就像是决定这种吸引力大小的一个神秘的“蚂蚁长老”的力量。
如果k变大了,那就好比这个“蚂蚁长老”突然变得超级强大,蚂蚁们之间的吸引或者排斥的力量就会变得超级大。
要是k变小了呢,那这种力量就会变得很微弱,就像小蚂蚁们之间只是轻轻地打个招呼,而不是紧紧抱在一起或者用力推开对方了。
再从数学的角度来看k的表达式。
这个表达式可不仅仅是一个简单的数字哦。
它包含了力的单位牛顿(N)、距离的单位米(m)还有电荷的单位库仑(C)。
这就像一个大杂烩,把这些不同的物理量都融合在一起,来给电荷之间的相互作用力下一个明确的定义。
你说奇妙不奇妙?有时候我就想啊,这k是不是大自然故意设置的一个小机关呢?为什么偏偏是这个数值而不是其他的呢?难道就像我们生活中有些习惯一样,是一种固定下来的“传统”?你看啊,在我们日常生活中,有些东西的大小、重量、比例都是固定的,比如一个标准的乒乓球的大小。
库仑定律的概念和公式

库仑定律的概念和公式
库仑定律是静电学中的基本定律,用于描述两个静止点电荷之间的相互作用力。
这个定律的公式是F=kQ1Q2/r^2,其中F表示力,k是库仑常数,Q1和Q2是两个点电荷的电量,r是它们之间的距离。
库仑定律指出,两个点电荷之间的作用力与它们的电量的乘积成正比,与它们之间的距离的平方成反比。
这意味着,如果两个点电荷的电量加倍,它们之间的作用力将增加四倍;如果它们之间的距离加倍,它们之间的作用力将减少四倍。
库仑定律具有普适性,适用于任何静止的点电荷之间。
它与牛顿的万有引力定律在数学形式上相似,但是点电荷之间的相互作用力只与它们之间的距离有关,而不受它们的质量分布、形状、速度等因素的影响。
库仑定律的成立条件是真空中的静止点电荷,因为在实际应用中,如果存在其他介质或电荷在运动,那么它们之间的相互作用力可能会受到其他因素的影响。
此外,库仑定律也假定点电荷的线度远小于它们之间的距离,以避免由于电荷分布的有限大小和形状而引起的误差。
库仑定律在静电学中具有广泛应用,例如在计算电场、电势、电容、电感等物理量时都需要用到这个定律。
同时,它也是电磁学中的基础之一,对于理解电磁波的传播、电磁场的性质等方面都有着重要的作用。
静电力常数k的数值 -回复
静电力常数k的数值-回复静电力常数k是一个物理常数,用于描述电荷之间相互作用的强度。
它是描述电场强度的物理量,也被称为库仑常数或真空电介质常数。
静电力常数k的数值是一个能够解释电荷之间相互作用的参数,它的具体数值为8.99 * 10^9 N·m^2/C^2。
静电力是一种力,它以静电荷的存在为基础,可以通过电磁理论进行描述。
电荷是物质的一个基本属性,它可以是正电荷或负电荷。
当两个电荷距离足够近时,它们之间会产生电荷力,即静电力。
静电力遵循库仑定律,即静电力与电荷之间的距离成反比,与电荷量的平方成正比。
静电力常数k在库仑定律中起到了重要的作用。
它是一个量化电荷相互作用强度的常数。
通过电荷分布情况和静电力常数k的数值,我们可以计算出电荷之间的相互作用力大小。
静电力常数k的数值为8.99 * 10^9 N·m^2/C^2,意味着当两个电荷之间的距离为1米,电荷量为1库仑时,它们之间的静电力为8.99 * 10^9牛顿。
静电力常数k的数值是通过实验测量得到的。
在测量过程中,通常会选择一对已知电荷量的电荷,通过测量它们之间的相互作用力来确定静电力常数k的数值。
实验结果表明,不同的电荷距离和电荷量之间确实存在着一种固定的关系,这就是库仑定律所描述的电荷相互作用规律。
静电力常数k的值在不同的物理环境中是相同的。
它不受物质介质的影响,只与真空中电荷相互作用的强度有关。
在真空中,静电力常数k的数值为8.99 * 10^9 N·m^2/C^2。
而在介质中,静电力的大小由介质的电介质常数影响,但静电力常数k的数值保持不变。
静电力常数k具有重要的应用价值。
在物理学和工程学中,我们经常利用静电力常数k来计算电荷之间的相互作用力。
在电场强度的计算中,静电力常数k也起到了关键的作用。
通过确定电场强度的大小和方向,我们能够了解电荷在空间中的分布规律,进而探索电荷之间的相互作用法则。
总结一下,静电力常数k是描述电荷之间相互作用强度的物理常数,它的数值为8.99 * 10^9 N·m^2/C^2。
真空中的库伦定律
真空中的库伦定律在物理学中,康布朗定律又称为库仑定律,是描述电荷之间相互作用的基本定律。
它是由法国物理学家查理·奥古斯特·德·库伦在18世纪末发现的。
康布朗定律指出,两个电荷之间的相互作用力与它们之间的距离成反比,与它们之间的电荷量的乘积成正比。
具体来说,如果两个电荷的电荷量分别为q1和q2,它们之间的距离为r,那么它们之间的相互作用力F可以用以下公式表示:F = k * q1 * q2 / r²其中,k是一个常量,被称为库仑常数,它的值为8.9875517923 × 10⁹ N·m²/C²。
康布朗定律在真空中适用,这意味着它适用于没有其他介质的情况下。
在这种情况下,电荷之间的相互作用完全由库伦定律描述。
康布朗定律的生动应用可以通过以下实例来了解。
假设我们有两个电荷,一个正电荷和一个负电荷。
根据库仑定律,正电荷会受到负电荷的吸引力,而负电荷会受到正电荷的吸引力。
随着它们之间的距离缩短,相互作用力增大,反之亦然。
这一现象可以用来解释为什么物体之间可以相互吸引或排斥。
康布朗定律的全面性在于它涵盖了电荷之间的相互作用的所有特征。
不仅仅是电荷量的大小会影响相互作用力的大小,电荷之间的距离也起着关键的作用。
当距离越远,力减小得越快;而距离越近,力增加得越快。
这使得电荷之间的相互作用力具有非常特殊的特征,同时也为我们提供了研究电场和电势能的基础。
康布朗定律对于我们的理解和应用都有指导意义。
例如,在电学工程中,我们必须考虑电荷之间的相互作用力,以便设计安全的电路和电子设备。
此外,康布朗定律还是其他重要概念的基础,如电场和电势能的计算以及电荷分布的描述。
综上所述,康布朗定律是描述电荷之间相互作用的重要定律,它在真空中适用,并且对于我们理解电荷之间的相互作用、研究电场和电势能等方面具有重要的指导意义。
通过深入研究和应用库伦定律,我们能够更好地理解电荷之间的相互作用力,促进电学和电磁学的进一步发展。
物理学常量k
物理学常量k物理学常量k是一个与电荷和电场有关的常量,也叫做库仑常量。
相比于其他科学常数,它的数值比较小,但是却在物理学领域中扮演着非常重要的角色。
本文将从多个角度探讨物理学常量k的相关内容。
一、物理学常量k的概念物理学常量k是一个量度电荷之间相互作用强度的物理学常数。
它的数值约为9×109牛顿·米²·库仑的平方,表示两个相同电荷之间作用力的大小,当它们之间的距离为1米时。
二、物理学常量k的公式物理学常量k在公式中的表示如下:F=k(q1×q2/r²)其中,F表示电荷之间的相互作用力;q1和q2分别代表电荷的电量;r表示电荷之间的距离;k为库伦常量,其值为9×109牛顿·米²·库仑的平方。
三、物理学常量k的应用1. 电场的计算和描述电荷和电场是密不可分的,因为电荷是产生电场的源头。
而物理学常量k 是电荷之间相互作用强度的衡量,因此,电荷之间的相互作用,会随着物理学常量k的变化而发生相应的变化。
在电场中,当我们需要计算某两个电荷之间的相互作用力时,就需要用到物理学常量k。
2. 电势能电荷之间的相互作用力与它们之间的距离有关,随着距离的增加而减弱。
这样的电场与电荷之间的相互作用是由电势能来描述的。
而电势能的大小与物理学常量k成正比。
3. 静电场静电场是指在任何时候电荷的分布都不随时间变化的电场。
在静电场中,当我们要计算电荷之间的相互作用力时,需要考虑空间中所有与其它电荷的相互作用,同时也要考虑物理学常量k。
四、物理学常量k的重要性物理学常量k是库伦定律的一部分,库伦定律是描述电荷之间相互作用强度的一个重要定律。
因此,物理学常量k在电荷和电场的相关计算中起着非常重要的作用。
库伦定律是所有电路、静电场和电磁波理论中基础的定律之一。
总的来说,物理学常量k是与电荷和电场有关的常量,是描述电荷之间相互作用强度的物理学常数。
库仑定律公式
库仑定律公式
库仑定律是电学中最基本的定律之一,它是描述电荷之间相互作用的定律,具体定义是在真空中两个点电荷之间的相互吸引或排斥的力与它们之间的距离
的平方成正比,与电荷的大小成正比。
库仑定律可以用数学公式表示出来,形式为:
$F=k\\frac{q_1q_2}{r^2}$
其中,$F$表示两个电荷之间的相互作用力大小,$q_1$和$q_2$分别表示
两个电荷的电荷大小,$r$表示两个电荷之间的距离,$k$表示库仑常数,它的
值为$9\\times10^9N\\cdot m^2/C^2$。
库仑定律的公式主要包含了三个要素:电荷大小、距离以及库仑常数。
电
荷大小是电荷所带的物理量,可以用库伦(C)为单位进行表示;距离是指两个电荷之间的空间距离,可以用米(m)为单位进行表示;库仑常数是一个恒定值,它表示了在真空中两个电荷之间相互作用力的大小。
在实际应用中,库仑定律的公式是非常重要的,它被广泛应用于电学领域
中的各种问题中,如电荷分布、电势、电场和电容等。
在这些应用中,人们可
以通过库仑定律的公式去计算和预测电学现象中出现的各种变化和趋势,从而
为电学研究和应用提供了有力的工具和手段。
总之,库仑定律是电学中最基本的定律之一,它描述了电荷之间相互作用的规律,并被广泛应用于电学领域的各种问题中。
掌握库仑定律的公式和相关知识对于电学学习和应用都具有重要的意义和价值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
库仑定律中k值
摘要:
一、库仑定律简介
1.库仑定律的定义
2.库仑定律在电学领域的应用
二、k 值的含义和作用
1.k 值的定义
2.k 值与电荷量、距离的关系
3.k 值在库仑定律中的重要性
三、k 值的测量和计算
1.库仑扭秤实验
2.计算方法
四、k 值的影响因素和测量误差
1.环境因素对k 值的影响
2.测量设备的精度对k 值的影响
五、我国对k 值的研究和应用
1.k 值在我国的研究历程
2.k 值在我国的测量和应用现状
正文:
库仑定律是电学领域中一个基本的定律,它描述了两个电荷之间相互作用力的规律。
根据库仑定律,两个电荷之间的作用力与它们的电荷量成正比,与
它们之间的距离的平方成反比。
这个定律可以用公式F=k*q1*q2/r^2 来表示,其中F 是两个电荷之间的作用力,q1 和q2 是两个电荷的电荷量,r 是两个电荷之间的距离,k 是一个常数,称为库仑常数。
在库仑定律中,k 值是一个非常重要的参数,它的大小直接影响到两个电荷之间作用力的计算结果。
k 值是由英国科学家库仑在18 世纪末通过扭秤实验测量出来的,其值约为8.99*10^9 N*m^2/C^2。
然而,由于实验条件的限制,库仑当时测得的k 值存在一定的误差。
在现代科学研究中,k 值通常通过更精确的实验方法来测量,例如库仑扭秤实验、微波法等。
此外,k 值也可以通过计算方法来得到,例如基于量子电动力学的计算方法。
尽管测量和计算k 值的方法已经非常精确,但由于环境因素和测量设备的精度等因素的影响,k 值的测量结果仍然存在一定的误差。
在我国,库仑定律和k 值的研究历史悠久。
早在20 世纪初,我国科学家就开始研究库仑定律和k 值,并取得了许多重要的成果。
近年来,我国在k 值的研究和应用方面也取得了显著的进展。
例如,我国科学家成功研发了基于库仑定律的高精度电荷量测量装置,并在k 值的测量和应用方面取得了国际领先的研究成果。
总之,库仑定律中的k 值是电学领域中一个基本而重要的参数。
对k 值的研究和理解,不仅有助于我们更好地掌握电学的基本规律,也为各种电学应用提供了理论基础。
