鲁教版数学六上第三章《整式及其加减》测试题
鲁教版六年级数学上册第三章整式及其加减复习

第10个图形有
个五角星.
【解析】第1个图形有1×2+1个,第2个图形有2×3+2个; 第3个图形有3×4+3个;第4个图形有4×5+4个;…; 第n个图形有n×(n+1)+n个. 当n=10时,n×(n+1)+n=10×11+10=120, 即第10个图形有120个五角星. 答案:120
第三章
【答案速填】 ①数与字母的乘积的代数式; ②单项式中的数字因数; ③单项式中所有字母的指数和; ④几个单项式的和; ⑤组成多项式的每个单项式; ⑥次数最高的项的次数; ⑦所含字母相同,并且相同字母的指 数也相同; ⑧把同类项的系数相加,字母和字母 的指数不变; ⑨括号前是“+”号,把括号和它前面 的“+”号去掉后,原括号里各项的符 号都不改变;括号前是“-”号,把括 号和它前面的“-”号去掉后,原括号 里各项的符号都要改变; ⑩n个整式相加减,如果有括号就先去 括号,然后再合并同类项.
有个幸福温暖的家庭,是大家眼里的好孩子;安生叛逆桀骜,父亲去世母女相爱相杀,是个缺爱的女孩。偏偏两个人好得要命,彼此踩着对方的影子,恨不能一辈子在一起, 一起洗澡,一起翘课……15岁那年,她们都喜欢了一个男孩子家明。家明的出现,让七月和安生之间的情感发生了不可言喻的变化,而家明的摇摆不定,也让两个女孩面对 友情与爱情,备受煎熬。最终,安生在确认自己也爱上家明以后,选择把家明让给七月,自己离开小镇,去流浪。她说,在七月与家明之间,她选择七月。七月明白安生的 离开,是成全,但还是任由安生的列车徐徐驶离,爱情在某个时刻,会战胜友情。但是,分开的两个人,仍然彼此牵挂。七月羡慕安生的自由,安生羡慕七月的岁月静好。 再次见面,却又像刺猬一样彼此伤害,然后各自哭泣疗伤。电影结尾,七月难产去世,临终前,将孩子托付给安生。不管我们之间有多少误会和伤害,我还是选择最信任你, 把孩子托付给你。这也许就是最动人的友情。想起《乱世佳人》里梅兰妮和斯嘉丽。一个相貌平平,但是优雅得体、善解人意的贵族小姐,女人中的女人;一个妩媚动人, 任性倔强热情似火的庄园主女儿,女人中的男人。一开始,斯嘉丽便把梅兰妮当作情敌,认为是梅兰妮夺走了自己暗恋的阿希礼。 所以,她心怀嫉恨,处处刁难,把梅兰妮
六年级上册数学鲁教版整式及其加减单元测试4

第三章 整式及其加减(本检测题满分:100分,时间90分钟)一、选择题(每小题3分,共30分)1.(海南模拟)“x 与3的差的2倍”用代数式表示为( ) A .2x-3, B .2(x-3), C .3(x-2), D .3x-22. (娄底)已知a 2+2a=1,则代数式2a 2+4a-1的值为( ) A .0, B .1, C .-1, D .-23.(玉林)下列运算中,正确的是( ) A .3a+2b=5ab, B .2a 3+3a 2=5a 5 C .3a 2b-3ba 2=0, D .5a 2-4a 2=14.(山东济宁中考)化简()160.5x --的结果是( )A. 160.5x --B. 5.016+xC. 816-xD. 168x -+ 5.(长沙县模拟)若2a-b=3,则9-4a+2b 的值为( ) A .3, B .6, C .12, D .06.已知a 是两位数,b 是一位数,把a 接写在b 的后面,就成为一个三位数.这个三位数可表示成( ) A.10b a +B.baC.100b a +D.10b a +7.一个代数式的2倍与2a b -+的和是2a b +,这个代数式是( ) A.3a b +B.1122a b -+C.3322a b +D.3122a b + 8.已知,a b 两数在数轴上的位置如图所示,则化简代数式12a b a b +--++的结果是( ) A.1B.23b +C.23a -D.-1第8题图 第9题图9.在排成每行七天的月历表中取下一个33⨯方块(如图).若所有日期数之和为189,则n 的值为( )A.21B.11C.15D.910.某商品进价为a 元,商店将其进价提高30%作为零售价销售,在销售旺季过后,商店又以8折(即售价的80%)的价格开展促销活动,这时一件商品的售价为( ) A.a 元B.0.8a 元C.0.92a 元D. 1.04a 元二、填空题(每小题3分,共24分) 11.若4x y +=,a ,b 互为倒数,则21的值是 .12.(江苏苏州中考)若a -2b =3,则9-2a +4b 的值为_______. 13.如图:(1)阴影部分的周长是: ; (2)阴影部分的面积是: ; (3)当,时,阴影部分的周长是 ,面积是 .14.(湖南株洲中考)如果手机通话每分钟收费m 元,那么通话n 分钟收费 元.15.去括号:3264(5)x x x ⎡⎤---+=⎣⎦ .16.一个学生由于粗心,在计算35a -的值时,误将“-”看成“+”,结果得63,则35a -的值应为____________.17.(沈阳中考)如果x =1时,代数式2ax 3+3bx +4的值是5,那么x =-1时,代数式2ax 3+3bx +4的值是 .18.已知甲、乙两种糖果的单价分别是x 元/千克和12元/千克.为了使甲、乙两种糖果分别销售与把它们混合成什锦糖后再销售收入保持不变,则由20千克甲种糖果和y 千克乙种糖果混合而成的什锦糖的单价应是 元/千克. 三、解答题(共46分) 19.(10分)化简并求值. (1),其中,; (2),其中.20.(5分)化简关于的代数式.当为何值时,代数式的值是常数?第13题图21.(5分)一个两位数,把它十位上的数字与个位上的数字对调,得到一个新的两位数.试说明原来的两位数与新两位数的差一定能被9整除.22.(6分)用同样大小的黑色棋子按如图所示的规律摆放:第22题图(1)第5个图形有多少枚黑色棋子?(2)第几个图形有2 013枚黑色棋子?请说明理由.23.(6分)观察下面的变形规律:211211-=⨯;3121321-=⨯;4131431-=⨯;… 解答下面的问题:(1)若n 为正整数,请你猜想=)1(1+n n _____________; (2)证明你猜想的结论; (3)求和:0122011 21431321211⨯++⨯+⨯+⨯Λ.24.(7分)一种蔬菜x 千克,不加工直接出售每千克可卖y 元;如果经过加工质量减少了20%,价格增加了40%.问:(1)x 千克这种蔬菜加工后可卖多少钱?(2)如果这种蔬菜1 000千克,不加工直接出售每千克可卖1.5元,问加工后原1 000千克这种蔬菜可卖多少钱?比加工前多卖多少钱?25.(7分)任意写出一个各数位不含零的三位数,任取三个数字中的两个,组合成所有可能的两位数(有6个).求出所有这些两位数的和,然后将它除以原三位数的各个数位上的数字之和.例如,对三位数223,取其两个数字组成所有可能的两位数:22,23,22,23,32,32.它们的和是154.三位数223各数位上÷=.再换几个数试一试,你发现了什么?请写出你按的数字的和是7,154722上面方法的探索过程和所发现的结果,并运用代数式的相关知识说明所发现的结果的正确性.第三章 整式及其加减参考答案 一、选择题1.B 解析:本题看清题意,x 与3的差的2倍,按题目要求写出代数式,先写出x 与3的差即x-3,然后x-3的二倍即2(x-3),即得答案.2.B 解析:原式前两项提取变形后,将已知等式代入计算即可求出值 解:∵a 2+2a=1,∴原式=2(a 2+2a )-1=2-1=1, 故选B3.C 解析:先根据同类项的概念进行判断是否是同类项,然后根据合并同类项的法则,即系数相加作为系数,字母和字母的指数不变计算进行判断4.D 解析:()160.5168x x --=-+,D 正确.5.A 解析:原式后两项提取-2变形后,把已知等式代入计算即可求出值 解:∵2a-b=3,∴原式=9-2(2a-b )=9-6=3, 故选A6.C 解析:两位数的表示方法:十位数字×10个位数字;三位数的表示方法:百位数字×100十位数字×10个位数字.是两位数,是一位数,依据题意可得扩大了100倍,所以这个三位数可表示成100b a +.7.D 解析:这个代数式的2倍为,所以这个代数式为3122a b +.8.B 解析:由数轴可知,且,所以,故12(1)(2)1223a b a b a b a b a b a b b +--++=+--++=+-+++=+.9.A 解析:月历的排列是有一定规律的,在月历表中取下一个3×3方块, 若中间的数是,则它上面的数是,下面的数是,左边的数是,右边的数是,左边最上面的数是,最下面的数是, 右边最上面的数是,最下面的数是.若所有日期数之和为189, 则,即,解得,故选A .10.D 解析:依题意可得:(元),故选D .二、填空题11.7 解析:因为a b ,互为倒数,所以, 所以2121.12.3 解析:∵ a -2b =3,∴ 原式=9-2(a -2b )=9-6=3. 13.(1)(2)(3)46,77解析:阴影部分的面积是:.14. mn 解析:根据收费=单价×通话时间,可得收费为 mn 元. 15.32645x x x --++解析:3232326[4(5)]6(45)645x x x x x x x x x ---+=----=--++. 16.7 解析:由题意可知,故.所以.17.3 解析:本题考查了代数式的求值技巧———整体代入法.把x =1代入代数式2ax 3+3bx +4=5中,得2a +3b +4=5,∴ 2a +3b =1. 把x =-1代入代数式2ax 3+3bx +4,得-2a -3b +4.∵ 2a +3b =1,∴ -2a -3b =-1,∴ -2a -3b +4=-1+4=3. 18.yy x ++201220 解析:先求出20千克甲种糖果和千克乙种糖果的总价钱,即元,混合糖果的质量是千克,由此我们可以求出20千克甲种糖果和千克乙种糖果混合而成的什锦糖的单价应为yy x ++201220(元/千克). 三、解答题19.解:(1)将原式去括号、合并同类项,得81x y --. 将2,0.5==-x y 代入得.(2)将原式去括号、合并同类项,得224a a --.将2=-a 代入得22242(2)4(2)2480--=-⨯--⨯-=-⨯+=a a . 20.解:将去括号,得222231x x kx x x +-+-+,合并同类项,得()251k x -+. 若代数式的值是常数,则,解得.故当时,代数式的值是常数.21.解:设原来的两位数是,则调换位置后的新数是,∴.∴ 这个数一定能被9整除.22.解:(1)第1个图形有棋子6枚, 第2个图形有棋子9枚, 第3个图形有棋子12枚, 第4个图形有棋子15枚, 第5个图形有棋子18枚, …第n 个图形有棋子枚.答:第5个图形有18枚黑色棋子. (2)设第n 个图形有2 013枚黑色棋子, 根据(1)得,解得,所以第670个图形有2 013枚黑色棋子. 23.(1)解:111+n n-;(2)证明:右边==+=+-+=++++)1(1)1(1)1()1(1111n n n n n n n n n n n n n n-=-左边, 所以猜想成立.(3)解:原式=01221011 2141313121211-++-+-+-Λ0122011 2012 211=-=. 24.解:(1)千克这种蔬菜加工后质量为千克,价格为元,故千克这种蔬菜加工后可卖(元).(2)加工后可卖1.12×1 000×1.5=1 680(元),(元),比加工前多卖180元.25.解:举例1:三位数578:57757887588522;578+++++=++举例2:三位数123:12211331233222.123+++++=++猜想:一个各数位不含零的三位数,任取三个数字中的两个,组合成所有可能的两位数的和除以这个三位数的各个数位上的数字之和恒等于22. 证明如下:设三位数为()10010,,0a b c a b c ++≠,则 所有的两位数是.故101010101010a b b a a c c a b c c ba b c+++++++++++++()2222222222a b c a b c a b c a b c++++===++++.。
鲁教版五四制六年级数学上册《整式及其加减》单元测试试题及解析【试卷】.docx

单元评价检测(三)第三章(45分钟 100分)一、选择题(每小题4分,共28分)1.足球每个m 元,篮球每个n 元,桐桐为学校买了4个足球,7个篮球共需要() A.(7m+4n)元 B.28mn 元C.(4m+7n)元D.11mn 元2.已知代数式-3x m-1y 3与52y n x n+1是同类项,那么m,n 的值分别是 ( )A.n=-3,m=-1B.n=-3,m=-3C.n=3,m=5D.n=2,m=33.多项式a 3b 2+4ax 2y-ab 2+36的次数和项数分别为 ( )A.次数为6,项数为4B.次数为5,项数为4C.次数为6,项数为2D.次数为5,项数为24.下列计算正确的是 ( )A.7a+a=7a 2B.5y-3y=2C.3x2y-2yx2=x2yD.3a+2b=5ab5.如果代数式4y2-2y+5的值为7,那么代数式-2y2+y-1的值为( )A.-3B.2C.-2D.0【变式训练】已知x2-2y+1=0,则整式2x2-4y+5的值等于( )A.3B.4C.6D.76.如图,淇淇和嘉嘉做数学游戏:假设嘉嘉抽到牌的点数为x,淇淇猜中的结果应为y,则y= ( )A.2B.3C.6D.x+37.若M表示a与b的和的平方,N表示a与b的平方和,则当a=7,b=-5时,M-N的值是( )A.-70B.-28C.42D.0二、填空题(每小题5分,共25分)8.代数式:-x,b 5a ,23abc,2a−13,x+5y ,π,b3中,单项式为 ,多项式为 . 9.一个多项式加上-2+x-x 2得x 2-1,则这个多项式是 .【变式训练】(6x 2-7x-5)- =5x 2-2x+3.10.若x 2-2x=3,则代数式2x 2-4x+3的值为 .11.如图,下列图形都由同样大小的十字星图案按一定的规律组成,其中第一个图形有1个十字星图案,第二个图形有2个十字星图案,第三个图形有5个十字星图案,第四个图形有10个十字星图案,…,则第101个图形有 个十字星图案.12.一组按规律排列的式子:a 2,a 43,a 65,a 87,….则第n 个式子是 . 三、解答题(共47分)13.(12分)化简:(1)3(4x 2-3x+2)-2(1-4x 2+x).(2)a2-2[a2-(2a2-b)].b+2),而第三边比第14.(10分)三角形的第一边等于(2a+b),第二边比第一边小(12b−2),这个三角形的周长是多少?一边大(1215.(12分)为鼓励节约用电,某地用电收费标准规定:如果每月每户用电不超过150度,那么每度电0.5元;如果该月用电超过150度,那么超过部分每度电0.8元. (1)小张家一月份用电128度,那么这个月应缴电费多少元?(2)如果小张家一个月用电a(a>150)度,那么这个月应缴电费多少元?(用含a的式子表示)(3)如果小张家八月份用电241度,那么这个月应缴电费多少元?16.(13分)先阅读下面例题的解题过程,再回答下面的问题:例:已知多项式9-6y-4y2=7,求2y2+3y+7的值.解:由9-6y-4y2=7,得-6y-4y2=7-9,即6y+4y2=2.因此2y2+3y=1,所以2y2+3y+7=8.问题:已知多项式14x+5-21x2的值是-2,求6x2-4x+5的值.单元评价检测(三)第三章(45分钟 100分)一、选择题(每小题4分,共28分)1.足球每个m 元,篮球每个n 元,桐桐为学校买了4个足球,7个篮球共需要( )A.(7m+4n)元B.28mn 元C.(4m+7n)元D.11mn 元【解析】选C.4个足球,7个篮球共需要价钱为(4m+7n)元.2.已知代数式-3x m-1y 3与52y n x n+1是同类项,那么m,n 的值分别是 ( ) A.n=-3,m=-1B.n=-3,m=-3C.n=3,m=5D.n=2,m=3【解析】选C.由同类项的定义,得n=3,且m-1=n+1,所以n=3,m=5.【易错提醒】同类项是指字母相同,相同字母的指数也相同的项,本题要注意字母的排列顺序不同,不要误选D.3.多项式a 3b 2+4ax 2y-ab 2+36的次数和项数分别为 ( )A.次数为6,项数为4B.次数为5,项数为4C.次数为6,项数为2D.次数为5,项数为2【解析】选B.多项式a 3b 2+4ax 2y-ab 2+36的次数是5,项数是4.【易错提醒】单项式的次数是所有字母的指数和,与常数的指数无关,多项式的次数是指次数最高项的次数,所以本题的次数是5而不是6.4.下列计算正确的是( )A.7a+a=7a2B.5y-3y=2C.3x2y-2yx2=x2yD.3a+2b=5ab【解析】选C.根据合并同类项法则可知:7a+a=8a,5y-3y=2y,故A,B都错误,C正确;D中两项不是同类项,不能合并,故D错误.5.如果代数式4y2-2y+5的值为7,那么代数式-2y2+y-1的值为( )A.-3B.2C.-2D.0【解析】选C.因为4y2-2y+5=7,所以4y2-2y=7-5,所以2(2y2-y)=2,所以2y2-y=1. 所以-2y2+y-1=-(2y2-y)-1=-1-1=-2.【变式训练】已知x2-2y+1=0,则整式2x2-4y+5的值等于( )A.3B.4C.6D.7【解析】选A.因为x2-2y+1=0,即x2-2y=-1,所以2x2-4y+5=2(x2-2y)+5=-2+5=3.6.如图,淇淇和嘉嘉做数学游戏:假设嘉嘉抽到牌的点数为x,淇淇猜中的结果应为y,则y= ( )A.2B.3C.6D.x+3 【解析】选B.根据题意得:y=12(2x+6)-x=x+3-x=3.7.若M 表示a 与b 的和的平方,N 表示a 与b 的平方和,则当a=7,b=-5时,M-N 的值是 ( )A.-70B.-28C.42D.0【解析】选A.由题意可得:M=(a+b)2,N=a 2+b 2,M-N=(a+b)2-(a 2+b 2),将a=7,b=-5代入,可得:M-N=-70.二、填空题(每小题5分,共25分)8.代数式:-x,b 5a ,23abc,2a−13,x+5y ,π,b3中,单项式为 ,多项式为 . 【解析】根据整式,单项式,多项式的概念可知,单项式有:-x,23abc,π,b3;多项式有:2a−13. 答案:-x,23abc,π,b 3 2a−13【知识归纳】整式概念中要注意的四个问题(1)单项式和多项式统称为整式.(2)整式中可以包含加、减、乘、除四种运算.(3)整式中除式不能含有字母.(4)单项式中没有加减法,多项式中有加减法.9.一个多项式加上-2+x-x 2得x 2-1,则这个多项式是 .【解析】设这个多项式为M,则M=(x 2-1)-(-x 2+x-2)=x 2-1+x 2-x+2=2x 2-x+1.答案:2x 2-x+1【变式训练】(6x 2-7x-5)- =5x 2-2x+3.【解析】6x 2-7x-5-(5x 2-2x+3)=6x 2-7x-5-5x 2+2x-3=x 2-5x-8.答案:x 2-5x-810.若x 2-2x=3,则代数式2x 2-4x+3的值为 .【解析】2x 2-4x+3=2(x 2-2x)+3=2×3+3=9.答案:911.如图,下列图形都由同样大小的十字星图案按一定的规律组成,其中第一个图形有1个十字星图案,第二个图形有2个十字星图案,第三个图形有5个十字星图案,第四个图形有10个十字星图案,…,则第101个图形有 个十字星图案.【解析】因为第一个图形有1个十字星图案;第二个图形有2个十字星图案,可以认为是在第一个图形上增加一个十字星图案,即当n=2时,第二个图形有1+1个十字星图案;第三个图形有5个十字星图案,可以认为是在第一个图形上增加四个十字星图案,即当n=3时,第三个图形有4+1=22+1个十字星图案;第四个图形有10个十字星图案,可以认为是在第一个图形上增加九个十字星图案,即当n=4时,第四个图形有9+1=32+1个十字星图案;…探究第101个图形是在第一个图形上增加1002个十字星图案,即当n=101时,第101个图形有10000+1=10001个十字星图案.答案:1000112.一组按规律排列的式子:a 2,a 43,a 65,a 87,….则第n 个式子是 .【解析】已知式子可写成:a 21,a 43,a 65,a 87,…分母为奇数,可写成2n-1,分子中字母a 的指数为偶数2n.答案:a 2n2n−1(n 为正整数)三、解答题(共47分)13.(12分)化简:(1)3(4x 2-3x+2)-2(1-4x 2+x).(2)a 2-2[a 2-(2a 2-b)].【解析】(1)原式=12x 2-9x+6-2+8x 2-2x=20x 2-11x+4.(2)原式=a 2-2(a 2-2a 2+b)=a 2-2a 2+4a 2-2b=3a 2-2b.14.(10分)三角形的第一边等于(2a+b),第二边比第一边小(12b +2),而第三边比第一边大(12b −2),这个三角形的周长是多少? 【解析】周长=(2a+b)+[(2a +b)−(12b +2)]+(2a+b)+(12b −2) =2a+b+(2a+b)-(12b +2)+(2a+b)+(12b −2) =2a+b+2a+b-12b-2+2a+b+12b-2 =6a+3b-4.15.(12分)为鼓励节约用电,某地用电收费标准规定:如果每月每户用电不超过150度,那么每度电0.5元;如果该月用电超过150度,那么超过部分每度电0.8元.(1)小张家一月份用电128度,那么这个月应缴电费多少元?(2)如果小张家一个月用电a(a>150)度,那么这个月应缴电费多少元?(用含a的式子表示)(3)如果小张家八月份用电241度,那么这个月应缴电费多少元?【解析】(1)128×0.5=64(元).答:这个月应缴电费64元.(2)150×0.5+0.8(a-150)=75+0.8a-120=(0.8a-45)(元).答:如果小张家一个月用电a(a>150)度,那么这个月应缴电费(0.8a-45)元.(3)当a=241时,0.8a-45=0.8×241-45=147.8(元).答:这个月应缴电费147.8元.16.(13分)先阅读下面例题的解题过程,再回答下面的问题:例:已知多项式9-6y-4y2=7,求2y2+3y+7的值.解:由9-6y-4y2=7,得-6y-4y2=7-9,即6y+4y2=2.因此2y2+3y=1,所以2y2+3y+7=8.问题:已知多项式14x+5-21x2的值是-2,求6x2-4x+5的值. 【解析】由14x+5-21x2=-2,得-21x2+14x=-7,即21x2-14x=7,因此3x2-2x=1.所以6x2-4x+5=2(3x2-2x)+5=2×1+5=7.。
2021-2022学年鲁教版六年级数学上册《第3章整式及其加减》期末综合复习训练(附答案)

2021-2022学年鲁教版六年级数学上册《第3章整式及其加减》期末综合复习训练(附答案)1.下列说法正确的是()A.的系数是﹣5B.单项式x的系数为1,次数为0C.xy+x﹣1是二次三项式D.﹣22xyz2的次数是62.多项式合并同类项后不含xy项,则k的值是()A.B.C.D.03.下列各式中,与3x3y2是同类项的是()A.2x5B.C.D.3x2y34.若单项式a m+1b2与的和是单项式,则m n的值是()A.3B.4C.6D.85.多项式2x3﹣8x2+x﹣1与多项式3x3+2mx2﹣5x+3的和不含二次项,则m为()A.2B.﹣2C.4D.﹣46.已知a﹣b=﹣3,c+d=2,则(b+c)﹣(a﹣d)的值为()A.1B.5C.﹣5D.﹣17.长方形长为3x+2y,宽为x﹣y,则这个长方形的周长为()A.4x+y B.8x+2y C.10x+10y D.12x+8y8.有理数a,b,c在数轴上的位置如图,化简|a|﹣|a+b|+|c﹣a|+|b﹣c|的结果为()A.﹣a B.2a﹣2b C.2c﹣a D.a9.已知代数式﹣2x a y4与bx3y4和为0,则a+b=()A.﹣1B.0C.1D.510.如图,两个正方形的面积分别为16,9,两阴影部分的面积分别为a,b(a>b),则(a ﹣b)等于()A.8B.7C.6D.511.观察下列关于x的单项式:﹣x,4x2,﹣7x3,10x4,﹣13x5,16x6,…,按照上述规律,第2021个单项式是.12.如果单项式3a2x b y与单项式﹣2a y b x+2是同类项,则y x的值为.13.若多项式2x3﹣8x2+x﹣1与多项式3x3+2mx2﹣5x+3相加后不含二次项,则m的值为.14.一根铁丝的长为5a+4b,剪下一部分围成一个长为a宽为b的长方形,则这根铁丝还剩下.15.已知A=4x2﹣4xy+y2,B=x2+xy﹣5y2,计算A﹣3B=.16.当k=时,多项式中不含xy项.17.先化简,再求值:5x2y﹣7(x2y﹣xy2)﹣3xy2,其中x=2,y=﹣1.18.已知代数式A=x2+3xy+x﹣12,B=2x2﹣xy+4y﹣1(1)当x=y=﹣2时,求2A﹣B的值;(2)若2A﹣B的值与y的取值无关,求x的值.19.先化简,再求值:5ab+2(2ab﹣3a2)﹣(6ab﹣7a2),其中a=﹣1,b=.20.一位同学做一道题:“已知两个多项式A、B,计算2A+B”.他误将“2A+B”看成“A+2B”,求得的结果为9x2﹣2x+7.已知B=x2+3x﹣2,求正确答案.21.观察下列算式:=1﹣,=﹣,=﹣,….(1)通过观察以上算式,猜想并写出:(n为正整数).(2)计算:++++…++.22.观察下列一列数:1,﹣3,5,﹣7,9,﹣11,13,﹣15,17,…(1)请写出这一列数中的第99个数和第2020个数;(2)在前2021个数中,正数和负数分别有多少个?(3)2019、2021、﹣2023是否都在这一列数中?若在,请指出它们分别是第几个数;若不在,请说明理由.参考答案1.解:A的系数是﹣,故A错误,不符合题意;B单项式x的系数为1,次数为1,故B错误,不符合题意;C xy+x﹣1是二次三项式,故C正确,符合题意;D﹣22xyz2的次数是4,故D错误,不符合题意;故选:C.2.解:原式=x2+(﹣3k)xy﹣3y2﹣8,因为不含xy项,故﹣3k=0,解得:k=.故选:C.3.解:与3x3y2是同类项的是﹣x3y2.故选:C.4.解:∵整式a m+1b2与的和为单项式,∴m+1=3,n=2,∴m=2,n=2,∴m2=22=4.故选:B.5.解:∵多项式2x3﹣8x2+x﹣1与多项式3x3+2mx2﹣5x+3相加后不含x的二次项,∴﹣8x2+2mx2=(2m﹣8)x2,∴2m﹣8=0,解得m=4.故选:C.6.解:因为(b+c)﹣(a﹣d)=b+c﹣a+d=(b﹣a)+(c+d)=﹣(a﹣b)+(c+d)…(1),所以把a﹣b=﹣3、c+d=2代入(1)得:原式=﹣(﹣3)+2=5.故选:B.7.解:长方形额周长为:2[(3x+2y)+(x﹣y)]=2(3x+2y+x﹣y)=2(4x+y)=8x+2y,故选:B.8.解:由数轴可得,a<b<0<c,|c|>|a|>|b|,∴a+b<0,c﹣a>0,b﹣c<0,∴|a|﹣|a+b|+|c﹣a|+|b﹣c|=﹣a+a+b+c﹣a﹣b+c=2c﹣a,故选:C.9.解:根据题意得:a=3,b=2.则a+b=3+2=5.故选:D.10.解:设空白出的面积为c,根据题意得:a+c=16,b+c=9,则a﹣b=(a+c)﹣(b+c)=16﹣9=7.故选:B.11.解:∵一列关于x的单项式:﹣x,4x2,﹣7x3,10x4,﹣13x5,16x6……,∴第n个单项式为:(﹣1)n•(3n﹣2)x n,∴第2021个单项式是(﹣1)2021•(3×2021﹣2)x2021=﹣6061x2021,故答案为:﹣6061x2021.12.解:因为单项式3a2x b y与单项式﹣2a y b x+2是同类项,所以2x=y,y=x+2,解得x=2,y=4,所以y x=42=16,故答案为:16.13.解:据题意两多项式相加得:5x3﹣8x2+2mx2﹣4x+2,∵相加后结果不含二次项,∴当2m﹣8=0时不含二次项,即m=4.14.解:剪下的长方形的周长为2(a+b)则这根铁丝还剩下5a+4b﹣2(a+b)=3a+2b.15.解:∵A=4x2﹣4xy+y2,B=x2+xy﹣5y2,∴A﹣3B=4x2﹣4xy+y2﹣3(x2+xy﹣5y2)=4x2﹣4xy+y2﹣3x2﹣3xy+15y2=x2﹣7xy+16y2.故答案为:x2﹣7xy+16y2.16.解:根据题意得:﹣3k﹣=0,解得:k=﹣.故答案是:﹣.17.解:5x2y﹣7(x2y﹣xy2)﹣3xy2=5x2y﹣7x2y+7xy2﹣3xy2=﹣2x2y+4xy2,当x=2,y=﹣1时,原式=﹣2×22×(﹣1)+4×2×(﹣1)2=﹣2×4×(﹣1)+8=8+8=16.18.解:(1)2A﹣B=2(x2+3xy+x﹣12)﹣(2x2﹣xy+4y﹣1)=2x2+6xy+2x﹣24﹣2x2+xy﹣4y+1=7xy+2x﹣4y﹣23.当x=y=﹣2时,原式=7×(﹣2)×(﹣2)+2×(﹣2)﹣4×(﹣2)﹣23=9.(2)∵2A﹣B=7xy+2x﹣4y﹣23=(7x﹣4)y+2x﹣23.由于2A﹣B的值与y的取值无关,∴7x﹣4=0∴x=.19.解:原式=5ab+4ab﹣6a2﹣6ab+7a2=a2+3ab,当a=﹣1,b=时,原式=1﹣1=0.20.根据题意得A=9x2﹣2x+7﹣2(x2+3x﹣2)=9x2﹣2x+7﹣2x2﹣6x+4=(9﹣2)x2﹣(2+6)x+4+7=7x2﹣8x+11.∴2A+B=2(7x2﹣8x+11)+x2+3x﹣2=14x2﹣16x+22+x2+3x﹣2=15x2﹣13x+20.21.解:(1)由题意可得,=,故答案为:=;(2)++++…++=1﹣++…+=1﹣=,故答案为:.22.解:(1)通过观察可得:数字的绝对值的规律是奇数为2n﹣1,符号规律为正负交替,第奇数个为正号,第偶数个为负号,∴第99个数为2×99﹣1=197,第2020个数为﹣(2×2020﹣1)=﹣4039.(2)在前2021个数中,正数有1011个,负数有1010个.(3)2019不在这列数中,2021、﹣2023在这一列数中,∵2019=2n﹣1,∴n=1010,第偶数个应该为负号,故2019不在这列数中,∵2021=2n﹣1,∴n=1011,第奇数个为正号,故2021在这列数中,∵2023=2n﹣1,∴n=1012,第偶数个应该为负号,故﹣2023在这列数中.。
六年级上册数学鲁教版整式的加减同步练习3
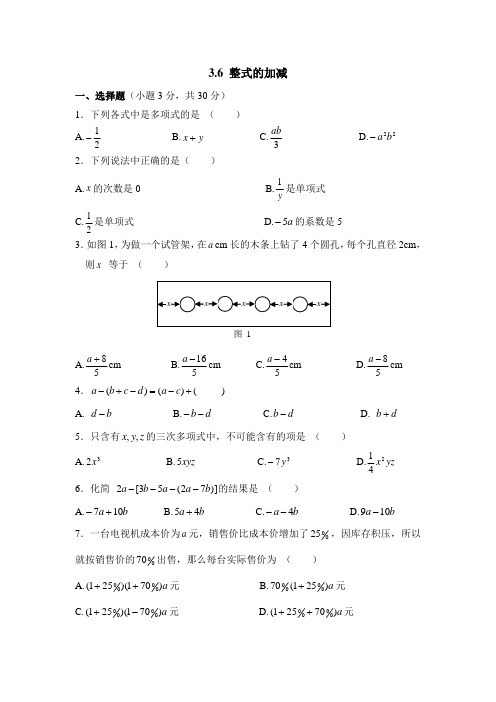
3.6 整式的加减一、选择题(小题3分,共30分) 1.下列各式中是多项式的是 ( ) A.21-B.y x +C.3abD.22b a -2.下列说法中正确的是( )A.x 的次数是0B.y1是单项式 C.21是单项式 D.a 5-的系数是5 3.如图1,为做一个试管架,在a cm 长的木条上钻了4个圆孔,每个孔直径2cm ,则x 等于 ( ) A.58+a cm B.516-a cm C.54-a cm D.58-a cm 4.+-=-+-)()(c a d c b a ( )A. b d -B.d b --C.d b -D. d b + 5.只含有z y x ,,的三次多项式中,不可能含有的项是 ( ) A.32x B.xyz 5 C.37y - D.yz x 241 6.化简 )]72(53[2b a a b a ----的结果是 ( )A.b a 107+-B.b a 45+C.b a 4--D.b a 109- 7.一台电视机成本价为a 元,销售价比成本价增加了0025,因库存积压,所以就按销售价的0070出售,那么每台实际售价为 ( )A.a )701)(251(0000++元B.a )251(700000+元C.a 701)(251(0000-+元D.a )70251(0000++元图 18.下面是小芳做的一道多项式的加减运算题,但她不小心把一滴墨水滴在了上面.⎪⎭⎫ ⎝⎛-+-22213y xy x 222 2123421y x y xy x +-=⎪⎭⎫ ⎝⎛-+--,阴影部分即为被墨迹弄污的部分.那么被墨汁遮住的一项应是 ( )A .xy 7- B. xy 7+ C. xy - D .xy + 9.用棋子摆出下列一组三角形,三角形每边有n 枚棋子,每个三角形的棋子总数是S .按此规律推断,当三角形边上有n 枚棋子时,该三角形的棋子总数S 等于( )A. 33-nB. 3-nC. 22-nD. 32-n 10.把(x -3)2-2(x -3)-5(x -3)2+(x -3)中的(x -3)看成一个因式合并同类 项,结果应( )A. -4(x -3)2+(x -3)B. 4(x -3)2-x (x -3)C. 4(x -3)2-(x -3) D . -4(x -3)2-(x -3) 二、填空题(每小题3分,共30分)11.单项式853ab -的系数是 ,次数是 .12.144mn mn -= ; 13.一个两位数,个位数字是a ,十位数字比个位数字大2,则这个两位数是_____. 14.当2x =-时,代数式651x x+-的值是 ; 15.计算:22224(2)(2)a b ab a b ab --+= ;16.规定一种新运算:1+--⋅=∆b a b a b a ,如1434343+--⨯=∆,请比较大小:()()34 43-∆∆-(填“>”、“=”或“>”).()3,2==S n ()6,3==S n ()9,4==S n ()12,5==S n17.根据生活经验,对代数式a b +作出解释: ;18.下面是一组数值转换机,写出(1)的输出结果(写在横线上),找出(2)的转换步骤(填写在框内).19.某城市按以下规定收取每月的煤气费:用气不超过60立方米,按每立方米0.8元收费;如果超过60立方米,超过部分每立方米按1.2元收费.已知某户用煤气x 立方米(x >60),则该户应交煤气费 元.20.观察下列单项式:0,3x 2,8x 3,15x 4,24x 5,……,按此规律写出第13个单项式是______。
高学校鲁教版六年级上册第三章整式的加减练习二十一(附答案)
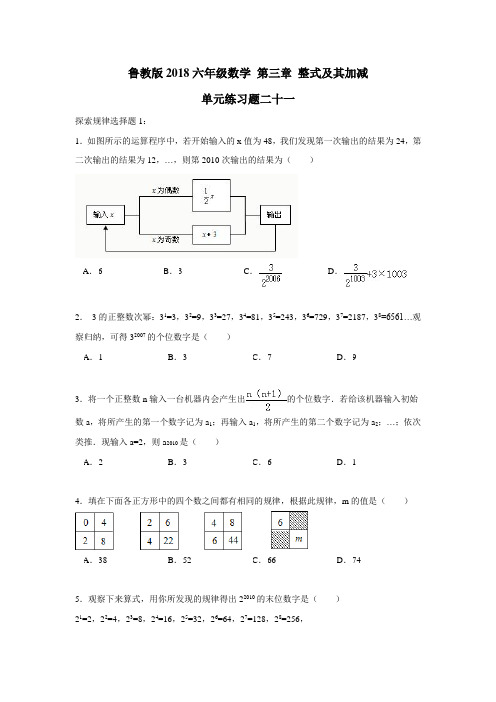
鲁教版2018六年级数学第三章整式及其加减单元练习题二十一探索规律选择题1:1.如图所示的运算程序中,若开始输入的x值为48,我们发现第一次输出的结果为24,第二次输出的结果为12,…,则第2010次输出的结果为()2.3的正整数次幂:31=3,32=9,33=27,34=81,35=243,36=729,37=2187,38=6561…观察归纳,可得32007的个位数字是()3.将一个正整数n输入一台机器内会产生出的个位数字.若给该机器输入初始数a,将所产生的第一个数字记为a1;再输入a1,将所产生的第二个数字记为a2;…;依次类推.现输入a=2,则a2010是()4.填在下面各正方形中的四个数之间都有相同的规律,根据此规律,m的值是()5.观察下来算式,用你所发现的规律得出22010的末位数字是()21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,6.下面是按一定规律排列的一列数:第1个数:;第2个数:;第3个数:;…第n个数:.那么,在第10个数,第11个数,第12个数,第13个数中,最大的数是()7.观察下列各式:,,,…计算:3×(1×2+2×3+3×4+…+99×100)=()8.四个电子宠物排座位,一开始,小鼠、小猴、小兔、小猫分别坐在1,2,3,4号座位上(如图所示),以后它们不停地变换位置,第一次上下两排交换,第二次是在第一次换位后,再左右两列交换位置,第三次再上下两排交换,第四次再左右两列交换…这样一直下去,则第2005次交换位置后,小兔所在的号位是()9.下面两个多位数1248624…、6248624…,都是按照如下方法得到的:将第一位数字乘以2,若积为一位数,将其写在第2位上,若积为两位数,则将其个位数字写在第2位.对第2位数字再进行如上操作得到第3位数字…,后面的每一位数字都是由前一位数字进行如上操作得到的.当第1位数字是3时,仍按如上操作得到一个多位数,则这个多位数前100位的所有数字之和是()10.某校生物教师李老师在生物实验室做试验时,将水稻种子分组进行发芽试验;第1组取3粒,第2组取5粒,第3组取7粒…即每组所取种子数目比该组前一组增加2粒,按此规律,那么请你推测第n组应该有种子数()粒.11.有一列数a1,a2,a3,a4,a5,…,a n,其中a1=5×2+1,a2=5×3+2,a3=5×4+3,a4=5×5+4,a5=5×6+5,…,当a n=2009时,n的值等于()12.为了求1+2+22+23+...+22008的值,可令S=1+2+22+23+...+22008,则2S=2+22+23+ (22009)因此2S﹣S=22009﹣1,所以1+2+22+23+…+22008=22009﹣1.仿照以上推理计算出1+5+52+53+…+52009的值是()13.观察下面几组数:1,3,5,7,9,11,13,15,…2,5,8,11,14,17,20,23,…7,13,19,25,31,37,43,49,…这三组数具有共同的特点.现在有上述特点的一组数,并知道第一个数是3,第三个数是11.则其第n个数为()14.23,33,43分别可以按如图所示方式“分裂”成2个、3个和4个连续奇数的和,63也能按此规律进行“分裂”,则63“分裂”出的奇数中最大的是()15.小时候我们就用手指练习过数数,一个小朋友按图中的规则练习数数,数到2009时应对应的指头是()答案:BCDDB ACAAA DDCAA。
六年级数学上册第三章整式及其加减习题归类八(探索规律)测试试题(无答案)鲁教版五四制(2021年整
山东省龙口市兰高镇六年级数学上册第三章整式及其加减习题归类八(探索规律)同步测试试题(无答案)鲁教版五四制编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(山东省龙口市兰高镇六年级数学上册第三章整式及其加减习题归类八(探索规律)同步测试试题(无答案)鲁教版五四制)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为山东省龙口市兰高镇六年级数学上册第三章整式及其加减习题归类八(探索规律)同步测试试题(无答案)鲁教版五四制的全部内容。
(探索规律)利用图形探索规律1.(重庆)观察下列图形,则第n 个图形中三角形的个数是( )A .22n +B .44n +C .44n -D .4n 、2.(广西梧州)下图是用火柴棍摆成的边长分别是1,2,3 根火柴棍时的正方形.当边长为n 根火柴棍时,设摆出的正方形所用的火柴棍的根数为s ,则s = . (用n 的代数式表示s )利用式子探索规律3、(重庆綦江)观察下列等式:(1)221.4135-=⨯; (2)222.5237-=⨯; (3)223.6339-=⨯ (4)224.74311-=⨯;…………则第n (n 是正整数)个等式为________.4、(牡丹江市)有一列数1234251017--,,,,…,那么第7个数是 . 5、(咸宁市)如图所示的运算程序中,若开始输入的x 值为48,我们发现第1次输出的结果为24,……n =1n =2n =3……第1个第2个第3个⑴1+8=?1+8+16=?⑵ ⑶ 1+8+16+24=?第8题……第2次输出的结果为12,……第2009次输出的结果为___________. 6、计算()()=⨯+⋅⋅⋅⋅⋅⋅+⨯+⨯+⨯=⨯+⋅⋅⋅⋅⋅⋅+⨯+⨯+⨯200920071751531311)2(200920072752532312)1(练习7、如图,四个电子宠物排座位:一开始,小鼠、小猴、小兔、小猫分别坐在1、2、3、4号的座位上,以后它们不停地交换位置,第一次上下两排交换位置,第二次是在第一次交换位置后,再左右两列交换位置,第三次是在第二次交换位置后,再上下两排交换位置,第四次是在第三次交换位置后,再左右两列交换位置,…,这样一直继续交换位置,第2008次交换位置后,小鼠所在的座号是( )。
初中数学鲁教版六年级上册《第三章6整式的加减》习题
《整式的加减》
一、基础题
选择题
1.小明身上带着a 元去商店里买学习用品,付给服务员b 元,找回c 元,小明身上还有( )
A.c 元 B .(a+c )元 C .(a-b+c )元 D.(a-b )元.
2.对于代数式a+,下列描述正确的是( )
A.a 与的平方的和
B.a 与b 的平方和
C.a 与b 的和的平方
D.a 与b 的平方的和
3.下列各组单项式中,是同类项的是( )
A. 与
B.与
C.与1
D. 与 二、综合题
1.填空题
(1)“x的2倍与1的和”用代数式表示为___.
(2)一个三位数,百位数字是3,十位数字和个位数字都是b,用代数式表示这个三位数是
(3)若与是同类项,则m= , n= .
(4)一个多项式加上得到,则这个多项式是
三、提高题
1.先化简,再求值
(1),其中a =-2
(2),其中x =-1,y =2.
2b 2b 3
2b a b a 2y x 2323xy a bc 2abc 2n y x 3225y x m -22x x -+-12
-x 233(4333)(4)a a a a a +-+--+22222222(22)(33)(33)x y xy x y x y x y xy ⎡⎤---++-⎣⎦
参考答案
四、基础题
选择题
1.A
2.D
3.A
五、综合题
1.填空题
(1)X2+1 (2)300+11b (3) 3 2 (4)2x2-x+1 六、提高题
(1)7 (2)-6。
2019年六年级数学上册 第三章 6《整式的加减》习题 鲁教版五四制
2019年六年级数学上册 第三章 6《整式的加减》习题 鲁教版五四制一、基础题选择题1.小明身上带着a 元去商店里买学习用品,付给服务员b 元,找回c 元,小明身上还有( )A.c 元 B .(a+c )元 C .(a-b+c )元 D.(a-b )元.2.对于代数式a+,下列描述正确的是( )A.a 与的平方的和B.a 与b 的平方和C.a 与b 的和的平方D.a 与b 的平方的和3.下列各组单项式中,是同类项的是( )A. 与B.与C.与1D. 与二、综合题1.填空题(1)“x的2倍与1的和”用代数式表示为___.(2)一个三位数,百位数字是3,十位数字和个位数字都是b,用代数式表示这个三位数是(3)若与是同类项,则m= , n= .(4)一个多项式加上得到,则这个多项式是三、提高题1.先化简,再求值(1),其中a =-2(2)22222222(22)(33)(33)x y xy x y x y x y xy ⎡⎤---++-⎣⎦,其中x =-1,y =2.参考答案四、基础题选择题1.A2.D3.A五、综合题1.填空题(1)X2+1 (2)300+11b (3) 3 2 (4)2x2-x+1六、提高题(1)7 (2)-6附送:2019年六年级数学上册第三章 6《整式的加减》学案鲁教版五四制一、学习目标知识与技能目标:通过对以前所学知识的综合复习,从而顺利过渡到整式的加减运算;在整式的加减中,能灵活结合各方面的关系,使得运算的正确性,灵活性。
过程与方法目标:探索和寻求整式加减的合理解释,形成分析解决问题的一些基本策略,提高创造性解决问题的愿望与能力。
情感态度与价值观目标:通过组织教学,体验只有用科学的方法,科学的态度才能学好数学的情感。
二、学习过程1.讨论教材提供的问题情境。
使用‘学乐师生’APP录像、拍照,分享给全班同学。
2.讨论教材中的“议一议”:因此引出整式的加减运算的法则:进行整式加减运算时,如果遇到括号要先去括号,再合并同类项。
第三章 整式及其加减 单元测试
第三章 整式及其加减 单元测试(能力提升)一、单选题1.下列代数式中,符合代数式书写要求的是()A .3mn B .2135x y C .()3m n ´+D .3ab ×2.下列判断中错误的个数有()(1)23a bc 与2bca -不是同类项; (2)25m n 不是整式;(3)单项式32x y -的系数是-1;(4)2235x y xy -+是二次三项式.A .4个B .3个C .2个D .1个3.某人骑自行车t (小时)走了()km s ,若步行()km s ,则比骑自行车多用3(小时),那么骑自行车每小时比步行多走()()km .A .3s s t t --B .3s s t t -+C .()s t s +D .(3)s t -4.下列各组中的两项是同类项的是( )A .2a b 和2ab -B .214x y 和5xy -C .a 和3a D .m 和7n5.已知一个多项式的 2 倍与3x 2+ 9x 的和等于-x 2+5x -2,则这个多项式是()A .-4x 2-4x -2B .-2x 2-2x -1C .2x 2+14x -2D .x 2+7x -16.已知3x 2﹣4x ﹣1的值是8,则15x 2﹣20x+7的值为( )A .45B .47C .52D .537.一个多项式M 减去多项式2 253x x -+-,小马虎同学却误解为先加上这个多项式,结果得237x x ++,则多项式M 是( )A .23210x x -+B .284x x -++C .2310x x -+D .284x x --8.某天数学课上老师讲了整式的加减运算,小颖回家后拿出自己的课堂笔记,认真地复习老师在课堂上所讲的内容,她突然发现一道题目:5(2a 2+3ab-b 2)-(-3+ab+5a 2+b 2)=5a 2■-6b 2+3被墨水弄脏了,请问被墨水遮盖住的一项是()A .+14abB .+3abC .+16abD .+2ab9.设P 为一个二次三项式,Q 为一个一次二项式,且P Q ¸的商为一个整式.则P 与Q 的和、差、商之和的项数至少是()A .3B .2C .1D .010.代数式4x 3–3x 3y +8x 2y +3x 3+3x 3y –8x 2y –7x 3的值A .与x ,y 有关B .与x 有关C .与y 有关D .与x ,y 无关二、填空题11.在式子1x y +、12、x -、61xy +、22a b -中,多项式有______个.12.2018年电影《我不是药神》反映了用药贵的事实,从而引起了社会的广泛关注.国家针对部分药品进行了改革,看病贵将成为历史.据调查,某种原价为345元的药品进行了两次降价,第一次降价15%,第二次降价x %,则该药品两次降价后的价格变为__________________元.13.小雷说“我有一个整式2()a b +”小宁说“我也有一个整式,我们两个整式的和为3(2)a b -”,那么小宁的整式是________.14.已如22321,42A B x x B C x -=-+-=-,则C A -=_________.15.关于x 的多项式222514x mx nx x x -++--+,它的值与x 的取值无关,则m n +=________.16.已知381P ax x =-+,23Q x ax =--,无论x 取何值时,329P Q -=恒成立,则a 的值为______.17.按下面的程序计算:当输入100x =时,输出结果是299;当输入50x =时,输出结果是_________.18.某同学做一道代数题:“求代数式9876543210987654321x x x x x x x x x +++++++++,当1x =时的值”,由于将式中某一项前的“+”号错看为“-”号,误得代数式的值为37,那么这位同学看错了______次项前的符号.19.已知x 2+2xy =﹣12,xy ﹣y 2=﹣4,则2x 2+5xy ﹣y 2的值为_____.20.将数1个1,2个12,3个13,…,n 个1n(n 为正整数)顺次排成一列1,12,12,13,13,13,…1n ,1n …记11a =,211122a a =++,32111333a a =+++,…,11S a =,212S a a =+,3123S a a a =++,…,12n n S a a a =++¼+,则20212019S S -=__________.三、解答题21.上海与南京间的公路长为364km ,一辆汽车以xkm/h 的速度开往南京,请用代数式表示:(1)汽车从上海到南京需多少小时?(2)如果汽车的速度增加2km/h ,从上海到南京需多少小时?(3)如果汽车的速度增加2km/h ,可比原来早到几小时?22.一个三位数,它的个位数字是m ,十位数字是个位数字的5倍少1,百位数字比个位数字大3.(1)用含m 的式子表示此三位数;(2)若交换个位数字和百位数字,其余不变,得到新的三位数,求原来的三位数比新得到的三位数多了多少?23.已知多项式﹣x 2y 2m +1+xy ﹣6x 3﹣1是五次四项式,且单项式πx n y 4m ﹣3与多项式的次数相同,求m ,n 的值.24.(1)求2212312(1)2323x x y x y æöæö--+-++-ç÷ç÷èøèø的值,其中11,42x y =-=-.(2)已知2(2)|23|0b a b -+-+=,求15(2)2(622)432a b a b a b æö---++--ç÷èø的值.25.设2222232,4623A x xy y x y B x xy y x y =-+-+=-+--,若2|2|(3)0x a y -++=且2B A a -=,求A 的值.26.对于多项式22222735x xy y x kxy y +++-+,老师提出了两个问题,第一个问题是:当k 为何值时,多项式中不含xy 项?第二个问题是:在第一问的前提下,如果2x =,1y =-,多项式的值是多少?(1)小明同学很快就完成了第一个问题,也请你把你的解答写在下面吧;(2)在做第二个问题时,马小虎同学把1y =-,错看成1y =,可是他得到的最后结果却是正确的,你知道这是为什么吗?27.有这样一道题:求整式33223320.520.5a b ab b a b ab -+-+233223b a b b ++--的值,其中 2.3a =,0.25b =-.有一个同学指出式子的值与条件 2.3a =,0.25b =-无关,他的说法有没有道理?说明理由.28.观察下列关于自然数的等式:①221743´=-;②222853´=-;③223963´=-;…根据上述规律解决下列问题:(1)完成第四个等式:4´_______=________;(2)写出你猜想的第n 个等式(用含n 的式子表示).29.如图,某校的“图书码”共有7位数字,它是由6位数字代码和校验码构成,其结构分别代表“种类代码、出版社代码、书序代码和校验码”.其中校验码是用来校验图书码中前6位数字代码的正确性.它的编制是按照特定的算法得来的.以上图为例,其算法为:a=++=;步骤1:计算前6位数字中偶数位数字的和a,即91313b=++=;步骤2:计算前6位数字中奇数位数字的和b,即6028c=´+=;步骤3:计算3a与b的和c,即313847d=;步骤4:取大于或等于c且为10的整数倍的最小数d,即50X=-=.步骤5:计算d与c的差就是校验码X,即50473请解答下列问题:(1)《数学故事》的图书码为978753Y,则“步骤3”中的c的值为______,校验码Y的值为______.(2)如图①,某图书码中的一位数字被墨水污染了,设这位数字为m,你能用只含有m的代数式表示上述步骤中的d吗?从而求出m的值吗?写出你的思考过程.(3)如图②,某图书码中被墨水污染的两个数字的差是4,这两个数字从左到右分别是多少?请直接写出结果.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章 《整式及其加减》测试题
一、耐心填一填(每小题3分,共30分)
1.三个连续奇数,中间的一个是21n,则第一个是___ ______,第三个是__ ______,
这三个数的和是____ _____.
2.如果1233mxymxyx为四次三项式,则m________。
3.边长是x厘米的正方形,每边都减少2厘米后,所得的正方形面积将减少___ ___
平方厘米.
4.一个两位数,个位数字是a,十位数字是b;这个两位数用代数式表示为________.
5.用拖拉机耕地100公顷,原计划每天耕地x公顷,如果每天多耕5公顷,实际只需_______
天耕完.
6.周长是πD厘米的圆的面积是_ __平方厘米.
7.如果2231,27AmmBmm,且0ABC,那么C=__ _
8.某行政单位原有工作人员m人,现精减机构,减少15%的工作人员,则精减后该单位有
____ ____人.
9.已知甲、乙两地相距s千米,货车需t小时走完全程,客车少用1小时,则客车每小时行
驶___ __千米.
10.甲种糖果每千克12元,乙种糖果每千克14元,丙种糖果每千克9元,从这三种糖果中
分别取出a,b,c千克混合销售,比单独销售快,要使混合销售所得收入与分别销售收入
相同,则混合糖果每千克应定价为__ ___元.
二、精心选一选(每小题3分,共24分)
11.在代数式21215,5,,,,,233xyzxyaxyxyzy中有( )
A.5个整式 B.4个单项,3个多项式
C.6个整式,4个单项式 D.6个整式,单项式与多项式个数相同
12.当12a,13b时,代数式2ab等于( )
A.16 B.112 C.124 D.136
13.下列各组代数式中,属于同类项的是( )
A.212ab与212ab B.2ab与2ac C.34与43 D.p与q
14.某商店上月的营业额是a万元,本月比上月增长15%,那么本月的营业额是( )
A.(a+1)15%万元 B.15%a万元 C.115%a万元 D.2115%a万
15.一个多项式加上2233xyxy,得323xxy,则这个多项式为( )
A.323xxy B.323xxy C.32263xxyxy D.33363xxyxy
16.用火柴棒摆“金鱼”,如图,按照图上的规律,第n个“金鱼”图需要火柴棒的根数为
( )根。
A. 6n-2 B. 8n-2 C. 6n+2 D. 8n+2
17.当2x时,代数式2420xRx的值0,则R的值等于( )
A.18 B.18 C.2 D.2
18.如果2120ab,则ab的值为( )
A.1 B.2 C.3 D.4
三、细心做一做(共30分,19-24题每题5分)
19. 2222(835)(223)aabbaabb 20. )(2)2(333cbacbaba
21. 13431354baba 22. 2223[723()1]aaaaa
23. 222(43)(24)(21),2aaaaaaa其中
24.若0322ba,求3a2b-[2ab2-2(ab-1.5a2b)+ab]+3ab2的值;
四、先认真想一想,再细心做一做(共36分)
25.(6分)某空调器销售商,今年四月份销出空调1a台,五月份销售空调比四月份的2
倍少1台,六月份销售空调比前两个月的总和的4倍还多5台.
(1)用代数式表示该销售商今年第二季度共销售空调多少台?
(2)若a=220,求第二季度销售的空调总数.
26.(6分)某农场有耕地1000亩,种粮食、棉花和蔬菜.其中蔬菜用地a亩,粮食用地比
蔬菜用地的6倍还多b亩,求棉花用地多少亩?当a=120,b=4时,棉花用地多少亩?
27.(8分)某城市大剧院地面的一部分为扇形,观众席的座位按下列方式设置:
排数 1 2 3 4 …
座位数 50 53 56 59 …
按这种方式排下去;
(1) 第5、6排各有多少个座位?
(2)第n排有多少个座位?
(3)在(2)的代数式中,当第n排为28时,有多少个座位?
28.(6分)观察下列图形:
它们是按照一定规律排列的,依照此规律,第9个图形中共有几个★,第n个呢?
29.(10分)阅读下列材料:
11111111111
1;,13233523557257
11111111111
113355723235257
111111113
11233557277
解答问题:
⑴111133557…12121nn
⑵模仿上面的解法,计算111266101014…13842
