2019版一轮优化探究理数(苏教版)练习:选修4-5 第三节 柯西不等式与排序不等式 Word版含解析
2019版一轮优化探究理数(苏教版)练习:第三章第三节导数在研究函数中的应用与生活中的优化问题举例

又函数 f(x)在 x=1 处有极值 12,
f′ 1 =0,
所以
1
f 1 =2
2a+b=0, .即 1
a= 2.
解得 a=12, b=- 1.
(2),其定义域是 (0,+ ∞ ),
且
1 f′ (x)=x-x=
x+ 1 x-1 x
.
当 x 变化时, f′ (x), f (x)的变化情况如下表:
答案: m<-12
4π 5π 8.已知函数 f(x)=xsin x,x∈R,则 f(- 4),f( 3 ),f(- 4 )的大小关系为 ________(用
“ <连”结 ).
解析: f′(x)= sin x+xcos x,当
x∈
[
54π,
4π 3 ]时,
sin
x<0,cos
x<0,∴
f′(
x)
=sin
1
令 3x2+6ax+3(a+2)= 0,即 x2+ 2ax+ a+ 2= 0.
∵函数 f(x)有极大值和极小值, ∴方程 x2+2ax + a+ 2= 0 有两个不相等的实根. 即 Δ=4a2-4a- 8>0,∴ a>2 或 a<-1.
答案: a>2 或 a<-1
5.已知函数 f(x)= 12x4-2x3+3m,x∈R,若 f(x)+9≥0 恒成立,则实数 m 的取
一、填空题 1.函数 y=1+3x- x3 的极大值,极小值分别为 ________. 解析: 由 y= 1+ 3x-x3, 得 y′=- 3x2+3, 令 y′=0,即- 3x2+ 3= 0. 得 x=±1. ∵当 x<-1 时, y′ <0; 当- 1<x<1 时, y′>0; 当 x>1 时, y′ <0. ∴当 x=1 时,有 y 极大值 = 1+ 3- 1=3; 当 x=- 1 时,有 y 极小值 = 1- 3+ 1=- 1. 答案: 3,- 1 2.函数 y=x3-3x2+1 的单调递减区间为 ________. 解析: f′(x)= (x3-3x2+1)′=3x2-6x, ∵当 f′(x)<0 时, f( x)单调递减, ∴ 3x2- 6x<0,即 0<x<2. 故单调递减区间为 (0,2). 答案: (0,2) 3.已知 t 为常数,函数 f(x)=|x3-3x-t+1|在区间 [- 2,1]上的最大值为 2,则实 数 t= ________. 解析: 由题意知- 2≤ x3-3x- t+1≤2 在 x∈[ -2,1]上恒成立,不等式左右两边 分别分离变量,可得 x3-3x- 1≤ t≤x3- 3x+3 在 x∈[ -2,1]上恒成立,得 1≤ t≤1, 所以 t=1.本题还可以通过数形结合的方法讨论解决. 答案: 1 4.函数 f(x)=x3+ 3ax2+3[( a+2)x+1]既有极大值又有极小值,则 a 的取值范围 是 ________. 解析: ∵ f(x)= x3+3ax2+ 3[( a+2)x+1] , ∴ f′(x)=3x2+6ax+3(a+2).
高中数学 第三讲 柯西不等式与排序不等式章末归纳提升

3 .
思想方法
新课标 ·数学 选修4-5
解决数学问题时,常遇到一些直接求解较为困难的问 题,通过观察、分析、类比、联想等思维过程,选择运用恰 当的数学方法进行变换,将原问题转化为一个新问题.
本章常把要证明的不等式通过换元或配凑等转化手段, 转化为柯西不等式或排序不等式的形式加以解决.
已知a>b>c,求证:a-1 b+b-1 c≥a-4 c.
新课标 ·数学 选修4-5
利用柯西不等式、排序不等式求最值 有关不等式的问题往往要涉及到对式子或量的范围的限 制,柯西不等式、排序不等式为我们通过不等式求最值提供 了新的有力工具,但一定要注意取等号的条件能否满足.
设a、b、c为正实数,且a+2b+3c=13,求 3a+ 2b+ c的最大值.
]【解】 由于a、b、c为正实数,根据柯西不等式,知 (a+2b+3c)(3+1+13) =[( a)2+( 2b)2+( 3c)2][( 3)2+12+( 13)2]
【证明】 因为a,b,c是实数,且a+b+c=1,令m= ( 13a+1, 13b+1, 13c+1),
n=(1,1,1).
新课标 ·数学 选修4-5
则|m·n|2=( 13a+1+ 13b+1+ 13c+1)2, |m|2·|n|2=3[(13a+1)+(13b+1)+(13c+1)] =3[13(a+b+c)+3]=48. ∵|m·n|2≤|m|2·|n|2, ∴( 13a+1)+ 13b+1+ 13c+1)2≤48. ∴ 13a+1+ 13b+1+ 13c+1≤4 3.
又a+x+b+y=2(a+b)>0,
所以a+a2 x+b+b2 y≥a+2 b.
新课标 ·数学 选修4-5
排序原理在不等式证明中的应用
2019版一轮优化探究理数(苏教版)练习选修4-5 第一节 绝对值不等式 Word版含解析
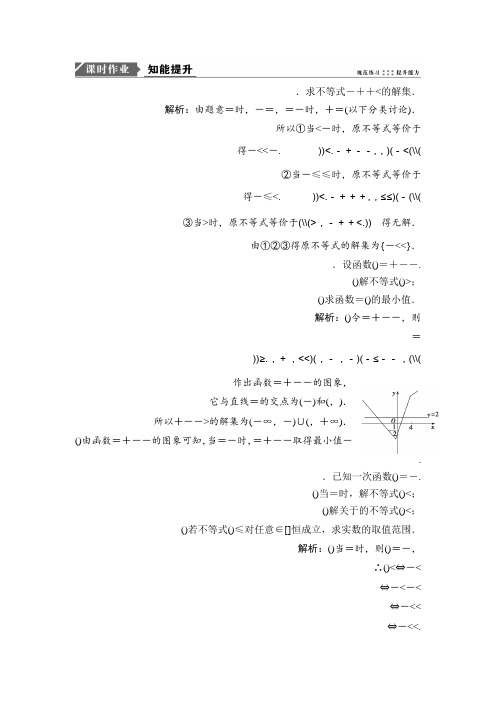
.求不等式-++<的解集.解析:由题意=时,-=,=-时,+=(以下分类讨论).所以①当<-时,原不等式等价于(\\(<-(),,-+--<.))得-<<-.②当-≤≤时,原不等式等价于(\\(-()≤≤,,-+++<.))得-≤<.③当>时,原不等式等价于(\\(>,-++<.))得无解.由①②③得原不等式的解集为{-<<}..设函数()=+--.()解不等式()>;()求函数=()的最小值.解析:()令=+--,则=(\\(--,≤-(),-,-()<<,+,≥.))作出函数=+--的图象,它与直线=的交点为(-)和(,).所以+-->的解集为(-∞,-)∪(,+∞).()由函数=+--的图象可知,当=-时,=+--取得最小值-..已知一次函数()=-.()当=时,解不等式()<;()解关于的不等式()<;()若不等式()≤对任意∈[]恒成立,求实数的取值范围.解析:()当=时,则()=-,∴()<⇔-<⇔-<-<⇔-<<⇔-<<.∴不等式的解集为{-<<}.()()<⇔-<⇔-<-<⇔-<<.当>时,不等式的解集为{-<<};当<时,不等式的解集为{<<-}.()()≤⇔-≤⇔-≤-≤⇔-≤≤⇔(\\(≤,≥-.))又∈[],∴-≤≤,且≠..已知关于的不等式-+-<.()当=时,解上述不等式;()如果关于的不等式-+-<的解集为空集,求实数的取值范围.解析:()∵=,∴-+-<,当<时,原不等式化为-<,解得>,∴<<;当≤≤时,原不等式化为<,∴≤≤;当>时,原不等式化为-<,解得<,∴<<.综上可知,原不等式的解集为{<<}.()作出=-+-与=的图象,若使不等式-+-<的解集为空集,则必有=-+-的图象在=的图象的上方,或=与=重合,∴≤.∴的取值范围为(-∞,].。
高二数学选修4-5 几个著名的不等式之一:柯西不等式

高二数学选修4-5 几个著名的不等式之一:柯西不等式目的要求: 重点难点: 教学过程: 一、引入:除了前面已经介绍的贝努利不等式外,本节还将讨论柯西不等式、排序不等式、平均不等式等著名不等式。
这些不等式不仅形式优美、应用广泛,而且也是进一步学习数学的重要工具。
1、什么是柯西不等式:定理1:(柯西不等式的代数形式)设d c b a ,,,均为实数,则22222)())((bd ac d c b a +≥++,其中等号当且仅当bc ad =时成立。
证明:几何意义:设α,β为平面上以原点O 为起点的两个非零向量,它们的终点分别为A (b a ,),B (d c ,),那么它们的数量积为bd ac +=•βα, 而22||b a +=α,22||d c +=β,所以柯西不等式的几何意义就是:||||||βαβα•≥⋅,其中等号当且仅当两个向量方向相同或相反(即两个向量共线)时成立。
2、定理2:(柯西不等式的向量形式)设α,β为平面上的两个向量,则||||||βαβα•≥⋅,其中等号当且仅当两个向量方向相同或相反(即两个向量共线)时成立。
3、定理3:(三角形不等式)设332211,,,,,y x y x y x 为任意实数,则: 分析:思考:三角形不等式中等号成立的条件是什么?4、定理4:(柯西不等式的推广形式):设n 为大于1的自然数,ii b a ,(=i 1,2,…,n )为任意实数,则:211212)(∑∑∑===≥ni i i ni in i i b a ba ,其中等号当且仅当nn a b a b a b === 2211时成立(当0=i a 时,约定0=i b ,=i 1,2,…,n )。
证明:构造二次函数:2222211)()()()(n n b x a b x a b x a x f -++-+-=即构造了一个二次函数:∑∑∑===+-=ni i n i i i ni ib x b a x ax f 121212)(2)()(由于对任意实数x ,0)(≥x f 恒成立,则其0≤∆, 即:0))((4)(4121221≤-=∆∑∑∑===ni i n i i ni i i b a b a ,即:))(()(121221∑∑∑===≤ni i ni i n i i i b a b a ,等号当且仅当02211=-==-=-n n b x a b x a b x a ,即等号当且仅当nn a b a b a b === 2211时成立(当0=i a 时,约定0=i b ,=i 1,2,…,n )。
柯西不等式与排序不等式章末总结课件

利用排序不等式证明不等式 排序不等式具有自己独特的体现:多个变量的排序与其大小顺 序有关,特别是与多变量间的大小顺序有关的不等式问题,利 用排序不等式解决往往很简捷.
已知 a,b,c∈R+,求证a2+2cb2+b22+ac2+c2+2ba2≥a+b +c. 【证明】 设 a≥b≥c>0.于是 a2≥b2≥c2,1c≥1b≥1a. 由排序不等式得:
【解】 (1)因为(x+2y+· 3)2 ≤[x2+( 2y)2+( 3z)2]·[12+( 2)2+( 3)2]
=(x2+2y2+3z2)(1+2+3)=18.
当且仅当x1=
2y= 2
3z, 3
即 x=y=z 时,等号成立.
所以-3 2≤x+2y+3z≤3 2,
根据排序不等式,得 F=xx221+xx223+…+xx2n-n 1+xx2n1 ≥x21·x11+x22·x12+…+x2n·x1n=x1+x2+…+xn =P(定值).当且仅当 x1=x2=…=xn=Pn时取等号. 即 F=xx221+xx223+…+xx2n-n 1+xx2n1的最小值为 P.
a2·1a+b2·1b+c2·1c ≤a2·1b+b2·1c+c2·1a,① a2·1a+b2·1b+c2·1c ≤a2·1c+b2·1a+c2·1b.②
①+②得 2a2·1a+b2·1b+c2·1c ≤a2·1b+b2·1c+c2·1a+a2·1c+b2·1a+c2·1b, 即 2(a+b+c)≤a2+c b2+b2+a c2+c2+b a2, 所以a2+2cb2+b22+ac2+c2+2ba2≥a+b+c 成立.
1111 等号成立⇔a1=b1=1c=d1⇔ba=bc=dc=ad
bcda ⇔a=b=c=d. 又已知 a,b,c,d 不全相等,则①中等号不成立.
2019版高考新创新一轮复习理数江苏专版课时达标检测六

课时达标检测(六十二) 选修4-5《不等式选讲》1.(2018·贵阳模拟)已知函数f (x )=2|x +1|+|x -2|.(1)求f (x )的最小值m ;(2)若a ,b ,c 均为正实数,且满足a +b +c =m ,求证:b 2a +c 2b +a 2c ≥3. 解:(1)当x <-1时,f (x )=-2(x +1)-(x -2)=-3x ∈(3,+∞);当-1≤x <2时,f (x )=2(x +1)-(x -2)=x +4∈[3,6);当x ≥2时,f (x )=2(x +1)+(x -2)=3x ∈[6,+∞).综上,f (x )的最小值m =3.(2)证明:a ,b ,c 均为正实数,且满足a +b +c =3,因为b 2a +c 2b +a 2c+(a +b +c ) =⎝⎛⎭⎫b 2a +a +⎝⎛⎭⎫c 2b +b +⎝⎛⎭⎫a 2c +c ≥2⎝⎛⎭⎫ b 2a ·a + c 2b ·b + a 2c ·c =2(a +b +c ). (当且仅当a =b =c =1时,取等号)所以b 2a +c 2b +a 2c ≥a +b +c ,即b 2a +c 2b +a 2c ≥3.2.(2018·南通模拟)已知x >0,y >0,z >0,且xyz =1,求证:x 3+y 3+z 3≥xy +yz +xz . 证明:因为x >0,y >0,z >0,所以x 3+y 3+z 3≥3xyz ,x 3+y 3+1≥3xy ,y 3+z 3+1≥3yz ,x 3+z 3+1≥3xz .将以上各式相加,得3x 3+3y 3+3z 3+3≥3xyz +3xy +3yz +3xz ,又因为xyz =1,从而x 3+y 3+z 3≥xy +yz +xz .3.(2018·常州期初)设不等式-2<|x -1|-|x +2|<0的解集为M ,a ,b ∈M .(1)证明:⎪⎪⎪⎪13a +16b <14;(2)比较|1-4ab |与2|a -b |的大小,并说明理由.解:(1)证明:记f (x )=|x -1|-|x +2|=⎩⎪⎨⎪⎧ 3,x ≤-2,-2x -1,-2<x <1,-3,x ≥1.由-2<-2x -1<0解得-12<x <12, 则M =⎝⎛⎭⎫-12,12.所以⎪⎪⎪⎪13a +16b ≤13|a |+16|b |<13×12+16×12=14. (2)由(1)得a 2<14,b 2<14. 因为|1-4ab |2-4|a -b |2=(1-8ab +16a 2b 2)-4(a 2-2ab +b 2)=(4a 2-1)(4b 2-1)>0. 所以|1-4ab |2>4|a -b |2,故|1-4ab |>2|a -b |.4. (2018·苏南四市模拟)已知函数f (x )=3x +6,g (x )=14-x ,若存在实数x 使f (x )+g (x )>a 成立,求实数a 的取值范围.解:存在实数x 使f (x )+g (x )>a 成立,等价于f (x )+g (x )的最大值大于a ,因为f (x )+g (x )=3x +6+14-x =3×x +2+1×14-x ,由柯西不等式:(3×x +2+1×14-x )2≤(3+1)·(x +2+14-x )=64,所以f (x )+g (x )=3x +6+14-x ≤8,当且仅当x =10时取“=”,故常数a 的取值范围是(-∞,8).5.(2018·盐城模拟)已知正数x ,y ,z 满足x +2y +3z =1,求1x +2y +3z的最小值. 解:1x +2y +3z =⎝⎛⎭⎫1x +42y +93z (x +2y +3z )=1+4+9+2y x +3z x +4x 2y +12z 2y +9x 3z +18y 3z≥14+22y x ·4x 2y +23z x ·9x 3z +212z 2y ·18y 3z=36, 当且仅当x =y =z =16时等号成立,所以1x +2y +3z 的最小值为36. 6. (2018·宿迁模拟)已知a ,b ∈R ,a >b >e(其中e 是自然对数的底数),求证:b a >a b .证明:因为b a >0,a b >0,a >b >e ,所以要证b a >a b ,只要证a ln b >b ln a ,只要证ln b b>ln a a .取函数f (x )=ln x x ,因为f ′(x )=1-ln x x 2, 所以当x >e 时,f ′(x )<0,所以函数f (x )在(e ,+∞)上单调递减.所以,当a >b >e 时,有f (b )>f (a ),即ln b b >ln a a ,所以b a >a b .7.(2018·无锡期末)已知正实数a ,b ,c ,d 满足a +b +c +d =1.求证:1+2a +1+2b +1+2c +1+2d ≤2 6.证明:因()1+2a+1+2b+1+2c+1+2d2≤(1+1+1+1)×(1+2a+1+2b+1+2c+1+2d)=4×[4+2×(a+b+c+d)],又a+b+c+d=1,所以(1+2a+1+2b+1+2c+1+2d)2≤24,即1+2a+1+2b+1+2c+1+2d≤2 6.。
2019版一轮优化探究理数(苏教版)练习:第三章 第三节 导数在研究函数中的应用与生活中的优化
一、填空题1.函数y=1+3x-x3的极大值,极小值分别为________.解析:由y=1+3x-x3,得y′=-3x2+3,令y′=0,即-3x2+3=0.得x=±1.∵当x<-1时,y′<0;当-1<x<1时,y′>0;当x>1时,y′<0.∴当x=1时,有y极大值=1+3-1=3;当x=-1时,有y极小值=1-3+1=-1.答案:3,-12.函数y=x3-3x2+1的单调递减区间为________.解析:f′(x)=(x3-3x2+1)′=3x2-6x,∵当f′(x)<0时,f(x)单调递减,∴3x2-6x<0,即0<x<2.故单调递减区间为(0,2).答案:(0,2)3.已知t为常数,函数f(x)=|x3-3x-t+1|在区间[-2,1]上的最大值为2,则实数t=________.解析:由题意知-2≤x3-3x-t+1≤2在x∈[-2,1]上恒成立,不等式左右两边分别分离变量,可得x3-3x-1≤t≤x3-3x+3在x∈[-2,1]上恒成立,得1≤t≤1,所以t=1.本题还可以通过数形结合的方法讨论解决.答案:14.函数f(x)=x3+3ax2+3[(a+2)x+1]既有极大值又有极小值,则a的取值范围是________.解析:∵f(x)=x3+3ax2+3[(a+2)x+1],∴f′(x)=3x2+6ax+3(a+2).令3x 2+6ax +3(a +2)=0,即x 2+2ax +a +2=0.∵函数f (x )有极大值和极小值,∴方程x 2+2ax +a +2=0有两个不相等的实根.即Δ=4a 2-4a -8>0,∴a >2或a <-1.答案:a >2或a <-15.已知函数f (x )=x 4-2x 3+3m ,x ∈R ,若f (x )+9≥0恒成立,则实数m 的取12值范围是________.解析:因为函数f (x )=x 4-2x 3+3m ,12所以f ′(x )=2x 3-6x 2,令f ′(x )=0,得x =0或x =3,经检验知x =3是函数的最小值点,所以函数的最小值为f (3)=3m -,272不等式f (x )+9≥0恒成立,即f (x )≥-9恒成立,所以3m -≥-9,解得m ≥.27232答案:m ≥326.函数y =x +2cos x 在[0,]上取得最大值时x 的值为________.π2解析:y ′=(x +2cos x )′=1-2sin x ,令1-2sin x =0,且x ∈[0,]时,x =.π2π6当x ∈[0,]时,f ′(x )≥0,f (x )是单调增函数,π6当x ∈[,]时,f ′(x )≤0,f (x )单调递减.π6π2∴f (x )max =f ().π6答案:π67.设m ∈R ,若函数y =e x +2mx (x ∈R)有大于零的极值点,则m 的取值范围是________.解析:因为函数y =e x +2mx (x ∈R)有大于零的极值点,所以y ′=e x +2m =0有大于0的实根.令y 1=e x ,y 2=-2m ,则两曲线的交点必在第一象限.由图象可得-2m >1,即m <-.12答案:m <-128.已知函数f (x )=x sin x ,x ∈R ,则f (-4),f (),f (-)的大小关系为4π35π4________(用“<”连结).解析:f ′(x )=sin x +x cos x ,当x ∈[,]时,sin x <0,cos x <0,∴f ′(x )5π44π3=sin x +x cos x <0,则函数f (x )在x ∈[,]上为减函数,∴f ()<f (4)<f (),5π44π34π35π4又函数f (x )为偶函数,∴f ()<f (-4)<f (-).4π35π4答案:f ()<f (-4)<f (-)4π35π49.f (x )=x (x -c )2在x =2处有极大值,则常数c 的值为________.解析:f (x )=x 3-2cx 2+c 2x ,f ′(x )=3x 2-4cx +c 2,f ′(2)=0⇒c =2或c =6.若c =2,f ′(x )=3x 2-8x +4,令f ′(x )>0⇒x <或x >2,f ′(x )<0⇒<x <2,2323故函数在(-∞,)及(2,+∞)上单调递增,在(,2)上单调递减,∴x =2是极2323小值点.故c =2不合题意,c =6.答案:6二、解答题10.已知函数f (x )=ax 2+b ln x 在x =1处有极值.12(1)求a ,b 的值;(2)判断函数y =f (x )的单调性并求出单调区间.解析:(1)因为函数f (x )=ax 2+b ln x ,所以f ′(x )=2ax +.bx 又函数f (x )在x =1处有极值,12所以Error!.即Error!解得Error!(2)由(1)可知f (x )=x 2-ln x ,其定义域是(0,+∞),12且f ′(x )=x -=.1x (x +1)(x -1)x当x 变化时,f ′(x ), f (x )的变化情况如下表:x (0,1)1(1,+∞)f ′(x )-0+f (x )极小值所以函数y =f (x )的单调递减区间是(0,1),单调递增区间是(1,+∞).11.已知函数f (x )=(x >0,x ≠1).xln x (1)求函数f (x )的极值;(2)若不等式>x 对任意实数x 恒成立,求实数a 的取值范围.解析:(1)函数f (x )=的定义域为(0,1)∪(1,+∞),xln x f ′(x )=.ln x -1ln2x 令f ′(x )=0,解得x =e.当x 变化时,f ′(x ),f (x )的变化情况如下表:x (0,1)(1,e)e (e ,+∞)f ′(x )--0+f (x )极小值f (e)由表得函数f (x )的单调减区间为(0,1)和(1,e),单调增区间为(e ,+∞).所以存在极小值为f (e)=e ,无极大值.(2)当x ≤0时,对任意a ≠0,不等式恒成立.当x >0时,在不等式>x 两边同时取自然对数,得>ln x .(*)xa ①当0<x ≤1时,ln x ≤0,当a >0,不等式恒成立;如果a <0,ln x <0,a ln x >0,不等式(*)等价于a <,xln x 由(1)得,此时∈(-∞,0),xln x 不等于(*)不恒成立.②当x >1时,ln x >0,则a >0,不等式(*)等价于a <,由(1)得,此时的最xln x xln x 小值为e ,得0<a <e.综上所述,a 的取值范围是(0,e).12.设函数f (x )=e x -1-x -ax 2.(1)若a =0,求f (x )的单调区间;(2)若当x ≥0时,f (x )≥0,求a 的取值范围.解析:(1)若a =0,f (x )=e x -1-x ,f ′(x )=e x -1.当x ∈(-∞,0)时,f ′(x )<0;当x ∈(0,+∞)时,f ′(x )>0.故f (x )的单调递减区间是(-∞,0),单调递增区间是(0,+∞).(2)f ′(x )=e x -1-2ax .由(1)知e x ≥1+x ,当且仅当x =0时等号成立,故f ′(x )≥x -2ax =(1-2a )x ,从而当1-2a ≥0,即a ≤时,f ′(x )≥0(x ≥0).12∴f (x )在[0,+∞)上单调增加.而f (0)=0,于是当x ≥0时,f (x )≥0.由e x >1+x (x ≠0)可得e -x >1-x (x ≠0).从而当a >时,12f ′(x )<e x -1+2a (e -x -1)=e -x (e x -1)(e x -2a ),令e -x (e x -1)(e x -2a )<0得1<e x <2a ,∴0<x <ln 2a .故当x ∈(0,ln 2a )时,f ′(x )<0,∴f (x )在(0,ln 2a )上单调减少.而f (0)=0,于是当x ∈(0,ln 2a )时,f (x )<0.不符合要求.综上可得a 的取值范围为(-∞,].12。
2019苏教版高考一轮优化探究理数练习:选修4-5 第一节 绝对值不等式 Word版含解析
单像空间后方交会姓名:学号:时间:Echo did this for you .2013/4/25目录一、作业任务 .............................................................................................................. - 4 -二、计算原理 .............................................................................................................. - 4 -三、算法流程 .............................................................................................................. - 8 -四、源程序 .................................................................................................................. - 9 -五、计算结果 .............................................................................................................. - 9 -六、结果分析 .............................................................................................................. - 9 -七、心得与体会 .......................................................................................................... - 9 -八、附页 ...................................................................................................................... - 9 -1.c++程序........................................................................................................... - 9 -2.C++程序截图..................................................................................................- 16 -3.matlb程序.....................................................................................................- 17 -一、 作业任务 已知条件:摄影机主距f=153.24mm ,x0=0,y0=0, 像片比例尺为1:40000,有四对点的像点坐标与相应的地面坐标如下表。
柯西不等式与排序不等式章末总结课件
【例 1】 设 x+y+z=1,求 w=2x2+3y2+z2 的最小值. 【 分 析 】 将 已 知 条 件 变 形 为 : 12 = (x + y + z)2 =
1 2·
2x+
1 3·
3y+1·z2
就可以应用柯西不等式.
【解】 ∵x+y+z=1,
∴1=(x+y+z)2
三 用柯西不等式解决实际应用问题 解决实际应用问题,主要在于数学模型的建立和目标函数的求 解,只要找好这两点问题便迎刃而解.
【例 5】 在半径为 R 的圆中,求周长最大的内接长方形. 【分析】 首先表示出内接长方形的周长,得出目标函数,再 利用柯西不等式求解.
【解】 如图,设内接长方形 ABCD 的长为 x,则宽为 4R2-x2.
a+b+c
求证:>0, 则 lga≥lgb≥lgc, 由排序不等式,得 alga+blgb+clgc=alga+blgb+clgc, alga+blgb+clgc≥algb+blgc+clga. alga+blgb+clgc≥algc+blga+clgb.
于是长方形 ABCD 的周长为 L=2x+ 4R2-x2 =21×x+1× 4R2-x2 ≤2x2+ 4R2-x2212·(12+12)12 =2 2·2R=4 2R. 当且仅当1x= 4R12-x2,即 x= 2R 时,取等号,此时宽为 2R. 所以,周长最大的内接长方形为正方形,其周长为 4 2R.
47<n+1 1+n+1 2+…+21n<
2 2.
由柯西不等式,有 n+1 1+n+1 2+…+21nn+1+n+2+…+2n>n2, 于是n+1 1+n+1 2+…+21n
n2 >n+1+n+2+…+2n =3n2+n 1=3+2 1n≥3+2 12=47.
2019-2020学年人教版高中数学选修4-5教材用书:第三讲柯西不等式与排序不等式一二维形式的柯西不等式Wo
解:∵ (4 x2+ 9y2)(2 2+ 22) ≥ (4 x+ 6y) 2= 4,∴ 4x2+ 9y2≥1. 2
当且仅当 2×2x=3y×2,即 2x= 3y 时,等号成立.
1
1
又 2x+ 3y= 1,得 x= 4, y= 6,
故当
x=
1 4,
1 y=6时,
4x2+
9y
2
的最小值为
1 2.
6.求函数 f ( x) = x- 6+ 12- x的最大值及此时 x 的值.
等号成立的条件必须一致,不能自相矛盾,否则就会出现错误.多次反复运用柯西不等式的方法也是常用技 巧之一.
4.已知 2x2+ y2= 1,求 2x+ y 的最大值.
解: 2x+ y= 2× 2x+1× y≤
2 + 12×
2 + y2= 3× 2x2+ y2= 3.
3 当且仅当 x= y= 3 时,等号成立.∴ 2x+ y 的最大值为 3. 5.已知 2x+ 3y=1,求 4x2+ 9y2 的最小值.
-
+-
+-
.
事实上,在平面直角坐标系中,设点 P1,P2,P3 的坐标分别为 ( x1,y1) ,( x2,y2) ,( x3,y3) ,根据△ P1P2P3
的边长关系有 | P1P3| + | P2P3| ≥ | P1P2| ,当且仅当三点 P1,P2, P3 共线,并且点 P1, P2 在 P3 点的异侧时,等号
a2+ b2· c2+ d2≥ | ac+ bd|( a, b,c, d∈ R);
a2+ b2· c2+ d2≥ | ac| + | bd|( a, b, c, d∈ R).
2.柯西不等式的向量形式
定理 2:设 α , β 是两个向量,则 | α ·β | ≤ | α | ·|β| ,当且仅当 β 是零向量,或存在实数 k,使
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019版一轮优化探究理数练习
苏教版
1、若n为大于1的自然数,求证:nnn+1
=2+32+43+54+…+n+1n
≥n·n2·32·43·…·n+1n
=n·nn+1=左边、
∵2≠32≠43,故不取等号、
∴不等式nnn+1
(2)求函数y=2x+91-2x,x∈(0,12)的最小值、
解析:(1)证明:因为m,n>0,利用柯西不等式,得
(m+n)(a2m+b2n)≥(a+b)2,
所以a2m+b2n≥a+b2m+n.
(2)由(1),y=2x+91-2x=222x+321-2x≥2+322x+1-2x=25,
所以函数y=2x+91-2x(x∈ (0,12))的最小值为25,当且仅当x=15时取得、
3、设△ABC的三边长分别为a,b,c,
(1)判定b+c-a,a+b-c,c+a-b的符号;
2019版一轮优化探究理数练习
苏教版
(2)求证:a2b+c-a+b2c+a-b+c2a+b-c≥a+b+c.
解析:(1)因为a,b,c为三角形的三边,
所以b+c-a>0,c+a-b>0,a+b-c>0.
(2)证明:a2b+c-a+b2c+a-b+c2a+b-c
=1a+b+c(a2b+c-a+b2c+a-b+c2a+b-c)·[(b+c-a)+(c+a-b)+(a+b-c)]
≥1a+b+c(a2b+c-a·b+c-a+b2c+a-b·c+a-b+
c
2
a+b-c
·a+b-c)2
=1a+b+c(a+b+c)2=a+b+c.
4、已知a,b,c∈(0,+∞),且1a+2b+3c=2,求a+2b+3c的最小值及取得最
小值时a,b,c的值、
解析:(1a+2b+3c)(a+2b+3c)=[( 1a)2+( 2b)2+( 3c)2][(a)2+(2b)2+
(3c)2]≥( 1a·a+2b·2b+3c·3c)2=36.
又1a+2b+3c=2,∴a+2b+3c≥18,
当且仅当1aa=2b2b=3c3c,即a=b=c=3时等号成立、
∴当a=b=c=3时,a+2b+3c取得最小值18.
5、已知函数f(x)=m-|x-2|, m∈R,且f(x+2)≥0的解集为[-1,1]、
(1)求m的值;
(2)若a,b,c∈R+,且1a+12b+13c=m,求证:a+2b+3c≥9.
2019版一轮优化探究理数练习
苏教版
解析:(1)因为f(x+2)=m-|x|,
所以f(x+2)≥0等价于|x|≤m,
由|x|≤m有解,得m≥0,
且其解集为{x|-m≤x≤m}、
又f(x+2)≥0的解集为[-1,1],故m=1.
(2)由(1)知1a+12b+13c=1,又a,b,c∈R+,由柯西不等式得a+2b+3c=(a+2b
+3c)(1a+12b+13c)≥(a·1a+2b·12b+3c·13c)2=9.
6、某自来水厂要制作容积为500 m3的无盖长方体水箱,现有三种不同规格的长
方形金属制箱材料(单位:m):
①19×19;②30×10;③25×12.
请你选择其中的一种规格材料,并设计出相应的制作方案(要求:①用料最省;
②简便易行)、
解析:设无盖长方体水箱的长、宽、高分别为a m、b m、c m,
由题意,可得abc=500,
长方体水箱的表面积为:S=2bc+2ac+ab.
由均值不等式,知S=2bc+2ac+ab≥332bc·2ac·ab=334×5002=300.
当且仅当2bc=2ca=ab,即a=b=10,c=5时,
S=2bc+2ca+ab=300为最小,
这表明将无盖长方体的尺寸设计为10×10×5(即2∶2∶1)时,其用料最省、
如何选择材料并设计制作方案,就要研究三种供选择的材料,哪一种更易制作成
长方体水箱的平面展开图、
逆向思维,先将无盖长方体展开成平面图,如图(1),进一步剪拼成图(2)的长30 m,
宽10 m(长∶宽=3∶1)的长方形、因此,应选择规格30×10的制作材料,制作方
2019版一轮优化探究理数练习
苏教版
案如图(3)、
可以看出,图(3)这种“先割后补”的方案不但可使用料最省,而且简便易行、
SJ
