中考数学易错题精选-反比例函数练习题及答案.docx

中考数学易错题精选 -反比例函数练习题及答案
一、反比例函数
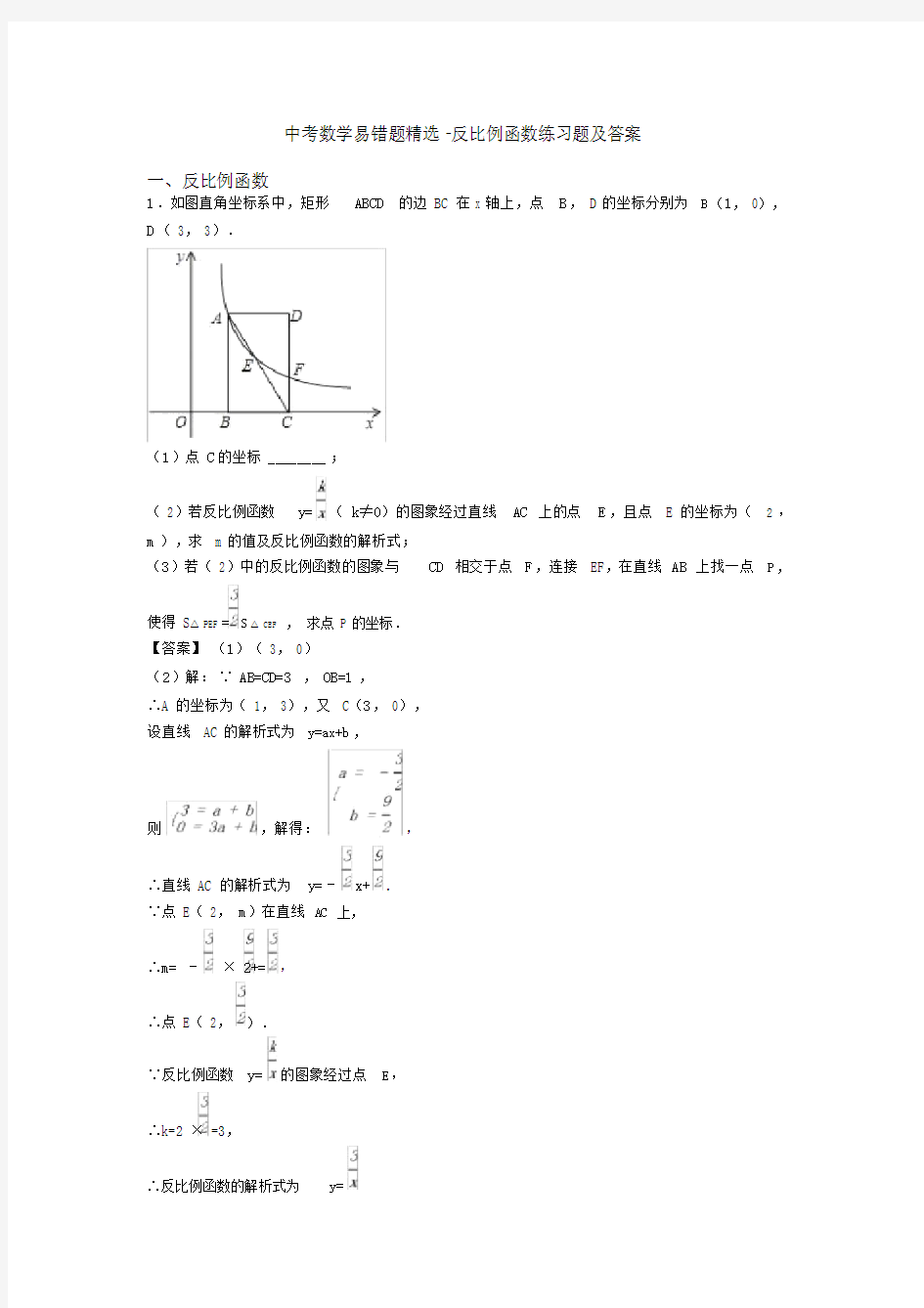
1.如图直角坐标系中,矩形ABCD的边 BC 在 x 轴上,点B, D 的坐标分别为B(1, 0),D( 3, 3).
(1)点 C的坐标 ________;
( 2)若反比例函数y=(k≠0)的图象经过直线AC 上的点E,且点 E 的坐标为( 2 ,m),求 m 的值及反比例函数的解析式;
(3)若( 2)中的反比例函数的图象与CD 相交于点F,连接 EF,在直线AB 上找一点P,
使得 S△PEF=S△CEF,求点 P 的坐标.
【答案】(1)( 3, 0)
(2)解:∵ AB=CD=3, OB=1,
∴A 的坐标为( 1, 3),又 C(3, 0),
设直线 AC 的解析式为y=ax+b,
则,解得:,
∴直线 AC 的解析式为y=﹣x+.
∵点 E( 2, m)在直线AC 上,
∴m= ﹣× 2+=,
∴点 E( 2,).
∵反比例函数y=的图象经过点E,
∴k=2 × =3,
∴反比例函数的解析式为y=
(3)解:延长 FC 至 M ,使 CM=CF,连接 EM,则 S△
EFM=
△
).S EFC, M( 3,﹣ 0.5
在 y= 中,当 x=3 时, y=1,
∴F(3, 1).
过点 M 作直线 MP∥ EF交直线 AB 于 P,则 S△PEF=S△MEF.
设直线 EF的解析式为y=a'x+b',
∴,解得,
∴y=﹣ x+ .
设直线 PM 的解析式为y=﹣x+c,
代入 M( 3,﹣ 0.5),得: c=1,
∴y=﹣ x+1.
当 x=1 时, y=0.5,
∴点 P( 1, 0.5).
同理可得点P( 1, 3.5).
∴点 P 坐标为( 1, 0.5)或( 1, 3.5).
【解析】【解答】解:(1)∵ D( 3, 3),
∴OC=3,
∴C(3,0).
故答案为( 3, 0);
【分析】( 1)由 D 的横坐标为3,得到线段OC=3,即可确定出 C 的坐标;( 2)由矩形的对边相等,得到AB=CD,由 D 的纵坐标确定出CD的长,即为AB 的长,再由 B 的坐标确定出 OB 的长,再由 A 为第一象限角,确定出 A 的坐标,由 A 与 C 的坐标确定出直线AC 的解析式,将 E 坐标代入直线AC 解析式中,求出m 的值,确定出 E 的坐标,代入反比例解
析式中求出k 的值,即可确定出反比例解析式;(3)延长FC 至 M ,使CM= CF,连接
EM,则 S△EFM= S△EFC, M ( 3,﹣ 0.5).求出 F( 3,1),过点 M 作直线 MP∥ EF交直线 AB 于 P,利用平行线间的距离处处相等得到高相等,再利用同底等高得到 S△PEF=S△MEF.此时直线 EF 与直线 PM 的斜率相同,由 F 的横坐标与 C 横坐标相同求出 F
的横坐标,代入反比例解析式中,确定出 F 坐标,由 E 与 F 坐标确定出直线 EF 斜率,即为直线 PM 的斜率,再由 M 坐标,确定出直线 PM 解析式,由 P 横坐标与 B 横坐标相同,将横坐标代入直线
PM 解析式中求出 y 的值,即为 P 的纵坐标,进而确定出此时 P 的坐 B
标.
2.一次函数y=ax+b( a≠0)的图象与反比例函数y=(k≠0)的图象相交于y 轴交于点C,与x 轴交于点D,点 D 的坐标为(﹣ 1 , 0 ),点A tan∠ CDO=2.过点 B 作 BH⊥ y 轴交 y 轴于 H,连接 AH.
A, B 两点,与的横坐标是 1 ,
(1)求一次函数和反比例函数的解析式;
(2)求△ ABH 面积.
【答案】(1)解:∵点 D 的坐标为(﹣ 1, 0), tan∠ CDO=2,∴C O=2,即 C( 0, 2),
把 C(0, 2), D(﹣ 1, 0)代入 y=ax+b 可得,
,解得,
∴一次函数解析式为y=2x+2,
∵点 A 的横坐标是1,
∴当 x=1 时, y=4,即 A( 1,4),
把 A( 1, 4)代入反比例函数 y= ,可得 k=4,
∴反比例函数解析式为 y=
(2)解:解方程组,可得或,∴B(﹣ 2,﹣ 2),
又∵ A( 1, 4), BH⊥y轴,
∴△ ABH 面 =× (2×4+2)=6.
【解析】【分析】( 1)先由 tan∠ CDO=2 可求出 C 坐,再把 D 点坐代入直解析式,
可求出一次函数解析式,再由直解析式求出 A 坐,代入双曲解析式,可求出双曲
解析式;( 2)△ ABH 面可以 BH 底,高 =y A-y B=4-(-2)=6.
3.如,四形 OP1A1B1、 A1P2A2B2、 A2P3 A3B3、?、 A n﹣1P n A n B n都是正方形,角OA1、
AA、AA、?、A A 都在 y 上( n≥1的整数),点P ( x, y ),点 P (x
2,
1223n﹣1 n1112
y2),?, P n( x n, y n)在反比例函数y=(x>0)的象上,并已知B1( 1,1).
(1)求反比例函数 y= 的解析式;
(2)求点 P2和点 P3的坐;
( 3)由( 1)、( 2)的果或律猜想并直接写出:△ P n B n O的面________ ,点
P n的坐 ________ (用含【答案】(1)解:在正方形B1与 P1关于 y 称,∵B1( 1,1),
∴P1( 1,1).n的式子表示).
OP1A1B1中, OA1是角,
k=1×1=1,即反比例函数解析式y=
(2)解:接P2B2、 P3B3,分交 y 于点 E、 F,
又点 P1的坐( 1, 1),
∴OA1=2,
点 P2的坐( a,a+2),
代入 y= 得 a= -1,
故点 P2的坐(-1,+1),
A1E=A2E=2 -2, OA2=OA1+A1A2=2 ,
点 P3的坐( b, b+2),
代入 y= ( >0)可得 b=-,
故点 P3的坐(- ,+ )
(3) 1;( -,+)
【解析】【解答】解:( 3)∵=2=2× =1,=2=2× =1,?
∴△ P n B n O 的面1,
由 P1( 1, 1)、 P2(1,+1)、 P3(,+)知点 P n的坐(,+),
故答案: 1、(,+).
【分析】( 1)由四形 OP1 11111
A B 正方形且OA 是角知B与 P 关于 y 称,得出
点 P1(1, 1),然后利用待定系数法求解即可;
(2)接 P2B2、 P3B3,分交 y 于点 E、 F,由点 P1坐及正方形的性知OA1=2,P2的坐( a, a+2),代入解析式求得 a 的即可,同理可得点P3的坐;
(3)先分求得 S△P1 B1 O、 S△P2B2O 的,然后找出其中的律,最后依据律行算即可 .
4.抛物y=+x+m 的点在直y=x+3 上,点F( 2,2)的直交抛物于点
M、 N 两点(点M 在点 N 的左边), MA ⊥x 轴于点 A, NB⊥ x 轴于点 B.
(1)先通过配方求抛物线的顶点坐标(坐标可用含m 的代数式表示),再求m 的值;(2)设点 N 的横坐标为a,试用含 a 的代数式表示点N 的纵坐标,并说明NF=NB;
(3)若射线NM 交 x 轴于点 P,且 PA?PB=,求点M的坐标.
【答案】(1)解: y= x2+x+m=(x+2)2+(m﹣1)
∴顶点坐标为(﹣2, m﹣ 1)
∵顶点在直线y=x+3 上,
∴﹣ 2+3=m﹣ 1,
得 m=2;
(2)解:过点 F 作 FC⊥ NB 于点 C,
∵点 N 在抛物线上,
∴点 N 的纵坐标为:a2 +a+2,
即点 N( a,a2+a+2)
在 Rt△ FCN中, FC=a+2, NC=NB﹣ CB= a2+a,
∴NF2=NC2+FC2=( a2+a)2+( a+2)2,
=(a2+a)2 +( a2+4a) +4,
而 NB2=(a2+a+2)2,
=(a2+a)2 +( a2+4a) +4
∴N F2=NB2,
NF=NB
(3)解:连接AF、 BF,
由 NF=NB,得∠ NFB=∠ NBF,由( 2)的思路知, MF=MA ,
∴∠ MAF=∠ MFA,
∵MA ⊥ x 轴, NB⊥ x 轴,
∴MA ∥ NB,
∴∠ AMF+∠BNF=180 °
∵△ MAF 和△ NFB 的内角总和为360 ,°
∴2∠ MAF+2∠ NBF=180 ,°∠ MAF+∠
NBF=90 ,°∵∠ MAB+∠ NBA=180 ,°
∴∠ FBA+∠ FAB=90 ,°又∵
∠ FAB+∠ MAF=90°,
∴∠ FBA=∠ MAF=∠ MFA,
又∵∠ FPA=∠ BPF,
∴△ PFA∽△ PBF,
∴=,PF2=PA× PB=,
过点 F 作 FG⊥ x 轴于点 G,在 Rt△ PFG中,
PG==,
∴PO=PG+GO=,
∴P(﹣,0)
设直线 PF: y=kx+b,把点 F(﹣ 2, 2)、点 P(﹣,0)代入y=kx+b,解得 k=,b=,
∴直线 PF: y= x+,
解方程x2+x+2= x+,
得 x=﹣ 3 或 x=2(不合题意,舍去),
当 x=﹣ 3 时, y=,
∴M (﹣ 3,).
【解析】【分析】( 1)利用配方法将二次函数化成顶点式,写出顶点坐标,由顶点再直线
y=x+3 上,建立方程求出m 的值。
(2)过点 F 作 FC⊥ NB 于点C,根据已知条件点N 在抛物线上,可得出N 点坐标,在Rt△ FCN 中,利用勾股定理得出NF2=NC2+FC2,用含 a 的代数式分别表示出进而得出
NF2、 NB2,即可得出到NF=NB。
(3)要求点M 的坐标,需要先求出直线PF 的解析式.首先由(2)的思路得出MF=MA ,然后连接AF、 FB,再通过证明△ PFA∽ △ PBF,利用相关的比例线段将PA?PB 的值转化为PF2的值,进而求出点 F 的坐标和直线 PF 的解析式,由图像可知直线 PF 和抛物线相较于点M,
建立方程求解,即可得点 M 的坐标。
5.平面直角坐标系 xOy 中,点 A、 B 分别在函数 y1= ( x> 0)与 y2=﹣(x< 0)的图象上, A、B 的横坐标分别为 a、 b.
(1)若 AB∥ x 轴,求△ OAB 的面积;
(2)若△ OAB 是以 AB 为底边的等腰三角形,且a+b≠0,求 ab 的值;
(3)作边长为 2 的正方形ACDE,使 AC∥ x 轴,点 D 在点 A 的左上方,那么,对大于或等
于 3 的任意实数a,CD 边与函数y1=(x>0)的图象都有交点,请说明理由.
【答案】(1)解:由题意知,点A( a,),B(b,﹣),
∵AB∥ x 轴,
∴,
∴a=﹣ b;
∴A B=a﹣ b=2a,
∴S△OAB= ?2a?=3
(2)解:由( 1)知,点A( a,),B(b,﹣),
222222
∴OA =a +(),OB =b +(﹣),
∴OA=OB,
∴OA2=OB2,
∴a2+()2=b2+(﹣)2,
∴a2﹣ b2=()2﹣()2,
∴( a+b)( a﹣ b) =(+)(﹣)=,
∵a> 0, b< 0,
∴ab< 0, a﹣ b ≠0,
∵a+b ≠0,
∴1=,
∴a b=3(舍)或 ab=﹣3,
即: ab 的值为﹣ 3;
(3)解:对大于或等于 3 的任意实数 a, CD 边与函数 y1=(x> 0)的图象都有交点.理由:如图,
∵a ≥3, AC=2,
∴直线 CD 在 y 轴右侧且平行于y 轴,
∴直线 CD 一定与函数y1=(x>0)的图象有交点,
∵四边形 ACDE是边长为 2 的正方形,且点 D 在点 A( a,)的左上方,
∴C( a﹣ 2,),
∴D( a﹣ 2,+2),
设直线 CD 与函数 y1=(x>0)相交于点F,
∴F(a﹣ 2,),
∴FC=﹣=,
∴2﹣ FC=2﹣=,
∵a ≥3,
∴a﹣ 2>0, a﹣3 ≥0,
∴≥0,
∴2﹣ FC≥0,
∴F C≤2,
∴点 F 在线段 CD 上,
即:对大于或等于 3 的任意实数a, CD 边与函数y1=(x>0)的图象都有交点.
【解析】【分析】( 1)先判断出a=﹣ b,即可得出AB=2a,再利用三角形的面积公式即可
得出结论;( 2 )利用等腰三角形的两腰相等建立方程求解即可得出结论;(3)先判断出
直线 CD 和函数出 FC,再判断
y1=
FC
与
( x>0 )必有交点,根据
点 2 的大小即可.
A 的坐标确定出点C, F 的坐标,进而得
6.如图,在平面直角坐标系中,直线AB 与 x 轴交于点B,与 y 轴交于点A,与反比例函数 y=的图象在第二象限交于点C, CE⊥ x 轴,垂足为点E, tan ∠ABO=,OB=4,
OE=2.
(1)求反比例函数的解析式;
(2)若点 D 是反比例函数图象在第四象限上的点,过点 D 作 DF⊥y 轴,垂足为点F,连接OD、 BF.如果 S△BAF=4S△DFO,求点 D 的坐标.
【答案】(1)解:∵OB=4, OE=2,∴ BE=OB+OE=6.
∵CE⊥ x 轴,
∴∠ CEB=90 .°
在 Rt△ BEC中,∠ CEB=90°, BE=6, tan∠ ABO=,
∴C E=BE?tan∠ ABO=6 × =3,
结合函数图象可知点 C 的坐标为(﹣ 2, 3).
∵点 C 在反比例函数y=的图象上,
∴m= ﹣ 2 × 3=﹣ 6,
∴反比例函数的解析式为y=﹣
(2)解:∵点 D 在反比例函数y=﹣第四象限的图象上,∴ 设点D的坐标为(n,﹣)( n> 0).
在 Rt△ AOB 中,∠ AOB=90°, OB=4, tan∠ABO=,
∴O A=OB?tan∠ ABO=4 × =2.
∵S△BAF= AF?OB=(OA+OF)?OB=(2+)× 4=4+.
∵点 D 在反比例函数y=﹣第四象限的图象上,
∴S=×|﹣6|=3 .
△DFO
=4S,
∵S△BAF△DFO
∴4+=4 ×3,
解得: n=,
经验证, n=是分式方程4+=4×3的解,
∴点 D 的坐标为(,﹣4).
【解析】【分析】( 1)由边的关系可得出BE=6,通过解直角三角形可得出CE=3,结合函
数图象即可得出点 C 的坐标,再根据点 C 的坐标利用反比例函数图象上点的坐标特征,即
可求出反比例函数系数m,由此即可得出结论;(2)由点 D 在反比例函数在第四象限的
图象上,设出点 D 的坐标为( n,﹣)(n>0).通过解直角三角形求出线段OA 的长
度,再利用三角形的面积公式利用含n 的代数式表示出S△BAF,根据点 D 在反比例函数图
形上利用反比例函数系数k 的几何意义即可得出S△DFO的值,结合题意给出的两三角形的
面积间的关系即可得出关于n 的分式方程,解方程,即可得出n 值,从而得出点 D 的坐标.
7.如图,在平面直角坐标系xOy 中,直线y=kx+b( k≠0)与双曲线y=(m≠0)交于点A
(2,﹣ 3)和点 B(n ,2).
(1)求直线与双曲线的表达式;
(2)对于横、纵坐标都是整数的点给出名称叫整点.动点P 是双曲线y=(m≠0)上的整
点,过点P 作垂直于x 轴的直线,交直线AB 于点 Q,当点P 位于点Q 下方时,请直接写
出整点 P 的坐标.
【答案】(1)解:∵双曲线 y=(m≠0)经过点A( 2,﹣ 3),∴m=﹣6.
∴双曲线的表达式为y=﹣.
∵点 B(n,2)在双曲线y=﹣上,
∴点 B 的坐标为(﹣ 3, 2).
∵直线 y=kx+b 经过点 A( 2,﹣ 3)和点 B(﹣ 3, 2),
∴
解得,
∴直线的表达式为y=﹣x﹣ 1
(2)解:符合条件的点P的坐标是(1,﹣6)或(6,﹣
1).
【解析】【分析】( 1)把 A 的坐标代入可求出 m,即可求出反比例函数解析式,把 B 的坐标代
入反比例函数解析式,即可求出 n,把 A, B 的坐标代入一次函数解析式即可求出
点一次函数解析式;(2)根据图象和函数解析式得出即可.
8.已知抛物线与轴的两个交点间的距离为2.
(1)若此抛物线的对称轴为直线,请判断点(3,3)是否在此抛物线上?
(2)若此抛物线的顶点为(S, t ),请证明;
(3)当时,求的取值范围
【答案】(1)解:抛物线的对称轴为直线,且抛物线与轴的两个交点间的距离
为 2,可得抛物线与轴的两个交点为(0, 0)和( 2, 0),
所以抛物线的解析式为与
当时,
所以点( 3,3)在此抛物线上.
( 2)解:抛物线的顶点为
间的距离为2,
可得抛物线与轴的两个交点为(,则对称轴为直线
,, 0 )和(
,且抛物线与
, 0)
轴的两个交点
所以抛物线的解析式为与
由得
所以;
(3)解:由( 2)知即整理得
由对称轴为直线,且二次项系数
可知当时,b的随a的增大而增大
当 a=10 时,得
当 a=20 时,得
所以当时,
【解析】【分析】( 1)根据已知条件得出两个交点坐标,利用待定系数法求出解析式,然
后验证点( 3,3)是否在这条抛物线上即可;(2)先确定对称轴为直线,再得出与x 轴的两交点坐标为(, 0)和(,0),再利用待定系数法求出解析式的顶点
式可得解;( 3)把 t=-1 代入顶点坐标公式,得到二次函数解析式,根据函数的增减性分别计算a=10 和 20 时 b 的值从而得解 .
9.已知,抛物线的图象经过点,.
(1)求这个抛物线的解析式;
(2)如图1,是抛物线对称轴上一点,连接,,试求出当的值最小时点的坐标;
( 3)如图2,是线段上的一点,过点作轴,与抛物线交于点,若直线把分成面积之比为的两部分,请求出点的坐标.
【答案】( 1)解:将,的坐标分别代入.
得
解这个方程组,得,
所以,抛物线的解析式为
(2)解:如图1,由于点、关于轴对称,所以连接,直线与轴的交点即为所求的点,
由,令,得,
解得,,
点的坐标为,
又,
易得直线的解析式为:.
当时,,
点坐标
(3)解:设点的坐标为,
所以所在的直线方程为.那么,与直线的交点坐标为,与抛物线的交点坐标为.
由题意,得
①,即,
解这个方程,得或(舍去).
②,即,
解这个方程,得或(舍去),
综上所述,点的坐标为,或,.
【解析】【分析】( 1)将点、的坐标代入可得出、的值,继而得出这个抛物线的
解析式;( 2)由于点、关于轴对称,所以连接,直线与轴的交点即为所求
的点,利用待定系数法确定直线的解析式,然后求得该直线与轴的交点坐标即可;( 3 )如图2,交于,设,根据一次函数和二次函数图象上点的坐标特
征,设点的坐标为,,.
然后分类讨论:分别利用或,列关于的方程,然后分别解关于的方程,从而得到点坐标
10.如图,抛物线与轴交于两点(在的左侧),与轴交于点,点与点关于抛物线的对称轴对称.
(1)求抛物线的解析式及点的坐标 :
(2)点是抛物线对称轴上的一动点,当的周长最小时,求出点的坐标 ;
(3)点在轴上,且,请直接写出点的坐标 .
【答案】( 1)解:根据题意得,
解得
抛物线的解析式为
抛物线的对称轴为直线
点与点关于抛物线的对称轴对称
点的坐标为
(2)解:连接
点与点关于抛物线的对称轴对称.
为定值,
即由当的值最小
三点在同一直线上时
解得,
的周长最小
在由当
的左侧,
两点坐标可求得直线
时,
的解析式为
当的周长最小时,点的坐标为
(3)解:点坐标为或
【解析】【分析】( 1)利用待定系数法即可求出n,利用对称性C、 D 关于对称轴对称即可求出点 D 坐标 .( 2) A, P, D 三点在同一直线上时△ PAC的周长最小,求出直线AD 的解析式即可解决问题.(3)分两种情形① 作DQ∥AC交x轴于点Q,此时∠ DQA=∠DAC,满足条件 . ②设线段AD 的垂直平分线交AC 于 E,直线DE 与x 的交点为Q′,此时∠Q′ DA= ′,CAD满足条件,分别求解即可.
11.已知函数
(1)判断该函数的图象与轴的交点个数.
(2)若,求出函数值在时的取值范围.
(3)若方程在内有且只有一个解,直接写出的范围.
【答案】( 1)解:△,当时,图象与轴只有一个交点,当时,图象与轴有两个交点
(2)解:时,,
当时,函数有最小值,
当时,,
故:
(3)解:若方程在内有且只有一个解,
即为和函数只有一个交点,
函数,与轴的交点为:,函数的顶点坐标为:,故在时,
和函数只有一个交点时,或
【解析】【分析】( 1 )△,即可求解;( 2)时,,当时,函数有最小值,当时,,即可求解;( 3 )若方程在
内有且只有一个解,即为和函数只有一个交点,即可求解
12.综合与探究
如图,抛物线的图象经过坐标原点O,且与轴的另一交点为(,0).
(1)求抛物线的解析式;
(2)若直线与抛物线相交于点 A 和点 B(点 A 在第二象限 ),设点 A′是点 A 关于原点 O 的对称点,连接A′B,试判断AA′B的形状,并说明理由;
(3)在问题 (2)的基础上,探究:平面内是否存在点P,使得以点A, B, A′,P 为顶点的四边形是菱形?若存在直接写出点P 的坐标;若不存在,请说明理由.
【答案】( 1)解:∵抛物线 y=x2+bx+c 的图象经过点(0,0)和 (, 0),
∴,
解得:;
∴.
(2)解:AA′B是等边三角形;
∵,
解得:,
∴A(), B(),
过点 A 分别作 AC⊥轴,AD⊥ A′B,垂足分别为C, D,
∴A C= ,OC= ,在 Rt
AOC中
OA=,
∵点 A′与点 A 关于原点对称,
∴A′ (), AA′ =,
∵B(),
∴A′ B=2-(- )=,
又∵ A(), B(),
∴A D= ,BD= ,在 Rt
ABD中
AB=,
∴AA′ =A ′,B=AB
∴Δ AA′B是等边三角形
(3)解:存在正确的点 P,且以点 A、 B、 A′、 P 为顶点的菱形分三种情况;设点 P 的坐标为:( x,y).
①当 A′B为对角线时,有,
解得:,
∴点 P为:;
②当 AB 为对角线时,有,
解得:,
∴点 P为:;
