相似三角形基础测试卷资料
相似三角形测试题及答案(全)

1、两个相似三角形对应边之比是1:5,那么它们的周长比是( )。 (A)
;(B)1:25;(C)1:5;(D)
。 2、如果两个相似三角形的相似比为1:4,那么它们的面积比为( )。 (A)1:16;(B)1:8;(C)1:4;(D)1:2。 3、如图,锐角三角形ABC的高CD和高BE相交于O,则与△DOB相似的三角 形个数是( )。 (A)1;(B)2;(C)3;D)5。
3、如图,△ABC中,D是AC中点,AF∥DE, =1:3,则 =( )。 (A)1:2;(B)2:3;(C)3:4;(D)1:1。 4、如图,平行四边形ABCD中,O1、O2、O3为对角线BD上三点,且BO1= O1O2=O2O3=O3D,连结AO1并延长交BC于点E,连结EO3并延长交AD于F, 则AD:FD等于( )。 (A)19:2;(B)9:1;(C)8:1;(D)7:1。 三、(本题8分) 如图,已知矩形ABCD中,AB=10cm,BC=12cm,E为DC中点,AF⊥BE于 点F,求AF长。 四、(本题8分) 如图,D、E分别是△ABC边AB和AC上的点,∠1=∠2,求证:AD·AB= AE·AC。 五、(本题8分) 如图,ABCD是平行四边形,点E在边BA延长线上,连CE交AD于点F, ∠ECA=∠D,求证:AC·BE=CE·AD。
4、如图,∠ACD=∠B,AC=6,AD=4,则AB=________。
5、如图ABCD是平行四边形,F是DA延长线上一点,连CF交BD于G,交AB 于E,则图中相似三角形(包括全等三角形在内)共有________对。 6、如图,△ABC中,BC=15cm,DE、FG均平行于BC且将△ABC面积分成 三等分,则FG=________ cm。 7、如图,AF∥BE∥CD,AF=12,BE=19,CD=28,则FE:ED的值等于 ________。 8、如图,△ABC,DE∥GF∥BC,且AD=DG=GB,则 =________。
相似三角形基础测试卷.doc
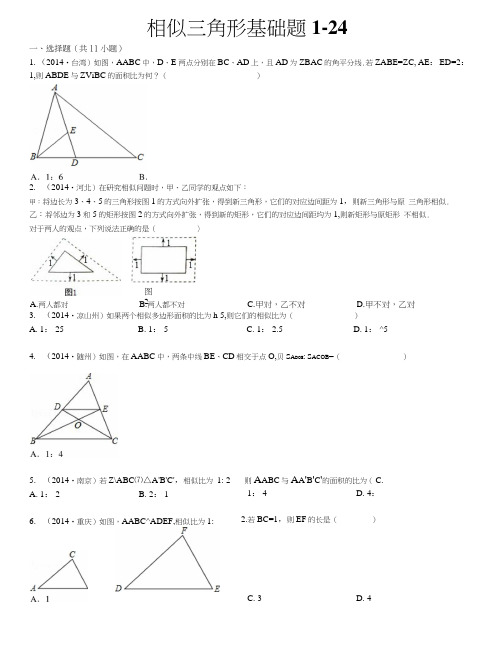
C. 3D. 4相似三角形基础题1-24一、选择题(共11小题)1. (2014•台湾)如图,AABC 中,D 、E 两点分别在BC 、AD 上,且AD 为ZBAC 的角平分线.若ZABE=ZC, AE : ED=2: 1,则ABDE 与ZViBC 的面积比为何?()2. (2014•河北)在研究相似问题时,甲、乙同学的观点如下:甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原 三角形相似.乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形 不相似.对于两人的观点,下列说法正确的是(〉3. (2014•凉山州)如果两个相似多边形面积的比为h 5,则它们的相似比为()A. 1: 25B. 1: 5C. 1: 2.5D. 1: ^54. (2014•随州)如图,在AABC 中,两条中线BE 、CD 相交于点O,贝S A DOE : S ACOB =()A.两人都对图2 B.两人都不对C.甲对,乙不对D.甲不对,乙对5. (2014•南京)若Z\ABC ⑺△A'B'C',相似比为 1: 2 A. 1: 2B. 2: 16. (2014•重庆)如图,AABC^ADEF,相似比为1:则A ABC 与A A 'B 'C '的面积的比为( C.1: 4D. 4:2.若BC=1,则EF 的长是()8. (2014•佛山)若两个相似多边形的而积之比为1: 4,贝它们的周长之比为()A. 1: 4B. 1: 2C. 2: 1D. 4: 19. (2014•包头)如图,在AABC 中,点D,E,F 分别在边AB,AC, BC 上,且DE//BC,EF//AB.若AD=2BD,10. (2014•贵阳)如图,在方格纸中,A ABC和A EPD的顶点均在格点上,要使A ABC〜A EPD,则点P所在的格点为()—r ——n——r- - -i r — -1■r • •• •r ••r ••■一L■Ah ••• •■ -J_ _ _ ’哀• •1■ ••• r ••r ••内将线段AB缩小为原来的1后得到线段CD,则端点C的坐韧为(B. (4, 3)C. (3, 1)D. (4, 1)A. i B- J."2"c•丄1A. P|B. P2C. P3D. P411. (2014•南平)如图,AABC 中,AD、BE 是两条中线,贝U S A EDC:S A A BC=(A. 1: 2B. 2: 3C. 1: 3D. 1: 4二、填空题(共9小题)(除非特别说明,请填准确值)12. (2014•沛县模拟)在平面直角坐标系中,点O为坐标原点,点A的坐标为(3, 4),点B的坐标为(6, 0), D, E分别是线段AO, AB上的点,以DE所在直线力对称轴,把AADE作轴对称变换得AA'DE,点A'恰好在x轴上若ZXOA'D与AOAB相似,则OA'的长为 ___________________________________________ .13.(2014•北京)在某一时刻,测得一根高为1.8m的竹竿的影长为3m,同时测得一根旗杆的影长为25m,那么这根旗杆的高度为________________ m.14.(2014•黔南州)如图,在AABC巾,点D、E分别在AB、AC上,DE//BC.若AD=4, DB=2,则@的值为15. (2014•张家界)如图,AABC中,D、E分别为AB、AC的巾点,则AADE与AABC的而积比为__________________16.(2014•阜新)己知AABC⑺ADEF,其中AB=5,BC=6, CA=9, DE=3,那么ADEF 的周长是______________________ .17.(2014•海南)如图,AD是AABC的高,AE是AABC的外接圆OO的直径,且AB=4^,AC=5,AD=4,则©0的直径AE= ___________ .18. (2014•铁岭)将(n+1)个边长为1的正方形按如图所示的方式排列,点A、Ai、A2、A3、...A n+1和点M、Mn M2、M3, ...M n是正方形的顶点,连结AM H A J M2, A2M3, ...AM n,分别交正方形的边AiM, A2M I,A3M2, ...A n M n -i于点N H N2, N3, ...,N n,叫边形MMAiA]的面积为S P叫边形M2N2A2A3的面积是S2,…四边形M n N n A n A n+119. (2014•牡丹江)在同一时刻两根木竿在太阳光下的影子如图所示,•其屮木竿AB=2m,它的影子BC=1.6m,木竿PQ的影子有一部分落在了墙上,FM=1.2m, MN=0.8m,则木竿PQ的长度为________________________________ m.O II I■I20. (2014•槐荫区二模)正方形ABCD与正方形OEFG中,点D和点F的坐标分别为(-3, 2)和(1, -1),则这两个正方形的位似屮心的坐标为_______________________________ .V AA D0EB CG4A c?三、解答题(共4小题)(选答题,不自动判卷)21. (2014•厦门)如图,在AABC屮,点D, E分别在边AB,AC上,若DE//BC,DE=2, BC=3,求的值.C22. (2014•安徽)如阁,在边长为1个单位长度的小正方形组成的网格屮,给出了格点AABC (顶点是网格线的交点). (1)将AABC向上平移3个单位得到AAiBiCH请画出(2)请画一个格点AA2B2C2,使AA2B2C2⑺AABC,且相似比不为1.23. (2014•南宁)如图,AB//FC, D是AB上一点,DF交AC于点E,DE=FE,分别延长FD和CB交于点G.(1)求证:AADE空ACFE;(2)若GB=2, BC=4, BD=1,求AB 的长.24. (2014•南平)如图,已知AABC中,点D在AC上且ZABD=ZC, 求证:AB2=AD*AC.【章节训练】第27章相似-1参考答案与试题解析一、选择题(共11小题)1. (2014•台湾)如图,AABC 中,D 、E 两点分别在BC 、AD 上,且AD 为ZBAC 的角平分线.若ZABE=ZC, AE : ED=2:1,则ABDE 与Z^ABC 的面积比为何?( )D. 2: 15相似三角形的判定与性质;全等三角形的判定与性质.根掘已知条件先求得S AABE : S ABED =2: 1» PJ 根据三角形相似求得S AACD —SA ABE —S ABED ,根掘S AABC =S AABE +S AACD +S ABED 即⑴求得.解:VAE : ED=2: 1,••AE: AD=2: 3,/ZABE=ZC, ZBAE=ZCAD, ••△ABE ⑺ AACD,'•S AABE : S AACD =4: 9, ••S AACD =~^S AABE ,4••AE: ED=2: 1,••S AABE : S ABED =2: 1, **S AABE =2S ABED »•9 9 •S AACD =—S AABE =—S ABED »42•,S AABC =S AABE +S AACD +S ABED =2S ABED +-^S ABED +S ABED =4^S A 2 2 '•S ABDE : S AABC =2: 15,故选D.本题考查了相似三角形的判定和性质,不同底等高的三角形面积的求法等,等量代换是本题的关键2. (2014•河北)在研究相似问题吋,甲、乙同学的观点如下:甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为丨,则新三角形与原 三角形相似. 乙:将邻边为3和5的矩形按阁2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形 不相似. 对于两人的观点,下列说法正确的是()考点. 分析:解答:点评: B. 1: 9C. 2: 13BED:相似三角形的判定;相似多边形的性质. :数形结合.:甲:根据题意得:AB//A'B', AC//AV, BC//BV,即可证得 ZA=ZA Z , ZB=ZB Z ,可得 AABC ⑺ AA'B'C';乙:根据题意得:AB=CD=3, AD=BC=5,则 A'B'=C'D'=3+2=5, A /D ,=B /C /=5+2=7,则可得、祕、类,如,, A 7D 7即新矩形与原矩形不相似.解答:解:甲:根据题意得:AB//A'B',AC//AV, BC//B'C',A ZA=ZA z , ZB=ZB\ •••△ABC ⑺△A'B'C',.•.甲说法正确;乙:•••根据题意得:AB 二CD=3, AD=BC=5,则 A'B'=C'D'=3+2=5,A'D'=B'C'=5+2=7,> AB _ CD _3 AD _ BC _5 "A y B z :C 、D z A z D z :B z C z > AB AD •*A yD 7/.新矩形与原矩形不相似. •••乙说法正确.故选:A.点评:此题考查了相似三角形以及相似多边形的判定.此题难度不大,注意掌握数形结合思想的应用.3. (2014•凉山州)如果两个相似多边形面积的比为1: 5,则它们的相似比为( )A. 1: 25B. 1: 5C. 1: 2.5D. 1: ^5考点:相似多边形的性质. 专题:计算题.分析:根据相似多边形的面积的比等于相似比的平方解答. 解答:解:Y 两个相似多边形面积的比为h 5,人它们的相似比为1: 故选:D.点评:本题考查了相似多边形的性质,熟记性质是解题的关键.4. (2014•随州)如图,在AABC 中,两条中线BE 、CD 相交于点O,则S ADOE : S ACOB =(A.两人都对图2B.两人都不对C.甲对,乙不对D.甲不对,乙对点题析考专分考点:相似三角形的判定与性质;三角形中位线定理. 专题:计算题.W :根据三角形的屮位线得出DE//BC, DE=^BC,根据平行线的性质得山相似,根据相似三角形的性质求山 2即可.解答:解:YBE 和CD 是AABC 的中线,•••DE=』BC, DE//BC,2••U, A DOE ^A COB , BC 2故选:A.点评:本题考查了相似三角形的性质和判定,三角形的中位线的应用,注意:相似三角形的面积比等于相似比的 平方,三角形的屮位线平行于第三边,并且等于第三边的一半.5. (2014•南京〉若AABC ⑺△ATBX7,相似比为1: 2,则AABC 与AA'B'C'的面积的比为( )A. 1: 2B. 2: 1C. 1: 4D. 4: 1考点:相似三角形的性质.分析:根据相似三角形面积的比等于相似比的平方计算即可得解. 解答:解:•••△ABC ⑺AA'B'C',相似比力1: 2,•••△ABC 与AA'B'C'的面积的比为1: 4.故选:C.点评:本题考查了相似三角形的性质,熟记相似三角形面积的比等于相似比的平方是解题的关键.6. (2014•重庆)如图,AABC ⑺ADEF ,相似比为1: 2.若BC=1,则EF 的长是()考点:相似三角形的性质.分析:根据相似三角形对应边的比等于相似比即可求解. 解答:解:VAABC^ADEF,相似比为1: 2,• BC_1• • --------------------- 9EF 2 AEF=2BC=2.sr -------- A. 1: 4B. 2: 3C. 1: 3D. 1:2^ACOB BC 24故选:B.点评:本题考查了相似三角形的性质:相似三角形对应边的比等于相似比.7. (2014•武汉)如阁,线段AB两个端点的坐标分别为A (6, 6), B (8, 2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的1后得到线段CD,则端点C的坐标为(B. (4, 3)C. (3, 1)D. (4, 1)考点:位似变换;坐标与图形性质.专题:几何图形问题.分析:利用位似图形的性质结合两图形的位似比进而得出C点坐标.解答:解:Y线段AB的两个端点坐标分别为A (6, 6),B (8, 2),以原点O力位似巾心,在第一象限内将线段AB缩小为原来的1后得到线段CD,2端点C的横坐标和纵坐标都变为A点的一半,•••端点C的坐标为:(3, 3).故选:A.8. (2014•佛山)若两个相似多边形的面积之比为1: 4,则它们的周长之比乂J ()A. 1: 4B. 1: 2C. 2: 1D. 4: 1考/X: 分析: 解答: 相似多边形的性质.根据相似多边形的而积之比等于相似比的平方, 解:Y两个相似多边形面积比为1: 4,周长之比等于相似比,就可求解.点评: /.周长之比为2.故选:B.本题考查相似多边形的性质.相似多边形对应边之比、周长之比等于相似比,而面积之比等于相似比的平方.9. (2014•包头)如图,在AABC 中,点D,E,F 分别在边AB, AC, BC 上,且DE//BC, EF//AB.若AD=2BD,则I的值为()平行线分线段成比例.儿何图形问题. 根据平行线分线段成比例定理得出即可得出答案.BD EC CF解:VDE//BC, EF//AB, AD=2BD,• CF_1.. ------------- ,BF 2故选:A.本题考查了平行线分线段成比例定理的应用,注意:一组平行线截两条直线,所截得的对应线段成比例.10. (2014•贵阳)如图,在方格纸屮,AABC 和AEPD 的顶点均在格点上,要使A ABC 〜AEPD,则点P 所在的A. P,B. P 2C. P 3D. P 4考点:相似三角形的判定.专题:网格型. 由于ZBAC=ZPED=90°,而则当时,可根裾两组对应边的比相等且夹角对应相等的两个三角 AC 2 ED 2形相似判断AABC ⑺AEPD,然后利用DE=4,所以EP=6,则易得点P 落在P 3处.解答:解:YZBAOZPED ,而■’AC 2时,A A BC ⑺ZMEPD ,ED 2•••DE:4,AEP=6,.••点P 落在P 3处.故选:C.点评:本题考査了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似.11. (2014•南平)如图,AABC 中,AD 、BE 是两条中线,则 S A EDC : S AABC =(A. 1"2D- 2 1考占. ■j ✓、、、• 专题:分析: 解答: • AD =AE =2 • H 一 AE.BF_2EC CF点评:A. 1: 2B. 2: 3C. 1: 3D. 1: 4考点:相似三角形的判定与性质;三角形中位线定理.分析:在AABC中,AD、BE是两条中线,可得DE是AABC的中位线,即可证得△EDC〜Z\ABC,然后由相似三角形的而积比等于相似比的平方,即可求得答案.解答:解:Y/XABC中,AD、BE是两条中线,••.DE是AABC的屮位线,ADE//AB, DE=^AB,2/.A EDC^A ABC,•••S AEDC:S AABC=(巷)2~- AB 4故选:D.点评:此题考查了相似三角形的判定与性质与三角形中位线的性质.此题比较简单,注意中位线的性质的应用,注意掌握相似三角形的面积的比等于相似比的平方定理的应用是解此题的关键.二、填空题(共9小题)(除非特别说明,请填准确值)12. (2014•沛县模拟)在平面直角坐标系中,点O为坐标原点,点A的坐标为(3, 4〉,点B的坐标为(6, 0), D, E分别是线段AO, AB上的点,以DE所在直线为对称轴,把AADE作轴对称变换得AA'DE,点A'恰好在x轴上若AOA'D与AOAB相似,则OA'的长为延或3 •_11考点:相似三角形的判定与性质;坐标与图形性质;轴对称的性质.专题:压轴题.分析:由点A的坐标为(3, 4),点B的坐标为(6, 0),可得OA=5, OB=6, AB=5,然后分别从△OA'D^AOAB 与A OA'D…A OBA 去分析,根据相似三角形的对应边成比例,即可取得答案.解答:解:Y点A的坐标为(3, 4),点B的坐标为(6, 0),•••OA=5, OB=6,AB=5,若A OA'D⑺ A OAB,'0A OB AB 设AD=x,则OD二5 - x,A'D二OA'=x,解得:X=^, 11••.OA 、=々; 11若 A OA 'D ⑺ A OBA ,' OB OA AB设 AD=AD'=y ,则 OD=5-y ,贝ij y=5 - y ,解得:y=2.5,可得:OA'=3.点评:此题考査了相似三角形的性质与折叠的知识.此题综合性较强,难度较大,注意数形结合与方程思想的应 用,小心别漏解.13. (2014•北京)在某一时刻,测得一根岛为1.8m 的竹竿的影长为3m,同时测得一根旗杆的影长为25m ,那么这 根旗杆的高度为15 m.:相似三角形的应用.:根裾同时同地物髙与影长成正比列式计算即可得解. :解:设旗杆高度为x 米, 由题意得, 3 25 解得x=15. 故答案为:15. 点评:本题考查了相似三角形的应用,主要利用了同时同地物高与影长成正比,需熟记. 14. (2014•黔南州)如图,在AABC 中,点D 、E 分别在AB 、AC 上,DE//BC.若AD=4, DB=2,则^的值为 BC -考点:相似三角形的判定与性质.分析:由AD=3, DB=2,即可求得AB 的长,又由DE//BC ,根据平行线分线段成比例定理,可得DE: BC=AD : AB,则可求得答案.解答:解:VAD=4, DB=2,故答案为:@或3.点析答考分解2—• .AB=AD+BD=4+2=6,VDE//BC,△ADE ⑺A A BC ,/. AD_DE =_4_2?AB BC 6 3故答案力:人 3点评:此题考查Y 平行线分线段成比例定理.此题比较简单,注意掌握比例线段的对应关系是解此题的关键.15. (2014•张家界)如图,AABC 中,D 、E 分别为AB 、AC 的中点,则AADE 与AABC 的面积比为1: 4 .考点:相似三角形的判定与性质;三角形屮位线定理.根据三角形的中位线得出DE=^BC, DE//BC,推出AADEmAABC,根据相似三角形的性质得出即可.2解答:解:YD 、E 分别为AB 、AC 的屮点,/.DE=-BC, DE//BC,2/.A ADE ^A ABC ,• S AADE _ , DE 、2一 1• • ------------- \ ------- ) ------- ,S AABC BC 4 故答案为:1: 4.点评:本题考查了三角形的性质和判定,三角形的中位线的应用,注意:相似三角形的面积比等于相似比的平方.16. (2014•阜新)己知AABC ⑺ADEF ,其中 AB=5,BO6,CA:9, DE=3,那么/^DEF 的周长是 12.:相似三角形的性质.:计算题. :鵬似的性质得即长4然醐比例的性质计算即可. 解答:解:•••△ABC ⑺ADEF , .AABC 的周长_AB m, 5+6+9 _ 5 .*ADEF 的周长、ADEF 的周长 •••△DEF 的周长=12. 故答架为:12.点评:本题考查了相似三角形的性质:相似三角形的对应角相等,对应边的比相等;相似三角形(多边形)的周 长的比等于相似比;相似三角形的对应线段(对应中线、对应角平分线、对应边上的高)的比也等于相似 比.17. (2014•海南)如图,AD 是AABC 的高,AE 是AABC 的外接圆OO 的直径,且AB=4^,AC=5,AD=4,贝lj OO 的直径AE: 5收•点题析 考专分:相似三角形的判定与性质;圆周角定理.:首先根据两个对应角相等可以证明三角形相似,再根据相似三角形的性质得出关于AE 的比例式,计算即可. :解:由圆周角定理可知,ZE=ZC,V ZABE=ZADC=90°, ZE =ZC ,/.A ABE ^A ACD ./.AB : AD=AE : AC,•••AB:4V^,AC 二5,AD=4,/.4V2: 4=AE : 5,/.AE=5V2,故答案为:5^2.点评:本题考查了圆周角定理,相似三角形的性质和判定的应用,解此题的关键是求出AADC 〜A ABE .18. (2014•铁岭)将(n+1)个边长为1的正方形按如图所示的方式排列,点A 、八丨、A 2、A 3、...A n+i 和点M 、M!、 M 2、M 3, ...M n 是正方形的顶点,连结 AM!,A]M 2, A2M3, ...AM n ,分别交正方形的边 A|M, A 2M I ,A 3M 2, ...A n M n -1于点Nn N 2, N 3, N n ,四边形的面积为S H 四边形M 2N 2A 2A 3的面积是S 2,...四边形M n N n A n A n+1考点:相似三角形的判定与性质;正方形的性质.专题:规律型.分析:根据题意得出:△M 1MN 1mAM 1EA ,进而求出MNH 的长,进而得出同理得出S 2,进而得出511的值. 解答:解:由题意可得出:AMiMNi ⑺AMiEA ,EH 7"'A F~1,故MN r 故四边形M J N I A J A O 的面积为S,=l故醐形M 2騎〜的醐是S 2=l十十同理可得出:EH AE 3则四边形雌仏+1麵ws"小故答案为:点评:此题主要考査了相似三角形的判宙与性质以及数字变化规律,得出四边形的面积变化规律是解题关键.19. (2014•牡丹江)在同一时刻两根木竿在太阳光丁的影子如图所示,其中木竿AB=2m,它的影子BC=1.6m,木竿PQ的影子有一部分落在了墙上,PM=1.2m, MN=().8m,则木竿PO的长度为2.3 m.AQN1■11"1 11 I 1 1 1 1 1 11 1I I1 1B C ,P M考点:相似三角形的应用.专题:儿何图形问题.分析:先根据同一时刻物高与影长成正比求出MN的影长,再根据此影长列出比例式即可. 解答:解:解:过N点作ND丄PQ于D,.BC DN ••--~-- ,AB QD又...AB:〕,BC=1.6, PM=1.2, NM=0.8,AQD=^5H=1.5,BC••• PQ=QD+DP=QD+NM= 1.5+0.8=2.3 (米).故答案为:2.3.点评:在运用相似三角形的知识解决实际问题时,要能够从实际问题屮抽象出简单的数学模型,然后列出相关数据的比例关系式,从而求出结论.20. (2014•槐荫区二模)正方形ABCD与正方形OEFG中,点D和点F的坐标分别为(-3, 2)和(1, -1),则这两个正方形的位似中心的坐标为(-1, 0)或(5, -2)..位似变换;坐标与图形性质. 计算题;压轴题.由图形可得两个位似图形的位似中心必在X 轴上,连接AF 、DG,其交点即为位似屮心,进而再由位似比 即可求解位似中心的坐标.解:当位似中心在两正方形之间,连接AF 、DG,交于H,如图所示,则点H 为其位似中心,在x 轴上,Y 点D 的纵坐标为2,点F 的纵坐标为1,•••其位似比为2: 1,•••CH=2HO ,B|J OH=^OC,3又 C ( - 3, 0), •••003,•••OH=1,所以其位似中心的坐标为(-1,0);当位似中心在正方形0EFG 的右侧时,如图所示,连接DE 并延长,连接CF 并延长, 两延长线交于M,过M 作MN 丄x 轴,Y 点D 的纵坐标为2,点F 的纵坐标为1,其位似比为2: 1,••• EF=】DC, BP EF 为AMDC 的中位线,2•••ME 二DE,又ZDEOZMEN ,ZDCE=ZMNE=90O ,/.A DCE ^A MNE ,/. CE=EN=0C+0E=3+1 =4,即 0N=5, MN=DC=2, 则M 坐标为(5, -2),综上,位似中心为:(-1,0)或(5, -2). 故答案为:(_ 1,0)或(5,- 2)AD E%BC 钃 A点评:本题主要考查了位似变换以及坐标与图形结合的问题,能够熟练运用位似的性质求解一些简单的位似计算 问题.三、解答题(共4小题)(选答题,不自动判卷)21'謹•则如图’伽C 中’点D ,。
相似三角形基础测试卷

相似三角形基础题1-24一、选择题(共11小题)1.(2014•台湾)如图,△ABC中,D、E两点分别在BC、AD上,且AD为∠BAC的角平分线.若∠ABE=∠C,AE:ED=2:1,则△BDE与△ABC的面积比为何?()2.(2014•河北)在研究相似问题时,甲、乙同学的观点如下:甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形不相似.对于两人的观点,下列说法正确的是()4.(2014•随州)如图,在△ABC中,两条中线BE、CD相交于点O,则S△DOE:S△COB=()6.(2014•重庆)如图,△ABC∽△DEF,相似比为1:2.若BC=1,则EF的长是()7.(2014•武汉)如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的后得到线段CD,则端点C的坐标为()9.(2014•包头)如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,且DE∥BC,EF∥AB.若AD=2BD,则的值为().C D.10.(2014•贵阳)如图,在方格纸中,△ABC和△EPD的顶点均在格点上,要使△ABC∽△EPD,则点P所在的格点为()11.(2014•南平)如图,△ABC中,AD、BE是两条中线,则S△EDC:S△ABC=()二、填空题(共9小题)(除非特别说明,请填准确值)12.(2014•沛县模拟)在平面直角坐标系中,点O为坐标原点,点A的坐标为(3,4),点B的坐标为(6,0),D,E分别是线段AO,AB上的点,以DE所在直线为对称轴,把△ADE作轴对称变换得△A′DE,点A′恰好在x轴上若△OA′D与△OAB相似,则OA′的长为_________.13.(2014•北京)在某一时刻,测得一根高为1.8m的竹竿的影长为3m,同时测得一根旗杆的影长为25m,那么这根旗杆的高度为_________m.14.(2014•黔南州)如图,在△ABC中,点D、E分别在AB、AC上,DE∥BC.若AD=4,DB=2,则的值为_________.15.(2014•张家界)如图,△ABC中,D、E分别为AB、AC的中点,则△ADE与△ABC的面积比为_________.16.(2014•阜新)已知△ABC∽△DEF,其中AB=5,BC=6,CA=9,DE=3,那么△DEF的周长是_________.17.(2014•海南)如图,AD是△ABC的高,AE是△ABC的外接圆⊙O的直径,且AB=4,AC=5,AD=4,则⊙O 的直径AE=_________.18.(2014•铁岭)将(n+1)个边长为1的正方形按如图所示的方式排列,点A、A1、A2、A3、…A n+1和点M、M1、M2、M3,…M n是正方形的顶点,连结AM1,A1M2,A2M3,…AM n,分别交正方形的边A1M,A2M1,A3M2,…A n M n 于点N1,N2,N3,…,N n,四边形M1N1A1A2的面积为S1,四边形M2N2A2A3的面积是S2,…四边形M n N n A n A n+1﹣1的面积是S n,则S n=_________.19.(2014•牡丹江)在同一时刻两根木竿在太阳光下的影子如图所示,其中木竿AB=2m,它的影子BC=1.6m,木竿PQ的影子有一部分落在了墙上,PM=1.2m,MN=0.8m,则木竿PQ的长度为_________m.20.(2014•槐荫区二模)正方形ABCD与正方形OEFG中,点D和点F的坐标分别为(﹣3,2)和(1,﹣1),则这两个正方形的位似中心的坐标为_________.三、解答题(共4小题)(选答题,不自动判卷)21.(2014•厦门)如图,在△ABC中,点D,E分别在边AB,AC上,若DE∥BC,DE=2,BC=3,求的值.22.(2014•安徽)如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).(1)将△ABC向上平移3个单位得到△A1B1C1,请画出△A1B1C1;(2)请画一个格点△A2B2C2,使△A2B2C2∽△ABC,且相似比不为1.23.(2014•南宁)如图,AB∥FC,D是AB上一点,DF交AC于点E,DE=FE,分别延长FD和CB交于点G.(1)求证:△ADE≌△CFE;(2)若GB=2,BC=4,BD=1,求AB的长.24.(2014•南平)如图,已知△ABC中,点D在AC上且∠ABD=∠C,求证:AB2=AD•AC.【章节训练】第27章相似-1参考答案与试题解析一、选择题(共11小题)1.(2014•台湾)如图,△ABC中,D、E两点分别在BC、AD上,且AD为∠BAC的角平分线.若∠ABE=∠C,AE:ED=2:1,则△BDE与△ABC的面积比为何?()=====S S2.(2014•河北)在研究相似问题时,甲、乙同学的观点如下:甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形不相似.对于两人的观点,下列说法正确的是()∴,∴:4.(2014•随州)如图,在△ABC中,两条中线BE、CD相交于点O,则S△DOE:S△COB=()DE=∴,∴((6.(2014•重庆)如图,△ABC∽△DEF,相似比为1:2.若BC=1,则EF的长是()∴,7.(2014•武汉)如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的后得到线段CD,则端点C的坐标为()后得到线段周长之比为9.(2014•包头)如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,且DE∥BC,EF∥AB.若AD=2BD,则的值为().C D.==∴=2,=2∴,10.(2014•贵阳)如图,在方格纸中,△ABC和△EPD的顶点均在格点上,要使△ABC∽△EPD,则点P所在的格点为(),而=,则当==∴时,11.(2014•南平)如图,△ABC中,AD、BE是两条中线,则S△EDC:S△ABC=()AB.二、填空题(共9小题)(除非特别说明,请填准确值)12.(2014•沛县模拟)在平面直角坐标系中,点O为坐标原点,点A的坐标为(3,4),点B的坐标为(6,0),D,E分别是线段AO,AB上的点,以DE所在直线为对称轴,把△ADE作轴对称变换得△A′DE,点A′恰好在x轴上若△OA′D与△OAB相似,则OA′的长为或3.=,=x=;=,故答案为:13.(2014•北京)在某一时刻,测得一根高为1.8m的竹竿的影长为3m,同时测得一根旗杆的影长为25m,那么这根旗杆的高度为15m.由题意得,=14.(2014•黔南州)如图,在△ABC中,点D、E分别在AB、AC上,DE∥BC.若AD=4,DB=2,则的值为.,∴,故答案为:15.(2014•张家界)如图,△ABC中,D、E分别为AB、AC的中点,则△ADE与△ABC的面积比为1:4.DE=DE=∴(=16.(2014•阜新)已知△ABC∽△DEF,其中AB=5,BC=6,CA=9,DE=3,那么△DEF的周长是12.根据相似的性质得,即,然后利用比例的性质计算即可.∴,即,17.(2014•海南)如图,AD是△ABC的高,AE是△ABC的外接圆⊙O的直径,且AB=4,AC=5,AD=4,则⊙O 的直径AE=5.AB=44AE=518.(2014•铁岭)将(n+1)个边长为1的正方形按如图所示的方式排列,点A、A1、A2、A3、…A n+1和点M、M1、M2、M3,…M n是正方形的顶点,连结AM1,A1M2,A2M3,…AM n,分别交正方形的边A1M,A2M1,A3M2,…A n M n 于点N1,N2,N3,…,N n,四边形M1N1A1A2的面积为S1,四边形M2N2A2A3的面积是S2,…四边形M n N n A n A n+1﹣1的面积是S n,则S n=.=,=××﹣;=,××﹣,﹣.故答案为:19.(2014•牡丹江)在同一时刻两根木竿在太阳光下的影子如图所示,其中木竿AB=2m,它的影子BC=1.6m,木竿PQ的影子有一部分落在了墙上,PM=1.2m,MN=0.8m,则木竿PQ的长度为 2.3m.∴QD==1.520.(2014•槐荫区二模)正方形ABCD与正方形OEFG中,点D和点F的坐标分别为(﹣3,2)和(1,﹣1),则这两个正方形的位似中心的坐标为(﹣1,0)或(5,﹣2)..OCEF=DC三、解答题(共4小题)(选答题,不自动判卷)21.(2014•厦门)如图,在△ABC中,点D,E分别在边AB,AC上,若DE∥BC,DE=2,BC=3,求的值.,然后由相似三角形的对应边成比例,求得∴=.22.(2014•安徽)如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).(1)将△ABC向上平移3个单位得到△A1B1C1,请画出△A1B1C1;(2)请画一个格点△A2B2C2,使△A2B2C2∽△ABC,且相似比不为1.23.(2014•南宁)如图,AB∥FC,D是AB上一点,DF交AC于点E,DE=FE,分别延长FD和CB交于点G.(1)求证:△ADE≌△CFE;(2)若GB=2,BC=4,BD=1,求AB的长.24.(2014•南平)如图,已知△ABC中,点D在AC上且∠ABD=∠C,求证:AB=AD•AC.∴。
三角形相似证明基础50题

33、如图,已知△ABC中,∠ACB=90°,AC=BC,点E、F在AB 上,∠ECF=45°.(1)求证:△ACF∽BEC;(2)设△ABC的面积为S,求 证:AF·BE=2S.
45° A E F B C
34、如图,在ABCD中,过点B作BE⊥CD,垂足为E,连结AE,F为AE上一点,且 ∠BFE=∠C.(1)求证:△ABF∽△EAD;(2)若AB=4,∠BAE=30°,求AE 的长;(3)在(1)(2)的条件下,若AD=3,求BF的长.
CD的中点,△ADQ与△QCP是否相似?为什么?
5、如图,CD是Rt△ABC的斜边AB上的高,∠BAC的平分线分别交 BC、CD于点E、F,AC·AE=AF·AB吗?说明理由。
6、如图,AD是Rt△ABC斜边BC上的高,DE⊥DF,且DE和DF分别交 AB、
7、已知:如图,D是△ABC的边AC上一点,且CD=2AD,AE⊥BC于E, 若BC=13, △BDC的面积是39, 求AE的长。
8、已知:如图,在△ABC中,AB=AC,AD⊥AB,AD交BC于点E, DC⊥BC,与AD交于点D. 求证:AC2=AE·AD.
B C D A E
9、已知:如图,在△ABC中,∠CAB=90°,AD⊥BC于点D,点E是 AC边的中点,ED的延长线与AB的延长线交于点F. 求证:△AFD ∽△DFB.
B C D M N E A
40、如图,等腰三角形ABC中,AB=AC,D为CB延长线上一点,E为BC延长线上 点,且满足AB2=DB·CE. (1)求证:△ADB∽△EAC;(2)若∠BAC=40°,求∠DAE的度数
A B C E D
45、如图ΔABC中,∠C=900, BC = 8cm, AC = 6cm,点P从B出发,沿BC方 向以2cm/s的速度移动,点Q从C出发,沿CA方向以1cm/s的速度移动.若P、 Q分别同时从B、C出发,经过多少时间以C、P、Q为顶点的三角形与以C、 B、A为顶点的三角形相似? 9分
人教版初三数学 相似三角形的判定基础练习题(含答案)

相似三角形的判定(基础)一、选择题1. 下列判断中正确的是( )A. 全等三角形不一定是相似三角形B. 不全等的三角形一定不是相似三角形C. 不相似的三角形一定不全等D. 相似三角形一定不是全等三角形2.已知△ABC的三边长分别为、、2, △A′B′C′的两边长分别是1和, 如果△ABC与△A′B′C′相似, 那么△A′B′C′的第三边长应该是( )A. B. C. D.3.如图,在大小为4×4的正方形网格中,是相似三角形的是().①②③④A.①和②B.②和③C.①和③D.②和④4. 在△ABC和△DEF中,①∠A=35°,∠B=100°,∠D=35°,∠F=45°;②AB=3cm,BC=5cm,∠B=50°,DE=6cm,DF=10cm,∠D=50°;其中能使△ABC与以D、E、F为顶点的三角形相似的条件( )A. 只有①B. 只有②C. ①和②分别都是D. ①和②都不是5.在矩形ABCD中,E、F分别是CD、BC上的点,若∠AEF=90°,则一定有()A.ΔADE∽ΔAEF B.ΔECF∽ΔAEF C.ΔADE∽ΔECF D.ΔAEF∽ΔABF6. 如图所示在平行四边形ABCD中,EF∥AB,DE:EA=2:3,EF=4,则CD的长为( )A. B. 8 C. 10 D. 16二、填空题7. 如图所示,D、E两点分别在AB、AC上且DE和BC不平行,请你填上一个你认为合适的条件___使△ADE∽△ACB.8. 如图所示,∠C=∠E=90°,AD=10,DE=8,AB=5,则AC=________.9. 如图所示,在直角坐标系中有两点A(4,0),B(0,2),如果点C在x轴上(C与A不重合),当点C的坐标为________或________时,使得由点B、O、C组成的三角形与△AOB相似(至少找出两个满足条件的点的坐标).10. 如图,已知AB⊥BD,ED⊥BD,C是线段BD的中点,且AC⊥CE,ED=1,BD=4,那么AB=__________.11. 如图,CD∥AB,AC、BD相交于点O,点E、F分别在AC、BD上,且EF∥AB,则图中与△OEF相似的三角形为____.12.如图,点E是平行四边形ABCD的边BC延长线上一点,连接AE交CD于点F,则图中相似三角形共有_________对.三.解答题13. 如图,在△ABC中,DE∥BC,AD=3,AE=2,BD=4,求的值及AC、EC的长度.14. 如图在梯形ABCD中,AD∥BC,∠A=90°,且,求证:BD⊥CD.15. 已知在Rt△ABC中,∠C=90°,AB=10,BC=6.在Rt△EDF中,∠F=90°,DF=3,EF=4,则△ABC和△EDF相似吗?为什么?【答案与解析】一.选择题1.【答案】C2.【答案】A【解析】根据三边对应成比例,可以确定,所以第三边是3.【答案】C【解析】设方格边长为1,求出每个三角形的各边长,运用三边对应成比例的两个三角形相似的判定方法来确定相似三角形.4.【答案】C5.【答案】C【解析】∵∠AEF=90°, ∴∠1+∠2=90°,又∵∠D=∠C=90°,∴∠3+∠2=90°,即∠1=∠3,∴△ADE∽△ECF.6.【答案】C【解析】∵EF∥AB,∴,∵,∴,,∴CD=10,故选C.二. 填空题7.【答案】∠ADE=∠C或∠AED=∠B或.【解析】据判定三角形相似的方法来找条件.8.【答案】3 .【解析】∵∠C=∠E,∠CAB=∠EAD,∴△ACB∽△AED,∴,BC=4,在Rt△ABC中,.9.【答案】;10.【答案】4【解析】∵AB⊥BD,ED⊥BD,∴∠B=∠D=90°,又∵AC⊥CE,∴∠BCA+∠DCE=90°,∴∠BCA=∠E,∴△ABC∽△CDE.∵C是线段BD的中点,ED=1,BD=4∴BC=CD=2∴,即AB=4.11.【答案】△OAB,△OCD12.【答案】3.【解析】∵平行四边形ABCD,∴AD∥BE.AB∥CD∴△EFC∽△EAB; △EFC∽△AFD; △AFD∽△EAB.三综合题13.【解析】∵DE∥BC,∴△ADE∽△ABC,∵,,∴,∴AC=,∴EC=AC-AE=.14.【解析】∵AD∥BC,∴∠ADB=∠DBC,又∵,∴△ABD∽△DCB,∴∠A=∠BDC,∵∠A=90°,∴∠BDC=90°,∴BD⊥CD.15.【解析】已知△ABC和△EDF都是直角三角形,且已知两边长,所以可利用勾股定理分别求出第三边AC 和DE,再看三边是否对应成比例.在Rt△ABC中,AB=10,BC=6,∠C=90°.由勾股定理得.在Rt△DEF中,DF=3,EF=4,∠F=90°.由勾股定理,得.在△ABC和△EDF中,,,,∴,∴△ABC∽△EDF(三边对应成比例,两三角形相似).。
相似三角形测试卷

初三年级数学相似三角形单元测试卷一、填空题 (每题3分, 满分36分) 1.已知 ,则 ........2. 如图,L1 ∥ L2 ∥L3,AB=4,DF=8,BC=6,则DE= .3. 在比例尺为1∶50000的地图上,图距为4厘米,则实际距离为 千米.4. 如图,△ABC 中,CD 平分∠ACB 交AB 于D,DE ∥BC 交AC 与点E,AC=6,DE=4,则BC= .5. 两相似三角形的面积之比为9∶16,若小三角形的周长为6厘米,则大三角形的周长为 厘米.6. Rt △ABC,∠ACB= ,CD ⊥A 于D,AC=4,AB=5,则AD = .7. 如图,若G 是△ABC 的重心,GD ∥BC,则 ∶ = .8. 如图矩形ABCD 的长和宽分别为2和4,BP ⊥PQ,AP ∶PD=3∶7,则BP ∶PQ= . 9. 如图AB ∥EF ∥CD,AB=2,CD=8,AE ∶EC=1∶5,则EF= .(10题图) (11题图) (12题图) 10. 如图, 已知菱形ADEF, AC=15, AB=10, 则CF= . 11.如图,在梯形ABCD 中,AB ∥CD. ∶ =1∶4.则 ∶ 的值...12. 如图,在矩形ABCD 中,AB=3,BC=4,将矩形折叠,使点C 与点A 重合,则折痕EF= .二、选择题(每题4分, 满分16分)13. 一个三角形的三边长分别为3,4,5,另一个与它相似的三角形中有一条边长为6.则这个三角形的周长不可能是………………………( )(A)572(B) 18 (C) 48 (D) 24 14.已知D.E 分别是△ABC 的AB.AC 上的一点, DE ∥BC, 且 =1: 3, 那么AD: DB等..................... .. )(A )41 (B) 21(C) 1 (D) 3315. 如图,DE ∥BC, DF ∥AC, 则下列比例式中正确的是……………( )(8题图)(9题图)(A) BC DFEC AE =(B) FB CFEC AE =(C) ACDF BC DE =(D) ACECBC FC =16.下列所给条件中, 能判定△ABC ∽△ 的是…( )(A )/////A A CB BC B A AB ∠=∠=, (B )︒=∠︒=∠︒=∠=∠507060//C B A A ,, (C )42/////==∆∆C B A ABC S S CB BC, (D )//B A B A ∠=∠∠=∠, 三、简答题(17.18每题8分, 19、20每题10分, 满分36分)17. 如图,已知AD ∥BE, ,求证:∠C=∠OBD.18. 如图,四边形EFGH 是△ABC 的内接矩形,EF ∶EH=5∶9,若BC=36,高AD=12,求矩形EFGH 的周长。
九年数学下第27章《相似三角形》测试题及答案【基础题】
九年数学下第27章《相似三角形》测试题及答案【基础题】答案在18页图形的放缩与比例线段(1)一、填空题(每小题4分,共40分)1、如果,那么=________。
2、已知:,则=________。
3、与的比例中项是________。
4、对一段长为20cm的线段进行黄金分割,那么分得的较长线段长为________cm。
(不取近似值)5、如图,DE∥BC,AD=1,DB=2,则的值为________。
6、如图,DE∥BC,AB=12,AC=16,AE=10,则AD=________。
7、如图,线段AB=10cm,,,则CD=________cm。
8、已知:线段AB=10cm,点C是AB的黄金分割点,且AC>CB,则BC=_____cm。
(不取近似值)9、如图,AD∥EF∥BC,,DF=4cm,则DC=_______cm。
10、如图,AB∥EF∥DC,AB=,DC=,,则EF=_______。
(用式子表示)二、选择题(每小题4分,共16分)1、若,则下列等式中不正确的是()。
(A);(B);(C);(D)。
2、如图,△ABC中,DE∥BC,则下列等式中不成立的是()。
(A);(B);(C);(D)。
3、如图,△ABC中,DE∥BC,AD=1,EC=3,则下列等式中成立的是()。
(A);(B);(C);(D)。
4、如图,△ABC中,DE∥BC,AD=1,DB=DE=2,则BC长是()。
(A)3;(B)4;(C)5;(D)6。
三、(本题8分)如图,△ABC中,DE∥BC,EF∥AB,,FC=2,AC=6,求DE和CE长四、(本题8分)如图,△ABC中,AD=2DC,G是BD中点,AC延长线交BC于E,求的值。
五、(本题8分)如图,△ABC中,DE∥BC,AH⊥BC于F,AH交DE于G,DE=10,BC=15,AG=12,求线段AH 长。
六、(本题10分)如图,平行四边形ABCD中,E是AB的中点,G是AC上一点,,连EC延长交AD 于F,求的值。
相似三角形测试题及答案
第27章相似三角形测试题一、选择题:(每小题3分共30分)1、下列命题中正确的是()①三边对应成比例的两个三角形相似②二边对应成比例且一个角对应相等的两个三角形相似③一个锐角对应相等的两个直角三角形相似④一个角对应相等的两个等腰三角形相似A、①③B、①④C、①②④D、①③④2、如图,已知DE∥BC,EF∥AB,则下列比例式中错误的是( )A B C D3、如图,D、E分别是AB、AC上两点,CD与BE相交于点O,下列条件中不能使ΔABE和ΔACD相似的是()A. ∠B=∠C B。
∠ADC=∠AEBC. BE=CD,AB=ACD. AD∶AC=AE∶AB4、如图,E是平行四边形ABCD的边BC的延长线上的一点,连结AE交CD于F,则图中共有相似三角形()A 1对B 2对C 3对D 4对5、在矩形ABCD中,E、F分别是CD、BC上的点,若∠AEF=90°,则一定有()A ΔADE∽ΔAEFB ΔECF∽ΔAEFC ΔADE∽ΔECFD ΔAEF∽ΔABF6、如图1,∽,若,则与的相似比是()A.1:2 B.1:3 C.2:3 D.3:27、一个三角形三边的长分别为3,5,7,另一个与它相似的三角形的最长边是21,则其它两边的和是( )A.19 B.17 C.24 D.218、在比例尺为1:5000的地图上,量得甲,乙两地的距离25cm,则甲,乙的实际距离是( )A.1250km B。
125km C。
12。
5km D。
1。
25km9、在相同时刻,物高与影长成正比。
如果高为1。
5米的标杆影长为2。
5米,那么影长为30米的旗杆的高为( )A 20米B 18米C 16米D 15米10、.如图3,小正方形的边长均为1,则图中三角形(阴影部分)与相似的是( )二、填空题: (每小题3分,共,24分)11、已知,则12、两个相似三角形的面积之比为4:9,则这两个三角形周长之比为 。
13、如图,在△ABC 中,D 为AB 边上的一点,要使△ABC ~△AED 成立,还需要添加一个条件为 。
《相似》基础测试题及参考答案(精编)
《相似》基础测试题及参考答案(精编)一、选择题1.下列长度的各组线段中,成比例线段的是 ( ) A.2,3,4,5 B.2,3,4,8 C.2,3,4,7 D.2,3,4,62.在△ABC 和△A 1B 1C 1中,∠A=∠A 1=90°,添加下列条件不能判定两个三角形相似的是 ( ) A.∠B=∠B 1 B.ABA1B 1=ACA1C 1C.ABA1B 1=BCB1C 1D.ABB1C 1=ACA1C 13.如图,在平行四边形ABCD 中,EF//AB,DE:EA=2:3,EF=4,则CD 的长为 ( ) A.163 B.8 C.10 D.16第3题 第4题 第5题 第6题4.如图,AC,BD 相交于点O,AB//DC,M 是AB 的中点,MN//AC,交BD 于点N,若DO:OB=1:2,AC=12,则MN 的长为 ( ) A.2 B.4C.6D.85.如图,在平行四边形ABCD 中,AB=6,BC=9,∠ABC 和∠BCD 的平分线分别交AD 于点E 和点F,BE 与CF 交于点O,则△EFO 与△BCO 的面积之比是 ( ) A.1.3 B.1.9C.2.3D.9.16.如图,在平行四边形ABCD 中,点E 是边AD 上一点,且AE=2ED,EC 交对角线BD 于点F,则EF:FC 的值为 ( ) A.12 B.13 C.23 D.327.若△ABC ∽△DEF,相似比为1:2,则△ABC 与△DEF 的面积比为 ( ) A.1.2 B.1.4 C.2:1 D.4:18.如图,在Rt △ABC 中,∠ACB=90°,CD ⊥AB,若AC=4,AD=2,则AB 的值为 ( ) A.6 B.8 C.9 D.109.如图,AB,CD 相交于点E,且AC//EF//DB,点C,F,B 在同一条直线上,已知AC=p,EF=r,DB=q,则p,q,r 之间满足的数量关系式是 ( )A.1r +1q =1p B.1p +1r =2q C.1p +1q =1r D.1q +1r =2p第8题 第9题 第10题10.如图,在平面直角坐标系中,正方形ABCD 与正方形BEFG 是以原点O 为位似中心的位似图形,相似比为13,点A,B,E 在x 轴上.若正方形BEFG 的边长为6,则点C 的坐标为 ( ) A.(2,2) B.(3,1) C.(3,2) D.(4,2)11.如图,E 是平行四边形ABCD 的边BC 延长线上一点,连接AE,交CD 于点F,连接BF,若CD=3CF,则S △ADF :S △BEF 等于 ( )A.4:1B.3:1C.4:3D.9:412.如图,在△ABC 中,DE//BC 分别交AC,AB 于点D,E,EF//AC 交BC 于点F.若AE BE=25,BF=8,则DE 的长为 ( )A.165B.167C.2D.3第 12题 第 13题 第14题 第15题13.如图,在平行四边形ABCD 中,F 为BC 的中点,延长AD 至点E,使DE:AD=1:3,连接EF 交DC 于点G,则S △DEG :S△CFG为 ( )A.2:3B.3:2C.9:4D.4:914.如图,在△ABC 中,点D,E 分别在边AB,AC 上,下列四个条件:①∠AED=∠B ②DE CB=AE AB③AD AC=AE AB④AD ·BC =DE ·AC.其中能证明△ADE ∽△ACB 的有 ( ) A.1个 B.2个 C.3 个 D.4 个15.如图,在平面直角坐标系中,已知点A(-3,6),B(-9,-3),以原点O 为位似中心,相似比为13,把△ABO 缩小,则点A 的对应点A ’的坐标是 ( )A.(-3,6)B.(-9,18)C.(-9,18)或(9,-18)D.(-1,2)或(1,-2)二、填空题16.如图,在△ABC中,∠ADE=∠B,ADAB =23,则图中的相似三角形为____,其相似比为__.第16题第17题第 18题第19题17.如图,在Rt△ABC中,∠B=90°,D为BC上一点,过点D作DE⊥AC于点E,若BC=12,DECE =512,则AC的长为___.18.如图,在矩形ABCD中,AD=2,AB=4,剪去一个矩形AEFD后,余下的矩形EBCF∽矩形BCDA,则CF的长为___.19.如图,小强用长2米的竹竿CD做测量工具,测量学校旗杆的高度AB,移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面的同一点O.此时,OD=3米,DB=9米,则旗杆AB的高为___米.20.如图,在△ABC中,AB=5,D,E分别是边AC和AB上的点,且∠AED=∠C,若AD·BC=252,则DE的长为____.第20题第21题第 22题21.如图,已知直线l1//l2//l3,直线AC与直线l1,l2,l3分别交于A,B,C三点,直线DF与直线l1,l2,l3分别交于D,E,F三点,AC与DF交于点O.若BC=2OA=2OB,OD=1,则OF的长为____.22.为测量旗杆的高度,小霞的测量方法如下:如图,将直角三角形硬纸板△DEF的斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上,测得DE=0.5m,EF=0.25 m,目测点D到地面的距离DG=1.6m,到旗杆的水平距离DC=18m.按此方法,可计算出旗杆的高度为____m.三、解答题23.如图,在△ABC中,点D,E分别在边AB,AC上,若DE//BC,AD=3,AB=5.求DEBC的值.24.如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.求证:△ADF∽△DEC.25.如图,已知AD·AB=AF·AC,求证:△DEB∽△FEC.26.如图,在矩形ABCD中,E是AD边上一点,连接CE,且AE=CE,O是AC的中点,连接BO并延长交CE于点F.(1)求证:△AEC∽△BOC;的值.(2)若AE=4,BC=6,求S△OFCS△EDC参考答案一、选择题1-5 DDCBB 6-10 BBBCC 11-15 CADBD二、填空题16.△ADE∽△ABC,2317. 1318. 119. 820.5221. 322. 10.6三、解答题23.3524.略25.略26(1)略(2)34。
相似三角形测试题
相似三角形测试题 题目一 已知两个三角形的边长比分别为3:4:5和6:8:10,问这两个三角形是否相似? 解析 两个三角形的边长比相等,即第一个三角形的边长与第二个三角形的边长相等,且对应边的比例相等。即3/6 = 4/8 = 5/10,所以这两个三角形是相似的。
结论 这两个三角形是相似的。 题目二 已知两个三角形的边长比分别为5:12:13和8:15:17,问这两个三角形是否相似?
解析 两个三角形的边长比相等,即第一个三角形的边长与第二个三角形的边长相等,且对应边的比例相等。但是5/8 ≠ 12/15 ≠ 13/17,所以这两个三角形不相似。
结论 这两个三角形不相似。 题目三 已知两个三角形的边长分别为7、24、25和15、20、25,问这两个三角形是否相似?
解析 两个三角形的边长比相等,即第一个三角形的边长与第二个三角形的边长相等,且对应边的比例相等。即7/15 = 24/20 = 25/25,所以这两个三角形是相似的。
结论 这两个三角形是相似的。 题目四 已知两个三角形的边长分别为9、40、41和12、16、20,问这两个三角形是否相似?
解析 两个三角形的边长比相等,即第一个三角形的边长与第二个三角形的边长相等,且对应边的比例相等。但是9/12 ≠ 40/16 ≠ 41/20,所以这两个三角形不相似。
结论 这两个三角形不相似。 题目五 已知两个三角形的边长分别为2、3、4和4、6、8,问这两个三角形是否相似? 解析 两个三角形的边长比相等,即第一个三角形的边长与第二个三角形的边长相等,且对应边的比例相等。即2/4 = 3/6 = 4/8,所以这两个三角形是相似的。
结论 这两个三角形是相似的。 以上是相似三角形的测试题,根据两个三角形的边长比较可以判断它们是否相似。相似的三角形具有相等的边长比例,而不一定是边长相等。在解析过程中,通过对边长比例的比较,可以得出两个三角形是否相似的结论。在实际应用中,相似三角形的性质可以用于解决许多几何问题,例如计算不直接测量的边长或角度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相似三角形基础题1-24 一、选择题(共11小题) 1.(2014•台湾)如图,△ABC中,D、E两点分别在BC、AD上,且AD为∠BAC的角平分线.若∠ABE=∠C,AE:ED=2:1,则△BDE与△ABC的面积比为何?( )
A. 1:6 B. 1:9 C. 2:13 D. 2:15 2.(2014•河北)在研究相似问题时,甲、乙同学的观点如下: 甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似. 乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形不相似. 对于两人的观点,下列说法正确的是( )
A. 两人都对 B. 两人都不对 C. 甲对,乙不对 D. 甲不对,乙对 3.(2014•凉山州)如果两个相似多边形面积的比为1:5,则它们的相似比为( ) A. 1:25 B. 1:5 C. 1:2.5 D. 1:
4.(2014•随州)如图,在△ABC中,两条中线BE、CD相交于点O,则S△DOE:S△COB
=( )
A. 1:4 B. 2:3 C. 1:3 D. 1:2 5.(2014•南京)若△ABC∽△A′B′C′,相似比为1:2,则△ABC与△A′B′C′的面积的比为( ) A. 1:2 B. 2:1 C. 1:4 D. 4:1
6.(2014•重庆)如图,△ABC∽△DEF,相似比为1:2.若BC=1,则EF的长是( )
A. 1 B. 2 C. 3 D. 4 相似三角形基础题1-24 7.(2014•武汉)如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的后得到线段CD,则端点C的坐标为( )
A. (3,3) B. (4,3) C. (3,1) D. (4,1) 8.(2014•佛山)若两个相似多边形的面积之比为1:4,则它们的周长之比为( ) A. 1:4 B. 1:2 C. 2:1 D. 4:1
9.(2014•包头)如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,且DE∥BC,EF∥AB.若AD=2BD,则的值为( )
A. B. C. D. 10.(2014•贵阳)如图,在方格纸中,△ABC和△EPD的顶点均在格点上,要使△ABC∽△EPD,则点P所在的格点为( )
A. P1 B. P2 C. P3 D. P4
11.(2014•南平)如图,△ABC中,AD、BE是两条中线,则S△EDC:S△ABC
=( ) 相似三角形基础题1-24 A. 1:2 B. 2:3 C. 1:3 D. 1:4 二、填空题(共9小题)(除非特别说明,请填准确值) 12.(2014•沛县模拟)在平面直角坐标系中,点O为坐标原点,点A的坐标为(3,4),点B的坐标为(6,0),D,E分别是线段AO,AB上的点,以DE所在直线为对称轴,把△ADE作轴对称变换得△A′DE,点A′恰好在x轴上若△OA′D与△OAB相似,则OA′的长为 _________ .
13.(2014•北京)在某一时刻,测得一根高为1.8m的竹竿的影长为3m,同时测得一根旗杆的影长为25m,那么这根旗杆的高度为 _________ m.
14.(2014•黔南州)如图,在△ABC中,点D、E分别在AB、AC上,DE∥BC.若AD=4,DB=2,则的值为 _________ .
15.(2014•张家界)如图,△ABC中,D、E分别为AB、AC的中点,则△ADE与△ABC的面积比为 _________ . 16.(2014•阜新)已知△ABC∽△DEF,其中AB=5,BC=6,CA=9,DE=3,那么△DEF的周长是 _________ . 17.(2014•海南)如图,AD是△ABC的高,AE是△ABC的外接圆⊙O的直径,且AB=4,AC=5,AD=4,则⊙O的直径AE= _________ . 相似三角形基础题1-24 18.(2014•铁岭)将(n+1)个边长为1的正方形按如图所示的方式排列,点A、A1、A2、A3、…An+1和点M、M1、M2、M3,…Mn是正方形的顶点,连结AM1,A1M2,A2M3,…AMn,分别交正方形的边A1M,A2M1,A3M2,…AnMn
﹣1于点N1,N2,N3,…,Nn,四边形M1N1A1A2的面积为S1,四边形M2N2A2A3的面积是S2,…四边形MnNnAnAn+1的面积是Sn,则Sn= _________ .
19.(2014•牡丹江)在同一时刻两根木竿在太阳光下的影子如图所示,其中木竿AB=2m,它的影子BC=1.6m,木竿PQ的影子有一部分落在了墙上,PM=1.2m,MN=0.8m,则木竿PQ的长度为 _________ m.
20.(2014•槐荫区二模)正方形ABCD与正方形OEFG中,点D和点F的坐标分别为(﹣3,2)和(1,﹣1),则这两个正方形的位似中心的坐标为 _________ .
三、解答题(共4小题)(选答题,不自动判卷) 21.(2014•厦门)如图,在△ABC中,点D,E分别在边AB,AC上,若DE∥BC,DE=2,BC=3,求的值. 相似三角形基础题1-24 22.(2014•安徽)如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点). (1)将△ABC向上平移3个单位得到△A1B1C1,请画出△A1B1C1; (2)请画一个格点△A2B2C2,使△A2B2C2∽△ABC,且相似比不为1.
23.(2014•南宁)如图,AB∥FC,D是AB上一点,DF交AC于点E,DE=FE,分别延长FD和CB交于点G. (1)求证:△ADE≌△CFE; (2)若GB=2,BC=4,BD=1,求AB的长.
24.(2014•南平)如图,已知△ABC中,点D在AC上且∠ABD=∠C, 求证:AB2=AD•AC. 相似三角形基础题1-24 【章节训练】第27章 相似-1 参考答案与试题解析 一、选择题(共11小题) 1.(2014•台湾)如图,△ABC中,D、E两点分别在BC、AD上,且AD为∠BAC的角平分线.若∠ABE=∠C,AE:ED=2:1,则△BDE与△ABC的面积比为何?( )
A. 1:6 B. 1:9 C. 2:13 D. 2:15 考点: 相似三角形的判定与性质;全等三角形的判定与性质. 分析: 根据已知条件先求得S△ABE:S△BED=2:1,再根据三角形相似求得S△ACD=S△ABE=S△BED
,根据
S△ABC=S△ABE+S△ACD+S△BED
即可求得.
解答: 解:∵AE:ED=2:1, ∴AE:AD=2:3, ∵∠ABE=∠C,∠BAE=∠CAD, ∴△ABE∽△ACD, ∴S△ABE:S△ACD=4:9,
∴S△ACD=S△ABE,
∵AE:ED=2:1, ∴S△ABE:S△BED=2:1,
∴S△ABE=2S△BED,
∴S△ACD=S△ABE=S△BED,
∵S△ABC=S△ABE+S△ACD+S△BED=2S△BED+S△BED+S△BED=S△BED,
∴S△BDE:S△ABC=2:15,
故选D. 点评: 本题考查了相似三角形的判定和性质,不同底等高的三角形面积的求法等,等量代换是本题的关键.
2.(2014•河北)在研究相似问题时,甲、乙同学的观点如下: 甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似. 乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形不相似. 对于两人的观点,下列说法正确的是( ) 相似三角形基础题1-24 A. 两人都对 B. 两人都不对 C. 甲对,乙不对 D. 甲不对,乙对 考点: 相似三角形的判定;相似多边形的性质. 专题: 数形结合. 分析: 甲:根据题意得:AB∥A′B′,AC∥A′C′,BC∥B′C′,即可证得∠A=∠A′,∠B=∠B′,可得△ABC∽△A′B′C′;
乙:根据题意得:AB=CD=3,AD=BC=5,则A′B′=C′D′=3+2=5,A′D′=B′C′=5+2=7,则可得,即新矩形与原矩形不相似. 解答: 解:甲:根据题意得:AB∥A′B′,AC∥A′C′,BC∥B′C′, ∴∠A=∠A′,∠B=∠B′, ∴△ABC∽△A′B′C′, ∴甲说法正确;
乙:∵根据题意得:AB=CD=3,AD=BC=5,则A′B′=C′D′=3+2=5,A′D′=B′C′=5+2=7, ∴,,
∴, ∴新矩形与原矩形不相似. ∴乙说法正确. 故选:A.
点评: 此题考查了相似三角形以及相似多边形的判定.此题难度不大,注意掌握数形结合思想的应用. 3.(2014•凉山州)如果两个相似多边形面积的比为1:5,则它们的相似比为( ) A. 1:25 B. 1:5 C. 1:2.5 D. 1:
考点: 相似多边形的性质. 专题: 计算题. 分析: 根据相似多边形的面积的比等于相似比的平方解答. 解答: 解:∵两个相似多边形面积的比为1:5, ∴它们的相似比为1:.
故选:D. 点评: 本题考查了相似多边形的性质,熟记性质是解题的关键.
4.(2014•随州)如图,在△ABC中,两条中线BE、CD相交于点O,则S△DOE:S△COB
=( )
