2020山东女子学院高数期末考试试题
2020年度大学高等数学(下)测试题及答案4

高等数学(下)试题四一、填空题(18分)1 设yxy x f arctan),(=,则=)1,1(df 。
2 曲面1222=++z y x 2在点(2,-2,2)处的切平面方程为 。
3 设{}2,20:),(≤≤≤≤=y x x y x D ,则=⎰⎰-Dy dxdy e 2。
4 如果Γ是从点(1,2,3)到点(0,0,0)的直线段,则=++⎰Γydz x dy y dx x 2233 。
5幂级数∑∞=--11212n n n x 的收敛区间为 。
6以xx e y xe y ==,为特解的二阶线性齐次微分方程为 。
二、选择题(18分)1 在点处),(y x f 可微的充分条件是( )(A )),(y x f 的所有二阶偏导数连续 (B )),(y x f 连续(C )),(y x f 的所有一阶偏导数连续 (D )),(y x f 连续且),(y x f 对y x ,的偏导数都存在。
2 已知222),,(z y x z y x u ++=,则=u ( )(A ){}z y x 2,2,2 (B )222444z y x ++ (C ){}z y x ,, (D ){}1,1,1。
3 设D :4122≤+≤y x ,则=+⎰⎰dxdy y x D22( )(A )dr r d ⎰⎰10220πθ (B )dr r d ⎰⎰41220πθ (C )dr r d ⎰⎰21220πθ (D )dr r d ⎰⎰2120πθ。
4 设L 是圆周:x y x 222-=+的正向,则=-+-⎰dy y x dx y x L)()(33( )(A )π2- (B )0 (C )π3 (D )π2。
5 将函数2)(x ex f -=展开成x 的幂级数得到( )(A )∑∞=02!n nn x (B )∑∞=-02!)1(n n n n x (C )∑∞=0!n n n x (D )∑∞=-0!)1(n n n n x6 函数xx ec e c y -+=21是微分方程( )的通解(A )0''=+y y (B )0''=-y y (C )0'''=+y y (D )0'''=-y y三、 计算与求解(49分)1 设方程z y x z y x 32)32sin(2-+=-+确定函数),(y x z z =,求yz x z ∂∂+∂∂。
2020年全国大学高等数学考试及答案解析
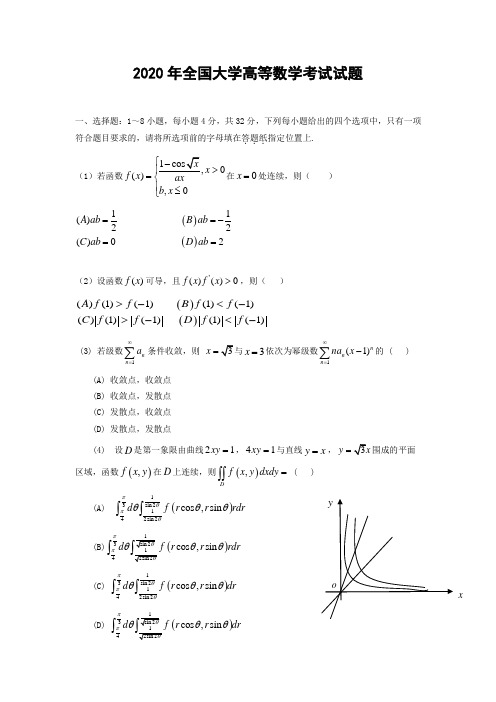
2020年全国大学高等数学考试试题一、选择题:1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求的,请将所选项前的字母填在答题纸...指定位置上. (1)若函数1,0(),0x f x axb x ⎧->⎪=⎨⎪≤⎩在0x =处连续,则( ) ()()11()22()02A abB abC abD ab ==-==(2)设函数()f x 可导,且'()()0f x f x >,则( )()()()(1)(1)(1)(1)()(1)(1)(1)(1)A f fB f fC f fD f f >-<->-<-(3) 若级数1∞=∑nn a条件收敛,则=x 3=x 依次为幂级数1(1)∞=-∑n n n na x 的 ( )(A) 收敛点,收敛点 (B) 收敛点,发散点 (C) 发散点,收敛点 (D) 发散点,发散点(4) 设D 是第一象限由曲线21xy =,41xy =与直线y x =,y =围成的平面区域,函数(),f x y 在D 上连续,则(),Df x y dxdy =⎰⎰ ( )(A)()13sin 2142sin 2cos ,sin d f r r rdr πθπθθθθ⎰⎰(B)()34cos ,sin d f r r rdr ππθθθ⎰(C)()13sin 2142sin 2cos ,sin d f r r dr πθπθθθθ⎰⎰(D)()34cos ,sin d f r r dr ππθθθ⎰x(5)设α是n 维单位列向量,E 为n 阶单位矩阵,则( )()()()()22T T TT A E B E C E D E αααααααα-++-不可逆不可逆不可逆不可逆(6)设矩阵200210100021,020,020*********A B C ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,则( ) ()()(),,(),,A A C B C B A C B C C A C B C D A C B C 与相似与相似与相似与不相似与不相似与相似与不相似与不相似(7) 若A,B 为任意两个随机事件,则 ( )(A) ()()()≤P AB P A P B (B) ()()()≥P AB P A P B (C) ()()()2≤P A P B P AB (D) ()()()2≥P A P B P AB(8)设随机变量,X Y 不相关,且2,1,3===EX EY DX ,则()2+-=⎡⎤⎣⎦E X X Y ( )(A) 3- (B) 3 (C) 5- (D) 5二、填空题:9-14小题,每小题4分,共24分,请将答案写在答题纸...指定位置上. (1) 已知函数21()1f x x=+,则(3)(0)f =__________ (2) 微分方程'''230y y y ++=的通解为y =_________(3) 若曲线积分221L xdx aydy x y -+-⎰在区域{}22(,)|1D x y x y =+<内与路径无关,则 a =__________(4)设Ω是由平面1++=x y z 与三个坐标平面平面所围成的空间区域,则(23)__________.x y z dxdydz Ω++=⎰⎰⎰(5)设二维随机变量(,)x y 服从正态分布(1,0;1,1,0)N ,则{0}________.P XY Y -<=三、解答题:15—23小题,共94分.请将解答写在答题纸...指定位置上.解答应写出文字说明、证明过程或演算步骤. (1)(本题满分10分)设函数(,)f u v 具有2阶连续偏导数,(,cos )xy f e x =,求0x dy dx=,22x d y dx=(2)(本题满分10分)求21lim ln 1nn k kk nn →∞=⎛⎫+ ⎪⎝⎭∑(3)(本题满分10分)已知函数()y x 由方程333320x y x y +-+-=确定,求()y x 的极值(4)(本题满分 10 分)(I )设函数()()u x ,v x 可导,利用导数定义证明u x v x u x v x u x v x '''=+[()()]()()()()(II )设函数()()()12n u x ,u x ,,u x 可导,n f x u x u x u x =12()()()(),写出()f x 的求导公式.(5)(本题满分 10 分)已知曲线L的方程为,z z x ⎧=⎪⎨=⎪⎩起点为()A,终点为()0,B ,计算曲线积分()()2222d d ()d LI y z x z x y y x y z =++-+++⎰.(6) (本题满11分)设向量组1,23,ααα内3R 的一个基,113=2+2k βαα,22=2βα,()313=++1k βαα.(I )证明向量组1β2β3β为3R 的一个基;(II )当k 为何值时,存在非0向量ξ在基1,23,ααα与基1β2β3β下的坐标相同,并求所有的ξ.(7)(本题满分11分)设二次型222123123121323(,,)2282f x x x x x ax x x x x x x =-++-+在正交变换X QY =下的标准型221122y y λλ+,求a 的值及一个正交矩阵Q(8)(本题满分11分)设随机变量,X Y 相互独立,且X 的概率分布为1(0)(2)2P X P X ====,Y 的概率密度为201()0,y y f y <<⎧=⎨⎩,其他()I 求()P Y EY ≤()∏求Z X Y =+的概率密度。
2022年山东女子学院计算机科学与技术专业《计算机组成原理》科目期末试卷A(有答案)

2022年山东女子学院计算机科学与技术专业《计算机组成原理》科目期末试卷A(有答案)一、选择题1、局部性原理是一个持久的概念,对硬件和软件系统的设计和性能都有着极大的影响。
局部性通常有两种不同的形式:时间局部性和空间局部性。
程序员是否编写出高速缓存友好的代码,就取决于这两方面的问题。
对于下面这个函数,说法正确的是()。
int sumvec(int v[N]){int i, sum=0;for(i=0;i<N;i++)sum+= v[i]eturn sum;}A.对于变量i和sum,循环体具有良好的空间局部性B.对于变量i、sum和v[N],循环体具有良好的空间局部性C.对于变量i和sum,循环体具有良好的时间局部性D.对于变量i、sum和v[N],循环体具有良好的时间局部性22、主存按字节编址,地址从0A4000H到0CBFFFH,共有()字节;若用存储容量为32K×8位的存储芯片构成该主存,至少需要()片。
A.80K,2B.96K,2C.160K,5 C.192K,53、某机器字长为8位,采用原码表示法(其中一位为符号位),则机器数所能表示的范围是()。
A.-127~+127B.-127~+128C.-128~+127D.-128~+1284、下列关于各种移位的说法中正确的是()。
I.假设机器数采用反码表示,当机器数为负时,左移时最高数位丢0,结果出错;右移时最低数位丢0,影响精度Ⅱ在算术移位的情况下,补码左移的前提条件是其原最高有效位与原符号位要相同Ⅲ.在算术移位的情况下,双符号位的移位操作中只有低符号位需要参加移位操作()A. Ⅲ、ⅡB.只有ⅡC.只有ⅢD.全错5、设x为整数,[x]补=1.x1x2x3x4x5,若要x<-16,x1~ x5应满足的条件是()。
A. x1~ x5至少有一个为1B.x1必须为1,x2~x5至少有一个为1C.x1必须为0,x2~x5至少有一个为1D.x1必须为0,x2~x5任意6、按数据传送格式,总线常被划分为()。
山东农业大学高等数学期末考试试卷(含答案)

山东农业大学高等数学期末考试试卷(含答案) 一、高等数学选择题
1.设函数,则.
A、正确
B、不正确
【答案】B
2. ( ).
A、
B、
C、
D、
【答案】D
3.设函数,则().
A、
B、
C、
D、
【答案】C
4.设函数,则.
A、正确
B、不正确
【答案】A
5.设,则微分.
A、正确
B、不正确
【答案】B
二、二选择题
6.函数的图形如图示,则是函数的
( ).
A、极小值点也是最小值点
B、极小值点但非最小值点
C、最大值点
D、极大值点
【答案】A
7.是偶函数.
A、正确
B、不正确
【答案】B
8. ( ).
A、
B、
C、
D、
【答案】B
9.设函数,则().
A、
B、
C、
D、
【答案】D
10.函数的定义域为.
A、正确
B、不正确
【答案】A
11..
A、正确
B、不正确
【答案】B
12.设,则.
A、正确
B、不正确
【答案】B
13.不定积分.A、
B、
C、
D、
【答案】B
14.函数在点处连续.
A、正确
B、不正确
【答案】A
15.函数的导数.
A、正确
B、不正确
【答案】B。
2020届山东省烟台市高三上学期期末考试数学试题(PDF版)【附参考答案】

2019-2020学年度第一学期期末学业水平诊断高三数学注意事项:1.本试题满分150分,考试时间为120分钟。
2.答卷前务必将姓名和准考证号填涂在答题纸上。
3.使用答题纸时,必须使用0.5毫米的黑色签字笔书写,要字迹工整,笔迹淸晰。
超出答题区书写的答案无效;在草稿纸、试题卷上答题无效。
一、单项选择题:本题共8小題,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合題目要求的。
1.己知集合A={X|X2-X-2≤0},B={x|y=,则A∪B=A.{x|-l≤x≤2}B. {x|0≤x≤2}C. {x|x≥-l}D. {x|x≥0}2.“x∈R,x2-x+l>0”的否定是A.x∈R, X2-X+1≤0B. x∈R, x2-x+1<0C. x∈R, x2-x+l<0D. x∈R, x2-x+l≤03.若双曲线(a>0,b>0)的离心率为,则其渐近线方程为A. 2x±3y=0B. 3x±2y=0C. x±2y=0D. 2x±y=04.设a=log0.53,b=0.53,c=,则a,b,c的大小关系为A.a<b<cB. a<c<bC. b<a<cD. b<c<a5.为弘扬我国古代的“六艺文化”,某夏令营主办单位计划利用暑期开设“礼”“乐”“射”“御”“书”“数”六门体验课程,每周一门,连续开设六周.若课程“乐”不排在第一周,课程“御”不排在最后一周,则所有可能的排法种数为A. 216B. 480C. 504D. 6246.函数y=|x|+sinx的部分图象可能是7.若x=α时,函数f(x)=3sinx+4cosx取得最小值,则sinα=A. B. C. D.8.函数,若方程f(x)=-2x+m有且只有两个不相等的实数根,则实数m的取值范围是A. (-∞,4)B. (-∞,4]C. (-2,4)D. (-2,4]二、多项选择题:本題共4小题,每小题5分,共20分。
山东省2020年数学高二下学期理数期末考试试卷A卷

山东省2020年数学高二下学期理数期末考试试卷A卷姓名:________ 班级:________ 成绩:________一、一.选择题 (共10题;共20分)1. (2分)(2020·临沂模拟) 已知复数,在复平面内对应的点分别为,,则的共轭复数为()A .B .C .D .2. (2分)(2018·绵阳模拟) 某车间加工零件的数量与加工时间的统计数据如下表:零件数(个)102030加工时间(分钟)213039现已求得上表数据的回归方程中的值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为()A . 84分钟B . 94分钟C . 102分钟D . 112分钟3. (2分)已知曲线的一条切线的斜率为,则切点的横坐标为()A . 3B . 2C . 1D .4. (2分) (2020高二下·新余期末) 已知函数,,,…,,,那么()A .B .C .D .5. (2分) (2020高三上·嵊州期末) 设,随机变量的分布列是-101则当在内变化时,()A . 增大B . 减小C . 先增大后减小D . 先减小后增大6. (2分) (2017高二下·陕西期中) 设(2﹣x)5=a0+a1x+a2x2…+a5x5 ,那么的值为()A . ﹣B . ﹣C . ﹣7. (2分) (2017高二下·遵义期末) 为了研究学生性别与是否喜欢数学课之间的关系,得到列联表如下:喜欢数学不喜欢数学总计男4080120女40140180总计80220300并计算:K2≈4.545P(K2≥k)0.1000.0500.0100.001k 2.706 3.841 6.63510.828参照附表,得到的正确结论是()A . 有95%以上把握认为“性别与喜欢数学课有关”B . 有95%以上把握认为“性别与喜欢数学课无关”C . 在犯错误的概率不超过0.5%的前提下,认为“性别与喜欢数学课有关”D . 在犯错误的概率不超过0.5%的前提下,认为“性别与喜欢数学课无关”8. (2分) (2019高二下·泗县月考) 已知,则()A . 0.6B . 3.6C . 2.16D . 0.2169. (2分) (2017高二下·定西期中) 若A =2A ,则m的值为()A . 5B . 3D . 710. (2分) (2016高三上·湖北期中) 已知函数f(x)= ,若函数y=f(x)﹣4有3个零点,则a的值为()A . 3B . 4C . 5D . 6二、二.填空题 (共5题;共5分)11. (1分)若复数z满足z2﹣z+1=0,则|z|=________12. (1分) (2018高二下·黑龙江期中) 从1,2,3,…,9一共九个数中,任意取出三个数,则这三个数互不相邻的取法有________种.(用数字作答)13. (1分) (2017高二下·西华期中) 已知函数f(x)=x3+ax2+bx(a,b∈R)的图象如图所示,它与直线y=0在原点处相切,此切线与函数图象所围区域(图中阴影部分)的面积为,则a的值为________.14. (1分)(2017·闵行模拟) 一名工人维护3台独立的游戏机,一天内3台需要维护的概率分别为0.9、0.8和0.85,则一天内至少有一台游戏机不需要维护的概率为________(结果用小数表示)15. (1分)在二项式的展开式中,含x5的项的系数是________.三、三.解答题 (共5题;共55分)16. (5分)如果复数z=(其中i为虚数单位,b为实数)的实部和虚部互为相反数.①求z.②求|z|.③负数z在复平面内对应的点在第几象限.④若z(m+i)是纯虚数,求m的值.⑤求()2016 .17. (15分) (2016高二下·曲靖期末) 20名学生某次数学考试成绩(单位:分)的频率分布直方图如图:(1)求频率分布直方图中a的值;(2)分别求出成绩落在[50,60)与[60,70)中的学生人数;(3)从成绩在[50,70)的学生任选2人,求此2人的成绩都在[60,70)中的概率.18. (10分)综合题。
2020年全国大学高等数学考试试题及答案
.
因为 在 可导,且为极值,所以 ,则
.
(3)(本题满分10分)
【解析】显然 为方程一个实根.
当 时,令
.
令 ,
,
即 .
又因为 ,
即当 时, ; 当 时, .
当 时, ;当 时, .
所以当 时, 单调递减,当 时, 单调递增
又由 ,
,
所以当 时,由零点定理可知 在 , 内各有一个零点;
当 时,则 在 , 内均无零点.
(5)若二次曲面的方程 ,经过正交变换化为 ,则 .
(6)设二维随机变量 服从正态分布 ,则 =.
三、解答题:15~23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.
(1)(本题满分10分)
求极限 .
(2)(本题满分9分)
设函数 ,其中函数 具有二阶连续偏导数,函数 可导且在 处取得极值 ,求 .
综上所述,当 时,原方程有三个根.当 时,原方程有一个根.
(4)(本题满分10分)
设奇函数 上具有2阶导数,且 证明:
(III)存在
(IV)存在 ,使得
【解析】(1)令
则 使得
(2)令 则
又由于 为奇函数,故 为偶函数,可知 ,
则 使
即 ,即
(5)(本题满分10分)
设直线L过 两点,将L绕Z轴旋转一周得到曲面 所围成的立体为 ,
又 ,从而 。
(7)设 是随机变量,且 ,
则( )
(A)
(B)
(C)
(D)
【答案】(A)
【解析】由 知,
,
,故 .
由根据 及概率密度的对称性知, ,故选(A)
(8)设随机变量 给定 常数c满足 ,则 ( )
山东省2020年数学高二下学期文数期末考试试卷D卷
山东省2020年数学高二下学期文数期末考试试卷D卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分) (2020高二下·南昌期末) 已知全集为,集合 , ,则()A .B .C .D .2. (2分) (2019高二下·双鸭山期末) 以下四个命题中,真命题的是()A .B . “对任意的”的否定是“存在”C . ,函数都不是偶函数D . 中,“ ”是“ ”的充要条件3. (2分)“”是“”的()A . 充分而不必要条件B . 必要而不充分条件C . 充分必要条件D . 既不充分也不必要条件4. (2分)已知椭圆与双曲线有共同的焦点,,椭圆的一个短轴端点为,直线与双曲线的一条渐近线平行,椭圆与双曲线的离心率分别为,则取值范围为()A .B .C .D .5. (2分)若p是真命题,q是假命题。
以下四个命题① p且q ② p或q ③ 非p ④非q。
其中假命题的个数是()A . 1B . 2C . 3D . 46. (2分) (2016高二下·临泉开学考) 抛物线y2=8x上到其焦点F距离为4的点有()个.A . 1B . 2C . 3D . 47. (2分)(2018·昌吉月考) 若关于的不等式,在上恒成立,,则实数的最大值为()A .B .C .8. (2分)方程+=1的图象表示曲线C,则以下命题中甲:曲线C为椭圆,则1<t<4;乙:若曲线C为双曲线,则t>4或t<1;丙:曲线C不可能是圆;丁:曲线C表示椭圆,且长轴在x轴上,则1<t<.正确的有()A . 1个B . 2个C . 3个D . 4个9. (2分)设曲线在点处的切线与直线平行,则实数等于()A .B .C . 2D .10. (2分)已知函数f(x)=sinx﹣cosx且f′(x)=2f(x),则tanx=()A . -3B . 3C . 1D . -111. (2分) (2020高二上·天津期末) 若抛物线的准线经过双曲线的一个焦点,则()B . 10C .D .12. (2分)定义在R上的可导函数f(x),且f(x)图像连续,当x≠0时, ,则函数的零点的个数为()A . 1B . 2C . 0D . 0或2二、填空题 (共4题;共4分)13. (1分)已知全集U=R,集合A={x|x2﹣2x﹣3>0},则∁UA=________14. (1分) (2019高二上·泉港月考) 已知双曲线的一条渐近线的倾斜角为,且的一个焦点到的距离为,则双曲线的方程为________.15. (1分)(2020·江西模拟) 双曲线上一点P,过双曲线中心O的直线交双曲线于A、B两不同(点A,B异于点P).设直线PA、PB的斜率分别为、,当最小时,双曲线的离心率为________.16. (1分) (2016高一上·德州期中) 下列几个命题:①函数y= + 是偶函数,但不是奇函数;②方程x2+(a﹣3)x+a=0的有一个正实根,一个负实根,则a<0;③f(x)是定义在R上的奇函数,当x<0时,f(x)=2x2+x﹣1,则x≥0时,f(x)=﹣2x2+x+1④函数y= 的值域是(﹣1,).其中正确命题的序号有________.三、解答题 (共5题;共35分)17. (5分) (2016高二下·孝感期末) 已知命题p:方程 =1所表示的图形是焦点在y轴上的双曲线,命题q:复数z=(m﹣3)+(m﹣1)i对应的点在第二象限,又p或q为真,p且q为假,求实数m的取值范围.18. (5分)已知双曲线中心在原点,离心率等于2,且一个焦点坐标为(4,0),求此双曲线方程.19. (10分) (2018高二上·寿光月考) 已知, .(1)求函数的最小值;(2)对一切,恒成立,求实数的取值范围.20. (10分)(2018·广东模拟) 已知椭圆的左焦点与抛物线的焦点重合,椭圆的离心率为,过点作斜率不为0的直线,交椭圆于两点,点,且为定值.(1)求椭圆的方程;(2)求面积的最大值.21. (5分) (2019高二下·哈尔滨月考) 已知曲线 .(Ⅰ) 求曲线在处的切线方程;(Ⅱ) 求曲线过原点的切线方程.四、选做题 (共2题;共10分)22. (5分)(2017·厦门模拟) 已知曲线C的参数方程为(φ为参数),以原点为极点,x轴的非负半轴为极轴建立极坐标系.(Ⅰ)求曲线C的极坐标方程;(Ⅱ)已知倾斜角为135°且过点P(1,2)的直线l与曲线C交于M,N两点,求的值.23. (5分)(2017·深圳模拟) 已知函数f(x)=|x+1﹣2a|+|x﹣a2|,a∈R.(Ⅰ)若f(a)≤2|1﹣a|,求实数a的取值范围;(Ⅱ)若关于x的不等式f(x)≤1存在实数解,求实数a的取值范围.参考答案一、选择题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共5题;共35分)17-1、18-1、19-1、19-2、20-1、20-2、21-1、四、选做题 (共2题;共10分) 22-1、23-1、。
山东省2020年数学高二下学期文数期末考试试卷(I)卷
山东省2020年数学高二下学期文数期末考试试卷(I)卷姓名:________ 班级:________ 成绩:________一、选择题 (共10题;共20分)1. (2分)命题""的否定为()A .B .C .D .2. (2分)(2017·仁寿模拟) 已知双曲线E:﹣ =1(a>0,b>0)的左、右焦点分别为F1、F2 ,|F1F2|=6,P是E右支上一点,PF1与y轴交于点A,△PAF2的内切圆在边AF2上的切点为Q,若|AQ|= ,则E 的离心率是()A . 2B .C .D .3. (2分)(2019·广州模拟) 设是函数的导函数,且,(为自然对数的底数),则不等式的解集为()A .B .C .D .4. (2分) (2019高二下·江西期中) 已知圆:,圆:,是椭圆:的半焦距,若圆,都在椭圆内,则椭圆离心率的范围是()A .B .C .D .5. (2分)命题“存在x0∈R,2≤0”的否定是()A . 不存在x0∈R,2>0B . 存在x0∈R,2≥0C . 对任意的x∈R,2x≤0D . 对任意的x∈R,2x>06. (2分) (2018高二下·葫芦岛期末) 下列结论中正确的是()A . 若两个变量的线性关系性越强,则相关系数的绝对值越接近于0B . 回归直线至少经过样本数据中的一个点C . 独立性检验得到的结论一定正确D . 利用随机变量来判断“两个独立事件的关系”时,算出的值越大,判断“ 有关”的把握越大7. (2分) (2020高二下·武汉期中) 已知复数(其中为虚数单位),则其共轭复数的虚部为()A .B .C .D .8. (2分)用反证法证明命题“+是无理数”时,假设正确的是()A . 假设是有理数B . 假设是有理数C . 假设或是有理数D . 假设+是有理数9. (2分) (2018高二上·齐齐哈尔期中) 抛物线的焦点到准线的距离为()A .B . 1C . 2D . 310. (2分) (2016高二上·吉林期中) 若双曲线的标准方程为 =1,则它的渐近线方程和离心率分别是()A . y=± x,e=B . y=± x,e=C . y=± x,e=D . y=± x,e=二、填空题 (共5题;共5分)11. (1分) (2017高三下·赣州期中) 点P在双曲线﹣ =1(a>0,b>0)的右支上,其左、右焦点分别为F1 , F2 ,直线PF1与以坐标原点O为圆心、a为半径的圆相切于点A,线段PF1的垂直平分线恰好过点F2 ,则该双曲线的渐近线的斜率为________.12. (1分) (2020高二上·贵阳月考) 在下列四个结论中,正确的有________(填序号)① 动点P到两定点AB的距离之差且为常数是P点的轨迹是双曲线的充要条件;② 如果点M 在运动过程中,总满足关系式,则点M的轨迹是椭圆;③ “ ”是“ ”的必要不充分条件;④ 若“ ”是真命题,则实数m的最小值为0.13. (1分)(2012·重庆理) 过抛物线y2=2x的焦点F作直线交抛物线于A,B两点,若,则|AF|=________.14. (1分) (2017高三上·赣州期中) 在△ABC中,a,b,c为∠A,∠B,∠C的对边,a,b,c成等比数列,,则 =________.15. (1分) (2017高三上·南通开学考) 设实数a>1,b>1.则“a<b”是“lna﹣lnb>a﹣b”成立的________条件.(请用“充分不必要”,“必要不充分”,“充要”,“既不充分也不必要”中之一填空.)充要.三、解答题 (共6题;共41分)16. (10分) (2017高二下·长春期末) 已知复数 .(1)若,求z;(2)若z在复平面内对应的点位于第一象限,求a的取值范围.17. (5分)如图,命题“a是平面π内的一条直线,b是π外的一条直线(b不垂直于π),c是直线b在π上的投影,若a⊥b,则a⊥c”.(1)写出上述命题的逆否命题并判断其真假;(2)写出上述命题的逆命题,判断其真假并证明.18. (5分) (2017高二下·原平期末) 设函数,其中,若在上为增函数,求的范围19. (10分) (2020高二上·绵阳期中) 在圆上任取一点,过点作轴的垂线段,为垂足.当点在圆上运动时,线段的中点的轨迹为曲线,直线过点且与曲线交于两点.(1)求的轨迹方程;(2)求面积的最大值.20. (1分)函数f(x)=x2﹣f′(2)x,则f′(2)=________.21. (10分) (2019高一上·杭州期中) 某厂家拟举行双十一促销活动,经调查测算,该产品的年销售量(即该厂的年产量)m万件与年促销费用x万元()满足.已知年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).(1)将该产品的年利润y万元表示为年促销费用x万元的函数;(2)该厂家年促销费用投入多少万元时,厂家的利润最大?参考答案一、选择题 (共10题;共20分)答案:1-1、考点:解析:答案:2-1、考点:解析:答案:3-1、考点:解析:答案:4-1、考点:解析:答案:5-1、考点:解析:答案:6-1、考点:解析:答案:7-1、考点:解析:答案:8-1、考点:解析:答案:9-1、考点:解析:答案:10-1、考点:解析:二、填空题 (共5题;共5分)答案:11-1、考点:解析:答案:12-1、考点:解析:答案:13-1、考点:解析:答案:14-1、考点:解析:答案:15-1、考点:解析:三、解答题 (共6题;共41分)答案:16-1、答案:16-2、考点:解析:答案:17-1、考点:解析:答案:18-1、考点:解析:答案:19-1、答案:19-2、考点:解析:答案:20-1、考点:解析:答案:21-1、答案:21-2、考点:解析:。
山东省2020年数学高二下学期文数期末考试试卷D卷
山东省2020年数学高二下学期文数期末考试试卷D卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分) (2020高二上·湛江期末) 已知命题,,则是().A . ,B . ,C . ,D . ,2. (2分)已知函数f(x)=sinx+ex+x2013 ,令f1(x)=f′(x),f2(x)=f1′(x),f3(x)=f2′(x),…,fn+1=fn′(x),则f2014(x)=()A . sinx+exB . cosx+exC . ﹣sinx+exD . ﹣cosx+ex3. (2分)曲线(t为参数)与x轴的交点坐标是()A . (8,0),(﹣7,0).B . (﹣8,0),(﹣7,0)C . (8,0),(7,0).D . (﹣8,0),(7,0)4. (2分) (2020高二下·上饶期末) 已知是双曲线的左右焦点,过的直线与圆相切,切点T,且交双曲线右支于点,若,则双曲线C的离心率为()A . 2B .C .D .5. (2分)命题;命题若函数为奇函数 , 则函数的图像关于点成中心对称,下列命题正确的是()A . 真B . 真C . 真D . 假6. (2分) (2019高三上·西安月考) 下列说法正确的是()A . 命题“若,则”的否命题是“若,则”B . “ ”是“ ”的必要不充分条件C . 命题“ ”的否定是“ ”D . 命题“若,则”的逆否命题是真命题。
7. (2分)已知函数f(x)=x3+bx的图象在点A(1,f(1))处的切线的斜率为4,则函数g(x)= sin2x+bcos2x 的最大值是()A . 1B . 2C .D .8. (2分) (2016高一上·石家庄期中) 下列根式、分数指数幂的互化中,正确的是()A .B .C . (x,y≠0)D .9. (2分) (2018高二下·黑龙江月考) 已知函数,其导函数的图象如图,则对于函数的描述正确的是()A . 在上为减函数B . 在处取得最大值C . 在上为减函数D . 在处取得最小值10. (2分)极坐标和参数方程(t为参数)所表示的图形分别是()A . 直线、直线B . 直线、圆C . 圆、圆D . 圆、直线11. (2分) (2019高三上·葫芦岛月考) 已知定义在R上的函数满足,且的图象关于点对称,当时,,则()A .B . 4C .D . 512. (2分)(2017·上饶模拟) 设函数f(x)=ex(2x﹣3)﹣ax2+2ax+b,若函数 f(x)存在两个极值点x1 ,x2 ,且极小值点x1大于极大值点x2 ,则实数a的取值范围是()A .B .C .D .二、填空题 (共4题;共4分)13. (1分) (2017高二上·如东月考) 抛物线的准线方程是________.14. (1分) (2020高二下·林州月考) 平面直角坐标系中,若点经过伸缩变换后的点为,则极坐标系中,极坐标为的点到极轴所在直线的距离等于________.15. (1分) (2019高二下·临海月考) 若函数是R上的单调函数,则实数的取值范围是________16. (1分)(2020·鄂尔多斯模拟) 双曲线:的左、右焦点分别为、,是右支上的一点,与轴交于点,的内切圆在边上的切点为,若,则的离心率为________.三、解答题 (共6题;共40分)17. (5分) (2017高三上·南通开学考) 已知命题p:∀x∈[2,4],x2﹣2x﹣2a≤0恒成立,命题q:f(x)=x2﹣ax+1在区间上是增函数.若p∨q为真命题,p∧q为假命题,求实数a的取值范围.18. (5分)已知定点O(0,0),A(3,0),动点P到定点O距离与到定点A的距离的比值是.(Ⅰ)求动点P的轨迹方程,并说明方程表示的曲线;(Ⅱ)当λ=4时,记动点P的轨迹为曲线D.F,G是曲线D上不同的两点,对于定点Q(﹣3,0),有|QF|•|QG|=4.试问无论F,G两点的位置怎样,直线FG能恒和一个定圆相切吗?若能,求出这个定圆的方程;若不能,请说明理由.19. (10分) (2018高二上·浙江月考) 已知抛物线:和:的焦点分别为,交于两点(为坐标原点),且 .(1)求抛物线的方程;(2)过点的直线交的下半部分于点,交的左半部分于点,点坐标为,求△ 面积的最小值.20. (5分) (2017高三上·赣州期中) 某工艺品厂要设计一个如图1所示的工艺品,现有某种型号的长方形材料如图2所示,其周长为4m,这种材料沿其对角线折叠后就出现图1的情况.如图,ABCD(AB>AD)为长方形的材料,沿AC折叠后AB'交DC于点P,设△ADP的面积为S2 ,折叠后重合部分△ACP的面积为S1 .(Ⅰ)设AB=xm,用x表示图中DP的长度,并写出x的取值范围;(Ⅱ)求面积S2最大时,应怎样设计材料的长和宽?(Ⅲ)求面积(S1+2S2)最大时,应怎样设计材料的长和宽?21. (5分) (2019高二上·雨城期中) 椭圆C: (a>b>0)的左、右焦点分别为,离心率为,过焦点且垂直于x轴的直线被椭圆C截得的线段长为1.(Ⅰ)求椭圆C的方程;(Ⅱ)已知点M(0,-1),直线l经过点N(2,1)且与椭圆C相交于A,B两点(异于点M),记直线MA的斜率为,直线MB的斜率为,证明为定值,并求出该定值.22. (10分) (2020高三上·长春月考) 设函数.(1)当时,求函数的单调区间;(2)当时,求证:参考答案一、选择题 (共12题;共24分)答案:1-1、考点:解析:答案:2-1、考点:解析:答案:3-1、考点:解析:答案:4-1、考点:解析:答案:5-1、考点:解析:答案:6-1、考点:解析:答案:7-1、考点:解析:答案:8-1、考点:解析:答案:9-1、考点:解析:答案:10-1、考点:解析:答案:11-1、考点:解析:答案:12-1、考点:解析:二、填空题 (共4题;共4分)答案:13-1、考点:解析:答案:14-1、考点:解析:答案:15-1、考点:解析:答案:16-1、考点:解析:三、解答题 (共6题;共40分)答案:17-1、考点:解析:答案:18-1、考点:解析:答案:19-1、答案:19-2、考点:解析:答案:20-1、考点:解析:答案:21-1、考点:解析:答案:22-1、答案:22-2、考点:解析:。
