2018年广州二模理科数学试题(含详细答案)
2018年高考仿真模拟试题(新课标全国卷ⅡⅢ)理科数学(五)答案

2018年高考仿真模拟试题(新课标全国卷Ⅱ/Ⅲ)理科数学(五)答案1.A 【解析】A ={x |223x x -- 0}={x |−1 x 3},故A ∪B =[−1,4],选A .2.C 【解析】由(1+i)z=2−i ,得z=2i (2i)(1i)13i1i (1i)(1i)2----==++-, 由共轭复数的概念知z =13i 22+. 3.B 【解析】解法一 因为sin α+cos α=15,α是第四象限角,所以sin α=−35,cos α=45, 则tan 2α=sin2cos 2αα=22sin 22sin cos 22ααα=1cos sin αα-=13-. 4.D 【解析】由三视图知,几何体的表面积S =2×12×3×+2×12××该几何体的体积V =13×12×3××=272,设其内切球半径为r ,则V =13×S ×r=272,得rV 球=43πr 3=43.5.B 【解析】14 356=8 251×1+6 105,8 251=6 105×1+2 146, 6 105=2 146×2+1 813, 2 146=1 813×1+333, 1 813=333×5+148, 333=148×2+37,148=37×4+0,此时r =0,输出m 的值为37. 6.B 【解析】通解 设M (0x ,0),由已知可设P (02x ,0y ),因而20y =2p ×02x ,即0y由于△OPM02x ,则0x =4p ,所以P (2p ,±2p ),F (2p,0),从而|PF52p =,故选B . 优解 设P (0x ,0y ),因为△OPM 为等腰三角形,且OP ⊥MP ,因而0x =|0y |,所以20x =2p 0x ,则P (2p ,±2p ),故|PF |=0x +2p =52p ,故选B . 7.C 【解析】由()f x 是奇函数和(2)f x -=()f x 知,()f x 是周期为4的周期函数,且关于直线x =1+2k (k ∈Z)对称,关于点(2k ,0)(k ∈Z)对称, 因此y=()f x 在(−4,2]上的零点分别是1e −4,−2−1e , −2 ,1e −2, −1e ,0 , 1e ,2−1e,2,共9个零点. 8.D 【解析】∵()f x =sin(2x +φcos(2x +φ)=2sin(2x +φ+3π),∴将函数()f x 的图象向左平移4π个单位长度后,得到y =2sin[2(x +4π)+φ+3π]=2cos(2x +φ+3π)的图象.∵该图象关于点(2π,0)对称,对称中心在函数图象上,∴2cos(2×2π+φ+3π)=2cos(π+φ+3π)=0,解得π+φ+3π=k π+2π,k ∈Z ,解得φ=k π−56π,k ∈Z .∵0<φ<π,∴φ=6π.∴()cos()6g x x π=+,∵[,]26x ππ∈-,∴[,]633x πππ+∈-,∴1cos()[,1]62x π+∈,则函数()cos()g x x ϕ=+在[,]26ππ-上的最小值是12.故选D .9.D 【解析】通解 由n a =−1143n n a a --++=−1−113n a -+,得n a +2=1−113n a -+=1123n n a a --++,易知n a ≠−2,所以12n a +−112n a -+=1,所以数列{12n a +}是等差数列,且首项为112a +=2,公差为1,则12n a +=2+(n −1)×1=n +1,n a =11n +−2,99a =1100 −2=−199100. 优解 由1a =−32及n a =−1143n n a a --++,得2a =−342332-+-+=−53,3a =−542532-+-+=−74,……,归纳知,n a =−211n n ++,故99a =−199100,故选D .10.B 【解析】连接DN 并延长交F A 于点P ,连接BP .由△APN ∽△EDN 得,点P 为F A的中点,则23DN DM DP DB ==,∴MN ∥BP ,∴BP 与平面ABCD 所成的角即直线MN 与平面ABCD 所成的角.设AP =1,则AB =4,BPsin ∠PBA.11.D 【解析】由双曲线的定义,知221||||PF PF =211(2||)||a PF PF +=1||PF +214||a PF +4a ,已知点P在双曲线左支上,因而1||PF c −a .①当c −a 2a ,即1<e 3时,由基本不等式得,当且仅当1||PF =2a 时,1||PF +214||a PF +4a 取得最小值8a ,不符合题意;②当c −a >2a ,即e >3时,由于函数y =t +24a t 在[c −a ,+∞)上单调递增,因而当且仅当1||PF =c −a 时,1||PF +214||a PF +4a 取得最小值2()c a c a +-=9a ,即2e −7e +10=0,解得e =5或2,其中e =2舍去,故选D .12.C 【解析】根据题意设y=()f x 上的切点为(1x ,1y ),y=()g x 上的切点为(2x ,2y ),()f x '=−x e −1,()g x '=a −2sin x .根据已知,对任意1x ,存在2x ,使得(−1x e −1)(a −2sin2x )=−1,即2sin 2x =a −111x e +对任意1x ∈R 均有解2x ,故−2 a −111x e + 2对任意1x ∈R 恒成立,则a −2 111x e + 2+a 恒成立.又111x e +∈(0,1),所以2021a a -≤⎧⎨+≥⎩解得−1 a 2,所以实数a 的取值范围是[−1,2].故选C .13.5【解析】因为a =(1,y ),b =(−2,4),且a ⊥b ,所以a ·b =1×(−2)+4y =0,得y =12, 所以2a +b =(2,1)+(−2,4)=(0,5),所以|2a +b |=5.14.2号和3号【解析】若要开启1号阀门,由(i)知,必须开启2号阀门,关闭5号阀门,由(ii)知,关闭4号阀门,由(iii)知,开启3号阀门,所以同时开启2号阀门和3号阀门. 15.[0,1]【解析】由已知作出可行域如图中阴影部分所示,z=1y x+的几何含义为可行域内的点与定点A (0,−1)连线的斜率,其中过A (0,−1),且与函数y=ln x 的图象相切的直线的斜率最大,设y=ln x 图象上点P (0x ,0y )处的切线过A (0,−1),则切线方程为 y−ln 0x =01x (x −0x ),则−1−ln 0x =01x (0−0x ),得0x =1,则PA k =1, 由图易知点A (0,−1)与可行域内的点连线的斜率的最小值为0,因而z=1yx+的取值范围为[0,1].16.22【解析】如图,设AB=AC=a,AD=BD=b,由3BC=2AB得,BC=233a.在△ABC中,由余弦定理得,cos∠ABC=22222223()3322323a aAB BC ACAB BCa a+-+-==⨯⨯⨯⨯,∴∠ABC是锐角,则sin∠ABC=261cos ABC-∠=.在△ABD中,由余弦定理2AD=2AB+2BD−2×AB×BD×cos∠ABD,得2b=2a+2b−2×a×b×3,解得a=23b.解法一由正弦定理sin sinAD ABABD ADB=∠∠sin6aADB=∠,解得sin∠ADB22,又222b a>,∴ADB∠为锐角,∴21cos1sin3ADB ADB∠=-∠=,tan ADB∠=22.解法二由余弦定理得,cos∠ADB=2222AD BD ABAD BD+-⨯=2222123b b ab+-=,∴sin∠ADB221cos3ADB-∠=,tan ADB∠=22.17.【解析】(1)由22a ,4a ,33a 成等差数列可得24a =22a +33a ,即21a 3q =21a q +31a 2q ,又q >1,1a =1,故22q =2+3q ,即22q −3q −2=0,得q =2,(3分) 因此数列{n a }的通项公式为n a =12n -.(4分) (2)n b =2n ×12n -=n ×2n ,(5分)n T =1×2+2×22+3×23+…+n ×2n ①,2n T =1×22+2×23+3×24+...+n ×12n + ②. (7分) ①−②得−n T =2+22+23+ (2)−n ×12n +,−n T =2(21)21n --−n ×12n +,n T =(n −1)×12n ++2.(12分)【备注】数列问题是高考的热点,但是无论怎样命题,肯定少不了考查等差数列与等比数列的基本概念、基本公式,如通项公式、前n 项和公式,同时数列的求和方法(如错位相减法、裂项相消法等)也是考查重点,数列与函数、不等式、方程等知识交汇仍然是这类问题的常见命题规律,但万变不离其宗,在复习备考中只要把数列部分的基础知识落实好,就能在高考中游刃有余,解题时得心应手. 18.【解析】(1)两种抽取方法得到的概率不同.方法一:由于题库中题目总数非常大,可以认为每抽取1个题目,抽到自然科学类题目的概率均为35,抽到文化生活类题目的概率均为25,所以抽取的3个题目中恰好有1个自然科学类题目和2个文化生活类题目的概率为13C ×35 (25)2=36125.(5分)方法二:按照题目类型用分层抽样抽取的10个题目中有6个自然科学类题目和4个文化生活类题目,从这10个题目中抽取3个题目,恰好有1个自然科学类题目和2个文化生活类题目的概率为1264310C C C =310.(5分)(2)由题意得,X 的所有可能取值为0,1,2,3. P (X =0)=111433⨯⨯=136,P (X =1)=311433⨯⨯ +112433⨯⨯+121433⨯⨯=736, P (X =2)=312433⨯⨯ +321433⨯⨯+122433⨯⨯=49,P (X =3)= 322433⨯⨯=13.(10分)所以X 的分布列为X 的数学期望E (X )=0×36+1×36+2×9+3×3=12.(12分)【备注】超几何分布往往会与二项分布混淆,即将超几何分布问题视作二项分布问题.而二项分布需同时满足以下两个条件:(1)在一次试验中,试验结果只有A 与A 两种,而且事件A 发生的概率为p ,事件A 发生的概率为1−p ;(2)试验可以独立重复地进行,即每重复做一次试验,事件A 发生的概率都是p ,事件A 发生的概率都为1−p .19.【解析】(1)在矩形ABCD 中,∵CE =1,AB BC =3,∴tan ∠EDC =CECD tan ∠ACB =AB BC = ∴∠EDC =∠ACB .∵∠DCA +∠ACB =2π, ∴∠EDC +∠DCA =2π,∴∠DHC =2π,∴AC ⊥DE ,∴D H '⊥AC .(3分)又△CHE ∽△AHD ,且CE ∶AD =1∶3, ∴D H '=DH =34DE =32,HE =14DE =12.∵ED '=2,∴2D H '+2HE =2D E ',∴D H '⊥HE . ∵直线AC 与HE 是平面ABC 内的两条相交直线,∴D H '⊥平面ABC .又AE ⊂平面ABC ,∴D H '⊥AE .(5分)(2)建立如图所示的空间直角坐标系H−xyz,则HA=34AC33HC3,于是H(0,0,0),A 33,0,0),E(0,12,0),C3,0,0),D'(0,0,32).(6分)设平面CD E'的法向量为m=(x,y,z),∵CE 312,0),ED '=(0,−12,32),∴EDCE⎧'⋅=⎪⎨⋅=⎪⎩mm,即13223122y zx y⎧-+=⎪⎪⎪+=⎪⎩,令x3,则y=−3,z=−1,则m3−3,−1)为平面CD E'的一个法向量.(9分)又平面D HE'的一个法向量为n=(1,0,0),设二面角H−ED'−C的平面角为θ,则cos θ=||339 ||||1313⋅==m nm n,∴二面角H−ED'−C的余弦值为3913.(12分)【备注】解决图形的翻折问题的关键是了解翻折前后点、线、面之间的位置关系的变化情况.解题时应注意:(1)翻折后,若线与线在同一个平面内,则它们的位置关系不发生任何变化;(2)若翻折后,线与线由在同一个平面内转变为不在同一个平面内,则应注意其位置关系变化的结果;(3)点与点的重合问题及点的位置的变化;(4)利用平面图形解决空间图形中线段的长度及其他量的问题.20.【解析】(1)解法一 设椭圆C 的左、右焦点分别为1F ,2F ,则1F (0),2F,0),由椭圆的定义可得 2a, 解得a,(3分)∴2b =2a −2c =6−3=3.∴椭圆C 的标准方程为22163x y +=. (4分) 解法二 ∵c,∴2a −2b =3,又椭圆22221x y a b +=(a >b >0)过点 T,则有23a +264b=1,故233b ++232b=1,(3分) 化简得24b −32b −9=0,得2b =3,∴2a =6,∴椭圆C 的标准方程为22163x y +=.(4分) (2)设直线l 的方程为x =my +3,P (1x ,1y ),Q (2x ,2y ),当直线AP 的斜率不存在时,直线BP 与椭圆C 相切,不符合题意,同理可得直线AQ 的斜率存在,故直线AP 的方程为y −1=1112y x --(x −2),则M (11121y x y --,0),(5分) 即M (11(2)31m y y ---,0), 直线AQ 的方程为y −1=2212y x --(x −2),则N (22221y x y --,0),即N (22(2)31m y y ---,0).(7分)由223163x my x y =+⎧⎪⎨+=⎪⎩,得(2+2m )2y +6my +3=0,由Δ=362m −12(2+2m )>0得2m >1, 又1y +2y =−262m m +,1y 2y =232m+,(9分)所以|DM |·|DN |=[52−11(2)31m y y ---][52−22(2)31m y y ---]=212121212(12)(12)()14[()1]m y y m y y y y y y +++++-++=2222236(12)(12)()122364(1)22mm m m m m m m+++-+++++++=22223121261224(362)m m m m m m m ++--+++++=22654(65)m m m m ++++=14, 故|DM |·|DN |为定值,且|DM |·|DN |=14.(12分) 21.【解析】(1)函数()f x =ln(x +1)−x +212x ,定义域为(−1,+∞) ,则()f x '=21x x +>0,所以()f x 的单调递增区间为(−1,+∞),无单调递减区间.(3分) (2)由(1)知,当x 0时, 有()f x (0)f =0,即ln(x +1) x −212x .(4分) ()g x '=ln(x +1)+2(a −1)x +212x (x −212x )+2(a −1)x +212x =(2a −1)x .(i)当2a −1 0,即a 12时,且x 0时,()g x ' 0,所以()g x 在[0,+∞)上是增函数,且(0)g =0,所以当x 0时,()g x 0,所以a12符合题意.(6分) (ii)当a <12时,令()g x '=ln(x +1)+2(a −1)x +212x =()x ϕ,()x ϕ'=11x ++2(a −1)+x =2(21)211x a x a x +-+-+, 令2x +(2a −1)x +2a −1=0,则其判别式Δ=(2a −1)(2a −5)>0, 两根1x<0,2x =12(21)(25)a a a -+-->0 ,(9分)当x ∈(0,2x )时,()x ϕ'<0,所以()x ϕ在(0,2x )上单调递减,且(0)ϕ=0,即x ∈(0,2x )时,()g x '<(0)g '=0,()g x 在(0,2x )上单调递减,所以存在0x ∈(0,2x ),使得0()g x <(0)g =0,即当x 0时,()g x 0不恒成立. 所以a <12不符合题意. 综上所述,a 的取值范围为[12,+∞).(12分) 【备注】求解函数、导数、不等式问题时,首先,利用导数求出函数的单调区间,注意函数的定义域;其次,把恒成立问题转化为最值问题求解;最后,用分析法等进行探求,寻找比所证的不等式更精简的不等式,合理构造函数,利用函数的单调性或图象求解. 22.【解析】(1)当tan α=1时,将直线1C 的参数方程化为普通方程为y =x +1.曲线2C 的直角坐标方程为(x −1)2+y 2=1,则曲线2C 是以2C (1,0)为圆心,r =1为半径的圆,则圆心2C 到直线1C 的距离d =2=2>1,所以直线1C 与曲线2C 的位置关系为相离.(5分)(2)由直线1C 的方程可知,直线恒过定点Q (1,2),如图,弦AB 的中点P 满足2C P ⊥QP ,故点P 到2C Q 的中点D (1,1)的距离为定值1.现在考虑极限情况,当直线1C 与圆2C 相切时,切点分别记为E ,F ,则可得E (1312),F 3,12). 则点P 的轨迹的普通方程为(x −1)2+(y −1)2=1(y <12),P 的轨迹为一段圆弧.(10分)23.【解析】(1)因为()f x =16,2124,126,1x x x x x x ⎧--⎪⎪⎪+-<<⎨⎪⎪⎪⎩≤≥, 所以()f x 在(−∞,−12]上单调递减,在(−12,+∞)上单调递增, 所以m =()f x min =f (−12)=3.(5分) (2)因为a ,b ,c 是正数,则1a ,1b ,1c 也是正数, 所以111a b c ++=>0,当且仅当a =b =c 时取等号. 又a +b +c,故(111a b c ++)(a +b +c ), 又a +b +c =m =3, 所以111a b c ++ 9a b c ++=3,即111a b c ++ m . (10分)。
2018年高考仿真模拟试题(新课标全国卷ⅡⅢ)理科数学(一)答案

2018年高考仿真模拟试题(新课标全国卷Ⅱ/Ⅲ)理科数学(一)本试卷分必考和选考两部分.必考部分一、选择题:本题共12小题,每小题5分,在每小题给出的四个选项中,只有一项符合题目要求的.1.设全集U =R ,A ={x |2x −2x >0},B ={x |y =1x -错误!未找到引用源。
},则A ∪U B ð=A .(2,+∞)B .(−∞,0)∪(2,+∞)C .(−∞,1)∪(2,+∞)D .(−∞,0) 2.若(1+i)z =2,则|z |=A .2B .3C .2D .13.已知()f x 是定义在R 上的偶函数,且满足(4)f x +=()f x ,当x ∈[−2,0]时,()f x =−2x,则(1)f +(4)f 等于 A .32 B .−32C .−1D .1 4.执行如图所示的程序框图,则输出y 的值是A .6B .8C .10D .125.已知点x ,y 满足约束条件2024020x y x y x +-⎧⎪-+⎨⎪-⎩≥≥≤错误!未找到引用源。
,则z =3x +y 的最大值与最小值之差为A .5B .6C .7D .86.已知命题p :存在n ∈R ,使得()f x =22n nnx+是幂函数,且在(0,+∞)上单调递增; 命题q :“∃x ∈R ,2x +2>3x ”的否定是“∀x ∈R ,2x +2<3x ”.则下列命题为真命题的是 A .p ∧q B .¬p ∧q C .p ∧¬q D .¬p ∧¬q7.早在公元前三百多年我国已经运用“以度审容”的科学方法,其中商鞅铜方升是公元前344年商鞅督造的一种标准量器,其三视图如图所示(单位:寸),若π取3,其体积为12.6(立方寸),则图中的x 为A .1.2B .1.6C .1.8D .2.4 8.如图,已知P ,Q 是函数()f x =A sin(ωx +φ)(A >0,ω>0,|φ|<2π)的图象与x 轴的两个相邻交点,R 是函数()f x 的图象的最高点,且RP RQ ⋅u u u r=3,若函数()g x 的图象与()f x 的图象关于直线x =1对称,则函数()g x 的解析式是A .()g x =3sin(错误!未找到引用源。
2018年全国高考理科数学试题及答案-广东002 精品

试卷类型:A2018年普通高等学校招生全国统一考试(广东卷)数学(理科)本试题共4页,21小题,满分150分,考试用时120分钟。
注意事项:1、答卷前,考生务必用黑色自己的钢笔或签字笔将自己的姓名、和考生号、试室号、座位号,填写在答题卡上。
用2B 铅笔将试卷类型(A )填涂在答题卡相应位置上。
将条形码横贴在答题卡右上角“条形码粘贴处”。
2、选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案。
答案不能答在试卷上。
3、非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求做大的答案无效。
4、作答选做题时,请先用2B 铅笔填涂选做题的题号对应的信息点,再做答。
漏涂、错涂、多涂的,答案无效。
5、考生必须保持答题卡得整洁。
考试结束后,将试卷和答题卡一并交回。
参考公式:柱体的体积公式V=Sh 其中S 为柱体的底面积,h 为柱体的高线性回归方程 y bx a =+ 中系数计算公式 其中,x y 表示样本均值。
N 是正整数,则()n n a b a b -=-12(n n a a b --++…21n n ab b --+)一、选择题:本大题共8小题,每小题5分,满分40分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 设复数z 满足()12i z +=,其中i 为虚数单位,则z = A .1i + B. 1i - C. 22i + D.22i -2.已知集合(){,A x y = ∣,x y 为实数,且}221x y +=,(){,B x y =,x y 为实数,且}y x =,则A B ⋂的元素个数为A.0 B.1 C.2 D.33. 若向量a,b,c满足a∥b且a⊥b,则(2)c a b ∙+=A.4 B.3 C.2 D.04. 设函数()f x 和()g x 分别是R上的偶函数和奇函数,则下列结论恒成立的是 A.()()f x g x +是偶函数 B.()()f x g x -是奇函数 C.()()f x g x +是偶函数 D.()()f x g x -是奇函数5. 在平面直角坐标系xOy 上的区域D由不等式组02x y x ⎧≤≤⎪≤⎨⎪≤⎩给定。
广州市第二中学2018 学年第一学期期中考高二年级理科数学卷答案

广州市第二中学2018 学年第一学期期中考 高二年级理科数学试卷参考答案 2018.11.81.D2. B3.A4.B5.C6.B7.A8.B9.D 10.B 11.C 12.D1.【解析】由240x -≥得22x -≤≤,由10x ->得1x <,故{|22}{|1}{|21}A B x x x x x x =-≤≤<=-≤<,选D.2.3.解:甲=>乙, 乙≠>甲45. 22.5,160,x y ==则160422.570,a =-⨯=当24x =时,ˆ42470y=⨯+166=,选C.6. 选B. 解:12l l ⊥13102121-==⇔=+⇔a a B B A A 或 7. 【解析】由题意得,其中,所以,又,所以,所以,,由得,故选A . 8.【答案】B9.10. 根据程序可知P 为频率,它趋近于在边长为1的正方形中随机取一点落在扇形内的的概率41412πππ=⨯⨯125282118k k ωϕωϕππ⎧+=π+⎪⎪⎨π⎪+=π⎪⎩12,k k ∈Z 2142(2)33k k ω=--22T ωπ=>π01ω<<23ω=11212k ϕ=π+πϕ<π12ϕπ=第11题0a b <<,且()()f a f b =即ba b a b a 110|lg ||lg |=<<<∴=且 )(122b f b b b a =+=+∴,3)1()(1),22[)(=>∴>+∞f b f b b f 上递增,而在,所以选C 第12题法二:二、填空题:(本大题共4小题,每小题5分, 共20分)13. 答1,1,3,3 14.答15.4321<<a . 16.答93213. 解:平均数和中位数都是2,标准差s=1得方差s 2=1,484)2()2()2()2(4324321242322212=+=+++=-+-+-+-=∴x x x x x x x x x x s ,,四个数都为正整数,由方差知各数与2差不超过2,只可能为1,2,3,4由后式知可知中间两数只能为1,3或者2,2,代入前式可知四个数只能为1,1,3,314.【解析】设正方体的边长为,则,故这个球的体积. 15.()y f x =在区间)0,1(-及)21,0(内各有一个零点充要条件是 (1)0(0)01()02f f f ⎧⎪->⎪<⎨⎪⎪>⎩ 即340120304a a a ⎧⎪->⎪-<⎨⎪⎪->⎩, 解得4321<<a .92πa 2618a a =⇒=23R ==34π3V R ==4279ππ382⨯=16. [解析] 设小王到校的时间为x ,小张到校的时间为y ,(x ,y )可以看成平面中的点.法二 :三、解答题(要求写出必要的过程与理由说明,17题10分,18~22各12分,共70分) 17.解:(1)因为13n S +是6与2n S 的等差中项,所以1626n n S S ++=(*N n ∈),即1311+=+n n S S ,(*N n ∈) ……………1分由此得)23(31213123)131(231-=-=-+=-+n n n n S S S S (*N n ∈), …………3分又21232311-=-=-a S ,所以3123231=--+n n S S (*N n ∈), ……………4分 所以数列}23{-n S 是以21-为首项,31为公比的等比数列. ……………5分(2)由(1)得1)31(2123-⨯-=-n n S ,即1)31(2123--=n n S (*N n ∈),……………6分所以,当2≥n 时,121131])31(2123[])31(2123[----=---=-=n n n n n n S S a ,又1=n 时,11=a 也适合上式, 所以)(31*1N n a n n ∈=-…8分n a b n n -==∴1log 3 , {}n b 是首项为0,公差为1-的等差数列 …………9分2)(2)(1n n b b n T n n -=+=∴1 …………10分18.【答案】.......6分.........12分19.解法一:(I )融合指数在内的“省级卫视新闻台”记为,,;融合指数在内的“省级卫视新闻台”记为,.从融合指数在和内的“省级卫视新闻台”中随机抽取家的所有基本事件是:,,,,,,,,,,共个. ................3分其中,至少有家融合指数在内的基本事件是:,,,,,,,,,共个.所以所求的概率. .........................6分 (II )频率分布直方图如下:......................9分[]7,81A 2A 3A [)4,51B 2B [)4,5[]7,82{}12,A A {}13,A A {}23,A A {}11,A B {}12,A B {}21,A B {}22,A B {}31,A B {}32,A B {}12,B B 101[]7,8{}12,A A {}13,A A {}23,A A {}11,A B {}12,A B {}21,A B {}22,A B {}31,A B {}32,A B 9910P =据此估计这家“省级卫视新闻台”的融合指数平均数等于=x . ........................12分解法二:(I )融合指数在内的“省级卫视新闻台”记为,,;融合指数在内的“省级卫视新闻台”记为,.从融合指数在和内的“省级卫视新闻台”中随机抽取家的所有基本事件是:,,,,,,,,,,共个.其中,没有家融合指数在内的基本事件是:,共个.所以所求的概率. (II )同解法一.20.(1)证明:连结11B D ,BD ,因为四边形1111A B C D 是正方形,所以1111AC B D ⊥. (...1分) 在正方体1111ABCD A B C D -中,1DD ⊥平面1111A B C D , 11AC ⊂平面1111A B C D ,所以111AC DD ⊥. (...2分)因为1111B D DD D =,11B D ,1DD ⊂平面11BB D D ,所以11AC ⊥平面11BB D D . (...3分)因为EF ⊂平面11BB D D ,所以11EF AC ⊥. (......4分) (2)解:取1C C 的中点H ,连结BH ,由正方体易知. 在平面11BB C C 中,过点F 作,则. 连结EG ,则A ,E ,G ,F 四点共面. (...7分)因为11122CH C C a ==,11133HG BF C C a ===, 所以1C G 116C C CH HG a =--=. 故当1C G 16a =时,A ,E ,G ,F 四点共面. (......8分)(3)如图,在面AA 1B 1B 内作FH//AB,因正方体中D D AA FH D D AA AB 1111面面⊥∴⊥D D AA 11面内作AE HM ⊥于E ,连结FM , 由三垂线定理知 AE FM ⊥ 则FMH ∠为面AEF 与D D AA 11面所成二面角的平面角.................................................................10分侧D D AA 11面为正方形,所以AHM∆EAD ∆ 2028734.5 5.5 6.57.5 6.0520202020⨯+⨯+⨯+⨯=[]7,81A 2A 3A [)4,51B 2B [)4,5[]7,82{}12,A A {}13,A A {}23,A A {}11,A B {}12,A B {}21,A B {}22,A B {}31,A B {}32,A B {}12,B B 101[]7,8{}12,B B 11911010P =-=1D A BCDEF 1A1B1C 1DA BCDEF 1A1B 1CG H所以=HM AH AD EA ,而,,2⊥==∴a AD DE DE AD a AE 3//,//a BF AH BF AH FH AB ==∴HM ∴=2cos 7HF HM MF HM FMH MF ⊥∴==∴∠==即平面AEF 与平面D D AA 11所成锐二面角的余弦值27.........................12分法二(向量法)以A 为原点O ,AB ,AD ,AA 1 分别为x,y,z 轴建立空间坐标系 则A(0,0,0), (0,,),(,0,0),(,0,)23aa E a B a F a ,11(0,0,),(,,)A a C a a a(1) 1111(,,0),(,,)()0()066aa AC a a EF a a AC EF a a a a ==--∴⋅=⨯+⨯-+⨯-= 11EF AC ∴⊥(2) G 在CC 1上可设CG=m, (,,),(0,,),(0,,)32a aG a a m FG a m AE a ∴=-=正方体相对侧面平行,所以A ,E ,G ,F 四点共面155//32666a a a a aAE FG AE FG m CG m C G a λ⇔⇔=∴-=∴==∴=-=.(3) 设(,,)n x y z =为平面AEF 的一个法向量,则002(2,3,6)003a n AE ay z n a n AF ax z ⎧⋅=++=⎪⎪∴=-⎨⎪⋅=++=⎪⎩可取 正方体中1111(,0,0)AB AAD D AAD DAB a ⊥∴=侧面侧面的一个法向量为 设平面AEF 与平面D D AA 11所成锐二面角为θ,则2cos |cos ,|7n AB n AB n ABθ⋅=<>==⋅(每小题各4分,方法公式一半分,计算结果一半分)21.解:⑴ 二次函数中0≠a设]1,1[,sin -∈∴∈=s R x x s ,若(sin )f x (x R ∈)的最大值为54即关于S 的二次函数s as s g +=2)(在区间上有最大值54, 由二次函数图象性质可知此最大值只能是)21(),1(),1(ag g g --之一........2分 若49451)1(-=⇒=--=-a a g ,此时二次函数开口向下且对称轴]1,1[9221-∈=-=a s ,函数在区间上最大值在顶点处取得,不是)1(-g ,不合题意;若41451)1(=⇒=+=a a g ,此时二次函数开口向上且对称轴1221-<-=-=as ,最大值是 )1(-g ,符合题意若151()245g a a -=⇒=-,此时二次函数开口向下且对称轴15[1,1]22s a =-=∉-,并不在顶点处有最大值,不符合题意 综上所述14a =. ...............6分 ⑵对于任意的R x ∈,总有|(sin cos )f x x |1≤,令111sin cos sin2[,]222t x x x ==∈-,则命题转化为11[,]22t ∀∈-,不等式|()|1f t ≤恒成立, ……………………7分当0t =时,()0f t =使()1f t ≤成立;当0t ≠时,有222211111241111124a t t t a t t t ⎧⎛⎫≤-=--⎪ ⎪⎪⎝⎭⎨⎛⎫⎪≥--=-++ ⎪⎪⎝⎭⎩ 对于任意的11[,0)(0,]22t ∈-恒成立; …………………………..10分1111[,0)(0,]2222t t t ∈-∴≥≤-或,则2111()224t --≥,故要使①式成立,则有2a ≤,又2111()224t -++≤-,故要使②式成立,则有2a ≥-,由题设知0a ≠.综上,[2,0)(0,2]a ∈-⋃为所求。
2018广州广东实验初三二模(电子版有答案)

广东实验中学2017—2018学年(下)初三级毕业班综合测试(二)注意:1.考试时间为120分钟.满分为110分。
2.试卷分为第Ⅰ卷(选择题)与第Ⅱ卷(非选择题)两部分。
3.选择题答案必须用2B铅笔在答题卡对应题号答题框内填涂,非选择题需在问卷指定位置作答。
第I卷(选择题)共75分一、语法选择(共15题, 每小题1分,满分15分)阅读下面短文,按照句子结构的语法性和上下文连贯性的要求,从各题所给的A、B、C和D项中选出最佳选项。
One's attitude is always important. If you are lazy and weak, you will never taste any success. But if you are____1____, success and happiness will be more likely to come to you.I love eating persimmons (柿子). But you can't get them until autumn. If you try them before the right time, they probably____2____bad.In Grade 9, because of my poor grades, my parents were worried that I wouldn't be able to get into____3____ excellent high school. They pushed me to study harder, but I didn't really understand ____4____ they were so anxious.Summer came, and I studied hard. The hot weather made me____5____ sleepy and I couldn't focus on my textbooks. But every time I wanted to stop____6____, Mom would shout, "Hey you! Think about your future, if you don't work hard, you'll regret it!" I had to sit back down again and return to my textbooks____7____ were full of words. But all I thought about was playing ____8____my friends and eating persimmons.My mom would say to me, with a serious look on____9____face, "If a persimmon tree doesn't grow in summer, it can't bear ____10____ fruit in autumn! Only by hard work can you get the good result of your work."Although I didn't understand it at that time, I____11____came to see the truth of her words. A few months later, I succeeded in getting into the key high school. It was autumn.Walking in my new school, I could see quite a few persimmon trees. It was ____12____ a red fruit that it looked as if it was on fire. Suddenly, I realized that working hard____13____ be bitter but its fruit is sweet.My mom was right, if a persimmon tree doesn't grow during summer, it can't bear fruit in autumn. I smiled. I had grown through the summer____14____now it was autumn. The fruits of my labors could ____15____ by me now!( ) 1. A. work hard B. working hardly C. hardly work D. hardworking( ) 2. A. tasted B. taste C. tastes D. have tasted( ) 3. A. a B. an C. the D. /( ) 4. A. what B. how C. why D. that( ) 5. A. feeling B. to feel C. felt D. feel( ) 6. A. to work B. working C. work D. worked( ) 7. A. whose B. who C. what D. which( ) 8. A. about B. to C. with D. on( ) 9. A. her B. hers C. herself D. she( ) 10. A. hundred B. hundreds of C. hundreds D. two hundreds( ) 11. A. graduation B. gradual C. gradually D. graduated( ) 12. A. very B.so C. such D. too( ) 13. A. may B. should C. must D. need to( ) 14. A. and B. however C. or D. so( ) 15. A. be enjoyed B. enjoy C. enjoying D. enjoyed二、完形填空(共10题, 每小题1.5分,满分15分)阅读下面短文,掌握其大意,然后从各题所给的A、B、C和D项中,选出最佳选项。
2018年(理科数学)(新课标Ⅱ)试卷真题+参考答案+详细解析
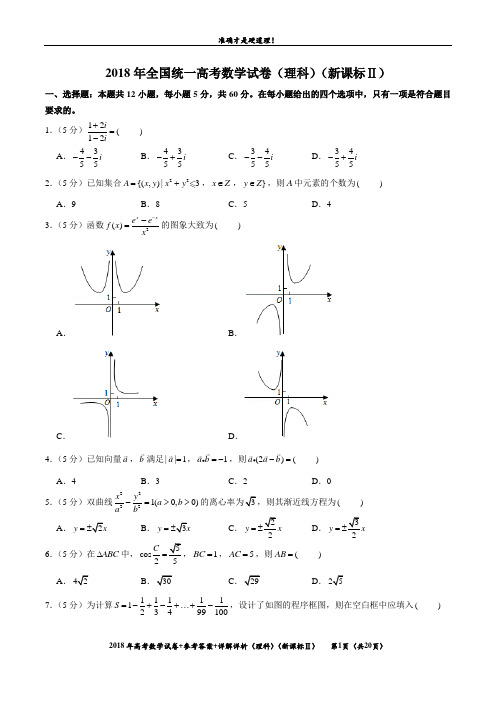
2018年全国统一高考数学试卷(理科)(新课标Ⅱ)一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(5分)12(12ii+=- ) A .4355i --B .4355i -+C .3455i --D .3455i -+2.(5分)已知集合22{(,)|3A x y x y =+,x Z ∈,}y Z ∈,则A 中元素的个数为( ) A .9B .8C .5D .43.(5分)函数2()x x e e f x x--=的图象大致为( ) A . B .C .D .4.(5分)已知向量a ,b 满足||1a =,1a b =-,则(2)(a a b -= ) A .4B .3C .2D .05.(5分)双曲线22221(0,0)x y a b a b-=>>3( )A .2y x =B .3y x =C .2y = D .3y = 6.(5分)在ABC ∆中,5cos 2C =,1BC =,5AC =,则(AB = ) A .42B 30C 29D .257.(5分)为计算11111123499100S =-+-+⋯+-,设计了如图的程序框图,则在空白框中应填入( )A .1i i =+B .2i i =+C .3i i =+D .4i i =+8.(5分)我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如30723=+.在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是( ) A .112B .114C .115D .1189.(5分)在长方体1111ABCD A B C D -中,1AB BC ==,13AA =,则异面直线1AD 与1DB 所成角的余弦值为( )A .15B 5C 5D 210.(5分)若()cos sin f x x x =-在[a -,]a 是减函数,则a 的最大值是( )A .4πB .2π C .34π D .π11.(5分)已知()f x 是定义域为(,)-∞+∞的奇函数,满足(1)(1)f x f x -=+,若(1)2f =,则(1)(2)(3)(50)(f f f f ++++= )A .50-B .0C .2D .5012.(5分)已知1F ,2F 是椭圆2222:1(0)x y C a b a b+=>>的左、右焦点,A 是C 的左顶点,点P 在过A 且斜3的直线上,△12PF F 为等腰三角形,12120F F P ∠=︒,则C 的离心率为( ) A .23 B .12 C .13 D .14二、填空题:本题共4小题,每小题5分,共20分。
2018年广东高考(理科)数学试题及答案
2018年普通高等学校招生全国统一考试(全国一卷)理科数学一、选择题:(本题有12小题,每小题5分,共60分。
) 1、设z=,则∣z ∣=( )A.0B. 12 C.1 D. √2 2、已知集合A={x|x 2-x-2>0},则C R A =( ) A 、{x|-1<x<2} B 、{x|-1≤x ≤2} C 、{x|x<-1}∪{x|x>2} D 、{x|x ≤-1}∪{x|x ≥2}3、某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番,为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例,得到如下饼图:则下面结论中不正确的是( )A. 新农村建设后,种植收入减少B. 新农村建设后,其他收入增加了一倍以上C. 新农村建设后,养殖收入增加了一倍D. 新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半4、记S n 为等差数列{a n }的前n 项和,若3S 3 = S 2+ S 4,a 1 =2,则a 5 =( ) A 、-12 B 、-10 C 、10 D 、125、设函数f (x )=x ³+(a-1)x ²+ax .若f (x )为奇函数,则曲线y= f (x )在点(0,0)处的切线方程为( )A.y= -2xB.y= -xC.y=2xD.y=x6、在∆ABC 中,AD 为BC 边上的中线,E 为AD 的中点,则EB→ =( ) A. 34 AB → - 14 AC → B. 14 AB → - 34 AC → C. 34 AB→ +14AC → D. 14 AB → + 34 AC→7、某圆柱的高为2,底面周长为16,其三视图如右图。
圆柱表面上的点M 在正视图上的对应点为A ,圆柱表面上的点N 在左视图上的对应点为B ,则在此圆柱侧面上,从M 到N 的路径中,最短路径的长度为( )A. 2√17B. 2√5C. 3D. 28.设抛物线C :y ²=4x 的焦点为F ,过点(-2,0)且斜率为23的直线与C 交于M ,N 两点,则FM → ·FN→ =( ) A.5 B.6 C.7 D.8 9.已知函数f (x )=g (x )=f (x )+x+a ,若g (x )存在2个零点,则a 的取值范围是( )A. [-1,0)B. [0,+∞)C. [-1,+∞)D. [1,+∞)10.下图来自古希腊数学家希波克拉底所研究的几何图形。
2018年新课标2卷高考数学试卷文档解析版(理科)
2018年新课标2卷高考数学试卷文档解析版(理科)2018年全国统一高考数学试卷(理科)(新课标Ⅱ)一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(5分)=()A.i B. C. D.【解答】解:==+.故选:D.2.(5分)已知集合A={(x,y)|x2+y2≤3,x∈Z,y∈Z),则A中元素的个数为()A.9 B.8 C.5 D.4【解答】解:当x=﹣1时,y2≤2,得y=﹣1,0,1,当x=0时,y2≤3,得y=﹣1,0,1,当x=1时,y2≤2,得y=﹣1,0,1,即集合A中元素有9个,故选:A.3.(5分)函数f(x)=的图象大致为()A.B.C.D.【解答】解:函数f(﹣x)==﹣=﹣f(x),则函数f(x)为奇函数,图象关于原点对称,排除A,当x=1时,f(1)=e﹣>0,排除D.当x→+∞时,f(x)→+∞,排除C,故选:B.4.(5分)已知向量,满足||=1,=﹣1,则?(2)=()A.4 B.3 C.2 D.0【解答】解:向量,满足||=1,=﹣1,则?(2)=2﹣=2+1=3,故选:B.5.(5分)双曲线=1(a>0,b>0)的离心率为,则其渐近线方程为()A.y=±x B.y=±x C.y=±x D.y=±x【解答】解:∵双曲线的离心率为e==,则=====,即双曲线的渐近线方程为y=±x=±x,故选:A.6.(5分)在△ABC中,cos=,BC=1,AC=5,则AB=()A.4 B. C. D.2【解答】解:在△ABC中,cos=,cosC=2×=﹣,BC=1,AC=5,则AB====4.故选:A.7.(5分)为计算S=1﹣+﹣+…+﹣,设计了如图的程序框图,则在空白框中应填入()A.i=i+1 B.i=i+2 C.i=i+3D.i=i+4【解答】解:模拟程序框图的运行过程知,该程序运行后输出的是S=N﹣T=(1﹣)+(﹣)+…+(﹣);累加步长是2,则在空白处应填入i=i+2.故选:B.8.(5分)我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如30=7+23.在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是()A.B.C.D.【解答】解:在不超过30的素数中有,2,3,5,7,11,13,17,19,23,29共10个,从中选2个不同的数有=45种,和等于30的有(7,23),(11,19),(13,17),共3种,则对应的概率P==,故选:C.9.(5分)在长方体ABCD﹣A1B1C1D1中,AB=BC=1,AA1=,则异面直线AD1与DB1所成角的余弦值为()A.B.C.D.【解答】解:以D为原点,DA为x轴,DC为y轴,DD1为z 轴,建立空间直角坐标系,∵在长方体ABCD﹣A1B1C1D1中,AB=BC=1,AA1=,∴A(1,0,0),D1(0,0,),D(0,0,0),B1(1,1,),=(﹣1,0,),=(1,1,),设异面直线AD1与DB1所成角为θ,则cosθ===,∴异面直线AD1与DB1所成角的余弦值为.故选:C.10.(5分)若f(x)=cosx﹣sinx在[﹣a,a]是减函数,则a的最大值是()A.B.C. D.π【解答】解:f(x)=cosx﹣sinx=﹣(sinx﹣cosx)=,由,k∈Z,得,k∈Z,取k=0,得f(x)的一个减区间为[,],由f(x)在[﹣a,a]是减函数,得,∴.则a的最大值是.故选:A.11.(5分)已知f(x)是定义域为(﹣∞,+∞)的奇函数,满足f(1﹣x)=f (1+x),若f(1)=2,则f(1)+f(2)+f(3)+…+f(50)=()A.﹣50 B.0 C.2 D.50【解答】解:∵f(x)是奇函数,且f(1﹣x)=f(1+x),∴f(1﹣x)=f(1+x)=﹣f(x﹣1),f(0)=0,则f(x+2)=﹣f(x),则f(x+4)=﹣f(x+2)=f(x),即函数f(x)是周期为4的周期函数,∵f(1)=2,∴f(2)=f(0)=0,f(3)=f(1﹣2)=f(﹣1)=﹣f(1)=﹣2,f(4)=f(0)=0,则f(1)+f(2)+f(3)+f(4)=2+0﹣2+0=0,则f(1)+f(2)+f(3)+…+f(50)=12[f(1)+f(2)+f(3)+f(4)]+f(49)+f(50)=f(1)+f(2)=2+0=2,故选:C.12.(5分)已知F1,F2是椭圆C:=1(a>b>0)的左、右焦点,A是C的左顶点,点P在过A且斜率为的直线上,△PF1F2为等腰三角形,∠F1F2P=120°,则C的离心率为()A.B.C.D.【解答】解:由题意可知:A(﹣a,0),F1(﹣c,0),F2(c,0),直线AP的方程为:y=(x+a),由∠F1F2P=120°,|PF2|=|F1F2|=2c,则P(2c,c),代入直线AP:c=(2c+a),整理得:a=4c,∴题意的离心率e==.故选:D.。
(完整word版)2018年全国2卷理科数学试卷及答案
2018年普通高等学校招生全国统一考试全国2卷数学(理科)4.已知向量a, b 满足,a 1 , a b 1,则a 2a b ( )12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是复合题目要求的。
,1 2i1.()1 2iA4 3. r 4 3.A._l B.-l 5 5552.已知集合 Ax , y 2 2 一 X y <3,x Z ,A . 9B . 8C . 3 4.— 3 4i D .—5 55 5y Z ,则A 中元素的个数为()C . 5D . 4、选择题:本题共e xe x3•函数f X -2—的图象大致是( )XA . 4B .3 2 25.双曲线—2^7a1 a >0 , b >0的离心力为A . y2xB . y 3x6 .在 A ABC 中, C5 cos —25BC 1, ACA . 4.2B. 、30C . 2D ..3,则其渐近线方程为()C 曇C . yx 2D .3 y—25,贝U AB =()C .29D .2 52 1 34&我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是1117 •为计算S 1 1 112 3 4图,1 99 1100设计了右侧的程序框则在空白框中应填入( )A. i i 1B. i i 2C. i i 3D.i i 4每个大于2的偶数可以表23 •在不超过 30的素数中,随机选取两个不同的数,其和等于30 的概率是()A.—12B.—14C .1 15D .丄189.在长方体 ABCD AB 1G D 1中,AB BC 1 , AA 3,则异面直线 AQ 与DB 1所成角的余弦值为 A.-B VC VD.565210.若 f xcosx sin x 在 a , a疋减函数,则a 的取大值疋()A .B.—C . 3D .42411.已知 f x 是定义域为, 的奇函数,满足 f 1 X ' f 1 x .若f 12,则f 1f 2 f 3f 50 ()A . 50B . 0C . 2D.50斜率为—的直C .()2 212 •已知F 1 , F 2是椭圆C : X 2 占1 a > b >0的左、右焦点交点, A 是C 的左顶点,点P 在过A 且 a b二、填空题,本题共4小题,每小题5分,共20分.13.曲线y 21 n x 1在点0, 0处的切线方程为 __________________ .x 2y 5》014 •若x , y满足约束条件x 2y 3>0,则z x y的最大值为 __________________ .x 5<015 .已知sin cos 1 , cos sin 0 ,贝U sin __________ .16. 已知圆锥的顶点为S,母线SA, SB所成角的余弦值为 -,SA与圆锥底面所成角为45 .若8△SAB的面积为5 15,则该圆锥的侧面积为____________ .三、解答题:共70分,解答应写出文字说明、证明过程或演算步骤。
(完整word版)2018全国高考II卷理科数学试题及答案解析(2),推荐文档
绝密★启用前2018年普通咼等学校招生全国统考试理科数学注意事项:1. 答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2. 作答时,将答案写在答题卡上。
写在本试卷及草稿纸上无效。
3. 考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1 4-2i1.1 21[4引4 3r 3 4 3 4lA. -------- 1 --- b C. : D.-7 +5 5 5 5 5]>【答案】D【解析】分析:根据复数除法法则化简复数,即得结果详解:'•.选D.1-21 5 5点睛:本题考查复数除法法则,考查学生基本运算能力2. 已知集合厂「..厂•「则中元素的个数为A. 9B. 8C. 5D. 4【答案】A【解析】分析:根据枚举法,确定圆及其内部整点个数详解:选入九/冬久E乙"X- - l,0j|,当b = 时,[;:'■ ■」.丨当卜■取时,当 b ■-〕时,f所以共有9个,选A.点睛:本题考查集合与元素关系,点与圆位置关系,考查学生对概念理解与识别3. 函数心、的图像大致为A B C DA. AB. BC. CD. D【答案】B【解析】分析:通过研究函数奇偶性以及单调性,确定函数图像-谑异畑为奇函数,舍去A,详解:x2r (亡"亠亡K)x1-(e x-e K)2X (x-2)e x + (x + 2)e_li r,所以舍去C;因此选B.点睛:有关函数图象识别问题的常见题型及解题思路(1)由函数的定义域,判断图象左右的位置,由函数的值域,判断图象的上下位置;②由函数的单调性,判断图象的变化趋势;③由函数的奇偶性,判断图象的对称性;④由函数的周期性,判断图象的循环往复.4. 已知向量,卜满足用i,则且“『通-心;:TA. 4B. 3C. 2D. 0【答案】B【解析】分析:根据向量模的性质以及向量乘法得结果详解:因为 a -(坯 & - - b -加'-(-】) 2+1-3.所以选B.点睛:向量加减乘:.-'■: I、m. ■ I -i ;•- :■■ ;;. I:2 25. 双曲线的离心率为|门|,则其渐近线方程为A. \qB.” ■ 土占羞c.\一r\y 三土—x D.2y = i —x£【解析】分析:根据离心率得 a,c 关系,进而得 a,b 关系,再根据双曲线方程求渐近线方程,得结果详解:b" c"-a"r b jr- c -1 ■ 3 - 1 ■ 2 " - ■ J2,2口口M,所以渐近线方程为.,选A.【答案】A【解析】分析:先根据二倍角余弦公式求 cosC,再根据余弦定理求 AB.详解:因为 所以? -- 1 亠 25-2 1 ■ ?,选 A.点睛:解三角形问题,多为边和角的求值问题, 这就需要根据正、余弦定理结合已知条件灵活转化边和角 之间的关系,,设计了下面的程序框图,则在空白框中应填入因为渐近线方程为ya 2b 32 2Kv b 0 刊■ ± -x . ? a A.卜同 B. .. C.D.I 11 1A. B.【解析】分析:根据程序框图可知先对奇数项累加,偶数项累加,最后再相减 •因此累加量为隔项•详解:由得程序框图先对奇数项累加,偶数项累加,最后再相减•因此在空白框2 3 499 100中应填入厂帀,选B.点睛:算法与流程图的考查,侧重于对流程图循环结构的考查•先明晰算法及流程图的相关概念,包括选择结构、循环结构、伪代码,其次要重视循环起点条件、循环次数、循环终止条件,更要通过循环规律,明 确流程图研究的数学问题,是求和还是求项8.我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果. 哥德巴赫猜想是“每个大于 2的偶数可以表示为两个素数的和”,如 卜迓;(•在不超过30的素数中,随机选取两个不同的数,其和 等于30的概率是 1 1 1 1A.B.C. D.12】41518【答案】C【解析】分析:先确定不超过 30的素数,再确定两个不同的数的和等于 30的取法,最后根据古典概型概率公式求概率•详解:不超过30的素数有2, 3, 5, 7, 11, 13, 17, 19, 23, 29,共10个,随机选取两个不同的数,共 有减 f 种方法,因为773 ■ I 「旧 戸丄17-30,所以随机选取两个不同的数,其和等于30的有3种3 r方法,故概率为R-,选C.禎 15点睛:古典概型中基本事件数的探求方法:(1)列举法• (2)树状图法:适合于较为复杂的问题中的基本事件的探求•对于基本事件有“有序”与“无序”区别的题目,常采用树状图法 • (3)列表法:适用于多元素 基本事件的求解问题,通过列表把复杂的题目简单化、抽象的题目具体化 • (4)排列组合法:适用于限制条件较多且元素数目较多的题目9.在长方体卩•,飞•匸|中,卜庶■段打■ :.|,啟卸「.讯 则异面直线 与所成角的余弦值为5| |6【答案】C【解析】分析:先建立空间直角坐标系,设立各点坐标,利用向量数量积求向量夹角,再根据向量夹角与 线线角相等或互补关系求结果详解:以D 为坐标原点,DA,DC,DD 为x,y,z 轴建立空间直角坐标系,贝U ',所以血1麻Db 广(1丄间,A.B. C. D.因为. . 土,所以异面直线与 所成角的余弦值为IADJIDBJ 2 忻 5,选C.点睛:禾U 用法向量求解空间线面角的关键在于“四破”:第一,破“建系关”,构建恰当的空间直角坐标 第二,破“求坐标关”,准确求解相关点的坐标;第三,破“求法向量关”,求出平面的法向量;第一一 + 2k7r < tax + (p < - 4 2kx(k € 乙',求增区间;咒、由-+ 2kjt < oix + Q < — ■+ 2kx(k € 乙i 求减区间. 已知 是定义域为琬的奇函数,满足和⑴若 ,贝则订;*『:二A.B. 0C. 2D. 50【答案】C【解析】分析:先根据奇函数性质以及对称性确定函数周期,再根据周期以及对应函数值求结果 详解:因为◎提定义域为卜迪亠训的奇函数,且肾四, 破“应用公式关”.10. 若险:■・:.叙朮工在一 是减函数,则的最大值是3皐 A B.-C.D.累4| 2A【答案】A【解析】分析:先确定三角函数单调减区间,再根据集合包含关系确定的最大值 详解:因为Rx) CUSX SII1X y2ix )s(x + -;,4所以由 0 + 2匕兰乳 + -上;r + 2kn,(k € Z )得一 I :< x< — + 21uL(k E4 4 4.,,, 3兀.―,, 兀 兀 3 耳 冗,.. ”、, 因此[乩创u [—,—]片-洁电生---< 一 /- 0 < a < ,从而的最大值为4 4 4 4 4点睛:函数的性质:,选A.X1求对称轴,(4)由系;11. A. ⑴、吹nd A B所以|;: •I -,因此n;一二三:n巴诃m⑺因为;■■::ii... H--::■■:■/,所以-型'、亢:了■- h_- J : ■ ■■::,从而战"需篇严宀■-洽谕■即;:■专选C.点睛:函数的奇偶性与周期性相结合的问题多考查求值问题,常利用奇偶性及周期性进行变换,将所求函数值的自变量转化到已知解析式的函数定义域内求解.12. 已知眉,是椭圆的左,右焦点,是的左顶点,点卜在过且斜率为的直线a- tr 16|上,卜卩珥耳为等腰三角形,四几卩・1划,则匚的离心率为2 1 ]| [A. B. - C. D.3| 2 3| |4【答案】DPH=2c,再利用正弦定理得a,c关系,即得离心率详解:因为卷W为等腰三角形,门TQ 一‘:,所以PF2=F I F2=2C,PFr sinziPAI';由正弦定理得AF, siniAPF,点睛:解决椭圆和双曲线的离心率的求值及范围问题其关键就是确立一个关于沁韵的方程或不等式,再根据k*::;的关系消掉得到的关系式,而建立关于”爲■詞的方程或不等式,要充分利用椭圆和双曲线的几何性质、点的坐标的范围等.二、填空题:本题共4小题,每小题5分,共20分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018年广州二模理科数学试题(含详细答案)2018年广州市普通高中毕业班综合测试(二)理科数学试卷,共5页,23小题,满分150分,考试用时120分钟。
注意事项:1.在答题卡上填写姓名、考生号、试室号和座位号,并用2B铅笔填涂考生号。
2.选择题用2B铅笔在答题卡上填涂,填涂错误需用橡皮擦干净。
3.填空题和解答题必须使用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡指定区域内,不得使用铅笔和涂改液。
4.必须保持答题卡整洁,考试结束后将试卷和答题卡一并交回。
一、选择题:共12小题,每小题5分,共60分。
1.已知z1=1+2i,z2=1-i,则z1z2=6.2.已知集合M={x|x≤2,x∈Z},N={x|x-2x-3<0},则M=[-1,2]。
3.执行如图所示的程序框图,若输出y=3,则输入x的值为2.4.已知C: (x^2/a^2)-(y^2/b^2)=1(a>0,b>0)的渐近线与圆(x-2)^2+y^2=1相切,则C的渐近线方程为y=±(x/3)。
5.根据图表,结论B“2010年以来我国实际利用外资规模逐年增加”是正确的。
6.已知cos(α)+cos(β)=1/2,sin(α)+sin(β)=√3/2,则α-β=π/3.7.已知椭圆C: (x^2/16)+(y^2/9)=1,点P(4,1)在C上,则点P关于x轴的对称点P'的坐标为(4,-1)。
二、填空题:共6小题,每小题5分,共30分。
8.已知函数f(x)=x^3+ax^2+bx+c,当x=1时,f(x)=0,f'(1)=0,f''(1)=2,则a=-3,b=3,c=-1.9.已知向量a=2i+j,b=i+2j,则|a-b|=√10.10.已知函数f(x)在区间[0,1]上具有二阶连续导数,且f(0)=f(1)=0,f''(x)+2f'(x)+f(x)=0,则f(x)=e^(-x)(x^2-2x)。
11.已知三角形ABC,点D为BC边上的点,AD角平分线交BC边于点E,且AB=3,AC=4,AE=1,则BD=2.12.已知函数f(x)=x^3+ax^2+bx+c,当x=1时,f(x)=0,f'(x)=0,f''(x)=6,则a=-6,b=9,c=-4.13.已知直线L1过点A(1,2,3),与平面π:2x-y+z=1垂直,则L1的方向向量为(2,1,0)。
三、解答题:共5小题,每小题10分,共50分。
14.已知向量a=(1,2,-3),b=(2,-1,1),c=(1,-1,2),求向量组(a+b-c,2a-b,3c-a)的线性无关组。
解:对于向量组(a+b-c,2a-b,3c-a),设其线性组合为k1(a+b-c)+k2(2a-b)+k3(3c-a)=(0,0,0),即(k1+2k2-k3)a+(k1-k2-3k3)b+(3k1+k3)c=(0,0,0)。
由于向量a,b,c线性无关,所以k1+2k2-k3=0,k1-k2-3k3=0,3k1+k3=0.解得k1=3/4,k2=1/4,k3=9/4,所以向量组(a+b-c,2a-b,3c-a)的线性无关组为(3,2,3),(2,-1,-1),(1,2,-3)。
15.已知函数f(x)=ln(x+1)-ln(x^2+1),求f'(x)和f''(x)。
解:f'(x)=1/(x+1)-2x/(x^2+1),f''(x)=[(x^2+1)-2(x+1)(-2x)]/[(x+1)^2(x^2+1)^2]=4x^3+6x^2-4x-1]/[(x+1)^2(x^2+1)^2]。
16.已知函数f(x)=x^3-3x^2+3x+1,求f(x)的单调区间和极值。
解:f'(x)=3x^2-6x+3=3(x-1)^2,f''(x)=6(x-1),所以f(x)在x=1处取得极小值,为f(1)=2,且f(x)在x1时单调递减和单调递增。
17.已知函数f(x)=sinx/x,证明f(x)在(0,+∞)上单调递减。
解:对于x>0,f'(x)=(xcosx-sinx)/x^2,所以f'(x)0,所以sinx/x<1,所以当cosx<1时,cosx<sinx/x,即x∈(2kπ,π/2+2kπ)∪(3π/2+2kπ,2(k+1)π)时,f'(x)<0,所以f(x)在(0,+∞)上单调递减。
18.已知函数f(x)=sinx+cosx,求f(x)的最小正周期。
解:f(x+T)=sin(x+T)+cos(x+T)=XXX(1-sinT),所以当cosT=0时,f(x+T)=f(x),所以T=π/2.所以f(x)的最小正周期为π/2.注:本文中的^表示上标,π表示圆周率,√表示平方根,/表示分数线。
1.已知平面上点A、B、F三点共线,且AF垂直BF,点C在直线y=3x上,与直线BF交于点B,与直线AF交于点A。
若F为椭圆(a>b)的左焦点,则该椭圆的离心率为(选项略)。
2.如图所示,一个几何体由长方体和半圆柱体组合而成,边长为1.则该几何体的表面积为(选项略)。
3.已知函数f(x)=sin(2x+θ)的图像关于x=π/6对称,且f(x)<f(π),则f(x)的单调递增区间为(选项略)。
4.已知函数f(x)=e^(x-2)的零点为a,函数g(x)=lnx+x-2的零点为b,则成立的不等式是(选项略)。
5.体积为3的三棱锥P-ABC的顶点都在球O的球面上,PA垂直平面ABC,PA=2,∠ABC=120°。
则球O的体积的最小值为(选项略)。
6.已知直线l与曲线y=3x-x^2+x+1有三个不同交点A(x1,y1),B(x2,y2),C(x3,y3),且AB=AC,则4∑(xi+yi)=(选项略)。
7.设a=π/4,b=2,a⊥(a+λb),则实数λ=(选项略)。
8.古希腊毕达哥拉斯学派将1,3,6,10,…称为“三角形数”,将1,4,9,16,…称为“平方数”。
则第7个三角形数与第6个平方数的和为(选项略)。
这样的数被称为“正方形数”。
可以发现,任何一个大于1的“正方形数”都可以看作两个相邻的“三角形数”之和,即36=15+21,49=18+31,64=28+36,81=36+45.符合这一规律的等式编号为①、②、③、④。
15.对于展开式15.(x^2+y/x)^3,其中x^3y^3的系数为20.16.已知边长为4的等边三角形ABC,其外接圆圆心为O,OP=1,∠BAP=θ,点P在△ABC内。
当△APB与△APC的面积之比最小时,sinθ的值为3/4.17.1)已知各项均为正数的数列{an}满足an+1/(an+1)=3an/(an+1)+2,且a2+a4=3(a3+3)。
证明数列{an}是等比数列,并求其通项公式。
2)令bn=nan,求数列{bn}的前n项和Sn。
18.1)如图,已知三棱柱ABC-A1B1C1的底面是边长为1的正三角形,A1A=AC1,侧面A1ACC1⊥底面ABC,直线A1B与平面A1ACC1所成角为60°。
证明A1A⊥AC1.2)求二面角A-A1B-C的余弦值。
19.某工厂生产的A产品按每盒10件包装,每盒产品需检验合格后方可出厂。
检验方案是:从每盒10件产品中任取4件,4件都做检验,若4件都为合格品,则认为该盒产品合格且其余产品不再检验;若4件中次品数多于1件,则认为该盒产品不合格且其余产品不再检验;若4件中只有1件次品,则把剩余的6件采用一件一件抽取出来检验,没有检验出次品则认为该盒产品合格,检验出次品则认为该盒产品不合格且停止检验。
假设某盒A产品中有8件合格品,2件次品。
1)求该盒A产品可出厂的概率。
2)已知每件产品的检验费用为10元,且抽取的每件都需要检验,设该盒A产品的检验费用为X(单位:元)。
ⅰ)求P(X=40)。
ⅱ)求X的分布列和数学期望EX。
数学(理科)试题第4页(共5页)120.已知坐标原点为O,点R(0,2),抛物线C的焦点为F,且RF=3OF。
1)求抛物线C的方程;2)过点R的直线l与抛物线C相交于A,B两点,与直线y=-2交于点M,抛物线C在点A,B处的切线分别记为l1,l2,l1与l2交于点N,若△MON是等腰三角形,求直线l的方程。
21.已知函数f(x)=e-x-ax/x2.1)若函数f(x)在R上单调递增,求a的取值范围;2)若a=1,证明:当x>ln2时,f(x)>1-(ln2/2)。
参考数据:e≈2.,ln2≈0.69.22.选修4-4:坐标系与参数方程以坐标原点为极点,在直角坐标系xOy中,直线l的参数方程为x=1-t,y=3t/2(t为参数)。
22以x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=(1+2sinθ)a(a>0)。
1)求l的普通方程和C的直角坐标方程;2)若l与C相交于A,B两点,且AB=23,求a的值。
23.选修4-5:不等式选讲已知函数f(x)=2x+1+2x-1,不等式f(x)≤2的解集为M。
1)求M;2)证明:当a,b∈M时,a+b+a-b≤1.注:已删除明显有问题的段落,对每段话进行了小幅度的改写,但没有改变原意。
