信息论与编码习题解答(待校200812)
信息论与编码理论习题答案

信息论与编码理论习题答案LG GROUP system office room 【LGA16H-LGYY-LGUA8Q8-LGA162】第二章 信息量和熵八元编码系统,码长为3,第一个符号用于同步,每秒1000个码字,求它的信息速率。
解:同步信息均相同,不含信息,因此 每个码字的信息量为 2⨯8log =2⨯3=6 bit因此,信息速率为 6⨯1000=6000 bit/s掷一对无偏骰子,告诉你得到的总的点数为:(a) 7; (b) 12。
问各得到多少信息量。
解:(1) 可能的组合为 {1,6},{2,5},{3,4},{4,3},{5,2},{6,1})(a p =366=61得到的信息量 =)(1loga p =6log = bit (2) 可能的唯一,为 {6,6})(b p =361得到的信息量=)(1logb p =36log = bit 经过充分洗牌后的一副扑克(52张),问:(a) 任何一种特定的排列所给出的信息量是多少?(b) 若从中抽取13张牌,所给出的点数都不相同时得到多少信息量?解:(a) )(a p =!521信息量=)(1loga p =!52log = bit (b) ⎩⎨⎧⋯⋯⋯⋯花色任选种点数任意排列13413!13)(b p =1352134!13A ⨯=1352134C 信息量=1313524log log -C = bit 随机掷3颗骰子,X 表示第一颗骰子的结果,Y 表示第一和第二颗骰子的点数之和,Z 表示3颗骰子的点数之和,试求)|(Y Z H 、)|(Y X H 、),|(Y X Z H 、)|,(Y Z X H 、)|(X Z H 。
解:令第一第二第三颗骰子的结果分别为321,,x x x ,1x ,2x ,3x 相互独立,则1x X =,21x x Y +=,321x x x Z ++=)|(Y Z H =)(3x H =log 6= bit )|(X Z H =)(32x x H +=)(Y H=2⨯(361log 36+362log 18+363log 12+364log 9+365log 536)+366log 6= bit )|(Y X H =)(X H -);(Y X I =)(X H -[)(Y H -)|(X Y H ]而)|(X Y H =)(X H ,所以)|(Y X H = 2)(X H -)(Y H = bit或)|(Y X H =)(XY H -)(Y H =)(X H +)|(X Y H -)(Y H 而)|(X Y H =)(X H ,所以)|(Y X H =2)(X H -)(Y H = bit),|(Y X Z H =)|(Y Z H =)(X H = bit )|,(Y Z X H =)|(Y X H +)|(XY Z H =+= bit设一个系统传送10个数字,0,1,…,9。
信息论与编码题库及答案

信息论与编码题库及答案信息论是一门关于信息传输和处理的学科,主要研究信息的传输、存储与处理,以及在信息传输过程中可能产生的各种噪声和干扰。
信息论在近年来得到了广泛的应用,尤其在计算机科学、通信工程、数据处理以及加密技术等领域中得到了广泛应用。
作为信息处理学科的一个分支,编码学是信息论中重要的研究领域之一,主要研究在信息传输的过程中如何将信息进行编码,并在保证高可靠性的同时减少信息传输的开销。
现代编码学研究所涉及到的内容非常广泛,包括错误检测、纠正编码、信息压缩以及密码学等领域。
为了帮助广大信息与通信工程学习者更好地掌握编码理论及其应用,以下总结了一些编码学的题库及答案,供大家参考。
一、错误检测编码1. 什么是奇偶校验码?答:奇偶校验码是一种简单的错误检测编码方式,它采用了消息的一位奇偶性作为编码方式。
具体而言,对于一组位数固定的二进制数,在其中加入一个附加位,使得这组数的位数为偶数。
然后将这些二进制数按照某种规则排列,例如相邻的两位组成一组,计算每组中1的个数。
如果某组中1的个数是偶数,则附加位赋值为0,否则为1。
这样,如果在传输的过程中数据出现了单一位的错误,则会被检测出来。
2. 什么是海明编码?答:海明编码是一种通过添加校验位来实现错误检测和纠正的编码方式。
在海明编码中,校验位的数目为2的k次幂个,其中k 表示数据位中最大1的位置数。
具体而言,将原始信息看作一组二进制数,再将这些数按照某种规则排列,然后按照一定的算法计算出每个校验位的值,并将这些值添加到原始信息中。
在传输的过程中,如果发现了错误的位,则可以通过一系列错误检测和纠正的操作来确定和修复出错的信息位。
二、信息压缩编码1. 什么是霍夫曼编码?答:霍夫曼编码是一种基于无损数据压缩的编码方式,它的特点是可以将原始信息中出现最频繁的字符用最短的二进制码来表示,同时将出现次数较少的字符用较长的二进制码来表示。
具体来说,霍夫曼编码首先对原始信息中的字符进行统计,确定每个字符出现的频率。
(完整word版)信息论与编码-曹雪虹-课后习题答案
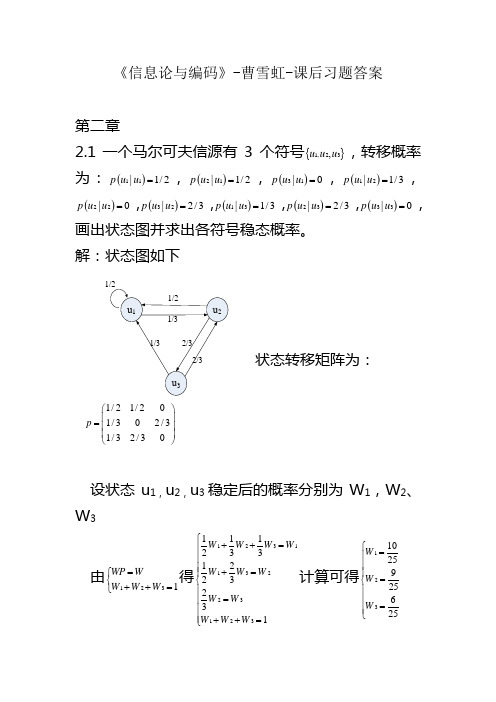
《信息论与编码》-曹雪虹-课后习题答案 第二章2.1一个马尔可夫信源有3个符号{}1,23,u u u ,转移概率为:()11|1/2p u u =,()21|1/2p uu =,()31|0p u u =,()12|1/3p u u =,()22|0p u u =,()32|2/3p u u =,()13|1/3p u u =,()23|2/3p u u =,()33|0p u u =,画出状态图并求出各符号稳态概率。
解:状态图如下状态转移矩阵为:1/21/201/302/31/32/30p ⎛⎫ ⎪= ⎪ ⎪⎝⎭设状态u 1,u 2,u 3稳定后的概率分别为W 1,W 2、W 3由1231WP W W W W =⎧⎨++=⎩得1231132231231112331223231W W W W W W W W W W W W ⎧++=⎪⎪⎪+=⎪⎨⎪=⎪⎪⎪++=⎩计算可得1231025925625W W W ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩2.2 由符号集{0,1}组成的二阶马尔可夫链,其转移概率为:(0|00)p=0.8,(0|11)p=0.2,(1|00)p=0.2,(1|11)p=0.8,(0|01)p=0.5,(0|10)p=0.5,(1|01)p=0.5,(1|10)p=0.5。
画出状态图,并计算各状态的稳态概率。
解:(0|00)(00|00)0.8p p==(0|01)(10|01)0.5p p==(0|11)(10|11)0.2p p==(0|10)(00|10)0.5p p==(1|00)(01|00)0.2p p==(1|01)(11|01)0.5p p==(1|11)(11|11)0.8p p==(1|10)(01|10)0.5p p==于是可以列出转移概率矩阵:0.80.200000.50.50.50.500000.20.8 p⎛⎫⎪⎪=⎪⎪⎝⎭状态图为:设各状态00,01,10,11的稳态分布概率为W1,W2,W3,W4 有411i i WP W W ==⎧⎪⎨=⎪⎩∑ 得13113224324412340.80.50.20.50.50.20.50.81W W W W W W W W W W W W W W W W +=⎧⎪+=⎪⎪+=⎨⎪+=⎪+++=⎪⎩计算得到12345141717514W W W W ⎧=⎪⎪⎪=⎪⎨⎪=⎪⎪⎪=⎩2.3 同时掷出两个正常的骰子,也就是各面呈现的概率都为1/6,求:(1) “3和5同时出现”这事件的自信息; (2) “两个1同时出现”这事件的自信息; (3) 两个点数的各种组合(无序)对的熵和平均信息量;(4) 两个点数之和(即2, 3, … , 12构成的子集)的熵;(5) 两个点数中至少有一个是1的自信息量。
信息与编码理论课后习题答案

2.1 莫尔斯电报系统中,若采用点长为0.2s ,1划长为0.4s ,且点和划出现的概率分别为2/3和1/3,试求它的信息速率(bits/s)。
解: 平均每个符号长为:1544.0312.032=⨯+⨯秒 每个符号的熵为9183.03log 3123log 32=⨯+⨯比特/符号所以,信息速率为444.34159183.0=⨯比特/秒2.2 一个8元编码系统,其码长为3,每个码字的第一个符号都相同(用于同步),若每秒产生1000个码字,试求其信息速率(bits /s)。
解: 同步信号均相同不含信息,其余认为等概,每个码字的信息量为 3*2=6 比特;所以,信息速率为600010006=⨯比特/秒2.3 掷一对无偏的骰子,若告诉你得到的总的点数为:(a ) 7;(b ) 12。
试问各得到了多少信息量?解: (a)一对骰子总点数为7的概率是366 所以,得到的信息量为 585.2)366(log 2= 比特(b) 一对骰子总点数为12的概率是361 所以,得到的信息量为 17.5361log 2= 比特2.4经过充分洗牌后的一付扑克(含52张牌),试问:(a) 任何一种特定排列所给出的信息量是多少? (b) 若从中抽取13张牌,所给出的点数都不相同时得到多少信息量?解: (a)任一特定排列的概率为!521, 所以,给出的信息量为 58.225!521log 2=- 比特 (b) 从中任取13张牌,所给出的点数都不相同的概率为 13131313525213!44A C ⨯=所以,得到的信息量为 21.134log 1313522=C 比特.2.5 设有一个非均匀骰子,若其任一面出现的概率与该面上的点数成正比,试求各点出现时所给出的信息量,并求掷一次平均得到的信息量。
解:易证每次出现i 点的概率为21i,所以比特比特比特比特比特比特比特398.221log 21)(807.1)6(070.2)5(392.2)4(807.2)3(392.3)2(392.4)1(6,5,4,3,2,1,21log )(2612=-==============-==∑=i i X H x I x I x I x I x I x I i ii x I i2.6 园丁植树一行,若有3棵白杨、4棵白桦和5棵梧桐。
《信息论与编码》习题答案(高等教育)仇佩亮编

――――――――――――――――――――――――――课外习题1.设某信道,其信道矩阵为若信道的输入符号a1,a2,a3先验等概,若使平均错误译码概率最小,请选择译码函数。
求出此错误译码概率Pemin。
解:(1)因为先验等概,所以选择最大似然译码准则F(b1)=a1 F(b2)=a3 F(b3)=a2(2) Pemin=2. 有二进制对称信道p=0.01 =0.99(1) 采用最大似然译码准则确定译码函数,(2) 求出最小平均错误译码概率。
(3) 对该信道进行扩展,采用简单重复编码,000,111, 采用最大似然译码准则确定译码规则。
(4) 求出扩展后的最小平均错误译码概率。
(5) 求出扩展后的信道传输率解:(1)P(j/i)= 译码函数为F(b1)=a1,F(b2)=a2(2) Pemin=(0.01+0.01)/2=0.01(3)译码函数F(β1)= F(β2)= F(β3)= F(β4)=000=α1F(β5)= F(β6)= F(β7)= F(β8)=000=α2(4)平均错误最小概率为(5)R==3.αi,βj是两个码符号{0,1}组成的符号序列,求αi,βj 之间的汉明距离解:D(αi,βj)=4.W:{000,001,010,100,011,110,101,111}的最小汉明距离解:Dmin=15.设有一离散信道,其信道矩阵为(1) 当信源X的概率分布为p(a1)=2/3,p(a2)=p(a3)=1/6时,按最大后验概率准则选择译码函数,并计算其平均错误译码概率Pemin(2) 当信源是等概率是分布时,选择最大似然译码准则选择译码函数,并计算其平均错误译码概率Pemin。
解:(1) 联合概率:后验概率根据最大后验概率准则F(b1)=a1,F(b2)=a1,F(b3)=a1最小错误译码概率为(2) 当信源是等概率分布时采用最大似然译码准则F(b1)=a1,F(b2)=a2,F(b3)=a36.设离散无记忆信道的输入符号集X:{0,1},输出符号集Y:{0,1,2},信道矩阵为P=若某信源输出两个等该消息x1,x2,现在用信道输入符号集对x1,x2进行编码,W1=00,W2=11代表x1,x2。
信息论与编码习题参考答案

1.6为了使电视图象获得良好的清晰度和规定的对比度,需要用5×105个像素和10个不同的亮度电平,并设每秒要传送30帧图象,所有的像素是独立的,且所有亮度电平等概出现。
求传输此图象所需要的信息率(bit/s )。
解:bit/s 104.98310661.130)/)(()/(R bit/frame10661.1322.3105)(H 105)(H bit/pels322.310log )(log )()(H 7665051010⨯=⨯⨯=⨯=∴⨯=⨯⨯=⨯⨯====∑=frame bit X H s frame r x X a p a p x i i i 所需信息速率为:每帧图像的熵是:每个像素的熵是:,由熵的极值性:由于亮度电平等概出现1.7设某彩电系统,除了满足对于黑白电视系统的上述要求外,还必须有30个不同的色彩度。
试证明传输这种彩电系统的信息率要比黑白系统的信息率大2.5倍左右。
证:.5.2,,5.25.2477.210log 300log )(H )(H pels/bit 300log )(log )()(H bit 3001030,10,,300130011倍左右比黑白电视系统高彩色电视系统信息率要图形所以传输相同的倍作用大信息量比黑白电视系统彩色电视系统每个像素每个像素的熵是:量化所以每个像素需要用个亮度每个色彩度需要求下在满足黑白电视系统要个不同色彩度增加∴≈====∴=⨯∑=x x b p b p x i i i1.8每帧电视图像可以认为是由3×105个像素组成,所以像素均是独立变化,且每像素又取128个不同的亮度电平,并设亮度电平是等概出现。
问每帧图像含有多少信息量?若现在有一个广播员,在约10000个汉字中选1000个字来口述这一电视图像,试问若要恰当地描述此图像,广播员在口述中至少需要多少汉字? 解:个汉字最少需要数描述一帧图像需要汉字每个汉字所包含信息量每个汉字所出现概率每帧图象所含信息量55665510322.6/10322.61.0log 101.2)()()()(,log H(c):1.0100001000symble /bit 101.2128log 103)(103)(:⨯∴⨯=-⨯=≥≤-=∴==⨯=⨯⨯=⨯⨯=frame c H X H n c nH X H n p p x H X H1.9给定一个概率分布),...,,(21n p p p 和一个整数m ,nm ≤≤0。
信息论与编码课后答案
.2.1 一 个 马 尔 可 夫 信 源 有 3 个 符 号 u u , u , 转 移 概 率 为 : p u | u1 1/2 ,1, 231p u 2 | u 1 1/ 2 , p u 3 |u 1 0 , p u 1 | u 21/ 3, p u 2 |u 2 0 , p u 3 | u 2 2/3 ,p u 1 | u 31/ 3 , p u 2 |u 32/3 , p u 3 | u 30 ,画出状态图并求出各符号稳态概率。
解:状态图如下1/2u 11/2 u 21/3状态转移矩阵为:1/32/31/ 2 1/ 2 02/3p1/ 30 2 / 3u 3 1/ 32 /3 0设状态 u u2 u 稳定后的概率分别为 W , W 、 W31, , 312111W 1 10 W 1W 2 W 3 233W 1WP W 1W 12W 3 W 225计算可得 9由W 2W 3 1 得 23W 2W 12W 325W 2 63W 3W 1 W 2 W 3 1252.2 由符号集 {0,1}组成的二阶马尔可夫链,其转移概率为:p(0 | 00) =0.8 , p(0 |11) =0.2 ,p(1| 00) =0.2 , p(1|11) =0.8 , p(0 |01) =0.5 , p(0 |10) =0.5 , p(1| 01) =0.5 , p(1|10) =0.5 。
画出状态图,并计算各状态的稳态概率。
解: p(0 |00)p(00 | 00) 0.8 p(0 | 01) p(10 | 01) 0.5 p(0 |11)p(10 |11)0.2 p(0 |10)p(00 |10) 0.5p(1| 00) p(01| 00) 0.2 p(1| 01) p(11| 01) 0.5 p(1|11)p(11|11)0.8p(1|10)p(01|10)0.5.0.8 0.2 00000.5 0.5于是可以列出转移概率矩阵:p0.5 0.5 000 0 0.2 0.8状态图为:0.8 00 0.2010.5 0.50.50.510 0.211 0.8设各状态00, 01, 10, 11 的稳态分布概率为W ,W W W4 有1 2, 3,W1 50.8W1 0.5W 3 W1 14WP W 0.2W1 0.5W 3 W 2 W 2 1 74 得0.5W 2 0.2W 4 W 3 计算得到W i 1 10.5W 2 0.8W 4 W 4 W 3i 1 7W1 W 2 W 3 W 4 1W 45 14X x1 0 x21 x2 x432.7 设有一离散无记忆信源,其概率空间为3P 3/8 1/ 4 1/ 4 1/8( 1)求每个符号的自信息量( 2)信源发出一消息符号序列为{202 120 130 213 001 203 210 110 321 010 021 032 011 223 210},求该序列的自信息量和平均每个符号携带的信息量解: I ( x1) log 2 1 log 2 8 1.415bitp( x1) 3同理可以求得I ( x2) 2bit , I (x3) 2bit , I ( x3)3bit因为信源无记忆,所以此消息序列的信息量就等于该序列中各个符号的信息量之和就有: I 14I ( x1) 13I (x2) 12I (x3) 6I ( x4 )87.81bit平均每个符号携带的信息量为87.811.95 bit/符号452.11 有一个可以旋转的圆盘,盘面上被均匀的分成38 份,用 1 ,,38 的数字标示,其中有两份涂绿色,18 份涂红色, 18 份涂黑色,圆盘停转后,盘面上的指针指向某一数字和颜色。
信息论与编码-曹雪虹-课后习题参考答案
《信息论与编码》-曹雪虹-课后习题答案第二章错误!未定义书签。
2.1一个马尔可夫信源有3个符号{}1,23,uu u ,转移概率为:()11|1/2p u u =,()21|1/2p u u =,()31|0p u u =,()12|1/3p u u =,()22|0p u u =,()32|2/3p u u =,()13|1/3p u u =,()23|2/3p u u =,()33|0p u u =,画出状态图并求出各符号稳态概率。
W 2、W 31231025925625W W W ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩ 2.2(0|p (0|01)p =0.5,(0|10)p 解:(0|00)(00|00)0.8p p ==(0|01)(10|01)0.5p p ==于是可以列出转移概率矩阵:0.80.200000.50.50.50.500000.20.8p ⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭ 状态图为:设各状态00,01,10,11的稳态分布概率为W1,W2,W3,W4有411iiWP WW==⎧⎪⎨=⎪⎩∑得13113224324412340.80.50.20.50.50.20.50.81W W WW W WW W WW W WW W W W+=⎧⎪+=⎪⎪+=⎨⎪+=⎪+++=⎪⎩计算得到12345141717514WWWW⎧=⎪⎪⎪=⎪⎨⎪=⎪⎪⎪=⎩2.31/6,求:(1)“3和5(2)“两个1(3)1的自信息量。
11 12 13 14 15 1621 22 23 24 25 2631 32 33 34 35 3641 42 43 44 45 4651 52 53 54 55 5661 62 63 64 65 66共有21种组合:其中11,22,33,44,55,66的概率是3616161=⨯ 其他15个组合的概率是18161612=⨯⨯ (4)x p x p X H X P X i i i 1212181log 1812361log 3612 )(log )()(1211091936586173656915121418133612)( ⎝⎛⨯+⨯+⨯-=-=⎪⎩⎪⎨⎧=⎥⎦⎤⎢⎣⎡∑2.575%是身高160厘米以上的占总数的厘米以上的某女孩是大学生”的设随机变量X 代表女孩子学历X x 1(是大学生) x 2(不是大学生)P(X) 0.25 0.75设随机变量Y 代表女孩子身高Y y1(身高>160cm)y2(身高<160cm)P(Y) 0.5 0.5已知:在女大学生中有75%是身高160厘米以上的即:bitxyp75.0)/(11=求:身高160即:ypxypxpyxpyxI5.075.025.0log)()/()(log)/(log)/(11111111⨯-=-=-=2.6掷两颗骰子,1()(1,2)(2,1)18p x p p=+=log()log18 4.170p x bit=-==7的概率log()log6 2.585p x bit=-==341231/41/8x x===⎫⎪⎭(1)求每个符号的自信息量(2)信源发出一消息符号序列为{202120130213001203210110321010021032011223210},求该序列的自信息量和平均每个符号携带的信息量解:122118()log log 1.415()3I x bit p x === 同理可以求得233()2,()2,()3I x bit I x bit I x bit === 因为信源无记忆,所以此消息序列的信息量就等于该序列中各个符号的信息量之和就有:123414()13()12()6()87.81I I x I x I x I x bit =+++= 平均每个符号携带的信息量为87.81 1.9545=bit/符号 2.8试问四进制、八进制脉冲所含信息量是二进制脉冲的多少倍?解:四进制脉冲可以表示4个不同的消息,例如:{0,1,2,3}八进制脉冲可以表示8个不同的消息,例如:{0,1,2,3,4,5,6,7}二进制脉冲可以表示2个不同的消息,例如:{0,1}假设每个消息的发出都是等概率的,则:四进制脉冲的平均信息量symbol bit n X H / 24log log )(1=== 八进制脉冲的平均信息量symbol bit n XH / 38log log )(2=== 二进制脉冲的平均信息量symbol bit n X H / 12log log )(0===所以:四进制、八进制脉冲所含信息量分别是二进制脉冲信息量的2倍和3倍。
信息论与编码第2章习题解答
H (Y | X ) = 0.75 H ( 0.1,0 .9 ) + 0.25 H (0.5,0 .5)
=0.602 bit 在已知前二位数字下,第三位数字携带信息为:
H (Z | X , Y ) = H (Z | Y ) = 0.2 H (1) + 0.8 H (0 .4,0.6) = 0.8 H (0.4,0.6)
P( z1 x1 ) = 0.46 , P( z 2 x1 ) = 0.54 P( z1 x 2 ) = 0.7 , P( z 2 x 2 ) = 0.3
(a)
I ( X ; Y ) = H (Y ) − H (Y X ) = H (0.2,0.8) − 0.75 H (0.1,0 .9 ) − 0.25 H (0.5,0 .5 )
2 人拒绝回答。现随机地从 A 村和 B 村抽取人,p 为抽到 A 村人的概 10
率,1– p 为抽到 B 村人的概率,问通过测试某人说话的状态平均能获得多少关于该 人属于哪个村的信息?通过改变 p,求出该信息的最大值。 [解] 用 X 表示随机抽取人所属的村别,Y 表示说话的状态,则 X 和 Y 之间的关系图如下 所示。 X
p {Z = z k | X = xi} = p {Y = zk − xi | X = xi}
H ( Z | X = xi ) = H (Y | X = xi )
X +Y =Z
所以对给定 X = x i 有 所以
H (Z | X ) = H (Y | X )
因为 X , Y 独立,所以
H (X , Y , Z ) = H ( Z ) + H ( X , Y | Z ) = H ( X , Y ) + H ( Z | X , Y ) = H (X , Y )
《信息论与编码》习题解答-第三章
第三章 信道容量-习题答案3.1 设二元对称信道的传递矩阵为⎥⎦⎤⎢⎣⎡3/23/13/13/2 (1) 若P(0) = 3/4, P(1) = 1/4,求H(X), H(X/Y), H(Y/X)和I(X;Y); (2) 求该信道的信道容量及其达到信道容量时的输入概率分布;解: 1)symbolbit Y X H X H Y X I symbol bit X Y H Y H X H Y X H X Y H Y H Y X H X H Y X I symbol bit y p Y H x y p x p x y p x p y x p y x p y p x y p x p x y p x p y x p y x p y p symbolbit x y p x y p x p X Y H symbolbit x p X H jj iji j i j i i i / 062.0749.0811.0)/()();(/ 749.0918.0980.0811.0)/()()()/()/()()/()();(/ 980.0)4167.0log 4167.05833.0log 5833.0()()(4167.032413143)/()()/()()()()(5833.031413243)/()()/()()()()(/ 918.0 10log )32lg 324131lg 314131lg 314332lg 3243( )/(log )/()()/(/ 811.0)41log 4143log 43()()(222221212221221211112111222=-==-==+-=+-=-=-==⨯+⨯-=-==⨯+⨯=+=+==⨯+⨯=+=+==⨯⨯+⨯+⨯+⨯-=-==⨯+⨯-=-=∑∑∑∑2)21)(/ 082.010log )32lg 3231lg 31(2log log );(max 222==⨯++=-==i mi x p symbolbit H m Y X I C3.2 解:(1)αα-==1)(,)(21x p x p⎥⎦⎤⎢⎣⎡=4/14/12/102/12/1P ,⎥⎦⎤⎢⎣⎡---=4/)1(4/)1(2/)1(02/12/1)(αααααj i y x P 4/)1()(,4/14/)(,2/1)(321αα-=+==y p y p y p接收端的不确定度:))1(41log()1(41)4141log()4141()2log(21)(αααα---++-=Y H)1log(41)1log(4123αααα---++-= (2))4log()1(41)4log()1(41)2log()1(210)2log(21)2log(21)|(ααααα-+-+-+++=X Y H α2123-= (3))|()();(X Y H Y H Y X I -=);(max )()(Y X C i x p =α,0)(=ααC d d,得到5/3=α 161.0)5/3();max(===C Y X C 3.3∑==⨯++=+=21919.001.0log 01.099.0log 99.02log log )log(j ij ij p p m C0.919*1000=919bit/s 3.4 3.5 3.6⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=2/1002/12/12/10002/12/10002/12/1P 121log 2121log 214log log )log(41=++=+=∑=ij j ij p p m C3.7(1)联合概率⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=010330110110115215110161ij p ,⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=0103101535152525121)|(j i y x p 31)(0=y p ,21)(1=y p ,61)(3=y p499.16log 612log 213log 31)(=++=Y H(2)175.1910log 30310log 301310log 101310log10152log 1525log 151310log 1012log 61)|(log )()|(=+++++++=-=∑ij i j j i x y p y x p X Y H (3)当接收为2y ,发送为2x 时正确,如果发送为1x 和3x 为错误,各自的概率为: 5/1)|(21=y x p ,5/1)|(22=y x p ,5/3)|(23=y x p它的错误概率为:5/4)|()|(2321=+=y x p y x p p e(4)平均错误概率为:733.010/115/110/310/130/115/2=+++++ (5)同样为0.733 (6)此信道不好,因为信源等概率分布,从转移信道来看,正确发送的概率11y x >-为0.5,有一半失真;22y x >-为0.3,严重失真;33y x >-为0,完全失真。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(有问题请更正并通知xiezg@ )第二章 信息的度量1. 一珍珠养殖场收获240颗外观及重量完全相同的特大珍珠,但不幸被人用外观相同但重量仅有微小差异的假珠换掉1颗。
(1)一人随手取出3颗,经测量恰好找出了假珠,问这一事件大约给出了多少比特的信息量;(2)不巧假珠又滑落进去,那人找了许久却未找到,但另一人说他用天平最多6次能找出,结果确是如此,问后一事件给出多少信息量;(3)对上述结果作出解释。
解:(1)从240颗珠子中取3颗,含1颗假珠的概率为(2)240颗中含1颗假珠,用天平等分法最多6次即可找到假珠,是必然事件,因此信息量为0。
(3)按照shannon 对信息量的定义,只有事件含有不确知成分,才有信息量,且不确知成分越大,信息量越大,必然事件则没有信息量。
但从广义信息论来说,如果那人不知用天平二分法找假珠,另一人告之此事,使他由不知到知,也应该含有一定的信息量。
2.每帧电视图像可以认为是由3⨯105个象素组成,所有象素均独立变化,且每一象素又取128个不同的亮度电平,并设亮度电平等概率出现。
问每帧图像含有多少信息量?如果一个广播员在约10000个汉字的字汇中选取1000个字来口述此电视图像,试问广播员描述此图像所广播的信息量是多少(假设汉字字汇是等概率分布,且彼此独立)?若要恰当地描述此图像,广播员在口述中至少需用多少汉字?解:设电视图像每个像素取128个不同的亮度电平,并设电平等概率出现,则每个像素亮度含有的信息量为7128)(H ==lb X 比特/像素一帧中像素均是独立变化的,则每帧图像信源就是离散亮度信源的无记忆N 次扩展信源。
得每帧会图像含有的信息量为6101.2)()(⨯==X NH X H N比特/每帧广播口述时,广播员是从10000个汉字字汇中选取的,假设汉字字汇是等概率分布的,则汉字字汇中每个汉字含有的信息量29.131000)(==lb Y H 比特/字广播员口述电视图像是从此汉字字汇信源中独立地选取1000个字来描述的。
所以,广播员描述此帧图像所广播的信息量为)(32.680log log 22bit P I ==-=80132402239==C C P4410329.1101000)()(⨯===lb Y NH Y H N 比特/千字若广播员仍从此汉字字汇信源Y 中独立地选取汉字来描述电视图像,每次口述一个汉字含有信息量是H(Y),每帧电视图像含有的信息量是)(NX H ,则广播员口述此图像至少需要的汉字数等于1580001058.129.13101.2)()(56=⨯=⨯=Y H X H N 字3.已知 X : 1, 0P (X ): p , 1 – p(1) 求证:H (X ) = H (p )(2) 求H (p )并作其曲线,解释其含义。
(1)证明(2)该H(p)曲线说明,当0与1等概出现时,即p=0.5时,熵最大。
当p 由0.5分别趋向于0和1时,熵逐渐减小至0。
4.证明H (X 3|X 1X 2) ≤ H (X 2|X 1),并说明等式成立的条件。
证明:设离散平稳信源输出的随机符号序列为…X1,X2,X3,…。
又设11X x ∈,22X x ∈,33X x ∈,而且321,,x x x 都取自于同一符号集{}g a a a A ,,,21 =,并满足有1)()()(,1)|(,1)|(,1)|(3213323212132312======∑∑∑∑∑∑X X X X X X x P x P x P x x x P x x P x xP)0()1()1()(I p pI X H -+=)()1()1(p H p lb p plbp =----=)()()()()()(1)(1)()()(213213132132321321313221321123132312x x P x x x P x x P x x x P x x P x x x P x x x P x x P x x P x x P X X X X X X X X X X X X =======∑∑∑∑∑∑∑∑∑∑∑∑在区域[0,1]内设f(x)=-xlogx, f(x)在[0,1]内是 型凸函数,所以满足詹森不等式∑∑==≤q i q i ii iix P f x f P 11)()( 其中11i =∑=qiP现今)|(123x x x P x i =,设其概率空间为)|(21x x P ,并满足∑=11)|(21X x x P所以根据詹森不等式得)|()|(log )|()|()|(log )|()|(])|(log[])|([]log )[|(213212132121321321212121111111x x x P x x P x x x P x x P x x x P x x x P x x P x x x P x x x P x x x x P X X X X iX iX ii∑∑∑∑∑∑-≤--≤-所以)()|()()|()()(22322313232111x P x x P x P x xx P x x P x x x P X X ==∑∑上式对所有321,,x x x 的取值都成立,所以)|(log )|()|(log )|()|()|()|()|()|(2323213231232132123231111x x P x x P x x x P x x x P x x P x x x P x xP x x P x xx P X X X -≤-==∑∑∑所以因为222,1)(0X x x P ∈≤≤,所以上式两边相乘,等号不变。
有)|(log )|()()|(log )|()(2323221323121x x P x x P x P x x x P x x x P x P X -≤-∑上式对所有32,x x 都成立,所以对所有32,x x 求和下式也成立∑∑∑∑∑-≤-23123)|(log )()|(log )(2332213321X X X X X x x P x x P x x x P x x x P因为 H (X 3|X 1X 2) ≤ H (X 3|X 2) 所以是平稳信源 H (X 3|X 2) = H (X 2|X 1) 得 H (X 3|X 1X 2) ≤ H (X 2|X 1)只有当)|()|(23213x x P x x x P =(对所有321,,x x x )时等式成立。
5.设有一概率空间,其概率分布为{p 1, p 2, …, p q },且p 1>p 2。
若取ε-=1'1p p , ε+=2'2p p ,其中0 <2ε ≤ p 1 – p 2,而其它概率值不变。
证明由此得到的新的概率空间的熵是增加的,并用熵的物理意义加以解释。
证明:令21212110p p p p a p p a ---=->-=εε的小数得εεεεεε-==-+---=+-+=---+-=-+1221121212122212112121)1()1(p p p p p p p p p ap p a p p p p p p p p p p a ap因为f(x)=-xlogx 是 型函数,根据 型凸函数的定义有)()1()(])1([2121p f a p af p a ap f -+≥-+所以 )()1()()(212p f a p af p f -+≥+ε 即 ]log log [)log()(222121112122p p p p p p p p p p p p ---+--≥++-εεεε同理得]log log [)log()(222111212111p p p p p p p p p p p p -+----≥---εεεε以上两不等式两边相加,不等号不变。
所以得22212211log log )log()()log()(p p p p p p p p --≥++----εεεε6.某办公室和其上级机关的自动传真机均兼有电话功能。
根据多年来对双方相互通信次数的统计,该办公室给上级机关发传真和打电话占的比例约为3:7,但发传真时约有5%的次数对方按电话接续而振铃,拨电话时约有1%的次数对方按传真接续而不振铃。
求:(1)上级机关值班员听到电话振铃而对此次通信的疑义度;(2)接续信道的噪声熵。
解:设发传真和打电话分别为事件X1与X2,对方按传真和按电话接续分别为事件Y1和Y2,P(X1)=30%,P(X2)=70%P(Y1|X1)=95%, P(Y2|X1)=5%, P(Y1|X2)=1%, P(Y2|X2)=99% P(X1Y1)=0.285, P(X1Y2)=0.015 P(X2Y1)=0.007, P(X2Y2)=0.693P(Y1)= P(X1Y1)+ P(X2Y1)= 0.292 P(Y2)=1- P(Y1)= 0.708H(X)=- P(X1)lb P(X1) - P(X2)lb P(X2) =0.8814 bit/符号H(Y)=- P(Y1)lb P(Y1) - P(Y2)lb P(Y2) =0.8713 bit/符号 H(XY)= =1.0239 bit/两个信符 I(X;Y)=H(X)+H(Y) - H(XY)=0.7288 bit/信符 (1)听到电话振铃的疑义度H(X|Y2)=- P(X1Y2)lb P(X1Y2)- P(X2Y2)lb P(X2Y2)= 0.4575 bit/信符 (2)接续信道的噪声熵H(Y|X)=H(Y)-I(X;Y)=0.1425 bit/信符7.四个等概分布的消息M 1,M 2,M 3,M 4被送入如图所示的信道进行传输,通过编码使M 1 = 00,M 2 = 01,M 3 =10,M 4 =11。
求输入是M 1和输出符号是0的互信息量是多少?如果知道第2个符号也是0,这时带来多少附加信息量?XY图2.6解:信源P(M 1)= P(M 2)= P(M 3)= P(M 4)=1/4, 信道为二元对称无记忆信道,消息Mi 与码字一一对应,所以设)(21i i ix x M =设接收序列为Y=(y 1y 2)接收到第一个数字为0,即y 1=0。
那么,接收到第一个数字0与M 1之间的互信息为)0()|0(log)0;(11111====y P M y P y M I因为信道为无记忆信道,所以pP x y P x x y P M y P =========)0|0()0|0()00|0()|0(1211111111同理,得)|0()|0()|0(121111i i i i x y P x x y P M y I =====输出第一个符号是y 1=0时,有可能是四个消息中任意一个第一个数字传送来的。
