高考数学讲义三角函数.知识框架

三角函数

要求层次重难点

任意角的概念和弧度

制

B 掌握角的概念的推广，终边相同的角的表示弧度与角度的互化 B

掌握弧度与角度的转化关系，扇形面积及弧

长公式，能正确地进行弧度和角度的互化任意角的正弦、余弦、

正切的定义

C

理解任意角的正弦、余弦、正切的定义；了

解任意角的余切、正割、余割的定义

用单位圆中的三角函

数线表示正弦、余弦

C

会利用单位圆中的有向线段表示正弦、余

弦、正切

高考要求

模块框架

三角函数

和正切 诱导公式

C

熟练运用诱导公式——“奇变偶不变，符号看象限”，并能运用这些公式进行求值、化简与证明

同角三角函数的基本关系式

C

理解同角三角函数的基本关系式：

22sin cos 1x x +=，

sin tan cos x

x x

=；借助单位圆的直观性探索正弦、余弦和正切的诱导公式，并掌握其应用 sin y x

=，

cos y x =，tan y x

=的图象和性质

C

了解正弦、余弦、正切、余切函数的图象的画法

函数

sin()

y A x ω?=+的图象

C

会用“五点法”画正弦、余弦函数和函数

sin()y A x ω?=+的简图，理解,,A ω?的

物理意义，掌握由函数sin y x =的图象到函数sin()y A x ω?=+的图象的变换原理和方法

用三角函数的图象解

决一些简单的实际问题

B

掌握正弦、余弦、正切函数图象的对称轴或对称中心

三角函数的定义域和值域

B

掌握三角函数的定义域、值域的求法 三角函数的性质 C

掌握三角函数的奇偶性与单调性，并能应用它们解决一些问题,会求经过简单的恒等变

形可化为sin()y A x ω?=+的三角函数的性质

三角函数的图象和性质的应用

C

掌握三角函数奇偶性的判断及三角函数单调区间的求解及其应用

两角和与差的正弦、余弦、正切公式

C

掌握两角和与差的三角函数公式，掌握二倍角公式；能运用这些公式进行三角化简，求值等有关运算问题

能正确地运用三角函数的有关公式进行三角函数式的求值，化简与恒等式的证明． 二倍角的正弦、余弦、正切公式 C

掌握两角和与差的三角函数公式，掌握二倍角公式；能运用这些公式进行三角化简，求值等有关运算问题

能正确地运用三角函数的有关公式进行三角函数式的求值，化简与恒等式的证明．

简单的恒等变形

B

任意角与弧度制

1. 角的概念的推广

⑴角：一条射线绕着端点从一个位置旋转到另一个位置所成的图形.其中顶点，始边，终边称为角的三要素.角可以是任意大小的. ⑵角按其旋转方向可分为：正角，零角，负角.

①正角：习惯上规定，按照逆时针方向旋转而成的角叫做正角； ②负角：按照顺时针方向旋转而成的角叫做负角；

③零角：当射线没有旋转时，我们也把它看成一个角，叫做零角. ⑶在直角坐标系中讨论角：

①角的顶点在原点，始边在x 轴的非负半轴上，角的终边在第几象限，就说这个角是第几象限角.

②若角的终边在坐标轴上，就说这个角不属于任何象限，它叫轴线角.

<教师备案>可通过初中角的概念的定义引出角的概念的推广.

①初中角的概念：有公共端点的两条射线组成的图形叫做角，这个公共端点叫做角的顶点，这两条射线叫做角的边.

②角还可以看成是一条射线绕它的端点从一个位置旋转到另一个位置所成的图形.初中学此定义时，不考虑旋转方向，旋转的绝对量是一样的，而且旋转的绝对量不超过一个周角.

③转角：旋转生成的角，又常叫做转角.各角和的旋转量等于各角旋转量的和. 2.终边相同的角的集合：设α表示任意角，所有与α终边相同的角，包括α本身构成一个集合，这个集合可记为{}360,Z S k k ββα==+??∈.集合S 的每一个元素都与α的终边相同，当0k =时，对应元素为α.

<教师备案>①终边相同的角不一定相等，但相等的角的终边一定相同； ②终边相同的角有无数多个，它们相差360?的整数倍. ③正确理解角：

“0~90??间的角”指的是：090θ?

“第一象限的角”，“锐角”，“小于90?的角”，这三种角的集合分别表示为：

{}36036090,k k k θθ??<

3.弧度制和弧度制与角度制的换算

⑴角度制：把圆周360等分，其中1份所对的圆心角是1度，用度作单位来度量角的制度叫做角度制.

<教师备案>一些特殊角的度数与弧度数的对应表： 度数

0? 15° 30?

45?

60? 75° 90?

120?

135?

150?

弧度

0 π12

π6 π4 π3

5π12

π2 2π3 3π4

5π6

度数

180?

210°

225°

240°

270?

300°

315°

330°

360?

知识内容

弧度 π

7π6 5π4 4π3

3π2

5π3 7π4 11π

6

2π

⑵1弧度的角：长度等于半径长的圆弧所对的圆心角叫做1弧度的角. 规定：正角的弧度数为正数，负角的弧度数为负数，零角的弧度数为零.任一已

知角α的弧度数的绝对值l

r

α=，这种以“弧度”作为单位来度量角的制度叫做

弧度制.

⑶弧度与角度的换算：180πrad =o ，1801rad 57.305718π???

'=≈?=? ???

<教师备案>比值l

r

与所取圆的半径大小无关，而仅与角的大小有关.

度量角的制度除角度制和弧度制外，还有军事上常用的密位制，密位制的单位

是“密位”，1密位就是圆周的1

6000

的弧所对的圆心角.因为3606000?=密位，

所以6000116.7360?=≈密位密位；1密位3600.066000

?

==?.除了以上三种以外，还有

其他的角的度量单位，这里不再一一介绍.

1.三角函数定义

在直角坐标系中，设α是一个任意角，α终边上任意一点P （除了原点）的坐标为(,)x y ，

它与原点的距离为2222(||||0)r r x y x y +=+，那么

⑴比值

y r 叫做α的正弦，记作sin α，即sin y

r α=； ⑵比值x r 叫做α的余弦，记作cos α，即cos x

r α=；

⑶比值y x

叫做α的正切，记作tan α，即tan y

x α=；

⑷比值x

y 叫做α的余切，记作cot α，即cot x y α=；

⑷比值

r x 叫做α的正割，记作sec α，即sec r

x

α=； ⑸比值r

y 叫做α的余割，记作csc α，即csc r y α=.

<教师备案>①α的始边与x 轴的非负半轴重合，α的终边没有表明α一定是正角或负

角，以及α的大小，只表明与α的终边相同的角所在的位置；

②根据相似三角形的知识，对于确定的角α，六个比值不以点(,)P x y 在α的终边上的位置的改变而改变大小；

③当π()2

k k π

α=+∈Z 时，α的终边在y 轴上，终边上任意一点的横坐标x 都等

于0，所以tan y x α=与sec r

x

α=无意义；同理，当π()k k α=∈Z 时，x coy y α=与

csc r

y

α=无意义；

④除以上两种情况外，对于确定的值α，比值

y r 、x r 、y x

、x y 、r

x 、r y 分别是

一个确定的实数，所以正弦、余弦、正切、余切、正割、余割是以角为自变量，

以比值为函数值的函数，以上六种函数统称为三角函数.

2.三角函数的定义域、值域

函数 定义域 值域 sin y α=

R [1,1]- cos y α=

R

[1,1]-

tan y α=

π|π,2k k αα??

≠+∈????

Z

R

3.三角函数的符号

由三角函数的定义，以及各象限内点的坐标的符号，我们可以得知：

⑴正弦值y

r

对于第一、二象限为正（0,0y r >>），对于第三、四象限为负

（0,0y r <>）；

⑵余弦值x

r

对于第一、四象限为正（0,0x r >>），对于第二、三象限为负

（0,0x r <>）；

⑶正切值y

x

对于第一、三象限为正（,x y 同号），对于第二、四象限为负（,x y 异号）.

可以用下图表示：

说明：若终边落在轴线上，则可用定义求出三角函数值.

<教师备案>三角函数在各象限的符号是学习诱导公式的基础，因此建议教师在此处多举

例让学生口答，灵活掌握这部分知识，在例题中没有放此类题目.可按以下方式举例：

如⑴cos2500?<；⑵πsin 04

??-< ???

；⑶tan(672)0-?>；（4）11π

tan

03

>，⑸cot(3)0->.

关于3rad 的判断方法，可根据

π

3π2

<<，则3rad 所在的象限为第二象限.

4.同角三角函数的基本关系式：

平方关系：22sin cos 1x x +=，22sec tan 1x x -=，22csc cot 1x x -=

商数关系：

sin tan cos x x x =，cos cot sin x

x x

= 倒数关系：111

sec ,csc ,tan cos cos cot x x x x x x

===

<教师备案>①注意“同角”，至于角的形式无关重要，如22sin 4cos 41αα+=等；

②注意这些关系式都是对于使它们有意义的角而言的，如π

tan cot 1(,)2

k k ααα?=≠∈Z ；

③对这些关系式不仅要牢固掌握，还要能灵活运用（正用、反用、变形用），如：

2cos 1sin αα=-，22sin 1cos αα=-，sin cos tan α

αα

=

等. ④特殊角的三角函数值

角α 0 π6 π4 π3 π2

2π3 3π4 5π

6

π 3π

2

2π sin α 0 12 2

2

32 1 32 2

2 12 0 1- 0

cos α 1 32 2

2

12

12- 22- 32

- 1- 0

1 tan α 0

33

1

3 不存

在

3-

1- 33

-

不存在

6.诱导公式：

⑴角α与2π()k k α+?∈Z 的三角函数间的关系；

sin(2π)sin k αα+=,cos(2π)cos k αα+=,tan(2π)=tan k αα+;

⑵角α与α-的三角函数间的关系；

sin()sin αα-=-,cos()cos αα-=,tan()tan αα-=-; ⑶角α与(21)π()k k α++∈Z 的三角函数间的关系；

[]sin (21)πsin k αα++=-,[]cos (21)πcos k αα++=-,[]tan (21)πtan k αα++=;

⑷角α与2

π

α+

的三角函数间的关系.

πsin cos 2αα??+= ???,πcos sin 2αα??+=- ???,πtan cot 2αα?

?+=- ??

?.

<教师备案>诱导公式的记忆方法：“奇变偶不变，符号看象限”，具体指的是对于任意三

角函数，以πsin 2y m ???

=?+ ???

为例，若m 为π2的偶数倍，则函数名不改变，

根据角?所在象限判断变换后的三角函数的符号，若m 为

π

2

的奇数倍，则函数名改变成余弦，符号同理仍然看象限.

4.三角函数式的化简与三角恒等式的证明是个难点，需要学生熟悉并灵活运用所学的公式与知识，一般情况下，化简的基本思路是：减少角的种数，减少三角函数的种数，适当配凑和拆分，统一切割化弦等等. ⑴单位圆：

半径等于单位长的圆叫做单位圆.设单位圆的圆心与坐标原点重合，则单位圆与x轴交点分别为(1,0)

A，(1,0)

A'-，而与y轴的交点分别为(0,1)

B，(0,1)

B'-.由三角函数的定义可知，点P的坐标为(cos,sin)

αα，即(cos,sin)

Pαα.其中cos OM

α=，sin ON

α=.

N

B'(0,-1)

A'(-1,0)

P(cosα,sinα)

A(1,0)

B(0,1)

M

O

y

x

α

T'

T(1,tanα)

x

y

O

A(1,0)

α终边与单位圆交点的横坐标和纵坐标.过点(1,0)

A作单位圆的切线，它与角α的终边或其反向延长线交与点T（或T'），则tan AT

α=(或AT').

⑵有向线段：

坐标轴是规定了方向的直线，那么与之平行的线段亦可规定方向.具有方向的线段叫做有向线段.

规定：与坐标轴方向一致时为正，与坐标方向相反时为负.

⑶三角函数线的定义：

设任意角α的顶点在原点O，始边与x轴非负半轴重合，终边与单位圆相交于点P(,)

x y，过P作x轴的垂线，垂足为M；过点(1,0)

A作单位圆的切线，它与角α的终边或其反向延长线交与点T.我们就分别称有向线段MP

u u u r

，OM

u u u u r

，AT

u u u r

为正弦线、余弦线、正切线.

<教师备案>①三条有向线段的位置：正弦线为α的终边与单位圆的交点到x轴的垂直线段；余弦线在x轴上；正切线在过单位圆与x轴正方向的交点的切线上，三条

有向线段中两条在单位圆内，一条在单位圆外.

②三条有向线段的方向：正弦线由垂足指向α的终边与单位圆的交点；余弦线

由原点指向垂足；正切线由切点指向与α的终边的交点.

③三条有向线段的书写：有向线段的起点字母在前，终点字母在后面.

④由于三角函数线的知识是下面学习同角三角函数的基本关系式及诱导公式

的基础，因此建议教师作即时性练习，此知识点的练习不作为例题出现.以下列

各角为例，作出各角的正弦线、余弦线、正切线.

⑴

π

3

；⑵

7π

6

-；⑶

2π

3

-；⑷

11π

6

.

⑤在本讲还没有学习三角函数的图象前，适当引导学生用三角函数线来观察函

数值的变化情况，取值范围等等，增强学生的“数形结合”意识.

三角函数的性质

1.三角函数的图象

<教师备案>会用正弦线、正切线画出正弦函数、正切函数的图象，并能够在此基础上利

用诱导公式画出余弦函数和余切函数的图象.

2.函数()()sin 0,0,y A x A x ω?ω=+>>∈R 的图象的作法――五点法

①确定函数的最小正周期2π

T ω

=；

②令x ω?+＝0、

π2、π、3π2、2π，得x ?ω=-、1π()2?ω-、1(π)?ω

-、13π()2?ω-、1(2π)?ω-，于是得到五个关键点(,0)?ω-、1π

((),1)2?ω-、1((π),0)?ω-、13π((),1)2?ω--、1

((2π),0)?ω

-； ③描点作图，先作出函数在一个周期内的图象，然后根据函数的周期性，把函数在一个周期内的图象向左、右扩展，得到函数

()

()sin 0,0,y A x A x ω?ω=+>>∈R 的图象．

3.()

()sin 0,0,y A x A x ω?ω=+>>∈R 的图象

函数()

()sin 0,0,y A x A x R ω?ω=+>>∈的图象可以用下面的方法得到：先

M

A P T

O

y

x

（1） P

M

A T

O

y

x （2） x

y

O

T

A

M P

（3） x

y O

T

A

M P

（4）

y

x

O

2π

π

-π

-2π

y =sin x x -2π

-π

π

O

y

2π

x

y =cos x

-π/2

π/23π/2

-3π/2-π

π

O

y

x

y =tan x

把sin y x = 的图象上所有点向左(0)?>或向右(0)?<平行移动||?个单位；再把所得各点的横坐标缩短(1)ω>或伸长(01)ω<<到原来的

1

ω

倍（纵坐标不变）；再把所得的各点的纵坐标伸长(1)A >或缩短(01)A <<到原来的A 倍（横坐标不变），从而得到sin()y A x ω?=+的图象．当函数sin()y A x ω?=+表示一个振动量时：A 叫做振幅；T 叫做周期；

1

T

叫做频率；x ω?+叫做相位，?叫做初相． 上面是一种函数的平移缩放的过程，可以用这种方法来把一种三角函数转换成另外一种三角函数．下面把这个过程分解一下： (1)相位变换

要得到函数sin()(0)y x ??=+≠的图象，可以令x x ?=+，也就是原来的x 变成了现在的x ?+，相当于x 减小了(0)??<，即可以看做是把sin y x =的图象上的各点向左(0)?>或向右(0)?<平行移动||?个单位而得到的．这种由

sin y x =的图象变换为sin()y x ?=+的图象的变换，使相位由x 变为x ?+，我

们称它为相位变换．它实质上是一种左右平移变换．

(2)周期变换

要得到函数sin (0,1)y x ωωω=>≠的图象，令x x ω=，即现在的x 缩小到了原来的ω倍，就可以看做是把sin y x =的图象上的各点的横坐标缩短(1)ω>或伸长

(01)ω<<到原来的

1

ω

倍（纵坐标不变）得到，由sin y x =的图象变换为sin y x ω=的图象，其周期由2π变为2π

ω

，这种变换叫周期变换．周期变换是一种横向的伸缩．

(3)振幅变换

要得到sin (0,1)y A x A A =>≠且的图象，令y

y A

=

，即相当于y 变为原来的A 倍，也就是把sin y x =的图象上的各点的纵坐标伸长(1)A >或缩短(01)A <<到原来的A 倍（横坐标不变）而得到的．这种变换叫做振幅变换．振幅变换是一种纵向的伸缩．

【说明】本题的所有变换都是针对x 和y 来的，也就是说所有的转换都是用在x 和y 身

上的，他们的系数也不包括在内．例如()

()

sin 0,0,y A x A x R ω?ω=+>>∈的图象，如果先把sin y x =各点的横坐标缩短(1)ω>或伸长(01)ω<<到原来

的

1

ω

倍（纵坐标不变）变成sin y x ω=，再把所得的各点的纵坐标伸长(1)A >或缩短(01)A <<到原来的A 倍（横坐标不变），得到sin y A x ω=，而最后才所有点向左(0)?>或向右(0)?<平行移动||?个单位，这样得到就是

sin ()y A x ω?=+，而不是sin()y A x ω?=+．希望大家能够从中理解“坐标

变换是针对x 和y 做的” 这句话的意义．

<教师备案>1．函数图象平移基本结论小结如下：

(0)

()()a a y f x y f x a >=??????→=+左移个单位 (0)()()a a y f x y f x a >=??????→=-右移个单位

(0)()()a a y f x y a f x >=??????→-=上移个单位 (0)()()a a y f x y a f x >=??????→+=下移个单位

1

()()y f x y f x ω

ω=????????→=各点横坐标变成原来的倍

()()y f x Ay f x =????????→=1

各点纵坐标变成原来的倍

A

()()x y f x y f x =????→-=绕轴翻折 ()()y f x y f x =????→=-绕y 轴翻折

这些新的解析式可以由图象上任意一点变换后的对应关系得出，以左移a 个单位的解析式变化为例：

设00(,)P x y 为()y f x =左移a 个单位后所得图象上的任意一点，则将Ｐ右移a 个单位得到的00'(,)P x a y +必在()y f x =的图象上，故

00()y f x a =+，又00(,)P x y 点任意，故()y f x =的图象左移a 个单位得到

的新的函数的解析式为：()y f x a =+．

函数变换可以用下图表示：

横坐标缩短

1ω

倍(ω>1)

横坐标扩大

1ω倍(0<ω<1)向右平移

?

ω(?<0)向左平移

?

ω(?>0)

向下平移b (b <0)

向上平移b (b >0)纵坐标缩短为A 倍(0

纵坐标扩大为A 倍(A >1)

y=sin(ωx+?)

y=A sin(ωx+?)+b

y=A sin(ωx+?)

向下平移

b A

(b<0)

纵坐标缩短为A 倍(0

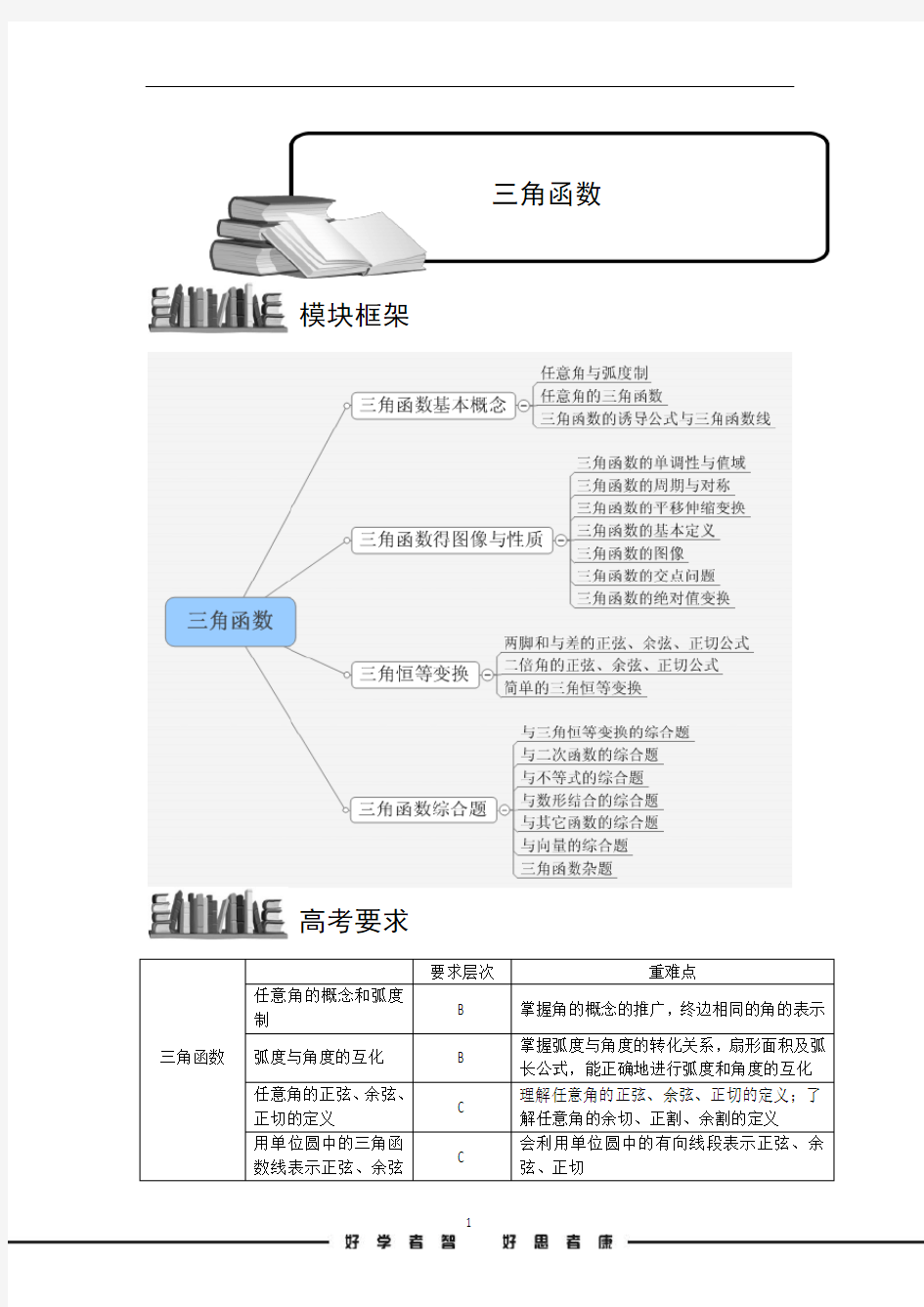
向上平移b A (b>0)纵坐标扩大为A 倍(A >1)向右平移?(?<0)

向左平移?(?>0)横坐标缩短

1ω

倍(ω>1)

横坐标扩大

1ω倍(0<ω<1)

y=sin(ωx +?)

y=sin(x+?)

y=sin x

y=sin ωx

函数

sin y x =

cos y x = tan y x =

cot y x =

定义域

R R

{|,,}

2

x x R x k k π

π∈≠

+

∈Z 且

{|,,

}

x x R x k k π∈≠∈Z 且

值域 [1,1]-

[1,1]-

R

R

奇偶性 奇函数 偶函数 奇函数 奇函数 有界性 有界函数|sin |1x ≤

有界函数

|cos |1x ≤

无界函数

无界函数

周期性（最小正周期）

2πT = 2πT = πT = πT =

单调性

ππ

[2π,2π]22π3π

[2π,2π]22

(π)

k k k k -+++∈Z Z

]在在

[(21)π,

2π],[2π,(21)π]()k k k k k -+∈Z Z ]在

π

[(π,

2π

π]2()

k k k -+∈Z Z 在

[(π,ππ]()

k k k +∈Z ]在

最值

π

2π,2x k =+

max 1y =;

π

2π2x k =-,

min 1y =-(k ∈Z)

2π,x k =

max 1y =; (21)πx k =+,

min 1

y =-(k ∈Z)

无

无

对称轴

π

π(2x k k =+∈Z)

π(x k k =∈Z)

无 无

对称点

(π,0)()k k ∈Z

π(π+,0)

2

(k k ∈Z)

(π,0)(k k ∈Z)

π

(π+,0)(2

k k ∈Z)

2.sin y x =与sin y x =的性质

函数 sin y x =

sin y x =

定义域 R

R

值域 [0,1]

[1,1]-

奇偶性 偶函数 偶函数 周期 πT =

不是周期函数

单调性

π

[π,π]2

k k +为增区间，

ππ,ππ2k k ??++????

为减区间()k ∈Z 增减区间规律不明显，只能就具体

区间分析

三角恒等变换

1.两角和与差的三角函数公式：

sin()sin cos cos sin αβαβαβ±=± cos()cos cos sin sin αβαβαβ±=m

tan tan tan()1tan tan αβ

αβαβ

±±=

m

2.倍角公式

sin 22sin cos ααα=；

2

2

2

2

cos 2cos sin 12sin 2cos 1ααααα=-=-=- 22tan tan 21tan α

αα

=

-

3

sin 33sin 4sin ααα=-；3

cos34cos 3cos ααα=-；323tan tan tan 313tan αα

αα

-=-

3.半角公式 1cos sin

2

2α

α-=1cos cos 22αα

+= 1cos 1cos sin tan

2

1cos sin 1cos α

ααα

ααα

--===++

4.万能公式

2

2tan

2sin 1tan 2

α

αα

=

+；22

1tan 2cos 1tan 2

ααα

-=

+；2

2tan

2tan 1tan 2

α

αα

=-

5.积化和差公式

1

sin cos [sin()sin()]

2

αβαβαβ=++-；

1

cos sin [sin()sin()]2

αβαβαβ=+--；

1

cos cos [cos()cos()]

2

αβαβαβ=++-；

1

sin sin [cos()cos()]2

αβαβαβ=-+--

6.和差化积公式 sin sin 2sin

cos

22αβ

αβ

αβ+-+=；sin sin 2cos

sin

22αβ

αβ

αβ+--=；

cos cos 2cos cos 22αβαβαβ+-+=；cos cos 2sin sin 22

αβαβ

αβ+--=- 【说明】这里的三倍角公式、万能公式、积化和差公式、和差化积公式都属于了解内容，

不要求必须掌握.

不建议大家去记这些公式，首先sin()sin cos cos sin αβαβαβ+=+这个公式比较容易记，而且如果大家不记其他公式不记其他公式的话，应该很容易了．下面给出其

他公式通过这个公式的推导过程：

2.公式的推导：

sin()sin[()]sin cos()cos sin()αβαβαβαβ-=+-=-+-sin cos cos sin αβαβ=-

cos()sin[()]sin[()()]22

ππ

αβαβαβ+=-+=-+-

sin()cos()cos()sin()cos cos sin sin()22

ππ

αβαβαβαβ=--+--=+-

cos cos sin sin αβαβ=-

cos()sin[()]sin[()]22

ππ

αβαβαβ-=--=-+ sin()cos cos()sin cos cos sin sin 22

ππ

αβαβαβαβ=-+-=+ sin()sin cos cos sin tan()cos()cos cos sin sin αβαβαβ

αβαβαβαβ

+++=

=+-

两边同时除以cos cos αβ可得tan()αβ+=

tan tan 1tan tan αβ

αβ

+-

tan tan()tan tan tan()tan[()]1tan tan()1tan tan a αβαβ

αββαβαβ

+---=+-=

=--+

然后把上面各式中的β代换为α，则可得到二倍角公式

sin 2sin()sin cos cos sin 2sin cos ααααααααα=+=+=

22cos 2cos()cos cos sin sin cos sin ααααααααα=+=?-?=-

再利用22sin cos 1αα+=，可得：

2222cos2cos sin 2cos 112sin ααααα=-=-=-

()2tan tan 2tan tan 2tan 1tan tan 1tan ααα

αααααα

+=+==

-?- 2

2sin sin 1cos 22tan

2

1cos cos

cos 2

2

αα

α

αα

αα-===+sin 2sin

sin

1cos 22

2tan

2

sin cos

2sin cos 2

22

αα

α

α

αα

ααα-===

sin 2cos

sin

sin 22

2tan

2

1cos cos

2cos cos

2

22

αα

α

α

αα

ααα===+ 1.倍角、半角、和差化积、积化和差等公式的运用

(1)并项功能：

222

1sin 2sin cos 2sin cos (sin cos )ααααααα±=+±=± (2)升次功能

2222cos 2cos sin 2cos 112sin ααααα=-=-=-

(3)降次功能

221cos 21cos 2cos ,sin 22

αα

αα+-=

=

(4)一个重要的构造

2222

22

sin cos (

cos )b

a b a b a b a b αααα+=++

++

令2

2

sin a b

β=

+，则2

2

cos a b

β=

+

22cos cos sin )a b αβαβ++（2

2

sin a b

β=

+）

可知：22sin cos a b a b αα++≤2.三角变换中常用的数学思想方法技巧有：

⑴角的变换：和、差、倍、半、互余、互补的相对性，有效沟通条件与结论中角的差异，

比如：3015453060452

?

?=?-?=?-?=

, ()()22

α

ααββαββ=-+=+-=?

()()()()ππ

2()()44

ααβαβαββααα=++-=+--=+--

()()222βαβαβαααβα?

?-=-+=-=-- ??

?

ππππππ244362

αααααα??????????+-=++-=++-= ? ? ? ? ???????????

π3ππ2ππ5ππ443366αααααα????????????++-=++-=++-= ? ? ? ? ? ?????????????

⑵函数名称的变换：三角变形中，常常需要变函数名称为同名函数，在三角函数中正余弦是基础，通常化切为弦，变异名为同名；有时可以使用万能公式将所有函数名化为正切； ⑶常数代换：在三角函数运算、求值、证明中，有时需要将常数转化为三角函数值，

例如：

2222ππππ1sin cos sec tan sin

tan 2sin 22464

αααα=+=-====； ⑷幂的变换：降幂是三角变换时常用的方法，常用的降幂公式有：

21cos2cos 2

αα+=，21cos2sin 2

αα-=

但降幂并非绝对，有时也需要对某些式子进行升幂处理，比如： 221cos22cos ,1cos22sin αααα+=-=；21sin 2(sin cos )ααα±=±；

⑸公式变形：三角公式是变换的依据，应熟练掌握三角公式的顺用，逆用及变形应用，

例如：tan tan tan()(1tan tan )αβαβαβ±=±??m ；

⑹辅助角公式的运用：在求值问题中，要注意辅助角公式

()22 sin cos y a b a b ααα?=+=++的应用，其中tan b

a

?=

，?所在的象限由,a b 的符号确定．