(北师大版)北京市必修二第二章《解析几何初步》测试题(答案解析)
高一北师大版数学必修2第二章 解析几何初步练习题含答案解析 双基限时练19

双基限时练(十九)一、选择题1.过(1,2),(5,3)的直线方程是( ) A .y -25-1=x -13-1 B .y -23-2=x -15-1 C .y -15-1=x -35-3D .x -25-2=y -32-3解析 由两点式,可知答案为B . 答案 B2.已知直线2x +ay +b =0在x 轴、y 轴上的截距分别为-1,2,则a ,b 的值分别为( )A .-1,2B .-2,2C .2,-2D .-2,-2 解析 令x =0,y =-b a =2,令y =0,x =-b2=-1,得b =2,a =-1,故选A .答案 A3.已知点(x 0,y 0)在直线3x -9y -27=0上,则x 0-3y 0的值为( )A .27B .18C .9D .无法确定解析 由题可知,3x 0-9y 0-27=0,∴x 0-3y 0=9. 答案 C4.经过点M(1,1),且在两坐标轴上截距相等的直线是( ) A .x +y =2 B .x +y =1 C .x +y =2或x =yD .x =1或y =1解析 若截距为0,则直线方程为y =x ,若截距不为0,设l 的方程为x +y =a ,又l 过M 点,∴1+1=a ,∴a =2,故l 为x +y =2,故选C . 答案 C5.如果AC<0且BC<0,那么直线Ax +By +C =0不通过( ) A .第一象限 B .第二象限 C .第三象限D .第四象限解析 令x =0,y =-C B >0,令y =0,x =-CA >0,知l 过一、二、四象限,不过第三象限,故选C .答案 C6.已知直线Ax +By +C =0的斜率为5,且A -2B +3C =0,则该直线方程为( )A .15x -3y -7=0B .15x +3y -7=0C .3x -15y -7=0D .3x +15y -7=0解析由题意得⎩⎨⎧-A B=5,A -2B +C =0,∴⎩⎨⎧A =-5B ,C =73B.∴直线方程为-5x +y +73=0,即15x -3y -7=0.答案 A 二、填空题 7.经过A(1,3)和B(a,4)的直线方程为________________________________________________________________________.解析 当a =1时,直线AB 的斜率不存在,所求直线的方程为x =1;当a ≠1时,由两点式,得y -3x -1=4-3a -1=1a -1,得y =1a -1(x -1)+3,即x -(a -1)y +3a -4=0.答案 x =1,或x -(a -1)y +3a -4=08.经过点P(-5,-4)且与两坐标轴围成的三角形的面积为5的直线方程为________________________________________________ ________________________.解析 设所求的直线方程为x a +yb =1. ∵直线过点P(-5,-4),∴-5a +-4b =1 即4a +5b =-ab ① 又12|a||b|=5,即|ab|=10②将①②联立⎩⎪⎨⎪⎧4a +5b =-ab ,|ab|=10,得⎩⎨⎧a =-52,b =4,或⎩⎪⎨⎪⎧a =5,b =-2. 故所求的直线方程为x -52+y 4=1,或x 5+y-2=1.即8x -5y +20=0,或2x -5y -10=0. 答案 8x -5y +20=0,或2x -5y -10=09.过A(1,4)且在两坐标轴上的截距的绝对值相等的直线共有________条.解析 一条是截距为0,一条是截距相等(不为0),一条是截距互为相反数(不为0)共三条.答案 3 三、解答题10.已知直线l 在x 轴上的截距比在y 轴上的截距大1,且过定点(6,-2),求直线l 的方程.解 设直线l 在y 轴上的截距为b ,则直线l 在x 轴上的截距为b +1,∴直线l 的方程为x b +1+y b=1,又直线l 过点(6,-2),∴6b +1+-2b =1,得b =1或b =2.∴直线l 的方程为x 2+y =1或x 3+y2=1.11.已知△ABC 的三个顶点A(3,-4),B(0,3),C(-6,0),求它的三条边所在的直线方程.解 ∵A(3,-4),B(0,3),C(-6,0), ∴k AB =3-(-4)0-3=-73.∴AB 的直线方程为y -3=-73(x -0). 即7x +3y -9=0.由截距式得BC 所在的直线方程为x -6+y3=1,即x -2y +6=0.由k AC =0-(-4)-6-3=-49,由点斜式得AC 所在的直线方程为 y -0=-49(x +6), 即4x +9y +24=0.12.直线l 过点(1,2)和第一、二、四象限,若直线l 的横截距与纵截距之和为6,求直线l 的方程.解 设直线l 的横截距为a(a ≠0),由题意,得纵截距为6-a , ∴直线l 的方程为x a +y6-a =1.∵(1,2)在直线l 上,∴1a +26-a=1,解得a =2,或a =3.当a =2时,直线l :x 2+y4=1经过第一、二、四象限,当a =3时,直线方程为x 3+y3=1,直线经过第一、二、四象限. 综上得所求直线l 的方程为2x +y -4=0,或x +y -3=0.思 维 探 究13.已知直线l 的斜率为-3且该直线与两坐标轴围成的三角形面积S 不大于3,试求直线l 在y 轴上的截距b 的取值范围.解 据题意可设直线l 方程为y =-3x +b.其中b ≠0. 令y =0,得x =b 3 .因此S =12⎪⎪⎪⎪⎪⎪b 3 ||b|=b 223≤ 3 .解得-6≤b ≤6,又因为b ≠0,故b ∈[-6,0)∪(0,6].。
高中数学 第二章 解析几何初步 1.2.2 直线方程的两点式和一般式练习(含解析)北师大版必修2-北
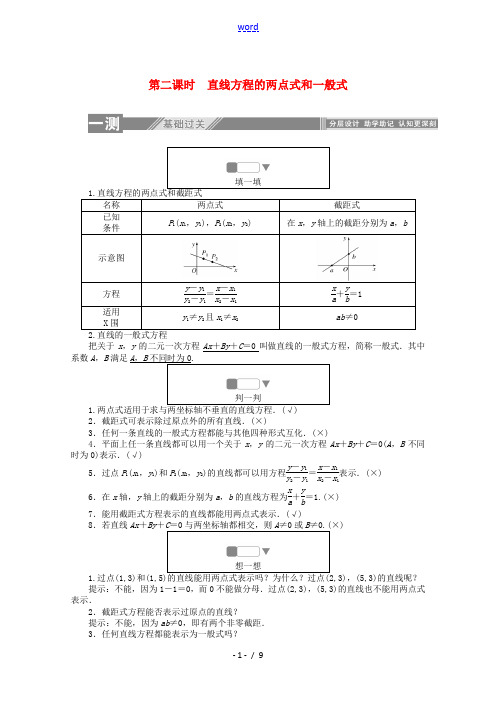
第二课时 直线方程的两点式和一般式填一填1.直线方程的两点式和截距式名称 两点式 截距式已知条件 P 1(x 1,y 1),P 2(x 2,y 2)在x ,y 轴上的截距分别为a ,b示意图方程y -y 1y 2-y 1=x -x 1x 2-x 1 x a +y b=1 适用X 围y 1≠y 2且x 1≠x 2 ab ≠02.直线的一般式方程把关于x ,y 的二元一次方程Ax +By +C =0叫做直线的一般式方程,简称一般式.其中系数A ,B 满足A ,B 不同时为0.判一判1.两点式适用于求与两坐标轴不垂直的直线方程.(√) 2.截距式可表示除过原点外的所有直线.(×)3.任何一条直线的一般式方程都能与其他四种形式互化.(×)4.平面上任一条直线都可以用一个关于x ,y 的二元一次方程Ax +By +C =0(A ,B 不同时为0)表示.(√)5.过点P 1(x 1,y 1)和P 2(x 2,y 2)的直线都可以用方程y -y 1y 2-y 1=x -x 1x 2-x 1表示.(×)6.在x 轴,y 轴上的截距分别为a ,b 的直线方程为x a +y b=1.(×) 7.能用截距式方程表示的直线都能用两点式表示.(√)8.若直线Ax +By +想一想1.过点(1,3)和,(5,3)的直线呢? 提示:不能,因为1-1=0,而0不能做分母.过点(2,3),(5,3)的直线也不能用两点式表示.2.截距式方程能否表示过原点的直线?提示:不能,因为ab ≠0,即有两个非零截距. 3.任何直线方程都能表示为一般式吗?提示:能.因为平面上任意一条直线都可以用一个关于x ,y 的二元一次方程表示. 4.当A ,B 同时为零时,方程Ax +By +C =0表示什么?提示:当C =0时,方程对任意的x ,y 都成立,故方程表示整个坐标平面; 当C ≠0时,方程无解,方程不表示任何图像.故方程Ax +By +C =0,不一定代表直线,只有当A ,B 不同时为零时,即A 2+B 2≠0时才代表直线.思考感悟:练一练1.直线x a +y b=1(ab <0)的图像可能是( )答案:C2.过两点(2018,2019),(2018,2020)的直线方程是( ) A .x =2018 B .x =2019 C .y =2018 D .x +y =2020 答案:A3.直线x -y +5=0的倾斜角为( ) A .45° B.60° C .120° D.135° 答案:A4.在x 轴、y 轴上的截距分别是5,-3的直线的截距式方程为( ) A.x 5+y 3=1 B.x 5-y 3=1 C.y 3-x5=1 D.x 5+y3=0 答案:B5.直线2x +3y -6=0与坐标轴围成的三角形面积为________. 答案:3知识点一 直线的两点式方程1.已知直线l 经过点A (1,-2),B (-3,2),则直线l 的方程为( ) A .x +y +1=0 B .x -y +1=0 C .x +2y +1=0 D .x +2y -1=0解析:由两点式得直线l 的方程为y +22--2=x -1-3-1,即y +2=-(x -1).故选A.答案:A2.过两点(-1,1)和(3,9)的直线在x 轴上的截距为( )A .-32B .-23C.25D .2 解析:由直线的两点式方程可得直线方程为y -19-1=x +13+1,即2x -y +3=0,令y =0得x=-32.故选A.答案:A知识点二 直线的截距式方程3.过点A (4,1)且在两坐标轴上截距相等的直线方程为( ) A .x +y =5 B .x -y =5C .x +y =5或x -4y =0D .x -y =5或x -4y =0解析:当直线过点(0,0)时,直线方程为y =14x ,即x -4y =0;当直线不过点(0,0)时,可设直线方程为x a +y a=1(a ≠0),把(4,1)代入,解得a =5,∴直线方程为x +y =5.综上可知,直线方程为x +y =5或x -4y =0.选C. 答案:C4.两条直线l 1:x a -y b =1和l 2:x b -y a=1在同一平面直角坐标系中的图像可以是( )解析:将两直线方程化成截距式为l 1:x a +y -b =1,l 2:x b +y-a=1,则l 1与x 轴交于(a,0),与y 轴交于(0,-b ),l 2与x 轴交于(b,0),与y 轴交于(0,-a ).结合各选项,先假定l 1的位置,判断出a ,b 的正负,然后确定l 2的位置,知A 项符合.选A.答案:A知识点三直线的一般式方程5.已知直线l 的方程为x -3y +2=0,则直线l 的倾斜角为( ) A .30° B.45° C .60° D .150°解析:设直线l 的倾斜角为θ,则tan θ=13,则θ=30°.答案:A6.设直线l 的方程为(a +1)x +y +2-a =0(a ∈R ),若l 不经过第二象限,则实数a 的取值X 围是________.解析:将直线l 的方程化为y =-(a +1)x +a -2. 则⎩⎪⎨⎪⎧ -a +1>0,a -2≤0或⎩⎪⎨⎪⎧-a +1=0,a -2≤0,∴a ≤-1. 答案:(知识点四 直线方程的应用7.(1)求证:不论a 为何值,直线l 总经过第一象限; (2)为使直线不经过第二象限,求a 的取值X 围.解析:(1)证明:方法一 将直线l 的方程整理为 y -35=a ⎝ ⎛⎭⎪⎫x -15, ∴l 的斜率为a ,且过定点A ⎝ ⎛⎭⎪⎫15,35,而点A ⎝ ⎛⎭⎪⎫15,35在第一象限,故不论a 为何值,l 恒过第一象限.方法二 直线l 的方程可化为(5x -1)a +(3-5y )=0. 当定点为(x ,y )时,上式对任意的a 总成立,必有⎩⎪⎨⎪⎧5x -1=0,3-5y =0,即⎩⎪⎨⎪⎧x =15,y =35,即l 过定点A ⎝ ⎛⎭⎪⎫15,35.以下同方法一.(2)如图,直线OA 的斜率为 k =35-015-0=3. 要使l 不经过第二象限,需它在y 轴上的截距不大于零,即令x =0时,y =-a -35≤0,∴a ≥3.8.已知直线l :y =kx +2k +1.(1)求证:对于任意的实数k ,直线l 恒过一个定点;(2)当-3<x <3时,直线l 上的点都在x 轴的上方,某某数k 的取值X 围. 解析:(1)由y =kx +2k +1, 得y -1=k (x +2).由直线的点斜式方程,可知直线l 恒过定点(-2,1). (2)设函数f (x )=kx +2k +1.若-3<x <3时,直线l 上的点都在x 轴的上方,则⎩⎪⎨⎪⎧f -3≥0,f 3≥0,即⎩⎪⎨⎪⎧-3k +2k +1≥0,3k +2k +1≥0,解得-15≤k ≤1.所以实数k 的取值X 围是⎣⎢⎡⎦⎥⎤-1,1. 综合知识 直线的方程9.(1)经过点(-1,3),且斜率为-3; (2)经过两点A (0,4)和B (4,0);(3)经过点(2,-4)且与直线3x -4y +5=0平行; (4)经过点(3,2),且垂直于直线6x -8y +3=0.解析:(1)根据条件,写出该直线的点斜式方程为 y -3=-3(x +1),即y -3=-3x -3, 整理得其一般式为3x +y =0.(2)根据条件,写出该直线的截距式为x 4+y4=1,整理得其一般式为x +y -4=0.(3)设与直线3x -4y +5=0平行的直线为3x -4y +c =0,将点 (2,-4)代入得6+16+c =0,所以c =-22.故所求直线的一般式为3x -4y -22=0.(4)设与直线6x -8y +3=0垂直的直线为8x +6y +c =0,代入点(3,2)得24+12+c =0,c =-36.从而得8x +6y -36=0,即所求直线的一般式为4x +3y -18=0.10.已知△ABC 的三个顶点为A (0,3),B (1,5),C (3,-5). (1)求边AB 所在的直线方程; (2)求中线AD 所在直线的方程.解析:(1)设边AB 所在的直线的斜率为k ,则k =5-31-0=2.它在y 轴上的截距为3.所以,由斜截式得边AB 所在的直线的方程为y =2x +3.(2)B (1,5)、C (3,-5),1+32=2,5+-52=0,所以BC 的中点D (2,0).由截距式得中线AD 所在的直线的方程为x 2+y3=1.基础达标一、选择题1.下列四个命题中的真命题是( )A .经过定点P 0(x 0,y 0)的直线都可以用方程y -y 0=k (x -x 0)表示B .经过任意两个不同点P 1(x 1,y 1)、P 2(x 2,y 2)的直线都可以用方程(y -y 1)(x 2-x 1)=(x -x 1)(y 2-y 1)表示C .不经过原点的直线都可以用方程x a +yb=1表示D .经过定点A (0,b )的直线都可以用方程y =kx +b 表示解析:当直线与y 轴平行或重合时,斜率不存在,直线方程不能用点斜式、斜截式,选项A 、D 不正确;当直线垂直于x 轴或y 轴时,直线方程不能用截距式表示,选项C 不正确;选项B 正确.故选B.答案:B2.已知直线l :ax +y -2-a =0在x 轴和y 轴上的截距相等,则a 的值是( ) A .1 B .-1 C .-2或-1 D .-2或1解析:①当a =0时,y =2不合题意.②当a ≠0时,令x =0,得y =2+a ,令y =0,得x =a +2a ,则a +2a=a +2,得a =1或a =-2.故选D.答案:D3.直线l 过点P (1,3),且与x ,y 轴正半轴围成的三角形的面积等于6的直线方程是( ) A .3x +y -6=0 B .x +3y -10=0 C .3x -y =0 D .x -3y +8=0 解析:设所求的直线方程为x a +yb=1. 所以⎩⎪⎨⎪⎧1a +3b =1,12|ab |=6,解得a =2,b =6.故所求的直线方程为3x +y -6=0.故选A.答案:A4.如果AB <0,且BC <0,那么直线Ax +By +C =0不通过( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限解析:因为直线Ax +By +C =0可化为y =-A B x -C B ,又AB <0,BC <0,所以-A B >0,-C B>0,所以直线过第一、二、三象限,不过第四象限.故选D. 答案:D5.已知m ≠0,则过点(1,-1)的直线ax +3my +2a =0的斜率为( ) A .3 B .-3 C.13 D .-13解析:由题意,得a -3m +2a =0,所以a =m ,又因为m ≠0,所以直线ax +3my +2a =0的斜率k =-a 3m =-13.故选D.答案:D6.已知两条直线的方程分别为l 1:x +ay +b =0,l 2:x +cy +d =0,它们在坐标系中的位置如图所示,则( )A .b >0,d <0,a <cB .b >0,d <0,a >cC .b <0,d >0,a >cD .b <0,d >0,a <c解析:由题图可知,直线l 1的斜率-1a >0,在y 轴上的截距-ba<0,因此a <0,b <0;直线l 2的斜率-1c >0,在y 轴上的截距-d c >0,因此c <0,d >0.且l 1的斜率大于l 2的斜率,即-1a >-1c,因此a >c ,故选C.答案:C7.若方程(2m 2+m -3)x +(m 2-m )y -4m +1=0表示一条直线,则实数m 满足( )A .m ≠0 B.m ≠-32C .m ≠1 D.m ≠1且m ≠-32且m ≠0解析:∵当2m 2+m -3=0时,m =1或m =-32;当m 2-m =0时,m =0或m =1,要使方程(2m 2+m -3)x +(m 2-m )y -4m +1=0表示一条直线,则2m 2+m -3,m 2-m 不能同时为0,∴m ≠1,故选C.答案:C 二、填空题 8.经过A (1,3)和B (a,4)的直线方程为________________________________________________________________________.解析:当a =1时,直线AB 的斜率不存在,所求直线的方程为x =1;当a ≠1时,由两点式,得y -34-3=x -1a -1,即x -(a -1)y +3a -4=0.这个方程中,对a =1时方程为x =1也满足. 所以,所求的直线方程为x -(a -1)y +3a -4=0. 答案:x -(a -1)y +3a -4=09.过点(5,2),且在x 轴上的截距是在y 轴上的截距的2倍的直线方程是________________。
高一北师大版数学必修2第二章 解析几何初步练习题含答案解析 双基限时练22

双基限时练(二十二)一、选择题1.直线3x +y -5=0与x +y -1=0的交点是( ) A .(2,-1) B .(-1,2) C .(-2,1)D .(-2,-1)解析 由⎩⎪⎨⎪⎧ 3x +y -5=0,x +y -1=0,得⎩⎪⎨⎪⎧x =2,y =-1.答案 A2.若(-1,-2)为直线ax +3y +8=0与x -by =0的交点,则a ,b 的值分别为( )A .2,12 B .12,2 C .-2,-12D .-2,12解析 ∵(-1,-2)为两条直线的交点,∴⎩⎪⎨⎪⎧-a -6+8=0,-1+2b =0,得⎩⎨⎧a =2,b =12.答案 A3.若直线x +y +3m +2=0与x -y -5m +6=0的交点在第三象限,则m 的取值范围是( )A .12<m<4 B .-4<m<-12 C .m>4D .m<12解析 由⎩⎪⎨⎪⎧ x +y +3m +2=0,x -y -5m +6=0,得⎩⎪⎨⎪⎧x =m -4,y =-4m +2,由⎩⎪⎨⎪⎧m -4<0,-4m +2<0,得12<m<4. 答案 A4.已知三条直线y =2x ,x +y =3,mx +ny +5=0交于一点,则坐标(m ,n)可能是( )A .(1,-3)B .(3,-1)C .(-3,1)D .(-1,3)解析 由⎩⎪⎨⎪⎧ y =2x ,x +y =3,得⎩⎪⎨⎪⎧x =1,y =2.由三条直线相交于一点,可知m ×1+n ×2+5=0即m +2n +5=0,结合选项可知A 项正确. 答案 A5.已知直线l 1:2x +y -10=0,l 2⊥l 1,且l 2过(-10,0),则l 1与l 2的交点坐标为( )A .(6,2)B .(2,-6)C .(-6,2)D .(2,6)解析 ∵kl 1=-2,l 2⊥l 1,∴kl 2=12. 又l 2过(-10,0),∴l 2:x -2y +10=0.由⎩⎪⎨⎪⎧ x -2y +10=0,2x +y -10=0,得⎩⎪⎨⎪⎧x =2,y =6.答案 D6.无论k 为何值,直线(k +2)x +(1-k)y -5-4k =0都过一个定点,则这个定点的坐标为( )A .(1,3)B .(-1,3)C .(3,1)D .(3,-1)解析 原直线可化为(2x +y -5)+k(x -y -4)=0,由⎩⎪⎨⎪⎧ 2x +y -5=0,x -y -4=0,得⎩⎪⎨⎪⎧x =3,y =-1.∴交点(3,-1). 答案 D 二、填空题7.直线l 1:3x +4y -5=0与直线l 2:2x -3y +8=0的交点坐标为________.解析 由⎩⎪⎨⎪⎧ 3x +4y -5=0,2x -3y +8=0,得⎩⎪⎨⎪⎧x =-1,y =2.答案 (-1,2)8.经过直线x +y -1=0和x -y +1=0的交点,且与3x +2y +6=0垂直的直线方程为________.解析 所求的直线方程为x +y -1+λ(x -y +1)=0,即(λ+1)x -(λ-1)y +λ-1=0,k =λ+1λ-1,由k·⎝ ⎛⎭⎪⎫-32=-1,则λ+1λ-1=23,得λ=-5,故所求的直线方程为-4x +6y -6=0,即2x -3y +3=0.答案 2x -3y +3=09.已知l 1:x -y -1=0,l 2:2x -y +3=0,l 3:x +my -5=0,若l 1,l 2,l 3只有两个交点,则m =________.解析 ∵l 1与l 2相交,故只需l 1∥l 3,或l 2∥l 3即可,得m =-1,或m =-12.答案 -1或-12 三、解答题10.设直线l 经过2x -3y +2=0和3x -4y -2=0的交点,且与两坐标轴围成等腰直角三角形,求直线l 的方程.解 设所求的直线方程为(2x -3y +2)+λ(3x -4y -2)=0,整理得(2+3λ)x -(4λ+3)y -2λ+2=0由题意,得2+3λ3+4λ=±1,解得λ=-1,或λ=-57.∴所求的直线方程为x -y -4=0,或x +y -24=0.11.三条直线ax +2y +8=0,4x +3y =10和2x -y =10相交于一点,求a 的值.解 解方程组⎩⎪⎨⎪⎧ 4x +3y =10,2x -y =10得⎩⎪⎨⎪⎧x =4,y =-2,所以交点坐标为(4,-2).代入直线方程ax +2y +8=0,得a ×4+2×(-2)+8=0,解得a =-1.12.设直线l 的方程为(a +1)x +y +(2-a)=0(a ∈R ). (1)证明直线l 恒过定点;(2)若l 在两坐标轴上的截距相等,求直线l 的方程.解 (1)证明:直线l 的方程可化为(x -1)a +x +y +2=0(a ∈R )令⎩⎪⎨⎪⎧ x -1=0,x +y +2=0,得⎩⎪⎨⎪⎧x =1,y =-3.∴无论a 为任何实数,直线l 总经过定点(1,-3). (2)∵直线l 在两坐标轴上截距相等,l 的方程为 (a +1)x +y +2-a =0,∴l 的两截距一定存在, ∴a ≠-1,令y =0,x =a -2a +1,令x =0,y =a -2,由a -2a +1=a -2,得a =2,或a =0. ∴所求直线l 的方程为3x +y =0,或x +y +2=0.思 维 探 究13.求经过两直线2x +y -8=0与x -2y +1=0的交点,且在y 轴上的截距为x 轴上截距的两倍的直线l 的方程.解 设所求的直线方程为2x +y -8+λ(x -2y +1)=0即:(2+λ)x +(1-2λ)y +λ-8=0,由题意得2+λ≠0且1-2λ≠0.令x >0,得y =λ-82λ-1;令y =0,得x =8-λ2+λ.由题意得2·8-λ1-2λ=8-λ2+λ,得λ=8或λ=-34.当λ=8时,直线方程为10x -15y =0,即2x -3y =0; 当λ=-34时,直线方程为:54x +52y -354=0,即x +2y -7=0. ∴所求的直线方程为2x -3y =0或x +2y -7=0.。
高中数学 第二章 解析几何初步 3 空间直角坐标系练习(含解析)北师大版必修2-北师大版高中必修2数
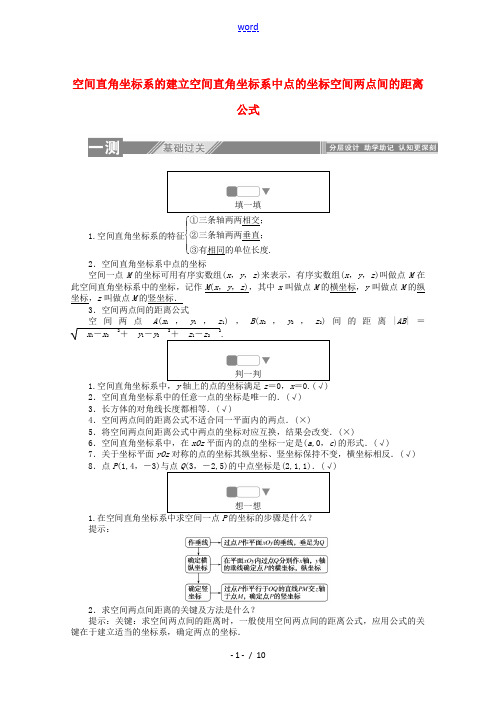
空间直角坐标系的建立空间直角坐标系中点的坐标空间两点间的距离公式填一填1.空间直角坐标系的特征⎩⎪⎨⎪⎧①三条轴两两相交;②三条轴两两垂直;③有相同的单位长度.2.空间直角坐标系中点的坐标空间一点M 的坐标可用有序实数组(x ,y ,z )来表示,有序实数组(x ,y ,z )叫做点M 在此空间直角坐标系中的坐标,记作M (x ,y ,z ),其中x 叫做点M 的横坐标,y 叫做点M 的纵坐标,z 叫做点M 的竖坐标.3.空间两点间的距离公式空间两点A (x 1,y 1,z 1),B (x 2,y 2,z 2)间的距离|AB |=x 1-x 22+y 1-y 22+z 1-z 22.判一判1.空间直角坐标系中,y 轴上的点的坐标满足z =0,x =0.(√) 2.空间直角坐标系中的任意一点的坐标是唯一的.(√) 3.长方体的对角线长度都相等.(√)4.空间两点间的距离公式不适合同一平面内的两点.(×)5.将空间两点间距离公式中两点的坐标对应互换,结果会改变.(×)6.空间直角坐标系中,在xOz 平面内的点的坐标一定是(a,0,c )的形式.(√)7.关于坐标平面yOz 对称的点的坐标其纵坐标、竖坐标保持不变,横坐标相反.(√) 8.点P (1,4,-3)与点Q (3,-2,5)的中点坐标是(2,1,1).(√)想一想1.在空间直角坐标系中求空间一点P 的坐标的步骤是什么? 提示:2.求空间两点间距离的关键及方法是什么?提示:关键:求空间两点间的距离时,一般使用空间两点间的距离公式,应用公式的关键在于建立适当的坐标系,确定两点的坐标.(2)方法:确定点的坐标的方法视具体题目而定,一般说来,要转化到平面中求解,有时也利用几何图形的特征,结合平面直角坐标系的知识确定.3.求空间对称点的方法是什么?提示:空间的对称问题可类比平面直角坐标系中点的对称问题,要掌握对称点的变化规律,才能准确求解.对称点的问题常常采用“关于谁对称,谁保持不变,其余坐标相反”这个结论.4.两点间距离公式在几何中的两个应用是什么? 提示:(1)求立体几何中线段长度问题①建系:将立体图形放在空间直角坐标系中.②定坐标:在空间直角坐标系中,根据条件确定有关的点的坐标. ③定距离:利用空间两点间距离公式确定所求线段的长. (2)判断三角形形状①利用两点间距离公式求三边长.②结合三边长及三角形有关知识判断三角形的形状. 思考感悟:练一练1.点Q (0,0,3)的位置是( )A .在x 轴上B .在y 轴上C .在z 轴上D .在面xOy 上 答案:C2.点A (-3,1,5),点B (4,3,1)的中点坐标是( ) A.⎝ ⎛⎭⎪⎫72,1,-2 B.⎝ ⎛⎭⎪⎫12,2,3 C .(-12,3,5) D.⎝ ⎛⎭⎪⎫13,43,2 答案:B3.已知点A (-1,2,7),则点A 关于x 轴对称的点的坐标为( ) A .(-1,-2,-7) B .(-1,-2,7) C .(1,-2,-7) D .(1,2,-7) 答案:A4.已知点A (2,3,5),B (-2,1,3),则|AB |等于( ) A. 6 B .2 6 C. 2 D .2 2 答案:B5.已知长方体ABCD -A 1B 1C 1D 1的对角线长为6,且底面是边长为4的正方形,则该长方体的高为( )A .9 B.92C .4D .2 答案:D知识点一空间中点的坐标及其位置1.如图所示,正方体ABCD -A 1B 1C 1D 1的棱长为1,则点B 1的坐标是( ) A .(1,0,0) B .(1,0,1) C .(1,1,1) D .(1,1,0)解析:点B 1到三个坐标平面的距离都为1,易知其坐标为(1,1,1),故选C. 答案:C 2.如图所示,已知四棱锥P -ABCD ,PB ⊥AD ,侧面PAD 为边长等于2的等边三角形,底面ABCD 为菱形,侧面PAD 与底面ABCD 所成的二面角为120°,G 是棱PB 的中点,请建立适当的空间直角坐标系,求出点P ,A ,B ,C ,D ,G 的坐标.解析:如图所示,过点P 作PO ⊥平面ABCD ,垂足为点O .连接PE .因为AD ⊥PB ,PO ⊥AD ,PO ∩PB =P ,所以AD ⊥平面POB ,所以AD ⊥OB .因为PA =PD ,所以OA =OD . 于是OB 平分AD ,点E 为AD 的中点, 所以PE ⊥AD .所以以垂足O 为原点,以OB ,OP 及在底面ABCD 内过O 且垂直于OB 的直线分别为y 轴、z 轴、x 轴建立如图所示的空间直角坐标系O -xyz .由题意可得∠PEB =120°,∠PEO =180°-120°=60°. 又等边三角形PAD 的边长等于2, 所以AE =ED =1,PE = 3.所以在Rt△POE 中,OE =PE ·cos 60°=32,PO =PE ·sin 60°=32.又底面ABCD 为菱形,所以AD =BC =AB =CD =2.所以在Rt△AEB 中,BE =AB 2-AE 2=3,所以OB =OE +BE =332.所以所求坐标分别为P ⎝ ⎛⎭⎪⎫0,0,32,A ⎝ ⎛⎭⎪⎫1,32,0,B ⎝ ⎛⎭⎪⎫0,332,0,C ⎝ ⎛⎭⎪⎫-2,332,0,D ⎝⎛⎭⎪⎫-1,32,0. 又因为G 是棱PB 的中点,所以由中点坐标公式可得G ⎝⎛⎭⎪⎫0,334,34.知识点二 空间中点的对称问题3.在空间直角坐标系中,若P (3,-2,1),则P 点关于坐标平面xOz 的对称点坐标为( )A .(-3,-2,-1)B .(3,2,1)C .(-3,2,-1)D .(3,-2,-1)解析:设所求的点为Q (x ,y ,z ),因为点Q (x ,y ,z )与点P (3,-2,1)关于平面xOz 对称,所以P ,Q 两点的横坐标和竖坐标相等,而纵坐标互为相反数,即x =3,y =2,z =1,得Q 点坐标为(3,2,1),故选B.答案:B4.点P (1,3,5)关于坐标原点对称的点P ′的坐标是( ) A .(-1,-3,-5) B .(1,-3,5) C .(-1,-3,5) D .(-1,3,5)解析:把点P (1,3,5)的横坐标、纵坐标、竖坐标均变为原来的相反数即可,故点P ′的坐标为(-1,-3,-5).答案:A知识点三 空间两点间的距离5.已知空间中两点A (1,2,3),B (4,2,a ),且|AB |=10,则a 的值为( )A .2B .4C .0D .2或4解析:由空间两点间的距离公式得|AB |=4-12+2-22+a -32=10,即9+a 2-6a +9=10,所以a 2-6a +8=0, 所以a =2或a =4.故选D. 答案:D6.在空间直角坐标系中,给定点M (2,-1,3),若点A 与点M 关于xOy 平面对称,点B 与点M 关于x 轴对称,则|AB |等于( )A .2B .4C .2 5D .37解析:由题可知,A (2,-1,-3),B (2,1,-3),所以|AB |=2-22+1+12+-3+32=2.故选A. 答案:A7.已知A (x,5-x,2x -1),B (1,x +2,2-x ),当|AB |取最小值时,x 的值为( )A .19B .-87C.87D.1914解析:|AB |=x -12+3-2x 2+3x -32=14x 2-32x +19,∴当x =--322×14=87时,|AB |最小.答案:C知识点四 距离公式的综合应用8.在空间直角坐标系中,已知A (3,0,1)和B (1,0,-3). (1)在y 轴上是否存在点M ,满足|MA |=|MB |?(2)在y 轴上是否存在点M ,使△MAB 为等边三角形?若存在,试求出点M 的坐标. 解析:(1)假设在y 轴上存在点M ,满足|MA |=|MB |,设M (0,y,0),由|MA |=|MB |,可得32+y 2+12=12+y 2+32,显然,此式对任意y ∈R 恒成立.这就是说,y 轴上所有点都满足|MA |=|MB |. (2)假设在y 轴上存在点M (0,y,0),使△MAB 为等边三角形. 由(1)可知,对y 轴上任一点都有|MA |=|MB |,所以只要|MA |=|AB |就可以使得△MAB 是等边三角形.因为|MA |=3-02+0-y 2+1-02=10+y 2,|AB |=1-32+0-02+-3-12=20,于是10+y 2=20,解得y =±10,故在y 轴上存在点M ,使△MAB 为等边三角形,点M 的坐标为(0,10,0)或(0,-10,0).综合知识 空间直角坐标系9.点A (1,2,-1),点C 与点A 关于平面xOy 对称,点B 与点A 关于x 轴对称,则|BC |的值为( )A .2 5B .4C .2 2D .27解析:点A 关于平面xOy 对称的点C 的坐标是(1,2,1),点A 关于x 轴对称的点B 的坐标是(1,-2,1),故|BC |=1-12+2+22+1-12=4.答案:B10.已知ABCD 为平行四边形,且A (1,2,3),B (2,-5,1),C (-3,2,-1),求D 点坐标. 解析:设D (x ,y ,z ),A 、C 的中点坐标(-1,2,1)∴⎩⎪⎨⎪⎧x +22=-1y -52=2z +12=1∴⎩⎪⎨⎪⎧x =-4y =9z =1∴D 点坐标为(-4,9,1)基础达标一、选择题1.若A (1,3,-2),B (-2,3,2),则A ,B 两点间的距离为( ) A.61 B .25 C .5 D.57解析:|AB|=1+22+3-32+-2-22=5.答案:C2.空间直角坐标系O-xyz中的点P(1,2,3)在xOy平面内的射影是点Q,则点Q的坐标为( )A.(1,2,0) B.(0,0,3)C.(1,0,3) D.(0,2,3)解析:因为空间直角坐标系O-xyz中,在xOy平面内的点的竖坐标是0,所以点Q的坐标为(1,2,0).答案:A3.在空间直角坐标系中,点M(-5,3,1)关于x轴的对称点的坐标为( )A.(-5,-3,-1) B.(5,3,-1)C.(5,-3,1) D.(5,-3,-1)解析:关于x轴的对称点的坐标中,横坐标不变,其余坐标变为相反数,故点M关于x 轴的对称点的坐标为(-5,-3,-1).答案:A4.点B是点A(2,-3,5)关于xOy平面的对称点,则A,B两点间的距离为( )A.10 B.10C.38 D.38解析:由于A,B关于xOy平面对称,则A,B的横、纵坐标相等,竖坐标互为相反数,故点B的坐标为(2,-3,-5),所以|AB|=2-22+-3+32+5+52=10.答案:A5.已知A点坐标为(1,1,1),B(3,3,3),点P在x轴上,且|PA|=|PB|,则P点坐标为( ) A.(6,0,0) B.(6,0,1)C.(0,0,6) D.(0,6,0)解析:设P(x,0,0),|PA|=x-12+1+1,|PB|=x-32+9+9,由|PA|=|PB|得x=6,故选A.答案:A6.在空间直角坐标系中,已知三点A(1,0,0),B(1,1,1),C(0,1,1),则三角形ABC是( ) A.直角三角形 B.等腰三角形C.等腰直角三角形 D.等边三角形解析:由题|AB|=1-12+0-12+0-12=2,|AC|=0-12+1-02+1-02=3,|BC|=0-12+1-12+1-12=1,所以AC2=AB2+BC2,所以三角形ABC是直角三角形.答案:A7.已知点A(1,2,2),B(1,-3,1),点C在yOz平面上,且点C到点A,B的距离相等,则点C的坐标可以为( )A.(0,1,-1) B.(0,-1,6)C.(0,1,-6) D.(0,1,6)解析:由题意设点C的坐标为(0,y,z),所以1+y-22+z-22=1+y+32+z-12,即(y-2)2+(z-2)2=(y+3)2+(z-1)2.经检验知,只有选项C满足.答案:C二、填空题8.点P(1,4,-3)与点Q(3,-2,5)的中点坐标是________________________________________________________________________.解析:设点P 与点Q 的中点坐标为(x ,y ,z ),则x =1+32=2,y =4-22=1,z =-3+52=1.所以中点坐标是(2,1,1).答案:(2,1,1)9.已知P ⎝ ⎛⎭⎪⎫32,52,z 到直线AB 中点的距离为3,其中A (3,5,-7),B (-2,4,3),则z =________.解析:AB 中点C ⎝ ⎛⎭⎪⎫12,92,-2,|PC |=3. 而⎝ ⎛⎭⎪⎫32-122+⎝ ⎛⎭⎪⎫52-922+[z --2]2=3,解为z =0,或z =-4. 答案:0或-410.已知平行四边形ABCD 中,A (4,1,3),B (2,-5,1),C (3,7,-5),则点D 的坐标为________.解析:设平行四边形ABCD 的两条对角线的交点为点P ,则P 为AC ,BD 的中点.由A (4,1,3),C (3,7,-5),得点P 的坐标为⎝ ⎛⎭⎪⎫72,4,-1.又点B (2,-5,1),所以点D 的坐标为(5,13,-3).答案:(5,13,-3)11.在空间直角坐标系中,点M (-2,4,-3)在xOz 平面上的射影为M ′点,则M ′点关于原点的对称点的坐标是________.解析:点M (-2,4,-3)在平面xOz 上的射影M ′(-2,0,-3),M ′关于原点的对称点的坐标是(2,0,3).答案:(2,0,3)12.三棱锥P -ABC 各顶点的坐标分别为A (0,0,0),B (1,0,0),C (0,2,0),P (0,0,3),则三棱锥P -ABC 的体积为________.解析:由A ,B ,C ,P 四点的坐标,知△ABC 为直角三角形,AB ⊥AC ,PA ⊥底面ABC .由空间两点间的距离公式,得|AB |=1,|AC |=2,|PA |=3,所以三棱锥P -ABC 的体积V =13Sh =13×12×1×2×3=1. 答案:1 三、解答题13.如图,在长方体ABCD -A 1B 1C 1D 1中,AD =AA 1=2,AB =4,DE ⊥AC ,垂足为E ,求B 1E 的长.解析:如图,以点D 为原点,以DA ,DC ,DD 1所在直线分别为x 轴,y 轴,z 轴,建立空间直角坐标系D -xyz .则D (0,0,0),B 1(2,4,2),A (2,0,0),C (0,4,0),设点E 的坐标为(x ,y,0),在坐标平面xOy 内,直线AC 的方程为x 2+y4=1,即2x +y -4=0,又DE ⊥AC ,直线DE 的方程为x -2y =0.由⎩⎪⎨⎪⎧2x +y -4=0,x -2y =0得⎩⎪⎨⎪⎧x =85,y =45,∴E ⎝ ⎛⎭⎪⎫85,45,0.∴|B 1E |=⎝ ⎛⎭⎪⎫85-22+⎝ ⎛⎭⎪⎫45-42+0-22=6105,即B 1E 的长为6105.14.已知正方形ABCD ,ABEF 的边长都是1,且平面ABCD ⊥平面ABEF ,点M 在AC 上移动,点N 在BF 上移动,若|CM |=|BN |=a (0<a <2).(1)求|MN |的长;(2)当a 为何值时,|MN |的长最小. 解析:∵平面ABCD ⊥平面ABEF , 平面ABCD ∩平面ABEF =AB ,AB ⊥BE , ∴BE ⊥平面ABCD ,∴AB ,BC ,BE 两两垂直. 过点M 作MG ⊥AB ,MH ⊥BC , 垂足分别为G ,H , 连接NG ,易证NG ⊥AB . ∵|CM |=|BN |=a ,∴|CH |=|MH |=|BG |=|GN |=22a ,∴以B 为原点,以BA ,BE ,BC 所在的直线分别为x 轴、y 轴、z 轴,建立如图所示的空间直角坐标系B -xyz ,则M ⎝⎛⎭⎪⎫22a ,0,1-22a ,N ⎝ ⎛⎭⎪⎫22a ,22a ,0.(1)|MN |=⎝ ⎛⎭⎪⎫22a -22a 2+⎝ ⎛⎭⎪⎫0-22a 2+⎝ ⎛⎭⎪⎫1-22a -02=a 2-2a +1=⎝ ⎛⎭⎪⎫a -222+12.(2)由(1)得,当a =22时,|MN |最短,最短为22,这时M ,N 恰好为AC ,BF 的中点.能力提升15.已知三点A (-1,1,2),B (1,2,-1),C (a,0,3),是否存在实数a ,使A 、B 、C 共线?若存在,求出a 的值;若不存在,说明理由.解析:AB =-1-12+1-22+2+12=14,AC =-1-a 2+1-02+2-32=a +12+2,BC =1-a 2+2-02+-1-32=a -12+20,因为BC >AB ,所以,若A ,B ,C 三点共线,有BC =AC +AB 或AC =BC +AB ,若BC =AC +AB ,整理得:5a 2+18a +19=0, 此方程无解;若AC =BC +AB ,整理得:5a 2+18a +19=0,此方程也无解. 所以不存在实数a ,使A 、B 、C 共线. 16.如图,以正方体的三条棱所在直线为坐标轴,建立空间直角坐标系,点P 在正方体的对角线AB 上,点Q 在正方体的棱CD 上.(1)当2|DQ |=|QC |时,求|PQ |;(2)当点P 为对角线AB 的中点,点Q 在棱CD 上运动时,探究|PQ |的最小值; (3)当点Q 为棱CD 的中点,点P 在对角线AB 上运动时,探究|PQ |的最小值. 解析:设正方体的棱长为a .(1)当点P 为对角线AB 的中点时,点P 的坐标是⎝ ⎛⎭⎪⎫a 2,a 2,a2. 由2|DQ |=|QC |,易知|QC |=23a ,故Q ⎝ ⎛⎭⎪⎫0,a ,23a 从而|PQ |=⎝ ⎛⎭⎪⎫a 2-02+a -a 22+⎝ ⎛⎭⎪⎫a 2-23a 2=196a . (2)∵点Q 在线段CD 上,设Q (0,a ,z ) ∴|PQ |=⎝ ⎛⎭⎪⎫-a 22+⎝ ⎛⎭⎪⎫a -a 22+⎝ ⎛⎭⎪⎫z -a 22 =⎝ ⎛⎭⎪⎫z -a 22+12a 2. 当z =a 2时,|PQ |的最小值为22a .即点Q 在棱CD 的中点时,|PQ |有最小值22a . (3)如图,当Q 为CD 的中点时,Q ⎝ ⎛⎭⎪⎫0,a ,a 2,设P 的坐标为(x ,x ,z ),则由三角形相似可得z a =2a -2x 2a,则z =a -x . ∴|PQ |2=x 2+(x -a )2+⎝ ⎛⎭⎪⎫a 2-x 2=3x 2-3ax +54a 2=3⎝ ⎛⎭⎪⎫x -a 22+a 22.当x =a 2时,|PQ |有最小值为22a ,此时P ⎝ ⎛⎭⎪⎫a 2,a 2,a2为AB 的中点.。
北师大版必修二第二章解析几何初步综合测试题

北师大版必修二第二章解析几何初步综合测试题一、单选题1.已知圆C 的标准方程为2221x y ,则它的圆心坐标是( ) A .()2,0- B .()0,2-C .()0,2D .()2,0 2.直线30x y a ++=是圆22240x y x y ++-=的一条对称轴,则a =( ) A .1- B .1 C .3- D .33.直线x +(m +1)y ﹣1=0与直线mx +2y ﹣1=0平行,则m 的值为( )A .1或﹣2B .1C .﹣2D .124.已知直线1l :210x ay +-=,与2l :()12102a x ay --+=平行,则a 的值是( ) A .0或1 B .0或14 C .0 D .145.已知两条直线()1:3450l a x y ++-=与()2:2580l x a y ++-=平行,则a 的值是( )A .7-B .1或7C .133-D .1-或7- 6.已知点(2,A 0,1),(4,B 2,3),P 是AB 的中点,则点P 的坐标为( )A .(3,1,2)B .(3,1,4)C .()0,2,1--D .(6,4,5)7.直线210x y --=与圆221x y +=的位置关系是( )A .相切B .相交且直线过圆心C .相交但直线不过圆心D .相离8.已知点A (-1,0),B (0,2),点P 是圆22:(1)1C x y -+=上任意一点,则△P AB 面积的最大值与最小值分别是( )A .2,2B .2,2C ,4D . +1-1 9.已知圆O 1的方程为x 2+(y +1)2=6,圆O 2的圆心坐标为(2,1).若两圆相交于A ,B 两点,且|AB |=4,则圆O 2的方程为( )A .(x -2)2+(y -1)2=6B .(x -2)2+(y -1)2=22C .(x -2)2+(y -1)2=6或(x -2)2+(y -1)2=22D .(x -2)2+(y -1)2=36或(x -2)2+(y -1)2=3210.已知点P 是圆()()22:31C x a y a ++-+=上一动点,点P 关于y 轴的对称点为M ,点P 关于直线1y x =+的对称点为N ,则MN 的最小值是( )A .4B .C .4D .8- 11.设P 为直线2x +y +2=0上的动点,过点P 作圆C :x 2+y 2-2x -2y -2=0的两条切线,切点分别为A ,B ,则四边形P ACB 的面积的最小值时直线AB 的方程为( ) A .2x -y -1=0 B .2x +y -1=0 C .2x -y +1=0 D .2x +y +1=012.若直线x +y ﹣m =0与曲线2y =没有公共点,则实数m 所的取值范围是( )A .[3-B .(-∞,)∪(4,+∞)C .,]D .(-∞,)∪,+∞)二、填空题13.已知直线1:10l mx y ++=,2:(1)20l x m y +-+=,若12l l ⊥,则m 值为________. 14.已知圆22:(4)4C x y ++=,过点(6,3)-与圆C 相切的直线方程为________. 15.已知点(2,2),(4,2)A B ---,点P 在圆224x y +=上运动,则22||||PA PB +的最小值是__________.16.已知圆C 的方程为2240x x y -+=,直线l :330kx y k -+-=与圆C 交于A ,B 两点,则当ABC 面积最大时,直线l 的斜率k =______.三、解答题17.已知两点(32)(54)M N -,,,,两直线12:270:10l x y l x y -+=+-=,. (1)求过点M 且与直线1l 平行的直线方程;(2)求过线段MN 的中点以及直线1l 与2l 的交点的直线方程.18.已知两圆222610x y x y +---=和2210120x y x y m +--+=.(1)m 取何值时两圆外切?(2)m 取何值时两圆内切?19.已知圆C 经过点(1,2)A -,(1,4)B ,且圆心C 在直线20x y -=上.(1)求圆C 的方程;(2)若过点(2,3)P -的直线l 与圆C 交于M ,N 两点,且MN =l 的方程.20.已知圆C 的方程:22240x y x y m +--+=.(1)求m 的取值范围;(2)当圆C 过A (1,1)时,求直线:240l x y +-=被圆C 所截得的弦MN 的长. 21.已知圆22:2220C x y x y ++--=,点(),1A m -、()4,2B m +,其中m R ∈. (1)若直线AB 与圆C 相切,求直线AB 的方程;(2)若以AB 为直径的圆D 与圆C 有公共点,求实数m 的取值范围.22.已知圆M 过点)P ,且与圆222:(1)(2)(0)N x y r r -+-=>关于直线0:20x y l +-=对称.(1)求两圆的方程;(2)若直线1:70l x y +-=,在1l 上取一点A ,过点A 作圆M 的切线,切点为B ,C .证明:BC ≠参考答案1.A【分析】根据标准方程,直接求圆心坐标.【详解】圆C 的标准方程为2221x y , 圆心坐标为()2,0-.故选:A【点睛】本题考查圆的标准方程,属于基础题型.2.B【分析】根据圆的对称性,得出圆心在直线30x y a ++=上,即可得出a 的值.【详解】由圆的对称性可知,该圆的圆心1,2在直线30x y a ++=上则()31121a =-⨯--⨯=故选:B3.C【分析】解方程m (m +1)﹣2=0,再检验即得解.【详解】由m (m +1)﹣2=0,解得m =﹣2或1.经过验证m =1时,两条直线方程都为x +2y ﹣1=0,可知两直线重合,所以舍去. 当m =﹣2时,满足题意.故选:C【点睛】本题主要考查两直线的位置关系,意在考查学生对这些知识的理解掌握水平.4.C根据直线一般式方程下直线平行的关系列式求解即可.【详解】解:因为对于直线1111:0l A x B y C ++=(11,A B 不同时为零),直线2222:0l A x B y C ++=(22,A B 不同时为零);当直线12l l //时,等价于1221122100AC A C A B A B -≠⎧⎨-=⎩; 所以有()()121022210a a a a ⎧+-≠⎪⎨⎪---=⎩,解得0a =.故选:C.【点睛】方法点睛:对于直线1111:0l A x B y C ++=(11,A B 不同时为零),直线2222:0l A x B y C ++=(22,A B 不同时为零);当直线12l l //时,等价于1221122100AC A C A B A B -≠⎧⎨-=⎩; 当直线12l l ⊥时,等价于12120A A B B +=;5.D【分析】根据两直线平行的条件,得出关于a 的方程,求得a 的值,即可得到答案.【详解】由题意,直线()1:3450l a x y ++-=与()2:2580l x a y ++-=相互平行,可得(3)(5)420a a ++-⨯=,整理的2870a a ++=,解得1a =-或7a =-.经验证,当1a =-或7a =-时,此时12l l //,所以a 的值是1-或7-.故选:D.6.A利用中点坐标公式直接求解即可【详解】根据题意,点(2,A 0,1),(4,B 2,3),P 是AB 中点,则点P 的坐标为240213,,222+++⎛⎫⎪⎝⎭,即(3,1,2). 故选:A.7.C【分析】 求出圆心到直线的距离,与半径比较大小,即可得到结论.【详解】圆221x y +=的圆心()0,0O ,半径1r =. 因为圆心()0,0O 到直线210x y --=的距离15d ==<. 所以直线与圆相交但直线不过圆心.故选:C8.B【分析】求得圆心到直线AB l 的距离d =,结合点与圆的位置关系,结合三角形的面积公式,即可求解.【详解】由题意知AB ==:220AB l x y -+=,又由圆22:(1)1C x y -+=的圆心坐标为(1,0),所以圆心到直线AB l的距离5d ==,所以PAB S 的最大值为11)22=,PAB S 的最小值为1(1)2252-=-. 9.C【分析】设出圆O 2的方程,进而可得直线AB 的方程,再由垂径定理运算即可得解.【详解】由题意,设圆O 2的方程为222(2)(1)(0)x y r r -+-=>因为圆O 1的方程为22(1)6x y ++=,所以圆O 1的圆心为()0,1-, 所以直线AB 的方程为244100x y r ++-=, 则圆心O 1到直线AB 的距离2d =, 所以2262AB d ⎛⎫= ⎪⎝⎭+即2246+=,解得26r =或22,故圆O 2的方程为22(2)(1)6x y -+-=或22(2)(1)22x y -+-=. 故选:C.10.C【分析】先设()P m n ,,则(),M m n -,()1,1N n m -+,由两点间距离公式,得到MN =由圆的性质,求出其最小值,即可得出结果.【详解】设()P m n ,,则(),M m n -,()1,1N n m -+,MN ==C 上的点()P m n ,到定点()0,1A 的距离,由题得,圆心(),3C a a --,半径1r =,根据圆的性质可得,11AP AC r ≥-==11=≥,当且仅当2a =时,等号成立;所以()14MN =≥=所以MN 的最小值是4故选:C.【点睛】关键点点睛:求解本题的关键在于,通过设点()P m n ,,得到M ,N 坐标,根据两点间距离公式,得到MN =. 11.D【分析】根据圆的切线性质可知四边形PACB 的面积转化为直角三角形的面积,结合最小值可求直线AB 的方程.【详解】由于,PA PB 是圆()()22:114C x y -+-=的两条切线,,A B 是切点,所以2||||2||PACB PAC S S PA AC PA ∆==⋅=== 当||PC 最小时,四边形PACB 的面积最小,此时PC :11(x 1)2y -=-,即210.y x --= 联立210,220y x x y --=⎧⎨++=⎩得1,,(1,0),0x P y =-⎧-⎨=⎩PC 的中点为1(0,),||2PC ==以PC 为直径的圆的方程为2215(),24x y +-=即2210x y y +--=, 两圆方程相减可得直线AB 的方程210,x y ++=故选:D.12.D【分析】将曲线方程等价变形,得到其表示下半圆,在同一个坐标系中画出图象,结合图形得到结果.【详解】 由2(2)y x x =--+等价变形得:(x +1)2+(y ﹣2)2=1(12y ≤≤),曲线2(2)y x x =--+表示以(﹣1,2)为圆心,半径为1的下半圆, 作出曲线2(2)y x x =--+,以及直线x +y ﹣m =0,由直线和圆(x +1)2+(y ﹣2)2=1相切, 即1212md -+-==,解得m =2m =2(舍去),当直线通过(0,2)时,0+2﹣m =0,即m =2,可得m <2或m >2时,直线x +y ﹣m =0与曲线2(2)y x x =-+ 故选:D .【点睛】该题考查的是有关根据曲线没有公共点求参数的取值范围的问题,涉及到的知识点有数形结合思想的应用,直线与圆的位置关系,属于简单题目.13.12【分析】本题考查两直线的垂直的条件,根据两直线垂直的条件列出关于m 的方程,求解.【详解】解:直线1:10l mx y ++=,2:(1)20l x m y +-+=,若12l l ⊥,则()1110m m ⨯+⨯-=,解得12m =, 故答案为:12.【点睛】两直线1110a x b y c ++=,2220a x b y c ++=垂直的充分必要条件是12120a a b b +=. 14.6x =-或51122y x =-+,(答案:6x =-或12560y x +-=也可以) 【分析】本题考查求圆的切线方程,分斜率存在与不存在,利用由圆心到切线的距离等于半径,求解即得. 【详解】解:圆22:(4)4C x y ++=的圆心坐标()4,0C -,半径2r =,过点(6,3)-的直线,当斜率不存在时,直线的方程为6x =-,显然到圆心的距离正好等于半径,故而是圆的一条切线;当斜率存在时,设斜率为k ,直线的方程为()36y k x -=+,即:630kx y k -++=,2=,解得512k =-, 故切线的方程为51122y x =-+, 故答案为:6x =-或51122y x =-+,(答案:6x =-或12560y x +-=也可以) 【点睛】关键是由首先验证斜率不存在时是否是圆的切线,一定要养成思维严密有序的良好习惯. 15.36- 【分析】设(,)P x y ,求出22||||PA PB +,再利用几何意义求得最小值. 【详解】设(,)P x y ,则22||||PA PB +22222222(2)(2)(4)(2)2(1)2(2)182(1)(2)18x y x y x y x y ⎡⎤=++++-++=-+++=-+++⎣⎦,又记(1,2)C -,CO =O 为坐标原点), 则22(1)(2)-++x y的最小值为22(2)2)9CO -==-所以22PA PB +的最小值为2(91836-+=-故答案为:36- 【点睛】本题考查用几何意义平面上的最值问题.对一些特殊的表达式可利用几何意义求解: 平方和形式:22()()x a y b -+-(,)P x y 与(,)Q a b 的距离, 分式形式:y bx a--表示(,)P x y 与定点(,)a b 连线斜率.这是两个常用的几何意义. 另外圆外的点到圆上点的最值可通过定点到圆心距离求解. 16.1或7- 【分析】由三角形面积公式求得ABC 面积最大时,2ACB π∠=,这样可求得圆心C 到直线BC 的距离,再由点到直线距离公式求得斜率k . 【详解】圆C 的标准方程为()2224x y -+=,直线l 可变形为()33y k x =-+,则圆心C 为()2,0,半径为2,直线l 过定点()3,3, 由面积公式可得21sin 2sin 22ABCS r ACB ACB =∠=∠≤, 所以当2ACB π∠=,即圆心C 到直线l的距离为d =ABC 的面积取得最大值,所以d ==1k =或7-.故答案为:1或7-. 【点睛】易错点睛:直线与圆相交于,A B ,圆心为C ,ABC 面积为21sin 2S r ACB =∠,当ACB ∠的最大值θ不小于2π时,2ABC π∠=时,S 取得最大值212r ,当ACB ∠的最大值2πθ<时,S 取得最大值21sin 2r θ.不是任何时候最大值都是212r .17.(1)280x y -+=;(2)30.y -=. 【分析】(1)根据两直线平行设出所求直线方程,代入点(3,2)M -的坐标可解得结果;(2)根据中点坐标公式求出线段MN 的中点,根据两条直线方程解出交点坐标,由此可得所求直线方程. 【详解】(1)因为所求直线与直线1l 平行,所以设所求直线方程为20x y C -+=(7)C ≠, 因为所求直线经过点(3,2)M -,所以2(3)20C ⨯--+=,得8C =, 所以所求直线方程为280x y -+=.(2)因为(32)(54)M N -,,,,所以线段MN 的中点为(1,3), 联立27010x y x y -+=⎧⎨+-=⎩,得23x y =-⎧⎨=⎩,即直线1l 与2l 的交点为(2,3)-故所求直线方程为30.y -= 【点睛】结论点睛:与直线0Ax By C ++=平行的直线方程可设为10Ax By C ++=;与直线0Ax By C ++=垂直的直线方程可设为10Bx Ay C -+=.18.(1)25m =+(2)25m =-. 【分析】(1)两圆位置关系外切,则圆心距等于半径之和; (2)两圆位置关系内切,则圆心距等于半径之差. 【详解】解:两圆的标准方程为:()()221311x y -+-=,()()225661x y m -+-=-, 圆心分别为()1,3M ,()5,6N,半径分别为1r =和2r =5MN ==.(1)当两圆外切时,圆心距12MNr r =+,即5=解得25m =+(2)当两圆内切时,因定圆的半径1r =小于两圆圆心间距离5,故为小圆,即12MN rr =-,5=25m =-19.(1)()()22124x y -+-=;(2)3y =或3460x y +-=. 【分析】(1)由已知先设出圆心C 的坐标为(,2)a a ,再求出AB 的中点E 的坐标,利用AB 与CE 垂直即可求出a 的值,进而可求出半径,即可求得圆的方程;(2)根据点斜率方程设出直线的方程,求出圆心到直线的距离,然后利用弦长的一半以及半径和圆心到直线的距离建立方程,即可求解 【详解】解:(1)由题意设圆心C 的坐标为(,2)a a ,由(1,2)A -,(1,4)B ,可得AB 的中点E 的坐标为(0,3), 因为ABCE ,所以1AB CE k k ⋅=-,即4223111a a--⋅=---,解得1a =, 则圆心(1,2)C ,半径2r AC ==, 所以圆C 的方程为()()22124x y -+-=.(2)设直线l 的方程为()32y k x -=+,圆心C 到直线l 的距离d =1=1=; 解方程得:0k =或34k =-所以直线l 的方程为3y =或3460x y +-=.20.(1)5m <;(2. 【分析】(1)将圆的方程整理成标准形式,可得不等式50m ->,即可得答案; (2)求出圆的方程,再根据圆的弦长公式,即可得答案; 【详解】解:(1)圆C 的方程可化为22(1)(2)5x y m -+-=-令50m ->得5m <(2)∵圆C 过A (1,1)代入得4m =,圆C 方程为22(1)(2)1x y -+-=圆心C (1,2),半径1r =,圆心C (1,2)到直线:240l x y +-=的距离为5d ==∴5MN ==. 21.(1)34170x y -+=或3430x y --=;(2)33.⎡⎤--⎣⎦【分析】(1)求出圆心C 的圆心坐标与半径长,求出直线AB 的方程,利用直线AB 与圆C 相切可得出圆心C 到直线AB 的距离等于圆C 的半径,可得出关于实数m 的等式,求出m 的值,进而可求得直线AB 的方程;(2)求出线段AB 的中点D 的坐标,由题意可得出关于m 的不等式,即可解得实数m 的取值范围. 【详解】(1)圆C 的标准方程为()()22114x y ++-=,圆心()1,1C -,半径为2r,直线AB 的斜率为()21344AB k m m +==+-,所以,直线AB 的方程为()314y x m +=-,即34340x y m ---=, 由于直线AB 与圆C 相切,则31125m --=,解得13m =-或7m =-,因此,直线AB 的方程为34170x y -+=或3430x y --=; (2)线段AB 的中点为12,2D m ⎛⎫+ ⎪⎝⎭,且5AB =, 由于以AB 为直径的圆D 与圆C 有公共点,则22AB ABr CD r -≤≤+,可得1922≤≤,解得33m --≤≤-,故实数m 的取值范围为33⎡⎤--⎣⎦.【点睛】关键点睛:本题考查利用两圆有公共点求参数的取值范围,若两圆圆心分别为1C 、2C ,半径分别为1r 、2r ,可将问题等价转化为121212r r C C r r -≤≤+来处理.22.(1)圆22:(1)9M x y +-=,圆22:(1)(2)9N x y -+-=;(2)证明见解析.【分析】(1)由MN 与0l 垂直,MN 的中点在0l 上,可求得M 点坐标,得圆半径,从而得两圆方程;(2)设点(,7)A a a -,设B ,C 中点为Q .,假设BC =,则BQ =,由切线性质求得AM 2=,如果此方程有解,则在在,此方程无解,则不存在,假设错误.从而可得结论. 【详解】解:(1)设点()00,M x y ,因为圆M 与圆N 关于直线0:20x y l +-=对称,且()1,2N ,根据直线MN 与直线0l 垂直,M ,N 中点在直线0l 上,得0000211122022y x x y -⎧=⎪-⎪⎨++⎪+-=⎪⎩,解得0001x y =⎧⎨=⎩,即(0,1)M ,所以||3MP ==,3r =,所以圆22:(1)9M x y +-=,圆22:(1)(2)9N x y -+-=.(2)由题可知1:70l x y +-=,设点(,7)A a a -,设B ,C 中点为Q .假设BC =,则BQ = 又∵3BM =,90BQM ∠=︒,∴MQ =, ∵BMQ 与AMB 相似,∴MQ BM BMAM=,∴22BM AM MQ===,= 整理得24521202a a -+=, ∵45144421602∆=-⨯⨯=-<,所以方程无解,假设BC =不成立,所以BC ≠【点睛】方法点睛:本题考查圆关于直线对称问题,考查圆的切点弦长问题.解题方法:关于直线对称的圆的方程,圆心关于直线的对称点即为对称圆的圆心,半径为变,由此易得.过圆外一点作圆的切线,切点弦长一般结合几何方法求解,即由图中的BMQ与AMB相似建立关系求解.。
2019_2020学年高中数学第二章解析几何初步1.5平面直角坐标系中的距离公式练习(含解析)北师大版必修2

1.5 平面直角坐标系中的距离公式填一填1.两点间的距离公式 (1)数轴上:一般地,数轴上两点A ,B 对应的实数分别是x A ,x B ,则|AB |=|x B -x A |. (2)平面直角坐标系中:一般地,若两点A ,B 对应的坐标分别为A (x 1,y 1),B (x 2,y 2),则|AB |=x 2-x 12+y 2-y 12. 2.点到直线的距离点P (x 0,y 0)到直线Ax +By +C =0的距离记为d ,则d =|Ax 0+By 0+C |A 2+B2. 3.两平行线间的距离两条平行直线的方程分别为l 1:Ax +By +C 1=0,l 2:Ax +By +C 2=0,两条直线间的距离记为d ,即d =|C 2-C 1|A 2+B2.判一判1.原点O 到点P (x ,y )的距离为|OP |=x 2+y 2.(√) 23.平面内任意两点间的距离均可使用两点间的距离公式.(√)4.直线l 1:Ax +By +C 1=0与l 2:Ax +By +C 2=0的距离是|C 1-C 2|.(×)5.原点到直线Ax +By +C =0的距离公式是|C |A 2+B2.(√)6.平行线间的距离是两平行线上两点间距离的最小值.(√) 7.连接两条平行直线上两点,即得两平行线间的距离.(×)8想一想1. 提示:点到直线的距离公式只适用直线方程的一般式.2.两条平行直线间的距离公式写成d =|C 1-C 2|A 2+B 2时对两条直线应有什么要求?提示:两条平行直线的方程都是一般式,并且x ,y 的系数分别对应相等. 3.两条平行直线间距离有哪几种求法? 提示:(1)直接利用两平行线间的距离公式.(2)在一条直线上任意选取一点利用点到直线的距离公式求解(一般要选特殊的点,如直线与坐标轴的交点、坐标为整数的点).(3)当两直线都与x 轴(或y 轴)垂直时,可利用数形结合来解决. ①当两直线都与x 轴垂直时,l 1:x =x 1,l 2:x =x 2,则d =|x 2-x 1|; ②当两直线都与y 轴垂直时,l 1:y =y 1,l 2:y =y 2,则d =|y 2-y 1|. 4.距离公式综合应用的常见类型有哪些? 提示:(1)最值问题.①利用对称转化为两点之间的距离问题.②利用所求式子的几何意义转化为点到直线的距离.③利用距离公式将问题转化为一元二次函数的最值问题,通过配方求最值. (2)求参数问题.利用距离公式建立关于参数的方程或方程组,通过解方程或方程组求值. (3)求方程的问题.立足确定直线的几何要素——点和方向,利用直线方程的各种形式,结合直线的位置关系(平行直线系、垂直直线系及过交点的直线系),巧设直线方程,在此基础上借助三种距离公式求解.思考感悟:练一练1.已知A (3,7),B A .5 B. 5 C .3 D .29 答案:B2.已知直线上两点A (a ,b ),B (c ,d ),且a 2+b 2-c 2+d 2=0,则( ) A .原点一定是线段AB 的中点 B .A ,B 一定都与原点重合C .原点一定在线段AB 上,但不是线段AB 的中点D .原点一定在线段AB 的垂直平分线上 答案:D3.点(1,-1)到直线x -y +1=0的距离是( )A .3 2 B.22C .3 D.322答案:D4.点(5,-3)到直线x +2=0的距离等于( ) A .7 B .5 C .3 D .2 答案:A5.直线l 1:x +y =0与直线l 2:2x +2y +1=0间的距离是________.答案:24知识点一两点间距离公式的应用1.已知点A (2,m )与点B (m,1)间的距离是13,则实数m =( )A .-1B .4C .-1或4D .-4或1 解析:∵|AB |=m -22+1-m 2=13,∴m 2-3m -4=0,解得m =-1或m =4. 答案:C2.已知点A (2,1),B (-2,3),C (0,1),则△ABC 中,BC 边上的中线长为________. 解析:BC 中点为(-1,2),所以BC 边上中线长为2+12+1-22=10. 答案:10知识点二 求点到直线的距离3.已知点(a,1)到直线x -y +1=0的距离为1,则a 的值为( ) A .1 B .-1 C. 2 D .± 2解析:由题意,得|a -1+1|12+-12=1,即|a |=2, 所以a =± 2.故选D. 答案:D4.点P (x ,y )在直线x +y -4=0上,O 是原点,则|OP |的最小值是( ) A.10 B .2 2 C. 6 D .2解析:由题意可知|OP |的最小值即原点(0,0)到直线x +y -4=0的距离d =|-4|2=2 2.知识点三 两条平行直线间的距离5.12b +c 等于( )A .-12B .48C .36D .-12或48解析:将l 1:3x +4y +5=0改写为6x +8y +10=0, 因为两条直线平行,所以b =8. 由|10-c |62+82=3,解得c =-20或c =40.所以b +c =-12或48.故选D. 答案:D6.已知直线3x +2y -3=0和6x +my +1=0互相平行,则它们之间的距离是( )A .4 B.21313C.51326 D.71326解析:由两直线平行可知36=2m ≠-31,故m =4.又方程6x +4y +1=0可化简为3x +2y +12=0,∴平行线间的距离为|12--3|22+32=71326.故选D. 答案:D知识点四 对称问题7.直线y =3xA .y =3x -10B .y =3x -18C .y =3x +4D .y =4x +3解析:在直线上任取两点A (1,-1),B (0,-4),则其关于点P 的对称点A ′,B ′可由中点坐标公式求得为A ′(3,-1),B ′(4,2),由两点式可求得方程为y =3x -10.答案:A8.直线2x +3y -6=0关于点(1,-1)对称的直线的方程是( ) A .3x -2y +2=0 B .2x +3y +7=0 C .3x -2y -12=0 D .2x +3y +8=0解析:由平面几何知识易知所求直线与已知直线2x +3y -6=0平行,则可设所求直线的方程为2x +3y +C =0(C ≠-6).在直线2x +3y -6=0上任取一点(3,0),其关于点(1,-1)对称的点为(-1,-2),则点(-1,-2)必在所求直线上,∴2×(-1)+3×(-2)+C =0,解得C =8. 故所求直线的方程为2x +3y +8=0. 答案:D综合知识 距离公式的综合应用9.已知△ABC 中,A (2,-1),B (4,3),C (3,-2). (1)求BC 边上的高所在直线方程的一般式; (2)求△ABC 的面积.解析:(1)因为k BC =3--24-3=5,所以BC 边上的高AD 所在直线斜率k =-15.所以AD 所在直线方程为y +1=-15(x -2).即x +5y +3=0.(2)BC 的直线方程为:y +2=5(x -3). 即5x -y -17=0,点A 到直线BC 的距离为|2×5--1-17|52+-12=626. 又因为|BC |=3-42+-2-32=26,所以△ABC 的面积S =12×626×26=3.10.已知直线l 1经过点A (0,1),直线l 2经过点B (5,0),且直线l 1∥l 2,l 1与l 2间的距离为5,求直线l 1,l 2的方程.解析:∵直线l 1∥l 2,∴当直线l 1,l 2垂直于x 轴时,直线l 1的方程为x =0,直线l 2的方程为x =5, 这时直线l 1,l 2之间的距离等于5,符合题意. 当直线l 1,l 2不垂直于x 轴时,可设其斜率为k , 依题意得,直线l 1的方程为y =kx +1,即kx -y +1=0,直线l 2的方程为y =k (x -5), 即kx -y -5k =0.由两条平行直线间的距离公式,得|1+5k |1+k2=5, 解得k =125.∴直线l 1的方程为12x -5y +5=0,直线l 2的方程为12x -5y -60=0.综上,符合题意的直线l 1,l 2的方程有两组:l 1:x =0,l 2:x =5或l 1:12x -5y +5=0,l 2:12x -5y -60=0.基础达标一、选择题1.点P (1,-1)到直线l :3y =2的距离是( )A .3 B.53C .1 D.22解析:点P (1,-1)到直线l 的距离d =|3×-1-2|02+32=53,选B. 答案:B2.已知点M (1,4)到直线l :mx +y -1=0的距离为3,则实数m =( )A .0 B.34C .3D .0或34解析:点M 到直线l 的距离d =|m +4-1|m 2+1=|m +3|m 2+1,所以|m +3|m 2+1=3,解得m =0或m =34,选D.答案:D3.两条平行直线3x +4y -12=0与ax +8y +11=0间的距离为( ) A.1310 B.135 C.72 D.235解析:直线3x +4y -12=0,即直线6x +8y -24=0,根据直线3x +4y -12=0与ax +8y +11=0平行,可得a =6,故两条平行直线3x +4y -12=0与ax +8y +11=0间的距离为|-24-11|36+64=72. 答案:C4.已知点A (1,3),B (3,1),C (-1,0),则△ABC 的面积等于( ) A .3 B .4 C .5 D .6解析:设AB 边上的高为h ,则S △ABC =12|AB |·h .|AB |=3-12+1-32=22,AB 边上的高h 就是点C 到直线AB 的距离.AB 边所在的直线方程为y -31-3=x -13-1,即x +y -4=0.点C 到直线x +y -4=0的距离为|-1+0-4|2=52,因此,S △ABC =12×22×52=5.答案:C5.直线l 垂直于直线y =x +1,原点O 到l 的距离为1,且l 与y 轴正半轴有交点.则直线l 的方程是( )A .x +y -2=0B .x +y +1=0C .x +y -1=0D .x +y +2=0解析:因为直线l 与直线y =x +1垂直,所以设直线l 的方程为y =-x +b .又l 与y 轴正半轴有交点,知b >0,即x +y -b =0(b >0),原点O (0,0)到直线x +y -b =0(b >0)的距离为|0+0-b |12+12=1,解得b =2(b =-2舍去),所以所求直线l 的方程为x +y -2=0. 答案:A6.已知△ABC 的三个顶点是A (-a,0),B (a,0)和C ⎝ ⎛⎭⎪⎫a2,32a ,则△ABC 的形状是( )A .等腰三角形B .等边三角形C .直角三角形D .斜三角形解析:因为k AC =32a a 2+a =33,k BC =32a a2-a=-3,k AC ·k BC =-1,所以AC ⊥BC ,又|AC |=⎝ ⎛⎭⎪⎫a 2+a 2+⎝ ⎛⎭⎪⎫32a 2=3|a |. |BC |=⎝ ⎛⎭⎪⎫a 2-a 2+⎝ ⎛⎭⎪⎫32a -02=|a |,|AC |≠|BC |. 所以△ABC 为直角三角形.答案:C7.若动点A (x 1,y 1),B (x 2,y 2)分别在直线l 1:x +y -7=0和l 2:x +y -5=0上移动,则AB 的中点M 到原点距离的最小值为( )A .3 2B .2 C. 2 D .4解析:由题意,知点M 在直线l 1与l 2之间且与两直线距离相等的直线上,设该直线方程为x +y +c =0,则|c +7|2=|c +5|2,即c =-6,∴点M 在直线x +y -6=0上,∴点M 到原点的距离的最小值就是原点到直线x +y -6=0的距离,即|-6|2=3 2.答案:A 二、填空题8.已知点A (-1,2),B (3,b )的距离是5,则b =________.解析:根据两点间的距离公式,可得3+12+b -22=5,解得b =5或b =-1. 答案:5或-19.若点(2,k )到直线5x -12y +6=0的距离是4,则k 的值是________.解析:∵|5×2-12k +6|52+122=4, ∴|16-12k |=52,∴k =-3,或k =173.答案:-3或17310.两直线3x +y -3=0与6x +my +n =0平行且距离为10,则m +n =________. 解析:因为两直线平行,所以m =2, 由两平行线的距离公式知⎪⎪⎪⎪⎪⎪-3-n 232+12=10, 解得n =14或n =-26.所以m +n =16或m +n =-24. 答案:16或-2411.已知直线l 过点P (3,4)且与点A (-2,2),B (4,-2)等距离,则直线l 的方程为________________________________________________________________________.解析:显然直线l 的斜率不存在时,不满足题意; 设所求直线方程为y -4=k (x -3), 即kx -y +4-3k =0,由已知,得|-2k -2+4-3k |1+k 2=|4k +2+4-3k |1+k 2, 所以k =2或k =-23.所以所求直线l 的方程为2x -y -2=0或2x +3y -18=0. 答案:2x -y -2=0或2x +3y -18=012.已知实数x ,y 满足2x +y +5=0,那么x 2+y 2的最小值为________.解析:求x 2+y 2的最小值,就是求2x +y +5=0上的点到原点的距离的最小值,转化为坐标原点到直线2x +y +5=0的距离d =522+12= 5. 答案: 5 三、解答题13.已知点P (2,-1).(1)求过P 点且与原点距离为2的直线l 的方程;(2)求过P 点且与原点距离最大的直线l 的方程,最大距离是多少?(3)是否存在过P 点且与原点距离为6的直线?若存在,求出方程;若不存在,请说明理由.解析:(1)过P 点的直线l 与原点距离为2,而P 点坐标为(2,-1),可见,过P 点垂直于x 轴的直线满足条件,此时直线l 的斜率不存在,其方程为x =2.若直线l 的斜率存在,设其方程为y +1=k (x -2),即kx -y -2k -1=0.由已知,得|-2k -1|k 2+1=2,解得k =34,此时l 的方程为3x -4y -10=0.综上,直线l 的方程为x =2或3x -4y -10=0.(2)过P 点且与原点O 距离最大的直线是过P 点且与OP 垂直的直线.由l ⊥OP ,得k l k OP=-1,所以k l =-1k OP=2.由直线方程的点斜式得y +1=2(x -2),即2x -y -5=0.即直线2x -y -5=0是过P 点且与原点O 距离最大的直线,最大距离为|-5|5= 5.(3)由(2)可知,存在过点P 且到原点距离最大为5的直线,因此不存在过点P 到原点距离为6的直线.14.已知直线l 1:x +3y -3m 2=0和直线l 2:2x +y -m 2-5m =0相交于点P (m ∈R ). (1)用m 表示直线l 1与l 2的交点P 的坐标;(2)当m 为何值时,点P 到直线x +y +3=0的距离最短?并求出最短距离.解析:(1)解方程组⎩⎪⎨⎪⎧x +3y -3m 2=0,2x +y -m 2-5m =0,得x =3m ,y =m 2-m ,∴直线l 1与l 2的交点P 的坐标为(3m ,m 2-m ).(2)设点P 到直线x +y +3=0的距离为d ,d =|3m +m 2-m +3|2=|m 2+2m +3|2=|m +12+2|2=m +12+22,∴当m =-1时,即P 点坐标为(-3,2)时,点P 到直线x +y +3=0的距离最短,最短距离为 2.能力提升15.已知两点A (2,3),B (4,1),直线l :x +2y -2=0,在直线l 上求一点P . (1)使|PA |+|PB |最小; (2)使||PA |-|PB ||最大.解析:(1)可判断A ,B 在直线l 的同侧,设A 点关于l 的对称点A 1的坐标为(x 1,y 1), 则有⎩⎪⎨⎪⎧x 1+22+2·y 1+32-2=0,y 1-3x 1-2·⎝ ⎛⎭⎪⎫-12=-1,解得⎩⎪⎨⎪⎧x 1=-25,y 1=-95.由直线的两点式方程得直线A 1B 的方程为y -1-95-1=x -4-25-4,即y =711(x -4)+1,由⎩⎪⎨⎪⎧x +2y -2=0,y =711x -4+1得直线A 1B 与l 的交点为P ⎝⎛⎭⎪⎫5625,-325,由平面几何知识可知,此时|PA |+|PB |最小.(2)由直线的两点式方程求得直线AB 的方程为y -31-3=x -24-2,即x +y -5=0.由⎩⎪⎨⎪⎧x +2y -2=0,x +y -5=0得直线AB 与l 的交点为P (8,-3),此时||PA |-|PB ||最大.16.已知三条直线l 1:mx -y +m =0,l 2:x +my -m (m +1)=0,l 3:(m +1)x -y +(m +1)=0,它们围成△ABC .(1)求证:不论m 取何值时,△ABC 中总有一个顶点为定点; (2)当m 取何值时,△ABC 的面积取最值?并求出最值. 解析:(1)证明:设直线l 1与直线l 3的交点为A .由⎩⎪⎨⎪⎧mx -y +m =0,m +1x -y +m +1=0,解得⎩⎪⎨⎪⎧x =-1,y =0,∴点A 的坐标为(-1,0),∴不论m 取何值,△ABC 中总有一个顶点A (-1,0)为定点.(2)由⎩⎪⎨⎪⎧ x +my -m m +1=0,m +1x -y +m +1=0,解得⎩⎪⎨⎪⎧x =0,y =m +1,即l 2与l 3交点为B (0,m +1).再由⎩⎪⎨⎪⎧mx -y +m =0,x +my -m m +1=0,解得⎩⎪⎨⎪⎧x =m m 2+1,y =m 3+m 2+mm 2+1,即l 1与l 2交点为C ⎝ ⎛⎭⎪⎫mm 2+1,m 3+m 2+m m 2+1.设边AB 上的高为h , ∴S △ABC =12|AB |·h =12·1+m +12·⎪⎪⎪⎪⎪⎪m m +1m 2+1-m 3+m 2+m m 2+1+m +1m +12+1=12·|m 2+m +1|m 2+1=12·m 2+m +1m 2+1=12⎝ ⎛⎭⎪⎫1+m m 2+1.当m =0时,S =12;当m ≠0时,S =12⎝⎛⎭⎪⎪⎫1+1m +1m . ∵函数f (x )=x +1x的值域为[2,+∞)∪(-∞,-2].∴-12≤1m +1m <0或0<1m +1m≤12,∴14≤S <12或12<S ≤34. 当m =1时,△ABC 的面积的最大值为34,当m =-1时,△ABC 的面积的最小值为14.。
北师大版高一数学必修2解析几何初步试题及答案
《解析几何初步》检测试题一、选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.过点(1,0)且与直线x-2y-2=0平行的直线方程是( ) A.x-2y-1=0 B.x-2y+1=0 C.2x+y-2=0 D.x+2y-1=0 2.若直线210ay -=与直线(31)10a x y -+-=平行,则实数a 等于( )A 、12B 、12- C 、13D 、13-3.若直线32:1+=x y l ,直线2l 与1l 关于直线x y -=对称,则直线2l 的斜率为 ( )A .21B .21- C .2 D .2- 4.在等腰三角形AOB 中,AO =AB ,点O(0,0),A(1,3),点B 在x 轴的正半轴上,则直线AB 的方程为( ) A .y -1=3(x -3) B .y -1=-3(x -3) C .y -3=3(x -1) D .y -3=-3(x -1)5.直线02032=+-=+-y x y x 关于直线对称的直线方程是 ( ) A .032=+-y xB .032=--y xC .210x y ++=D .210x y +-=6.若直线()1:4l y k x =-与直线2l 关于点)1,2(对称,则直线2l 恒过定点( )A .0,4B .0,2C .2,4D .4,27.已知直线mx+ny+1=0平行于直线4x+3y+5=0,且在y 轴上的截距为31,则m ,n 的值分别为A.4和3B.-4和3C.- 4和-3D.4和-3 8.直线x-y+1=0与圆(x+1)2+y 2=1的位置关系是( ) A 相切 B 直线过圆心 C .直线不过圆心但与圆相交 D .相离 9.圆x 2+y 2-2y -1=0关于直线x -2y -3=0对称的圆方程是( )A.(x -2)2+(y+3)2=12 B.(x -2)2+(y+3)2=2C.(x +2)2+(y -3)2=12 D.(x +2)2+(y -3)2=210.已知点(,)P x y 在直线23x y +=上移动,当24x y +取得最小值时,过点(,)P x y 引圆22111()()242x y -++=的切线,则此切线段的长度为( )A .2B .32C .12D .211.经过点(2,3)P -作圆22(1)25x y ++=的弦AB ,使点P 为弦AB 的中点,则弦AB 所在直线方程为( ) A .50x y --= B .50x y -+= C .50x y ++=D .50x y +-=12.直线3y kx =+与圆()()22324x y -+-=相交于M,N 两点,若MN≥k的取值范围是()A.34⎡⎤-⎢⎥⎣⎦,B.[]34⎡⎤-∞-+∞⎢⎥⎣⎦,,C.⎡⎢⎣⎦ D.23⎡⎤-⎢⎥⎣⎦,二填空题:(本大题共4小题,每小题4分,共16分.)13.已知点()1,1A-,点()3,5B,点P是直线y x=上动点,当||||PA PB+的值最小时,点P的坐标是。
北师大版数学必修二同步配套试题:第二章 解析几何初步测评
第二章测评(时间:120分钟满分:150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.过两点A(-2,m),B(m,4)的直线倾斜角是45°,则m的值是()A.-1B.3C.1D.-3解析由k AB==tan 45°=1,得m=1.★答案☆C2.点A到点B的距离为()A.B.3C.D.解析|AB|=.★答案☆D3.已知点A(1,2),B(-2,3),C(4,y)在同一直线上,则y的值为()A.-1B.C.1D.解析由A,B,C三点共线,得k AB=k AC,即,解得y=1,故选C.★答案☆C4.如果AC<0,且BC<0,那么直线Ax+By+C=0不经过()A.第一象限B.第二象限C.第三象限D.第四象限解析由已知得直线Ax+By+C=0在x轴上的截距->0,在y轴上的截距->0,故直线经过第一、第二、第四象限,不经过第三象限.★答案☆C5.已知直线l过圆x2+(y-3)2=4的圆心,且与直线x+y+1=0垂直,则l的方程是 ()A.x+y-2=0B.x-y+2=0C.x+y-3=0D.x-y+3=0解析已知圆的圆心为(0,3),直线x+y+1=0的斜率为-1,则所求直线的斜率为1,故所求直线的方程为y=x+3,即x-y+3=0.故选D.★答案☆D6.若直线(a+2)x+(1-a)y=a2(a>0)与直线(a-1)x+(2a+3)y+2=0互相垂直,则a的值是()A.1B.-1C.±1D.-2解析因为两直线垂直,所以(a+2)(a-1)+(1-a)·(2a+3)=0,解得a=±1,又a>0,所以a=1,故选A.★答案☆A7.已知点P(2,-1)是圆(x-1)2+y2=25的弦AB的中点,则弦AB所在直线的方程是()A.x-y-3=0B.x+y-1=0C.2x+y-3=0D.2x-y-5=0解析由圆心O(1,0),P(2,-1),得k PO=-1,由圆的性质可知AB与OP垂直,所以AB的斜率为1,所以AB的方程为x-y-3=0,故选A.★答案☆A8.已知P是圆O:x2+y2=1上的动点,则点P到直线l:x+y-2=0的距离的最小值为()A.1B.C.2D.2解析圆心O(0,0)到直线x+y-2=0的距离d==2,又圆的半径r=1,所以点P到直线距离的最小值为2-1=1.★答案☆A9.过点P(-2,4)作圆O:(x-2)2+(y-1)2=25的切线l,直线m:ax-3y=0与直线l平行,则直线l与m的距离为()A.4B.2C.D.解析因为点P(-2,4)在圆上,圆心O为(2,1),则k OP==-.所以切线l的斜率k=.即直线l的方程为y-4=(x+2),整理得4x-3y+20=0.又直线m与l平行,所以直线m的方程为4x-3y=0.故两平行直线的距离为d==4.★答案☆A10.已知圆x2+y2+2x-2y+a=0截直线x+y+2=0所得弦的长度为4,则实数a的值是()A.-2B.-4C.-6D.-8解析圆的方程可化为(x+1)2+(y-1)2=2-a,因此圆心为(-1,1),半径r=.圆心到直线x+y+2=0的距离d=,又弦长为4,因此,由勾股定理可得()2+=()2,解得a=-4.故选B.★答案☆B11.已知圆C:(x-3)2+(y-4)2=1和两点A(-m,0),B(m,0)(m>0).若圆C上存在点P,使得∠APB=90°,则m 的最大值为()A.7B.6C.5D.4解析因为A(-m,0),B(m,0)(m>0),所以使∠APB=90°的点P在以线段AB为直径的圆上,该圆的圆心为O(0,0),半径为m.而圆C的圆心为C(3,4),半径为1.由题意知点P在圆C上,故两圆有公共点.所以两圆的位置关系为外切、相交或内切,故m-1≤|CO|≤m+1,即m-1≤5≤m+1,解得4≤m≤6.所以m的最大值为6.故选B.★答案☆B12.导学号91134073过点P(-,-1)的直线l与圆x2+y2=1有公共点,则直线l的倾斜角的取值范围是()A. B.C. D.解析如图,直线l1,l2过点P分别与圆O相切于点A、点B.连接OP,OA,在Rt△OAP中,|OP|=2,|OA|=1,所以∠OPA=,同理∠OPB=.所以∠APB=.所以直线l1的倾斜角为,显然直线l2的倾斜角为0,所以直线l的倾斜角的取值范围是.故直线l的倾斜角范围为.★答案☆D二、填空题(本大题共4小题,每小题5分,共20分.把★答案☆填在题中的横线上)13.在空间直角坐标系中,点M(-2,4,-3)在平面xOz上的射影为点M',则点M'关于原点对称的点的坐标是.解析点M在平面xOz上的射影为(-2,0,-3),其关于原点对称点的坐标为(2,0,3).★答案☆(2,0,3)14.过点P(1,2),且与原点的距离最大的直线方程是.解析当过点P且与OP(O为坐标原点)垂直时,直线与原点距离最大,由题意知,k OP=2,则直线l的斜率为-.此时,直线方程为y-2=-(x-1),即x+2y-5=0.★答案☆x+2y-5=015.经过点P(0,-1)作直线l,若直线l与连接A(1,-2),B(2,1)的线段总有公共点,则直线l的倾斜角α的范围是.解析如图所示,k PA==-1,k PB==1,由图可观察出,直线l倾斜角α的范围是.★答案☆16.导学号91134074已知方程x2+y2+2mx-2my-2=0表示的曲线恒过第三象限内的一个定点A,若点A又在直线l:mx+ny+1=0上,则m+n=.解析由方程x2+y2-2+2m(x-y)=0知,该曲线系恒经过圆x2+y2-2=0与直线x-y=0的交点,由得所过定点为(-1,-1),(1,1),∵点A为第三象限内的点,∴A点的坐标为(-1,-1),将其代入直线l的方程得(-1)·m+(-1)·n+1=0,即m+n=1.★答案☆1三、解答题(本大题共6小题,共70分.解答时应写出文字说明、证明过程或演算步骤)17.(本小题满分10分)已知△ABC的三个顶点分别为A(-3,0),B(2,1),C(-2,3),求:(1)BC边所在直线的方程;(2)BC边上中线AD所在直线的方程;(3)BC边的垂直平分线DE的方程.解(1)因为直线BC经过B(2,1)和C(-2,3)两点,得BC的方程为,即x+2y-4=0.(2)设BC边的中点D(x,y),则x==0,y==2.BC边的中线AD过A(-3,0),D(0,2)两点,所在直线方程为=1,即2x-3y+6=0.(3)由(1)知,直线BC的斜率k1=-,则直线BC的垂直平分线DE的斜率k2=2.所求直线方程为y-2=2(x-0),即2x-y+2=0.18.(本小题满分12分)已知直线l1:ax+2y+6=0和l2:x+(a-1)y+a2-1=0.(1)试判断l1与l2是否平行;(2)当l1⊥l2时,求a的值.解(1)(方法1)当a=1时,直线l1的方程为x+2y+6=0,直线l2的方程为x=0,l1不平行于l2;当a=0时,直线l1的方程为y=-3,直线l2的方程为x-y-1=0,l1不平行于l2;当a≠1,且a≠0时,两条直线的方程可化为l1:y=-x-3,l2:y=x-(a+1),由l1∥l2⇔解得a=-1.综上可知,当a=-1时,l1∥l2,否则l1与l2不平行.(方法2)由A1B2-A2B1=0,得a(a-1)-1×2=0;由A1C2-A2C1≠0,得a(a2-1)-1×6≠0.因此l1∥l2,可有解得a=-1,故当a=-1时,l1∥l2,否则l1与l2不平行.(2)由A1A2+B1B2=0,得a+2(a-1)=0,故a=.19.(本小题满分12分)已知圆C:x2+y2-4x-14y+45=0及点Q(-2,3).(1)P(a,a+1)在圆上,求线段PQ的长及直线PQ的斜率;(2)若M为圆C上任一点,求|MQ|的最大值和最小值.解(1)∵点P(a,a+1)在圆上,∴a2+(a+1)2-4a-14(a+1)+45=0.∴a=4.∴P(4,5).∴|PQ|==2,k PQ=.(2)∵圆心C的坐标为(2,7),∴|QC|==4.又圆的半径是2,∴点Q在圆外.∴|MQ|max=4+2=6,|MQ|min=4-2=2.20.(本小题满分12分)自点A(-3,3)发出的光线l射到x轴上,被x轴反射,其反射光线所在直线与圆x2+y2-4x-4y+7=0相切,求光线l所在的直线方程.解设反射光线为l',由于l和l'关于x轴对称,l过点A(-3,3),点A关于x轴的对称点为A'(-3,-3),因此反射光线所在直线过A'(-3,-3).设反射光线所在直线的斜率为k,则反射光线所在直线的方程为y-(-3)=k[x-(-3)],即kx-y+3k-3=0,圆方程可化为(x-2)2+(y-2)2=1,圆心M的坐标为(2,2),半径r=1.因为反射光线所在直线和已知圆相切,所以M到反射光线所在直线的距离等于半径,即=1,整理得12k2-25k+12=0.解得k=或k=.所以反射光线所在直线的方程为y+3=(x+3)或y+3=(x+3),即4x-3y+3=0或3x-4y-3=0,因为l与l'关于x轴对称,所以光线l所在直线的方程为4x+3y+3=0或3x+4y-3=0.21.导学号91134075(本小题满分12分)设圆心在直线2x+y=0上的圆C,经过点A(2,-1),并且与直线x+y-1=0相切.(1)求圆C的方程;(2)圆C被直线l:y=k(x-2)分割成弧长的比值为的两段弧,求直线l的方程.解(1)设圆的标准方程为(x-a)2+(y-b)2=r2(r>0).由题意知,解得a=1,b=-2,r=,故圆C的方程为(x-1)2+(y+2)2=2.(2)设直线l与圆C交于B,D两点.∵圆C被直线l分成弧长的比值为的两段,∴∠BCD=120°,∴∠CBD=30°.∴圆心C到直线l的距离为r=.又直线l的方程为kx-y-2k=0,圆心C的坐标为(1,-2),由点到直线的距离公式,得,解得k=1或k=7,故所求直线方程为y=x-2或y=7x-14.22.导学号91134076(本小题满分12分)如图,已知以点A(-1,2)为圆心的圆与直线l1:x+2y+7=0相切.过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点.(1)求圆A的方程;(2)当|MN|=2时,求直线l的方程.解(1)设圆A的半径为R,由于圆A与直线l1:x+2y+7=0相切,∴R==2.∴圆A的方程为(x+1)2+(y-2)2=20.(2)①当直线l与x轴垂直时,易知x=-2符合题意;②当直线l与x轴不垂直时,设直线l的方程为y=k(x+2), 即kx-y+2k=0.如图,连接AQ,则AQ⊥MN.∵|MN|=2,∴|AQ|==1.则由|AQ|==1,得k=,∴直线l为3x-4y+6=0.故直线l的方程为x=-2或3x-4y+6=0.。
高一北师大版数学必修2第二章 解析几何初步练习题含答案解析 双基限时练26
双基限时练(二十六)一、选择题1.已知a 2+b 2=12c 2,则直线ax +by +c =0与x 2+y 2=4的位置关系是( )A .相交但不过圆心B .相交且过圆心C .相切D .相离解析 圆心到直线的距离d =|c |a 2+b 2=2<2∴直线与圆相交,又c ≠0(否则a =b =c =0), ∴圆心不在直线上. 答案 A2.设直线l 过点(-2,0),且与x 2+y 2=1相切,则l 的斜率为( ) A .±1 B .±12 C .±33D .±3解析 如图可知|OA |=2,r =1,∴∠P AO =30°=∠QAO . ∴切线l 的斜率为±33.答案C3.若圆心在x轴上,半径为5的圆位于y轴左侧,且与直线x +2y=0相切,则圆O的方程为()A.(x-5)2+y2=5 B.(x+5)2+y2=5C.(x-5)2+y2=5 D.(x+5)2+y2=5解析设圆心(a,0)(a<0),由题意,得5=|a|12+22,得|a|=5,即a=-5.所以圆O的方程为(x+5)2+y2=5.答案D4.已知圆C:(x-a)2+(y-2)2=4(a>0)及直线l:x-y+3=0,当直线l被圆C截得的弦长为23时,则a等于()A. 2 B.2-2C.2-1D.2+1解析由题可得|a-2+3|12+(-1)2=4-(3)2=1,得a=2-1或a=-2-1(舍).答案C5.如果直线ax+by=4与圆x2+y2=4有两个不同的交点,那么点P(a,b)与圆的位置关系是()A.P在圆外B.P在圆上C.P在圆内D.P与圆的位置关系不确定解析由题意,得4a2+b2<2,得a 2+b 2>4,即点P (a ,b )在圆x 2+y 2=4外. 答案 A6.设圆x 2+y 2-8x -9=0的弦AB 的中点为P (5,2),则直线AB 的方程为( )A .2x -5y =0B .2x -y -8=0C .x +2y -9=0D .5x -2y -21=0解析 ∵x 2+y 2-8x -9=0可化为(x -4)2+y 2=25 ∴圆心为C (4,0),故k PC =2-05-4=2.又PC ⊥AB ,∴k AB =-12.故AB 所在的直线方程为y -2=-12(x -5). 即x +2y -9=0. 答案 C 二、填空题7.圆心为(1,2)且与5x -12y -7=0相切的圆的方程为________. 解析 由题可知,(1,2)到5x -12y -7=0的距离d =|5-12×2-7|52+(-12)2=2613=2,故所求的圆的方程为(x -1)2+(y -2)2=4. 答案 (x -1)2+(y -2)2=48.直线2x +y +5=0与圆x 2+y 2=9相交于A ,B 两点,则|AB |=________.解析 圆心O 到2x +y +5=0的距离d =|5|22+12=5,即|AB |=29-5=4.答案 49.已知⊙C :(x -2)2+(y +3)2=25,过点A (-1,0)的弦中,弦长的最大值为M ,最小值为m ,则M -m =________.解析 弦长的最大值M =2r =10,当弦与过A 点与圆心的连线垂直时弦取得最小值m ,此时m =2·25-[(-1-2)2+(0+3)2]=27, 故M -m =10-27. 答案 10-27 三、解答题10.求过(2,3)点,且与(x -3)2+y 2=1相切的直线方程. 解 当直线l 的斜率不存在时,l :x =2, 此时l 与圆(x -3)2+y 2=1相切,当l 的斜率存在时,设l :y -3=k (x -2), 即kx -y -2k +3=0. 由题意,得|3k -2k +3|k 2+1=1, 得k =-43,故l 的方程为y -3=-43(x -2), 综上得所求的切线方程为x =2,或4x +3y -17=0.11.直线y =kx +3与圆(x -2)2+(y -3)2=4相交于M ,N 两点,若|MN |≥23,求k 的取值范围.解如图,设题中圆的圆心为C(2,3),作CD⊥MN于D,则|CD|=|2k|1+k2,于是有|MN|=2|MD|=2|CM2|-|CD|2=24-4k21+k2≥23,即4-4k21+k2≥3,解得-33≤k≤3 3.12.直线l经过点P(5,5),且和圆C:x2+y2=25相交,截得的弦长为45,求l的方程.解设所求的圆的方程为y-5=k(x-5),即:kx-y-5k+5=0,∵直线与圆截得的弦长为45,∴圆心到直线的距离为25-20= 5.即|5-5k|k2+1= 5.得k=2或k=12.∴所求的直线方程为2x-y-5=0或x-2y+5=0.思维探究13.已知圆C:x2+y2-2x+4y-4=0,问是否存在斜率为1的直线l,l被圆C截得的弦为AB,使以AB为直径的圆过原点?若存在,求出直线l的方程,若不存在,说明理由.解不妨设直线方程为y=x+b,A(x1,y1),B(x2,y2),将直线方程与圆的方程联立,消去y,可得2x2+(2b+2)x+b2+4b -4=0,∴x 1+x 2=-b -1,x 1x 2=b 2+4b -42, 故y 1y 2=(x 1+b )(x 2+b )=b 2+2b -42. ∵以AB 为直径的圆过原点,故OA ⊥OB ,即k OA ·k OB =-1,整理可知x 1x 2+y 1y 2=0,故b 2+4b -42+b 2+2b -42=0,解之得b =-4,或b =1,验证知,此时Δ>0,故存在这样的直线l ,其方程为y =x -4,或y =x +1.。
(常考题)北师大版高中数学必修二第二章《解析几何初步》测试卷(含答案解析)(3)
一、选择题1.圆C 1:x 2+y 2=4与圆C 2:x 2+y 2﹣4x +4y ﹣12=0的公共弦的长为( ) A .2B .3C .22D .322.已知0a ≠,直线()240ax b y +++=与直线()230ax b y +--=互相垂直,则ab 的最大值为( ) A .0B .2C .4D .23.圆()()22211x y r -++=上有且仅有四个点到直线43110x y +-=的距离等于32,则半径r 的取值范围为( ) A .72r >B .72r <C .12r >D .1722r << 4.已知圆()()2295x a y a -+=>上存在点M ,使2OM MQ =(O 为原点)成立,()2,0Q ,则实数a 的取值范围是( )A .7a >B .57a <<C .1373a ≤≤ D .57a <≤5.设双曲线()222210,0x y a b a b-=>>的右焦点为F ,右顶点为A ,过F 作AF 的垂线与双曲线交于B ,C 两点,过B ,C 分别作AC ,AB 的垂线,两垂线交于点D .若D 到直线BC 的距离等于22a a b ++,则该双曲线的离心率是( ) A .2B .3C .2D .56.如下图所示,在正方体1111ABCD A B C D -中,E 是平面11ADD A 的中心,M 、N 、F 分别是11B C 、1CC 、AB 的中点,则下列说法正确的是( )A .12MN EF =,且MN 与EF 平行 B .12MN EF ≠,且MN 与EF 平行 C .12MN EF =,且MN 与EF 异面 D .12MN EF ≠,且MN 与EF 异面7.在直角坐标平面内,过定点P 的直线:10l ax y +-=与过定点Q 的直线:30m x ay -+=相交于点M ,则22||||MP MQ +的值为( )A .102B .10C .5D .10 8.设m ,n 为两条不同的直线,α,β为两个不同的平面,给出下列命题:①若//m α,//m n ,则//n α; ②若m α⊥,//m β,则αβ⊥; ③若αβ⊥,n αβ=,m n ⊥,则m β⊥;④若//m n ,//αβ,则m 与α所成的角和n 与β所成的角相等.其中正确命题的序号是( )) A .①② B .①④C .②③D .②④9.已知三棱锥A BCD -的各棱长都相等,E 为BC 中点,则异面直线AB 与DE 所成角的余弦值为( ) A .136B .3 C .336D .11610.如图,在三棱锥P ABC -中,AB AC ⊥,AB AP =,D 是棱BC 上一点(不含端点)且PD BD =,记DAB ∠为α,直线AB 与平面PAC 所成角为β,直线PA 与平面ABC 所成角为γ,则( )A .,γβγα≤≤B .,βαβγ≤≤C .,βαγα≤≤D .,αβγβ≤≤11.正三棱柱111ABC A B C -各棱长均为1,M 为1CC 的中点,则点1B 到面1A BM 的距离为( ) A 2B .22C .12D .3212.已知四面体ABCD 中,二面角A BC D --的大小为60,且2AB =,4CD =,120CBD ∠=,则四面体ABCD 体积的最大值是( )A 43B 23C .83D .43二、填空题13.已知直线1:220l x by ++=与直线2:210l x y -+=平行,则直线1l ,2l 之间的距离为__________.14.在平面直角坐标系xOy 中,设直线y =-x +2与圆x 2+y 2=r 2(r >0)交于A ,B 两点.若圆上存在一点C ,满足5344OC OA OB =+,则r 的值为________. 15.圆22220x y x y a ++-+=截直线20x y ++=所得弦的长度为4,则实数a 的值是________.16.经点()2,3P -,作圆2220x y +=的弦AB ,使得P 平分AB ,则弦AB 所在直线方程是______.17.经过两条直线2310x y ++=和340x y -+=的交点,并且平行于直线3470x y +-=的直线方程是________.18.已知m R ∈,动直线1:20l x my +-=过定点A ,动直线2230l mx y m --+=:过定点B ,若1l 与2l 交于点P (异于点A B ,),则PA PB +的最大值为_________. 19.在正三棱锥P ABC -中,E ,F 分别为棱PA ,AB 上的点,3PE EA =,3BF FA =,且CE EF ⊥.若23PB =,则三棱锥P ABC -的外接球的体积为_________.20.在如图棱长为2的正方体中,点M 、N 在棱AB 、BC 上,且1AM BN ==,P 在棱1AA 上,α为过M 、N 、P 三点的平面,则下列说法正确的是__________.①存在无数个点P ,使面α与正方体的截面为五边形; ②当11A P =时,面α与正方体的截面面积为33③只有一个点P ,使面α与正方体的截面为四边形;④当面α交棱1CC 于点H ,则PM 、HN 、1BB 三条直线交于一点.21.在直三棱柱111ABC A B C -中,90ABC ∠=︒,13AA O ,已知三棱锥O ABC -3O 表面积的最小值为______. 22.已知三棱锥A BCD -中,2AB CD ==3AC BC AD BD ====,则三棱锥A BCD -的体积是____________.23.三棱锥P ABC -的各顶点都在同一球面上,PC ⊥底面ABC ,若1PC AC ==,2AB =,且60BAC ∠=︒,给出如下命题:①ACB △是直角三角形;②此球的表面积等于11π; ③AC ⊥平面PBC ;④三棱锥A PBC -的体积为3. 其中正确命题的序号为______.(写出所有正确结论的序号)24.在正方体1111ABCD A B C D -中,P 为线段1AB 上的任意一点,有下面三个命题:①//PB 平面11CC D D ;②1BD AC ⊥;③1BD PC ⊥.上述命题中正确命题的序号为__________(写出所有正确命题的序号).三、解答题25.已知四棱锥P ABCD -的底面是菱形,60,BCD PD AD ∠=︒⊥,点E 是BC 边的中点.(Ⅰ)求证:AD ⊥平面PDE ;(Ⅱ)若二面角P AD C --的大小等于60︒,且834,AB PD ==①点P 到平面ABCD 的距离;②求直线PB 与平面ABCD 所成角的大小.26.如图,在四棱锥P ABCD -中,底面ABCD 是正方形,32,3,PB PD PA AD ====点,E F 分别为线段,PD BC 的中点.(1)求证://EF 平面ABP ; (2)求证:平面AEF ⊥平面PCD ; (3)求三棱锥C AEF -的体积27.如图,在正三棱柱111ABC A B C -中,若12AB BB =,AD DC =,试证明:(1)1//AB 平面1BC D ; (2)11AB BC ⊥.28.已知圆锥的侧面展开图为半圆,母线长为23.(1)求圆锥的底面积;(2)在该圆锥内按如图所示放置一个圆柱,当圆柱的侧面积最大时,求圆柱的体积.【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【分析】两圆方程相减,得到公共弦所在的直线方程,然后利用其中一个圆,结合弦长公式求解. 【详解】因为圆C 1:x 2+y 2=4与圆C 2:x 2+y 2﹣4x +4y ﹣12=0, 两式相减得20x y --=,即公共弦所在的直线方程. 圆C 1:x 2+y 2=4,圆心到公共弦的距离为d =所以公共弦长为:l ==. 故选:C 【点睛】本题主要考查直线与圆,圆与圆的位置关系,还考查了运算求解的能力,属于基础题.2.B解析:B 【分析】根据两直线垂直,得到关于,a b 的等式224a b +=,再利用基本不等式即可求出ab 的最大值. 【详解】因为直线()240ax b y +++=与直线()230ax b y +--=互相垂直, 所以2(2)(2)0a b b ++-=,即224a b +=, 因为222a b ab +≥, 所以24ab ≤,即2ab ≤, 故选:B. 【点睛】本题将两直线位置关系与基本不等式相结合进行考查,难度不大.3.A解析:A 【分析】圆()()22211x y r -++=上有且仅有四个点到直线43110x y +-=的距离等于32,先求圆心到直线的距离,再根据题意求半径的范围即可. 【详解】由()()22211x y r -++=可知圆心为()1,1-,圆心到直线43110x y +-=的距离为2=,因为圆上有且仅有四个点到直线43110x y +-=的距离等于32,所以322->r ,解得72r >. 故选:A 【点睛】本题主要考查直线与圆的位置关系,属于中档题.4.D解析:D 【分析】根据2OM MQ =可得M 的轨迹方程.由点M 在圆()()2295x a y a -+=>上,可得M 的轨迹方程与圆()()2295x a y a -+=>有公共点,即可由其位置关系求解. 【详解】 由题意,设(),M x y则由2OM MQ =,()2,0Q=化简变形可得2281639x y ⎛⎫-+= ⎪⎝⎭ 所以M 的轨迹为以8,03⎛⎫ ⎪⎝⎭为圆心,以43为半径的圆 由题意可知M 为2281639x y ⎛⎫-+= ⎪⎝⎭与()()2295x a y a -+=>的公共点即两个圆有公共点,由圆与圆的位置关系可知48433333a -≤-≤+ 解得1373a ≤≤ 又因为5a >所以57a <≤ 故选:D 【点睛】本题考查了点的轨迹方程求法,圆与圆位置关系式的应用,属于中档题.5.A解析:A 【分析】依题意求得,,A B C 的坐标,求得直线,BD CD 的方程,联立,BD CD 的方程求得D 点坐标,根据D 到直线BC 的距离等于a . 【详解】依题意可知()22,0,,,,b b A a B c C c a a ⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭,所以()()22,AB CD a c a b k k a c a b -==--,()()22,ACBD a c a b k k a c a b -=-=-,所以直线BD :()()22a c ab y xc a b--=-①,直线CD :()()22a c ab y xc a b-+=--②, ①-②并化简得()42D b x c a c a =+-.由于D 到直线BC 的距离等于a a c =+,直线BC 方程为x c =,所以()42D b x c a a c a =+=--,化简得22,a b a b ==,所以双曲线为等轴双曲线,离心率为.故选:A 【点睛】本小题主要考查直线和直线交点坐标的求法,考查直线方程点斜式,考查两条直线垂直斜率的关系,考查双曲线离心率的求法,考查化归与转化的数学思想方法,属于中档题.6.D解析:D 【分析】设正方体1111ABCD A B C D -的棱长为2,利用正方体性质可求得MN =,EF =知12MN EF ≠,再利用三角形中位线性质知1//MN B C ,从而//MN ED ,又EF 与ED 相交,可知MN 与EF 异面,即可选出答案. 【详解】设正方体1111ABCD A B C D -的棱长为2,则MN ==作E 点在平面ABCD 的投影点G ,即EG ⊥平面ABCD ,连接,EG GF ,在直角EGF △中,1EG =,GF ==EF ===以12MN EF ≠,故排除A 、C 连接DE ,由E 是平面11ADD A 的中心,得112DE A D =又M N 、分别是11B C 、1CC 的中点,所以1//MN B C 又11//A D B C ,所以//MN ED , 又EF ED E ⋂=,所以MN 与EF 异面 故选:D.【点睛】关键点睛:本题考查正方体中的线面关系,线线平行的关系,及判断异面直线,解题的关键是熟记正方体的性质,考查学生的逻辑推理能力,属于基础题.7.D解析:D 【分析】由已知得(0,1)P ,(3,0)Q -,过定点P 的直线10ax y +-=与过定点Q 的直线30x ay -+=垂直,M 位于以PQ 为直径的圆上,由此能求出22||||MP MQ +的值即可.【详解】在平面内,过定点P 的直线10ax y +-=与过定点Q 的直线30x ay -+=相交于点M ,(0,1)P ∴,(3,0)Q -,过定点P 的直线10ax y +-=与过定点Q 的直线30x ay -+=垂直,M ∴位于以PQ 为直径的圆上,||9110PQ =+=22||||10MP MQ ∴+=,故选:D . 【点睛】本题考查圆的轨迹方程求解,解题时要认真审题,注意两点间距离公式的合理运用.8.D解析:D 【分析】①根据//n α或n ⊂α判断;②利用面面垂直的判定定理判断;③根据m β⊂,或//m β,或m 与β相交判断;④利用线面角的定义判断.【详解】①若//m α,//m n ,则//n α或n ⊂α,因此不正确;②若//m β,则β内必存在一条直线//m m ',因为m α⊥,所以m α'⊥,又因为m β'⊂,所以αβ⊥,正确;③若αβ⊥,n αβ=,m n ⊥,则m β⊂,或//m β,或m 与β相交,因此不正确;④若//m n ,//αβ,则m 与α所成的角和n 与β所成的角相等,正确. 其中正确命题的序号是②④. 故选:D . 【点睛】空间直线、平面平行或垂直等位置关系命题的真假判断,除了利用定理、公理、推理判断外,还常采用画图(尤其是画长方体)、现实实物判断法(如墙角、桌面等)、排除筛选法等;另外,若原命题不太容易判断真假,可以考虑它的逆否命题,判断它的逆否命题真假,原命题与逆否命题等价.9.B解析:B 【分析】取AC 中点F ,连接,EF DF ,证明FED ∠是异面直线AB 与DE 所成角(或其补角),然后在三角形中求得其余弦值即可得. 【详解】取AC 中点F ,连接,EF DF ,∵E 是BC 中点,∴//EF AB ,12EF AB =, 则FED ∠是异面直线AB 与DE 所成角(或其补角), 设1AB =,则12EF =,3DE DF ==, ∴在等腰三角形DEF 中,11324cos 632EF FED DE ∠===. 所以异面直线AB 与DE 所成角的余弦值为3. 故选:B .【点睛】思路点睛:平移线段法是求异面直线所成角的常用方法,其基本思路是通过平移直线,把异面直线的问题化归为共面直线问题来解决,具体步骤如下: (1)平移:平移异面直线中的一条或两条,作出异面直线所成的角;(2)认定:证明作出的角就是所求异面直线所成的角; (3)计算:求该角的值,常利用解三角形; (4)取舍:由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦,当所作的角为钝角时,应取它的补角作为两条异面直线所成的角.10.A解析:A 【分析】由AB AP =,PD BD =,可得ABD △≌APD △,从而得DAB DAP α∠=∠=,而直线PA 与平面ABC 所成角为γ,由最小角定理可得γα≤,再由P ABC B PAC V V --=,PACABCSS≤,进而可比较,βγ的大小【详解】解:因为AB AP =,PD BD =,所以ABD △≌APD △, 所以DAB DAP α∠=∠=,因为直线PA 与平面ABC 所成角为γ, 所以由最小角定理可得γα≤, 因为AB AC ⊥,所以12ABCS AB AC =⋅, 因为1sin 2PACS AC AP PAC =⋅∠,AB AP =, 所以PACABCSS≤,令点P 到平面ABC 的距离为1d ,点B 到平面PAC 的距离为2d , 因为P ABC B PAC V V --=,1211,33P ABC ABCB PAC PACV S d V Sd --=⋅=⋅所以12d d ≤,因为直线AB 与平面PAC 所成角为β,直线PA 与平面ABC 所成角为γ,所以21sin ,sin d d AB PAβγ== 因为AB AP =, 所以sin sin βγ≥因为,(0,]2πβγ∈所以βγ≥, 故选:A 【点睛】关键点点睛:此题考查直线与平面所成的角,考查推理能力,解题的关键是利用了等体积法转换,属于中档题11.B解析:B 【分析】 连接11A N B AB =,根据已知条件先证明11B A A B ⊥、1⊥MN AB ,再通过线面垂直的判定定理证明1AB ⊥平面1A BM ,由此确定出1B N 的长度即为点1B 到面1A BM 的距离,最后完成求解. 【详解】连接1B A 交1A B 于N ,连接11,,,,MB MN MB MA MA ,如图所示:因为11A ABB 为正方形,所以11B A A B ⊥, 又因为22111115142MB MC C B =+=+=2215142MA MC CA =+=+=, 所以1MB MA =且N 为1AB 中点,则MN 为等腰三角形1AMB 的中垂线, ∴1⊥MN AB 且1MNA B N =,∴1AB ⊥平面1A BM ,∴1B N 就是点1B 到截面1A BM 的距离, 又因为1111211222B N AB ==+=,所以点1B 到截面1A BM 的距离为22, 故选:B. 【点睛】方法点睛:求解平面外一点A 到平面α的距离的方法:(1)几何方法:通过线面垂直的证明,找到A 在平面α内的投影点A ',则AA '即为A 到平面α的距离;(2)向量方法:①建立合适空间直角坐标系,在平面α内取一点B ;②求解出AB 和平面α的法向量n ;③根据AB n d n⋅=即可求解出点A 到平面α的距离.12.D解析:D 【分析】在BCD △中,利用余弦定理和基本不等式可得163BC BD ⋅≤,由三角形的面积公式可得3BCDS≤,由二面角A BC D --的大小为60,可得A 到平面BCD 的最大距离为2sin 603h ==ABCD 体积的最大值.【详解】在BCD △中,由余弦定理可得2222cos120CD BC BD BC BD =+-⋅22BC BD BC BD =++⋅因为222BC BD BC BD +≥,所以23CD BC BD ≥⋅, 所以163BC BD ⋅≤,当且仅当BC BD =时等号成立,1116sin1202232BCDSBC BD =⋅≤⨯⨯= 因为二面角A BC D --的大小为60,所以点A 到平面BCD 的最大距离为2sin 603h ==所以114333A BCD BCDV S h -=⋅≤=, 所以四面体ABCD 体积的最大值是43, 故选:D 【点睛】关键点点睛:本题解题的关键点是利用余弦定理和基本不等式、三角形面积公式求出BCD S △最大值,再由二面角求出高的最大值.二、填空题13.【分析】利用直线平行与斜率之间的关系点到直线的距离公式即可得出【详解】解:因为直线与直线平行所以解得当时则故答案为:【点睛】熟练运用直线平行与斜率之间的关系点到直线的距离公式是解题关键【分析】利用直线平行与斜率之间的关系、点到直线的距离公式即可得出. 【详解】解:因为直线1:220l x by ++=与直线2:210l x y -+=平行,所以22(1)b =⨯-,解得1b =-,当1b =-时,1:220l x y -+=,2:210l x y -+=,则5d ==【点睛】熟练运用直线平行与斜率之间的关系、点到直线的距离公式,是解题关键.14.【详解】即整理化简得cos ∠AOB =-过点O 作AB 的垂线交AB 于D 则cos ∠AOB =2cos2∠AOD -1=-得cos2∠AOD =又圆心到直线的距离为OD =所以cos2∠AOD ===所以r2=10r =【详解】22225325539OC OA OB OA 2OA OB OB 44164416⎛⎫=+=+⋅⋅+ ⎪⎝⎭即222225159r r r cos AOB r 16816=+∠+,整理化简得cos ∠AOB =-35,过点O 作AB 的垂线交AB 于D ,则cos ∠AOB =2cos 2∠AOD -1=-35,得cos 2∠AOD =15.又圆心到直线的距离为OD=,所以cos 2∠AOD =15=22OD r=22r ,所以r 2=10,r . 15.-4【分析】将圆的方程化为标准方程求出圆心坐标与半径利用点到直线的距离公式算出圆心到直线的距离再根据截得弦的长度为得到关于的方程解出即可【详解】由圆可得圆心为半径直线方程为圆心到直线的距离截得弦的长解析:-4 【分析】将圆的方程化为标准方程,求出圆心坐标与半径r ,利用点到直线的距离公式,算出圆心到直线l 的距离,再根据截得弦的长度为4,得到关于a 的方程,解出即可 【详解】由圆22220x y x y a ++-+=可得()()22112x y a ++-=-∴圆心为()11-,,半径)2r a =<直线方程为20x y ++=∴圆心到直线的距离d ==截得弦的长度为42222a ∴+=-,解得4a =-故答案为4- 【点睛】结合弦长的长度求出圆的标准方程,只需将圆化为标准方程,然后运用弦长公式的求法求出参量即可16.【分析】由题意知圆的圆心从而可求出由从而可求出弦所在直线的斜率是由直线的点斜式可写出弦所在直线方程【详解】解:设圆的圆心为则由是的中点知因为所以点在圆内且所以弦所在直线的斜率是则弦所在的直线方程是整解析:23130x y --=. 【分析】由题意知圆2220x y +=的圆心()0,0O ,从而可求出32OP k =-,由AB OP ⊥,从而可求出弦AB 所在直线的斜率是123AB OP k k =-=,由直线的点斜式,可写出弦AB 所在直线方程. 【详解】解:设圆2220x y +=的圆心为O ,则()0,0O .由P 是AB 的中点,知AB OP ⊥.因为()22231320+-=<,所以点P 在圆O 内,且303202OP k --==--. 所以弦AB 所在直线的斜率是123AB OP k k =-=,则弦AB 所在的直线方程是23(2)3y x +=-, 整理可得,23130x y --=. 故答案为:23130x y --=. 【点睛】本题考查了直线的点斜式方程,考查了两直线垂直的应用.本题的关键是分析出AB OP ⊥,进而求出弦所在直线的斜率.17.【分析】先求出两相交直线的交点设出平行于直线的直线方程根据交点在直线上求出直线方程【详解】联立直线的方程得到两直线的交点坐标平行于直线的直线方程设为则所以直线的方程为:故答案为:【点睛】本题考查了直 解析:1934011x y ++= 【分析】先求出两相交直线的交点,设出平行于直线3470x y +-=的直线方程,根据交点在直线上,求出直线方程. 【详解】联立直线的方程23103470x y x y ++=⎧⎨+-=⎩,得到两直线的交点坐标135(,)1111-,平行于直线3470x y +-=的直线方程设为340x y c ++=, 则1353()4()+01111c ⋅-+⋅= 所以直线的方程为:1934011x y ++= 故答案为:1934011x y ++= 【点睛】本题考查了直线的交点,以及与已知直线平行的直线方程,考查了学生概念理解,转化与划归的能力,属于基础题.18.【分析】根据观察两条直线的位置关系结合不等式可得结果【详解】由题可知:动直线过定点动直线过定点且可知所以且所以即当且仅当时取=所以的最大值为故答案为:【点睛】本题考查直线过定点问题还考查了基本不等式解析:【分析】根据观察两条直线的位置关系,结合不等式,可得结果. 【详解】 由题可知:动直线1:20l x my +-=过定点()2,0A动直线2230l mx y m --+=:过定点()2,3B 且()110m m ⨯+⨯-=,可知12l l ⊥,所以PA PB ⊥,且2229PA PB AB +==所以2229222PA PB PA PB ⎛+⎫≤+= ⎪⎝⎭即PA PB +≤ 当且仅当PA PB =时取“=”所以PA PB +的最大值为故答案为:【点睛】本题考查直线过定点问题,还考查了基本不等式应用,属中档题.19.【分析】证明与垂直得线面垂直从而得正三棱锥的三条侧棱两两垂直结合正方体的性质得三条侧棱的平方和为外接球直径的平方求得球半径后可得球体积【详解】∵∴∴又∴取中点连接如图由于是正三棱锥∴而平面∴平面又平 解析:36π【分析】证明PB 与,CE AC 垂直得线面垂直,从而得正三棱锥的三条侧棱两两垂直,结合正方体的性质得三条侧棱的平方和为外接球直径的平方,求得球半径后可得球体积. 【详解】∵3PE EA =,3BF FA =,∴AE AFAP AB=,∴//EF PB ,又CE EF ⊥,∴PB CE ⊥,取AC 中点D ,连接,PD BD ,如图,由于P ABC -是正三棱锥,∴,PD AC BD AC ⊥⊥,而PD BD D ⋂=,,PD BD ⊂平面PBD ,∴AC ⊥平面PBD ,又PB ⊂平面PBD , ∴AC PB ⊥,∵ACCE C =,,AC CE ⊂平面PAC ,∴PB ⊥平面PAC ,而,PA PC ⊂平面PAC ,∴,PB PA PB PC ⊥⊥,同理正三棱锥中,PA PC ⊥.设三棱锥P ABC -外接球半径为R ,则22222(2)3(23)R PA PB PC =++=⨯,3R =,球的体积为343363V ππ=⨯=. 故答案为:36π.【点睛】结论点睛:三棱锥的外接球问题,解题关键是找到外接球的球心,三棱锥的外接球球心在过各面外心且与该面垂直的直线上.当从同一顶点出发的三条棱两两垂直时,可以把三棱锥补成一个长方体,而长方体的对角线就是三棱锥外接球的直径.20.①②④【分析】让从开始逐渐向运动变化观察所得的截面从而可得正确的选项【详解】由题设可得为所在棱的中点当时如图(1)直线分别交与连接并延长于连接交于则与正方体的截面为五边形故①正确当如图(2)此时与正解析:①②④ 【分析】让P 从A 开始逐渐向1A 运动变化,观察所得的截面,从而可得正确的选项.【详解】由题设可得,M N 为所在棱的中点. 当203AP <<时,如图(1),直线MN 分别交,AD DC 与,T S ,连接TP 并延长1DD 于G , 连接GS 交1CC 于H ,则α与正方体的截面为五边形,故①正确.当11A P =,如图(2),此时α2, 其面积为2362=33B 正确.当,A P 重合或1,A P 重合时,如图(3),α与正方体的截面均为四边形,故③错误.如图(4),在平面α内,设PM HN S ⋂=,则S PM ∈,而PM ⊂平面11A B BA , 故S ∈平面11A B BA ,同理S ∈平面11C B BC ,故S ∈平面11A B BA ⋂平面111C B BC BB =即PM 、HN 、1BB 三条直线交于一点. 故答案为:①②④. 【点睛】思路点睛:平面的性质有3个公理及其推理,注意各个公理的作用,其中公理2可用来证明三点共线或三线共点,公理3及其推理可用来证明点共面或线共面,作截面图时用利用公理2来处理.21.【分析】设球的半径为连接交于点取中点连接即为三棱柱外接球球心根据三棱锥体积可得间关系表示出根据基本不等式可求得的最小值从而得到球的表面积的最小值【详解】如图因为三棱柱是且设球的半径为连接交于点取中点 解析:27π【分析】设AB a ,BC b =,球的半径为r ,连接1AC ,1A C 交于点O ,取AC 中点D ,连接BD ,即O 为三棱柱外接球球心,根据三棱锥体积可得a b ,间关系,表示出r ,根据基本不等式可求得r 的最小值,从而得到球的表面积的最小值. 【详解】如图,因为三棱柱111ABC A B C -是 ,且90ABC ∠=︒,设AB a ,BC b =,球的半径为r ,连接1AC ,1A C 交于点O ,取AC 中点D ,连接BD ,则O 到三棱柱六个定点的距离相等,即O 为三棱柱外接球球心,11322OD AA ==, 又因为三棱锥O ABC -3 即1133322ab ⨯⨯=,即12ab =, 所以222222313332224a b r AD OD ab ⎛⎫⎛⎫+=+=+≥+=⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭, 当且仅当a b =时等号成立,所以球O 的表面积最小值为2427S r ππ==, 故答案为:27π. 【点睛】与球有关的组合体问题,一种是内切,一种是外接.解题时要认真分析图形,明确切点和接点的位置,确定有关元素间的数量关系,并作出合适的截面图,如球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径;球外接于正方体,正方体的顶点均在球面上,正方体的体对角线长等于球的直径.22.【分析】取中点连接由条件可证明平面由此将三棱锥的体积表示为计算可得结果【详解】取中点连接如下图所示:因为所以平面平面所以平面又因为所以所以又因为故答案为:【点睛】关键点点睛:解答本题的关键是通过找的 解析:23【分析】取AB 中点O ,连接,CO DO ,由条件可证明AB ⊥平面CDO ,由此将三棱锥A BCD -的体积表示为13CDO AB S⨯⨯,计算可得结果.【详解】取AB 中点O ,连接,CO DO ,如下图所示:因为AC BC AD BD ===,所以,AB CO AB DO ⊥⊥,CO DO O =,CO ⊂平面CDO ,DO ⊂平面CDO ,所以AB ⊥平面CDO , 又因为3AC BC AD BD ====,2AB CD ==()22210322CO DO ⎛⎫==-= ⎪ ⎪⎝⎭, 所以22110221222CDO S ⎛⎫⎛⎫=-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭, 又因为11221333A BCD CDO V AB S -=⨯⨯==, 故答案为:23. 【点睛】 关键点点睛:解答本题的关键是通过找AB 的中点,证明出线面垂直,从而将三棱锥的体积表示为13CDO AB S ⨯⨯,区别于常规的13⨯底面积⨯高的计算方法,本例实际可看成是两个三棱锥的体积之和.23.①③【分析】①先求出再得到最后判断①正确;②先判断三棱锥的外接球就是以为顶点以棱的长方体的外接球再求半径最后求出球的表面积判断②错误;③先证明最后证明平面判断③正确;④直接求出三棱锥的体积判断④错误解析:①③.【分析】①先求出BC =222AB BC AC =+,最后判断①正确;②先判断三棱锥P ABC -的外接球就是以C 为顶点,以CA ,CB ,CP 棱的长方体的外接球,再求半径r ,最后求出球的表面积,判断②错误;③先证明AC PC ⊥,AC BC ⊥,⋂=PC CB C ,最后证明AC ⊥平面PBC ,判断③正确;④直接求出三棱锥A PBC -的体积,判断④错误.【详解】解:①在ACB △,因为1AC =,2AB =,且60BAC ∠=︒,所以2222cos 3BC AB AC AB AC BAC =+-⋅⋅∠=,则BC =所以222AB BC AC =+,所以ACB △是直角三角形,故①正确;②由(1)可知AC BC ⊥,又因为PC ⊥底面ABC ,所以三棱锥P ABC -的外接球就是以C 为顶点,以CA ,CB ,CP 棱的长方体的外接球,则2r ==,则此球的表面积等于245S r ππ==,故②错误; ③因为PC ⊥底面ABC ,所以AC PC ⊥,由(1)可知AC BC ⊥,⋂=PC CB C , 所以AC ⊥平面PBC ,故③正确;④三棱锥A PBC -的体积11(1132V =⨯⨯⨯=,故④错误. 故答案为:①③.【点睛】本题考查判断三角形是直角三角形、求三棱锥的外接球的表面积、求三棱锥的体积、线面垂直的证明,是中档题. 24.①②③【分析】①证明线面平行可判断对错;②证明线面垂直可判断对错;③证明线面垂直可判断对错【详解】①如下图所示:因为平面平面平面所以平面故①正确;②连接如下图所示:因为平面所以又因为且所以平面又因为解析:①②③【分析】①证明线面平行可判断对错;②证明线面垂直可判断对错;③证明线面垂直可判断对错.【详解】①如下图所示:因为平面11//ABB A 平面11CC D D ,BP ⊂平面11ABB A ,所以//PB 平面11CC D D ,故①正确;②连接,AC BD ,如下图所示:因为1DD ⊥平面ABCD ,所以1DD AC ⊥,又因为AC BD ⊥且1DD BD D =,所以AC ⊥平面1DBD ,又因为1BD ⊂平面1DBD ,所以1BD AC ⊥,故②正确;③连接11,,,AC PC B C BC ,如下图所示:因为11D C ⊥平面11BCC B ,所以11D C ⊥1B C ,又因为11BC B C ⊥,且1111D C BC C ⋂=,所以1B C ⊥平面11BD C ,又1BD ⊂平面11BD C ,所以11B C BD ⊥,由②的证明可知1BD AC ⊥,且1AC B C C ⋂=,所以1BD ⊥平面1AB C ,又因为PC ⊂平面1AB C ,所以1BD PC ⊥,故③正确,故答案为:①②③.【点睛】本题考查空间线面平行、线线垂直关系的判断,涉及线面平行判定定理、线面垂直判定定理的运用,主要考查学生对空间中位置关系的逻辑推理能力,难度一般.三、解答题25.(Ⅰ)证明见解析;(Ⅱ)①4,②3π. 【分析】(Ⅰ)连接BD ,点E 是BC 边的中点,得出DE BC ⊥,DE AD ⊥再由DP AD ⊥,得出结果;(Ⅱ)DE AD ⊥,PD AD ⊥,PDE ∠为二面角P AD C --的平面角,60PDE ∠=︒,过P 在平面PDE 内做PK DE ⊥于K ,易证PK ⊥面ABCD ,PK 为点到面的距离,PBK ∠即为线面角.【详解】(Ⅰ)连接BD ,底面ABCD 是菱形,∠BDC =60°,∴△BCD 是正三角形.∵点E 是BC 边的中点,∴DE ⊥BC ,∵AD ∥BC ,∴DE ⊥AD .∵DP ⊥AD ,DP ∩AD =D ,∴AD ⊥平面PDE ;(Ⅱ)①∵DE ⊥AD ,PD ⊥AD ,∴PDE ∠为二面角P -AD -C 的平面角,∴60PDE ∠=︒,过P 在平面PDE 内做PK DE ⊥于K ,由(Ⅰ)易AD PK ⊥.∴PK ⊥面ABCD .∵833PD =,∴433DK =,4PK =, 即点P 到平面ABCD 的距离是4. ②AB =4,∴23DE =,∴23DK DE =,∴K 为BCD △重心. 连接BK ,∵BCD △为正三角形,所以BK 为BP 在面ABCD 内的射影.∴PB ⊥AB ,PBK ∠为直线PB 与平面ABCD 所成角,RT PKB △中,tan 3PK PK PKB KB DK ∠===,3PKB π∠=, 直线PB 与平面ABCD 所成角的大小为3π. 【点睛】求直线与平面所成的角的一般步骤: ①找直线与平面所成的角,即通过找直线在平面上的射影来完成;②计算,要把直线与平面所成的角转化到一个三角形中求解.26.(1)证明见解析;(2)证明见解析;(3)98. 【分析】(1)取PA 的中点G ,连接,BG EG ,证明四边形EFBG 为平行四边形,得出//EF BG ,再由线面平行的判定定理证明即可;(2)先证明PA ⊥平面ABCD ,从而得出PA CD ⊥,再由等腰三角形的性质得出AE PD ⊥,最后由面面垂直的判定定理证明即可;(3)以AFC △为底,12PA 为高,由棱锥的体积公式得出答案. 【详解】(1)如图,取PA 的中点G ,连接,BG EG .因为点,E G 分别为,PD PA 的中点,所以1//,2EG AD EG AD = 又因为F 是BC 的中点,四边形ABCD 是正方形,所以//BF EG 且BF EG = 故四边形EFBG 为平行四边形,所以//EF BG因为BG ⊂平面,ABP EF 不在平面ABP 内,所以//EF 平面ABP .(2)由条件知3PB PD PA AD AB =====,所以PAB △和PAD △都是等腰直角三角形,,PA AB PA AD ⊥⊥又因为,,AB AD A AB AD =⊂平面,ABCD 所以PA ⊥平面ABCD因为CD ⊂平面ABCD ,所以PA CD ⊥又因为,,AD CD PA AD A ⊥⋂=所以CD ⊥平面PAD ,所以CD AE ⊥因为E 是PD 的中点,所以AE PD ⊥又因为,,PD CD D PD CD ⋂=⊂平面PCD ,所以AE ⊥平面PCD因为AE ⊂平面,AEF 所以平面AEF ⊥平面PCD .(3)由图可知C AEF E ACF V V --=,1111319333232228E ACF ACF V S PA -=⨯=⨯⨯⨯⨯⨯=△, 即三棱锥C AEF -的体积为98【点睛】关键点睛:在证明线线平行时,关键是证明四边形EFBG 为平行四边形,从而得出//EF BG .27.(1)证明见解析;(2)证明见解析.【分析】(1)连接1B C 交1BC 于点E ,连接DE ,则E 为1B C 的中点,利用中位线的性质可得1//DE AB ,再利用线面平行的判定定理可证得结论成立;(2)取BC 中点F ,连接AF 、1B F ,证明出1BC ⊥平面1AB F ,进而可证得11AB BC ⊥.【详解】(1)连接1B C 交1BC 于点E ,连接DE ,在正三棱柱111ABC A B C -中,四边形11BB C C 为平行四边形,且11B CBC E =,则E 为1B C 的中点,又D 为AC 的中点,所以1//AB DE ,又1AB ⊄平面1BC D ,DE ⊂平面1BC D ,所以1//AB 平面1BC D ; (2)取BC 中点F ,连接AF 、1B F ,设11B FBC O =, 在正三棱柱111ABC A B C -中,1BB ⊥平面ABC ,AF ⊂平面ABC ,1AF BB ∴⊥, ABC 为正三角形,且F 为BC 的中点,AF BC ∴⊥,1BB BC B =,AF ∴⊥平面11BB C C ,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、选择题 1.在平面直角坐标系xOy中,直线l:40kxyk与曲线29yx交于A,B两
点,且2AB,则k( )
A.33 B.22 C.1 D.3
2.在棱长为2的正方体1111ABCDABCD中,点,EF分别是棱1,BCCC的中点,P是侧
面11BCCB内一点,若1AP平行于平面AEF,则线段1AP长度的最小值是( )
A.334 B.324 C.332 D.
32
2
3.已知12,FF是椭圆222210xyabab的两焦点,P是椭圆上任意一点,过一焦点
引12FPF的外角平分线的垂线,垂足为Q,则动点Q的轨迹为( ▲ ) A.圆 B.椭圆 C.双曲线 D.抛物线
4.圆224xy被直线32yx截得的劣弧所对的圆心角的大小为( )
A.30 B.60 C.90 D.
120
5.苏州有很多圆拱的悬索拱桥(如寒山桥),经测得某圆拱索桥(如图)的跨度
100AB米,拱高10OP米,在建造圆拱桥时每隔5米需用一根支柱支撑,则与OP相
距30米的支柱MN的高度是( )米.(注意:10取3.162)
A.6.48 B.4.48 C.2.48 D.以上都不对
6.已知圆2260xyx,过点(1,2)的直线被该圆所截得的弦的长度的最小值为
( ) A.1 B.2 C.3 D.4 7.已知平面图形PABCD,ABCD为矩形,4AB,是以P为顶点的等腰直角三角
形,如图所示,将PAD△沿着AD翻折至PAD△,当四棱锥PABCD体积的最大值
为163,此时四棱锥PABCD外接球的表面积为( )
A.12 B.16 C.24 D.
32
8.如图所示,A,B为正方体的两个顶点,M,N为其所在棱的中点,则异面直线
AB与MN所成角的大小为( )
A.30° B.45° C.60° D.90° 9.如图,在正方体1111ABCDABCD中,点F是线段1BC上的动点,则下列说法错误的
是( ) A.无论点F在上1BC怎么移动,都有
11
AFBD
B.当点F移动至1BC中点时,才有1AF与1BD相交于一点,记为点E,且
12AEEF
C.当点F移动至1BC中点时,直线1AF与平面1BDC所成角最大且为60° D.无论点F在1BC上怎么移动,异面直线1AF与CD所成角都不可能是30° 10.如图,正方形ABCD的边长为4,点E,F分别是AB,BC的中点,将ADE,
EBF△,FCD分别沿DE,EF,FD折起,使得A,B,C三点重合于点A,若点G及四
面体ADEF的四个顶点都在同一个球面上,则以FDE为底面的三棱锥G-DEF的高h的最大值为( )
A.263 B.463 C.4263 D.
2263
11.如下图所示是一个正方体的平面展开图,在这个正方体中①//BM平面ADE;
②DEBM;③平面//BDM平面AFN;④AM平面BDE.以上四个命题中,真
命题的序号是( )
A.①②③④ B.①②③ C.①②④ D.②③④ 12.某几何体的三视图如图所示,该几何体的体积为V,该几何体所有棱的棱长之和为L,
则( ) A.8,14253VL B.
8,1425VL
C.8,16253VL D.
8,1625VL
二、填空题 13.2020年是中国传统的农历“鼠年”,有人用3个圆构成“卡通鼠”的形象,如图:
(0,3)Q是圆Q的圆心,圆Q过坐标原点O;点L、S均在x轴上,圆L与圆S的半径都等
于2,圆S、圆L均与圆Q外切.已知直线l过点O.若直线l截圆L、圆S、圆Q所得弦长均等于d,则d=_____.
14.若圆221xy与圆22()(4)25xay相交,则实数a的取值范围是______. 15.经过两直线11370xy和12190xy的交点,且与3,2A,1,6B等
距离的直线的方程是______. 16.若点1,1P为圆2239xy的弦MN的中点,则弦MN所在直线方程为
__________. 17.若直线220,0axbyab始终平分圆22420xyxy的周长,则
12
ab
的最小值为______. 18.若点P在直线1:30lxy上,过点P的直线2l与曲线22:54Cxy相切于点M,则PM的最小值为__________. 19.正方体1111ABCDABCD棱长为点1,点E在边BC上,且满足2BEEC,动点
P
在正方体表面上运动,满足1PEBD,则动点P的轨迹的周长为__________. 20.如图,在三棱锥PABC中,PA平面ABC,ABBC,2PAAB,
22AC,M是BC的中点,则过点M的平面截三棱锥PABC的外接球所得截面的面积最小值为___
21.在三棱锥PABC中,4PAPB,42BC,8AC,ABBC.平面
PAB平面ABC,若球O是三棱锥PABC的外接球,则球O的半径为_________.
22.如图,正方体1111ABCDABCD的棱长为1,线段11BD上有两个动点E,F,且
22EF,现有如下四个结论:
①ACBE;
②//EF平面ABCD;
③三棱锥ABEF的体积为定值;
④直线AE与平面BEF所成的角为定值,
其中正确结论的序号是______. 23.如图,正方形BCDE的边长为a,已知3ABBC,将ABE△沿边BE折起,折
起后A点在平面BCDE上的射影为D点,则翻折后的几何体中有如下描述: ①AB与DE所成角的正切值是2;②//ABCE;③BACEV体积是316a;④平面
ABC平面ADC.
其中正确的有______.(填写你认为正确的序号) 24.在矩形ABCD中,1AB,3AD.将BCD沿对角线BD翻折,得到三棱锥
ABCD,则该三棱锥外接球的表面积为________.
三、解答题
25.如图,在直三棱柱111ABCABC中,1,2ACBCACBCCC.
(1)求三棱柱111ABCABC的体积; (2)求异面直线1CB与1AC所成角的大小; (3)求二面角1BACC的平面角的余弦值. 26.如图,已知长方体1111ABCDABCD,2AB,11AA,直线BD与平面
1
AABB
所成的角为30°,AE垂直BD于E. (1)若F为棱11AB上的动点,试确定F的位置使得//AE平面1BCF,并说明理由; (2)若F为棱11AB上的中点;求点A到平面BDF的距离; (3)若F为棱11AB上的动点(端点1A,1B除外),求二面角FBDA的大小的取值范围. 27.如图,在平面四边形AABC中,90CABCAA,M在直线AC上,
AAAC,ABAMMC,AAC绕AC旋转.
(1)若AAC所在平面与ABC所在平面垂直,求证:AC平面AAB. (2)若二面角AACB大小为60,求直线AB与平面ABM所成角的正弦值. 28.如图,在三棱柱111ABCABC中,平面11AACC平面ABC,2,ABBC 30ACB,13AA,11BCAC,E为AC的中点
.
(1)求证:1//AB平面1CEB; (2)求证:1AC平面1
CEB.
【参考答案】***试卷处理标记,请不要删除
一、选择题 1.C 解析:C 【分析】 求出圆心到直线的距离,再由垂径定理列式求解k值. 【详解】 解: 曲线29yx是圆心为原点,半径r=3的上半圆,如图:
圆心到直线l的距离241kdk, 222
2
1622921kABrdk
,
解得:1k, 当1k时,直线l与曲线29yx无交点,舍去. 故1k. 故选:C. 【点睛】 本题考查直线系方程的应用,考查直线与圆位置关系的应用,考查计算能力,是中档题. 2.D 解析:D 【分析】 以D为原点,DA为x轴,DC为y轴,1DD为z轴,建立空间直角坐标系,利用向量法能求出线段1AP长度取最小值. 【详解】 以D为原点,DA为x轴,DC为y轴,1DD为z轴,建立空间直角坐标系,
