六年级奥数中等难度练习题一
2022年小学六年级数学中等难度练习题(一)

小学六年级数学中等难度练习题(一)巧求整数部分题目:(中等难度)A 8.8 8.98 8.998 8.9998 8.99998,A的整数部分是_________.巧求整数部分答案:准确值:(中等难度)已知A、B、C都是非0自然数,的近似值是6.4,那么它的准确值是多少?准确值案:自然数和:(中等难度)在整数中,有用2个以上的连续自然数的和来表白一个整数的方法.例如9:9=4+5,9=2+3+4,9有两个用2个以上连续自然数的和来表白它的方法.准确值案:(1)请写出只有3种这样的表现方法的最小自然数.(2)请写出只有6种这样的表现方法的最小自然数.关于某整数,它的"奇数的约数的个数减1",就是用连续的整数的和的形式来表白种数.根据(1)知道,有3种表白方法,于是奇约数的个数为3+1=4,对4分解质因数4=2×2,最小的15(1、3、5、15);有连续的2、3、5个数相加;7+8;4+5+6;1+2+3+4+5;根据(2)知道,有6种表现方法,于是奇数约数的个数为6+1=7,最小为729(1、3、9、27、81、243、729),有连续的2,3、6、9、10、27个数相加:364+365;242+243+244;119+120+...+124;77+78+79+...+85;36+37+ (45)14+15+…+40分数方程:(中等难度)若干只同样的盒子排成一列,小聪把42个同样的小球放在这些盒子里然后外出,小明从每支盒子里取出一个小球,然后把这些小球再放到小球数最少的盒子里去。
再把盒子重排了一下.小聪回来,仔细查看,没有发现有人动过小球和盒子.问:一共有多少只盒子?准确值案:设原来小球数最少的盒子里装有a只小球,现在增加了b只,由于小聪没有发现有人动过小球和盒子,这说明现在又有了一只装有a个小球的盒子,而这只盒子里原来装有(a+1)个小球.同样,现在另有一个盒子装有(a+1)个小球,这只盒子里原来装有(a+2)个小球.类推,原来还有一只盒子装有(a+3)个小球,(a+4)个小球等等,故原来那些盒子中装有的小球数是一些连续整数.现在变成:将42分拆成若干个连续整数的和,一共有多少种分法,每一种分法有多少个加数?因为42=6×7,故可以看成7个6的和,又(7+5)+(8+4)+(9+3)是6个6,从而42=3+4+5+6+7+8+9,一共有7个加数;又因为42=14×3,故可将42:13+14+15,一共有3个加数;又因为42=21×2,故可将42=9+10+11+12,一共有4个加数.所以原问题有三个解:一共有7只盒子、4只盒子或3只盒子.跑步:(中等难度)狗跑5步的时间马跑3步,马跑4步的距离狗跑7步,现在狗已跑出30米,马开始追它。
小学六年级奥数训练(一)及其答案

小学六年级奥数训练试卷一 一、计算题:(每题5分,共10分) 1、(111×66-185×8)÷37=______.
2、1997+1996-1995-1994+1993+1992…-2+1=_______. 二、填空题:(每题5分,共25分) 1、某地区水电站规定,如果每月用电不超过24度,则每度收9分;如果超过24度,则多出度数按每度2角收费.若某月甲比乙多交了9.6角(甲、乙都是整数),则甲交了______角______分
2、乒乓球单打决赛在甲、乙、丙、丁四位选手中进行,赛前,有些人预测比赛结果,A说:甲第4;B说:乙不是第2,也不是第4;C说:丙的名次在乙的前面;D说:丁将得第1.比赛结果表明,四个人中只有一人预测错了.那么,甲、乙、丙、丁四位选手的名次分别为:_______. 3、41位数55…5□99…9(其中5和9各有20个)能被7整除,那么中间方格内的数字是_____. 4、如图,一长方形被一条直线分成两个长方形,这两个长方形的宽的比为1∶3,若阴影三角形面积为1平方厘米,则原长方形面积为______平方厘米.
5.字母A、B、C代表三个不同的数字,其中A比B大,B比C大,如果用数字A、B、C组成的三个三位数相加的和为777,其竖式如右,那么三位数ABC是______.
三、解答题:(1~7题每题5分,8,9,10题每题10分,共65分) 1.一列快车和一列慢车相向而行,快车的车长是280米,慢车的车长是385米.坐在快车上看见慢车驶过的时间是11秒,那么坐在慢车上看见快车驶过的时间是多少秒? 2.一堆苹果,2个2个地数剩1个,3个3个地数剩2个,4个4个地数剩3个,5个5个地数剩4个,6个6个地数剩5个,求这堆苹果至少有多少个?
3.甲、乙、丙三人去完成植树任务,已知甲植一棵树的时间,乙可以 然后丙休息了8天,乙休息了3天,甲没休息,最后一起完成任务.问:从开始植树算起,共用了多少天才完成任务?
【精编】六年级奥数天天练 (中难度).doc
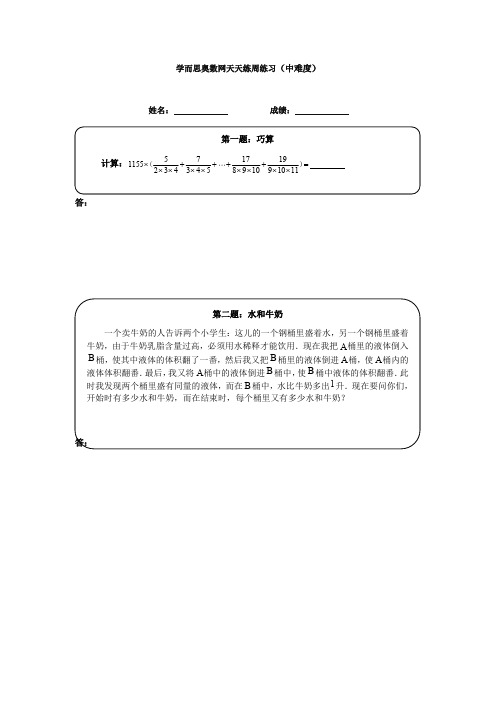
学而思奥数网天天练周练习(中难度)姓名:成绩:答:答:第一题:巧算计算:5717191155234345891091011⨯++++=⨯⨯⨯⨯⨯⨯⨯⨯()第二题:水和牛奶一个卖牛奶的人告诉两个小学生:这儿的一个钢桶里盛着水,另一个钢桶里盛着牛奶,由于牛奶乳脂含量过高,必须用水稀释才能饮用.现在我把A桶里的液体倒入B桶,使其中液体的体积翻了一番,然后我又把B桶里的液体倒进A桶,使A桶内的液体体积翻番.最后,我又将A桶中的液体倒进B桶中,使B桶中液体的体积翻番.此时我发现两个桶里盛有同量的液体,而在B桶中,水比牛奶多出1升.现在要问你们,开始时有多少水和牛奶,而在结束时,每个桶里又有多少水和牛奶?答:答:第三题:浓度问题瓶中装有浓度为15%的酒精溶液1000克,现在又分别倒入100克和400克的A、B两种酒精溶液,瓶中的浓度变成了14%.已知A种酒精溶液浓度是B种酒精溶液浓度的2倍,那么A种酒精溶液的浓度是百分之几?第四题:灌水问题公园水池每周需换一次水.水池有甲、乙、丙三根进水管.第一周小李按甲、乙、丙、甲、乙、丙……的顺序轮流打开1小时,恰好在打开某根进水管1小时后灌满空水池.第二周他按乙、丙、甲、乙、丙、甲……的顺序轮流打开1小时,灌满一池水比第一周少用了15分钟;第三周他按丙、乙、甲、丙、乙、甲……的顺序轮流打开1小时,比第一周多用了15分钟.第四周他三个管同时打开,灌满一池水用了2小时20分,第五周他只打开甲管,那么灌满一池水需用________小时.答:第五题:填数字请在下图的每个空格内填入1至8中的一个数字,使每行、每列、每条对角线上8个数字都互不相同.学而思奥数网天天练周练习(六年级)答案第一题答案:解答:本题的重点在于计算括号内的算式:571719234345891091011++++⨯⨯⨯⨯⨯⨯⨯⨯.这个算式不同于我们常见的分数裂项的地方在于每一项的分子依次成等差数列,而非常见的分子相同、或分子是分母的差或和的情况.所以应当对分子进行适当的变形,使之转化成我们熟悉的形式. 法一:观察可知523=+,734=+,……即每一项的分子都等于分母中前两个乘数的和,所以(法二) 上面的方法是最直观的转化方法,但不是唯一的转化方法.由于分子成等差数列,而等差数列的通项公式为a nd +,其中d 为公差.如果能把分子变成这样的形式,再将a与nd 分开,每一项都变成两个分数,接下来就可以裂项了.(法三) 本题不对分子进行转化也是可以进行计算的:(法四)对于这类变化较多的式子,最基本的方法就是通项归纳.先找每一项的通项公式:21(1)(2)n n a n n n +=++(2n =,3,……,9) 如果将分子21n +分成2n 和1,就是上面的法二;如果将分子分成n 和1n +,就是上面的法一.第二题答案:解答:假设一开始A 桶中有液体x 升,B 桶中有y 升.第一次将A 桶的液体倒入B 桶后,B 桶有液体2y 升,A 桶剩()x y -升;第二次将B 桶的液体倒入A 桶后,A 桶有液体2()x y -升,B 桶剩(3)y x -升;第三次将A 桶的液体倒入B 桶后,B 桶有液体(62)y x -升,A 桶剩(35)x y -升.由此时两桶的液体体积相等,得3562x y y x -=-,511x y =,:11:5x y =.现在还不知道A 桶中装的是牛奶还是水,可以将稀释牛奶的过程列成下表: A 桶 B 桶 原A 桶液体:原B 桶液体 原A 桶液体:原B 桶液体初始状态 11:0 0:5 第一次A 桶倒入B 桶6:0 5:5 第二次B 桶倒入A 桶9:3 2:2 第三次A 桶倒入B 桶6:2 5:3 由上表看出,最后B 桶中的液体,原A 桶液体与原B 桶液体的比是5:3,而题目中说“水比牛奶多1 升”,所以原A 桶中是水,原B 桶中是牛奶. 因为在5:3中,“53-”相当于1升,所以2个单位相当于1升.由此得到,开始时,A桶中有112升水,B 桶中有52升牛奶;结束时,A 桶中有3升水和1升牛奶,B 桶中有52升水和32升牛奶.第三题答案:解答:(法1)方程法.新倒入纯酒精:()100010040014%100015%60++⨯-⨯=(克).设A 种酒精溶液的浓度为x ,则B 种为2x.根据新倒入的纯酒精量,可列方程: 100400602xx +⨯=,解得20%x =,即A 种酒精溶液的浓度是20%.(法2)浓度三角法.设A 种酒精溶液的浓度为x ,则B 种为2x.根据题意,假设先把100克A 种酒精和400克B 种酒精混合,得到500克的酒精溶液,再与1000克15%的酒精溶液混合,所以A 、B 两种酒精混合得到的酒精溶液的浓度为()100014%15%14%12%500--⨯=.根据浓度三角,有()12%:12%400:1002x x ⎛⎫--= ⎪⎝⎭,解得20%x =.故A 种酒精溶液的浓度是20%.第四题答案:解答:如第一周小李按甲、乙、丙、甲、乙、丙……的顺序轮流打开1小时,恰好在打开丙管1小时后灌满空水池,则第二周他按乙、丙、甲、乙、丙、甲……的顺序轮流打开1小时,应在打开甲管1小时后灌满一池水.不合题意.如第一周小李按甲、乙、丙、甲、乙、丙……的顺序轮流打开1小时,恰好在打开乙管1小时后灌满空水池,则第二周他按乙、丙、甲、乙、丙、甲……的顺序轮流打开1小时,应在打开丙管45分钟后灌满一池水;第三周他按丙、乙、甲、丙、乙、甲……的顺序轮流打开1小时,应在打开甲管后15分钟灌满一池水.比较第二周和第三周,发现开乙管1小时和丙管45分钟的进水量与开丙管、乙管各1小时加开甲管15分钟的进水量相同,矛盾.所以第一周是在开甲管1小时后灌满水池的.比较三周发现,甲管1小时的进水量与乙管45分钟的进水量相同,乙管30分钟的进水量与丙管1小时的进水量相同.三管单位时间内的进水量之比为3:4:2.第五题答案: 解答:解此类数独题的关键在于观察那些位置较特殊的方格(对角线上的或者所在行、列空格比较少的),选作突破口.本题可以选择两条对角线上的方格为突破口,因为它们同时涉及三条线,所受的限制最严,所能填的数的空间也就最小.副对角线上面已经填了2,3,8,6四个数,剩下1,4,5和7,这是突破口.观察这四个格,发现左下角的格所在的行已经有5,所在的列已经有1和4,所以只能填7.然后,第六行第三列的格所在的行已经有5,所在的列已经有4,所以只能填1.第四行第五列的格所在的行和列都已经有5,所以只能填4,剩下右上角填5.再看主对角线,已经填了1和2,依次观察剩余的6个方格,发现第四行第四列的方格只能填7,因为第四行和第四列已经有了5,4,6,8,3.再看第五行第五列,已经有了4,8,3,5,所以只能填6.此时似乎无法继续填主对角线的格子,但是,可观察空格较少的行列,例如第四列已经填了5个数,只剩下1,2,5,则很明显第六格填2,第八格填1,第三格填5.此时可以填主对角线的格子了,第三行第三列填8,第二行第二列填3,第六行第六列填4,第七行第七列填5.继续依次分析空格较少的行和列(例如依次第五列、第三行、第八行、第二列……),可得出结果如下图.1346724578148627321567137865728635471288754321642431564835631852。
六年级数学经典奥数20题及答案解析

六年级数学经典奥数20题及答案解析【题-001】抽屉原理有5个小朋友,每人都从装有许多黑白围棋子的布袋中任意摸出3枚棋子.请你证明,这5个人中至少有两个小朋友摸出的棋子的颜色的配组是一样的。
【题-002】牛吃草:(中等难度)一只船发现漏水时,已经进了一些水,水匀速进入船内.如果10人淘水,3小时淘完;如5人淘水8小时淘完.如果要求2小时淘完,要安排多少人淘水?【题-003】奇偶性应用:(中等难度)桌上有9只杯子,全部口朝上,每次将其中6只同时“翻转”.请说明:无论经过多少次这样的“翻转”,都不能使9只杯子全部口朝下。
【题-004】整除问题:(中等难度)用一个自然数去除另一个整数,商40,余数是16.被除数、除数、商数与余数的和是933,求被除数和除数各是多少?【题-005】填数字:(中等难度)请在下图的每个空格内填入1至8中的一个数字,使每行、每列、每条对角线上8个数字都互不相同.【题-006】灌水问题:(中等难度)公园水池每周需换一次水.水池有甲、乙、丙三根进水管.第一周小李按甲、乙、丙、甲、乙、丙……的顺序轮流打开小1时,恰好在打开某根进水管1小时后灌满空水池.第二周他按乙、丙、甲、乙、丙、甲……的顺序轮流打开1小时,灌满一池水比第一周少用了15分钟;第三周他按丙、乙、甲、丙、乙、甲……的顺序轮流打开1小时,比第一周多用了15分钟.第四周他三个管同时打开,灌满一池水用了2小时20分,第五周他只打开甲管,那么灌满一池水需用________小时.【题-007】浓度问题:(中等难度)瓶中装有浓度为15%的酒精溶液1000克,现在又分别倒入100克和400克的A、B两种酒精溶液,瓶中的浓度变成了14%.已知A种酒精溶液浓度是B种酒精溶液浓度的2倍,那么A种酒精溶液的浓度是百分之几?【题-008】水和牛奶:(中等难度)一个卖牛奶的人告诉两个小学生:这儿的一个钢桶里盛着水,另一个钢桶里盛着牛奶,由于牛奶乳脂含量过高,必须用水稀释才能饮用.现在我把A桶里的液体倒入B桶,使其中液体的体积翻了一番,然后我又把B桶里的液体倒进A桶,使A桶内的液体体积翻番.最后,我又将A桶中的液体倒进B桶中,使B桶中液体的体积翻番.此时我发现两个桶里盛有同量的液体,而在B桶中,水比牛奶多出1升.现在要问你们,开始时有多少水和牛奶,而在结束时,每个桶里又有多少水和牛奶?【题-009】巧算:(中等难度)计算:【题-010】队形:(中等难度)做少年广播体操时,某年级的学生站成一个实心方阵时(正方形队列)时,还多10人,如果站成一个每边多1人的实心方阵,则还缺少15人.问:原有多少人?【题-011】计算:(中等难度)一个自然数,如果它的奇数位上各数字之和与偶数位上各数字之和的差是11的倍数,那么这个自然数是11的倍数,例如1001,因为1+0=0+1,所以它是11的倍数;又如1234,因为4+2-(3+1)=2不是11的倍数,所以1234不是11的倍数.问:用0、1、2、3、4、5这6个数字排成不含重复数字的六位数,其中有几个是11的倍数?【题-012】分数:(中等难度)某学校的若干学生在一次数学考试中所得分数之和是8250分.第一、二、三名的成绩是88、85、80分,得分最低的是30分,得同样分的学生不超过3人,每个学生的分数都是自然数.问:至少有几个学生的得分不低于60分?【题-013】四位数:(中等难度)某个四位数有如下特点:(1)这个数加1之后是15的倍数;(2)这个数减去3是38的倍数;(3)把这个数各数位上的数左右倒过来所得的数与原数之和能被10整除,求这个四位数.【题-014】行程:(中等难度)王强骑自行车上班,以均匀速度行驶.他观察来往的公共汽车,发现每隔12分钟有一辆汽车从后面超过他,每隔4分钟迎面开来一辆,如果所有汽车都以相同的匀速行驶,发车间隔时间也相同,那么调度员每隔几分钟发一辆车?【题-015】跑步:(中等难度)狗跑5步的时间马跑3步,马跑4步的距离狗跑7步,现在狗已跑出30米,马开始追它。
新版六年级奥数题及答案 20道题1

新版六年级奥数题及答案 20道题1 新版六年级奥数题及答案-20道题1 六年级奥林匹克数学试题和20个答案(中等难度) 【题-001】抽屉原理 共有五名儿童,他们每人从一个装有许多黑白棋子的布袋中随机摸出三个棋子。请证明五名儿童中至少有两人摸到了相同颜色的棋子。
【题-002】牛吃草:(中等难度) 当一艘船发现漏水时,它已经进入了一些水,水以匀速进入船内,如果10个人洗水,他们可以在3小时内完成;在用水冲洗8小时后,如果需要在2小时内清洗完,应安排多少人来清洗?
【题-003】奇偶性应用:(中等难度) 桌子上有九个杯子,都张着嘴,其中六个杯子是同时“翻转”的。请解释:无论这样“翻转”多少次,九个杯子都不能被翻转。
【题-004】整除问题:(中等难度) 将一个自然数除以另一个整数,即商40,余数为16。除数、除数、商和余数之和为933。除数和除数是什么?
【题-005】填数字:(中等难度) 请在下图中的每个空格中填写1到8之间的数字,以便每行、每列和每对角线上的8个数字彼此不同
精选 灌溉问题:(中等难度) 公园水池每周需换一次水.水池有甲、乙、丙三根进水管.第一周小李按甲、乙、丙、甲、乙、丙……的顺序轮流打开小1时,恰好在打开某根进水管1小时后灌满空水池.第二周他按乙、丙、甲、乙、丙、甲……的顺序轮流打开1小时,灌满一池水比第一周少用了15分钟;第三周他按丙、乙、甲、丙、乙、甲……的顺序轮流打开1小时,比第一周多用了15分钟.第四周他三个管同时打开,灌满一池水用了2小时20分,第五周他只打开甲管,那么灌满一池水需用________小时.
[问题007]注意力集中问题:(中等难度) 瓶中装有浓度为15%的酒精溶液1000克,现在又分别倒入100克和400克的a、b两种酒精溶液,瓶中的浓度变成了14%.已知a种酒精溶液浓度是b种酒精溶液浓度的2倍,那么a种酒精溶液的浓度是百分之几?
小学六年级奥数练习题:整除问题

小学六年级奥数练习题:整除问题
教案是教师为顺利而有效地开展教学活动,根据课程标准,教学大纲和教科书要求及学生的实际情况,以课时或课题为单位,对教学内容、教学步骤、教学方法等进行的具体设计和安排的一种实用性教学文书,包括教材简析和学生分析、教学目的、重难点、教学准备、教学过程及练习设计等,下面是由小编为大家整理的范文模板,仅供参考,欢迎大家阅读.
整除问题:(中等难度)
用一个自然数去除另一个整数,商40,余数是_.被除数、除数、商数与余数的和是933,求被除数和除数各是多少?
整除问题答案:
∵被除数=除数_商+余数,
即被除数=除数_40+_。
由题意可知:被除数+除数=933-40-_=877,
∴(除数_40+_)+除数=877,
∴除数_41=877-_,
除数=861÷41,
除数=_,
∴被除数=__40+_=856。
答:被除数是856,除数是_。
小学六年级奥数练习题:整除问题.到电脑,方便收藏和打印:。
六年级数学 中高难度奥数试题(含解析)(5)
小学六年级中高难度奥数题及答案解析(5)“奥数”是奥林匹克数学竞赛的简称。
学习奥数可以锻炼思维,是大有好处的。
学习奥数的年龄根据学生自身特点而定。
21世纪小学频道在这里精选了一些典型的小学六年级中高难度的奥数试题,并附有答案解析,大家来做做看吧!题1:(中等难度)若干只同样的盒子排成一列,小聪把42个同样的小球放在这些盒子里然后外出,小明从每支盒子里取出一个小球,然后把这些小球再放到小球数最少的盒子里去。
再把盒子重排了一下.小聪回来,仔细查看,没有发现有人动过小球和盒子.问:一共有多少只盒子【答案解析】设原来小球数最少的盒子里装有a只小球,现在增加了b只,由于小聪没有发现有人动过小球和盒子,这说明现在又有了一只装有a个小球的盒子,而这只盒子里原来装有(a+1)个小球.同样,现在另有一个盒子装有(a+1)个小球,这只盒子里原来装有(a+2)个小球.类推,原来还有一只盒子装有(a+3)个小球,(a+4)个小球等等,故原来那些盒子中装有的小球数是一些连续整数.现在变成:将42分拆成若干个连续整数的和,一共有多少种分法,每一种分法有多少个加数?因为42=6×7,故可以看成7个6的和,又(7+5)+(8+4)+(9+3)是6个6,从而42=3+4+5+6+7+8+9,一共有7个加数;又因为42=14×3,故可将42:13+14+15,一共有3个加数;又因为42=21×2,故可将42=9+10+11+12,一共有4个加数.所以原问题有三个解:一共有7只盒子、4只盒子或3只盒子.题2:(中等难度)在整数中,有用2个以上的连续自然数的和来表达一个整数的方法.例如9:9=4+5,9=2+3+4,9有两个用2个以上连续自然数的和来表达它的方法.【答案解析】(1)请写出只有3种这样的表示方法的最小自然数.(2)请写出只有6种这样的表示方法的最小自然数.关于某整数,它的"奇数的约数的个数减1",就是用连续的整数的和的形式来表达种数.根据(1)知道,有3种表达方法,于是奇约数的个数为3+1=4,对4分解质因数4=2×2,最小的15(1、3、5、15);有连续的2、3、5个数相加;7+8;4+5+6;1+2+3+4+5;根据(2)知道,有6种表示方法,于是奇数约数的个数为6+1=7,最小为729(1、3、9、27、81、243、729),有连续的2,3、6、9、10、27个数相加:364+365;242+243+244;119+120+…+124;77+78+79+…+85;36+37+…+45;14+15+…+40题3:(高等难度)求数的整数部分是几【答案解析】题4:(中等难度)(第六届小数报决赛)A ,A的整数部分是_________.【答案解析】题5:(中等难度)王母娘娘的蟠桃宴结束后,由于猪八戒吃的太多了,走不动了,第二天王母娘娘对猪八戒说只有完成一项任务才能让他走,任务是这样的,现有24米漂亮的小围栏,用这段围栏靠墙作一个长方形的小花圃(当然靠墙的一面就不用围栏了),为了种更多的花草,王母娘娘要求猪八戒围出的长方形花圃面积最大,同学们你能帮猪八戒想出最佳方案吗【答案解析】我们探索的结论是指封闭图形,但现在的长方形只有三条边,如何把它转化为封闭图形求解呢我们可以以墙面做对称轴,把周长乘二.(如下图)这时,矩形的周长为48米,那么,根据上面的定理,周长一定,正方形的面积最大.所以当这个长方形为正方形时,即边长为12米时,面积最大.而小花圃的面积是正方形面积的一半,则花圃的长为12米,宽为12÷2=6(米)那么,小花圃的面积为:12×6=72(平方米)题6:(中等难度)有5个小朋友,每人都从装有许多黑白围棋子的布袋中任意摸出3枚棋子.请你证明,这5个人中至少有两个小朋友摸出的棋子的颜色的配组是一样的。
六年级奥数题及答案:填数字(中等难度)
主对角线的格子了,第三行第三列填8,第二行第二列填3,第六行第六列填4,第七行第七列填5.
教师范读的是阅读教我读一句,让幼儿读一句,边读边记;第二通读,我大声读,我大声读,幼儿小声读,边学边仿;第三赏读,我借用录好配朗读磁带,一边放录音,一边幼儿反复倾听,在反复倾听中体验、品味。
与当今“教师”一称最接近的“老师”概念,最早也要追溯至宋元时期。金代元好问《示侄孙伯安》诗云:“伯安入小学,颖悟非凡貌,属句有夙性,说字惊老师。”于是看,宋元时期小学教师被称为“老师”有案可稽。清代称主考官也为“老师”,而一般学堂里的先生则称为“教师”或“教习”。可见,“教师”一说是比较晚的事了。如今体会,“教师”的含义比之“老师”一说,具有资历和学识程度上较低一些的差别。辛亥革命后,教师与其他官员一样依法令任命,故又称“教师”为“教员”。继续依次分析空格较少的行和列(例如依次第五列、第三行、第八行、第二列),可得出结果如下图.
语文课本中的文章都是精选的比较优秀的文章,还有不少名家名篇。如果有选择循序渐进地让学生背诵一些优秀篇目、精彩段落,对提高学生的水平会大有裨益。现在,不少语文教师在分析课文时,把文章解体的支离破碎,总在文章的技巧方面下功夫。结果教师费劲,学生头疼。分析完之后,学生收效甚微,没过几天便忘的一干二净。造成这种事倍功半的尴尬局面的关键就是对文章读的不熟。常言道“书读百遍,其义自见”,如果有目的、有计划地引导学生反复阅读课文,或细读、默读、跳读,或听读、范读、轮读、分角色朗读,学生便可以在读中自然领悟文章的思想内容和写作技巧,可以在读中自然加强语感,增强语言的感受力。久而久之,这种思想内容、写作技巧和语感就会自然渗透到学生的语言意识之中,就会在写作中自觉不自觉地加以运用、创造和发展。
六年级奥数题及答案:计算(中等难度)
我国古代的读书人,从上学之日起,就日诵不辍,一般在几年内就能识记几千个汉字,熟记几百篇文章,写出的诗文也是字斟句酌,琅琅上口,成为满腹经纶的文人。为什么在现代化教学的今天,我们念了十几年书的高中毕业生甚至大学生,竟提起作文就头疼,写不出像样的文章呢?吕叔湘先生早在1978年就尖锐地提出:“中小学语文教学效果差,中学语文毕业生语文水平低,……十几年上课总时数是9160课时,语文是2749课时,恰好是30%,十年的时间,二千七百多课时,用来学本国语文,却是大多数不过关,岂非咄咄怪事!”寻根究底,其主要原因就是腹中无物。特别是写议论文,初中水平以上的学生都知道议论文的“三要素”是论点、论据、论证,也通晓议论文的基本结构:提出问题――分析问题――解决问题,但真正动起笔来就犯难了。知道“是这样”,就是讲不出“为什么”。根本原因还是无“米”下“锅”。于是便翻开作文集锦之类的书大段抄起来,抄人家的名言警句,抄人家的事例,不参考作文书就很难写出像样的文章。所以,词汇贫乏、内容空洞、千篇一律便成了中学生作文的通病。要解决这个问题,不能单在布局谋篇等写作技方面下功夫,必须认识到“死记硬背”的重要性,让学生积累足够的“米”。
要练说,得练看。看与说是统的,看不准就难以说得好。练看,就是训练幼儿的观察能力,扩大幼儿的认知范围,让幼儿在观察事物、观察生活、观察自然的活动中,积累词汇、理解词义、发展语言。在运用观察法组织活动时,我着眼观察于观察对象的选择,着力于观察过程的指导,着重于幼儿观察能力和语言表达能力的提高。根据上述分析知:用0、1、2、3、4、5不能组成不包含重复数字的能被11整除的六位数.
小学六年级中高难度奥数题【含答案】(7)
小学六年级中高难度奥数题和答案解析(7)题1:(中等难度)一个卖牛奶的人告诉两个小学生:这儿的一个钢桶里盛着水,另一个钢桶里盛着牛奶,由于牛奶乳脂含量过高,必须用水稀释才能饮用.现在我把A桶里的液体倒入B桶,使其中液体的体积翻了一番,然后我又把B桶里的液体倒进A桶,使A桶内的液体体积翻番.最后,我又将A桶中的液体倒进B桶中,使B桶中液体的体积翻番.此时我发现两个桶里盛有同量的液体,而在B桶中,水比牛奶多出1升.现在要问你们,开始时有多少水和牛奶,而在结束时,每个桶里又有多少水和牛奶?【答案解析】 题2:(高等难度)有一堆苹果平均分给幼儿园大、小班小朋友,每人可得6个,如果只分给大班每人可得10个,问只分给小班时,每人可得几个?【答案解析】 题3:(高等难度)光明小学六年级选出的男生的1/11和12名女生参加数学竞赛,剩下的男生人数是剩下的女生人数的2倍.已知六年级共有156人,问男、女生各有多少人?【答案解析】 ②女生人数:156-99=57(人).题4:(中等难度)一个自然数,如果它的奇数位上各数字之和与偶数位上各数字之和的差是11的倍数,那么这个自然数是11的倍数,例如1001,因为1+0=0+1,所以它是11的倍数;又如1234,因为4+2-(3+1)=2不是11的倍数,所以1234不是11的倍数.问:用0、1、2、3、4、5这6个数字排成不含重复数字的六位数,其中有几个是11的倍数?【答案解析】 用1.2.3.4.5组成不含重复数字的六位数,,它能被11整除,并设a1+a3+a5≥a2+a4+a6,则对某一整数k≥0,有:a1+a3+a5-a2-a4-a6=11k (*)也就是:a1+a2+a3+a4+a5+a6=11k+2(a2+a4+a6)15=0+1+2+3+4+5=11k+2(a2+a4+a6)(**)由此看出k只能是奇数由(*)式看出,0≤k<2,又因为k为奇数,所以只可能k=1,但是当k=1时,由(**)式看出a2+a4+a6=2.但是在0、1、2、3、4、5中任何三个数之和也不等于2,可见k≠1.因此(*)不成立.对于a2+a4+a6>a1+a3+a5的情形,也可类似地证明(a2+a4+a6)-(a1+a3+a5)不是11的倍数.根据上述分析知:用0、1、2、3、4、5不能组成不包含重复数字的能被11整除的六位数.题5:(中等难度)某学校的若干学生在一次数学中所得分数之和是8250分.第一、二、三名的成绩是88、85、80分,得分最低的是30分,得同样分的学生不超过3人,每个学生的分数都是自然数.问:至少有几个学生的得分不低于60分?【答案解析】 除得分88、85、80的人之外,其他人的得分都在30至79分之间,其他人共8250-(88+85+80)=7997(分).为使不低于60分的人数尽量少,就要使低于60分的人数尽量多,即得分在30~59分中的人数尽量多,在这些分数上最多有3×(30+31+…+59)= 4005分(总分),因此,得60~79分的人至多总共得7997-4005=3992分.如果得60分至79分的有60人,共占分数3×(60+61+ …+ 79)= 4170,比这些人至多得分7997-4005= 3992分还多178分,所以要从不低于60分的人中去掉尽量多的人.但显然最多只能去掉两个不低于60分的(另加一个低于60分的,例如,178=60+60+58).因此,加上前三名,不低于60分的人数至少为61人.题6:(中等难度)某个四位数有如下特点:①这个数加1之后是15的倍数;②这个数减去3是38的倍数;③把这个数各数位上的数左右倒过来所得的数与原数之和能被10整除,求这个四位数.【答案解析】 因为该数加1之后是15的倍数,也是5的倍数,所以d=4或d=9.因为该数减去3是38的倍数,可见原数是奇数,因此d≠4,只能是d=9.这表明m=27、37、47;32、42、52.(因为38m的尾数为6)又因为38m+3=15k-1(m、k是正整数)所以38m+4=15k.由于38m的个位数是6,所以5|(38m+4),因此38m+4=15k等价于3|(38m+4),即3除m余1,因此可知m=37,m=52.所求的四位数是1409,1979.题7:(中等难度)王强骑自行车上班,以均匀速度行驶.他观察来往的公共汽车,发现每隔12分钟有一辆汽车从后面超过他,每隔4分钟迎面开来一辆,如果所有汽车都以相同的匀速行驶,发车间隔时间也相同,那么调度员每隔几分钟发一辆车?【答案解析】 汽车间隔距离是相等的,列出等式为:(汽车速度-自行车速度)×12=(汽车速度+自行车速度)×4得出:汽车速度=自行车速度的2倍. 汽车间隔发车的时间=汽车间隔距离÷汽车速度=(2倍自行车速度-自行车速度)×12÷2倍自行车速度=6(分钟).题8:(高等难度)如果多位数能被7整除,那么О内的数字是几?【答案解析】 2009÷3=669…2,从最后一位开始三位三位一段,则奇数段减去偶数段的差为:999-О99+222-22=200+О×100。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 六年级奥数中等难度练习题一 巧求整数部分题目:(中等难度) A 8.8 8.98 8.998 8.9998 8.99998,A的整数部分是_________. 巧求整数部分答案:
准确值:(中等难度) 已知A、B、C都是非0自然数, 的近似值是6.4,那么它的准确值是多少? 准确值案:
自然数和:(中等难度) 在整数中,有用2个以上的连续自然数的和来表达一个整数的方法.例如9:9=4+5,9=2+3+4,9有两个用2个以上连续自然数的和来表达它的方法. 准确值案: 2
(1)请写出只有3种这样的表示方法的最小自然数. (2)请写出只有6种这样的表示方法的最小自然数. 关于某整数,它的"奇数的约数的个数减1",就是用连续的整数的和的形式来表达种数. 根据(1)知道,有3种表达方法,于是奇约数的个数为3+1=4,对4分解质因数4=2×2,最小的15(1、3、5、15); 有连续的2、3、5个数相加;7+8;4+5+6;1+2+3+4+5; 根据(2)知道,有6种表示方法,于是奇数约数的个数为6+1=7,最小为729(1、3、9、27、81、243、729),有连续的2,3、6、9、10、27个数相加: 364+365;242+243+244;119+120+…+124;77+78+79+…+85;36+37+…+45;14+15+…+40 分数方程:(中等难度) 若干只同样的盒子排成一列,小聪把42个同样的小球放在这些盒子里然后外出,小明从每支盒子里取出一个小球,然后把这些小球再放到小球数最少的盒子里去。再把盒子重排了一下.小聪回来,仔细查看,没有发现有人动过小球和盒子.问:一共有多少只盒子? 准确值案: 设原来小球数最少的盒子里装有a只小球,现在增加了b只,由于小聪没有发现有人动过小球和盒子,这说明现在又有了一只装有a个小球的盒子,而这只盒子里原来装有(a+1)个小球. 同样,现在另有一个盒子装有(a+1)个小球,这只盒子里原来装有(a+2)个小球. 类推,原来还有一只盒子装有(a+3)个小球,(a+4)个小球等等,故原来那些盒子中装有的小球数是一些连续整数. 现在变成:将42分拆成若干个连续整数的和,一共有多少种分法,每一种分法有多少个加数? 因为42=6×7,故可以看成7个6的和,又(7+5)+(8+4)+(9+3)是6个6,从而42=3+4+5+6+7+8+9,一共有7个加数; 又因为42=14×3,故可将42:13+14+15,一共有3个加数; 又因为42=21×2,故可将42=9+10+11+12,一共有4个加数. 所以原问题有三个解:一共有7只盒子、4只盒子或3只盒子. 跑步:(中等难度) 狗跑5步的时间马跑3步,马跑4步的距离狗跑7步,现在狗已跑出30米,马开始追它。问:狗再跑多远,马可以追上它? 准确案: 根据"马跑4步的距离狗跑7步",可以设马每步长为7x米,则狗每步长为4x米。 根据"狗跑5步的时间马跑3步",可知同一时间马跑3*7x米=21x米,则狗跑5*4x=20x米。 3
可以得出马与狗的速度比是21x:20x=21:20 根据"现在狗已跑出30米",可以知道狗与马相差的路程是30米,他们相差的份数是21-20=1,现在求马的21份是多少路程,就是 30÷(21-20)×21=630米 行程:(中等难度) 王强骑自行车上班,以均匀速度行驶.他观察来往的公共汽车,发现每隔12分钟有一辆汽车从后面超过他,每隔4分钟迎面开来一辆,如果所有汽车都以相同的匀速行驶,发车间隔时间也相同,那么调度员每隔几分钟发一辆车? 行程答案: 汽车间隔距离是相等的,列出等式为:(汽车速度-自行车速度)×12=(汽车速度+自行车速度)×4 得出:汽车速度=自行车速度的2倍. 汽车间隔发车的时间=汽车间隔距离÷汽车速度=(2倍自行车速度-自行车速度)×12÷2倍自行车速度=6(分钟). 四位数:(中等难度) 某个四位数有如下特点:①这个数加1之后是15的倍数;②这个数减去3是38的倍数;③把这个数各数位上的数左右倒过来所得的数与原数之和能被10整除,求这个四位数. 四位数答案: 因为该数加1之后是15的倍数,也是5的倍数,所以d=4或d=9. 因为该数减去3是38的倍数,可见原数是奇数,因此d≠4,只能是d=9.
这表明m=27、37、47;32、42、52.(因为38m的尾数为6) 又因为38m+3=15k-1(m、k是正整数)所以38m+4=15k. 由于38m的个位数是6,所以5|(38m+4), 因此38m+4=15k等价于3|(38m+4),即3除m余1,因此可知m=37,m=52. 所求的四位数是1409,1979. 分数:(中等难度) 某学校的若干学生在一次数学考试中所得分数之和是8250分.第一、二、三名的成绩是88、85、80分,得分最低的是30分,得同样分的学生不超过3人,每个学生的分数都是自然数.问:至少有几个学生的得分不低于60分? 4
分数答案: 除得分88、85、80的人之外,其他人的得分都在30至79分之间,其他人共得分:8250-(88+85+80)=7997(分). 为使不低于60分的人数尽量少,就要使低于60分的人数尽量多,即得分在30~59分中的人数尽量多,在这些分数上最多有3×(30+31+…+59)= 4005分(总分),因此,得60~79分的人至多总共得7997-4005=3992分. 如果得60分至79分的有60人,共占分数3×(60+61+ …+ 79)= 4170,比这些人至多得分7997-4005= 3992分还多178分,所以要从不低于60分的人中去掉尽量多的人.但显然最多只能去掉两个不低于60分的(另加一个低于60分的,例如,178=60+60+58).因此,加上前三名,不低于60分的人数至少为61人. 计算:(中等难度) 一个自然数,如果它的奇数位上各数字之和与偶数位上各数字之和的差是11的倍数,那么这个自然数是11的倍数,例如1001,因为1+0=0+1,所以它是11的倍数;又如1234,因为4+2-(3+1)=2不是11的倍数,所以1234不是11的倍数.问:用0、1、2、3、4、5这6个数字排成不含重复数字的六位数,其中有几个是11的倍数? 计算答案: 用1.2.3.4.5组成不含重复数字的六位数,,它能被11整除,并设a1+a3+a5≥a2+a4+a6,则对某一整数k≥0,有: a1+a3+a5-a2-a4-a6=11k (*) 也就是: a1+a2+a3+a4+a5+a6=11k+2(a2+a4+a6) 15=0+1+2+3+4+5=11k+2(a2+a4+a6) (**) 由此看出k只能是奇数 由(*)式看出,0≤k<2 ,又因为k为奇数,所以只可能k=1,但是当k=1时,由(**)式看出a2+a4+a6=2. 但是在0、1、2、3、4、5中任何三个数之和也不等于2,可见k≠1.因此(*)不成立. 对于a2+a4+a6>a1+a3+a5的情形,也可类似地证明(a2+a4+a6)-(a1+a3+a5)不是11的倍数. 根据上述分析知:用0、1、2、3、4、5不能组成不包含重复数字的能被11整除的六位数. 队形:(中等难度) 做少年广播体操时,某年级的学生站成一个实心方阵时(正方形队列)时,还多10人,如果站成一个每边多1人的实心方阵,则还缺少15人.问:原有多少人? 5
队形答案: 当扩大方阵时,需补充10+15人,这25人应站在扩充的方阵的两条邻边处,形成一层人构成的直角拐角.补充人后,扩大的方阵每边上有(10+15+1)÷2=13人.因此扩大方阵共有13×13=169人,去掉15人,就是原来的人数 169-15=154人. 水和牛奶:(中等难度) 一个卖牛奶的人告诉两个小学生:这儿的一个钢桶里盛着水,另一个钢桶里盛着牛奶,由于牛奶乳脂含量过高,必须用水稀释才能饮用.现在我把A桶里的液体倒入B桶,使其中液体的体积翻了一番,然后我又把B桶里的液体倒进A桶,使A桶内的液体体积翻番.最后,我又将A桶中的液体倒进B桶中,使B桶中液体的体积翻番.此时我发现两个桶里盛有同量的液体,而在B桶中,水比牛奶多出1升.现在要问你们,开始时有多少水和牛奶,而在结束时,每个桶里又有多少水和牛奶? 水和牛奶答案:
浓度问题:(中等难度) 6
瓶中装有浓度为15%的酒精溶液1000克,现在又分别倒入100克和400克的A、B两种酒精溶液,瓶中的浓度变成了14%.已知A种酒精溶液浓度是B种酒精溶液浓度的2倍,那么A种酒精溶液的浓度是百分之几? 浓度问题答案:
灌水问题:(中等难度) 公园水池每周需换一次水.水池有甲、乙、丙三根进水管.第一周小李按甲、乙、丙、甲、乙、丙……的顺序轮流打开小1时,恰好在打开某根进水管1小时后灌满空水池.第二周他按乙、丙、甲、乙、丙、甲……的顺序轮流打开1小时,灌满一池水比第一周少用了15分钟;第三周他按丙、乙、甲、丙、乙、甲……的顺序轮流打开1小时,比第一周多用了15分钟.第四周他三个管同时打开,灌满一池水用了2小时20分,第五周他只打开甲管,那么灌满一池水需用________小时. 灌水问题答案: 如第一周小李按甲、乙、丙、甲、乙、丙……的顺序轮流打开1小时,恰好在打开丙管1小时后灌满空水池,则第二周他按乙、丙、甲、乙、丙、甲……的顺序轮流打开1小时,应在打开甲管1小时后灌满一池水.不合题意. 如第一周小李按甲、乙、丙、甲、乙、丙……的顺序轮流打开1小时,恰好在打开乙管1小时后灌满空水池,则第二周他按乙、丙、甲、乙、丙、甲……的顺序轮流打开1小时,应在打开丙管45分钟后灌满一池水;第三周他按丙、乙、甲、丙、乙、甲……的顺序轮流打开1小时,应在打开甲管后15分钟灌满一池水.比较第二周和第三周,发现开乙管1小时和丙管45分钟的进水量与开丙管、乙管各1小时加开甲管15分钟的进水量相同,矛盾.
