课堂新坐标2013届高三数学(文)一轮复习6-4
课堂新坐标2013届高三数学(文)一轮复习课时知能训练4-1

课时知能训练一、选择题1.对于非零向量a 、b ,“a +b =0”是“a ∥b ”的( ) A .充分不必要条件 B .必要不充分条件 C .充分必要条件 D .既不充分也不必要条件2.已知AB →=a +2b ,BC →=-5a +6b ,CD →=7a -2b ,则下列一定共线的三点是( )A .A 、B 、C B .A 、B 、D C .B 、C 、D D .A 、C 、D3.已知P 是△ABC 所在平面内的一点,若CB →=λPA →+PB →,其中λ∈R ,则点P 一定在( )A .△ABC 的内部B .AC 边所在直线上 C .AB 边所在直线上D .BC 边所在直线上4.(2012·揭阳模拟)已知点O 为△ABC 外接圆的圆心,且OA →+OB →+OC →=0,则△ABC 的内角A 等于( )A .30°B .60°C .90°D .120°5.设O 在△ABC 的内部,D 为AB 的中点,且OA →+OB →+2OC →=0,则△ABC 的面积与△AOC 的面积之比为( )A .3B .4C .5D .6 二、填空题6.若AB →=3e 1,CD →=-5e 1,且AD →与CB →的模相等,则四边形ABCD 是__________.7.已知向量a ,b 是两个非零向量,则在下列四个条件中,能使a 、b 共线的条件是________(将正确的序号填在横线上).①2a -3b =4e ,且a +2b =-3e ; ②存在相异实数λ、μ,使λ·a +μ·b =0; ③x ·a +y ·b =0(实数x ,y 满足x +y =0); ④若四边形ABCD 是梯形,则AB →与CD →共线. 8.如图4-1-3,在△ABC 中,图4-1-3点O 是BC 的中点.过点O 的直线分别交直线AB 、AC 于不同的两点M 、N ,若AB→=mAM →,AC →=nAN →,则m +n 的值为________. 三、解答题图4-1-49.(2012·肇庆质检)如图4-1-4所示,在△ABC 中,AN→=13NC →,P 是BN上的一点,若AP→=mAB →+211AC →,求实数m 的值.10.设a ,b 是两个不共线的非零向量,若a 与b 起点相同,t ∈R ,t 为何值时,a ,t b ,13(a +b )三向量的终点在一条直线上?11.设O 是平面上一定点,A ,B ,C 是平面上不共线的三点,动点P 满足OP →=OA →+λ(AB →|AB →|+AC →|AC →|),λ∈[0,+∞).求点P 的轨迹,并判断点P 的轨迹通过下述哪一个定点:①△ABC 的外心;②△ABC 的内心;③△ABC 的重心;④△ABC 的垂心.答案及解析1.【解析】 由a +b =0知道a 与b 互为相反向量,从而a ∥b ,充分性成立.由a ∥b 知a =λb ,λ≠-1时,a +b ≠0,∴必要性不成立. 【答案】 A2.【解析】 BD →=BC →+CD →=2a +4b =2AB →⇒BD →∥AB →⇒A 、B 、D 三点共线. 【答案】 B3.【解析】 ∵CB →=CP →+PB →,又CB →=λPA →+PB →, ∴CP →=λPA →,∴点P ∈AC . 【答案】 B4.【解析】 由OA →+OB →+OC →=0,知点O 为△ABC 重心,又O 为△ABC 外接圆的圆心, ∴△ABC 为等边三角形,A =60°. 【答案】 B5.【解析】 ∵D 为AB 的中点, 则OD→=12(OA →+OB →), 又OA→+OB →+2OC →=0, ∴OD→=-OC →,∴O 为CD 的中点, ∴S △AOC =12S △ADC =14S △ABC ,则S △ABCS △AOC =4.【答案】 B6.【解析】 ∵AB →=-35CD →,∴AB ∥CD ,且|AB |≠|CD |. 【答案】 等腰梯形7.【解析】 由①得10a -b =0,故①对.②对. 对于③当x =y =0时,a 与b 不一定共线,故③不对.若AB ∥CD ,则AB →与CD →共线,若AD ∥BC ,则AB →与CD →不共线,故④不对. 【答案】 ①②8.【解析】 ∵O 是BC 的中点, ∴AO →=12(AB →+AC →)又∵AB→=mAM →,AC →=nAN →, ∴AO→=m 2AM →+n 2AN →. ∵M ,O ,N 三点共线, ∴m 2+n2=1.则m +n =2. 【答案】 29.【解】 如题图所示,AP →=AB →+BP →,∵P 为BN 上一点,则BP =kBN →, ∴AP→=AB →+kBN →=AB →+k (AN →-AB →) 又AN→=13NC →,即AN →=14AC →, 因此AP →=(1-k )AB →+k 4AC →,所以1-k =m ,且k 4=211,解得k =811则m =1-k =311.10.【解】 设OA →=a ,OB →=t b ,OC →=13(a +b ).若A ,B ,C 三点共线,则有AB →=λAC →,∴OB→-OA →=λ(OC →-OA →), ∴t b -a =λ[13(a +b )-a ].化简整理得,(23λ-1)a =(13λ-t )b.∵a 与b 不共线,由平面向量基本定理得λ=32t =12. 故当t =12时,a ,t b ,13(a +b )的终点在一直线上.11.【解】 如图,记AM →=AB →|AB →|,AN →=AC →|AC →|,则AM→,AN →都是单位向量.∴|AM →|=|AN →|,AQ →=AM →+AN →,则四边形AMQN 是菱形.∴AQ 平分∠BAC ,∵OP →=OA →+AP →,由条件知OP →=OA →+λAQ →, ∴AP →=λAQ →(λ∈[0,+∞)),∴点P 的轨迹是射线AQ ,且AQ 通过△ABC 的内心.。
课堂新坐标2013届高考数学一轮复习课件:第七章第六节 空间向量及其运算(广东专用)
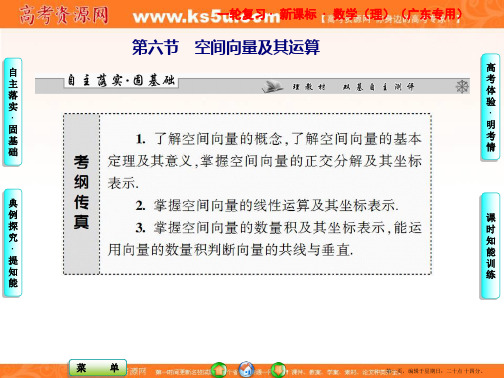
自 4.若三点A(1,5,-2),B(2,4,1),C(a,3,b+2)在同一条直线上,则a=
主
落
________,b=________.
实
高 考 体 验
·
固
基 础
【解析】 A→B=(1,-1,3),A→C=(a-1,-2,b+4),
· 明 考 情
因为三点共线,所以存在实数 λ 使A→C=λA→B,
自 主 落 实
高 考 体 验
· 固 基 础
1.选定空间不共面的三个向量作基向量,并用它们表示出指定
·
明
的向量,是用向量解决立体几何问题的基本要求.如本例用
考
情
表示 .解题时应结合已知和所求观察图形,联想相关的运算法
则和公式等,就近表示所需向量.
典
2.首尾相接的若干个向量的和,等于由起始向量的起点指向末尾
时 知
· 提
中 x+y+z=1).
能 训
知
练
能
菜单
第十六页,编辑于星期日:二十点 十四分。
一轮复习 ·新课标 ·数学(理)(广东专用)
自 主
已知 A、B、C 三点不共线,对平面 ABC 外的任一点 O,若
落 实 ·
点 M 满足O→M=13(O→A+O→B+O→C).
固 基
(1)判断M→A、M→B、M→C三个向量是否共面;
高 考 体 验
· 明 考 情
典
例
课
探
时
究
知
·能提训知练能
菜单
第十四页,编辑于星期日:二十点 十四分。
一轮复习 ·新课标 ·数学(理)(广东专用)
自 主
【思路点拨】 (1)在图形中,用向量A→B,A→A1表示向量M→N. (2)用共面向量的概念判定 MN 是否与平面 ABB1A1 平行.
课堂新坐标2013届高考数学一轮复习课件:选修4-5第一节 不等式和绝对值不等式(广东专用)
· 提
知
能
自
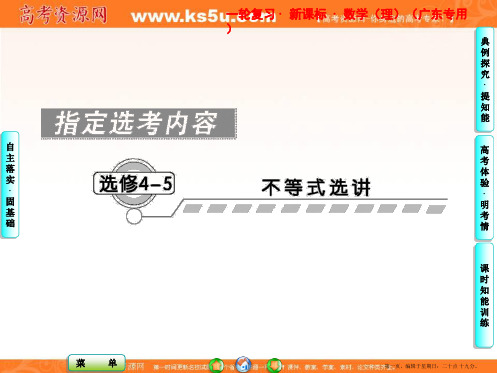
不等式
a>0
a=0
a<0
高
主 落
|x|<a
{x|-a<x<a}
∅
∅
考 体
实 ·
|x|>a
{x|x>a或x<-a}
{x∈R|x≠0}
R
验 ·
固
明
基
考
础
(2)|ax+b|≤c、|ax+b|≥c(c>0)型不等式的解法:
情
课 时 知 能 训 练
菜单
第五页,编辑于星期日:二十点 十九分。
一轮复习 ·新课标 ·数学(理)(广东专用
高 考
落 实 ·
当___a_=_b____时,等号成立.即两个正数的算术平均不小于(即大 体
于或等于)它们的几何平均.
验 ·
固 基 础
定理 3:如果 a,b,c 大于 0,那么a+3b+c≥__3__a_b_c_,当且仅
明 考 情
当__a_=__b_=__c___时,等号成立.
课 时 知 能 训 练
体 验 ·
固 基
注意 x+y=1 的应用,运用 a+b≥2 ab求最小值.
明 考
础
情
课 时 知 能 训 练
菜单
第二十一页,编辑于星期日:二十点 十九分。
一轮复习 ·新课标 ·数学(理)(广东专用
)
典
例
探
【尝试解答】 (1)∵x>0,
究 ·
∴f(x)=x+x42=x2+x2+x42≥3 3 x2·x2·x42=3,
菜单
第三页,编辑于星期日:二十点 十九分。
一轮复习 ·新课标 ·数学(理)(广东专用
)
课堂新坐标2013届高考数学一轮复习课件:选修4-4第一节 坐标系(广东专用)
情
课 时 知 能 训 练
菜单
第十一页,编辑于星期日:二十点 十九分。
一轮复习 ·新课标 ·数学(理)(广东专用)
典
例
探
究
平面直角坐标系下图形的变换
·
提
知
能
x′=3x,
自 主 落 实
· 固 基
在平面直角坐标系中,已知伸缩变换 φ:2y′=y.
高 考
(1)则点 A(13,-2)经过 φ 变换所得的点 A′的坐标为________;
高
落
考
实
体
·
验
固
【答案】 一个圆和一条射线
·
基
明
础
考
情
课 时 知 能 训 练
菜单
第九页,编辑于星期日:二十点 十九分。
一轮复习 ·新课标 ·数学(理)(广东专用)
典
例
3.(2011·北京高考)在极坐标系中,圆ρ=-2sin θ的圆心的极坐标是
探 究
________.
· 提
知
能
自 主 落
【解析】 ρ=-2sin θ=2cos(θ+π2),
一轮复习 ·新课标 ·数学(理)(广东专用)
【尝试解答】 (1)设点 A′(x′,y′),由伸缩变换 φ:
典
例
x′=3x 2y′=y
得yx′′==2y3,x,
探 究
· 提 知
自
∴x′=31×3=1,y′=-22=-1.
能
主
∴点 A′的坐标为(1,-1).
落 实
(2)设 P′(x′,y′)是直线 l′上任意一点.
高 考
实 · 固
∴圆心的极坐标为(1,-π2).
课堂新坐标2013届高三数学(文)一轮复习课时知能训练4-2

课时知能训练一、选择题1.(2012·湛江模拟)在△ABC 中,点P 在BC 上,且BP →=2PC →,点Q 是AC的中点,若PA →=(4,3),PQ →=(1,5),则BC →等于( )A .(-2,7)B .(-6,21)C .(2,-7)D .(6,-21)2.(2011·上海高考)设A 1,A 2,A 3,A 4,A 5是平面上给定的5个不同点,则使MA 1→+MA 2→+MA 3→+MA 4→+MA 5→=0成立的点M 的个数为( ) A .0 B .1C .5D .103.△ABC 中,M 为边BC 上任意一点,N 为AM 的中点,且AN→=λAB →+μAC →,则λ+μ的值为( )A.12B.13C.14D .1 4.已知向量a =(1,1),b =(2,x ).若a +b 与4b -2a 平行,则实数x 的值是( )A .-2B .0C .1D .25.设向量a =(1,0),b =(12,12,则下列结论中正确的是( ) A .|a |=|b | B .a ·b =22C .a -b 与b 垂直D .a ∥b二、填空题6.已知向量a =(-2,3),b ∥a ,向量b 的起点为A (1,2),终点B 在x 轴上,则点B 的坐标为________.7.已知向量OC →=(2,2),CA →=(2cos α,2sin α),则向量OA →的模的最大值是________.8.(2012·梅州调研)已知向量a =(2,-1),b =(-1,m ),c =(-1,2),若(a +b )∥c ,则m =________.三、解答题9.已知A (1,1)、B (3,-1)、C (a ,b ).(1)若A 、B 、C 三点共线,求a 、b 的关系式;(2)若AC→=2AB →,求点C 的坐标. 10.已知点O (0,0),A (1,2),B (4,5),且OP→=OA →+tAB →(t ∈R ),问: (1)t 为何值时,点P 在x 轴上?点P 在第二、四象限角平分线上?(2)四边形OABP 能否成为平行四边形?若能,求出相应的t 值;若不能,请说明理由.11.已知向量a =(sin θ,cos θ-2sin θ),b =(1,2).(1)若a ∥b ,求tan θ的值;(2)若|a |=|b |,0<θ<π,求θ的值.答案及解析1.【解析】 AC →=2AQ →=2(PQ →-PA →)=2(-3,2)=(-6,4),BC →=3PC →=3(PA →+AC→)=3(-2,7)=(-6,21). 【答案】 B2.【解析】 设M (x ,y ),A i (x i ,y i )(i =1,2,3,4,5),由MA 1→+MA 2→+MA 3→+MA 4→+MA 5→=0,∴(x 1+x 2+…+x 5-5x ,y 1+y 2+…+y 5-5y )=(0,0),∴x =x 1+x 2…+x 55,y =y 1+y 2+…+y 55, ∵A i 为定点,∴x ,y 为定值,因此点M 的个数为1.【答案】 B3.【解析】 如图所示,由B 、M 、C 共线,∴AM →=xAB →+(1-x )AC →,又N 为AM 的中点,∴AN →=12AM →=x 2AB →+1-x 2AC →, 由平面向量的基本定理,∴λ=x 2且μ=1-x 2,故λ+μ=12. 【答案】 A4.【解析】 由题意知a +b =(1,1)+(2,x )=(3,x +1), 且4b -2a =4(2,x )-2(1,1)=(6,4x -2).∵(a +b )∥(4b -2a ),∴3(4x -2)-6(x +1)=0,得x =2.【答案】 D5.【解析】 易知|a |=1,|b |= (12)2+(12)2=22. ∵a ·b =1×12+0×12=12, ∴a ·b ≠22,B 不正确. ∵a -b =(1,0)-(12,12)=(12,-12), ∴(a -b )·b =(12,-12)·(12,12)=0,C 正确. ∵1×12-0×12≠0,∴a 不平行于b .D 不正确. 【答案】 C6.【解析】 设B (x,0),则b =AB→=(x -1,-2),又b ∥a , ∴3(x -1)-(-2)×(-2)=0,∴x =73. 【答案】 (73,0) 7.【解析】 OA→=OC →+CA →=(2+2cos α,2+2sin α), ∴|OA→|2=(2+2cos α)2+(2+2sin α)2 =10+8sin(α+π4)≤18,故|OA →|≤3 2. 【答案】 3 28.【解析】 ∵a =(2,-1),b =(-1,m ),∴a +b =(1,m -1),又c =(-1,2),且(a +b )∥c ,∴2+m -1=0,∴m =-1.【答案】 -19.【解】 (1)由已知得AB→=(2,-2),AC →=(a -1,b -1), ∵A 、B 、C 三点共线,∴AB→∥AC →, ∴2(b -1)+2(a -1)=0,即a +b =2.(2)∵AC→=2AB →, ∴(a -1,b -1)=2(2,-2),∴⎩⎨⎧ a -1=4b -1=-4解之得⎩⎨⎧a =5b =-3. 因此点C 的坐标为(5,-3).10.【解】 (1)∵O (0,0),A (1,2),B (4,5),∴OA→=(1,2),AB →=(3,3), OP→=OA →+tAB →=(1+3t,2+3t ). 若P 在x 轴上,只需2+3t =0,t =-23;若P 在第二、四象限角平分线上,则1+3t =-(2+3t ),t =-12. (2)OA→=(1,2),PB →=(3-3t,3-3t ), 若OABP 是平行四边形,则OA→=PB →, ∴⎩⎨⎧ 3-3t =13-3t =2,此方程组无解. 所以四边形OABP 不可能为平行四边形.11.【解】 (1)因为a ∥b ,所以2sin θ=cos θ-2sin θ,于是4sin θ=cos θ,故tan θ=14. (2)由|a |=|b |知,sin 2θ+(cos θ-2sin θ)2=12+22, 所以1-2sin 2θ+4sin 2θ=5.从而-2sin 2θ+2(1-cos 2θ)=4,即sin 2θ+cos 2θ=-1.于是sin(2θ+π4)=-22. 又由0<θ<π知,π4<2θ+π4<9π4所以2θ+π4=5π4或2θ+π4=7π4. 因此θ=π2或θ=34π.。
课堂新坐标2013届高三数学(文)一轮复习课时知能训练4-5

课时知能训练一、选择题1.(2011·福建高考)i是虚数单位,若集合S={-1,0,1},则()A.i∈S B.i2∈S C.i3∈S D.2i∈S2.a为正实数,i为虚数单位,|a+ii|=2,则a=()A.2 B. 3 C. 2 D.13.(2011·天津高考)设i是虚数单位,复数1-3i1-i=()A.2+i B.2-iC.-1+2i D.-1-2i4.已知i是虚数单位,若实数x,y满足(1+i)(x+y i)=(1-i)(2+3i),则点P(x,y)所在的象限是()A.第一象限B.第二象限C.第三象限D.第四象限5.(2012·中山模拟)已知复数z1=cos 23°+isin 23°和复数z2=cos 37°+isin 37°,则z1·z2为()A.12+32i B.32+12iC.12-32i D.32-12i二、填空题6.(2011·江苏高考)设复数z满足i(z+1)=-3+2i(i为虚数单位),则z的实部是________.7.在复平面内,复数2i1-i对应的点的坐标为________.8.若复数z满足z(1+i)=1-i(i是虚数单位),则其共轭复数z=________.三、解答题9.计算(1)(1+i 1-i )4+2-i ;(2)(1+2i )23-4i. 10.已知复数z 1满足(z 1-2)i =1+i ,复数z 2的虚部为2,且z 1·z 2是实数,求z 2.11.已知z 是复数,z +2i ,z 2-i均为实数(i 为虚数单位),且复数(z +a i)2在复平面上对应的点在第一象限,求实数a 的取值范围.答案及解析1.【解析】 因为i 2=-1∈S ,i 3=-i ∉S ,2i=-2i ∉S . 【答案】 B2.【解析】 |a +i i|=|1-a i|=a 2+1=2,∴a =±3. 又a >0,∴a = 3.【答案】 B3.【解析】1-3i 1-i =(1-3i )(1+i )(1-i )(1+i )=4-2i 2=2-i. 【答案】 B4.【解析】 由条件,得(x -y )+(x +y )i =5+i ,根据复数相等的定义,得⎩⎨⎧x -y =5,x +y =1,解之得x =3,y =-2.∴点P (3,-2),在第四象限.【答案】 D5.【解析】 z 1·z 2=(cos 23°+isin 23°)(cos 37°+isin 37°)=(cos 23°cos 37°-sin 23°sin 37°)+i(cos 23°sin 37°+sin 23°cos 37°)=cos 60°+isin 60°=12+32i.【答案】 A6.【解析】 设z =a +b i(a 、b ∈R ),由i(z +1)=-3+2i , 得-b +(a +1)i =-3+2i ,∴a +1=2,∴a =1.【答案】 17.【解析】 ∵2i 1-i =2i (1+i )2i +i 2=-1+i , ∴复数2i 1-i对应的点的坐标为(-1,1). 【答案】 (-1,1)8.【解析】 z =1-i 1+i =(1-i )2(1+i )(1-i )=-i.∴z =i. 【答案】 i9.【解】 (1)∵1+i 1-i =(1+i )2(1-i )(1+i )=2i 2=i , ∴(1+i 1-i)4=i 4=1. 因此(1+i 1-i)4+2-i =3-i , (2)原式=1-4+4i 3-4i =-3+4i 3-4i =-(3-4i )3-4i=-1. 10.【解】 由(z 1-2)i =1+i ,得z 1=1+i i+2=(1+i)(-i)+2=3-i. ∵z 2的虚部为2.∴可设z 2=a +2i(a ∈R ).则z 1·z 2=(3-i)(a +2i)=(3a +2)+(6-a )i 为实数, ∴6-a =0,即a =6,因此z 2=6+2i.11.【解】 设z =x +y i(x ,y ∈R ),则z +2i =x +(y +2)i , 由题意得y =-2.z 2-i =x -2i 2-i =15(x -2i)(2+i) =15(2x +2)+15(x -4)i , 由题意得x =4.∴z =4-2i∵(z +a i)2=(12+4a -a 2)+8(a -2)i ,根据条件,可知⎩⎨⎧ 12+4a -a 2>0,8(a -2)>0,解得2<a <6. ∴实数a 的取值范围是(2,6).。
2013高三数学一轮复习课时提能演练 6.4 基本不等式 理 新课标
2013版高三新课标理科数学一轮复习课时提能演练 6.4 基本不等式(45分钟100分)一、选择题(每小题6分,共36分)1.下列不等式①a 2+1>2a ;②x 2+1x 2+1≥1;③a +b ab≤2;④sin 2x +4sin 2x ≥4. 其中正确的不等式的个数是( )(A)1 (B)2 (C)3 (D)42.已知x>0,y>0,且2x +1y=1,若x +2y>m 2+2m 恒成立,则实数m 的取值X 围 是()(A)m≥4或m≤-2(B)m≥2或m≤-4(C)-2<m<4(D)-4<m<23.设OA =(1,-2),OB =(a ,-1),OC =(-b,0),a>0,b>0,O 为坐标原点,若A 、B 、C 三点共线,则1a +2b的最小值是( ) (A)4 (B)6 (C)8 (D)104.(预测题)已知x >0,y >0,x +2y +2xy =8,则x +2y 的最小值是( ) (A)3 (B)4 (C)92 (D)1125.若a>0,b>0,且a +b =1,则ab +1ab 的最小值为( ) (A)2 (B)4 (C)174(D)2 2 6.设x ,y 满足约束条件⎩⎪⎨⎪⎧ 3x -y -6≤0x -y +2≥0x≥0,y≥0,若目标函数z =ax +by(a>0,b>0)的最大值为12,则3a +2b 的最小值为( )(A)4 (B)1325(C)1 (D)2 二、填空题(每小题6分,共18分)7.(2012·某某模拟)若x >0,y >0,2x +y =13,则1x +1y的最小值是. 8.(2012·某某模拟)若对任意x >0,x x 2+3x +1≤a 恒成立,则a 的取值X 围是. 9.(易错题)x ,y ,z 为正实数,x -y +2z =0,则xz y 2的最大值为. 三、解答题(每小题15分,共30分)10.已知x >0,y >0,且2x +8y -xy =0,求(1)xy 的最小值;(2)x +y 的最小值.11.(2012·某某模拟)某食品加工厂定期购买玉米,已知该厂每天需用玉米6吨,每吨玉米的价格为1 800元,玉米的保管等其他费用为平均每吨每天3元,购买玉米每次需支付运费900元.求该厂多少天购买一次玉米,才能使平均每天所支付的费用最少?【探究创新】(16分)设矩形ABCD(AB>AD)的周长为24,把它关于AC 折起来,AB 折过去后交CD 于点P ,如图,设AB =x ,求△ADP 的面积的最大值,及此时x 的值.答案解析1.【解析】选A.∵a 2+1-2a =(a -1)2≥0,故①错;∵x 2+1x 2+1=x 2+1+1x 2+1-1≥2-1=1, 等号成立的条件为x =0,故②对;当a ,b 均大于零时,a +b ≥2ab ,即a +b ab≥2,故③错;sin 2x +4sin 2x≥4等号不成立, 故④错,故选A.2.【解析】选D.∵x>0,y>0,且2x +1y=1, ∴x +2y =(x +2y)(2x +1y )=4+4y x +x y≥4+24y x ·x y =8,当且仅当4y x =x y ,即4y 2=x 2,x =2y ,又2x +1y=1即x =4,y =2等号成立.∴(x +2y)min =8,要使x +2y>m 2+2m 恒成立,只需(x +2y)min >m 2+2m 成立,即8>m 2+2m , 解得-4<m<2.3.【解析】选C.AB =OB -OA =(a -1,1), AC =OC -OA =(-b -1,2),∵AB 与AC 共线,∴2(a -1)+b +1=0,即2a +b =1.∵a>0,b>0, ∴1a +2b =(1a +2b)(2a +b) =4+b a +4a b≥4+4=8, 当且仅当b a =4a b,即b =2a 时等号成立. 4.【解析】选B.方法一:因为x +2y +2xy =8,所以y =8-x 2x +2,所以x +2y =x +8-x x +1=x +-(x +1)+9x +1=(x +1)+9x +1-2 ≥29-2=4(当且仅当x +1=9x +1, 即x =2时等号成立,此时y =1),选B.方法二:本题可以利用基本不等式转化为一元二次不等式求解. 因为x +2y ≥22xy ,所以2xy ≤(x +2y 2)2, 所以x +2y +2xy ≤x +2y +(x +2y)24, 设x +2y =A ,则A +A 24≥8,即A 2+4A -32≥0,解此不等式得A ≤-8(舍去)或A ≥4,即x +2y ≥4.∴最小值为4.5.【解题指南】由已知利用基本不等式得ab 的取值X 围而后换元利用函数的单调性求解.【解析】选C.由a +b =1,a>0,b>0得 2ab ≤a +b =1,∴ab ≤12,∴ab ≤14. 令ab =t ,则0<t ≤14, 则ab +1ab =t +1t ,结合函数的图象可知t +1t 在(0,14]上单调递减,故当t =14时,t +1t有最小值为14+4=174. 6.【解题指南】作出可行域确定最大值点,从而得a ,b 的关系式,利用“1”的代换求解.【解析】选A.作出可行域如图由图可知目标函数过A 点时z 取最大值,由⎩⎪⎨⎪⎧ 3x -y -6=0x -y +2=0得⎩⎪⎨⎪⎧ x =4y =6,故4a +6b =12,即a 3+b 2=1, ∴3a +2b =(3a +2b )(a 3+b 2)=1+3b 2a +2a 3b+1≥2+23b 2a ·2a 3b=4,当且仅当3b =2a 时等号成立,又2a +3b =6,即a =32,b =1时等号成立. 7.【解析】∵2x +y =13,∴6x +3y =1, 1x +1y =(1x +1y )(6x +3y)=9+3y x +6x y≥9+23y x ·6x y =9+62,当且仅当y =2x 时,等号成立,故最小值为9+6 2.答案:9+6 28.【解析】因为x >0,所以x +1x ≥2(当且仅当x =1时取等号),所以有x x 2+3x +1=1x +1x +3≤12+3=15,即x x 2+3x +1的最大值为15,故a ≥15. 答案:[15,+∞) 【方法技巧】不等式恒成立问题的解题方法不等式的恒成立问题与函数最值有密切的关系,解决不等式恒成立问题,通常先分离参数,再转化为最值问题来解:c ≥f(x)恒成立⇔c ≥f(x)max ;c ≤f(x)恒成立⇔c ≤f(x)min .【变式备选】已知x>0,y>0,xy =x +2y ,若xy ≥m -2恒成立,则实数m 的最大值是.【解析】由x>0,y>0,xy =x +2y ≥22xy ,得xy ≥8,等号当且仅当x =2y 时取得.又m -2≤xy 恒成立,故只需m -2≤8,即m ≤10.∴m 的最大值为10.答案:109.【解题指南】由已知用x ,z 代换y 后,分子分母同除以xz 后利用基本不等式求解.【解析】xz y 2=xz (x +2z)2=xz x 2+4xz +4z 2 =1x z +4z x+4≤18. 等号当且仅当x =2z 时取得.答案:1810.【解题指南】把2x +8y -xy =0转化为8x +2y=1即可. 【解析】(1)由2x +8y -xy =0,得8x +2y=1, 又x >0,y >0,则1=8x +2y ≥28x ·2y =8xy,得xy ≥64, 当且仅当8x =2y时,等号成立. 所以xy 的最小值为64.(2)方法一:由2x +8y -xy =0,得x =8y y -2, ∵x >0,∴y >2, 则x +y =y +8y y -2=(y -2)+16y -2+10≥18, 当且仅当y -2=16y -2,即y =6,x =12时,等号成立. ∴x +y 的最小值为18.方法二:由2x +8y -xy =0,得8x +2y=1, 则x +y =(8x +2y)·(x +y) =10+2x y +8y x ≥10+22x y ·8y x=18. 当且仅当2x y =8y x ,且8x +2y=1时等号成立, ∴x +y 的最小值为18. 11.【解题指南】平均每天所支付的费用=x 天支付的总费用天数x,先列出平均每天所支付的费用的函数解析式,再利用基本不等式求其最值.【解析】设该厂应每隔x 天购买一次玉米,其购买量为6x 吨,由题意知,玉米的保管等其他费用为3[6x +6(x -1)+6(x -2)+…+6×1] =3×x(6x +6)2=9x(x +1), 设平均每天所支付的费用为Y 1元,则Y 1=9x(x +1)+900x+1 800×6 =9x +900x +10 809≥29x ·900x+10 809=10 989, 当且仅当9x =900x,即x =10时取等号. 该厂每隔10天购买一次玉米,才能使平均每天所支付的费用最少.【变式备选】围建一个面积为360m 2的矩形场地,要求矩形场地的一面围墙利用旧墙(利用旧墙需维修),其他三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m 的进出口,已知旧墙的维修费用为45元/m ,新墙的造价为180元/m ,设利用的旧墙的长度为x(单位:m),所需费用为y 元.(1)将y 表示为x 的函数;(2)试确定x ,使修建此矩形场地围墙的总费用最少,并求出最少总费用.【解析】(1)设矩形的另一边长为a m ,则y =45x +180(x -2)+180×2a =225x +360a -360由已知xa =360,得a =360x, 所以y =225x +3602x-360(x>0). (2)∵x >0,∴225x +3602x≥2225×3602=10 800, ∴y =225x +3602x-360≥10 440. 当且仅当225x =3602x时,等号成立. 即当x =24 m 时,修建此矩形场地围墙的总费用最少,最少总费用是10 440元.【探究创新】【解析】∵AB =x ,∴AD =12-x ,又DP =PB ′,AP =AB ′-PB ′=AB -DP ,即AP =x -DP ,∴(12-x)2+PD 2=(x -PD)2,得PD =12-72x, ∵AB>AD ,∴6<x<12,∴△ADP 的面积S =12AD ·DP =12(12-x)(12-72x) =108-6(x +72x)≤108-6·272=108-72 2 当且仅当x =72x即x =62时取等号, ∴△ADP 面积的最大值为108-722,此时x =6 2.。
课堂新坐标2013届高三数学(文)一轮复习6-1
课时知能训练一、选择题1.(2012·梅州模拟)已知a ,b ,c 满足c <b <a 且ac <0,则下列选项中不一定能成立的是( )A.c a <b aB.b -a c>0 C.b 2c <a 2c D.a -c ac<0 2.若0<a <1,则下列不等式中正确的是( )A .(1-a )13>(1-a )12B .log (1-a )(1+a )>0C .(1-a )3>(1+a )2D .(1-a )1+a >13.设α∈(0,π2),β∈[0,π2],那么2α-β3的取值范围是( ) A .(0,5π6) B .(-π6,5π6) C .(0,π) D .(-π6,π) 4.若a ,b ,x ,y ∈R ,则⎩⎨⎧ x >a y >b 是⎩⎨⎧x +y >a +b (x -a )(y -b )>0成立的( ) A .充分不必要条件 B .必要不充分条件C .充要条件D .既不充分也不必要条件5.若a >b >0,则下列不等式中一定成立的是( )A .a +1b >b +1a B.b a >b +1a +1C .a -1b >b -1a D.2a +b a +2b >a b二、填空题6.x 2+y 2+1与2(x +y -1)的大小关系是________.7.(2012·潮州模拟)设x ,y 为实数,满足3≤xy 2≤8,4≤x 2y ≤9,则x 3y 4的最大值是________.8.如果一辆汽车每天行驶的路程比原来多19 km ,那么8天的行程就超过2 200 km ;如果它每天行驶的路程比原来少12 km ,那么它行驶同样的路程就得花9天多的时间,则这辆汽车原来每天行驶的路程(单位:km)的范围是______.三、解答题9.已知b >a >0,x >y >0,求证:x x +a >y y +b. 10.若实数a 、b 、c 满足b +c =5a 2-8a +11,b -c =a 2-6a +9,试比较a 、b 、c 的大小.11.下表为广州全运会官方票务网站分布的几种球类比赛的门票价格,某球迷赛前准备1 200元,预订15张下表中球类比赛的门票.该球迷想预订上表中三种球类比赛门票,其中篮球比赛门票数与乒乓球比赛门票数相同,且篮球比赛门票的费用不超过足球比赛门票的费用,求可以预订的足球比赛门票数.答案及解析1.【解析】 ∵c <b <a ,且ac <0,∴c <0,a >0,∴c a <b a ,b -a c >0,a -c ac<0, 但b 2与a 2的关系不确定,故b 2c <a 2c不一定成立. 【答案】 C2.【解析】 ∵0<a <1,∴0<1-a <1,∴(1-a )13>(1-a )12. 【答案】 A2.【解析】 由已知得0<2α<π,0≤β3≤π6∴-π6≤-β3≤0,∴-π6<2α-β3<π. 【答案】 D4.【解析】 ⎩⎨⎧ x >a ,y >b ,⇒⎩⎨⎧ x +y >a +b ,(x -a )(y -b )>0, 且⎩⎨⎧ x +y >a +b ,(x -a )(y -b )>0,⇒⎩⎨⎧x >a ,y >b .【答案】 C5.【解析】 ∵a >b >0,∴1b >1a >0,∴a +1b >b +1a. 【答案】 A6.【解析】 ∵(x 2+y 2+1)-2(x +y -1)=(x -1)2+(y -1)2+1>0,∴x 2+y 2+1>2(x +y -1).【答案】 x 2+y 2+1>2(x +y -1)7.【解析】 ∵3≤xy 2≤8,∴18≤1xy 213, ∵4≤x 2y ≤9,∴16≤x 4y 2≤81, ∴2≤x 3y 4≤27,故x 3y 4的最大值是27. 【答案】 278.【解析】 设原来每天行驶的路程为x km ,则⎩⎨⎧ 8(x +19)>2 200,8(x +19)>9(x -12),解得256<x <260. 【答案】 (256,260)9.【证明】x x +a -y y +b =x (y +b )-y (x +a )(x +a )(y +b ) =bx -ay (x +a )(y +b ). ∵b >a >0,x >y >0,∴bx >ay ,x +a >0,y +b >0,∴bx -ay (x +a )(y +b )>0, ∴x x +a >y y +b. 10.【解】 ∵b -c =a 2-6a +9=(a -3)2≥0,∴b ≥c .①又⎩⎨⎧b +c =5a 2-8a +11,b -c =a 2-6a +9.∴c =2a 2-a +1, 则c -a =2a 2-2a +1=2(a -12)2+12>0, ∴c >a .②由①②得b ≥c >a .11.【解】 设预订篮球比赛门票数与乒乓球比赛门票数都是n 张,则足球比赛门票预订(15-2n )张,由题意得 ⎩⎨⎧ 80n +60n +100(15-2n )≤1 200,80n ≤100(15-2n ),n ∈N *.解得5≤n ≤5514, 由n ∈N *知,n =5,∴15-2n =5,故可预订足球比赛门票5张.。
课堂新坐标2013届高三数学(文)一轮复习课时知能训练5-4
课时知能训练一、选择题1.数列{a n }中,a n +1=a 2n 2a n -5,已知该数列既是等差数列又是等比数列,则该数列的前20项的和等于( )A .100B .0或100C .100或-100D .0或-1002.数列{a n }的通项公式a n =1n +n +2(n ∈N *),若前n 项和为S n ,则S n为( )A.n +2-1B.n +2+n +1-2-1C.12(n +2-1)D.12(n +2+n +1-2-1) 3.(2012·惠州模拟)已知S n 为等差数列{a n }的前n 项和,若a 1=-2010,S 2 0102 010-S 2 0042004=6,则S 2011=( ) A .2011 B .2010 C .0 D .24.已知数列{a n }:12,13+23,14+24+34,…,110210+310+…+910,…,那么数列{b n }={1a n a n +1}的前n 项和S n 为( ) A.n n +1 B.4n n +1 C.3n n +1 D.5n n +1 5.设数列{x n }满足log a x n +1=1+log a x n (n ∈N *,a >0且a ≠1),且x 1+x 2+x 3+…+x 100=100,则x 101+x 102+x 103+…+x 200的值为( )A .100a 2B .101a 2C .100a 100D .101a 100二、填空题6.数列3,33,333,…的前n 项和S n =________.7.数列{a n }的前n 项和为S n ,a 1=1,a 2=2,a n +2-a n =1+(-1)n (n ∈N *),则S 100=________.8.已知{a n }是公差为-2的等差数列,a 1=12,则|a 1|+|a 2|+|a 3|+…+|a 20|=________.三、解答题9.(2012·韶关模拟)已知数列{a n }是各项均不为0的等差数列,S n 为其前n项和,且满足a 2n =S 2n -1,n ∈N *.(1)求数列{a n }的通项公式;(2)数列{b n }满足b n =1a n ·a n +1,求数列{b n }的前n 项和T n . 10.设函数y =f (x )的定义域为R ,其图象关于点(12,12)成中心对称,令a k =f (k n)(n 是常数且n ≥2,n ∈N *),k =1,2,…,n -1,求数列{a k }的前n -1项的和.11.(2012·汕头模拟)已知等差数列{a n }的前3项和为6,前8项和为-4.(1)求数列{a n }的通项公式;(2)设b n =(4-a n )q n -1(q ≠0,n ∈N *),求数列{b n }的前n 项和S n .答案及解析1.【解析】 由题意知a n +1=a n ≠0,由a n +1=a 2n 2a n -5得a 2n -5a n =0,∴a n =5, ∴S 20=100.【答案】 A2.【解析】 ∵a n =1n +n +2=12(n +2-n ), ∴S n =12(3-1+4-2+5-3+6-4+…+n -n -2+n +1-n -1+n +2-n )=12(-1-2+n +1+n +2) =12(n +2+n +1-2-1). 【答案】 D3.【解析】 设等差数列的公差为d ,则S n =na 1+n (n -1)2, ∴S n n =d 2n -2010-d 2, ∴数列{S n n }是以-2010为首项, 以d 2为公差的等差数列, 由S 20102010-S 20042004=6得6×d 2=6,∴d =2. ∴S 2011=2011×(-2010)+2011×20102×2=0. 【答案】 C4.【解析】 a n =1+2+3+…+n n +1=n 2, ∴b n =1a n a n +1=4n (n +1)=4(1n -1n +1), ∴S n =4[(1-12)+(12-13)+…+(1n -1n +1)] =4(1-1n +1)=4n n +1. 【答案】 B5.【解析】 log a x n +1=1+log a x n ,得x n +1=ax n 且a >0,a ≠1,x n >0,∴数列{x n }是公比为a 的等比数列,∴x 101+x 102+x 103+…+x 200=x 1a 100+x 2a 100+x 3a 100+…+x 100a 100=100a 100.【答案】 C6.【解析】 数列3,33,333,…的通项公式a n =13(10n -1), ∴S n =13(10-1)+13(102-1)+…+13n -1) =13[(10+102+103+…+10n )-n ] =13×10(1-10n )1-10-n 3=127×10n +1-10+9n 27. 【答案】 127×10n +1-10+9n 277.【解析】 由a n +2-a n =1+(-1)n 知a 2k +2-a 2k =2,a 2k +1-a 2k -1=0,∴a 1=a 3=a 5=…=a 2n -1=1,数列{a 2k }是等差数列,a 2k =2k .∴S 100=(a 1+a 3+a 5+…+a 99)+(a 2+a 4+a 6+…+a 100) =50+(2+4+6+…+100)=50+(100+2)×502=2 600. 【答案】 2 6008.【解析】 由题意知,a n =12+(n -1)×(-2)=-2n +14, 令-2n +14≥0,得n ≤7,∴当n ≤7时,a n ≥0;当n >7时,a n <0.∴|a 1|+|a 2|+|a 3|+…+|a 20|=(a 1+a 2+…+a 7)-(a 8+a 9+…+a 20)=2S 7-S 20=2[7×12+7×62×(-2)]-[20×12+20×192×(-2)] =224.【答案】 2249.【解】 (1)法一 设等差数列{a n }的公差为d ,首项为a 1, 在a 2n =S 2n -1中,令n =1,n =2,得⎩⎨⎧ a 21=S 1,a 22=S 3,即⎩⎨⎧a 21=a 1,(a 1+d )2=3a 1+3d , 解得a 1=1,d =2,∴a n =2n -1.法二 ∵{a n }是等差数列,则a 1+a 2n -1=2a n .∴S 2n -1=a 1+a 2n -12(2n -1)=(2n -1)a n . 由a 2n =S 2n -1,得a 2n =(2n -1)a n ,又∵a n ≠0,∴a n =2n -1,则a 1=1,d =2.∴a n =2n -1.(2)∵b n =1a n a n +1=1(2n -1)(2n +1)=12(12n -1-12n +1), ∴T n =12(1-13+13-15+…+12n -1-12n +1)=n 2n +1. 10.【解】 ∵y =f (x )的图象关于点(12,12)成中心对称, 所以f (x )+f (1-x )=1.令S n -1=a 1+a 2+…+a n -1则S n -1=f (1n )+f (2n )+…+f (n -1n), 又S n -1=f (n -1n )+f (n -2n )+…+f (1n), 两式相加,得2S n -1=[f (1n )+f (n -1n )]+[f (2n )+f (n -2n )]+…+[f (n -1n )+f (1n)]=n -1,∴S n -1=n -12. 11.【解】 (1)设{a n }的公差为d .由已知得⎩⎨⎧3a 1+3d =6,8a 1+28d =-4.解得a 1=3,d =-1.故a n =3-(n -1)=4-n .(2)由(1)可得,b n =n ·q n -1,于是S n =1·q 0+2·q 1+3·q 2+…+n ·q n -1. 若q ≠1,将上式两边同乘以q , qS n =1·q 1+2·q 2+…+(n -1)·q n -1+n ·q n . 两式相减得到(q -1)S n =nq n -1-q 1-q 2-…-q n -1=nq n -q n -1q -1=nq n +1-(n +1)q n +1q -1于是,S n =nq n +1-(n +1)q n +1(q -1)2若q =1,则S n =1+2+3+…+n =n (n +1)2, 所以,S n =⎩⎪⎨⎪⎧ n (n +1)2,(q =1),nq n +1-(n +1)q n +1(q -1)2,(q ≠1).。
课堂新坐标2013届高考数学一轮复习课件:第三章第七节 正弦定理和余弦定理(广东专用)
由余弦定理,a2=b2+c2-2bccos A,
课 时
∴bc=-2bc cos A,cos A=-21.
知 能 训
又 0<A<π,∴A=32π.
练
菜单
第十五页,编辑于星期日:二十点 十四分。
一轮复习 ·新课标 ·数学(理)(广东专用)
典
例
探
究
·
(2)由(1)知 sin2A=sin2B+sin2C+sin Bsin C,
课
【答案】 A
时 知
能
训
练
菜单
第六页,编辑于星期日:二十点 十四分。
一轮复习 ·新课标 ·数学(理)(广东专用)
典
例
探
2.在△ABC 中,a=15,b=10,A=60°,则 cos B=( )
究 ·
A.
6 3
B.23 2
提 知 能
自 主
C.-
6 3
落
D.-23 2
高 考
实 · 固
【解析】
由正弦定理,得
提
利用正弦、余弦定理解三角形
知 能
自
主 落
高
(2011·辽宁高考)△ABC 的三个内角 A,B,C 所对的边分别
考
实 ·
为 a,b,c,asin Asin B+bcos2A= 2a.
体 验
固 基 础
(1)求ab;
(2)若 c2=b2+ 3a2,求 B.
· 明 考 情
【思路点拨】 (1)利用正弦定理,化去角B的三角函数,再化简求值;
提
自 主 落 实
由余弦定理,cos∠ADC=AD2+2ADDC·D2-C AC2 =1020×+1306- ×6196=-12,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课时知能训练
一、选择题
1.(2011·重庆高考)若函数f (x )=x +1x -2
(x >2)在x =a 处取最小值,则a =( )
A .1+2
B .1+3
C .3
D .4
2.若M =a 2+4a
(a ∈R ,a ≠0),则M 的取值范围为( ) A .(-∞,-4]∪[4,+∞) B .(-∞,-4]
C .[4,+∞)
D .[-4,4]
3.(2011·上海高考)若a ,b ∈R ,且ab >0,则下列不等式中恒成立的是( )
A .a 2+b 2>2ab
B .a +b ≥2ab
C.1a +1b >2ab
D.b a +a b ≥2 4.已知a >0,b >0,且ab =1,α=a +4a ,β=b +4b
,则α+β的最小值为( ) A .8 B .9 C .10 D .12
5.已知x >0,y >0,x +2y +2xy =8,则x +2y 的最小值是( )
A .3
B .4 C.92 D.112
二、填空题
6.(2011·湖南高考)设x ,y ∈R ,且xy ≠0,则(x 2+1y 2)(1x
24y 2)的最小值为________.
7.若正数a ,b 满足1a +4b
=2,则ab 的最小值为________. 8.若a >0,b >0,a +b =2,则下列不等式对一切满足条件的a ,b 恒成立的是________(写出所有正确命题的编号).
①ab ≤1;②a +b ≤2;③a 2+b 2≥2;④a 3+b 3≥3.
三、解答题
9.已知a ,b ,c 是正实数,求证:bc a +ac b +ab c
≥a +b +c .
10.求函数y =x 2+x +3x +1
(x >-1)的值域. 11.某国际化妆品生产企业为了占有更多的市场份额,拟在2012年英国伦敦奥运会期间进行一系列促销活动,经过市场调查和测算,化妆品的年销量x 万件与年促销费t 万元之间满足3-x 与t +1成反比例,如果不搞促销活动,化妆品的年销量只能是1万件,已知2012年生产化妆品的设备折旧、维修等固定费用为3万元,每生产1万件化妆品需再投入32万元的生产费用,若将每件化妆品的售价定为其生产成本的150%与平均每件促销费的一半之和,则当年生产的化妆品正好能销完.
(1)将2012年的利润y (万元)表示为促销费t (万元)的函数.
(2)该企业2012年的促销费投入多少万元时,企业的年利润最大?
(注:利润=销售收入-生产成本-促销费,生产成本=固定费用+生产费用)
答案及解析
1.【解析】 ∵x >2,∴x -2>0,
∴f (x )=x +1x -2=(x -2)+1x -2+2≥2 (x -2)·1x -2
+2=4, 当且仅当x -2=1x -2
(x >2),即x =3时等号成立, ∴a =3.
【答案】 C
2.【解析】 M =a 2+4a =a +4a
, 当a >0时,M ≥4,当且仅当a =2时等号成立,
当a <0时,M ≤-4,当且仅当a =-2时等号成立,
故M 的取值范围是(-∞,-4]∪[4,+∞).
【答案】 A
3.【解析】 当a =b 时,a 2+b 2=2ab ,排除A ;当a <b ,b <0时,a +b
<0<2ab ,1a +1b <0<2ab
,排除B 、C ,选D.
【答案】 D
4.【解析】 α+β=(a +b )+4a +4b =(a +b )+4(a +b )ab
=5(a +b )≥10ab =10,
当且仅当a =b =1时等号成立.
【答案】 C
5.【解析】 ∵x +2y +2xy =8,∴y =8-x 2x +2
>0, ∴-1<x <8,∴x +2y =x +2·8-x 2x +2
=(x +1)+9x +12≥2 (x +1)·9x +1
-2=4, 当且仅当x +1=9x +1
时“=”成立,此时x =2,y =1. 【答案】 B
6.【解析】 (x 2+1y 2)(1x 2+4y 2)=5+4x 2y 2+1x 2y
2 ≥5+24x 2y 2·1x 2y 2
=9, 当且仅当4x 2y 2=1x 2y 2,即|xy |=22
时等号成立. 【答案】 9
7.【解析】 ∵a >0,b >0,
∴1a +4b ≥2 1a ·4b =4 1ab , ∴4 1ab
≤2,∴ab ≥4, 当且仅当1a =4b 且1a +4b
=2时等号成立. 【答案】 4
8.【解析】 ab ≤(a +b )2
4=1,当且仅当a =b 时取等号,①对; (a +b )2=a +b +2ab =2+2 ab ≤4,
当且仅当a =b 时取等号,得a +b ≤2,故②错误.
由于a 2+b 22≥(a +b )24
=1,故a 2+b 2≥2成立,故③正确. a 3+b 3=(a +b )(a 2+b 2-ab )=2(a 2+b 2-ab ),
∵ab ≤1,又a 2+b 2≥2,
∴a 2+b 2-ab ≥1,∴a 3+b 3≥2,故④错误.
【答案】 ①③
9.【证明】 ∵a ,b ,c 是正实数
∴bc a +ac b
≥2 bc a ·ac b =2c (当且仅当a =b 时取等号) ac b +ab c
≥2 ac b ·ab c =2a (当且仅当b =c 时取等号) ab c +bc a ≥2 ab c ·bc a
=2b (当且仅当a =c 时取等号) ∴2·(bc a +ac b +ab c
)≥2a +2b +2c , 故bc a +ac b +ab c
≥a +b +c . 10.【解】 y =x 2+x +3x +1=(x +1)2-(x +1)+3x +1
=x +1+3x +1
-1, 由x >-1,知x +1>0.
∴(x +1)+3x +12(x +1)×3x +1
=23, 当且仅当x +1=3x +1
,即x =3-1时等号成立, ∴y ≥23-1,
故函数的值域为[23-1,+∞).
11.【解】 (1)由题意可设3-x =k t +1
, 将t =0,x =1代入,得k =2.∴x =3-2t +1
. 当年生产x 万件时,
∵年生产成本=年生产费用+固定费用,
∴年生产成本为32x +3=32(3-2t +1
)+3. 当销售x (万件)时,年销售收入为
150%[32(3-2t +1)+3]+12
t . 由题意,生产x 万件化妆品正好销完,得年利润y =-t 2+98t +352(t +1)
(t ≥0). (2)y =-t 2+98t +352(t +1)=50-(t +12+32t +1
) ≤50-2t +12×32t +1
=50-216=42(万元), 当且仅当t +12=32t +1
,即t =7时,y max =42, ∴当促销费定在7万元时,年利润最大.。
