期望寿命的概念及计算方法
寿命评估
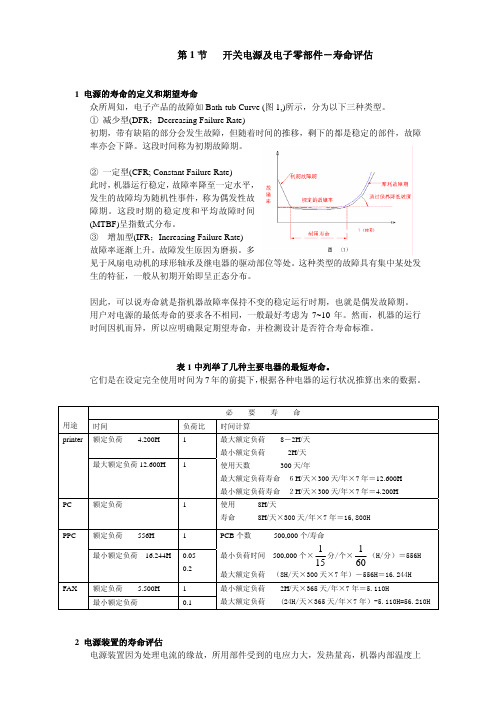
第1节 开关电源及电子零部件-寿命评估1 电源的寿命的定义和期望寿命众所周知,电子产品的故障如Bath-tub Curve (图1,)所示,分为以下三种类型。
① 减少型(DFR ;Decreasing Failure Rate)初期,带有缺陷的部分会发生故障,但随着时间的推移,剩下的都是稳定的部件,故障率亦会下降。
这段时间称为初期故障期。
② 一定型(CFR; Constant Failure Rate) 此时,机器运行稳定,故障率降至一定水平,发生的故障均为随机性事件,称为偶发性故障期。
这段时期的稳定度和平均故障时间(MTBF)呈指数式分布。
③ 增加型(IFR ;Increasing Failure Rate) 故障率逐渐上升。
故障发生原因为磨损。
多见于风扇电动机的球形轴承及继电器的驱动部位等处。
这种类型的故障具有集中某处发生的特征,一般从初期开始即呈正态分布。
因此,可以说寿命就是指机器故障率保持不变的稳定运行时期,也就是偶发故障期。
用户对电源的最低寿命的要求各不相同,一般最好考虑为7~10年。
然而,机器的运行时间因机而异,所以应明确限定期望寿命,并检测设计是否符合寿命标准。
表1中列举了几种主要电器的最短寿命。
它们是在设定完全使用时间为7年的前提下,根据各种电器的运行状况推算出来的数据。
2 电源装置的寿命评估电源装置因为处理电流的缘故,所用部件受到的电应力大,发热量高,机器内部温度上升快,所以寿命评估工作尤显重要。
机器的寿命基本上和使用部件的寿命挂钩。
部件寿命与热、电应力成函数关系,其中更以热应力为主。
从机器寿命设计的观点来看,如果将所有部件的寿命统一,则能达到理想的最优性价比,但部件的寿命性能(影响部件寿命的电力、环境特征)相差巨大,因而难以实现。
一般来说,尽可能降低短寿部件的应力,并极限化使用长寿部件,可以实现部件寿命的平均化。
电阻类、陶瓷电容器和薄膜电容器等半导体部件不接触强应力,寿命极长,因而可以说下面举出的部件的寿命才真正决定了电源的寿命。
寿命表PPT

现时寿命表
❖简略寿命表的编制
▪ 列8:生存人年数 Lx
• x岁尚存者在今后n年内的生存人年数
Lx
n lx
lxn 2
L5 5l5 l10 / 2 5(98484+98117)/2=491501
• 婴儿组的生存人年数根据0岁组死亡者的平均存活年数计算:
L0 l1 a0d0
• a0 系经验性常数,可查表得
基本概念
•特点
需要完整可靠的人口学资料和死亡登记
具有可比性:不受人口年龄构成的影响; 不同人群的寿命表指标具有良好的可比性
类型
•分类
现时寿命表:简称“寿命表” 定群寿命表
类型
•现时寿命表
根据特定人群的横断面调查资料提供的年龄别 死亡率编制
假定同时出生的一代人(10万)按照一定的年龄组 死亡率先后死去,直至死完为止。 计算这一代人各年龄组的死亡概率、死亡人数、 尚存人数和期望寿命等指标
0.000000 9818 9818 38481 38481
期望 寿命
e'x (13) 72.28 72.01 68.36 63.58 58.77 53.98 49.22 44.43 39.61 34.82 30.07 25.41 20.89 16.62 12.71 9.48 6.63 4.50 3.92
lx
(6)
100000 98983 98484 98117 97776 97380 96893 96372 95813 95078 93936 92108 89110 83803 75104 61004 44680 25171 7264
dx
(7)
1017 499 367 341 396 487 521 559 735
威布尔分布的平均寿命计算公式

威布尔分布的平均寿命计算公式概率密度函数:f(t) = (β/θ) * (t/θ)^(β-1) * exp(-(t/θ)^β)累积分布函数:F(t) = 1 - exp(-(t/θ)^β)其中,θ和β为分布的参数。
在威布尔分布中,平均寿命是一个重要的指标,用于描述一个产品或系统的预期使用寿命。
平均寿命可以通过计算概率密度函数f(t)的期望值来获得。
期望值的计算公式为:E(t) = ∫[0,∞] tf(t)dt将威布尔分布的概率密度函数代入上述公式中,可以得到平均寿命的计算公式为:E(t) = ∫[0,∞] t * (β/θ) * (t/θ)^(β-1) * exp(-(t/θ)^β) dt这个积分是一个复杂的定积分,无法通过简单的计算求出解析解。
通常情况下,可以通过数值积分的方法来近似计算平均寿命。
基于数值积分的方法有多种,例如格拉姆-查尔斯方法、辛普森方法、牛顿-科茨法等。
其中,辛普森方法被广泛应用于计算威布尔分布的平均寿命。
辛普森方法的计算步骤如下:1.将区间[0,∞]分成若干个小区间,每个小区间的宽度为h。
2. 在每个小区间中,选取三个点:起始点、中间点和终止点。
起始点的坐标为xi,中间点的坐标为xi+h/2,终止点的坐标为xi+h。
3.根据辛普森积分公式,计算每个小区间上的积分值。
积分值为三个点对应的函数值的加权平均值,权重为1、4和14.将每个小区间上的积分值相加,得到整个区间的近似积分值。
根据辛普森方法,可以得到平均寿命的近似计算公式:E(t) ≈ h/3 * [f(x0) + 4*f(x1+h/2) + 2*f(x2+h) + 4*f(x3+h/2) + ... + 4*f(xn-1+h/2) + f(xn)]其中,h表示小区间的宽度,n表示小区间的总数。
x0、x1、x2、..、xn为每个小区间的起始点的坐标。
通过选择适当的h和n的值,可以提高辛普森方法的计算精度。
通常情况下,可以通过反复计算并逐渐减小h和增大n的值,直至所得结果满足精度要求。
卫生统计学_寿命表

平均人 口数 Px 21865 44255 76411 98446 113452 127784 118925 99523 76224 59686 66580 55413 44331 33294 29448 18686 10282 8984
实际死 亡人数 Dx 256 58 45 60 96 131 128 100 92 135 252 356 682 888 1025 956 998 1023
期望寿 命 ex 71.46 71.30 67.67 62.86 58.04 53.28 48.54 43.79 38.99 34.22 29.58 25.09 20.83 17.30 14.41 11.68 9.38 8.78
0.001311 0.000589 0.000609 0.000846 0.001025 0.001076 0.001005 0.001207 0.002262 0.003785 0.006424 0.015384 0.026671 0.034807 0.051161 0.097063 0.113869
生存人 年数 Lx 99005 394282 490838 489370 487595 485320 482775 480268 477620 473503 466413 454698 430825 388360 333450 269913 189425 251974
生存总 人年数 Tx 7145634 7046629 6652347 6161509 5672139 5184544 4699224 4216449 3736181 3258561 2785058 2318645 1863947 1433122 1044762 711312 441399 251974
一个人从进入该特定人群,到最后
老年护理学——第一章绪论

四、人口老龄化
• (一)人口老龄化
• 人口老龄化(aging of population)简称人 口老化,是人口年龄结构的老龄化。它是 指老年人口占总人口的比例不断上升的一 种动态过程。出生率和死亡率的下降、平 均预期寿命的延长是世界人口趋向老龄化 的直接原因。
2.自由基理论
• 此理论认为老化是由于细胞代谢过程中自 由基产物有害作用的结果。随着年龄的增 长,人体内自由基水平随之增高,由其诱 导产生的有害物质不断积累,而对自由基 的防御能力却逐渐下降,导致自由基的损 伤作用增强,引起体内各种生理功能障碍, 最终促进了机体的老化与死亡。
3.差错灾难理论
• 认为老化是由于某种原因从DNA复制到最 终形成蛋白质的遗传信息传递过程中错误 积累的结果。在生物生命过程中,体内各 种蛋白质具有各种不同的功能,当错误蛋 白质逐渐增加,正常的生理功能遭受破坏, 从而促进了机体的老化与死亡,这就是所 谓“差错灾难”。
• 我国民间常以“年过半百”为进入老年, 并习惯以六十花甲、七十古稀、八十为耋、 九十为耄代表老年不同的时期,中华医学 会老年医学学会于1982年建议:我国以60 岁以上为老年人;老年分期按45~59岁为 老年前期(中老年人),60~89岁老年期 (老年人),90岁以上为长寿期(长寿老 人)。
人类年龄划分的其他标准
老年病的临床特征
1.起病隐匿,症状和体征不典型 2.病程迁延,并发症和后遗症多,死亡率高 3.同时患多种疾病 4.病因多元化或不明 5.易出现药物不良反应 6.病史采集困难 7.易发生意识障碍和水电解质紊乱
老年护理学总结

老年护理学总结老年护理学总结1、老化:人体从出生到成熟期后,随着年龄的增长,在形态和功能上发生进行性衰退性变化。
2、平均期望寿命:简称平均寿命,是指通过回顾性死因统计和其它统计学方法,计算出一定年龄组的人群能生存的平均年数。
3、健康期望寿命:是指去除残疾和残障后所得到的人类生存曲线,即个人在良好状态下的平均生存年数。
4、人口老龄化:指老年人口占人口的比例不断上升的一种动态过程。
出生率和死亡率的下降,平均预期寿命的延长是世界人口趋向老龄化的直接原因。
5、老年护理学:是研究、诊断和处理老年人对自身现存的潜在的健康问题的反映的学科,它是护理学一个分支,与社会科学,自然科学相互渗透。
6、老年人生活质量:指60岁或65岁以上的老年人群身体、精神、家庭和社会生活满意的程度和老年人对生活的全面评价。
、7、老年保健:指在平等享用卫生资源的基础上,充分利用现有的人力、物力以维护和促进老年人健康为目的,发展老年保健事业,使老年人得到基本的医疗、护理、康复、保健等服务。
8、自我保健:指人们为保护自己健康所采取的一些综合性的保健措施。
9心理健康:指在身体、智能以及感情上与他人的心理健康不相矛盾的范围内,将个人心境发展成最佳状态。
10、发达国家65岁以上为老年人,发展中国家60岁以上为老年(我国60以上老年,45-59为老年前期即中老年,60-89老年,90以上为长寿老年人)11、老年人口比例:发达,65岁以上占总人口7%以上为老龄化社会。
发展中60岁以上占10%为老龄化。
12、世界人口老龄化趋势特点:①人口老龄化速度加快②老年人口重心从发达国家向发展中国家转移③人口平均预期寿命不断延长④高龄老年人(80岁以上)增长速度快⑤老年妇女是老年人口的多数13、我国人口老龄化趋势特点:中国1999年进入老龄化社会①老年人口规模巨大②老龄化发展迅速③地区发展不平衡④城乡发展不平衡⑤女性老年人多于男性⑥老龄化超前于现代化。
14、人口老龄化影响:①社会负担加重②社会文化福利事业的发展与人口老龄化不适应③家庭养老功能减弱④老年人对医疗保健、生活服务的需求突出15、人口老龄化对策:①推动经济快速发展②完善养老福利政策和社会保障制度③健全老年人医疗保健防护体系④创建健康老龄化和积极老龄化⑤营造全社会的敬老、养老、助老风气16、老年学是一门研究老年及相关问题的学科,包括自然科学和社会科学的新兴综合性交叉学科,是老年生物学、老年医学、老年社会学、老年心理学、老年护理学的总称。
设计使用寿命的名词解释
设计使用寿命的名词解释设计使用寿命是指产品在设计阶段所预设的正常使用期限,也被称为设计寿命、预期寿命或目标寿命。
它是设计师在产品开发过程中所考虑的重要因素之一。
在不同的领域和行业,设计使用寿命的定义和评估方法可能会有所不同,但总体概念是相似的。
1. 设计使用寿命的意义设计使用寿命是为了满足用户对产品寿命的期望和需求。
它考虑了产品的可靠性、耐久性和性能。
通过设定合理的设计使用寿命,可以确保产品在正常使用条件下能够长时间稳定运行,减少维修和更换的频率,提高用户的满意度和品牌信誉。
2. 设计使用寿命的确定因素设计使用寿命的确定因素包括产品的设计质量、材料选择、产品的预期使用环境和负荷、设计阶段的可靠性分析等。
设计师需要综合考虑这些因素,并通过工程设计和测试来评估产品的使用寿命。
3. 设计使用寿命的评估方法设计使用寿命的评估方法多种多样,常见的方法包括可靠性试验、加速寿命试验、模拟测试等。
这些方法可以通过模拟产品在实际使用过程中的应力和环境来预测产品的使用寿命。
同时,还可以结合可靠性工程的理论和方法,进行可靠性分析和预测。
4. 设计使用寿命与经济效益设计使用寿命与产品的经济效益密切相关。
在产品设计过程中,过长的设计使用寿命可能会增加产品的成本和开发周期,过短的设计使用寿命则可能导致产品的寿命不符合用户的期望。
因此,设计师需要在考虑产品的使用寿命的同时,兼顾经济效益,寻求一个最佳的平衡点。
5. 设计使用寿命的例子设计使用寿命在各个行业和产品中都有应用。
以电子产品为例,如智能手机的设计使用寿命通常为2-3年,这是由于技术更新迭代快,用户对新功能和性能的需求不断提高。
而汽车的设计使用寿命通常为10-15年,这是由于汽车的投资和使用成本较高,用户期望能够长时间使用。
在建筑领域,房屋的设计使用寿命通常为30年以上,考虑到建筑的结构和耐久性需求。
总结:设计使用寿命是产品设计过程中的重要考虑因素,它关乎产品的可靠性、耐久性和用户的满意度。
2009第十三章寿命表2009-11-13
也称队列寿命表
根据某一特定人群中每一位观察对象从进 入该人群到死亡的实际过程,直接计算死亡 概率,最后算出预期寿命等各项寿命表指标。
应用:较短生命的寿命,如患某病后的寿
命、IUD的寿命。
2) 现时寿命表(current life table) 假定有同时出生的“一代人”(通常为 10万)按照某地某个时期年龄别死亡 率推算出的年龄别死亡概率陆续死去, 从而计算出这代人各年龄组“生存人 数”、“死亡人数”、“预期寿命”等 寿命表指标,以这些指标反映该地这一 时期人群的健康水平。
第二节 寿命表的编制原理与方法
1. 年龄组 x 表示年龄组的下限 0~ : 从出生到不满1周岁的儿童, 组距=1 ; 1~ : 从1周岁到不满5周岁, 组距=4 ; 5~ : 从5周岁到不满10周岁, 组距=5; 10~: ….. 85~: 85周岁及以上
2. 平均人口数
nPx
x: 年龄组的下限 n: 年龄组的组距
q
表示刚满x岁时的生存人数,在今后n年内的 死亡概率。
nd x lx
n年
lx+n
死亡率和死亡概率的区别: 死亡概率的分母为 lx , 死亡率的分母为(lx + lx+n)/2
5. 年龄别死亡概率
第一组:(0~组)
n
qx
某年婴儿死亡数 q0 婴儿死亡率 同年活产数
中间组:当 n<=5
2 n nmx n qx 2 n nmx
假定同时出生的一批人(一般定为10万人), 按照某一人口的年龄别死亡率计算出的年龄别 死亡概率而陆续死亡,直到全部死完为止,然 后计算出各年龄组“生存人数”、“死亡人 数”、“预期寿命”等寿命表指标,以这些指 标反映这一批人的整个生命过程。
寿命损失年计算方法
寿命损失年计算方法一、寿命损失年的概念1.1 寿命损失年是一个很重要的概念,它就像一把尺子,用来衡量因为某些原因,人们过早失去的健康生活的时间。
这可不是个干巴巴的数字,背后可是承载着许多生命的故事呢。
咱们打个比方,一个年轻人因为意外事故或者疾病,本来可以健健康康活个七八十岁,结果中途就没了,这中间少活的那些年就是寿命损失年。
这就好比是一盏灯,本来可以亮很久很久,结果突然被吹灭了,少亮的那段时间就是寿命损失年所关注的。
1.2 从健康的角度来看,寿命损失年能让我们清楚地看到哪些因素对人们的健康威胁最大。
这就像在战场上找出最厉害的敌人一样。
比如说,某些严重的疾病,像癌症或者心血管疾病,它们可能会一下子夺走很多人的健康岁月,这在寿命损失年的计算里就会体现得很明显。
这就好比是在一个大家庭里,突然有个败家子,把家里很多的财富(这里就是健康岁月)给败光了,这个败家子就是那些严重疾病。
二、寿命损失年的计算方法2.1 首先呢,要确定一个标准的寿命期望值。
这个就像定一个目标一样,一般是根据一个地区或者人群的平均寿命来确定的。
比如说,某个地区的人平均能活到75岁,那这个75岁就是我们计算的一个基础。
这就像是盖房子,得先有个地基一样。
如果一个人50岁就去世了,那初步算起来,他的寿命损失年就是75 50 = 25年。
这就像是本来计划走75里路,结果只走了50里,少走的那25里就相当于寿命损失年。
2.2 但是呢,这还不是全部。
我们还得考虑到不同年龄段的权重。
为啥呢?因为年轻人的生命价值和老年人的生命价值在某种意义上是不一样的。
就像一颗刚发芽的小树苗和一棵已经长了很多年的大树,小树苗如果夭折了,那损失就更大。
所以在计算寿命损失年的时候,对于年轻人的早逝,会给予更高的权重。
这就好比是在一个球队里,年轻有潜力的球员如果受伤不能踢球了,那对球队未来的影响可能比一个老球员受伤要大得多。
2.3 另外,我们还要考虑疾病或者伤害对生活质量的影响。
卫生统计学_寿命表
•
牢记安全之责,善谋安全之策,力务 安全之 实。2020年11月9日星 期一10时55分 48秒M onday, November 09, 2020
•
相信相信得力量。20.11.92020年11月9日星期 一10时 55分48秒20.11.9
谢谢大家!
•
加强做责任心,责任到人,责任到位 才是长 久的发 展。20.11.920.11.9Monday, November 09, 2020
•
每天都是美好的一天,新的一天开启 。20.11.920.11.910:5510:55: 4810:55:48Nov -20
•
相信命运,让自己成长,慢慢的长大 。2020年11月9日星期 一10时 55分48秒Monday, November 09, 2020
•
感情上的亲密,发展友谊;钱财上的 亲密, 破坏友 谊。20.11.92020年11月9日星 期一10时55分 48秒20.11.9
x岁到x n岁之间死亡人数
qx
活满x岁的人口数
死亡率的公式定义为 :
mx
x岁到x n岁之间死亡人数 x岁到x n岁之间的平均人口数
目前常用的计算死亡概率的公式为:
qx
2nmx 2 nmx
编制寿命表时,一般用婴儿死亡率或校正 婴儿死亡率作为0岁组死亡概率的估计值。 最后一组的死亡概率为1 。
安全象只弓,不拉它就松,要想保安 全,常 把弓弦 绷。20.11.910: 55:4810:55Nov-209- Nov-20
•
加强交通建设管理,确保工程建设质 量。10: 55:4810:55:4810:55Monday, November 09, 2020
•
安全在于心细,事故出在麻痹。20.11.920.11.910:55:4810: 55:48November 9, 2020
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
期望寿命的概念及计算方法
一、期望寿命的概念及相关
期望寿命(life expectancy?)又称平均预期寿命,或预期寿
命。X岁时平均预期寿命表示X岁尚存者预期平均尚能存活的年数。
刚满X岁者的平均预期寿命受X岁以后各年龄组死亡率的综合影
响。出生时的期望寿命简称平均寿命,它是各年龄死亡率的综合,
综合反映了居民的健康状况,是反映人群健康状况的综合指标,但
是,它只综合了有关死亡的信息,未包含疾病和伤残的情况,更未
反映疾病伤残结果的严重性。
期望寿命是评价居民健康状况、社会经济发展和人群生存质量
的重要指标,它不受人口年龄构成的影响,因此各地区平均期望寿
命可以直接比较。对一个地区人口学特征、期望寿命及影响因素进
行研究,可为制定科学、切合实际的卫生工作计划提供科学依据。
而另一个概念“健康期望寿命”(active life expectancy,
ALE),它是指人们能维持良好日常生活活动(ADL)功能的年限,
健康期望寿命与普通的期望寿命的差别是:普通的期望寿命是以死
亡为终点,而健康期望寿命以丧失日常生活能力为终点,它不仅能
客观反映人群生存质量,亦有助于卫生政策与卫生规划的制定。因
此2000年世界卫生组织推荐用“健康期望寿命”来反映居民健康
综合情况。
二、期望寿命的计算
我区期望寿命是由统计分析软件DeathReg 2005计算而来,原
理是编制我区居民简略寿命表。
寿命表又称为生命表(life table)是根据特定人群的年龄组
死亡率编制出来的一种统计表。寿命表有两种主要形式,队列寿命
表和现时寿命表。应用较广的是现时寿命表。它反映一定时期某地
区实际人口的死亡经历.是从一个断面来看当年一定时间段内人口
的死亡和生存经历,它完全取决于制表这一年的人口年龄别死亡
率。现时寿命表计算所得的预期寿命是假定一批婴儿在其一生中都
遵从当年资料所呈现的年龄别死亡率而死亡、生存的平均预期寿
命,即该预期寿命是该人群的平均水平.并不是每一个人的实际存
活年龄。现时寿命表的最大优点是不同地城、不同时期的寿命表指
标可以直接比较,不受原来的人口性别、年龄别构成的影响。目前
人们常说的预期寿命,基本上就是指现时寿命表的平均预期寿命。
队列和现时寿命表都有完全和简略寿命表之分。完全寿命是以
0岁为起点,逐年计算各种指标,直至生命的极限,其年龄的区间
是[x,x+1)。而简略寿命表的年龄区间则是(x,x+n),n除第一年
外均大于1年.典型的年龄区间是0一,1一,5一.10一,…,
85一,即每5岁一个间隔,直至最后一个年龄区间。简略寿命表
与完全寿命表相比,除减少计算量外,也可弥补完全寿命表的某些
不足:在完全寿命表中.各指标需按每岁一组纳资料编制,但每岁
一组的人口及死亡资料经诸不局获得,尤其当登记工作制度不健全
及非人口普查年年份时;或者有时虽可获得按年龄的人口及死亡资
料,但可能会受报告人错报年龄的影响,降低了资料的准确性;由
于年龄别死亡率不同,在按每岁年龄计算指标时,pJ
能会出现一些年龄组无死亡或死亡数多于存话数,尤其是在总人口
数较少的情况下;还合死亡是随机事件.
发生在一年内的死亡数有很大的波动等。以上多种原因,均可能影
响完全寿命表编制的准确性,采用简略寿命表可避免上述不足,提
高资料的准确性。
编制寿命表需要完整可靠的人口资料与死亡登记资料,现时寿
命表所依据的人口资料不一定限于某一年中,也可以是几年的资
料,这样做可以减少发生于一年中的异常死亡现象对分析结果的影
响。在编制寿命表时.有时会遇到统计资料有误或人口数太少出现
数据波动较大的情况,后者,在高龄组更易出现,可应用一些数学
方法对数据作…些修匀。
这里主要介绍简略寿命表。主要指标有:
1.年龄区间(z,z?”) 除第一区间是。一1岁,第二区间是
1—5岁外,其余区间均是5岁一个问阴,
一直到85岁及以上为最后一个区间。寿命表中的年龄s是“刚满
年龄(exa瓤age)”如“1一”,意即刚满一岁
(即刚过第1个生日)的儿童o
2.人口数(dPr)与死亡数(nD r) 人口数与死亡数是编制寿命
表的基本依据。按性别和年龄分组的可
靠的平均人闻数和准确的死亡登记资料是寿命表编制的必备条件。
编制寿命表一般以日历年度的人口资料
为依据,人口数与死亡数可由公安户籍部门或人口普查及专项调查
获取。在这些数据中,出生数及婴儿死亡
数据的准确性,对编制一份可信度高的寿命表十分重要。我国目前
在搜集人口出生、死亡资料过程中,普遍
存在的问题是新生儿出生与死亡数字的漏报,这对计算婴儿死亡率
的影响较大,从而宜接影响寿命表资料的
准确性。因此,在编制某国家或地区的寿命表时,应对人口及死亡
的基本数据进行认真的核查。
3.年龄别死亡率(nM r) 年龄别死亡率表示某年龄组人口在
一年或M年内的平均死亡率,它根据分年
龄组平均人口数及死亡数计算而来。即:
平均人口数也可用年中人口数代替。计算寿命表的关键步骤是
获得死亡概率,由于很难从调查数据中
直接获得计算死亡概率的数据.一般都是用一些特定的公式将死亡
率转换为死亡概率。从这一点上说,死亡
率的计算是寿命表编制的必备步骤。
4.年龄别死亡概率(;gz) 表示一批人在年龄2到年龄x?”
岁之间的死亡概率。分年龄组死亡概率
与分年龄组死亡率的概念不同,但两者问有一定的关系。”gj所表
示的是在那些已活满?岁的人中,有多大
比例将在他们到达2?n岁之前死亡。因此,死亡概率的公式定义为:
z岁到x?M岁之间死亡人数
Rg‘;—飞而了不石雨厂—
而死亡率的公式定A为: s岁到2?n岁之间死亡人数
”’=万聂万7:了百而乔面(i贡
可见,两者分母不同,当年龄分组为1岁时,gj比mf略小,
当年龄分组大于1岁时,即n>1时,则ng2
约比”M2大n倍。死亡率与死亡概率之间可以互相换算,现有许
多种由”mf推算”gJ的方法,各有其优缺点c
实践表明,同一资料用不同方法计算出ng2值咐获得的平均预期寿
命差
式中,人表示最后一个年龄组的生存人年数,jv表示生存人数,
M m表示死亡统计中的最后
率.如85岁及以上组死亡率为们:s(,)o
其余年龄组:
”L2=十〔jf‘J2t”)
8.生存总人年数(7,) 表示2岁及以上各年龄组的人口令后
还能存活人年数的总和。即:
由于o岁组即出生时的平均预期寿命do表示一批人出生后平
均一生可存活的年数,具有特殊的意义,
所以一般情况下的平均预期寿命多是指o岁组平均预期寿命‘。。
可见,有了”gJ,就可按上述关系式依次求
出所有其他各项寿命表指标。因此,寿命表上的关键指标是死亡概
率。
编制筒略寿命表的人口数据可以是一个国家的,也可以是一个
地区的;还可以针对某个特定的人口区域
编制寿命表,比如城市入口或者农村人口的寿命表。不同性别的人
口,死亡规律是有差异的,故寿命表的编
制一般按男、女性别分别编制。以下从实例来说明简略寿命表的编
制过程。
例13.1 编制某地1999年男性居民简略寿命表,资料见表
13.2。
WHO推荐的蒋庆琅式简略寿命表法
三、期望寿命的影响因素
