实验五典型环节和系统频率特性的测量
系统频率特性的测试1

系统频率特性的测试1简介在电子电路中,系统频率特性是非常重要的性能参数之一。
系统频率特性指的是系统对输入信号频率的响应能力,通俗地说,就是系统对于不同频率的信号的处理能力。
在设计一些高精度和高性能的电路的时候,对系统频率特性的测试就显得非常重要。
在本文中,我们将介绍常见的系统频率特性测试方法,并针对其中的一种方法进行详细的介绍。
常见系统频率特性测试方法Bode图法Bode图法是一种基于频率响应的方法,用于描述系统对输入信号频率的响应能力。
它通常通过Bode图来表示被测系统的频率特性。
Bode图是以频率为横轴、输入输出响应幅值比或相位差为纵轴的图形。
具体来说,Bode图法首先将被测系统激励输入电路,然后通过测量输出信号幅值和相位与输入信号的相对大小和差距来构建图形。
频率响应测试法频率响应测试法是一种基于一个频率输入信号测量系统的输出响应的方法。
具体操作过程是,选取一个频率范围作为输入信号,然后将各个频率的输入信号作为输入,测量对应的输出信号以得到系统的频率响应。
这种方法会输出一个基于不同频率的幅值和相位差的表格,以及对应的曲线图。
载频测试法又称为亚细分测试法,通过选取不同的载频对被测系统进行激励,测量电路的响应电流进行测试。
在实际的应用中,亚细分测试法可以用来评估系统处理高频信号和噪音的能力。
系统频率特性测试方法之一:Bode图法测试过程Bode图法将被测系统激励输入电路,随后测量输出电路随频率变化的幅值和相位,将结果用Bode图进行展示。
具体的测试步骤如下:1.激励输入电路。
在实际测试中,往往选取的是一个正弦波作为输入信号,将其施加到被测系统中。
2.测量输出信号的幅值和相位。
使用输入信号激励电路后,使用测量设备测量输出信号随时间变化的幅值和相位。
3.用Bode图展示幅值和相位的变化。
将得到的幅值和相位数据绘制成Bode图,用以表示对应信号频率下的系统响应能力。
Bode图的意义Bode图在系统性能测试中起着非常重要的作用。
控制系统的频率特性测量。

控制系统的频率特性测量1.一、实验目的1.加深了解系统及元件频率特性的物理概念。
2.掌握系统及元件频率特性的测量方法。
3.了解MATLAB测量系统频率特性的方法。
4.二、实验内容1.设计一阶惯性环节模拟电路,并完成频率特性曲线测试。
2.系统结构图如图所示(略)。
测试系统的频率响应,分析系统频率特性。
3.用MATLAB软件仿真求取一阶惯性环节频率特性和典型二阶系统开环频率特性曲线,并与实验所得结果比较。
三、理论分析与电路模拟四、软件仿真分析方法实验内容(1)一阶惯性环节:幅值=1、频率=1幅值=1、频率=5实验内容(2) 典型二阶系统:频率为1:频率为5:1.用LATLAB函数nyquist()和bode()绘制系统幅相曲线和对数曲线频率特性曲线。
参考程序:s=tf('s');G=1/(0.2*s+1);nyquist(G)bode(G)一介惯性环节开环幅相频率特性一介惯性环节开环对数频率特性num=[500];den=[1 10 500];sys=tf(num,den);bode(sys)[h,r,wg,wc]=margin(sys) 结果:h =Infr =36.8648wg =Infwc =30.0016典型二阶系统的开环幅相频率特性用LATLAB函数nyquist()和bode()绘制系统幅相曲线和对数曲线频率特性曲线。
参考程序:num=10;den=conv([1 1],[0.1 1]);G=tf(num,den);figure(1)nyquist(G)figure(2)bode(G)典型二阶系统的开环幅相频率特性。
5.1频率特性-5.2典型环节的极坐标图-5.3Nyquist图的绘制

jt jt x ( t ) ae a e o (4-2)
i 1
n
bi e pi t
(4-4)
因此,系统的稳态响应为:
t 趋向于零
xos (t ) ae jt ae jt
a G (s) R s2 R s2 2 ( s j ) s j G ( j ) 2 R R ( s j ) s j G ( j ) ( s j )(s j ) 2j R R ( s j ) s j G ( j ) ( s j )(s j ) 2j
第五章 系统的频率特性分析 2. 控制系统在正弦信号作用下的稳态输出
设系统的传递函数为 G ( s)
X o (s) U (s) X i (s) V (s)
已知输入 xi (t ) R sin( t ) 其拉氏变换 则系统输出为
X i ( s)
R s2 2
U (s) R U ( s ) R X o (s) G (s) X i (s) ( s p1 )( s p 2 ) ( s p n ) s 2 2 V (s) s 2 2
arctan T
第五章 系统的频率特性分析 • uo(t)表达式中第一项是瞬态分量,第二项是稳态 分量。显然上述RC电路的稳态响应为
lim uo (t )
t
U
2 2
1 T 1 1 U sin t 1 jT 1 jT
sin(t )
第五章 系统的频率特性分析 5.2.1 典型环节的极坐标图
• 用频域分析法研究控制系统的稳定性和动
态响应时,是根据系统的开环频率特性进
实验三 典型环节(或系统)的频率特性测量

实验三 典型环节(或系统)的频率特性测量一.实验目的1.学习和掌握测量典型环节(或系统)频率特性曲线的方法和技能。
2.学习根据实验所得频率特性曲线求取传递函数的方法。
二.实验内容1.用实验方法完成一阶惯性环节的频率特性曲线测试。
2.用实验方法完成典型二阶系统开环频率特性曲线的测试。
3.用软件仿真方法求取一阶惯性环节频率特性和典型二阶系统开环频率特性,并与实验所得结果比较。
三、实验原理及说明1.实验用一阶惯性环节传递函数参数、电路设计及其幅相频率特性曲线:对于1)(+=Ts Ks G 的一阶惯性环节,其幅相频率特性曲线是一个半圆,见图3.1。
取ωj s =代入,得)()(1)(ωϕωωωj e r T j Kj G =+=(3-2-1)在实验所得特性曲线上,从半园的直径(0)r ,可得到环节的放大倍数K ,K =(0)r 。
在特性曲线上取一点k ω,可以确定环节的时间常数T ,kk tg T ωωϕ)(-=。
(3-2-2)实验用一阶惯性环节传递函数为12.01)(+=s s G ,其中参数为R 0=200K Ω,R 1=200K Ω,C=1uF ,参数根据实验要求可以自行搭配,其模拟电路设计参阅下图3.2。
在进行实验连线之前,先将U13单元输入端的100K 可调电阻顺时针旋转到底(即调至最大),使输入电阻R 0的总阻值为200K;其中,R1、C1在U13单元模块上。
U8单元为反相器单元,将U8单元输入端的10K 可调电阻逆时针旋转到底(即调至最小),使输入电阻R 的总值为10K;注明:所有运放单元的+端所接的100K 、10K 电阻均已经内部接好,实验时不需外接。
图3.22.实验用典型二阶系统开环传递函数参数、电路设计及其幅相频率特性曲线:对于由两个惯性环节组成的二阶系统,其开环传递函数为12)1)(1()(2221++=++=Ts s T Ks T s T K s G ξ )1(≥ξ 令上式中 s j ω=,可以得到对应的频率特性 )(22)(12)(ωϕωωξωωj e r T j T Kj G =++-=二阶系统开环传递函数的幅相频率特性曲线,如图所示。
控制工程基础实验指导书(答案) 2讲解
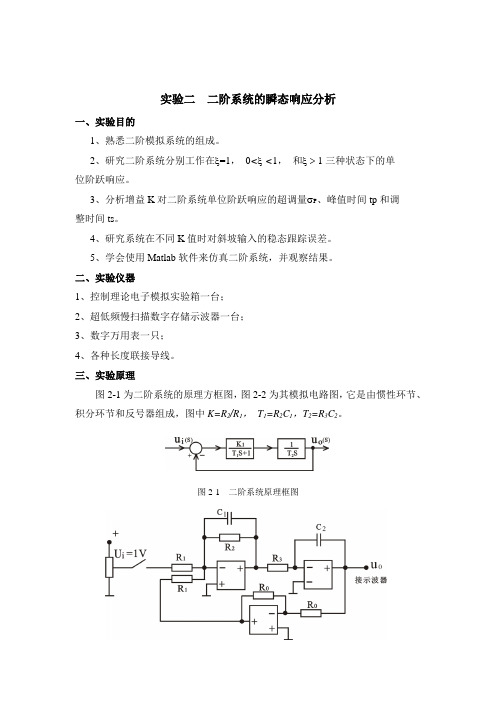
实验二二阶系统的瞬态响应分析一、实验目的1、熟悉二阶模拟系统的组成。
2、研究二阶系统分别工作在ξ=1,0<ξ<1,和ξ> 1三种状态下的单位阶跃响应。
3、分析增益K对二阶系统单位阶跃响应的超调量σP、峰值时间tp和调整时间ts。
4、研究系统在不同K值时对斜坡输入的稳态跟踪误差。
5、学会使用Matlab软件来仿真二阶系统,并观察结果。
二、实验仪器1、控制理论电子模拟实验箱一台;2、超低频慢扫描数字存储示波器一台;3、数字万用表一只;4、各种长度联接导线。
三、实验原理图2-1为二阶系统的原理方框图,图2-2为其模拟电路图,它是由惯性环节、积分环节和反号器组成,图中K=R2/R1,T1=R2C1,T2=R3C2。
图2-1 二阶系统原理框图图2-1 二阶系统的模拟电路由图2-2求得二阶系统的闭环传递函1222122112/() (1)()/O i K TT U S K U S TT S T S K S T S K TT ==++++ :而二阶系统标准传递函数为(1)(2), 对比式和式得n ωξ==12 T 0.2 , T 0.5 , n S S ωξ====若令则。
调节开环增益K 值,不仅能改变系统无阻尼自然振荡频率ωn 和ξ的值,可以得到过阻尼(ξ>1)、临界阻尼(ξ=1)和欠阻尼(ξ<1)三种情况下的阶跃响应曲线。
(1)当K >0.625, 0 < ξ < 1,系统处在欠阻尼状态,它的单位阶跃响应表达式为:图2-3 0 < ξ < 1时的阶跃响应曲线(2)当K =0.625时,ξ=1,系统处在临界阻尼状态,它的单位阶跃响应表达式为:如图2-4为二阶系统工作临界阻尼时的单位响应曲线。
(2) +2+=222nn nS S )S (G ωξωω1()1sin( 2-3n to d d u t t tgξωωωω--=+=式中图为二阶系统在欠阻尼状态下的单位阶跃响应曲线etn o n t t u ωω-+-=)1(1)(图2-4 ξ=1时的阶跃响应曲线(3)当K < 0.625时,ξ> 1,系统工作在过阻尼状态,它的单位阶跃响应曲线和临界阻尼时的单位阶跃响应一样为单调的指数上升曲线,但后者的上升速度比前者缓慢。
实验二、频率特性的测试与分析(4)

实验二、频率特性的测试与分析一、 实验目的1、 掌握频率特性的测试原理及方法。
2、 根据开环系统的对数频率特性,确定系统组成环节的参数。
3、 进一步掌握电模拟方法。
二、 实验设备和仪器1、自动控制系统教学模拟机 一台2、数字万用表 一块3、TD4010型频率响应分析仪 一台三、 实验原理及方法1、 概念:在XSin ωt 的作用下,线性定常系统的输出信号稳态分量Y (t )是和正弦输入信号同频率的正弦函数,其振幅Y 与输入正弦信号的振幅X 的比值是角频率ω的函数,它描述系统对不同频率的正弦输入信号在稳态情况下的衰减或放大特性。
定义系统输出信号的稳态分量Y (t )对正弦输入信号X (t )的相移Φ为该系统的相频特性,它描述系统的输出对不同频率的正弦输入信号在相位上产生的相角滞后和相角超前的特性。
上述的幅频特性|G (j ω)|和相频特性∠G(j ω)统称为系统的频率特性,记为:频率特性可以通过实验的方法来确定,即改变正弦输入信号XSin ωt 的角频率,测出与此相应的输出信号稳态分量Yw (t )的振幅以及Yw (t )相对于正弦输入信号X (t )的相移Φ,然后计算出Y/X 对于频率ω的函数曲线这便是幅频特性:求取相移Φ对于信号频率ω的函数曲线,这便是相频特性∠G(j ω)。
上述这种方法就是求取频率特性的实验法。
四、TD4010型频率响应分析仪使用说明TD4010型频率响应分析仪是用来测量自动控制系统,部件或元件等的频率特性,是在频率域内分析对象动态特性的重要工具。
1、 前面板示意图)(ωj G XY =e j G j j G j G )()()(ωωω∠=)()(ωωj G XY =前面板示意图见图2—1,除电源开关为按键外,其余均为轻触键。
显示方式发生器显示窗口过载指示灯分析器输入端子图2—1前面板示意图2、开机按下电源开关 POWER (POWER),仪器进入初始状态,预热10-15分钟即可使用。
5-2 典型环节的频率特性
K T 2 s 2 + 2ξTs + 1
0
ωr
对应频率特性 G( jω) 的起点为
G( j0) = K , ∠G( j0) = 0
(ω = 0 )
振荡环节的频率响应
阻尼比较小时,会产生谐振,谐振峰值 M r ( M 幅频特性的极值方程解出。
r
> 1) 和谐振频率 ω r 由
d d 2 2 2 1 − T ω + 4ξ 2T 2ω 2 = 0 G( jω ) = dω dω
∠G( jω ) = 0
频率特性如图所示。
°
Im
由图可看出放大环节的幅频特 性为常数K,相频特性等于零度, 它们都与频率无关。理想的放大环 节能够无失真和无滞后地复现输入 信号。
0
ω =0→∞
.
K
Re
放大环节的频率响应
(二) 积分环节
积分环节的传递函数为 其对应的频率特性是
1 G (s) = s
100
90o 45o 0 -45o -90o 0.01 0.1 1 10 100
ω
用伯德图分析系统有如下优点: (1) 将幅频特性和相频特性分别作图,使系统(或环节)
的幅值和相角与频率之间的关系更加清晰; (2) 幅值用分贝数表示,可将串联环节的幅值相乘变为相 加运算,可简化计算;
G ( jω ) = G1 ( jω )G2 ( jω ) LGn ( jω ) G ( jω ) = G1 ( jω ) ⋅ G2 ( jω ) L Gn ( jω ) L(ω ) = 20 lg G ( jω ) = 20 lg G1 ( jω ) + 20 lg G2 ( jω ) + L + 20 lg Gn ( jω )
实验五简支梁固有频率测试实验1
实验五 简支梁固有频率测试实验一、 实验目的:1、 掌握固有频率测试的工程意义及测试方法。
2、 掌握用共振法、李萨育图形法测量振动系统的固有频率的方法及步骤。
3、 加深了解常用简单振动测试仪器的使用方法。
二、实验设备和工具1.机械振动综合实验装置(安装简支梁) 1套2.激振器及功率放大器 1套3.加速度传感器 1台4.电荷放大器 1台5.数据采集仪 1台6.信号分析软件 1套三、实验内容1.用共振法测量简支梁固有频率共振法测量振动系统的固有频率是比较常用的方法之一。
共振是指当激振频率达到某一特定值时,振动量的振动幅值达到极大值的现象。
由弹性体振动理论可知,计算简支梁固有频率理论解为:APEJ L f 20115.49 式中,L 为简支梁长度(cm );E 为材料弹性系数(kg/cm 2);A 为梁横截面积(cm 2);P 为材料比重(kg/cm 3);J 为梁截面弯曲惯性矩(cm 4)。
用共振法测量简支梁固有频率的仪器连接如图1所示图1测量双简支梁固有频率框图2.用李萨育图形法测量简支梁固有频率李萨育图形是由运动方向相互垂直的两个简谐振动的合成运动轨迹。
李萨育图形可以通过示波器或数据采集软件的X-Y轨迹图观察到。
在图的X、Y 轴上同时输入简谐振动两个信号,这两个信号不同的相位差合成不同的李萨育图形如图2所示。
振动的位移、速度及加速度的幅值其各自达到极大值时频率是不同的,只有在无阻尼的情况下,它们频率才相等,并且等于振动系统的固有频率。
但在弱阻尼的情况下,三种共振频率接近系统的固有频率。
只有速度共振频率真正和固有频率相等,所以用速度共振的相位差判别共振。
判别依据是系统发生速度共振时,激振力和速度响应之间的相位差为90°,依据位移、速度、加速度响应判断速度共振的李萨育图形如图3~5所示。
θ=00 θ=450 θ=900 θ=1350 θ=1800图2 不同相位差信号合成的李萨育图形n ωω< n ωω= n ωω>图3用位移响应判断速度共振n ωω< n ωω= n ωω>图4用速度响应判断速度共振n ωω< n ωω= n ωω>图5用加速度响应判断速度共振四、实验原理固有频率是振动系统的一项重要参数。
第五章(典型环节的频率特性)
§5.1
频率特性的概念
§5.2 典型环节的频率特性 §5.3 系统的开环频率特性 §5.4 乃奎斯特稳定判据和系统的相对稳定性 §5.5 利用开环频率特性分析系统性能 §5.6 利用闭环频率特性分析系统性能
本章重点
1.开环频率特性的绘制(包括极坐标图和对数坐 标图); 2. 乃奎斯特稳定性判据及其在Bode图中的应用; 3. 对数频率特性和闭环系统性能的关系; 4. 开环频率特性指标; 5. 闭环频率特性指标。
稳定后输出 C(t)=CmSin(t+)
三要素: 频率: 不变
幅值: M Cm 关系为: 幅角: 0 关系为:
0 G(s) |S j
Cm A( ) G(s) S j X
系统频率响应与正弦输入信号之间的关系称为频率特性。
幅频特性 相频特性
可见:A( ) G ( j )
jt
dt C ( j ) c(t )e jt dt
经过傅氏反变换
1 c(t ) 2
G ( j ) R( j )e jt d
1 系统的单位脉冲响应为: g (t ) 2
G ( j )e jt d
频率特性
输入 r(t)=M Sin(t+0) 线性系统 通常令0=0
结论
Ar=1 ω=0.5
给稳定的系统输入一个正弦,其稳态输出是与输入 同频率的正弦,幅值随ω而变,相角也是ω的函数。
ω=1
ω=2
ω=2.5
ω=4
相角问题
AA ① 稳态输出 迟后于输入的 角度为: B φ= 360o A ②该角度与ω有 关系 , ∴为φ(ω) ③该角度与初始 角度无关 , ∴ …
奈奎斯特曲线
G(
j )
T
2
(
j )2
1
2T
(
j )
1
| G( j) |
1
(1 T 2 2 )2 (2 T)2
G(
j
)
tg
1
2T 1 T 2 2
当 0 时
| G( j) |1 G( j) 0o
当 时
| G( j) | 0,G( j) 180o
R
相频特性(): 稳态输出信号的相角与输入信号相角之差。
第五章 频域分析法
频率特性又称频率响应,它是系统(或元件)对不同频率正 弦输入信号的响应特性。(稳态)
频率特性=
输出的复数形式 输入的复数形式
W ( j ) X c ( j ) A( )e j X r ( j )
2
1.5
奈氏图
| G( j) |= U 2 V 2 K2 02 K
G( j) tg1 V tg1 0 0
U
K
第五章 频域分析法
2. 惯性环节:G(s)=1/(Ts+1)
G( j ) 1 Tj 1
1
j T U jV | G( j ) | e jG( j )
第五章 频域分析法
6.
二阶微分环节 G(s)
s2 wn2
2
wn
s 1 T 2s2
2Ts 1
A()
(1
T
2
2
)2
(2T
)2
,
(
)
tg 1
1
2T T 2
2
P() 1 T 2 2 , Q() 2 T
