2018届四川省宜宾市南溪区第二中学校高三上学期第5周周考数学(理)试题

合集下载

四川省宜宾市南溪区第二中学校2022届高三上学期第3周周考数学(文)试题 Word版含答案

K2= =11.538＞10.828，
所以该争辩小组有99.9%的把握认为，中同学使用手机对学习有影响；
（2）记A组推选的两名同学分别为C、D，
B组推选的三名同学分别为a、b、c，则从这5人中任取两人有
CD、Ca、Cb、Cc、Da、Db、Dc、ab、ac、bc，共10种取法，
其中一人来自A组、另一人来自B组有6种取法，
2、若z=1﹣i，则复数z+z2在复平面上对应的点的坐标为（）
A．（1，﹣3）B．（﹣3，1）C．（1，1）D．（﹣1，1）
3、设x∈R，向量 =（x，1）， =（1，﹣2），且 ⊥ ，则| + |=（）
A． B． C．2 D．10
4、下列函数中，既是偶函数，又在区间单调递减的函数是（）
A. B. C. D.
14、【答案】【解析】由函数的解析式结合题意可得： .
15、【答案】- 解： =4×4×cos90°=0，
2 = ， = ，
则 =（ ﹣ ）（ + ）=（ ﹣ ）（ + ）
= 2﹣ 2﹣ = ×16﹣ ×16=﹣ ．
16、【答案】①③
【解析】命题① 命题①正确；命题②当时不满足“远离区间”的定义命题②错误；命题③由图一可得该命题正确；命题④由图二可得该命题错误.综上真命题的是①③.
所以x﹣2=0，所以 =（2，1），所以 =（3，﹣1），
所以| + |= ，故选B．
4、【答案】D【解析】逐一考查所给的函数：
A. ，函数是奇函数；
B. 函数是偶函数，在区间是增函数；
C. 函数是偶函数，在区间不具有单调性；
D. 函数是偶函数，在区间单调递减；
5、【答案】C

2017-2018学年四川省宜宾市南溪区第二中学校高二上学期第15周周考数学(文)试题

2017-2018学年南溪二中高二上第15周周考试题（文科）1、命题“对x R ∀∈，都有20x ≥”的否定为（） A.x R ∃∈，使得20x < B.对x R ∀∈，使得20x < C.x R ∃∈，使得20x ≥ D.不存在x R ∈，使得20x <2、椭圆2222:1x y C a b+=(0)a b >>的左、右焦点为2,1F F ，过2F 作直线l 垂直于x 轴，交椭圆C于A ，B 两点，若若1F AB 为等腰直角三角形，且0190=∠B AF ，则椭圆C 的离心率为（）A 1B ．12-C ．2．23、椭圆22221124x y m m +=+-的焦距是（）A ．4B ．．8 D ．与m 有关 4、某程序框图如图所示，若输出的S=57，则判断框内为（ )A.k ＞4?B.k ＞5?C.k ＞6?D.k ＞7?5、下列四个图各反映了两个变量的某种关系，其中可以看作具有较强线性相关关系的是（）A ．①③B ．①④C ．②③D ．①②6、某产品分甲、乙、丙三级，其中乙、丙两级均属次品，若生产中出现乙级品的概率为0.03，丙级品的概率为0.01，则抽查一件产品抽得正品的概率为（）A ．0.09B ．0.98C ．0.97D ．0.967、甲、乙两人一起去游某公园，他们约定，各自独立地从1号到6号景点中任选4个进行游览，每个景点参观1小时，则最后一小时他们同在一个景点的概率是( )A.136B.19 C.536 D.168、某公司的班车在7:30，8:00，8:30发车，小明在7:50至8:30之间到达发车站乘坐班车，且到达发车站的时刻是随机的，则他等车时间不超过10分钟的概率是（ )A.13 B.12 C.23 D.349、将一根绳子对折，然后用剪刀在对折过的绳子上任意一处剪断，则得到的三条绳子的长度可以作为三角形的三边形的概率为（）A ．16 B ．14 C ．13 D ．1210、3+=kx y 与圆4)2(322=-+-y x ）（相交于N M ,两点，若32≥MN ，则k 的取值范围是A ．⎥⎦⎤ ⎝⎛-∞-43,B ．⎥⎦⎤⎢⎣⎡-0,43C ．⎥⎦⎤⎢⎣⎡-33,33 D ．⎥⎦⎤⎢⎣⎡-0,32 11、点（2，3，4）关于xoz 平面的对称点为（）A.（2，3，-4）B.（-2，3，4）C.（2，-3，4）D.（-2，-3，4）12、已知过定点()2,0P 的直线l与曲线y 相交于,A B 两点,O 为坐标原点,当AOB ∆的面积取最大值时，直线l 的倾斜角为（）A ．150B ．135C ．120D ．105 13、已知命题21:02p x x >--，则p ⌝对应的x 集合为___________． 14、取一个边长为2a 的正方形及其内切圆，随机地向正方形内丢一粒豆子，则豆子落入圆内的概率为 .15、已知两圆的方程分别为2240x y x +-=和2240x y y +-=，则这两圆公共弦的长等于__________.16、下列正确的是；①已知命题p ：|5x-2|＞3，命题q ：2145x x +-＞0，则？q 是？p 的必要不充分条件； ②在△ABC 中，A ＞B 是sinA ＞sinB 的充分不必要条件； ③在△ABC 中，tanAtanB ＞1是△ABC 为锐角三角形的充要条件； ④在△ABC 中，AB ⋅BC ＞0是△ABC 为钝角三角形的充要条件； ⑤在△ABC 中，AB ⋅AC =BA ⋅BC 是|AC |=|BC |的充要条件； ⑥两条直线互相平行是这两条直线斜率相等的充要条件；17、给定两个命题，p ：对任意实数x 都有210ax ax ++>恒成立；q ：28200a a +-<．如果p q ∨为真命题，p q ∧为假命题，求实数a 的取值范围．18、（Ⅰ）求经过点53(,)22-，且与椭圆22195x y +=有共同焦点的椭圆标准方程；（Ⅱ）已知椭圆以坐标轴为对称轴，且长轴长是短轴长的3倍，点(3,0)P 在该椭圆上，求椭圆的标准方程.19、已知以点C 为圆心的圆经过点A （﹣1，0）和B （3，4），且圆心在直线x+3y ﹣15=0上．（1）求圆C 的方程；（2）设点P 在圆C 上，求△PAB 的面积的最大值．20、某企业为了解下属某部门对本企业职工的服务情况，随机访问50名职工，根据这50名职工对该部门的评分，绘制频率分布直方图（如图所示），其中样本数据分组区间为[40,50),[50,60),...,[80,90),[90,100]（1）求频率分布直方图中a 的值；（2）估计该企业的职工对该部门评分不低于80的概率；（3）从评分在[40,60)的受访职工中，随机抽取2人，求此2人评分都在[40,50)的概率.21、已知集合[2,2]A =-，[1,1]B =-，设{()|}M x y x A y B ∈∈＝，，，在集合M 内随机取出一个元素(,)x y ．（1）求以(,)x y 为坐标的点落在圆221x y +=内的概率；（2）求以(,)x y 为坐标的点到直线0x y +=的距离不大于2的概率．22、已知中心在原点O ，左、右焦点分别为21,F F 的椭圆的离心率为36，焦距为22，A ，B 是椭圆上两点.（1）若直线AB 与以原点为圆心的圆相切，且OA ⊥OB ，求此圆的方程；（2）动点P 满足：3OP OA OB =+，直线OA 与OB 的斜率的乘积为31-，求动点P 的轨迹方程.第15周文科参考答案1、【答案】A2、【答案】A【解析】∵2AF x ⊥ 轴，∴2b A c a ⎛⎫⎪⎝⎭，．∵1F AB 为等腰直角三角形，∴122||F F AF = ，∴222222221b c ac b a c e e a=∴==-∴=-，，，化为()22100e e e +-=>，．解得212e -+== ．故选：A ．3、【答案】C4、【答案】A5、【答案】B6、【答案】D7、【答案】D【解析】甲、乙最后一小时他们所在的景点共有6×6＝36种情况，甲、乙最后一小时他们同在一个景点共有6种情况．由古典概型的概率公式知最后一小时他们同在一个景点的概率是P ＝636＝16. 8、【答案】B 【解析】设小明到达时间为y ，当y 在7：50至8：00，或8：20至8：30时，小明等车时间不超过10分钟，故201402P == 9、【答案】D 【解析】三边要能成为三角形，那么两边之和大于第三边，所以应在对折过的绳子的中点处和对折点之间的任意位置剪短，所以能构成三角形的概率21=P ,故 10、【答案】B 【解析】圆心（3,2）到直线3+=kx y 的距离为2113kk d ++=，所以32422≥-=d MN ,即d2≤1，则11)13(22≤++k k ，解得043≤≤-k . 11、【答案】C 12 【答案】A【解析】由题意知直线的斜率必然存在，设直线的斜率为k 且0k <，则直线方程为2y kx k =-，曲线y ==，解得1k =-，画图可知若使直线与半圆有两个交点则直线的斜率必须满足条件1k >-，即倾斜角要满足135α>，只有选项A 满足． 13、【答案】[1,2]- 14、【答案】π415、【答案】【解析】这两个圆的圆心分别为(2,0),(0,2)，半径都是2，两圆方程相减可得0x y -=，这是公共弦所在直线方程，d ==l ==16、【答案】①③⑤【解析】对于①，152315x x x ->⇔<->或，所以1:15P x ⌝-≤≤，210545x x x >⇔<-+-或1x >，所以:51q x ⌝-≤≤，由此可知,/p q qp ⌝⇒⌝⌝⇒⌝，所以①正确；对于②，在ABC ∆中，A B >是sin sin A B >的充要条件，故②错；对于③，tan tan 1tan 0,tan 0,A B A B >⇒>>所以角,A B 均为锐角，又tan tan tan tan[()]tan()01tan tan A BC A B A B A Bπ+=-+=-+=->-，所以角C 为锐角，当ABC ∆为锐角三角形时， tan 0,tan 0A B >>，且tan tan tan 01tan tan A BC A B+=->-，所以tan tan 1A B >，所以③正确；对于④0cos 0AB BC B B ⋅>⇒<⇒为钝角，当ABC ∆为钝角三角形时，例角A 为钝角时，0AB BC ⋅<，所以④错误；对于⑤，cos cos AB AC BA BC AB AC A BA BC B ⋅=⋅⇔⋅=⋅cos cos AC A BC B ⇔= sin cos sin cos sin()0B A A B A B A B ⇔=⇔-=⇔=，所以⑤正确；对于⑥，当两直线平行且垂直于x 轴时，这两第条直线的斜率不存在，故⑥错，所以应填①③⑤.17、【答案】10a 02a 4≤﹣＜＜或＜. （1）当p 真q 假时；（2）当p 假q 真时，从而得到实数a 的取值范围10a 02a 4≤﹣＜＜或＜.试题解析：解：命题p ：ax 2+ax+1＞0恒成立当a=0时，不等式恒成立，满足题意）当a ≠0时，，解得0＜a ＜4∴0≤a ＜4命题q ：a 2+8a ﹣20＜0解得﹣10＜a ＜2∵p q ∨为真命题，p q ∧为假命题∴,p q 有且只有一个为真，当p 真q 假时04102a a a ≤<⎧⎨≤-≥⎩或得24a ≤<当p 假q 真时04102a a a <≥⎧⎨-<<⎩或得100a -<<所以﹣10＜a ＜0或2≤a ＜418、【答案】（Ⅰ）221106x y +=（Ⅱ）221819y x += 或 2219x y += 19、【答案】（1）（x+3）2+（y ﹣6）2=40（2）16+（1）依题意，所求圆的圆心C 为AB 的垂直平分线和直线x+3y ﹣15=0的交点， ∵AB 中点为（1，2）斜率为1，∴AB 垂直平分线方程为y ﹣2=（x ﹣1）即y=﹣x+3（2分）联立，解得，即圆心（﹣3，6），半径（6分）∴所求圆方程为（x+3）2+（y ﹣6）2=40（7分）（2），（8分）圆心到AB 的距离为（9分）∵P 到AB 距离的最大值为（11分）∴△PAB 面积的最大值为（12分20、【答案】（1）0.006a =（2）该企业职工对该部门评分不低于80的概率的估计值为0.4.（3）1()10P A =21、【答案】（1）8π；（2）12．试题解析：（1）集合M 内的点形成的区域面积8S =．因221x y +=的面积1S π=，故所求概率为118S P S π==. （2，即11x y -≤+≤，形成的区域如图中阴影部分所示，面积24S =，所求概率为2212S P S ==. 22、【答案】（1）1322=+y x ；（2）)33(30322±≠=+x y x . 试题分析：（1）根据离心率为36，焦距为22烈方程组，解得,a b ，即可得椭圆方程，进而根据OA OB ⊥求得圆的半径即可；（2）3+=得⎩⎨⎧+=+=,3,32121y y y x x x ，312121-=x x y y ，即032121=+y y x x ，又,13,1322222121=+=+y x y x ，消去2211,,,y x y x 即可. 试题解析：（1）设椭圆方程为)0(12222>>=+b a by a x ，由已知⎪⎪⎩⎪⎪⎨⎧-===,,222,36222c a b c a c 得⎪⎩⎪⎨⎧===.2,1,3c b a ∴椭圆方程为1322=+y x . ①当直线AB 的斜率存在时，设直线AB 为m kx y +=，),(),,(2211y x B y x A ，代入椭圆方程得0)1(36)31(222=-+++m kmx x k .∴222122131)1(3,316km x x k km x x +-=+-=+. ∵OA ⊥OB ，∴0OA OB ⋅=，即22121221212121)()1())((m x x km x x k m kx m kx x x y y x x ++++=+++=+0)316(31)1(3)1(22222=++-⋅++-⋅+=m kkm km k m k ，即033422=--k m . ∵AB 与以原点为圆心的圆相切，∴圆半径12+=k m r ，则431222=+=k m r ，∴圆的方程为4322=+y x . ②当直线AB 的斜率存在时，易知AB 方程为23±=x 满足上述方程. 综上，所求圆的方程为4322=+y x . （2）设),(),,(),,(2211y x B y x A y x P ，由3OP OA OB =+得⎩⎨⎧+=+=,3,32121y y y x x x又直线OA ，OB 的斜率积为31-， ∴312121-=x x y y ，即032121=+y y x x . ∵A ，B 在椭圆上，∴,13,1322222121=+=+y x y x 联立得 ⎪⎪⎪⎩⎪⎪⎪⎨⎧=+=+=++=+=,33,33,03,3,32222212121212121y x y x y y x x y y y x x x 消去2211,,,y x y x ，得30322=+y x . 当OA 斜率不存在时，即01=x ，得3,0,1221±==±=x y y . 此时33±=x ，同理OB 斜率不存在时，33±=x ， ∴P 点的轨迹方程为)33(30322±≠=+x y x .。

四川省宜宾市南溪区第二中学校2018届高三4月月考数学(文)试题

南溪二中高三年级四月月考试题数学(文科)考生作答时，将答案答在答题卡上，在本试卷上答题无效。

考试结束后，将本试卷和答题卡一并交回。

注意事项：1．答题前，考生务必先将自己的姓名、准考证号填写在答题卡上，认真核对条形码上的姓名、准考证号，并将条形码粘贴在答题卡的指定位置上。

2．选择题答案使用2B 铅笔填涂，如需改动，用橡皮擦干净后，再选涂其他答案的标号；非选择题答题时使用0.5毫米的黑色中性（签字）笔或碳素笔书写，字体工整、笔迹清楚。

3．请按照题号在各题的答题区域(黑色线框)内作答，超出答题区域书写的答案无效。

4．保持卡面清洁，不折叠，不破损。

5．做选考题时，考生按照题目要求作答，并用2B 铅笔在答题卡上把所选题目对应的题号涂黑。

一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项符合题目要求 1.已知集合{0,1,2,3,4,5}A =，{1,0,1,2}B =-，则A B =A ．{1,2}B ．{0,1,2} C. {1,0,1}- D ．{0,1} 2.已知i 为虚数单位，则复数34ii-等于 A.43i -- B. 43i -+ C. 43i - D. 43i +3.已知向量(3,1)a =- ，(,2)b x =-，且a ⊥ b ，则x 等于A ．23 B ．23- C ．6- D ．64．已知等差数列{}n a 的公差为2,若431,,a a a 成等比数列, 则3a =A ．10-B ．6-C ．8-D ．4-5.已知双曲线的方程是2212x y -=，则其离心率等于A ．32B C D6．定义在R 上的偶函数)(x f 在[0,)+∞单调递增，且1)2(=-f ，则(2)1f x -≤的x 的取值范围是A ．]2,2[-B ．),2[]2,(+∞--∞C ．),4[]0,(+∞-∞D ．]4,0[7.设,x y 满足24122x y x y x y +≤⎧⎪-≥⎨⎪-≤⎩．则z x y =+的最大值是A ．1B ．73 C ．2 D ．538.如右图所示，网格纸上小正方形的边长为1，粗线画出的是某三棱锥的三视图，则此几何体的体积为A ．43 B ．2 C ．4 D ．23 9．函数f (x )＝2sin(ωx ＋φ)(ω＞0，x R ∈) 的部分图象如图所示，则该函数图象的一个对称中心是 A ．(,0)3πB ．2(,0)3π- C ．4(,0)3π-D ．4(,0)3π 10．阅读如图所示的程序框图,运行相应的程序,输出的s 值等于 A ．40 B ．38 C ．42 D ．4811．周末，某高校一学生宿舍甲,乙,丙,丁四位同学正在做四件不同事情:看书,写信,听音乐,玩游戏，下面是关于他们各自所做事情的一些判断:①甲不在看书,也不在写信； ②乙不在写信,也不在听音乐；③如果甲不在听音乐,那么丁也不在写信； ④丙不在看书,也不写信.若这些判断都是正确的，依据以上判断, 请问乙同学正在做的事情是 A ．玩游戏 B ．写信 C ．听音乐 D ．看书 12．已知F 1，F 2分别是双曲线3x 2－y 2＝3a 2(a ＞0)的左、右焦点，P 是抛物线y 2＝8ax 与双曲线的一个交点，若|PF 1|＋|PF 2|＝12，则抛物线的准线方程为 A ．x ＝－4 B ．x ＝－3 C ．x ＝－2 D ．x ＝－1二、填空题:本大题共4小题，每小题5分13．曲线3()3f x x x =-+在点(1,(1))P f 处的切线方程为 __________. 14．如图是我国三国时期著名数学家赵爽弦图.图中大正方形的面积是34，四个全等直角三角形围成一个小正方形，直角三角形的较短边长为3.现向大正方形内随机抛一粒绿豆，则绿豆落在小正方形内的概率为__________.15．把边长为1的正方形ABCD 沿对角线AC 折起,当以A B C D ，，，四点为顶点的三棱锥体积最大时，此三棱锥的外接球的表面积的大小等于____________.16．已知{}n a 是首项为1的等比数列，数列{}n b 满足21=b ，52=b ，且11()n n n n b b a a ++-=．则数列{}n b 的前n 项和为_____________.三、解答题：解答应写出文字说明，证明过程或演算步骤 17．（本小题满分12分）在ABC ∆中，内角A ，B ，C 所对的边长分别为a ，b ，c ，已知sin sin 2b Ba A=．（Ⅰ）求角A ；（Ⅱ）若b =ABC ∆a 的值． 18．（本小题满分12分）如图，四棱锥P ABCD -中，底面ABCD是边长为2的正方形， E 为AB 的中点，F 为PC 的中点．（Ⅰ）证明：//BF 平面PDE ；（Ⅱ）求三棱锥E BDF -的体积．19．（本小题满分12分）某养殖场的水产品在临近收获时，工人随机从水中捕捞100只，其质量分别在[100,150)，[150,200)，[200,250)，[250,300)，[300,350)，[350,400]（单位：克）中，经统计得频率分CABDPEF布直方图如图所示.（Ⅰ）求这组数据的众数；（Ⅱ）现按分层抽样从质量为[250,300)，[300,350)的水产品中随机抽取6只，再从这6只中随机抽取3只，求这3只水产品中恰有1只在[300,350)内的概率；(Ⅲ)某经销商来收购水产品时，该养殖场现还有水产品共计约10000只要出售，经销商提出如下两种收购方案：方案A：所有水产品以14元/只收购；方案B：对质量低于300克的水产品以10元/只收购，不低于300克的以28元/只收购.通过计算确定养殖场选择哪种方案获利更多？20．（本小题满分12分）已知动点P到定点F(1，0)和到直线x＝2的距离之比为22．设动点P的轨迹为曲线E，过点F作垂直于x轴的直线与曲线E相交于A，B两点．直线l：y＝mx＋n与曲线E交于C，D两点，与AB相交于一点(交点位于线段AB上，且与A，B不重合)．（Ⅰ）求曲线E的方程；（Ⅱ）当直线l与圆x2＋y2＝1相切时，四边形ACBD的面积是否有最大值？若有，求出其最大值及对应的直线l的方程；若没有，请说明理由．21．（本小题满分12分）已知函数f(x)＝ax－1－ln x(a>0).(Ⅰ)求函数f(x)的单调区间；(Ⅱ)若函数f(x)在x＝1处取得极值，对任意x∈(0，＋∞)，f(x)≥bx－2恒成立，求实数b的最大值.请考生在第22, 23题中任选一题作答，如果多做，则按所做的第一题记分.作答时请在答题卡涂上题号.22.（本小题满分10分）选修4-4 坐标系与参数方程已知曲线C 的极坐标方程为 ρ2＝364cos 2θ＋9sin 2θ. (Ⅰ)若以极点为平面直角坐标系的原点，极轴为x 轴的正半轴，建立平面直角坐标系，求曲线C 的直角坐标方程；(Ⅱ) 若P (x ，y )是曲线C 上的一个动点，求3x ＋4y 的最大值． 23.（本小题满分10分）选修4-5 不等式选讲已知函数()212f x x x =++-，集合(){|3}A x f x =<.(Ⅰ)求A ；(Ⅱ) 若,s t A ∈，求证：11t t s s-<-.南溪二中高三年级四月月考试题数学(文科) 参考答案一、选择题答案: BABD CDBA CADC二、填空题答案:13.14.15. 2π16.三、解答题答案：17．解：（Ⅰ）由得………………………………3分又，所以，得，即，所以……分（Ⅱ）由及可得……………………9分又在中，，即，得………………………………12分18.【解析】：（Ⅰ）【证法一】∵取的中点为，连、，∵为的中点，∴．∵为正方形，为的中点，∴，∴．∴四边形是，∴．又∵，故平面．………………………6分【证法二】取的中点为，连、，∵为正方形，为的中点，∴平行且等于，∴．又∵.∴.同理．又∵．∴平面平面，故平面．……………………………6分（Ⅱ）∵为的中点，，∴，∵为正四棱锥，∴在平面的射影为的中点，∵，，∴，∴，∴．……………………………12分19.【解析】：（Ⅰ）该样本的众数为275. ……………………………4分（Ⅱ）抽取的6只水产品中，质量在和内的分别有4只和2只.设质量在内的4只水产品分别为，质量在内的2只水产品分别为. 从这6只水产品中选出3只的情况共有，，，，，，，，，，，，，，，，，，，，共计20种，其中恰有一个在内的情况有，，，，，，，，，，，共计12种，因此概率. ……………………………8分(Ⅲ)方案A ：元；方案B ：低于300克：元，不低于300克：元，总计元.由，故B 方案获利更多，应选B 方案. ……………………………12分20.【解析】：（Ⅰ）设点P (x ，y )，由题意可得，|x －2|（x －1）2＋y2＝22，得2x2＋y 2＝1. ∴曲线E 的方程是2x2＋y 2＝1. ……………………………5分（Ⅱ）设，由条件可得.当m ＝0时，显然不合题意.当m ≠0时，∵直线l 与圆x 2＋y 2＝1相切，∴，得.联立消去y 得,则△，.，当且仅当，即时等号成立，此时代入得.经检验可知，直线和直线符合题意. ………………12分21.【解析】:（Ⅰ）f (x )的定义域为(0，＋∞)，＝a －x 1＝x ax －1.当a >0时，由<0，得0<x <a 1；由>0，得x >a 1，∴f (x )在a 1上递减，在，＋∞1上递增. ……………………………5分(Ⅱ) ∵函数f (x )在x ＝1处取得极值， ∴＝a －1＝0，则a ＝1，从而f (x )＝x －1－ln x ， x ∈(0，＋∞).因此，对任意x ∈(0，＋∞)，f (x )≥bx －2恒成立对任意x ∈(0，＋∞)，1＋x 1－x ln x≥b 恒成立，令g (x )＝1＋x 1－x ln x，则＝x2ln x －2，令＝0，得x ＝e 2，则g (x )在(0，e 2)上递减，在(e 2，＋∞)上递增，∴g (x )min ＝g (e 2)＝1－e21，即b ≤1－e21.故实数b 的最大值是1－e21.……………………………12分22.【解析】：(Ⅰ)由ρ2＝4cos 2θ＋9sin2θ36，得,即，故曲线C 的直角坐标方程.……………………………5分(Ⅱ)∵P(x，y)是曲线C上的一个动点，∴可设，则，其中.∵，∴当时，.………………………10分23.【解析】：(Ⅰ)函数首先画出与的图象，可得不等式解集为：.……………………………5分(Ⅱ)∵，∴.∴∴,故.……………………………10分。

四川省宜宾市南溪区第三初级中学2018届高三数学上学期补习部10月月考试题

四川省宜宾市南溪区第三初级中学2018届高三数学上学期补习部10月月考试题（无答案）考试时间：120分钟试卷分值：150分第Ⅰ卷（选择题）一、选择题（每小题5分，共60分）1. 若集合{2,1,0,1,2}A =--，则集合{|1,}y y x x A =+∈=（）A.{1,2,3}B.{0,1,2}C.{0,1,2,3}D.{1,0,1,2,3}-2．已知函数y=f （x+1）定义域是[﹣2，3]，则y=f （2x ﹣1）的定义域（）A ． [﹣3，7]B ．]25,0[ C ．[﹣5，5]D ． [﹣1，4]3.下列函数中，既是奇函数又是增函数的为（） A. 1y x =+B. 2y x =-C. 1y x=D. ||y x x =4. 已知幂函数y ＝f(x)的图像经过点)21,4(，则f(2)＝( )A.4B ．41C. 2D.22 5.若函数y=x 2-3x-4的定义域为［0,m ］，值域为［-425,-4］，则m 的取值范围( ) A. ［23,3］ B.［23,4］C.(0,]4D.［23,+∞) 6.下列说法正确的是( )A. 命题“0,x R ∃∈使得20230x x ++<”的否定是“2,230x R x x ∀∈++> B. “p q ∧为真命题”是“p q ∨为真命题”的必要不充分条件 C. 若命题:p “,sin cos 2x R x x ∀∈+≤”，则p ⌝是真命题 D. 若,a R ∈则“11a<”是“1a >”的必要不充分条件 7．若定义在闭区间上的连续函数有唯一的极值点，且为极小值，则下列说法正确的是（） A.函数有最小值，但不一定是B. 函数有最大值也可能是C.函数有最小值D. 函数不一定有最小值8．函数f(x)＝2x ＋sin x 的部分图像可能是( )9. 定义在R 上的函数()f x 满足：(1)(1)(1)f x f x f x -=+=-成立，且()f x 在[1,0]-上单调递增，设(3),(2),(2)a f b f c f ===，则a 、b 、c 的大小关系是( )A.c b a >>B.a c b >>C.b c a >>D.a b c >>10．函数()22f x x x =-，()2g x ax =+（0a >），对[]11,2x ∀∈-，[]01,2x ∃∈-，使()()10g x f x =，则a 的取值范围是（）A ．10,2⎛⎤ ⎥⎝⎦B ．[)3,+∞C ．1,32⎡⎤⎢⎥⎣⎦D ．(]0,311．对实数a 和b ，定义运算 “⊗”：⎩⎨⎧>-≤-=⊗1,1,b a b b a a b a 设函数.),1()2()(2R x x x x f ∈-⊗-=若函数c x f y -=)(的图像与x 轴恰有两个公共点，则实数c 的取值范围是 ( ) A ．),2(]1,1(+∞-B.]2,1[]1,2[ --C.]2,1(]1,2( --D ．]1,2[--12．已知函数()f x 在R 上可导，其导函数为()f x '，若()f x '满足()()01f x f x x '->-，22(2)()x f x f x e --=，则下列判断一定正确的是（）A ．(1)(0)f f <B ．3(3)(0)f e f >⋅ C ．(2)(0)f e f >⋅D ．4(4)(0)f e f <⋅第Ⅱ卷（非选择题）二、填空题（每空5分，共20分）13．【文科】函数)32(log )(221-+=x x x f 的递增区间是________________；【理科】 1(ln +1) ex dx =⎰14．当0,1a a >≠时,函数()log (1)1a f x x =-+的图象恒过定点A ，若点A 在直线mx-y+n=0上，则42m n +的最小值是；15．已知函数()|1|2(0xf x a a a =-->,且1a ≠)有两个零点，则a 的取值范围是；16．已知函数f （x ）=1sin )1(22+++x xx ，其导函数为f ´(x)，则--+'+)2018()2018()2018(f f f =-')2018(f 。

四川省宜宾市南溪区2018届高三数学10月月考试题文(无答案)

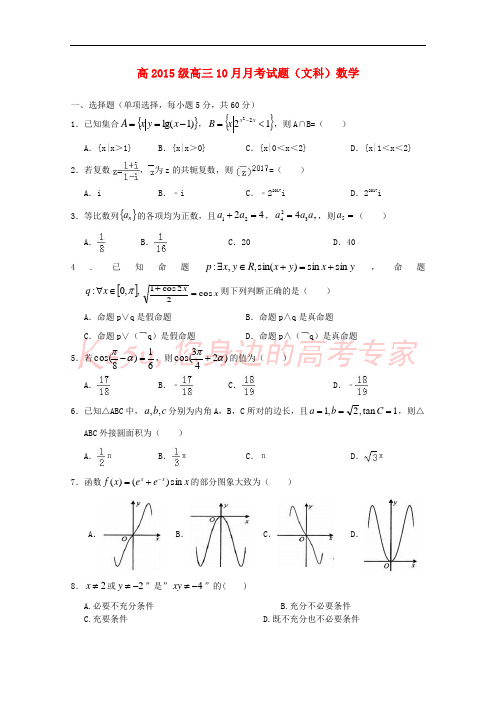
高2015级高三10月月考试题（文科）数学一、选择题（单项选择，每小题5分，共60分） 1．已知集合{})1lg(-==x y x A ，{}1222<=-xx x B ，则A∩B=（）A ．{x|x ＞1}B ．{x|x ＞0}C ．{x|0＜x ＜2}D ．{x|1＜x ＜2}2．若复数，为z 的共轭复数，则=（） A ．iB ．﹣iC ．﹣22017iD ．22017i3．等比数列{}n a 的各项均为正数，且4221=+a a ，73244a a a =，则=5a （）A ．B ．C ．20D ．404．已知命题yx y x R y x p sin sin )sin(,,:+=+∈∃，命题[],,0:π∈∀x q x x co s 22c o s1=+则下列判断正确的是（） A ．命题p ∨q 是假命题B ．命题p ∧q 是真命题C ．命题p ∨（￢q ）是假命题D ．命题p ∧（￢q ）是真命题5．若61)8cos(=-απ，则)243cos(απ+的值为（）A ．B ．﹣C ．D ．﹣6．已知△ABC 中，c b a ,,分别为内角A ，B ，C 所对的边长，且1tan ,2,1===C b a ，则△ABC 外接圆面积为（）A ．πB ．πC ．πD ．π7．函数x e e x f xxsin )()(-+=的部分图象大致为（）A ．B ．C ．D ．8．2x ≠或2y ≠-”是”4xy ≠-”的( ) A.必要不充分条件B.充分不必要条件C.充要条件D.既不充分也不必要条件9．已知函数⎪⎩⎪⎨⎧>+≤-=1,31log 1,)21()(x x x a x f a x ，当21x x ≠时，0)()(2121<--x x x f x f ，则a 的取值范围是（） A ．（0，]B ．[，]C ．（0，]D ．[，]10．已知函数21sin 232cos)(2-+=x xx f ωωR x ∈>),0(ω若)(x f 在区间（π，2π）内没有零点，则ω的取值范围是（） A ．（0，]B ．（0，]∪[，） C ．（0，]D ．（0，]∪[，]11．已知函数13)(23+-=x ax x f ，若)3(),(),(a f a f a f -成公差不为0的等差数列，则过坐标原点作曲线y=f （x ）的切线可以作（） A ．0条B ．1条C ．2条D ．3条12．如图所示，在△ABC 中，AD=DB ，点F 在线段CD 上，设AB =，=， AF =x +y ，则1y 4x 1++的最小值为（） A ．6+22B ．36C ．6+24D ．3+22二、填空题（每小题5分，共20分） 13．已知向量满足，则=______________.14．已知等差数列{}n a 的前n 项和为n S ，若5510=S ，则=+83a a ______________. 15．已知c b a ,,均为正数，且2))((=++c b c a ，则c b a 32++的最小值为______________.16．已知函数xe x xf -=)(（e 为自然对数的底数），1)(+=mx xg （R m ∈），若对于任意的x 1∈[﹣1，2]，总存在x 0∈[﹣1，1]，使得)()(10x f x g = 成立，则实数m 的取值范围为__________.三、解答题（17题为10分，其余每题为12分，共70分）17. 数列{a n }的前n 项和为n S ，n nn a S )12(-=，且a 1=1．（Ⅰ）求数列{a n }的通项公式；（Ⅱ）若n n na b =，求数列{n b }的前n 项和n T ．18.（Ⅰ）求函数()f x 的最小正周期；（Ⅱ）若()0f x m -=在恰有一实根，求m 的取值范围．19. 在ABC ∆中,角A 、B 、C 所对的边分别为a 、b 、c ，且（Ⅰ）求sin B ；（Ⅱ）若D 为AC 边的中点，且1BD =，求ABD ∆面积的最大值.20. 在ABC ∆中，角,,A B C 的对边分别为,,a b c ，（Ⅰ）求角B 的大小；（Ⅱ）若等差数列{}n a 的公差不为零，且B a 2cos 1=1，且248,,a a a 成等比数列，求的前n 项和n S ．21.已知函数()()ln 1f x x a x =+- （Ⅰ）讨论()f x 的单调性；（Ⅱ）当()f x 有最大值，且最大值大于2a-2时，求a 的取值范围。

2017-2018学年四川省宜宾市南溪区第二中学校高三数学上10月月考(文)试题(含答案)

宜宾市南溪区第二中学校高2015级10月阶段性测试文科数学学科试题考试时间120分钟，满分150分。

一、选择题（本题共12小题，共60分）1、设a ， b ， c R ∈，且0b a <<，则（）A. ac bc >B. 22ac bc >C.D. 2、已知点A （1，3），B （4，﹣1），则与向量的方向相反的单位向量是（）A ．（﹣，）B ．（﹣，）C ．（，﹣）D ．（，﹣） 3、函数xx x f 2)(+=的图象可能是（）A. B. C. D.4、在等差数列{}n a 中，若12011,a a 为方程x 2－10x ＋16＝0的两根，则210062010a a a ++=（）A ．10B ．15C ．20D ．405、不等式220ax bx ++>的解集是，则a b -的值等于（） A. －14 B. 14 C. －10 D. 106、等差数列{}n a 的公差为2，若2a ，4a ，8a 成等比数列，则{}n a 的前n 项和n s=（） A.()1n n + B.()1n n - C.()12n n + D.()12n n -7、已知ω>0，πϕ<<0，直线4π=x 和45π=x 是函数f (x )=sin(ωx +φ)图像的两条相邻的对称轴，则φ=（）A.π4B.π3C.π2D.3π48、已知单位向量m 和n 的夹角为60,记a =n -m , 2b =m , 则向量a 与b 的夹角为（）A. 30B.60 C. 120 D.1509、已知α为第二象限角，，则cos 2α=（）10、在△ABC 中，A 、B 、C 所对的边分别为a 、b 、c ，若bcosA+acosB=c 2，a=b=2，则△ABC 的周长为（） A ．7.5B ．7C ．6D ．511、已知函数y= f (x) 的周期为2，当x ∈[]11，-时 f (x) =x 2,那么函数 y = f (x) 的图像与函数y =x lg 的图像的交点共有（） A. 10个 B. 9个 C. 8个 D. 1个12、已知()f x 是定义在区间(0)+∞，上的函数，其导函数为()f x '，且不等式()2()x f x f x '< 恒成立，则（） A.4(1)(2)f f <B.4(1)(2)f f >C.(1)4(2)f f <D.(1)2(2)f f '<二、填空题（本题共4小题，共20分） 13、计算：lg 42lg5+= . 14、已知幂函数)(x f 的图像过点)22,21(，则)4(f = .15、等比数列{a n }的前n 项和为S n ，若S 3+3S 2=0，则公比q = .16、设曲线n+1*y =x,(n N )∈在点（1，1）处的切线与x 轴的交点的横坐标为n x ，令2log n n a x =，则1215a a a +++=… . 17、(12分)等差数列{n a }中，34574,6a a a a +=+=（I ）求{n a }的通项公式；(II)设n b =[n a ]，求数列{n b }的前10项和，其中[x]表示不超过x 的最大整数，如[0.9]=0,[2.6]=218、(12分)已知函数)(1cos 2)62sin()(2R x x x x f ∈-+-=π.（1）求)(x f 的单调递增区间；（2）在△ABC 中，三内角A ，B ，C 的对边分别为a ，b ，c ，已知21)(=A f ， b ，a ，c 成等差数列，且9=⋅，求a 的值.19、 (12分)已知数列{}n a 的前n 项和为n S ，，()*1212,n n S S n n N -=+≥∈. （1）求数列{}n a 的通项公式；（2的前n 项和n T .20、(12分)某花店每天以每枝5元的价格从农场购进若干枝玫瑰花，然后以每枝10元的价格出售.如果当天卖不完，剩下的玫瑰花做垃圾处理.（Ⅰ）若花店一天购进17枝玫瑰花，求当天的利润y (单位：元)关于当天需求量n （单位：枝，n ∈N ）的函数解析式.（Ⅱ）花店记录了100天玫瑰花的日需求量（单位：枝），整理得下表：(1)假设花店在这100天内每天购进17枝玫瑰花，求这100天的日利润（单位：元）的平均数；(2)若花店一天购进17枝玫瑰花，以100天记录的各需求量的频率作为各需求量发生的概率，求当天的利润不少于75元的概率.21.(12分)已知函数()ln ()af x a x x a R x=--∈ (Ⅰ) 若()f x 在其定义域内为单调递减函数，求a 的取值范围；(Ⅱ) 是否存在实数a ，使得当2[e e ]x ∈，时，不等式()0f x >恒成立，如果存在，求a 的取值范围，如果不存在，说明理由（其中e 是自然对数的底数，e ＝2.71828…）.22、[选修4―4：坐标系与参数方程]（10分）在直角坐标系xOy 中，曲线1C 的参数方程为t t y t x (1423⎩⎨⎧+=+-=为参数），以原点O 为极点，x 轴正半轴为极轴（两坐标系取相同的长度单位）的极坐标系中，曲线2C ：θρsin 2=。

2017-2018学年四川省宜宾市南溪区第二中学校高二上学期第15周周考数学试题

2017-2018学年高二数学理15周周考（模拟）一、选择题（60分）1、已知直线l 经过点(2,0)A -与点(5,3)B -，则该直线的倾斜角为（） A ．150° B ．75° C ．135° D ．45°2、2015年11月11日的“双十一”又掀购物狂潮，淘宝网站对购物情况做了一项调查，收回的有效问卷共500000份，其中购买下列四种商品的人数统计如下：服饰鞋帽198000人；家居用品94000人；化妆品116000人；家用电器92000人．为了解消费者对商品的满意度，淘宝网站用分层抽样的方法从中选出部分问卷进行调查，已知在购买“化妆品”这一类中抽取了116人，则在购买“家居用品”这一类中应抽取的问卷份数为（） A ．92 B ．94 C ．116 D ．1183、若直线()120x m y m +++-=和直线280mx y ++=平行，则m 的值为（） A ． 1 B ．2- C ．1或2- D ．23-4、若实数,x y 满足2288280x y x y +--+=，则22x y +的最小值为（）A. 18B. 36-25、若某程序框图如图所示，当输入50时，则该程序运算后输出的结果是 ( )A.5B.6C.7D.86、某市要对两千多名出租车司机的年龄进行调查，现从中随机抽出100名司机，已知抽到的司机年龄都在[)20,45岁之间，根据调查结果得出司机的年龄情况残缺的频率分布直方图如图所示，利用这个残缺的频率分布直方图估计该市出租车司机年龄的中位数．．．大约是（）A ．31.6岁B ．32.6岁C 33.6岁．D ．36.6岁7、下表是降耗技术改造后生产甲产品过程中记录的产量x （吨）与相应的生产能耗y （吨标准煤的几组对应数据，根据表中提供的数据，求出y 关于x 的线性回归方程0.70.35y x =+，那么表中m 的值为（）A.4B.3.15C.4.5D.38、设不等式组⎪⎪⎩⎪⎪⎨⎧≥-≥-≤+022y y x y x 所表示的区域为M ，函数21x y -=的图象与x轴所围成的区域为N ，向M 内随机投一个点，则该点落在N 内的概率为（）A ．π2B ．4π C．8πD ．16π9、如果圆22()()4x a y a -+-=上有且仅有两个点到原点的距离为2，那么实数a 的取值范围为( )A. (-B.C. (-⋃D. (1)(1--⋃ 10、已知直线ax+by=1（其中a ，b 为非零实数），与圆x+y 2=1相交于A ，B 两点，O为坐标原点，且△AOB 为直角三角形，则+的最小值为（）A ．4B ．2C ．5D ．811、已知实数y x ,满足2246120x y x y +-++=，则22x y --的最小值是（）A．5 B．4 C1 D．12、已知正实数,x y 满足22x y +=，则x +的最小值为（） A ．85 B ．45 C ．2 D二、填空题（20分）13、椭圆()2211mx y m +=>的短轴长为2m ,则m = ． 14、如果直线012=--y x 和1+=kx y 互相垂直，则实数k 的值为_____________. 15、从集合{}2,1,1A =--中随机选取一个数记为k ，从集合{}1,1,3B =-中随机选取一个数记为b ，则直线y kx b =+不．经过第四象限的概率为 . 16、已知圆O :x 2 + y 2 = 1,直线x - 2y + 5 = 0上动点P ,过点P 作圆O 的一条切线,切点为A ,则PO PA ⋅的最小值为__________三、解答题（每小题12分）17、已知直线l 经过直线3x+4y ﹣2=0与直线2x+y+2=0的交点P ，且垂直直线2x ﹣y ﹣1=0.（Ⅰ）求直线l 的方程；（Ⅱ）已知直线l 与圆x 2﹣2x+y 2=0相交于A ，B 两点，求弦AB 的长．18、已知圆22:()(2)4(0)C x a y a -+-=>及直线:30l x y -+=．当直线l 被圆C 截得的弦长为22时，求（Ⅰ）a 的值；（Ⅱ）求过点)5,3(并与圆C 相切的切线方程．19、如图，在四棱锥E ﹣ABCD 中，底面ABCD 为正方形，AE ⊥平面CDE ，已知AE=DE=2，F 为线段DE 的中点．（Ⅰ）求证：BE ∥平面ACF ；（Ⅱ）求二面角C ﹣BF ﹣E 的平面角的余弦值．20、如图甲，在平面四边形ABCD 中，已知45A ∠=,90C ∠=,105ADC ∠=,AB BD =,现将四边形ABCD 沿BD 折起，使平面ABD ⊥平面BDC （如图乙），设点E ，F 分别为棱AC ，AD 的中点．（1）证明DC ⊥平面ABC ；（2）求BF 与平面ABC 所成角的正弦值；（3）求二面角B EF A --的余弦值．21、如图,矩形ABCD 所在平面与平面PAD 垂直PA AD ⊥,且2,AD AB E =为BC 上的动点.（1）当E 为BC 的中点时,求证：PE DE ⊥；（2）若PA AB =,在线段BC 上是否存在点E ,使得二面角P ED A --的大小为4π.若存在,确定点E 的位置,若不存在,说明理由.参考答案一、单项选择1、【答案】C2、【答案】B3、【答案】A4、【答案】C5、【答案】B6、【答案】C7、【答案】D8、【答案】B9、【答案】C10、【答案】A11、【答案】A12、【答案】A二、填空题13、【答案】214、【答案】12.15、【答案】2916、【答案】4三、解答题17、【答案】（Ⅰ）2x+y ﹣2=0.（Ⅱ）．试题分析：（Ⅰ）联立两直线方程得到方程组，求出方程组的解集即可得到交点P 的坐标，根据直线l 与2x ﹣y ﹣1=0垂直，设出直线l 的方程，把P 代入即可得到直线l 的方程；（Ⅱ）求出圆心到直线的距离，利用勾股定理，求弦AB 的长．解：（Ⅰ）由，解得，∴P 的坐标是（﹣2，2）．∵所求直线l 与2x ﹣y ﹣1=0垂直，∴可设直线l 的方程为x+2y+m=0. 把点P 的坐标代入得﹣2+2×2+m=0，即m=﹣2. 所求直线l 的方程为2x+y ﹣2=0. （Ⅱ）由题意圆心（1，0），半径r=1. 圆心到直线的距离d=， ∴|AB|=2=．考点：直线与圆的位置关系．18、【答案】（Ⅰ）1=a （Ⅱ）045125=+-y x 或3=x试题分析：（Ⅰ）直线与圆相交时可利用圆心到直线的距离，圆的半径及弦长的一半构成的直角三角形勾股定理可求得a 的值；（Ⅱ）求切线方程可采用待定系数法，设出直线点斜式方程，利用圆心到直线的距离等于圆的半径可得到斜率值，注意验证斜率不存在的直线是否满足要求试题解析：（Ⅰ）依题意可得圆心2),2,(=r a C 半径，则圆心到直线:30l x y -+=的距离21)1(13222+=-++-=a a d由勾股定理可知222)222(r d =+，代入化简得21=+a ，则31-==a a 或，又0>a ，所以1=a（Ⅱ）由（Ⅰ）知圆4)2()1(:22=-+-y x C ，又点)5,3(在圆外∴①当切线方程的斜率存在时，设方程为)3(5-=-x k y由圆心到切线的距离2==r d 可解得125=k ∴切线方程为045125=+-y x ．②当过)5,3(斜率不存在直线方程为3=x 与圆相切．由①②可知切线方程为045125=+-y x 或3=x ．考点：直线与圆相交相切的位置关系19、【答案】1.见详解；2.20、【答案】（1）见解析；（2；（3）17-.试题分析：（1）利用已知的线面垂直关系建立空间直角坐标系，准确写出相关点的坐标，从而将几何证明转化为向量运算.其中灵活建系是解题的关键.（2）证明线面垂直，需证线线垂直，只需要证明直线的方向向量垂直；（3）把向量夹角的余弦值转化为两平面法向量夹角的余弦值;（4）空间向量将空间位置关系转化为向量运算，应用的核心是要充分认识形体特征，建立恰当的坐标系，实施几何问题代数化.同时注意两点：一是正确写出点、向量的坐标，准确运算；二是空间位置关系中判定定理与性质定理条件要完备..试题解析：（1）证明：在图甲中由AB BD =且45A ∠= 得45ADB ∠=,90ABC ∠=即AB BD ⊥在图乙中，因为平面ABD ⊥平面BDC ，且平面ABD 平面BDC ＝BD所以AB ⊥底面BDC ，所以AB ⊥CD ．又90DCB ∠=，得DC ⊥BC ,且AB BC B =所以DC ⊥平面ABC ．（2）解法1：由E 、F 分别为AC 、AD 的中点得EF //CD ，又由（1）知，DC ⊥平面ABC ，所以EF ⊥平面ABC ，垂足为点E 则FBE ∠是BF 与平面ABC 所成的角在图甲中，由105ADC ∠=,得60BDC ∠=,30DBC ∠= 设CD a =则2BD a =,BC =,BF ==,1122EF CD a == 所以在Rt FEB ∆中，sin EF FBE FB ∠=14a ==即BF 与平面ABC．解法2：如图，以B 为坐标原点，BD 所在的直线为x 轴建立空间直角坐标系如下图示，设CD a =，则2,BD AB a ==BC =，AD =可得(0,0,0)B ,(2,0,0)D a ,(0,0,2)A a,3(,0)2C a ，(,0,)F a a ，所以1(,,0)2CD a =,(,0,)BF a a = 设BF 与平面ABC 所成的角为θ 由（1）知DC ⊥平面ABC所以cos()2πθ-=||||CD BF CD BF⋅⋅214a ==即sin 4θ=（3）由（2）知EF ⊥平面ABC ，又因为BE ⊂平面ABC ，AE ⊂平面ABC ，所以FE ⊥BE ，FE ⊥AE ，所以AEB ∠为二面角B EF A --的平面角在AEB ∆中，12AE BE AC ==== 所以cos AEB ∠=222127AE BE AB AE BE +-=-⋅ 即所求二面角B EF A --的余弦为17-．考点：（1）证明直线与平面垂直；（2）利用空间向量解决线面角、二面角问题.21、【答案】（1）证明见解析；（2）E 在线段BC 上距B 点2试题分析：易证PA ⊥平面ABCD ,以A 为原点,,,AB AD AP 所在直线,,x y z 轴,建立空间直角坐标系.（1）计算0PE DE ⋅=可得PE DE ⊥；（2）设BE x =，利用向量法，根据二面角P ED A --的大小为4π可求得2x =试题解析：解：平面PAD ⊥平面ABCD ,平面PAD平面,,ABCD AD PA AD PA =⊥∴⊥平面ABCD ,以A 为原点,,,AB AD AP 所在直线,,x y z 轴,建立空间直角坐标系如图.（1）不妨设AP a =,则()()()0,0,,1,1,0,0,2,0P a E D ,从而()()1,1,,1,1,0PE a DE =-=-,于是()()1,11,1,0110PE DE a =--=-=,,PE DE PE DE ∴⊥∴⊥.（2）设BE x =,则()()()()()0,0,1,1,,0,0,2,0,1,,1,1,2,0P E x D PE x DE x =-=-. 易知向量()0,0,1AP =为平面AED 的一个法向量,设平面PDE 的法向量(),,n a b c =, 则00n PE n DE ⎧=⎪⎨=⎪⎩,即()020a bx c a b x +-=⎧⎪⎨+-=⎪⎩,解得2c b =,令1b =,则2,2c a x ==-,从而()2,1,2n x =-, 依题意2cos 42n APn AP π==,2=,解得12x =（舍去）,12x =所以点E 在线段BC 上距B 点2.【考点】空间向量与立体几何。

四川省宜宾市南溪区第二中学校2017-2018学年高二上学期第3周周考数学试题 Word版含答案

2017-2018学年高二上期第3周数学考试试卷姓名：__________ 班级：__________ 分数：__________（试卷总分130分，考试时间90分钟）一、选择题（每题5分，共60分）1、已知直线l 的倾斜角为60°，则直线l 的斜率为（）A ．1BCD 2、过两点A （1，3），B （4，32）的直线的倾斜角为（） A ．︒30 B.︒60 C.︒120 D.︒150 3、直线013=--y x 的倾斜角α=（）A ．30°B ．60°C ．120°D ．150° 4、直线210x y -+=与直线23y x =+的位置关系是（）A ．平行B ．垂直C ．相交但不垂直D ．重合 5、已知直线的方程是480x y -+=，那么此直线在y 轴上的截距为（） A. 2 B. 8- C.12D. 1 6、过点(1,3)P -且平行于直线24+10x y -=的直线方程为（）A.2+50x y -=B.2+10x y -=C.2+70x y -=D.250x y --= 7、若直线1:260l ax y ++=与直线()22:110l x a y a +-+-=平行，则a =（） A ．2或-1 B ．2 C ．-1 D ．以上都不对8、直线024=-+y mx 与直线052=+-n y x 垂直，垂足为),1(p ，则n 的值为（） A ．12- B ．2- C ．0 D ．109、设点A （2，－3），B （－3，－2），直线l 过点P （1,1）且与线段AB 相交，则l 的斜率k 的取值范围是（） A ．k≥34或k≤－4 B ．－4≤k≤34 C ．－34≤k≤4 D．以上都不对10、直线()()2110x a y a R +++=∈的倾斜角的取值范围是（） A ．0,4π⎡⎤⎢⎥⎣⎦ B ．3,4ππ⎡⎫⎪⎢⎣⎭C ．0,,42πππ⎡⎤⎛⎫ ⎪⎢⎥⎣⎦⎝⎭D ．3,,424ππππ⎡⎫⎡⎫⎪⎪⎢⎢⎣⎭⎣⎭二、填空题（每题5分，共20分）11、与直线10-=x 垂直的直线的倾斜角为．12、经过点(2,1)P --、(3,)Q a 的直线l 与倾斜角是45 的直线平行，则a 的值为．13、对于任给的实数m ，直线l ：5)12()1(-=-+-m y m x m 通过一定点，则该定点坐标为．14、已知两点()()4003 ，，，B A ，动点()y x P ，在线段AB 上运动，则11+-x y 的取值范围是．三、解答题（共60分）15、（12分）已知直线l 经过点（0，﹣2），其倾斜角的大小是60°．（1）求直线l 的方程；（2）求直线l 与两坐标轴围成三角形的面积．16、（12分）三角形的三个顶点是(4,0)B，(0,3)C．A，(6,7)（Ⅰ）求BC边上的高所在直线的方程；（Ⅱ）求BC边上的中线所在直线的方程．（Ⅲ）求线段BC的垂直平分线的方程．P ，直线m经过点P，且在两坐标轴上的截距相等，求直线17、（12分）已知点(2,1)m的方程；18、（12分）已知直线:230m x y --=与直线:30n x y +-=的交点为P ，直线l 过点P 且与,x y 正半轴交于A B 、两点，ABO ∆的面积为4，求直线l 的方程．19、（12分）已知△ABC 的顶点B （﹣1，﹣3），AB 边上的高CE 所在直线的方程为 x ﹣3y ﹣1=0，BC 边上中线AD 所在直线的方程为8x+9y ﹣3=0.求：（1）点A 的坐标；（2）直线AC 的方程．高二上期第3周数学考试试卷（答案）一、选择题（每题5分，共50分）1、【答案】D【解析】当直线的斜率存在时，直线的斜率等于倾斜角的正切值，即360tan tan =︒==αk .故选D ．2、【解析】由题直线经过点A （1，3），B （4，32）两点，则可利用斜率公式为；k ==tan .6k παα=== 3、【答案】A 【解析】直线斜率tan6k παα==∴=4、【答案】A【解析】直线210x y -+= 的斜率12k =,在y 轴上的截距为12b =.直线23y x =+的斜率22k =,在y 轴上的截距为23b =.由两斜率相等可知两直线平行,在y 轴上的截距不等可排除重合.故本题选A ． 5、【答案】A 【解析】试题分析：原方程可化为2,y x =+\直线在y 轴上的截距为2，故选A. 6、【答案】C【解析】试题分析：由平行可得所求直线的斜率为12，∴所求直线方程为13(1)2y x -=+，∴270x y -+=，故选C ． 7、【答案】C【解析】由题意(1)2a a -=，21a a ==-或，当2a =时，1l 方程为2260x y ++=，即30x y ++=，2l 方程为30x y ++=，两直线重合，不合题意，舍去，1a =-时，直线12,l l 的方程分别为260x y -++=，20x y -=，符合题意．所以1a =-．故选C ． 8、【答案】A【解析】直线024=-+y mx 与直线052=+-n y x 垂直，则10,0202==-m m ，直线024=-+y mx 可以写成02410=-+y x ，过点),1(p ，有2,02410-==-+p p ,点)2,1(-又在052=+-n y x 上，则12,0102-==++n n ，选A. 9、【答案】A【解析】根据题意，先表示出PA 的斜率为31=421----,直线PB 的斜率为，那么结合图像可知，过定点的直线的倾斜角为锐角，结合正切函数图像可知，直线l 的斜率为3k k -4 4≥≤或，故选A. 10、【答案】B【解析】直线()()2110x a y a R +++=∈的斜率为211a -+，由于21011a >-≥-+，设倾斜角为α，则0απ≤≤，1tan 0α-≤<，所以34παπ≤<，故选B ．二、填空题（每题5分，共20分）11、【答案】3π【解析】由两条直线垂直的条件，可知与直线10-=x 垂直的直线的斜率为k =3π12、【答案】4【解析】过点()(2)13P Q a --，，，的直线的斜率为132a ++倾斜角为45︒的直线的斜率为1，∴11432a a +=⇒=+． 13、【答案】)4,9(-【解析】把直线方程5)12()1(-=-+-m y m x m 化为5)12(-+=-+y x m y x ，令012=-+y x ，05=-+y x ，联立方程组得：4,9-==y x ，则对于任给的实数m ，直线l ：5)12()1(-=-+-m y m x m 通过一定点)4,9(-. 14、【答案】]3,41[- 【解析】11+-x y 看作点(),P x y 与)1,1(-C 连线斜率,连结AC 的斜率为41-，连结BC 的斜率为3，结合图形可知斜率的取值范围为]3,41[-三、解答题（共70分）15、已知直线l 经过点（0，﹣2），其倾斜角的大小是60°．（1）求直线l 的方程；（2）求直线l 与两坐标轴围成三角形的面积．【答案】（1）．（2）解：（1）因为直线l 的倾斜角的大小为60°，故其斜率为，又直线l 经过点（0，﹣2），所以其方程为y ﹣（﹣2）=x即．（2）由直线l 的方程知它在x 轴、y 轴上的截距分别是、﹣2，所以直线l 与两坐标轴围成三角形的面积．16、三角形的三个顶点是(4,0)A ，(6,7)B ，(0,3)C ．（Ⅰ）求BC 边上的高所在直线的方程；（Ⅱ）求BC 边上的中线所在直线的方程．（Ⅲ）求线段BC 的垂直平分线的方程．【答案】（Ⅰ）32120x y +-=；（Ⅱ）5200x y +-=.（Ⅲ）01923=-+y x 试题解析：（Ⅰ）BC 边所在直线的斜率320637=--=BC k 因为BC 所在直线的斜率与BC 高线的斜率乘积为—1所以BC 高线的斜率为23-又因为BC 高线所在的直线过A （4，0）所以BC 高线所在的直线方程为)4(230--=-x y ，即01223=-+y x（Ⅱ）设BC 中点为M 则中点M （3,5）所以BC 边上的中线AM 所在的直线方程为0205=-+y x （Ⅲ）BC 中点为（3,5），又因为320637=--=BC k因为BC 所在直线的斜率与BC 的垂直平分线的斜率乘积为—1 所以BC 的垂直平分线的斜率为23-．所以BC 的垂直平分线的方程为)3(235--=-x y ，即01923=-+y x17、已知点(2,1)P -，直线m 经过点P ，且在两坐标轴上的截距相等，求直线m 的方程；【答案】20x y +=或1x y +=；试题解析:①当截距为0时，设直线m 方程为y kx =，代入点P 坐标得：12k =-，所以此时直线m 方程为12y x =-，即20x y +=. ②当截距不为0时，设直线m 方程为1x ya a+=，代入点P 坐标得：1a =，所以此时直线m 方程为1x y +=.综上所述，直线m 方程为：20x y +=或1x y +=.18、已知直线:230m x y --=与直线:30n x y +-=的交点为P ，直线l 过点P 且与,x y 正半轴交于A B 、两点，ABO ∆的面积为4，求直线l 的方程．【答案】042=-+y x试题解析：由230,30x y m n x y --=⎧⇒⎨+-=⎩的交点为P (2,1)，方法一：由题可知，直线l 的斜率k 存在，且0k <．则直线1l 的方程为(2)121y k x kx k =-+=-+．令0x =，得120y k =->，令0y =，得210k x k-=>， ∴121(12)42ABO k S k k ∆-=-=，解得12k =-，故l 的方程为11(2)1222y x x =--+=-+，即042=-+y x方法二：由题可知，直线l 的横、纵截距a b 、存在，且00a b >>、，则1:1x yl a b+=，又1l 过点(2,1)，ABO ∆的面积为4，∴211142a b ab ⎧+=⎪⎪⎨⎪=⎪⎩，解得42a b =⎧⎨=⎩，故1l 方程为142x y +=，即即042=-+y x ．19、已知△ABC 的顶点B （﹣1，﹣3），AB 边上的高CE 所在直线的方程为x﹣3y﹣1=0，BC边上中线AD所在直线的方程为8x+9y﹣3=0.求：（1）点A的坐标；（2）直线AC的方程．试题解析：解：（1）∵CE⊥AB，且直线CE的斜率为，∴直线AB的斜率为﹣3，∴直线AB的方程为y+3=﹣3（x+1），即3x+y+6=0由，解得，∴A（﹣3，3）（2）设D（a，b），可得C（2a+1，2b+3）∴，解之得因此D（，﹣1），从而可得C（4，1）∴直线AC的方程为：，化简整理，得2x+7y﹣15=0，即为直线AC的方程。

南溪区高级中学2018-2019学年高三上学期11月月考数学试卷含答案

南溪区高级中学2018-2019学年高三上学期11月月考数学试卷含答案一、选择题1．抛物线y 2=2x 的焦点到直线x﹣y=0的距离是（）A．B．C．D．2．将n 2个正整数1、2、3、…、n 2（n ≥2）任意排成n 行n 列的数表．对于某一个数表，计算某行或某列中的任意两个数a 、b （a ＞b）的比值，称这些比值中的最小值为这个数表的“特征值”．当n=2时，数表的所有可能的“特征值”的最大值为（）A． B． C ．2 D ．33．设a是函数x 的零点，若x 0＞a ，则f （x 0）的值满足（）A ．f （x 0）=0B ．f （x 0）＜0C ．f （x 0）＞0D ．f （x 0）的符号不确定4．直线的倾斜角是（）A．B．C．D．5．某单位安排甲、乙、丙三人在某月1日至12日值班，每人4天．甲说：我在1日和3日都有值班；乙说：我在8日和9日都有值班；丙说：我们三人各自值班的日期之和相等．据此可判断丙必定值班的日期是（） A ．2日和5日 B ．5日和6日C ．6日和11日D ．2日和11日6．设函数F （x ）=是定义在R 上的函数，其中f （x ）的导函数为f ′（x ），满足f ′（x ）＜f （x ）对于x∈R 恒成立，则（） A ．f （2）＞e 2f （0），f B ．f （2）＜e 2f （0），f C ．f （2）＞e 2f （0），fD ．f （2）＜e 2f （0），f7．若f （x ）为定义在区间G 上的任意两点x 1，x 2和任意实数λ（0，1），总有f （λx 1+（1﹣λ）x 2）≤λf （x 1）+（1﹣λ）f （x 2），则称这个函数为“上进”函数，下列函数是“上进”函数的个数是（） ①f （x ）=，②f （x ）=，③f （x ）=，④f （x ）=．A ．4B ．3C ．2D ．18．已知点M （﹣6，5）在双曲线C：﹣=1（a ＞0，b ＞0）上，双曲线C 的焦距为12，则它的渐近线方程为（） A ．y=±x B ．y=±x C ．y=±xD ．y=±x9．设全集U={1，2，3，4，5，6}，设集合P={1，2，3，4}，Q={3，4，5}，则P ∩（∁U Q ）=（）班级_______________ 座号______ 姓名_______________ 分数__________________________________________________________________________________________________________________A ．{1，2，3，4，6}B ．{1，2，3，4，5}C ．{1，2，5}D ．{1，2}10．设双曲线焦点在y 轴上，两条渐近线为，则该双曲线离心率e=（）A ．5B ．C ．D ．11．设S n 为等比数列{a n }的前n 项和，若a 1=1，公比q=2，S k+2﹣S k =48，则k 等于（） A ．7B ．6C ．5D ．412．在“唱响内江”选拔赛中，甲、乙两位歌手的5次得分情况如茎叶图所示，记甲、乙两人的平均得分分别、，则下列判断正确的是（）A ．＜，乙比甲成绩稳定B ．＜，甲比乙成绩稳定C ．＞，甲比乙成绩稳定D ．＞，乙比甲成绩稳定二、填空题13．已知正四棱锥O ABCD -的体积为2，则该正四棱锥的外接球的半径为_________14．如图，一个空间几何体的正视图和侧视图都是边长为2的正三角形，俯视如图是一个圆，那么该几何体的体积是．15．将一张坐标纸折叠一次，使点()0,2与点()4,0重合，且点()7,3与点(),m n 重合，则m n +的值是．16．在复平面内，复数与对应的点关于虚轴对称，且，则____．17．已知x、y之间的一组数据如下：x 0 1 2 3y 8 2 6 4则线性回归方程所表示的直线必经过点．18．如图，E，F分别为正方形ABCD的边BC，CD的中点，沿图中虚线将边长为2的正方形折起来，围成一个三棱锥，则此三棱锥的体积是．三、解答题19．已知集合A={x|＞1，x∈R}，B={x|x2﹣2x﹣m＜0}．（Ⅰ）当m=3时，求；A∩（∁R B）；（Ⅱ）若A∩B={x|﹣1＜x＜4}，求实数m的值．20．已知函数f（x）=a﹣，（1）若a=1，求f（0）的值；（2）探究f（x）的单调性，并证明你的结论；（3）若函数f（x）为奇函数，判断|f（ax）|与f（2）的大小．21．已知m∈R，函数f（x）=（x2+mx+m）e x．（1）若函数f （x ）没有零点，求实数m 的取值范围；（2）若函数f （x ）存在极大值，并记为g （m ），求g （m ）的表达式；（3）当m=0时，求证：f （x ）≥x 2+x 3．22．（本小题满分12分）如图，四棱锥P ABCD -中，底面ABCD 是边长为2的菱形，且60oABC ∠=，侧面PDC 为等边三角形，且与底面ABCD 垂直，M 为PB 的中点．（Ⅰ）求证：PA ⊥DM ；（Ⅱ）求直线PC 与平面DCM 所成角的正弦值．23．（本题满分12分）在如图所示的几何体中，四边形ABCD 为矩形，直线⊥AF 平面ABCD ，AB EF //，12,2====EF AF AB AD ，点P 在棱DF 上.（1）求证：BF AD ⊥；（2）若P 是DF 的中点，求异面直线BE 与CP 所成角的余弦值；（3）若FD FP 31=，求二面角C AP D --的余弦值.24．如图，在五面体ABCDEF中，四边形ABCD是边长为4的正方形，EF∥AD，平面ADEF⊥平面ABCD，且BC=2EF，AE=AF，点G是EF的中点．（Ⅰ）证明：AG⊥平面ABCD；（Ⅱ）若直线BF与平面ACE所成角的正弦值为，求AG的长．南溪区高级中学2018-2019学年高三上学期11月月考数学试卷含答案（参考答案）一、选择题13．11 814．．15．34 516．-217．（，5）．18．．三、解答题19．20．21．22．23．24．。

南溪区高中2018-2019学年上学期高三数学10月月考试题

南溪区高中2018-2019学年上学期高三数学10月月考试题班级__________ 座号_____ 姓名__________ 分数__________一、选择题（本大题共12小题，每小题5分，共60分.每小题给出的四个选项中，只有一项是符合题目要求的.）1．棱长为2的正方体被一个平面截去一部分后所得的几何体的三视图如图所示，则该几何体的表面积为（）A ．B ．18C ．D ．2．已知三棱柱111ABC A B C - 的侧棱与底面边长都相等，1A 在底面ABC 上的射影为BC 的中点，则异面直线AB 与1CC 所成的角的余弦值为（）A B D ．343．若函数()()22f x x πϕϕ⎛⎫=+< ⎪⎝⎭的图象关于直线12x π=对称，且当12172123x x ππ⎛⎫∈-- ⎪⎝⎭，，，12x x ≠时，()()12f x f x =，则()12f x x +等于（）AB ．2D ．44．记集合{}22(,)1A x y x y =+?和集合{}(,)1,0,0B x y x y xy =+３?表示的平面区域分别为Ω1，Ω2，若在区域Ω1内任取一点M （x ，y ），则点M 落在区域Ω2内的概率为（） A ．12p B ．1p C ．2pD ．13p【命题意图】本题考查线性规划、古典概型等基础知识，意在考查数形结合思想和基本运算能力． 5．（文科）要得到()2log 2g x x =的图象，只需将函数()2log f x x =的图象（）A ．向左平移1个单位B ．向右平移1个单位C ．向上平移1个单位D ．向下平移1个单位 6．已知空间四边形ABCD ，M 、N 分别是AB 、CD 的中点，且4AC =，6BD =，则（） A ．15MN << B ．210MN << C ．15MN ≤≤ D ．25MN << 7．设{}n a 是递增等差数列，前三项的和为12，前三项的积为48，则它的首项是（）A ．1B ．2C ．4D ．6 8．在极坐标系中，圆的圆心的极坐标系是( )。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2017-2018学年高三上期第五周测试卷（理科数学）一、选择题(125⨯=60分)1．设集合2{|10},{|2,}x A x x B y y x A =-<==∈，则A B ⋂=（） A. ()0,1 B. ()1,2- C. ()1,+∞ D. 1,12⎛⎫ ⎪⎝⎭2．下列选项中说法正确的是（） A. 若，则B. 若向量满足，则与的夹角为锐角C. 命题“为真”是命题“为真”的必要条件D. “，”的否定是“，”3．i 为虚数单位， ()()211i z i +=-，则z =（）A. 1B. 2C. 2D.4．函数()()21log 121f x x x =-++的定义域为（） A. 1,2⎛⎫-∞ ⎪⎝⎭ B. 1,2⎛⎫+∞ ⎪⎝⎭ C. 11,,22⎛⎫⎛⎫-∞⋃+∞ ⎪ ⎪⎝⎭⎝⎭ D. ()1,11,2⎛⎫-∞-⋃- ⎪⎝⎭5．函数f(x)＝3-x a ＋1(a>0，a≠1)的图象恒过点（） A. (0,1) B. (1,2) C. (2,2) D. (3,2) 6．已知，且f （-2）=10，则f （2）= （）A. -26B. -18C. -10D. 107．已知函数()f x 是定义在R 上的偶函数，且当0x ≥时， ()()ln 1f x x =+，则函数()f x 的大致图象为（）A. B. C. D.8．()f x 是定义在R 上的函数，且()()2f x f x -=，当1x ≥时， ()2log f x x =，则有（） A. ()11232f f f ⎛⎫⎛⎫<< ⎪⎪⎝⎭⎝⎭ B. ()11223f f f ⎛⎫⎛⎫<< ⎪ ⎪⎝⎭⎝⎭C. ()11223f f f ⎛⎫⎛⎫<<⎪ ⎪⎝⎭⎝⎭ D. ()11223f f f ⎛⎫⎛⎫<< ⎪ ⎪⎝⎭⎝⎭9．若函数是上的减函数，则实数的取值范围是（）A.B.C.D.10．已知，则展开式中，项的系数为（）A.B.C.D.11．已知函数()()1324,1{log 1,1x x f x x x --≤=-+>且()2f a =-，则a 等于（）A. 5B. 2C. 8或2D. 812．已知()f x 是定义在R 上且以3为周期的奇函数，当30,2x ⎛⎫∈ ⎪⎝⎭时， ()()2ln 1f x x x =-+，则函数()f x 在区间[]0,6上的零点个数是（）A. 3B. 5C. 7D. 9二、填空题（45⨯=20分）13．随机变量ξ服从正态分布N (1,σ2)，已知P(ξ<0)=0.3，则P(ξ<2)= . 14．已知函数()31f x ax x =++的图像在点()()1,1f 的处的切线过点()2,7，则a = .15．已知奇函数满足的值为 .16．已知函数()2ln f x x x x =+，且0x 是函数()f x 的极值点。

给出以下几个命题： ①010x e <<；②01x e>；③()000f x x +<；④()000f x x +> 其中正确的命题是__________．（填出所有正确命题的序号）三、解答题（本大题共6小题，共70分）17．（本题12分）已知函数，若在区间上有最大值5，最小值2．（1）求的值；（2）若在上是单调函数，求m的取值范围.18．（本题12分）已知函数f（x）=x3﹣3x．（Ⅰ）求函数f（x）的极值；（Ⅱ）若关于x的方程f（x）=k有3个实根，求实数k的取值范围．19．（本题12分）某商场对甲、乙两种品牌的商品进行为期100天的营销活动，为调查者100天的日销售情况，随机抽取了10天的日销售量（单位：件）作为样本，样本数据的茎叶图如图，若日销量不低于50件，则称当日为“畅销日”.（1）现从甲品牌日销量大于40且小于60的样本中任取两天，求这两天都是“畅销日”的概率；列联表，（2）用抽取的样本估计这100天的销售情况，请完成这两种品牌100天销量的22并判断是否有99%的把握认为品牌与“畅销日”天数有关．附：()()()()()22n ad bcKa b c d a c b d-=++++（其中n a b c d=+++）20．（本题12分）某省2016年高中数学学业水平测试的原始成绩采用百分制，发布成绩使用等级制．各等级划分标准如下：85分及以上，记为A等；分数在[70，85）内，记为B等；分数在[60，70）内，记为C等；60分以下，记为D等．同时认定A，B，C为合格，D为不合格．已知某学校学生的原始成绩均分布在[50，100]内，为了了解该校学生的成绩，抽取了50名学生的原始成绩作为样本进行统计，按照[50，60），[60，70），[70，80），[80，90），[90，100]的分组作出样本频率分布直方图如图所示．（Ⅰ）求图中x 的值，并根据样本数据估计该校学生学业水平测试的合格率；（Ⅱ）在选取的样本中，从70分以下的学生中随机抽取3名学生进行调研，用X 表示所抽取的3名学生中成绩为D 等级的人数，求随机变量X 的分布列和数学期望．21．（本题12分）已知函数()()ln 1f x x ax a R =-+∈（1）若函数()f x 的图像在1x =处的切线l 垂直于直线y x =，求实数a 的值及直线l 的方程；（2）求函数()f x 的单调区间；（3）若1x >，求证： ln 1x x <-从22、23题中选做一题22．[选修4—4：坐标系与参数方程]在平面直角坐标系xOy 中，曲线1C 的参数方程为2{22x cos y sin αα==+（α为参数），直线2C的方程为y x =，以O 为极点，以x 轴非负半轴为极轴建立极坐标系.（1）求曲线1C 和直线2C 的极坐标方程；（2）若直线2C 与曲线1C 交于,P Q 两点，求OP OQ ⋅的值.23．选修4-5：不等式选讲设函数()313f x x ax =-++. （1）若1a =，解不等式()4f x ≤；（2）若()f x 有最小值，求实数a 的取值范围.高三上期第五周测试卷（理科数学）答案一、选择题(125⨯=60分)1．【答案】D 【解析】{}{}{}21|10|11,|2,{|2}2x A x x x x B y y x A y y =-<=-<<==∈=<<. 1,12A B ⎛⎫⋂= ⎪⎝⎭.2．【答案】C 【解析】解：,当时，结果不对. ,当两个向量夹角为零角时，向量点积仍为大于零，所以不对., 为真则两者均为真，为真两者有一个为真即可.3．【答案】C【解析】()()()()212121,1111i i i iz i z z ii i i ----====--∴===+++-4．【答案】D 【解析】由函数的性质可得： 120{ 10x x ->+≠，解得12x <且1x ≠-，故()f x 的定义域为： ()1,11,2⎛⎫-∞-⋃- ⎪⎝⎭，故选D. 5．【答案】D 【解析】当x －3＝0，即x ＝3时，＝1；f(3)＝1＋1＝2，故选D.6．【答案】A 【解析】,..,所以.故选A.7．【答案】C 【解析】先作出当0x ≥ 时， 1f x ln x =+（）（）的图象，显然图象经过点（00，），．再作此图象关于y 轴对称的图像，可得函数f x （）在R 上的大致图象，如图C 所示，故选：C ．8．【答案】C 【解析】由()()2f x f x -=，可知()()11f x f x -=+，∴()f x 的图象关于1x =对称．当1x ≥时， ()2log f x x =为增函数，∴1x <时， ()2log f x x =为减函数，∴()11223f f f ⎛⎫⎛⎫<<⎪ ⎪⎝⎭⎝⎭，故选C ．9．【答案】C 【解析】f (x )是R 上的减函数；解得10．【答案】B 【解析】==﹣1，则二项式的展开式的通项公式为T r+1=﹣•，令9﹣2r=3，求得r=3，∴展开式中x 3项的系数为﹣•=﹣，11．【答案】D 【解析】当1a ≤时， ()1242a f a -=-=-，解得2a =，不成立；当1a >时， ()()3log 12f a a =-+=-，解答8a =.综上8a =.故选D.12．【答案】C 【解析】∵当x ∈（0，1.5）时f （x ）=ln （x 2-x+1），令f （x ）=0，则x 2-x+1=1，解得x=1，又∵函数f （x ）是定义域为R 的奇函数， ∴在区间∈[-1.5，1.5]上，f （-1）=-f （1）=0，f （0）=0． ∴f （1.5）=f （-1.5+3）=f （-1.5）=-f （1.5）， ∴f （-1）=f （1）=f （0）=f （1.5）=f （-1.5）=0 又∵函数f （x ）是周期为3的周期函数，则方程f （x ）=0在区间[0，6]上的解有0，1，1.5，2，3，4，4.5，5，6，共9个.二、填空题（45⨯=20分）13．【答案】0.7【解析】随机变量ξ服从正态分布N (1,σ2)，∴曲线关于x =1对称，∴P (ξ<0)=P (ξ>2)=0.3，∴P (ξ<2)=1−0.3=0.7。

14．【答案】1【解析】试题分析：()()()()()()()2'31'131,12:231172f x ax f a f a l y a a x a =+⇒=+=+⇒-+=+-⇒-+()()31211a a =+-⇒=.15．【答案】【解析】∵满足f (x +2)=−f (x )，∴f (x +4)=f (x )，即函数的周期是4，∴f()=16．【答案】①③．【解析】试题分析：因为函数()2ln f x x x x =+，所以，所以．因为，，所以010x e<<，即①正确，②不正确；，即③正确，④不正确．三、解答题（本大题共6小题，共70分）17．试题解析：（I ），所以，在区间上是增函数,即所以(II ），则所以，所以，，即故，的取值范围是18．试题解析：（I ）∵3x 3f x x =（）﹣，∴'311f x x x =+（）（﹣）（），令'0f x =（），解得1x =﹣或1x =，列表如下：当x=﹣1时，有极大值f （﹣1）=2；当x=1时，有极小值f （1）=﹣2．（II ）要f x k =（）有3个实根，由（I ）知： 11f k f （）＜＜（﹣），即22k ﹣＜＜， ∴k 的取值范围是（﹣2，2）．19．试题解析：（1）由题意知，甲品牌日销量大于40且小于60的样本中畅销日有三天，分别记为1a ， 2a ， 3a ，非畅销日有三天，分别记为1b ， 2b ， 3b .从中任取2天的所有结果有： {}12,a a ， {}13,a a ， {}11,a b ， {}12,a b ， {}13,a b ， {}23,a a ，{}21,a b ， {}22,a b ， {}23,a b ， {}31,a b ， {}32,a b ， {}33,a b ， {}12,b b ， {}13,b b ， {}23,b b 共15个.根据题意，这些基本事件的出现是等可能的.其中两天都是畅销日的结果有： {}12,a a ， {}13,a a ， {}23,a a 共3个，所以两天都是畅销日的概率31155P ==. （2）()2220050703050256.635801201001003K ⨯-⨯==>⨯⨯⨯，所以有99%的把握认为品牌与“畅销日”天数有关. 20．试题解析：（Ⅰ）由题意可知，10x ＋0.012×10＋0.056×10＋0.018×10＋0.010×10＝1， ∴x＝0.004．∴合格率为1－10×0.004＝0.96．（Ⅱ）样本中C 等级的学生人数为0.012×10×50＝6，而D 等级的学生人数为0.004×10×50＝2．∴随机抽取3人中，成绩为D 等级的人数X 的可能取值为0，1，2， ∴()363820505614C P X C ====，()122638301515628C C PX C ====，()2126386325628C C P X C ====， ∴X 的分布列为数学期望()153213122828284E X =⨯+⨯== 21．试题解析：（1） ()()ln 1f x x ax a R =-+∈，定义域为()0,+∞， ∴ ()1f x a x '=- ∴函数()f x 的图像在1x =处的切线l 的斜率()11k f a ='=-切线l 垂直于直线y x =， ∴ 11a -=-， 2a ∴=∴ ()ln 21f x x x =-+， ()11f =-， ∴切点为()1,1-∴切线l 的方程为()11y x +=--，即0x y +=。