2018年312真题及答案

合集下载

2018年特岗中学美术真题【云南粉笔教育】

第3页（共11页）
中学美术试卷
第4页（共11页）
云南粉笔教育（一支粉笔三尺讲台）面授
编号： 312
教师资格：笔试不过全额退；面试不过双倍退！
”
微信18787171727 QQ群128466001资料下载
五、作品分析题（本大题共2小题，每小题5分，共10分）
00000000000000000 答0000000000000000 00000000000 000000 线0000000000000000000000 题 l ！封 TIll 密 t 线
六、论述题（本大题共1小题，共18分）
31.小李是东部地区某高校美术专业的本科毕业生，通过报考中央特岗计划教师招聘考试来到西部某县级市一中学教授美术。凭借自己优异的专业能力以及精实认真的工作态度，她，很快在学校里得到了各方面的认可。然而日复一日，她逐渐习惯于自己最初所构建的教学规范，工作目标逐渐模糊，热情递减，疏忽了对于学生在美术方面创新能力的指导，甚至形成了无效教学。面对这一情况，请从美术教学的角度分析出现此问题的原因，并思考解决之道。图5-2
云南粉笔教育（一支粉笔三尺讲台）面授
编号：312
教师资格：笔试不过全额退；面试不过双倍退！
微信18787171727 QQ群128466001资料下载
3.具体说来，一种色彩可以造成人的l�J［＼两方面联想？
00000000000000000 答0000000000000000 题00000000000000000 0000000000000000 000000 线 ’密 t 封线
“ 一
）
、单项选择题（在每小题的4个备选答案中，选出个符合题意的正确答案，并将其代码填写在题干后括号内。本大题共10小题，每小题1分，共10分）

2018年高考真题北京卷文综地理试题解析(解析版)详细答案

2018年高考真题北京卷文综地理试题解析(解析版)详细答案2018年普通高等学校招生全国统一考试文科综合能力测试地理（北京卷）共分为两部分，第一部分为选择题，共35小题，每小题4分，共140分。

第二部分为非选择题，共5大题，共160分。

考试时长为150分钟。

考生必须将答案填写在答题卡上，试卷上的作答无效。

考试结束后，考生必须将试卷和答题卡一并交回。

第一部分中的第一小题是关于川藏铁路成都至雅安段的问题。

根据图1，考生需要回答与成都相比，拉萨的哪个特点是正确的。

选项A表示日出早，白昼长，选项B表示正午太阳高度角小，选项C表示海拔高，日照强，选项D表示大气逆辐射强。

正确答案为选项C，因为拉萨地处青藏高原，海拔高，空气稀薄，大气对太阳辐射的削弱作用弱，日照强，晚上大气逆辐射弱。

而成都地处四川盆地，盆地地形，多阴雨天气，太阳辐射弱，大气逆辐射强。

第一部分中的第二小题是关于图示区域的问题。

考生需要根据图1回答区域的特点。

选项A表示地处板块的生长边界，选项B表示河流的流向自西向东，选项C表示自然景观为高寒荒漠，选项D表示跨地势第一、二级阶梯。

正确答案为选项D，因为图示区域跨越了地势的第一和第二级阶梯。

第一部分中的第三小题是关于川藏铁路开通后的问题。

考生需要根据图1回答哪些选项是正确的。

选项①表示缓解青藏铁路运输压力，选项②表示改善西藏物资供应，选项③表示消除区域内灾害的影响，选项④表示促进地域文化交流。

正确答案为选项B，因为川藏铁路开通后，增加了进藏通道，可以缓解青藏铁路运输压力，改善西藏物质供应，促进西藏和区外的文化交流和联系，但不能够消除区域内灾害的影响。

第一部分中的第四小题是关于图2的地质平面示意图的问题。

考生需要根据图2回答哪个选项是正确的。

选项A表示甲处的物质主要来源于地壳，选项B表示断层发生在花岗岩形成之后，选项C表示岩浆侵入可能导致乙处岩石变质，选项D表示丙处的溶洞景观由岩浆活动造成。

正确答案为选项C，因为根据图2，岩浆侵入可能导致乙处岩石变质。

2018年高考真题全国卷分类汇编(含答案)

2018年高考真题全国卷分类汇编（含答案）集合1.（全国1理）已知集合，则=A C R（）A ．B ．C ．D ．解答：或，则.选B2．（全国1文）已知集合{}02A =，，{}21012B =--，，，，，则A B =I （） A ．{}02，B ．{}12，C ．{}0D ．{}21012--，，，，解答：，选A.3．（全国2理）已知集合，则中元素的个数为（）A ．9B ．8C ．5D ．4解答：，，，，，，当时，，，；当时，，，；当时，，，；所以共有9个，选A ．4.（全国2文）已知集合，，则（） A ．B ．C ．D ．解答：，，，选C ．5．（全国3理）已知集合，，则（） A ． B ．C ．D ．解答：∵{|10}{|1}A x x x x =-≥=≥，{0,1,2}B =，∴{1,2}A B =I .选C. 6．（全国3文）已知集合，，则（） A ． B ． C ． D ．解答：∵{|10}{|1}A x x x x =-≥=≥，{0,1,2}B =，∴{1,2}A B =I .选C.复数1．（全国1文理）设，则（） A ． B ． C ． D解答：，∴，∴选C. 2．（全国2理）（） A ． B ．C ．D ．解答：，选D ．{}220A x x x =-->{}12x x -<<{}12x x -≤≤}{}{|1|2x x x x <->U }{}{|1|2x x x x ≤-≥U {|2A x x =>1}x <-{|12}R C A x x =-≤≤{0,2}A B ⋂=(){}223A x y xy x y =+∈∈Z Z ，≤，，A 223x y +≤Q 23x ∴≤x ∈Z Q 1x ∴=-011x =-1y =-010x =1y =-011x =-1y =-01{}1,3,5,7A ={}2,3,4,5B =A B =I {}3{}5{}3,5{}1,2,3,4,5,7{}1,3,5,7A =Q {}2,3,4,5B ={}3,5A B ∴=I {}|10A x x =-≥{}012B =，，A B =I {}0{}1{}12，{}012，，{|10}A x x =-≥{0,1,2}B =A B =I {0}{1}{1,2}{0,1,2}1i2i 1i z -=++||z =0121121i z i i i-=+=+1z =12i12i +=-43i 55--43i 55-+34i 55--34i 55-+()212i 12i 34i 12i 55++-+==-Q3．（全国2文）（）A ．B ．C ．D ．解答：，选D ．4．（全国3文理）（）A ．B ．C ．D ．解答：2(1)(2)23i i i i i +-=+-=+，选D.平面向量1．（全国1文理）在中，为边上的中线，为的中点，则（）A ．B ．C ．D ．解答：.2．（全国2文理）已知向量，满足，，则（）A ．4B ．3C ．2D ．0 解答：因为，所以选B ．3．（全国3文理）已知向量，，．若，则________．解答：2(4,2)a b +=r r ，∵//(2)c a b +r r r ，∴1240λ⨯-⨯=，解得12λ=.函数1．（全国1理）已知函数．若g （x ）存在2个零点，则a 的取值范围是（） A ．[–1，0） B ．[0，+∞） C ．[–1，+∞） D ．[1，+∞）解答：∵存在个零点，即与有两个交点，的图象如下：要使得与有两个交点，则有即，∴选C.2．（全国1文）设函数()201 0x x f x x -⎧=⎨>⎩，≤，，则满足()()12f x f x +<的x 的取值范围是（）A ．(]1-∞-，B ．()0+∞，C ．()10-，D ．()0-∞，解答：取，则化为，满足，排除；取，则化为，满足，排除，选.()i 23i +=32i -32i +32i --32i -+()2i 23i 2i 3i 32i +=+=-+()()1i 2i +-=3i --3i -+3i -3i +ABC △AD BC E AD EB =u u u r3144AB AC -u u u r u u u r 1344AB AC -u u u r u u u r 3144AB AC +u u u r u u u r 1344AB AC +u u ur u u u r 11131()22244EB AB AE AB AD AB AB AC AB AC =-=-=-⋅+=-u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u ur u u u r a b ||1=a 1⋅=-a b (2)⋅-=a a b ()()222221213⋅-=-⋅=--=+=a a b a a b a ()=1,2a ()=2,2-b ()=1,λc ()2∥c a +b λ=e 0()ln 0x x f x x x ⎧≤=⎨>⎩，，，，()()g x f x x a =++()()g x f x x a =++2()y f x =y x a =--)(x f y x a =--)(x f 1a -≤1a ≥-12x =-1()(1)2f f <-,A B 1x =-(0)(2)f f <-C D3．（全国1文）已知函数()()22log f x x a =+，若()31f =，则a =________．解答：可得，∴，.4．（全国2文理）已知是定义域为的奇函数，满足．若，则（）A ．B ．0C ．2D ．50解答：因为是定义域为的奇函数，且，所以，，，因此，，，，从而，选C ．5．（全国3理）设，，则（）A ．B ．C ．D ．解答：∵0.2log 0.3a =，2log 0.3b =，∴0.31log 0.2a =，0.31log 2b=， ∴0.311log 0.4a b +=，∴1101a b <+<即01a b ab+<<，又∵0a >，0b <，∴0ab a b <+<，选B.6．（全国3文）下列函数中，其图像与函数的图像关于直线对称的是（） A ． B ． C ． D ．解答：()f x 关于1x =对称，则()(2)ln(2)f x f x x =-=-.选B.7．（全国3文）已知函数，，则________．解答：())ln1()f x x x R -=+∈，()())1)1f x f x x x +-=+++22ln(1)22x x =+-+=， ∴()()2f a f a +-=，∴()2f a -=-.导数1．（全国1文理）设函数.若为奇函数，则曲线在点处的切线方程为（） A ．B ．C ．D ．解答：∵为奇函数，∴，即，∴，∴，∴切线方程为：，∴选D.2．（全国2理）曲线在点处的切线方程为__________．解答：，，． 3．（全国2文）曲线在点处的切线方程为__________．解答：由，得，则曲线在点处的切线的斜率为，则所求切线方程为，即．2log (9)1a +=92a +=7a =-()f x (,)-∞+∞(1)(1)f x f x -=+(1)2f =(1)(2)(3)(50)f f f f ++++=…50-()f x (),-∞+∞()()11f x f x -=+()()11f x f x +=--()()()311f x f x f x ∴+=-+=-4T ∴=()()()()()()()()()()1235012123412f f f f f f f f f f ++++=+++++⎡⎤⎣⎦L ()()()()3142f f f f =-=-Q ，()()()()12340f f f f ∴+++=()()()()22220f f f f =-=-∴=Q ()()()()()1235012f f f f f ++++==L 0.2log 0.3a =2log 0.3b =0a b ab +<<0ab a b <+<0a b ab +<<0ab a b <<+ln y x =1x =ln(1)y x =-ln(2)y x =-ln(1)y x =+ln(2)y x =+())1f x x =+()4f a =()f a -=32()(1)f x x a x ax =+-+()f x ()y f x =(0,0)2y x =-y x =-2y x =y x =()f x ()()f x f x -=-1a =3()f x x x =+'(0)1f =y x =2ln(1)y x =+(0,0)21y x '=+Q 2201k ∴==+2y x ∴=2ln y x =(1,0)()2ln y f x x ==()2f x x'=2ln y x =()1,0()12k f ='=()021y x -=-22y x =-4．（全国2文理）函数的图像大致为（）解答：，，为奇函数，舍去A ，，舍去D ；，，，所以舍去C ；选B ．5．（全国3文理）函数的图像大致为（）解答：当0x =时，2y =，可以排除A 、B 选项；又因为3424()(22y x x x x x '=-+=-+-，则()0f x '>的解集为(,)(0,)22-∞-U ，()f x单调递增区间为(,2-∞-，(0,)2；()0f x '<的解集为(()22-+∞U ，()f x单调递减区间为(,0)2-，)2+∞.结合图象，可知D 选项正确.6.（全国3理）曲线在点处的切线的斜率为，则________．解答：(1)x xy ae ax e =+，则(0)12f a '=+=-，所以3a =-.()2e e x xf x x --=0x ≠Q ()()2ee xxf x f x x ---==-()f x ∴()11e e 0f -=->Q ∴()()()()()243e e e e 22e 2e xx x x x xx xx x f x xx---+---++='=Q 2x ∴>()0f x '>422y x x =-++()1e xy ax =+()01，2-a =7．（全国1理）已知函数．（1）讨论的单调性；（2）若存在两个极值点，证明：．解答：（1）①∵，∴，∴当时，，，∴此时在上为单调递增. ②∵，即或，此时方程两根为，当时，此时两根均为负，∴在上单调递减.当时，，此时在上单调递减，在上单调递增，在上单调递减.∴综上可得，时，在上单调递减；时，在，上单调递减，在上单调递增.（2）由（1）可得，两根得，，令，∴，.∴，要证成立，即要证成立，∴，即要证() 令，可得在上为增函数，∴，∴成立，即成立. 8．（全国1文）已知函数()e ln 1xf x a x =--．（1）设2x =是()f x 的极值点，求a ，并求()f x 的单调区间；（2）证明：当1ea ≥时，()0f x ≥．1()ln f x x a x x=-+()f x ()f x 12,x x ()()12122f x f x a x x -<--1()ln f x x a x x =-+221'()x ax f x x-+=-22a -≤≤0∆≤'()0f x ≤()f x (0,)+∞0∆>2a <-2a >210x ax -+=12x x ==2a <-'()f x (0,)+∞2a >0∆>()fx ()fx ()fx )+∞2a ≤()f x (0,)+∞2a >()fx)+∞()fx 210x ax -+=12,x x 2a >1212,1x x a x x +=⋅=120x x <<121x x =1211221211()()ln (ln )f x f x x a x x a x x x -=-+--+21122()(ln ln )x x a x x =-+-12121212()()ln ln 2f x f x x x a x x x x --=-+⋅--1212()()2f x f x a x x -<--1212ln ln 1x x x x -<-1122212ln 0(1)xx x x x x x -+<>-2221212ln 0x x x x x --+∴<-22212ln 0x x x --+>21x >1()2ln (1)g x x x x x=--+>()g x (1,)+∞()(1)0g x g >=1212ln ln 1x x x x -<-1212()()2f x f x a x x -<--解答：（1）定义域为，.∵是极值点，∴，∴.∵在上增，，∴在上增. 又在上减，∴在上增.又， ∴当时，，减；当时，，增.综上，，单调增区间为，单调减区间为.（2）∵，∴当时有，∴. 令，.，同（1）可证在上增，又，∴当时，，减；当时，，增. ∴，∴当时，.9．（全国2理）已知函数．（1）若，证明：当时，；（2）若在只有一个零点，求．解答：（1）当时，等价于，设函数，则，当时，，所以在单调递减，而，故当时，，即．（2）设函数，在只有一个零点当且仅当在只有一个零点．当时，，没有零点；当时，．当时，；当时，．在单调递减，在单调递增．故是在的最小值． ①若，即，在没有零点；②若，即，在只有一个零点；③若，即，由于，所以在有一个零点，()f x (0,)+∞1()xf x ae x '=-2x =()f x (2)0f '=2211022ae a e-=⇒=x e (0,)+∞0a >xae (0,)+∞1x(0,)+∞()f x '(0,)+∞(2)0f '=(0,2)x ∈()0f x '<()f x (2,)x ∈+∞()0f x '>()f x 212a e=(2,)+∞(0,2)0x e ≥1a e ≥11x x x ae e e e-≥⋅=1()ln 1ln 1x x f x ae x e x -=--≥--1()ln 1x g x e x -=--(0,)x ∈+∞11()x g x e x -'=-()g x '(0,)+∞111(1)01g e -'=-=(0,1)x ∈()0g x '<()g x (1,)x ∈+∞()0g x '>()g x 11min ()(1)ln111010g x g e -==--=--=1a e≥()()0f x g x ≥≥2()e x f x ax =-1a =0x ≥()1f x ≥()f x (0,)+∞a 1a =()1f x ≥()21e 10xx -+-≤()()21e 1x g x x -=+-()()()2221e 1e x xg'x x x x --=--+=--1x ≠()0g'x <()g x ()0,+∞()00g =0x ≥()0g x ≤()1f x ≥()21e xh x ax -=-()f x ()0,+∞()h x ()0,+∞0a ≤()0h x >()h x 0a >()()2e xh x ax x -'=-()0,2x ∈()0h'x <()2,x ∈+∞()0h'x >()h x ∴()0,2()2,+∞()2421e ah =-()h x [)0,+∞()20h >2e 4a <()h x ()0,+∞()20h =2e 4a =()h x ()0,+∞()20h <2e 4a >()01h =()h x ()0,2由（1）知，当时，，所以．故在有一个零点，因此在有两个零点．综上，在只有一个零点时，．10．（全国2文）已知函数．（1）若，求的单调区间；（2）证明：只有一个零点．解答：（1）当时，，．令解得或当时，；当时，．故在，单调递增，在单调递减．（2）由于，所以等价于．设=，则，仅当时，所以在单调递增，故至多有一个零点，从而至多有一个零点．又，，故有一个零点．综上，只有一个零点．11．（全国3理）已知函数．（1）若，证明：当时，；当时，；（2）若是的极大值点，求．解答：（1）若0a =时，()(2)ln(1)2(1)f x x x x x =++->-，∴1()ln(1)(2)21fx x x x '=+++-+1ln(1)11x x =++-+. 令1()ln(1)11h x x x =++-+， ∴2211()1(1)(1)x h x x x x '=-=+++. ∴当0x >时，()0h x '>，()h x 在(0,)+∞上单调递增，当10x -<<时，()0h x '<，()h x 在(1,0)-上单调递减. ∴min ()(0)ln1110h x h ==+-=， ∴()0f x '≥恒成立，∴()f x 在(1,)-+∞上单调递增，又(0)2ln100f =-=，∴当10x -<<时，()0f x <；当0x >时，()0f x >.0x >2e x x >()()()33324421616161411110e 2e a a a a a h a a a =-=->-=->()h x ()2,4a ()h x ()0,+∞()f x ()0,+∞2e 4a =()()32113f x x a x x =-++3a =()f x ()f x 3a =()3213333f x x x x --=-()263x x f x -'-=()0f x '=3x =-3x =+(3–,x -∈∞U ()3++∞()0f x '=(3x -∈+()0f x '<()f x (–,3∞-()3++∞(3-+210x x ++>()0f x =32301x a x x -=++()g x 3231x a x x -++()()()22222310x x x x x g x ++++'=≥0x =()0g x '=()g x ()–∞+∞，()g x ()f x ()22111631260366a a a f a ⎛⎫-+-=--- ⎪⎝⎭=<-()03131f a +=>()f x ()f x ()()()22ln 12f x x ax x x =+++-0a =10x -<<()0f x <0x >()0f x >0x =()f x a（2）21()(21)ln(1)11ax f x ax x x +'=+++-+， 22212(1)1()2ln(1)01(1)ax ax x ax f x a x x x ++--''=+++≤++，222(1)ln(1)(21)(1)210a x x ax x ax ax +++++++-≤， 222(1)ln(1)340a x x ax ax x +++++≤， 22[2(1)ln(1)34]a x x x x x ++++≤-.设22()2(1)ln(1)34h x x x x x =++++，∴()4(1)ln(1)2(1)64h x x x x x '=++++++，(0)60h '=>，(0)0h =， ∴在0x =邻域内，0x >时，()0h x >，0x <时，()0h x <.0x >时，222(1)ln(1)34xa x x x x -≤++++，由洛必达法则得16a ≤-，0x <时，222(1)ln(1)34xa x x x x -≥++++，由洛必达法则得16a ≥-，综上所述，16a =-.12．（全国3文）已知函数．（1）求曲线在点处的切线方程；（2）证明：当时，．解答：（1）由题意：()21xax x f x e +-=得222(21)(1)22()()x x x x ax e ax x e ax ax x f x e e +-+--+-+'==，∴2(0)21f '==，即曲线()y f x =在点()0,1-处的切线斜率为2，∴(1)2(0)y x --=-，即210x y --=；（2）证明：由题意：原不等式等价于：1210x e ax x +++-≥恒成立；令12()1x g x e ax x +=++-，∴1()21x g x e ax +'=++，1()2x g x e a +''=+，∵1a ≥，∴()0g x ''>恒成立，∴()g x '在(,)-∞+∞上单调递增，∴()g x '在(,)-∞+∞上存在唯一0x 使0()0g x '=，∴010210x e ax +++=，即01021x e ax +=--，且()g x 在0(,)x -∞上单调递减，在0(,)x +∞上单调递增，∴0()()g x g x ≥.又01220000000()1(12)2(1)(2)x g x eax x ax a x ax x +=++-=+--=+-，111()1ag e a -'-=-，∵1a ≥，∴11011a e e -≤-<-，∴01x a≤-，∴0()0g x ≥，得证.综上所述：当1a ≥时，()0f x e +≥.21()e xax x f x +-=()y f x =(0,1)-1a ≥()e 0f x +≥三角函数1.（全国1理）已知函数，则的最小值是_____________．解答：∵，∴最小正周期为，∴，令，即，∴或.∴当，为函数的极小值点，即或,当∴，， ∴最小值为. 2．（全国1文）已知函数()222cos sin 2f x x x =-+，则（）A ．()f x 的最小正周期为π，最大值为3B ．()f x的最小正周期为π，最大值为4 C ．()f x 的最小正周期为2π，最大值为3 D ．()f x 的最小正周期为2π，最大值为4解答：， ∴最小正周期为，最大值为.3．（全国1文）已知角α的顶点为坐标原点，始边与x 轴的非负半轴重合，终边上有两点()1A a ，，()2B b ，，且2cos 2α=，则a b -=（）A ．15BCD ．1解答：由可得，化简可得；当时，可得，，即，此时；当时，仍有此结果. 4．（全国1文）△ABC 的内角A B C ，，的对边分别为a b c ，，，已知sin sin 4sin sin b C c B a B C +=，2228b c a +-=，则△ABC 的面积为________．解答：根据正弦定理有：，∴，∴.∵，∴，∴，∴.5．（全国2文理）在中，，，，则（） A ．BCD ．()2sin sin2f x x x =+()f x ()2sin sin 2f x x x =+()f x 2T π=2'()2(cos cos 2)2(2cos cos 1)f x x x x x =+=+-'()0f x =22cos cos 10x x +-=1cos 2x =cos 1x =-1cos 2=3x π=53x π=cos 1,x =-x π=5()3f π=()3f π=(0)(2)0f f π==()0f π=()f x 222()2cos (1cos )23cos 1f x x x x =--+=+π422cos22cos 13αα=-=222225cos 1cos 6sin cos tan 1ααααα===++tan α=tan α=1a =2b =a =b =5a b -=tan 5α=-sin sin sin sin 4sin sin sin B C C B A B C +=2sin sin 4sin sin sin B C A B C =1sin 2A =2228b c a +-=2224cos 2b c a A bc bc +-===bc =1sin 2S bc A ==ABC △cos2C =1BC =5AC =AB =解答：，，A ．6．（全国2理）若在是减函数，则的最大值是（）A ．B ．C ．D ．解答：因为，所以由得，因此，，，，从而的最大值为，选A ．7．（全国2文）若在是减函数，则的最大值是（）A ．B ．C ．D ．解答：因为，所以由，得，，因此，，从而的最大值为，选C ．8．（全国2理）已知，，则__________．解答：，，，，，因此．9.（全国2文）已知，则__________．解答：，解方程得． 10．（全国3文理）若，则（）A ．B ．C ．D ．解答：227cos 212sin199αα=-=-=.选B.11．（全国3文理）的内角的对边分别为，，，若的面积为，则（） 223cos 2cos 12125C C =-=⨯-=-⎝⎭Q 22232cos 125215325c a b ab C ⎛⎫∴=+-=+-⨯⨯⨯-= ⎪⎝⎭c ∴=()cos sin f x x x =-[,]a a -a π4π23π4π()cos sin 4f x x x x π⎛⎫=-=+ ⎪⎝⎭()022,4k x k k π+π≤+≤π+π∈Z ()322,44k x k k ππ-+π≤≤+π∈Z []π3π,,44a a ⎡⎤-⊂-⎢⎥⎣⎦π,4a a a ∴-<-≥-3π4a ≤π04a ∴<≤a π4()cos sin f x x x =-[0,]a a π4π23π4π()cos sin 4f x x x x π⎛⎫=-=+ ⎪⎝⎭0224k x k π+π≤+≤π+π()k ∈Z 32244k x k ππ-+π≤≤+π()k ∈Z []30,,44a ππ⎡⎤⊂-⎢⎥⎣⎦04a 3π∴<≤a 43πsin cos 1αβ+=cos sin 0αβ+=sin()αβ+=sin cos 1αβ+=Q cos sin 0αβ+=()()221sin cos 1αα∴-+-=1sin 2α∴=1cos 2β=()22111111sin sin cos cos sin cos 1sin 1224442αβαβαβαα+=+=⨯-=-+=-+=-5π1tan()45α-=tan α=5tan tan5tan 114tan 541tan 51tan tan 4αααααπ-π-⎛⎫-=== ⎪π+⎝⎭+⋅3tan 2α=1sin 3α=cos2α=897979-89-ABC △A B C ，，a b c ABC △2224a b c +-C =解答：2222cos 1cos 442ABC a b c ab C S ab C ∆+-===，又1sin 2ABC S ab C ∆=，故tan 1C =，∴4C π=.选C.12（全国3理）．函数在的零点个数为________．解答：由()cos(3)06f x x π=+=，有3()62x k k Z πππ+=+∈，解得39k x ππ=+，由039k πππ≤+≤得k 可取0,1,2，∴()cos(3)6f x x π=+在[0,]π上有3个零点.13．（全国3文）函数的最小正周期为（）A ．B ．C ．D ．解答：22222sin tan sin cos 1cos ()sin cos sin 2sin 1tan sin cos 21cos x x x x x f x x x x x x x x x=====+++，∴()f x 的周期22T ππ==.选C. 14．（全国1理）在平面四边形中，，，，.（1）求；（2）若，求.解答：（1）在中，由正弦定理得：,∴, ∵,∴. （2）,∴，∴,∴,∴.∴. ()πcos 36f x x ⎛⎫=+ ⎪⎝⎭[]0π，2tan ()1tan xf x x=+4π2ππ2πABCD 90ADC ∠=o45A ∠=o2AB =5BD =cos ADB∠DC =BC ABD ∆52sin 45sin ADB =∠o sin ADB ∠=90ADB ∠<o cos ADB ∠==2ADB BDC π∠+∠=cos cos()sin 2BDC ADB ADB π∠=-∠=∠cos cos()sin 2BDC ADB ADB π∠=-∠=∠222cos 2DC BD BC BDC BD DC+-∠=⋅⋅25=5BC =数列1．（全国1理）记为等差数列的前项和.若，，则（） A ． B ． C ． D ．解答：，∴. 2．（全国1理）记为数列的前项和.若，则_____________．解答：依题意，作差得，所以为公比为的等比数列，又因为，所以，所以，所以.3．（全国1文）已知数列{}n a 满足11a =，()121n n na n a +=+，设nn a b n=．（1）求123b b b ，，；（2）判断数列{}n b 是否为等比数列，并说明理由；（3）求{}n a 的通项公式．解答：依题意，，，∴，，. （1）∵，∴，即，所以为等比数列. （2）∵，∴. 4．（全国2文理）记为等差数列的前项和，已知，．（1）求的通项公式；（2）求，并求的最小值．解答：（1）设的公差为，由题意得，由得．所以的通项公式为．（2）由（1）得，当时，取得最小值，最小值为．5．（全国3文理）等比数列中，．（1）求的通项公式；（2）记为的前项和．若，求．解答：（1）设数列{}n a 的公比为q ，∴2534a q a ==，∴2q =±. ∴12n n a -=或1(2)n n a -=-.n S {}n a n 3243S S S =+12a ==5a 12-10-101211111132433(3)24996732022a d a d a d a d a d a d ⨯⨯+⨯=+++⨯⇒+=+⇒+=6203d d ⇒+=⇒=-51424(3)10a a d =+=+⨯-=-n S {}n a n 21n n S a =+6S =1121,21,n n n n S a S a ++=+⎧⎨=+⎩12n n a a +={}n a 211121a S a ==+11a =-12n n a -=-661(12)6312S -⋅-==--21224a a =⨯⨯=321(23)122a a =⨯⨯=1111a b ==2222a b ==3343a b ==12(1)n n na n a +=+121n na a n n+=+12n n b b +={}n b 1112n n nn a b b q n--===12n n a n -=⋅n S {}n a n 17a =-315S =-{}n a n S n S {}n a d 13315a d +=-17a =-2d ={}n a 29n a n =-228(4)16n S n n n =-=--∴4n =n S 16-{}n a 15314a a a ==，{}n a n S {}n a n 63m S =m（2）由（1）知，122112n nn S -==--或1(2)1[1(2)]123n n n S +-==--+， ∴2163mm S =-=或1[1(2)]633m m S =--=（舍），∴6m =.不等式1．(全国1文理）若，满足约束条件，则的最大值为_____________．解答：画出可行域如图所示，可知目标函数过点时取得最大值，.2．（全国2文理）若满足约束条件则的最大值为__________．解答：作可行域，则直线过点时取最大值9．3.（全国3文）若变量满足约束条件则的最大值是________．解答：由图可知在直线240x y -+=和2x =的交点(2,3)处取得最大值，故12333z =+⨯=.x y 220100x y x y y --≤⎧⎪-+≥⎨⎪≤⎩32z x y =+(2,0)max 32206z =⨯+⨯=,x y 25023050x y x y x +-≥⎧⎪-+≥⎨⎪-≤⎩，，，z x y =+z x y =+()5,4Az x y ，23024020.x y x y x ++≥⎧⎪-+≥⎨⎪-≤⎩，，13z x y =+立体几何1．（全国1文理）某圆柱的高为2，底面周长为16，其三视图如图．圆柱表面上的点在正视图上的对应点为，圆柱表面上的点在左视图上的对应点为，则在此圆柱侧面上，从到的路径中，最短路径的长度为（）A．B．C．3D．2解答：三视图还原几何体为一圆柱，如图，将侧面展开，最短路径为连线的距离，所以，所以选B.2．（全国1理）已知正方体的棱长为1，每条棱所在直线与平面α所成的角都相等，则α截此正方体所得截面面积的最大值为（）ABCD解答：由于截面与每条棱所成的角都相等，所以平面中存在平面与平面平行（如图），而在与平面平行的所有平面中，面积最大的为由各棱的中点构成的截面，而平面的面积.3．（全国1文）已知圆柱的上、下底面的中心分别为1O，2O，过直线12O O的平面截该圆柱所得的截面是面积为8的正方形，则该圆柱的表面积为（）A．B．12πC．D．10π解答：截面面积为，所以高，所以表面积为.4．（全国1文）在长方体1111ABCD A B C D-中，2AB BC==，1AC与平面11BB C C所成的角为30︒，则该长方体的体积为（）A．8B．C．D．解答：连接和，∵与平面所成角为，∴，∴，∴，∴，∴选C.MA N BM N17252,M N MN==α11AB D11AB DEFGHMN EFGHMN1622224S=⨯=8h=r=22212Sπππ=⋅⋅+=1AC1BC1AC11BB C C30o130AC B∠=o11tan30,ABBCBC==o1CC=22V=⨯⨯=5．（全国2理）在长方体中，，则异面直线与所成角的余弦值为（）A ． BCD解答：以D 为坐标原点，，，为，，轴建立空间直角坐标系，则，，，，，，，异面直线与，故选C ．6．（全国2理）已知圆锥的顶点为，母线，所成角的余弦值为，与圆锥底面所成角为45°，若的面积为，则该圆锥的侧面积为__________．解答：因为母线，所成角的余弦值为，所以母线，，因为的面积为，设母线长为，所以，，因与圆锥底面所成角为，所以底面半径为，因此圆锥的侧面积为． 7．（全国2文）在正方体中，为棱的中点，则异面直线与所成角的正切值为（）ABCD解答：在正方体中，，所以异面直线与所成角为，设正方体边长为，则由为棱的中点，可得，所以，则．故选C ． 8．（全国2文）已知圆锥的顶点为，母线，互相垂直，与圆锥底面所成角为，若的面积为，则该圆锥的体积为__________．解答：如下图所示，，，又，解得，所以，，所以该圆锥的体积为．1111ABCD A B C D -1AB BC ==1AA 1AD 1DB 15DA DC 1DD xy z ()0,0,0D ()1,0,0A (1B (1D (1AD ∴=-uuu r (1DB =u u u r111111cos<,>AD DB AD DB AD DB ⋅===uuu r uuu r uu uuu ruuu r Q uuu r u r ∴1AD 1DB S SA SB 78SA SAB △SA SB 78SA SB SAB △l 212l ⨯=280l ∴=SA 45︒cos 4l π22rl l π==1111ABCD A B C D -E 1CC AE CD 1111ABCD A B C D -CD AB ∥AE CD EAB ∠2a E 1CC CE a =BE =tan BE EAB AB ∠==S SA SB SA 30︒SAB △830SAO ∠=︒90ASB ∠=︒211822SAB S SA SB SA =⋅==△4SA =122SO SA ==AO =2183V OA SO =⋅π⋅⋅=π9．（全国3文理）中国古建筑借助榫卯将木构件连接起来，构件的凸出部分叫榫头，凹进部分叫卯眼，图中木构件右边的小长方体是榫头．若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是（）解答：根据题意，A 选项符号题意. 10．（全国3文理）设，，，是同一个半径为4的球的球面上四点，为等边三角形且其面积为，则三棱锥体积的最大值为（）A ．B ．C ．D ．解答：如图，ABC ∆为等边三角形，点O 为A ，B ，C ，D 外接球的球心，G 为ABC ∆的重心，由ABC S ∆=，得6AB =，取BC 的中点H，∴sin 60AH AB =⋅︒=23AG AH ==O 到面ABC的距离为2d ==，∴三棱锥D ABC -体积最大值1(24)3D ABC V -=⨯+=11．（全国1理）如图，四边形为正方形，分别为的中点，以为折痕把折起，使点到达点的位置，且.（1）证明：平面平面；（2）求与平面所成角的正弦值.解答：（1）分别为的中点，则，∴，又，，∴平面，平面，∴平面平面. （2），，∴，又，，∴平面，∴，A B C D ABC△D ABC-ABCD ,E F ,AD BC DF DFC △C P PF BF ⊥PEF ⊥ABFD DPABFD ,E F ,AD BC //EF AB EF BF ⊥PF BF ⊥EF PF F ⋂=BF ⊥PEF BE ⊂ABFD PEF ⊥ABFD PF BF ⊥//BF ED PF ED ⊥PF PD ⊥ED DP D ⋂=PF ⊥PED PF PE ⊥设，则，，∴，过作交于点，由平面平面，∴平面，连结，则即为直线与平面所成的角，由，∴，而，∴， ∴与平面所成角的正弦值.12．（全国1文）如图，在平行四边形ABCM 中，3AB AC ==，90ACM =︒∠，以AC 为折痕将△ACM 折起，使点M 到达点D 的位置，且AB DA ⊥．（1）证明：平面ACD ⊥平面ABC ；（2）Q 为线段AD 上一点，P 为线段BC 上一点，且23BP DQ DA ==，求三棱锥Q ABP -的体积．解答：（1）证明：∵为平行四边形且,∴,又∵,∴平面,∵平面,∴平面平面.（2）过点作,交于点，∵平面，∴,又∵,∴平面,∴,∴,∵,∴又∵为等腰直角三角形，∴，∴. 13．（全国2理）如图，在三棱锥中，，，为的中点．（1）证明：平面；（2）若点在棱上，且二面角为，求与平面所成角的正弦值．解答：（1）因为，为的中点，所以，且连结．因为，所以为等腰直角三角形，且，，由知，由知平面．4AB =4EF =2PF =PE =P PH EF ⊥EF H PEF ⊥ABFD PH ⊥ABFD DH PDH ∠DP ABFD PE PF EF PH ⋅=⋅PH ==4PD =sin 4PH PDH PD ∠==DP ABFD 4ABCM 90ACM ∠=oAB AC ⊥AB DA ⊥AB ⊥ACD AB ⊂ABC ABC ⊥ACD Q QH AC ⊥AC H AB ⊥ACD AB CD ⊥CD AC ⊥CD ⊥ABC 13HQ AQ CD AD ==1HQ =BC BC AM AD ====BP =ABC ∆1332ABP S ∆=⋅⋅=1131133Q ABD ABDV S HQ -∆=⋅⋅=⨯⨯=P ABC -AB BC ==4PA PB PC AC ====O AC PO ⊥ABC M BC M PA C --30︒PC PAM 4AP CP AC ===O AC OP AC ⊥OP =OB AB BC AC ==ABC △OB AC ⊥122OB AC ==222OP OB PB +=PO OB ⊥,OP OB OP AC ⊥⊥PO ⊥ABC（2）如图，以为坐标原点，的方向为轴正方向，建立空间直角坐标系．由已知得，，，，，，取平面的法向量，设，则，设平面的法向量为．由，，得，可取，，由已知得，，解得（舍去），，，又，所以．所以与平面． 14．（全国2文）如图，在三棱锥中，，，为的中点．（1）证明：平面；（2）若点在棱上，且，求点到平面的距离．解答：（1）因为，为的中点，所以，且．因为，所以为等腰直角三角形，且，．由知，．由，知平面．（2）作，垂足为．又由（1）可得，所以平面．故的长为点到平面的距离．O OB uu u r x O xyz -()0,0,0O ()2,0,0B ()0,2,0A -()0,2,0C (P (AP =uu u rPAC ()2,0,0OB =uu u r ()(),2,002M a a a -<≤(),4,0AM a a =-rPAM (),,x y z =n 0AP ⋅=uu u r n 0AM ⋅=uuu rn ()2040y ax a y ⎧+=⎪⎨+-=⎪⎩))4,a a =--n 4cos ,a OB -∴<uu u r n cos ,OB <>=uu u r n =4a =-43a =43⎛⎫∴=- ⎪ ⎪⎝⎭n (0,2,PC =-u u u r Q cos ,PC <uu u r n PC PAM P ABC -AB BC ==4PA PB PC AC ====O AC PO ⊥ABC M BC 2MC MB =C POM 4AP CP AC ===O AC OP AC ⊥OP =OB 2AB BC AC ==ABC △OB AC ⊥122OB AC ==222OP OB PB +=OP OB ⊥OP OB ⊥OP AC ⊥PO ⊥ABC CH OM ⊥H OP CH ⊥CH ⊥POM CH C POM由题设可知，，．所以，．所以点到平面．15.（全国3理）如图，边长为2的正方形所在的平面与半圆弧所在平面垂直，是上异于，的点．（1）证明：平面平面；（2）当三棱锥体积最大时，求面与面所成二面角的正弦值．解答：（1）∵正方形ABCD⊥半圆面CMD，∴AD⊥半圆面CMD，∴AD⊥平面MCD.∵CM在平面MCD内，∴AD CM⊥，又∵M是半圆弧CD上异于,C D的点，∴CM MD⊥.又∵AD DM D=I，∴CM⊥平面ADM，∵CM在平面BCM内，∴平面BCM⊥平面ADM.（2）如图建立坐标系：∵ABCS∆面积恒定，∴MO CD⊥，M ABCV-最大.(0,0,1)M，(2,1,0)A-，(2,1,0)B，(0,1,0)C，(0,1,0)D-,设面MAB的法向量为111(,,)m x y z=u r，设面MCD的法向量为222(,,)n x y z=r，(2,1,1)MA=--u u u r，(2,1,1)MB=-，(0,1,1)MC=-，(0,1,1)MD=--，11111120(1,0,2)20x y zmx y z--=⎧⇒=⎨+-=⎩u r，同理(1,0,0)n=r，，∴cosθ==，∴ sinθ=.16．（全国3文）如图，矩形所在平面与半圆弧所在平面垂直，是上异于，的点．（1）证明：平面平面；（2）在线段上是否存在点，使得平面？说明理由．122OC AC==23BCCM==45ACB∠=︒OMsinCOC MC AMHCBO⋅⋅∠==C POMABCD»CD M »CD C DAMD⊥BMCM ABC-MAB MCDABCD»CD M»CDC DAMD⊥BMCAM P MC∥PBD解答：（1）∵正方形ABCD ⊥半圆面CMD ，∴AD ⊥半圆面CMD ，∴AD ⊥平面MCD . ∵CM 在平面MCD 内，∴AD CM ⊥，又∵M 是半圆弧CD 上异于,C D 的点，∴CM MD ⊥.又∵AD DM D =I ，∴CM ⊥平面ADM ，∵CM 在平面BCM 内，∴平面BCM ⊥平面ADM .（2）线段AM 上存在点P 且P 为AM 中点，证明如下：连接,BD AC 交于点O ，连接,,PD PB PO ；在矩形ABCD 中，O 是AC 中点，P 是AM 的中点；∴//OP MC ，∵OP 在平面PDB 内，MC 不在平面PDB 内，∴//MC 平面PDB .圆锥曲线1．（全国1理）设抛物线C ：y 2=4x 的焦点为F ，过点（–2，0）且斜率为的直线与C 交于M ，N 两点，则=（）A ．5B ．6C ．7D ．8解答：由题意知直线的方程为，设，与抛物线方程联立有，可得或，∴，∴.2．（全国1理）已知双曲线C ：，O 为坐标原点，F 为C 的右焦点，过F 的直线与C 的两条渐近线的交点分别为M 、N .若为直角三角形，则|MN |=（）A ．B ．3C ．D ．4解答：渐近线方程为：，即，∵为直角三角形，假设，如图，∴，直线方程为.联立∴，即，∴ 3．（全国1文）已知椭圆C ：22214x y a +=的一个焦点为(20)，，则C 的离心率为（） A．13B ．12C ．2D．3解答：知，∴，，∴离心率. 4．（全国1文）直线1y x =+与圆22230x y y ++-=交于A B ，两点，则AB =________．解答：由，得圆心为，半径为，∴圆心到直线距离为∴23FM FN ⋅u u u u r u u u rMN 2(2)3y x =+1122(,),(,)M x y N x y 22(2)34y x y x⎧=+⎪⎨⎪=⎩1112x y =⎧⎨=⎩2244x y =⎧⎨=⎩(0,2),(3,4)FM FN ==u u u u r u u u r 03248FM FN ⋅=⨯+⨯=u u u u r u u u r 2213x y -=OMN △322203x y -=y x =OMN ∆2ONM π∠=NM k =MN 2)y x =-32)y x y x ⎧=-⎪⎨⎪=-⎩3(,2N ON =3MON π∠=3MN =2c =2228a b c =+=a =2e =22230x y y ++-=(0,1)-2d ==AB ==5．（全国2文理）双曲线，则其渐近线方程为（）A ． B． C ． D ．解答：，，因为渐近线方程为，所以渐近线方程为，选A ．6．（全国2理）已知，是椭圆的左、右焦点，是的左顶点，点在过的直线上，为等腰三角形，，则的离心率为（）A. B ． C ． D ．解答：因为为等腰三角形，，所以，由得，，，，由正弦定理得，，，，选D ．7．（全国2文）已知，是椭圆的两个焦点，是上的一点，若，且，则的离心率为（） A ． B ．CD解答：在中，，，设，则，，又由椭圆定义可知则离心率，选D ．8．（全国3文理）直线分别与轴，轴交于，两点，点在圆上，则面积的取值范围是（）A ．B ．C ．D ．解答：由直线20x y ++=得(2,0),(0,2)A B--，∴||AB ==22(2)2x y -+=的圆心为(2,0)，∴圆心到直线20x y ++==点P 到直线20x y ++=的距离的取值范围为d ≤≤d ≤≤，∴1||[2,6]2ABP S AB d ∆=⋅∈.22221(0,0)x y a b a b -=>>y =y =y =y =c e a ==Q 2222221312b c a e a a-∴==-=-=b a ∴by x a=±y =1F 2F 22221(0)x y C a b a b +=>>：A C P A 12PF F △12120F F P ∠=︒C 2312131412PF F △12120F F P ∠=︒2122PF F F c ==AP 2tan PAF ∠2sin PAF ∴∠=2cos PAF ∠=2222sin sin PF PAF AF APF ∠=∠2225sin 3c a c PAF ∴===+-∠ ⎪⎝⎭4a c ∴=14e =1F 2F C P C 12PF PF ⊥2160PF F ∠=︒C 12-112F PF △1290F PF ∠=︒2160PF F ∠=︒2PF m =1222c F F m ==1PF =)1221a PF PF m =+=212c c e a a====20x y ++=x y A B P ()2222x y -+=ABP △[]26，[]48，⎡⎣9．（全国3理）设是双曲线（）的左，右焦点，是坐标原点．过作的一条渐近线的垂线，垂足为．若，则的离心率为（）AB．2CD解答：∵2||PF b=，2||OF c=，∴ ||PO a=；又因为1|||PF OP=，所以1||PF=uu u r；在2RtPOF∆中，22||cos||PF bOF cθ==；∵在12Rt PF F∆中，2222121212||||||cos2||||PF FF PF bPF F F cθ+-==⋅⋅，222222224644633bb c a b c a c ac=⇒+-=⇒-=-223c a⇒=e⇒=.10．（全国3理）已知点和抛物线，过的焦点且斜率为的直线与交于，两点．若，则________．解答：依题意得，抛物线C的焦点为(1,0)F，故可设直线:(1)AB y k x=-，联立2(1),4,y k xy x=-⎧⎨=⎩消去y得2222(24)0k x k x k-++=，设11(,)A x y，22(,)B x y，则212224kx xk++=，121x x=，∴12124()2y y k x x kk+=+-=，2121212[()1]4y y k x x x x=-++=-.又11(1,1)MA x y=+-u u u r，22(1,1)MB x y=+-u u u r，∴1212(1)(1)(1)(1)MA MB x x y y⋅=+++--u u u r u u u r12121212()1()1x x x x y y y y=++++-++2224411410kk k+=++--+=，∴2k=.11．（全国3文）已知双曲线，则点到的渐近线的距离为（）A B．C．D．解答：由题意cea==1ba=，故渐近线方程为0x y±=，则点(4,0)到渐近线的距离为d==.故选D.12．（全国1理）设椭圆的右焦点为，过的直线与交于两点，点的坐标为.（1）当与轴垂直时，求直线的方程；（2）设为坐标原点，证明：.解答：（1）如图所示，将代入椭圆方程得，得，∴12F F，22221x yCa b-=：00a b>>，O2F C P1PF=C()11M-，24C y x=：C k CA B90AMB=︒∠k=22221(00)x yC a ba b-=>>：，(4,0)C2222:12xC y+=F F l C,A BM(2,0)l x AMO OMA OMB∠=∠1x=2112y+=2y=±，∴，∴直线的方程为：.（2）证明：当斜率不存在时，由（1）可知，结论成立；当斜率存在时，设其方程为，，联立椭圆方程有即，∴，，，∴，∴.13．（全国1文）设抛物线22C y x =：，点()20A ，，()20B -，，过点A 的直线l 与C 交于M ，N 两点．（1）当l 与x 轴垂直时，求直线BM 的方程；（2）证明：ABM ABN =∠∠．解答：（1）当与轴垂直时，的方程为，代入，∴或，∴的方程为：或.（2）设的方程为，设，联立方程，得，∴，，∴ ，∴，∴.14．（全国2文理）设抛物线的焦点为，过且斜率为的直线与交于，两点，．（1）求的方程（2）求过点，且与的准线相切的圆的方程．解答：（1）由题意得，的方程为，设，，由，得，，故，所以，由题设知，解得（舍去），．因此的方程为．(1,2A±2AM k =±AM 2)2y x =±-l l (1)y k x =-1122(,),(,)A x y B x y 22(1),12y k x x y =-⎧⎪⎨+=⎪⎩2222(21)4220k x k x k +-+-=2122421k x x k +=+21222221k x x k -=+1212121212[(23()4]22(2)(2)AM BM y y k x x x x k k x x x x -+++=+=----2222124412(4)21210(2)(2)k k k k k x x --+++==--AM BM k k =-OMA OMB ∠=∠l x l 2x =22y x =(2,2),(2,2)M N -(2,2),(2,2)M N -BM 220,y x ++=220y x --=MN 2x my =+1122(,),(,)M x y N x y 222x my y x =+⎧⎨=⎩2240y my --=12122,4y y m y y +==-11222,2x my x my =+=+121212122244BM BN y y y y k k x x my my +=+=+++++12121224()0(4)(4)my y y y my my ++==++BM BN k k =-ABM ABN ∠=∠24C y x =：F F (0)k k >l C A B ||8AB =l A B C ()1,0F l ()()10y k x k =->()11,A x y ()22,B x y ()214y k x y x⎧=-⎪⎨=⎪⎩()2222240k x k x k -++=216160k ∆=+>122224k x k x ++=()()122244||||||11k AB A x F BF k x +=+=+++=22448k k +=1k =-1k =l 1y x =-（2）由（1）得AB 的中点坐标为，所以AB 的垂直平分线方程为，即，设所求圆的圆心坐标为，则，解得或，因此所求圆的方程为或．15.（全国3理）知斜率为的直线与椭圆交于，两点，线段的中点为．（1）证明：；（2）设为的右焦点，为上一点，且．证明：，，成等差数列，并求该数列的公差．解答：（1）设直线l 方程为y kx t =+，设11(,)A x y ,22(,)B x y ,22143y kx tx y =+⎧⎪⎨+=⎪⎩联立消y 得222(43)84120k x ktx t +++-=，则2222644(412)(34)0k t t k ∆=--+>，得2243k t +>…①，且1228234kt x x k -+==+，121226()2234ty y k x x t m k+=++==+， ∵0m >，∴ 0t >且0k <.且2344k t k+=-…②.由①②得2222(34)4316k k k ++>，∴12k >或12k <-. ∵0k <，∴ 12k <-.（2）0FP FA FB ++=uu r uu r uu r r ，20FP FM +=uu r uuu r r , ∵(1,)M m ，(1,0)F ，∴P 的坐标为(1,2)m -.由于P 在椭圆上，∴ 214143m +=，∴34m =，3(1,)2M -，又2211143x y +=，2222143x y +=，两式相减可得1212121234y y x x x x y y -+=-⋅-+，又122x x +=，1232y y +=，∴1k =-，直线l 方程为3(1)4y x -=--，()3,2()23y x -=--5y x =-+()00,x y 00220005,(1)(1)162y x y x x =-+⎧⎪⎨-++=+⎪⎩0032x y =⎧⎨=⎩00116x y =⎧⎨=-⎩()()223216x y -+-=()()22116144x y -++=k l 22143x y C +=：A B AB ()()10M m m >，12k <-F C P C FP FA FB ++=0u u u r u u u r u u u r FA u u u r FP u u u rFB u u u r。

江西省2018年中考历史真题试卷(附解析)

2018年江西中考历史试题一、选择题（本大题共12小题，每小题2分，共24分。

在每小题列出的四个选项中，只有一项符合题目要求。

请将答案按要求填涂在答题卡的相应位置。

）1. “赵王闻秦反间之言，因使赵括代廉颇将以击秦。

括军败，卒四十万人降武安君（白起），（武安君）乃挟诈而尽坑杀之，遣其小者二百四十人归赵。

”材料描述的战争是A. 城濮之战B. 桂陵之战C. 长平之战D. 赤壁之战【答案】C【解析】提取题干的“赵括”结合所学知识可知，在公元前260年的长平之战中，赵王起用只会“纸上谈兵”的赵括，导致四十万赵军被秦军坑杀。

故材料描述的战争是长平之战。

故C符合题意；城濮之战发生在晋国和楚国之间，故A不符合题意；桂陵之战发生在齐国和魏国之间。

故B不符合题意；赤壁之战发生在曹军和孙刘联军之间。

故D不符合题意。

故选C。

2. “炀帝此举，为其国促数年之祚（国运），而为后世开万世之利，可谓不仁而有功者矣。

”“炀帝此举”是指A. 建立隋朝B. 统一全国C. 开通大运河D. 创立科举制【答案】C【解析】题干的“为其国促数年之祚（国运），而为后世开万世之利”大体意思是促进了多年的国运，造福后世。

结合所学知识可知，隋炀帝开通的大运河是我国古代最宏伟的工程之一，是贯通南北的交通大动脉，大大加强了南北联系，有利于国家的统一，同时促进了南北经济文化的交流，运河所经之地，城市兴起，经济繁荣，文化昌盛。

所以说这是为后世开万世之利。

故C符合题意；建立隋朝，统一全国的是隋文帝，故AB不符合题意；创立科举制的是隋炀帝，但与题干的“为其国促数年之祚（国运），而为后世开万世之利”不符合。

故D不符合题意。

故选C。

点睛：解题的关键是正确解读题干的“为其国促数年之祚（国运），而为后世开万世之利”，认识题干材料大意是隋炀帝的举措促进了多年的国运，造福后世。

隋炀帝开通的大运河，促进了南北经济文化的交流，为后世开万世之利。

3. 一个曾在中国海关任职的英国人说，上海“已经变成了无法无天的外国人们的一个真正黄金国……其中许多人都是属于这样一种类型的：只要有利可图，那么走私犯禁，一切都不顾忌，就是行凶杀人，也在所不惜。

【精校版】2018年全国卷Ⅰ文综高考试题(含答案)

2018年高考文综真题试卷全国卷Ⅰ总分数 130分时长:150分钟题型单选题简答题综合题题量12 1 4总分48 12 70一、选择题（本题共35小题，每小题4分，共140分。

在每小题给出的四个选项中，只有一项是符合题目要求的）（共12题 ,总计48分）1.（4分）（20182018年高考文综全国卷Ⅰ）《墨子》中有关于“圆”“直线”“正方形”“倍”的定义，对杠杆原理、声音传播、小孔成像等也有论述，还有机械制造方面的记载。

这反映出，《墨子》（）A. 汇集了诸子百家的思想精华B. 形成了完整的科学体系C. 包含了劳动人民智慧的结晶D. 体现了贵族阶层的旨趣2.（4分）（20182018年高考文综全国卷Ⅰ）据学者研究，唐朝“安史之乱”后百余年间的藩镇基本情况如表2所示。

由此可知，这一时期的藩镇（）A. 控制了朝廷财政收入B. 彼此之间攻伐不已C. 注重维护中央的权威D. 延续了唐朝的统治3.（4分）（20182018年高考文综全国卷Ⅰ）北宋前中期，在今四川井研县一带山谷中，密布着成百上千个采用新制盐技术的竹筒井，井主所雇工匠大多来自“他州别县”，以“佣身赁力”为生，受雇期间，若对工作条件或待遇不满意，辄另谋高就。

这反映出当时（）A. 民营手工业得到发展B. 手工业者社会地位高C. 雇佣劳动已经普及D. 盐业专卖制度已经解体4.（4分）（20182018年高考文综全国卷Ⅰ）图中的动物是郑和下西洋时外国使臣随船向明政府贡献的奇珍异兽。

明朝君臣认为，这就是中国传说中的“麒麟”。

明成祖遂厚赐外国使臣。

这表明当时（）A. 对外交流促使中国传统绘画出现新的类型B. 朝廷用中国文化对朝贡贸易贡品加以解读C. 海禁政策的解除促进了对外文化交流D. 外来物品的传入推动了传统观念更新5.（4分）（20182018年高考文综全国卷Ⅰ）甲午战争时期，日本制定舆论宣传策略，把中国和日本分别“包装”成野蛮和文明的代表，并运用公关手段让许多欧美舆论倒向日方。

【高考真题合集】2018全国文综历史真题及答案解析（I、II、III卷）

2018年普通高等学校招生全国统一考试•历史试题（I卷）一、选择题：本题共12小题，每小题4分，共48分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

24.《墨子》中有关于“圆"“直线"“正方形"“倍"的定义，对杠杆原理、声音传播、小孔成像等也有论述，还有机械制造方面的记载。

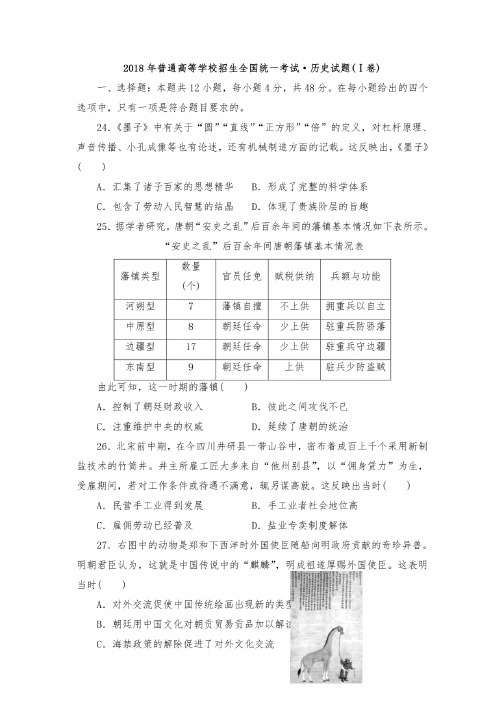
这反映出，《墨子》A.汇集了诸子百家的思想精华B,形成了完整的科学体系C.包含了劳动人民智慧的结晶D,体现了贵族阶层的旨趣25.据学者研究，唐朝“安史之乱"后百余年间的藩镇基本情况如下表所示。

“安史之乱"后百余年间唐朝藩镇基本情况表数量藩镇类型官员任免赋税供纳兵额与功能（个）河朔型7藩镇自擅不上供拥重兵以自立中原型8朝廷任命少上供驻重兵防骄藩边疆型17朝廷任命少上供驻重兵守边疆东南型9朝廷任命上供驻兵少防盗贼由此可知，这一时期的藩镇（）A.控制了朝廷财政收入B.彼此之间攻伐不已C.注重维护中央的权威D,延续了唐朝的统治26.北宋前中期，在今四川井研县一带山谷中，密布着成百上千个采用新制盐技术的竹筒井。

井主所雇工匠大多来自“他州别县"，以“佣身赁力"为生，受雇期间，若对工作条件或待遇不满意，辄另谋高就。

这反映出当时（）A.民营手工业得到发展B.手工业者社会地位高C,雇佣劳动已经普及 D.盐业专卖制度解体27.右图中的动物是郑和下西洋时外国使臣随船向明政府贡献的奇珍异兽。

明朝君臣认为，这就是中国传说中的“膜麟”，明成祖遂厚赐外国使臣。

这表明剧时再抻积说缉当时（）A.对外交流促使中国传统绘画出现新的类IWPH IIInB.朝廷用中国文化对朝贡贸易贡品加以解方C.海禁政策的解除促进了对外文化交流D.外来物品的传入推动了传统观念更新28.甲午战争时期，日本制定舆论宣传策略，把中国和日本分别“包装"成野蛮与文明的代表，并运用公关手段让许多欧美舆论倒向日方。

2018年广东省中考数学试卷(含答案解析版)

2018年广东省中考数学试卷一、选择题（本大题10小题，每小题3分，共30分）在每小题列出的四个选项中，只有一个是正确的，请把答题卡上对应题目所选的选项涂黑．1．（3分）（2018•广东）四个实数0、、﹣3.14、2中，最小的数是（）A．0 B．C．﹣3.14 D．22．（3分）（2018•广东）据有关部门统计，2018年“五一小长假”期间，广东各大景点共接待游客约14420000人次，将数14420000用科学记数法表示为（）A．1.442×107B．0.1442×107 C．1.442×108D．0.1442×1083．（3分）（2018•广东）如图，由5个相同正方体组合而成的几何体，它的主视图是（）A．B．C．D．4．（3分）（2018•广东）数据1、5、7、4、8的中位数是（）A．4 B．5 C．6 D．75．（3分）（2018•广东）下列所述图形中，是轴对称图形但不是中心对称图形的是（）A．圆B．菱形C．平行四边形D．等腰三角形6．（3分）（2018•广东）不等式3x﹣1≥x+3的解集是（）A．x≤4 B．x≥4 C．x≤2 D．x≥27．（3分）（2018•广东）在△ABC中，点D、E分别为边AB、AC的中点，则△ADE 与△ABC的面积之比为（）A．B．C．D．8．（3分）（2018•广东）如图，AB∥CD，则∠DEC=100°，∠C=40°，则∠B的大小是（）A．30°B．40°C．50°D．60°9．（3分）（2018•广东）关于x的一元二次方程x2﹣3x+m=0有两个不相等的实数根，则实数m的取值范围是（）A．m＜B．m≤C．m＞D．m≥10．（3分）（2018•广东）如图，点P是菱形ABCD边上的一动点，它从点A出发沿在A→B→C→D路径匀速运动到点D，设△PAD的面积为y，P点的运动时间为x，则y关于x的函数图象大致为（）A．B．C．D．二、填空题（共6小题，每小题3分，满分18分）11．（3分）（2018•广东）同圆中，已知弧AB所对的圆心角是100°，则弧AB所对的圆周角是．12．（3分）（2018•广东）分解因式：x2﹣2x+1=．13．（3分）（2018•广东）一个正数的平方根分别是x+1和x﹣5，则x=．14．（3分）（2018•广东）已知+|b﹣1|=0，则a+1=．15．（3分）（2018•广东）如图，矩形ABCD中，BC=4，CD=2，以AD为直径的半圆O与BC相切于点E，连接BD，则阴影部分的面积为．（结果保留π）16．（3分）（2018•广东）如图，已知等边△OA1B1，顶点A1在双曲线y=（x ＞0）上，点B1的坐标为（2，0）．过B1作B1A2∥OA1交双曲线于点A2，过A2作A2B2∥A1B1交x轴于点B2，得到第二个等边△B1A2B2；过B2作B2A3∥B1A2交双曲线于点A3，过A3作A3B3∥A2B2交x轴于点B3，得到第三个等边△B2A3B3；以此类推，…，则点B6的坐标为．三、解答题（一）17．（6分）（2018•广东）计算：|﹣2|﹣20180+（）﹣118．（6分）（2018•广东）先化简，再求值：•，其中a=．19．（6分）（2018•广东）如图，BD是菱形ABCD的对角线，∠CBD=75°，（1）请用尺规作图法，作AB的垂直平分线EF，垂足为E，交AD于F；（不要求写作法，保留作图痕迹）（2）在（1）条件下，连接BF，求∠DBF的度数．20．（7分）（2018•广东）某公司购买了一批A、B型芯片，其中A型芯片的单价比B型芯片的单价少9元，已知该公司用3120元购买A型芯片的条数与用4200元购买B型芯片的条数相等．（1）求该公司购买的A、B型芯片的单价各是多少元？（2）若两种芯片共购买了200条，且购买的总费用为6280元，求购买了多少条A型芯片？21．（7分）（2018•广东）某企业工会开展“一周工作量完成情况”调查活动，随机调查了部分员工一周的工作量剩余情况，并将调查结果统计后绘制成如图1和图2所示的不完整统计图．（1）被调查员工人数为人：（2）把条形统计图补充完整；（3）若该企业有员工10000人，请估计该企业某周的工作量完成情况为“剩少量”的员工有多少人？22．（7分）（2018•广东）如图，矩形ABCD中，AB＞AD，把矩形沿对角线AC所在直线折叠，使点B落在点E处，AE交CD于点F，连接DE．（1）求证：△ADE≌△CED；（2）求证：△DEF是等腰三角形．23．（9分）（2018•广东）如图，已知顶点为C（0，﹣3）的抛物线y=ax2+b（a ≠0）与x轴交于A，B两点，直线y=x+m过顶点C和点B．（1）求m的值；（2）求函数y=ax2+b（a≠0）的解析式；（3）抛物线上是否存在点M，使得∠MCB=15°？若存在，求出点M的坐标；若不存在，请说明理由．24．（9分）（2018•广东）如图，四边形ABCD中，AB=AD=CD，以AB为直径的⊙O经过点C，连接AC，OD交于点E．（1）证明：OD∥BC；（2）若tan∠ABC=2，证明：DA与⊙O相切；（3）在（2）条件下，连接BD交于⊙O于点F，连接EF，若BC=1，求EF的长．25．（9分）（2018•广东）已知Rt△OAB，∠OAB=90°，∠ABO=30°，斜边OB=4，将Rt△OAB绕点O顺时针旋转60°，如题图1，连接BC．（1）填空：∠OBC=°；（2）如图1，连接AC，作OP⊥AC，垂足为P，求OP的长度；（3）如图2，点M，N同时从点O出发，在△OCB边上运动，M沿O→C→B路径匀速运动，N沿O→B→C路径匀速运动，当两点相遇时运动停止，已知点M 的运动速度为1.5单位/秒，点N的运动速度为1单位/秒，设运动时间为x秒，△OMN的面积为y，求当x为何值时y取得最大值？最大值为多少？2018年广东省中考数学试卷参考答案与试题解析一、选择题（本大题10小题，每小题3分，共30分）在每小题列出的四个选项中，只有一个是正确的，请把答题卡上对应题目所选的选项涂黑．1．（3分）（2018•广东）四个实数0、、﹣3.14、2中，最小的数是（）A．0 B．C．﹣3.14 D．2【考点】2A：实数大小比较．【专题】1 ：常规题型．【分析】正实数都大于0，负实数都小于0，正实数大于一切负实数，两个负实数绝对值大的反而小，据此判断即可．【解答】解：根据实数比较大小的方法，可得﹣3.14＜0＜＜2，所以最小的数是﹣3.14．故选：C．【点评】此题主要考查了实数大小比较的方法，要熟练掌握，解答此题的关键是要明确：正实数＞0＞负实数，两个负实数绝对值大的反而小．2．（3分）（2018•广东）据有关部门统计，2018年“五一小长假”期间，广东各大景点共接待游客约14420000人次，将数14420000用科学记数法表示为（）A．1.442×107B．0.1442×107 C．1.442×108D．0.1442×108【考点】1I：科学记数法—表示较大的数．【专题】2B ：探究型．【分析】根据科学记数法的表示方法可以将题目中的数据用科学记数法表示，本题得以解决．【解答】解：14420000=1.442×107，故选：A．【点评】本题考查科学记数法﹣表示较大的数，解答本题的关键是明确科学记数法的表示方法．3．（3分）（2018•广东）如图，由5个相同正方体组合而成的几何体，它的主视图是（）A．B．C．D．【考点】U2：简单组合体的三视图．【专题】55F：投影与视图．【分析】根据主视图是从物体正面看所得到的图形解答即可．【解答】解：根据主视图的定义可知，此几何体的主视图是B中的图形，故选：B．【点评】本题考查的是简单几何体的三视图的作图，主视图、左视图、俯视图是分别从物体正面、侧面和上面看所得到的图形．4．（3分）（2018•广东）数据1、5、7、4、8的中位数是（）A．4 B．5 C．6 D．7【考点】W4：中位数．【专题】542：统计的应用．【分析】根据中位数的定义判断即可；【解答】解：将数据重新排列为1、4、5、7、8，则这组数据的中位数为5故选：B．【点评】本题考查了确定一组数据的中位数的能力．中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（最中间两个数的平均数），叫做这组数据的中位数．5．（3分）（2018•广东）下列所述图形中，是轴对称图形但不是中心对称图形的是（）A．圆B．菱形C．平行四边形D．等腰三角形【考点】R5：中心对称图形；P3：轴对称图形．【专题】1 ：常规题型．【分析】根据轴对称图形与中心对称图形的概念求解．【解答】解：A、是轴对称图形，也是中心对称图形，故此选项错误；B、是轴对称图形，也是中心对称图形，故此选项错误；C、不是轴对称图形，是中心对称图形，故此选项错误；D、是轴对称图形，不是中心对称图形，故此选项正确．故选：D．【点评】本题考查了中心对称图形与轴对称图形的概念：轴对称图形的关键是寻找对称轴，图形两部分沿对称轴折叠后可重合；中心对称图形是要寻找对称中心，旋转180度后与原图重合．6．（3分）（2018•广东）不等式3x﹣1≥x+3的解集是（）A．x≤4 B．x≥4 C．x≤2 D．x≥2【考点】C6：解一元一次不等式．【专题】11 ：计算题；524：一元一次不等式(组)及应用．【分析】根据解不等式的步骤：①移项；②合并同类项；③化系数为1即可得．【解答】解：移项，得：3x﹣x≥3+1，合并同类项，得：2x≥4，系数化为1，得：x≥2，故选：D．【点评】本题主要考查解一元一次不等式，解题的关键是掌握解一元一次不等式的步骤：①去分母；②去括号；③移项；④合并同类项；⑤化系数为1．7．（3分）（2018•广东）在△ABC中，点D、E分别为边AB、AC的中点，则△ADE 与△ABC的面积之比为（）A．B．C．D．【考点】S9：相似三角形的判定与性质；KX：三角形中位线定理．【专题】55D：图形的相似．【分析】由点D、E分别为边AB、AC的中点，可得出DE为△ABC的中位线，进而可得出DE∥BC及△ADE∽△ABC，再利用相似三角形的性质即可求出△ADE与△ABC的面积之比．【解答】解：∵点D、E分别为边AB、AC的中点，∴DE为△ABC的中位线，∴DE∥BC，∴△ADE∽△ABC，∴=（）2=．故选：C．【点评】本题考查了相似三角形的判定与性质以及三角形中位线定理，利用三角形的中位线定理找出DE∥BC是解题的关键．8．（3分）（2018•广东）如图，AB∥CD，则∠DEC=100°，∠C=40°，则∠B的大小是（）A．30°B．40°C．50°D．60°【考点】JA：平行线的性质．【专题】551：线段、角、相交线与平行线．【分析】依据三角形内角和定理，可得∠D=40°，再根据平行线的性质，即可得到∠B=∠D=40°．【解答】解：∵∠DEC=100°，∠C=40°，∴∠D=40°，又∵AB∥CD，∴∠B=∠D=40°，故选：B．【点评】本题考查了平行线性质的应用，运用两直线平行，内错角相等是解题的关键．9．（3分）（2018•广东）关于x的一元二次方程x2﹣3x+m=0有两个不相等的实数根，则实数m的取值范围是（）A．m＜B．m≤C．m＞D．m≥【考点】AA：根的判别式．【分析】根据一元二次方程的根的判别式，建立关于m的不等式，求出m的取值范围即可．【解答】解：∵关于x的一元二次方程x2﹣3x+m=0有两个不相等的实数根，∴△=b2﹣4ac=（﹣3）2﹣4×1×m＞0，∴m＜．故选：A．【点评】此题考查了根的判别式，一元二次方程根的情况与判别式△的关系：（1）△＞0⇔方程有两个不相等的实数根；（2）△=0⇔方程有两个相等的实数根；（3）△＜0⇔方程没有实数根．10．（3分）（2018•广东）如图，点P是菱形ABCD边上的一动点，它从点A出发沿在A→B→C→D路径匀速运动到点D，设△PAD的面积为y，P点的运动时间为x，则y关于x的函数图象大致为（）A．B．C．D．【考点】E7：动点问题的函数图象．【专题】31 ：数形结合．【分析】设菱形的高为h，即是一个定值，再分点P在AB上，在BC上和在CD 上三种情况，利用三角形的面积公式列式求出相应的函数关系式，然后选择答案即可．【解答】解：分三种情况：①当P在AB边上时，如图1，设菱形的高为h，y=AP•h，∵AP随x的增大而增大，h不变，∴y随x的增大而增大，故选项C不正确；②当P在边BC上时，如图2，y=AD•h，AD和h都不变，∴在这个过程中，y不变，故选项A不正确；③当P在边CD上时，如图3，y=PD•h，∵PD随x的增大而减小，h不变，∴y随x的增大而减小，∵P点从点A出发沿在A→B→C→D路径匀速运动到点D，∴P在三条线段上运动的时间相同，故选项D不正确；故选：B．【点评】本题考查了动点问题的函数图象，菱形的性质，根据点P的位置的不同，分三段求出△PAD的面积的表达式是解题的关键．二、填空题（共6小题，每小题3分，满分18分）11．（3分）（2018•广东）同圆中，已知弧AB所对的圆心角是100°，则弧AB所对的圆周角是50°．【考点】M5：圆周角定理．【专题】11 ：计算题．【分析】直接利用圆周角定理求解．【解答】解：弧AB所对的圆心角是100°，则弧AB所对的圆周角为50°．故答案为50°．【点评】本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．12．（3分）（2018•广东）分解因式：x2﹣2x+1=（x﹣1）2．【考点】54：因式分解﹣运用公式法．【分析】直接利用完全平方公式分解因式即可．【解答】解：x2﹣2x+1=（x﹣1）2．【点评】本题考查了公式法分解因式，运用完全平方公式进行因式分解，熟记公式是解题的关键．13．（3分）（2018•广东）一个正数的平方根分别是x+1和x﹣5，则x=2．【考点】21：平方根．【专题】11 ：计算题；511：实数．【分析】根据正数的两个平方根互为相反数列出关于x的方程，解之可得．【解答】解：根据题意知x+1+x﹣5=0，解得：x=2，故答案为：2．【点评】本题主要考查的是平方根的定义和性质，熟练掌握平方根的定义和性质是解题的关键．14．（3分）（2018•广东）已知+|b﹣1|=0，则a+1=2．【考点】23：非负数的性质：算术平方根；16：非负数的性质：绝对值．【专题】1 ：常规题型．【分析】直接利用非负数的性质结合绝对值的性质得出a，b的值进而得出答案．【解答】解：∵+|b﹣1|=0，∴b﹣1=0，a﹣b=0，解得：b=1，a=1，故a +1=2．故答案为：2．【点评】此题主要考查了非负数的性质以及绝对值的性质，正确得出a ，b 的值是解题关键．15．（3分）（2018•广东）如图，矩形ABCD 中，BC=4，CD=2，以AD 为直径的半圆O 与BC 相切于点E ，连接BD ，则阴影部分的面积为 π ．（结果保留π）【考点】MC ：切线的性质；LB ：矩形的性质；MO ：扇形面积的计算．【专题】11 ：计算题．【分析】连接OE ，如图，利用切线的性质得OD=2，OE ⊥BC ，易得四边形OECD 为正方形，先利用扇形面积公式，利用S 正方形OECD ﹣S 扇形EOD 计算由弧DE 、线段EC 、CD 所围成的面积，然后利用三角形的面积减去刚才计算的面积即可得到阴影部分的面积．【解答】解：连接OE ，如图，∵以AD 为直径的半圆O 与BC 相切于点E ，∴OD=2，OE ⊥BC ，易得四边形OECD 为正方形，∴由弧DE 、线段EC 、CD 所围成的面积=S 正方形OECD ﹣S 扇形EOD =22﹣=4﹣π，∴阴影部分的面积=×2×4﹣（4﹣π）=π．故答案为π．【点评】本题考查了切线的性质：圆的切线垂直于经过切点的半径．若出现圆的切线，必连过切点的半径，构造定理图，得出垂直关系．也考查了矩形的性质和扇形的面积公式．16．（3分）（2018•广东）如图，已知等边△OA1B1，顶点A1在双曲线y=（x ＞0）上，点B1的坐标为（2，0）．过B1作B1A2∥OA1交双曲线于点A2，过A2作A2B2∥A1B1交x轴于点B2，得到第二个等边△B1A2B2；过B2作B2A3∥B1A2交双曲线于点A3，过A3作A3B3∥A2B2交x轴于点B3，得到第三个等边△B2A3B3；以此类推，…，则点B6的坐标为（2，0）．【考点】G6：反比例函数图象上点的坐标特征；KK：等边三角形的性质．【专题】1 ：常规题型．【分析】根据等边三角形的性质以及反比例函数图象上点的坐标特征分别求出B2、B3、B4的坐标，得出规律，进而求出点B6的坐标．【解答】解：如图，作A2C⊥x轴于点C，设B1C=a，则A2C=a，OC=OB1+B1C=2+a，A2（2+a，a）．∵点A2在双曲线y=（x＞0）上，∴（2+a）•a=，解得a=﹣1，或a=﹣﹣1（舍去），∴OB2=OB1+2B1C=2+2﹣2=2，∴点B2的坐标为（2，0）；作A3D⊥x轴于点D，设B2D=b，则A3D=b，OD=OB2+B2D=2+b，A2（2+b，b）．∵点A3在双曲线y=（x＞0）上，∴（2+b）•b=，解得b=﹣+，或b=﹣﹣（舍去），∴OB3=OB2+2B2D=2﹣2+2=2，∴点B3的坐标为（2，0）；同理可得点B4的坐标为（2，0）即（4，0）；…，∴点B n的坐标为（2，0），∴点B6的坐标为（2，0）．故答案为（2，0）．【点评】本题考查了反比例函数图象上点的坐标特征，等边三角形的性质，正确求出B2、B3、B4的坐标进而得出点B n的规律是解题的关键．三、解答题（一）17．（6分）（2018•广东）计算：|﹣2|﹣20180+（）﹣1【考点】2C：实数的运算；6E：零指数幂；6F：负整数指数幂．【专题】1 ：常规题型．【分析】直接利用负指数幂的性质以及零指数幂的性质、绝对值的性质进而化简得出答案．【解答】解：原式=2﹣1+2=3．【点评】此题主要考查了实数运算，正确化简各数是解题关键．18．（6分）（2018•广东）先化简，再求值：•，其中a=．【考点】6D：分式的化简求值．【专题】11 ：计算题；513：分式．【分析】原式先因式分解，再约分即可化简，继而将a的值代入计算．【解答】解：原式=•=2a，当a=时，原式=2×=．【点评】本题主要考查分式的化简求值，解题的关键是熟练掌握分式混合运算顺序和运算法则．19．（6分）（2018•广东）如图，BD是菱形ABCD的对角线，∠CBD=75°，（1）请用尺规作图法，作AB的垂直平分线EF，垂足为E，交AD于F；（不要求写作法，保留作图痕迹）（2）在（1）条件下，连接BF，求∠DBF的度数．【考点】N2：作图—基本作图；KG：线段垂直平分线的性质；L8：菱形的性质．【专题】555：多边形与平行四边形．【分析】（1）分别以A、B为圆心，大于AB长为半径画弧，过两弧的交点作直线即可；（2）根据∠DBF=∠ABD﹣∠ABF计算即可；【解答】解：（1）如图所示，直线EF即为所求；（2）∵四边形ABCD是菱形，∴∠ABD=∠DBC=∠ABC=75°，DC∥AB，∠A=∠C．∴∠ABC=150°，∠ABC+∠C=180°，∴∠C=∠A=30°，∵EF垂直平分线线段AB，∴AF=FB，∴∠A=∠FBA=30°，∴∠DBF=∠ABD﹣∠FBE=45°．【点评】本题考查作图﹣基本作图，线段的垂直平分线的性质，菱形的性质等知识，解题的关键是灵活运用所学知识解决问题，属于常考题型．20．（7分）（2018•广东）某公司购买了一批A、B型芯片，其中A型芯片的单价比B型芯片的单价少9元，已知该公司用3120元购买A型芯片的条数与用4200元购买B型芯片的条数相等．（1）求该公司购买的A、B型芯片的单价各是多少元？（2）若两种芯片共购买了200条，且购买的总费用为6280元，求购买了多少条A型芯片？【考点】B7：分式方程的应用．【专题】34 ：方程思想；521：一次方程（组）及应用；522：分式方程及应用．【分析】（1）设B型芯片的单价为x元/条，则A型芯片的单价为（x﹣9）元/条，根据数量=总价÷单价结合用3120元购买A型芯片的条数与用4200元购买B型芯片的条数相等，即可得出关于x的分式方程，解之经检验后即可得出结论；（2）设购买a条A型芯片，则购买（200﹣a）条B型芯片，根据总价=单价×数量，即可得出关于a的一元一次方程，解之即可得出结论．【解答】解：（1）设B型芯片的单价为x元/条，则A型芯片的单价为（x﹣9）元/条，根据题意得：=，解得：x=35，经检验，x=35是原方程的解，∴x﹣9=26．答：A型芯片的单价为26元/条，B型芯片的单价为35元/条．（2）设购买a条A型芯片，则购买（200﹣a）条B型芯片，根据题意得：26a+35（200﹣a）=6280，解得：a=80．答：购买了80条A型芯片．【点评】本题考查了分式方程的应用以及一元一次方程的应用，解题的关键是：（1）找准等量关系，正确列出分式方程；（2）找准等量关系，正确列出一元一次方程．21．（7分）（2018•广东）某企业工会开展“一周工作量完成情况”调查活动，随机调查了部分员工一周的工作量剩余情况，并将调查结果统计后绘制成如图1和图2所示的不完整统计图．（1）被调查员工人数为800人：（2）把条形统计图补充完整；（3）若该企业有员工10000人，请估计该企业某周的工作量完成情况为“剩少量”的员工有多少人？【考点】VC：条形统计图；V5：用样本估计总体；VB：扇形统计图．【专题】1 ：常规题型；542：统计的应用．【分析】（1）由“不剩”的人数及其所占百分比可得答案；（2）用总人数减去其它类型人数求得“剩少量”的人数，据此补全图形即可；（3）用总人数乘以样本中“剩少量”人数所占百分比可得．【解答】解：（1）被调查员工人数为400÷50%=800人，故答案为：800；（2）“剩少量”的人数为800﹣（400+80+20）=300人，补全条形图如下：（3）估计该企业某周的工作量完成情况为“剩少量”的员工有10000×=3500人．【点评】本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．也考查了用样本估计总体．22．（7分）（2018•广东）如图，矩形ABCD中，AB＞AD，把矩形沿对角线AC所在直线折叠，使点B落在点E处，AE交CD于点F，连接DE．（1）求证：△ADE≌△CED；（2）求证：△DEF是等腰三角形．【考点】PB：翻折变换（折叠问题）；KD：全等三角形的判定与性质；LB：矩形的性质．【专题】14 ：证明题．【分析】（1）根据矩形的性质可得出AD=BC、AB=CD，结合折叠的性质可得出AD=CE、AE=CD，进而即可证出△ADE≌△CED（SSS）；（2）根据全等三角形的性质可得出∠DEF=∠EDF，利用等边对等角可得出EF=DF，由此即可证出△DEF是等腰三角形．【解答】证明：（1）∵四边形ABCD是矩形，∴AD=BC，AB=CD．由折叠的性质可得：BC=CE，AB=AE，∴AD=CE，AE=CD．在△ADE和△CED中，，∴△ADE≌△CED（SSS）．（2）由（1）得△ADE≌△CED，∴∠DEA=∠EDC，即∠DEF=∠EDF，∴EF=DF，∴△DEF是等腰三角形．【点评】本题考查了全等三角形的判定与性质、翻折变换以及矩形的性质，解题的关键是：（1）根据矩形的性质结合折叠的性质找出AD=CE、AE=CD；（2）利用全等三角形的性质找出∠DEF=∠EDF．23．（9分）（2018•广东）如图，已知顶点为C（0，﹣3）的抛物线y=ax2+b（a ≠0）与x轴交于A，B两点，直线y=x+m过顶点C和点B．（1）求m的值；（2）求函数y=ax2+b（a≠0）的解析式；（3）抛物线上是否存在点M，使得∠MCB=15°？若存在，求出点M的坐标；若不存在，请说明理由．【考点】HF：二次函数综合题．【专题】53：函数及其图象．【分析】（1）把C（0，﹣3）代入直线y=x+m中解答即可；（2）把y=0代入直线解析式得出点B的坐标，再利用待定系数法确定函数关系式即可；（3）分M在BC上方和下方两种情况进行解答即可．【解答】解：（1）将（0，﹣3）代入y=x+m，可得：m=﹣3；（2）将y=0代入y=x﹣3得：x=3，所以点B的坐标为（3，0），将（0，﹣3）、（3，0）代入y=ax2+b中，可得：，解得：，所以二次函数的解析式为：y=x2﹣3；（3）存在，分以下两种情况：①若M在B上方，设MC交x轴于点D，则∠ODC=45°+15°=60°，∴OD=OC•tan30°=，设DC为y=kx﹣3，代入（，0），可得：k=，联立两个方程可得：，解得：，所以M1（3，6）；②若M在B下方，设MC交x轴于点E，则∠OEC=45°﹣15°=30°，∴OE=OC•tan60°=3，设EC为y=kx﹣3，代入（3，0）可得：k=，联立两个方程可得：，解得：，所以M2（，﹣2），综上所述M的坐标为（3，6）或（，﹣2）．【点评】此题主要考查了二次函数的综合题，需要掌握待定系数法求二次函数解析式，待定系数法求一次函数解析式等知识是解题关键．24．（9分）（2018•广东）如图，四边形ABCD中，AB=AD=CD，以AB为直径的⊙O经过点C，连接AC，OD交于点E．（1）证明：OD∥BC；（2）若tan∠ABC=2，证明：DA与⊙O相切；（3）在（2）条件下，连接BD交于⊙O于点F，连接EF，若BC=1，求EF的长．【考点】MR：圆的综合题．【专题】15 ：综合题；55A：与圆有关的位置关系．【分析】（1）连接OC，证△OAD≌△OCD得∠ADO=∠CDO，由AD=CD知DE⊥AC，再由AB为直径知BC⊥AC，从而得OD∥BC；（2）根据tan∠ABC=2可设BC=a、则AC=2a、AD=AB==，证OE为中位线知OE=a、AE=CE=AC=a，进一步求得DE==2a，再△AOD 中利用勾股定理逆定理证∠OAD=90°即可得；（3）先证△AFD∽△BAD得DF•BD=AD2①，再证△AED∽△OAD得OD•DE=AD2②，由①②得DF•BD=OD•DE，即=，结合∠EDF=∠BDO知△EDF∽△BDO，据此可得=，结合（2）可得相关线段的长，代入计算可得．【解答】解：（1）连接OC，在△OAD和△OCD中，∵，∴△OAD≌△OCD（SSS），∴∠ADO=∠CDO，又AD=CD，∴DE⊥AC，∵AB为⊙O的直径，∴∠ACB=90°，∴∠ACB=90°，即BC⊥AC，∴OD∥BC；（2）∵tan∠ABC==2，∴设BC=a、则AC=2a，∴AD=AB==，∵OE∥BC，且AO=BO，∴OE=BC=a，AE=CE=AC=a，在△AED中，DE==2a，在△AOD中，AO2+AD2=（）2+（a）2=a2，OD2=（OF+DF）2=（a+2a）2=a2，∴AO2+AD2=OD2，∴∠OAD=90°，则DA与⊙O相切；（3）连接AF，∵AB是⊙O的直径，∴∠AFD=∠BAD=90°，∵∠ADF=∠BDA，∴△AFD∽△BAD，∴=，即DF•BD=AD2①，又∵∠AED=∠OAD=90°，∠ADE=∠ODA，∴△AED∽△OAD，∴=，即OD•DE=AD2②，由①②可得DF•BD=OD•DE，即=，又∵∠EDF=∠BDO，∴△EDF∽△BDO，∵BC=1，∴AB=AD=、OD=、ED=2、BD=、OB=，∴=，即=，解得：EF=．【点评】本题主要考查圆的综合问题，解题的关键是掌握等腰三角形的性质、全等三角形的判定与性质、相似三角形的判定与性质及勾股定理逆定理等知识点．25．（9分）（2018•广东）已知Rt△OAB，∠OAB=90°，∠ABO=30°，斜边OB=4，将Rt△OAB绕点O顺时针旋转60°，如题图1，连接BC．（1）填空：∠OBC=60°；（2）如图1，连接AC，作OP⊥AC，垂足为P，求OP的长度；（3）如图2，点M，N同时从点O出发，在△OCB边上运动，M沿O→C→B路径匀速运动，N沿O→B→C路径匀速运动，当两点相遇时运动停止，已知点M 的运动速度为1.5单位/秒，点N的运动速度为1单位/秒，设运动时间为x秒，△OMN的面积为y，求当x为何值时y取得最大值？最大值为多少？【考点】RB：几何变换综合题．【专题】152：几何综合题．【分析】（1）只要证明△OBC是等边三角形即可；（2）求出△AOC的面积，利用三角形的面积公式计算即可；（3）分三种情形讨论求解即可解决问题：①当0＜x≤时，M在OC上运动，N在OB上运动，此时过点N作NE⊥OC且交OC于点E．②当＜x≤4时，M在BC上运动，N在OB上运动．③当4＜x≤4.8时，M、N都在BC上运动，作OG⊥BC于G．【解答】解：（1）由旋转性质可知：OB=OC，∠BOC=60°，∴△OBC是等边三角形，∴∠OBC=60°．故答案为60．（2）如图1中，∵OB=4，∠ABO=30°，∴OA=OB=2，AB=OA=2，=•OA•AB=×2×2=2，∴S△AOC∵△BOC是等边三角形，∴∠OBC=60°，∠ABC=∠ABO+∠OBC=90°，∴AC==2，∴OP===．（3）①当0＜x≤时，M在OC上运动，N在OB上运动，此时过点N作NE⊥OC且交OC于点E．则NE=ON•sin60°=x，=•OM•NE=×1.5x×x，∴S△OMN∴y=x2．∴x=时，y有最大值，最大值=．②当＜x≤4时，M在BC上运动，N在OB上运动．作MH⊥OB于H．则BM=8﹣1.5x，MH=BM•sin60°=（8﹣1.5x），∴y=×ON×MH=﹣x2+2x．当x=时，y取最大值，y＜，③当4＜x≤4.8时，M、N都在BC上运动，作OG⊥BC于G．..MN=12﹣2.5x ，OG=AB=2， ∴y=•MN•OG=12﹣x ，当x=4时，y 有最大值，最大值=2，综上所述，y 有最大值，最大值为．【点评】本题考查几何变换综合题、30度的直角三角形的性质、等边三角形的判定和性质、三角形的面积等知识，解题的关键是学会用分类讨论的思想思考问题，属于中考压轴题．。

2018年中级会计《经济法》原题及答案(第2批)

一、单项选择题（本类题共30 小题，每小题1 分，共30 分。

多选、错选、不选均不得分）1、根据公司法律制度的规定，下列关于公司利润分配的表述中，正确的是（）。

A、公司股东大会可以决议在弥补亏损前向股东分配利润 B、有限责任公司股东可以约定不按出资比例分配利润 C、公司持有的本公司股份可以分配利润 D、股份有限公司章程不得规定不按持股比例分配利润【答案】B【解析】（1）选项 A：公司股东会、股东大会或者董事会“违反规定”，在公司弥补亏损和提取法定公积金之前向股东分配利润的，股东必须将违反规定分配的利润退还公司。

（2）选项BD：公司弥补亏损和提取公积金后所余税后利润，有限责任公司按照股东实缴的出资比例分配，但全体股东约定不按照出资比例分配的除外；股份有限公司按照股东持有的股份分配，但股份有限公司章程规定不按持股比例分配的除外。

（3）选项 C：公司持有的本公司股份不得分配利润。

（参考教材P74）【知识点】利润分配 2、根据专利法律制度的规定，下列行为中，构成假冒专利的是（）。

A、专利权终止前在依照专利方法直接获得的产品上标注专利标识，在专利权终止后许诺销售该产品的B、未经专利权人许可，为生产经营目的使用其专利产品 C、伪造专利证书D、专利权终止前在专利产品上标注专利标识，在专利权终止后销售该产品的【答案】C【解析】（1）选项AD：专利权终止前依法在专利产品、依照专利方法直接获得的产品或者其包装上标注专利标识，在专利权终止后许诺销售、销售该产品的，不属于假冒专利行为。

（2）选项B：未经专利权人许可，为生产经营目的制造、使用、许诺销售、销售、进口其专利产品，或者使用其专利方法以及使用、许诺销售、销售、进口依照该专利方法直接获得的产品，属于未经专利权人的许可，实施其专利的行为，不属于假冒专利行为。

（参考教材P411）【知识点】专利权的内容及其保护与限制 3、甲公司与乙公司签订买卖合同，约定甲公司先向乙公司支付货款，乙公司再向甲公司交付货物。

2018全国卷3语文(含答案)(K12教育文档)

(完整word)2018全国卷3语文(含答案)(word版可编辑修改)编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（(完整word)2018全国卷3语文(含答案)(word版可编辑修改)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为(完整word)2018全国卷3语文(含答案)(word版可编辑修改)的全部内容。

绝密★启用前2018年普通高等学校招生全国统一考试语文注意事项:1．答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答选择题时,选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时,将答案写在答题卡上.写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回.一、现代文阅读（36分）（一）论述类文本阅读（本题共3小题,9分）阅读下面的文字,完成1～3题.对城市而言，文明弹性是一个城市体在生存、创新、适应、应变等方面的综合状态、综合能力,是公共性与私人性之间、多样性与共同性之间、稳定性与变迁性之间、柔性与刚性之间的动态和谐,过于绵柔、松散，或者过于刚硬、密集，都是弹性不足或丧失的表现,是城市体出现危机的表征。

当代城市社会,尤其需要关注以下文明弹性问题。

其一，空间弹性。

城市具有良好空间弹性的一个重要表现，是空间的私人性与公共性关系能够得到较为合理的处理。

任何城市空间都是私人性与公共性的统一，空间弹性的核心问题,就是如何实现空间的公共性与私人性的有机统一、具体转换。

片面地强调空间的公共性或片面地强调空间的私人性,都会使城市发展失去基础。

目前，人们更多地要求空间的私人性，注重把空间固化为永恒的私人所有物、占有物。

2018年高考真题——理科综合(全国卷II)+Word版含答案

绝密★ 启用前2018 年一般高等学校招生全国一致考试理科综合能力测试一试题卷注意事项：1．答卷前，考生务势必自己的姓名、准考据号填写在答题卡上。

2．作答时，务势必答案写在答题卡上。

写在本试卷及底稿纸上无效。

3．考试结束后，将本试卷和答题卡一并交回。

可能用到的相对原子质量：H 1 C 12 N 14 O 16 Na 23 P 31 S 32 Fe 56一、选择题：此题共13 个小题，每题 6 分，共78 分。

在每题给出的四个选项中，只有一项为哪一项切合题目要求的。

1．以下对于人体中蛋白质功能的表达，错误的选项是A．浆细胞产生的抗体可联合相应的病毒抗原B．肌细胞中的某些蛋白质参加肌肉缩短的过程C．蛋白质联合Mg 2+形成的血红蛋白参加O2运输D．细胞核中某些蛋白质是染色体的重要构成成分2．以下有关物质跨膜运输的表达，正确的选项是A．巨噬细胞摄取病原体的过程属于辅助扩散B．固醇类激素进入靶细胞的过程属于主动运输C．神经细胞遇到刺激时产生的Na+内流属于被动运输D．护肤品中的甘油进入皮肤细胞的过程属于主动运输3．以下有关人体内激素的表达，正确的选项是A．运动时，肾上腺素水平高升，可使心率加快。

说明激素是高能化合物B．饥饿时，胰高血糖素水平高升，促使糖原分解，说明激素拥有酶的催化活性C．进食后，胰岛素水平高升，其既可加快糖原合成，也可作为细胞的构造组分D．青春期，性激素水平高升，随体液抵达靶细胞，与受体联合可促使机体发育4．有些作物的种子入库前需要经过风干办理，与风干前对比，以下说法错误的选项是A．风干种子中有机物的耗费减慢B．风干种子上微生物不易生长生殖C．风干种子中细胞呼吸作用的强度高D．风干种子中联合水与自由水的比值大5．以下对于病毒的表达，错误的选项是A ．从烟草花叶病毒中能够提取到RNAB ． T2噬菌体可感染肺炎双球菌致使其裂解C． HIV 可惹起人的获取性免疫缺点综合征D．阻断病毒的流传可降低其所致疾病的发病率6．在致癌因子的作用下，正常动物细胞可转变成癌细胞，有关癌细胞特色的表达错误的选项是A．细胞中可能发生单调基因突变，细胞间黏着性增添B．细胞中可能发生多个基因突变，细胞的形态发生变化C．细胞中的染色体可能遇到损害，细胞的增殖失掉控制D．细胞中遗传物质可能遇到损害，细胞表面的糖蛋白减少7．化学与生活亲密有关。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2018年考研心理学312真题一、单项选择题：1-65小题，每小题2分，共130分，下列每题给出的四个选项中，只有一个选项是符合题目要求的1、神经冲动的传导形式有( )A化学传导和声传导 B电传导和光传导C化学传导和电传导 D光传导和热传导2、根据鲁利亚的观点，由边缘系统与脑干网状结构等组成的机能系统是( )A平衡系统B调节系统C动力系统D信息接受、加工和存储系统3、人们在加工和处理与自己有关的信息时效率会更高，该现象被称为A自我图式 B自我意识 C自我确认 D自我参照效应4、当个体在弱光条件下直接观察物体时，往往看不清楚，但稍微移动一下物体，使其成像在视网膜边缘，则会看得清楚些。

产生这种现象的原因是：( )A视网膜边缘棒体细胞更多B视网膜边缘椎体细胞更多C视网膜中央窝对弱光最敏感D视网膜边缘对强光最敏感5、在阳光照射下，个体对波长为560nm的黄绿色光最敏感，而在黄昏时，对波长为505nm的蓝绿色光最敏感，这种现象被称为( )A.马赫带现象B.普肯耶现象C.闪光融合现象D.视觉掩蔽现象6、下列关于感觉和知觉关系的表述，错误的是( )A.知觉以感觉为基础B.知觉是个别感觉信息的累加C.知觉与感觉都是脑对直接作用于感官的事物的反映D.感觉是对事物个别属性的反映，知觉是对事物整体属性的反映7、学生很容易在作业本上看到教师用红笔写的评语，这体现的知觉特性是( )A随意注意 B不随意注意 C随意后注意 D随意前注意8、一个学生在解题时，被其他同学谈论的奇闻轶事所吸引，这种注意是( )A.随意注意B.不随意注意C.随意后注意D.随意前注意9、在睡眠的第二阶段中间或出现的频率高、波幅大的脑电波是( )A.α波B.β波C.Δ波D.纺锤波10、根据系列位置效应，个体按顺序学习一个由30个词组成的词表后，回忆正确率较低的部分是( )A开始B结尾C中间D开始和结尾11、一位老人回到阔别已久的家乡，当他走到村头时，触景生情，想起了童年往事，这个例子主要说明了（）A 痕迹衰退对于回忆的影响B 倒摄抑制对于回忆的影响C 提取线索对于回忆的影响D 动机性遗忘对于回忆的影响12、在布鲁纳的概念形成研究中，个体把第一个肯定实例所包含的全部属性都看作是未知概念的有关属性，以后每次只改变其中的一个属性，检验该属性与未知概念的关系，进而形成概念，这种概念形成的策略是（）A 保守性聚焦B 冒险性聚焦C 同时性扫描 D继时性扫描13、儿童观看“喜羊羊和灰太狼”动画片后，头脑中浮现的“灰太狼”形象是（）A 幻想B 表象C 图式D 创造想象14、有两所幼儿园可供家长选择，一所幼儿园离家远，但设施条件好，另一所幼儿园离家近，但设施条件一般，家长在做决定时由于不决，这种冲突时（）A 双趋冲突B 趋避冲突C 双避冲突D 多重趋避冲突15、动机的本能理论和驱动理论共同强调的是（）A 环境因素B 社会因素C 生物因素D 认知因素16、在情节反应中，与愤怒情绪产生关系最密切的神经中枢是A杏仁核B小脑C桥脑D延脑17、通常右图所表示的情绪理论是（）A 桑代克B 詹姆斯C 布鲁纳D 奥苏伯尔27、在某强化程序中，得到强化之前的反应数量是变化的、不可预期的。

该强化程序是（）A 固定比率程序B 可变比率程序C 固定时距程序D 可变时距程序28、奥苏伯尔解释有意义学习中的遗忘现象的理论是（）A 消退说B 同化说C 干扰说D 压抑说29、下列选项汇中，属于人本主义理论倡导的学习和教学方式的是（）A 生成学习B 结构教学C 自由学习D 程序教学30、容易导致习得性无助的归因方式是将失败归因为（）A 任务太难B 努力不够C 运气不佳D 能力不足31、学习拉丁语有助于改善记忆力，学习数学有提高推理能力。

持这种观点的迁移理论是（）A 概化理论B 相同因素说C 形式训练说D 认知迁移理论32、在“交通信号灯亮度对汽车驾驶员辨别信号灯所需时间的影响”的实验中，信号灯亮度和驾驶员辨别时间分别是（）A 自变量、因变量B 因变量、自变量C 自变量、控制变量D 因变量、控制变量33、在记忆研究中，为了防止复述产生的作用，通常采用的控制方法是（）A Donders 减因素法B Ebbinghaus 节省法C Stemberg 加因素法D Peterson-Peterson 分心法34、最早使用实验方法对注意选择性系统研究的是彻里（E.C.Cherry ）。

他的经典实验是（）A 视觉搜索实验B 双耳分听实验C 三耳人实验D 四耳人实验 35、为考察汉字字频（高频、低频）与声旁规则性（规则、不规则）对汉字阅读的影响，研究者将50名被随机分成两组，每组25名，一组既阅读高频规则字，也阅读高频不规则字，另一组既阅读低频规则字，也阅读低频不规则字。

该实验中的声旁规则性属于（）A 被试内变量B 被试间变量C 额外变量D 无关变量36、先让被试学一系列汉字，然后在测验时提供汉字的偏旁部首，让被试补写其余部分而构成一个有意义的汉字。

这种记忆测验方法是（）A 语词确定B 残词补全C 词于补笔D 语词识别37、用极限法测定绝对感觉阀限时，如果在递增序列中求得的阀限值显著大于递减序列的阀限值，则说明存在某种误差，这种误差是（）A 习惯误差B 期望误差C 练习误差D 疲劳误差38、在实验中，如果被试在自变量各个水平上的因变量作业成绩都很高且无明显差异，说明实验存在（）A 霍桑效应B 晕轮效应C 地板效应D 天花板效应39、用经典心得物理学方法测定感觉阀限容易产生序列效应，为了控制这种效应，通常采用的方法是（）A 恒定法B 消除法C 匹配法D ABBA 法40、在一项考察初中生英语学习效果的研究中，采用的教学方法有自学辅导式和启发式，使用的英语教材有A 、B 、C 三个版本。

该实验设计是（）A 二因素实验设计B 三因素实验设计C 五因素实验设计D 六因素实验设计41、在感受性测定的实验中，特定刺激条件下由被试采用不同的判断标准而得出的虚报率和击中率之间的关系曲线是（）A 回归曲线B 渐进曲线C 练习曲线D ROC 曲线42、下列关于纯音掩蔽的描述中，不正确的是（）A 掩蔽音对频率相近声音的影响最大B 掩蔽音越强，掩蔽的频率范围越大C 掩蔽音强度提高，掩蔽效果随之增加D 高频对低频的掩蔽效果要大于低频对高频的掩蔽效果更多资料，联系Q :2233548815A 连续数据B 顺序数据C 等距数据D 二分数据58、假定能力为正态分布，现取正负各三个标准差，欲将1000名被试按照能力测验成绩等距划分为好、中、差三组，下列选项中于分配到各组的被试人数最接近的是（）A 199,602,199B 179 642 179C 159 682 159D 139 722 13959、现有一列数据：4,1,4,6,6,5,7,7,4. 这列数据的中数与众数分别是（）A 6、4B 5、7C 4、4D 5、460、百分数P45=65 表示（）A 低于45分的人数占总人数的65%B 高于45分的人数占总人数的65%C 高于65分的人数占总人数的45%D 低于65分的人数占总人数的45%61、假定正常人情绪稳定性近似服从正态分布，某研究者拟根据3000正常人的情绪稳定性数据制定95%正常值范围，但计算时用了求99%置信区间的公式，产生的结果是（）A 提高了精确度B 降低了精确度C 该指标异常者容易被判为正常D 该指标正常者容易被判为异常根据下列材料，回答62-64题。

假定某门学科的测验成绩分布为正态分布，从某一学区随机抽取的65名考生的平均分为74，标准差为8.62、根据本次测验成绩，该测验分数的平均数的标准误（）A 8/√65-1B 8/√74-1 C74/√65 D 65/√7463、该学区所有考生平均成绩的99%的置信区间是（） A 73.20-74.80 B 72.04-75.96 C 72.36-75.64 D 71.42-76.5864、在其他有条件保持不变的情况下，下列叙述正确的是（）A 置信区间值越大，置信区间范围越宽B 置信区间值变小，置信区间范围不变C 显著性水平值越大，置信区间范围越宽D 显著性水平值越小，置信区间范围越窄65、如果测验的真分数方差减小，而观察分数方差不变，则误差分数方差（）A 减小B 增大C 与真分数方差的和增大D 与真分数方差的和减小二、多项选择题：66-75小题，每小题3分，共30分。

下列每题给出的四个选项中，至少有两个选项，是符合题目要求的，多选少选均不得分66、下列选项中，属于知觉恒常性的有：A 形状恒常性B 大小恒常性C 明度恒常性D 时间恒常性67、影响推理的因素有A 知识经验B 工作记忆的容量C 对前提信息加工的充分性D 前提中使用逻辑量词的气氛68、人际吸引的规则包括A 熟悉性B 表面性C 通常性D 邻近性69在下列选项中，属于卡特尔人格特质分类的有：A 根源特质B 情绪特质C 表面特质D 理智特质70、按照罗斯（E. Ross ）的研究，濒临灭亡者体验的内容有A 否认死亡B 接受死亡C 沮丧情绪D 愤怒情绪71、班杜拉认为，影响自我效能感的因素效能感的因素有更多资料，联系Q :2233548815A 直接经验B 替代经验C 言语说服D 情绪唤起72、在内隐记忆研究中，加工分离程序需要的测试条件包括A 独立条件B 结合条件C 包含条件D 排除条件73、取样时应遵循的原则有A 随机化B 代表性C 数量化D 置换性74、建立一元线性回归模型的主要方法有A 因素分析法B 平均数方法C 最小二乘法D 逐步回归法75表示测验等值结果的方法有A 图示法B 公式法C 列表法D 数轴法参考答案单选答案：1-10 ：CCDAB BDBDC11-20：CABDC ABCAB21-30：DBCAB ABBCD31-40：CADBA CADDA41-50：DDCBA CABCB51-60：ABCAD BDCDC61-65：CADAB多选答案：66：ABD 67.ABCD 68：AD 69：AC 70：ABCD71：ABCD 72：CD 73：ABD 74：BC75：ABC 三、简答题：76-80小题，每小题10分，共50分76、什么是观察法？它有何优缺点【解析】1、含义观察法是在自然条件下，对表现心理现象的外部活动讲行系统的、有计划的观察，从中发现心理现象产生和发展的规律性的方法。

例如：观察学生在课堂上的表现，可以了解其注意的稳定性、情绪状态等2、适用范围（1）对所研究的对象无法加以控制；（2）在控制条件下，可能影响某种行为的出现（3）由于社会道德的要求，不能对某种现象进行控制3、优点（1）适用范围较大（2）简便易行（3）对被观察者的行为进行直接的了解，因而能收集到第一手资料（4）被观察者处于自然状态，所得材料比较真实4、缺点（1）存在偶然性，不能揭示因果关系（2）难以讲行重复观察，观察的结果也难以进行检验和证实（3）得到的结果难以讲行精确的分析（4）由于对条件未加控制，观察时可能出现不需要研究的现象，而要研究的现象却没有出现（难以控制目标现象的出现）更多资料，联系Q :2233548815（5）观察容易“各取所需”，即观察的结果容易受至U 观察者本人的兴趣、愿望、知识经验和观察技能的影响。