2011年东城区普通校联考试卷3月
东城区一般校3月联考文科数学答案定稿
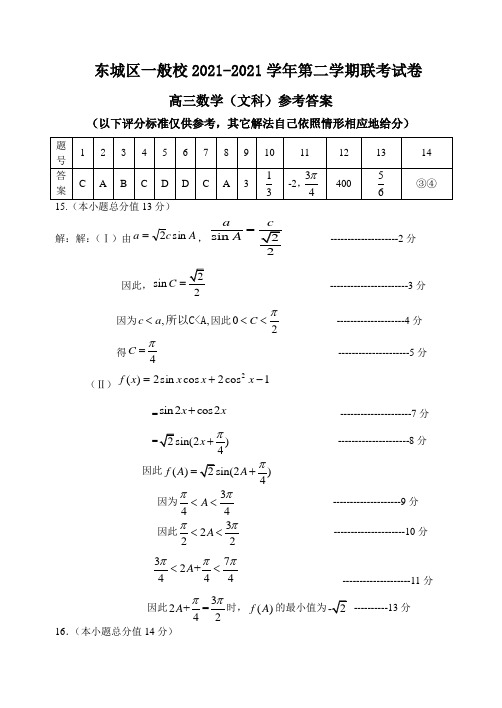
东城区一般校2021-2021学年第二学期联考试卷高三数学(文科)参考答案(以下评分标准仅供参考,其它解法自己依照情形相应地给分)15.(本小题总分值13分) 解:解:(Ⅰ)由A c a sin 2=,sin aA=--------------------2分因此,sin 2C =-----------------------3分 因为,,c a <所以C<A 因此02C π<<--------------------4分得4C π=---------------------5分(Ⅱ)1cos 2cos sin 2)(2-+=x x x x f=sin 2cos2x x + ---------------------7分)4x π+ ---------------------8分因此())4f A A π=+因为344A ππ<< --------------------9分 因此3222A ππ<< ---------------------10分 372+444A πππ<<--------------------11分 因此32+=42A ππ时,()f A的最小值为 ----------13分 16.(本小题总分值14分)解:(Ⅰ)取CE 的中点P ,连结FP 、BP , ∵F为CD 的中点,∴FP DE FP 12DE AB DE AB .21DE AB FP AB FP ABPF ∴AF BP AF ⊄BCE BP ⊂BCE AF BCE ACD ∆F CD AF CD ∵AB ACD ⊥平面,DE ∥AB ,∴DE ⊥平面ACD又AF ⊂平面ACD ,∴DE ⊥AF .又AF ⊥CD ,CD ⋂DE =D ,∴AF ⊥平面CDE -----------9分 又BP ∥AF ,∴BP ⊥平面CDE ,又BP ⊂平面BCE ,∴平面BCE ⊥平面CDE---------10分(Ⅲ)过C 作CM ⊥AD 于M ,易证 CM ⊥平面ABED ,因此CM 为四棱锥C ABED -的高 ∵直角梯形ABED 的面积为12232+⨯=, CM =323⨯=, ∴四棱锥C ABED -的体积为13333V =⨯⨯=. 即多面体C ABED -的体积为3.---------------------14分17.(本小题总分值14分)(Ⅰ)解:由于图中所有小矩形的面积之和等于1,因此10(0.0050.010.02⨯++0.0250.01)1a +++=. ----------------1分 解得0.03a =. ----------------2分 (II )解:成绩在[)40,50分数段内的人数为400.052⨯=人,别离记为A ,B . 成绩在[]90,100分数段内的人数为400.14⨯=人,别离记为C ,D ,E ,F .PM-------------------6分假设从成绩在[)40,50与[]90,100两个分数段内的学生中随机选取两名学生,那么所有的大体事件有:(),A B ,(),A C ,(),A D ,(),A E ,(),A F ,(),B C ,(),B D (),B E ,(),B F ,(),C D ,(),C E ,(),C F ,(),D E ,(),D F ,(),E F共15种. ----------------------9分若是两名学生的成绩都在[)40,50分数段内或都在[]90,100分数段内,那么这两名学生的地理成绩之差的绝对值必然不大于10.-----------------------10分 记“这两名学生的成绩之差的绝对值不大于10”为事件M ,则事件M 包括的大体事件有:(),A B ,(),C D ,(),C E ,(),C F ,(),D E ,(),D F ,(),E F 共7种.因此所求概率为()715P M =. --------------------------12分 (Ⅲ)解:依照频率散布直方图,成绩不低于60分的频率为110(0.0050.01)-⨯+0.85=.---------------------------------------13分由于该校高三年级共有学生640人,可估量该校高三年级地理成绩不低于60分的人数约为6400.85544⨯=人. -----------------------------------------14分 18.(本小题总分值13分)的概念域为),,0(+∞---------------------2分 若,0≤a 则'()0,f x >)(x f ∴在),0(+∞上单调递增,分(Ⅱ) )(x f ≤a 恒成立,即)(x f 在概念域内的最大值小于或等于a 恒成立。
2010-2011东城区高三期末统测数学(文)含答案

北京东城区2010—2011学年度第一学期期末教学统一检测数学(文)试题本试卷分第Ⅰ卷和第Ⅱ卷两部分,共150分,考试时长120分钟,考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷(选择题,共40分)一、本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项。
1.设全集U R =,集合{|1},{|05},A x x B x x =≥=≤<则集合()U C A B( )A .{|01}x x <<B .{|01}x x ≤<C .{|01}x x <≤D .{|01}x x ≤≤ 2.在复平面内,复数(1)i i -对应的点在( )A .第一象限B .第二象限C .第三象限D .第四象限 3.在等差数列4572{},15,15,n a a a a a +==中若则的值为 ( )A .—3B .0C .1D .24.直线l 过点(—4,0)且与圆22(1)(2)25x y ++-=交于A 、B 两点,如果|AB|=8,那么直线l 的方程为( )A .512200x y ++=B .512200x y -+=或40x +=C .512200x y -+=D .512200x y ++=40x +=5.已知,αβ为不重合的两个平面,直线,m α⊂那么“m β⊥”是“αβ⊥”的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件6.若0.311321log 2,log 3,()2a b c ===,则( )A .a b c <<B .a c b <<C .b c a <<D .b a c <<7.已知斜率为2的直线l 过抛物线2y ax =的焦点F ,且与y 轴相交于点A ,若OAF ∆(O为坐标原点)的面积为4,则抛物线方程为 ( )A .24y x =B .28y x =C .2244y x y x ==-或D .2288y x y x ==-或8.已知函数()f x 的定义域为R ,若存在常数0,,|()|||m x R f x m x >∈≤对任意有,则称()f x 为F 函数,给出下列函数:①()0f x =;②2()f x x =;③()s i n c o s f x x x ==;④2()1xf x x x =++;⑤()f x 是定义在R 上的奇函数,且满足对一切实数12,x x 均有1212|()()|2||.f x f x x x -≤-其中是F 函数的序号为( )A .①②④B .②③④C .①④⑤D .①②⑤第Ⅱ卷(共10分)二、填空题:本大题共6小题,每小题5分,共30分 9.已知α为第二象限角,且1sin ,3α=那么sin 2α= 。
北京东城区2011-2012学年中考数学模拟试卷(含答案)

北京东城区2011-2012年中考数学模拟试卷(满分:150分时间:120分钟)一、选择题:(本大题共8小题。
每小题3分,共24分.在每小题给出的四个选项中.只有一项是符合题目要求的,请将你认为正确的答案填涂在答题纸上)1.下列计算正确的是A.011303-⎛⎫⨯=⎪⎝⎭B.x5+x5=x10C.x8÷x2=x4 D.(-a3) 2=a62.2009年1月9日,住房和城乡建设部部长在全国建设工作会议上透露,2008年全国住房公积金缴纳规模达到了2.02万亿元,请用科学记数法表示2.02万亿元应为A.2.02×1010元B.2.02×1011元C.2.02×1012元D.2.02×1013元3. 如图所示零件的左视图是4.不等式组312840xx->⎧⎨-≥⎩的解集在数轴上表示为5.估计132128⨯+的运算结果应在A.3到4之间B.4到5之间C.5到6之间D.6到7之间6.如图,四边形ABCD是菱形,过点A作BD的平行线交CD的延长线于点E,则下列式子不成立...的是A.DA=DE B.BD=CEC.∠EAC=90° D.∠ABC=2∠E7.如图,直线32y x=-与双曲线kyx=(k>0)在第一象限内的交点为R,与x轴的交点为P,与y轴的交点为Q;作RM⊥x轴于点M,若△OPQ与△PRM的面积是4:1,则k等于正面(第3题)A.B.C.D.A.233B.3C.2 D.3第6题图第7题图第8题图8.如图1,在矩形ABCD中,动点P从点B出发,沿BC、CD、DA运动至点A停止,设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则矩形ABCD的面积是A.10 B.16 C.18 D.20二、填空题:(本大题共10小题.每小题3分.共30分.把答案填在答题纸上)9.函数y=3x中,自变量x的取值范围是▲10.因式分解:2a3-8a=▲ .11.已知一组数据:3,3,4,5,5,6,6,6.这组数据的众数是▲.12.为解决群众看病难的问题,一种药品连续两次降价,每盒的价格由原来的60元降至48.6元,则平均每次降价的百分率为▲ .13已知实数a,b同时满足a2+b2-11=0,a2-5b-5=0,则b= ▲ .14.一连串分数,共有6个,是按照一种简单规律排成的. 由于抄写的人笔头较慢,别人抄下来前3个,他只抄了前两个,把第3个空着;别人把后面3个也抄好了,他才抄了第4个和第5个,把第6个也空着. 请你帮他补上:1 20、110、、15、14、.15.如图,该图形经过折叠可以围成一个正方体,折好以后,与“静”字相对的字是▲.16.如图,在平行四边形ABCD中,DB=DC,∠A=70°,CE⊥BD于E,则∠BCE= ▲°.17.如图,将矩形纸片ABCD沿AE折叠,使点B落在直角梯形AECD的中位线FG上,若AB=3cm,则AE的长为 ▲ cm .18.如图,MN=3,以MN 为直径的⊙O 1,与一个半径为5的⊙O 2相切于点M ,正方形ABCD 的顶点A ,B 在大圆上,小圆在正方形的外部且与CD 切于点N ,则正方形ABCD 的边长为 ▲ .三、解答题:(本大题共10小题,共96分,解答应写出必要的计算过程、推演步骤或文字说明)19.(本小题满分8分)计算20.(本小题满分8分) 请先将下式化简,再选择一个适当的无理数...代入求值.2221112444x x x x ⎛⎫--÷ ⎪+--+⎝⎭36)21(60tan 1)2(100+-----π如图,方格纸上的每个小方格都是边长为1的正方形,我们把格点间连线为边的三角形称为“格点三角形”,图中的△ABC就是一个格点三角形.(1)在△ABC中,BC= ▲,tanB= ▲;(2)请在方格中画出一个格点三角形DEF,使△DEF∽△ABC,并且△DEF与△ABC的相似比为2.22.(本小题满分10分)已知:如图,在梯形ABCD中,AD∥BC,BC=DC,CF平分∠BCD,DF∥AB,BF的延长线交DC于点E.求证:(1)△BFC≌△DFC;(2)AD=DE.“农民也能报销医疗费了!”这是国家推行新型农村医疗合作的成果.村民只要每人每年交10元钱,就可以加入合作医疗,每年先由自己支付医疗费,年终时可得到按一定比例返回的返回款,这一举措极大地增强了农民抵御大病风险的能力.小华与同学随机调查了他们乡的一些农民,根据收集到的数据绘制了以下的统计图.第23题图根据以上信息,解答以下问题:(1)本次调查了▲名村民,被调查的村民中,有▲人参加合作医疗得到了返回款?(2)若该乡有10000名村民,请你估计有多少人参加了合作医疗?要使两年后参加合作医疗的人数增加到9680人,假设这两年的年平均增长率相同,求年平均增长率.24.(本小题满分10分)一个不透明的布袋内装有形状、大小、质地等完全相同的4个小球,分别标有数字1,2,3,4.(1)从布袋中随机地取出一个小球,则小球上所标的数字恰好为4的概率是▲;(2)从布袋中随机地取出一个小球,记录小球上所标的数字为x,不将取出的小球放回.........布袋,再随机地取出一个小球,记录小球上所标的数字为y,这样就确定点P的一个坐标为(x,y),求点P落在直线y=x+1上的概率;(3)从布袋中随机地取出一个小球,用小球上所标的数字作为十位上的数字,将取出小球放回.......布袋后,再随机地取出一个小球,用小球上所标的数字作为个位上的数字,求组成的两位数恰好是3的倍数的概率.BC的中点,OE交弦BC于点D,过点C作⊙O切25.(本小题满分10分)如图,AB是半圆O上的直径,E是⌒线交OE的延长线于点F. 已知BC=8,DE=2.⑴求⊙O的半径;⑵求CF的长;⑶求tan∠BAD的值AB26.(本小题满分10分)某市种植某种绿色蔬菜,全部用来出口.为了扩大出口规模,该市决定对这种蔬菜的种植实行政府补贴,规定每种植一亩这种蔬菜一次性补贴菜农若干元.经调查,种植亩数y(亩)与补贴数额x(元)之间大致满足如图1所示的一次函数关系.随着补贴数额x的不断增大,出口量也不断增加,但每亩蔬菜的收益z(元)会相应降低,且z与x之间也大致满足如图2所示的一次函数关系.(1)在政府未出台补贴措施前,该市种植这种蔬菜的总收益额为多少?(2)求政府补贴政策实施后,种植亩数y、每亩蔬菜的收益z分别与政府补贴数额x之间的函数关系式;(3)要使全市种植这种蔬菜的总收益w(元)最大,政府应将每亩补贴数额x定为多少?并求出总收益w的最大值.图1 x/元(第26题)图2x/元27.(本小题满分10分)两个全等的直角三角形ABC和DEF重叠在一起,其中∠A=60°,AC=1.固定△ABC不动,将△DEF进行如下操作:(1)如图1,△DEF沿线段AB向右平移(即D点在线段AB内移动),连结DC、CF、FB,四边形CDBF的形状在不断的变化,但它的面积不变化,四边形CDBF面积为▲;(2)如图2,当D点移到AB的中点时,请你猜想四边形CDBF的形状,并说明理由.(3)如图3,△DEF的D点固定在AB的中点,然后绕D点按顺时针方向旋转△DEF,使DF落在AB边上,此时F点恰好与B点重合,连结AE,请你求出sin∠AED的值.28.(本小题满分12分) 如图①,在平面直角坐标系中,已知△ABC 是等边三角形,点B 的坐标为(12,0),动点P 在线段AB 上从点A 向点Bt 秒.以点P 为顶点,作等边△PMN ,点M ,N 在x 轴上.(1)当t 为何值时,点M 与点O 重合.(2)求点P 坐标和等边△PMN 的边长(用t 的代数式表示).(3)如果取OB 的中点D ,以OD 为边在△AOB 内部作如图②所示的矩形ODEF ,点E 在线段AB 上.设等边△PMN 和矩形ODEF 重叠部分的面积为S ,请求出当02t ≤≤秒时S 与t 的函数关系式,并求出S 的最大值.参考答案及评分标准说明:本评分标准每题只给出了一种解法供参考,如果考生的解法与本解答不同,参照本评分标准的精神给分.一、选择题(每小题3分,共计24分)题号 1 2 3 4 5 6 78 答案 DCBCCBBD二、填空题(每小题3分,共计30分)9.X ≤3 10.2a(a+2)(a-2)11.612.10% 13. 1 14.203,103 15.着 16.20 17.23 18. 6三、解答题(本大题共10小题,共计96分)19.(本题8分)解=1-|1-3|-2+23 (4分)=1+1-3-2+23 (7分) =3 (8分)20.(本题8分)21.(本题8分)36)21(60tan 1)2(100+-----π(2)画图正确给4分23.(本题10分)24.(本题10分)25.(本题10分)(本题10分)(6分)(8分)(9分)(10分).⑴ r =5 (3分) ⑵ CF =203(3分) ⑶ tan ∠BAD =617(4分) 26.(本题10分)解:(1)政府没出台补贴政策前,这种蔬菜的收益额为30008002400000⨯=(元). ·················· 2分 (2)由题意可设y 与x 的函数关系为800y kx =+,将(501200),代入上式得120050800k =+, 得8k =,所以种植亩数与政府补贴的函数关系为8800y x =+. ········ 4分 同理可得,每亩蔬菜的收益与政府补贴的函数关系为33000z x =-+. · 5分 (3)由题意(8800)(33000)u yz x x ==+-+ ·············· 7分224216002400000x x =-++224(450)7260000x =--+. ·················· 8分所以当450x =,即政府每亩补贴450元时,全市的总收益额最大,最大值为7260000元. ································ 10分注:本卷只在第26题中,学生若出现答题时未写单位或未答分别扣除1分. 27.(本题10分)28.(本题12分)(1)如图①,点M与点O重合.∵△ABC是等边三角形,∴∠ABO=30°,∠BAO=60°.由OB=12,∴AB,AO.∵△PON是等边三角形,∴∠PON=60°.∴∠AOP=60°.∴AO=2AP,即.解得t=2.∴当t=2时,点M与点O重合.………………4分2)如图②,过P分别作PQ⊥OA于点Q,PS⊥OB于点S.可求得AQ=12AP PS=QO∴点P坐标为(t23,.………………6分在Rt△PMS中,sin60°=PSPM,∴PM=(-=8-t.………………8分(3)(Ⅰ)当0≤t≤1时,见图③.设PN交EF于点G,则重叠部分为直角梯形FONG,作GH⊥OB于点H.∵∠GNH=60°,GH HN=2.∵MP=8-t,∴BM=2MP=16-2t.∴OM=BM-OB=16-2t-12=4-2t.∴ON=MN-OM=8-t-(4-2t)=4+t.∴FG=OH=ON-HN=4+t-2=2+t.∴S=12(2+t+4+t+∵S随t的增大而增大,∴当t=1时,S最大.…10分(Ⅱ)当1<t≤2时,见图④.设PM交EF于点I,交FO于点Q,PN交EF于点G.重叠部分为五边形OQIGN.OQ,FQ-FI =2t -2.∴三角形QFP 的面积=12-t -(t 2-2t +1).由(Ⅰ)可知梯形OFGN 的面积+∴S +t 2-2t +1)=-t 2-3t -2).∵-0,∴当t =32时,S 有最大值,S 最大.综上所述:当0≤t ≤1时,S +1<t ≤2时,S =-2++;∵2>,∴S 的最大值是2. ……………………12分。
北京东城区2011-2012学年中考数学模拟试卷(含答案)

14.一连串分数,共有 6 个,是按照一种简单规律排成的 . 由于抄写的人笔头较慢,别人抄下来前 3 个,
他只抄了前两个,把第 3 个空着;别人把后面 3 个也抄好了,他才抄了第 4 个和第 5 个,把第 6 个也空
着 . 请你帮他补上:
1、 1、 20 10
、1、1、
.
54
15.如图,该图形经过折叠可以围成一个正方体,折好以后,与“静”字相对的字是
( 6 分)
( 8 分) ( 9 分) ( 10 分)
25.(本题 10 分)
- 11 - / 14
. ⑴ r =5 (3 分) ⑵ CF= 20 ( 3 分) ⑶ tan ∠BAD= 6 (4 分)
3
17
26.(本题 10 分)
解:( 1)政府没出台补贴政策前,这种蔬菜的收益额为
3000 800 2400000(元). ·················· 2 分
上,小圆在正方形的外部且与 CD切于点 N,则正方形 ABCD的边长为
▲.
三、解答题: ( 本大题共 10 小题,共 96 分,解答应写出必要的计算过程、推演步骤或文字说明
)
19. ( 本小题满分 8 分 ) 计算
(
2)0
1 tan 600
1 ()
1
6
2
3
20. ( 本小题满分 8 分 ) 请先将下式化简,再选择一个适当的无理数...代入求值.
7260000 元.
································
10 分
注:本卷只在第 26 题中,学生若出现答题时未写单位或未答分别扣除
1 分.
27.(本题 10 分)
2011年东城区中考一模语文试题及答案【word版】

二、填空(共8分)7.默写(5分)(1)不畏浮云遮望眼,。
(王安石《登飞来峰》)(1分)(2),零丁洋里叹零丁。
(文天祥《过零丁洋》)(1分)(3)人有悲欢离合,,此事古难全。
(苏轼《水调歌头·明月几时有》)(1分)(4)《小石潭记》中写出潭水空明澄澈的句子是:,。
(2分)8.名著阅读(3分)《朝花夕拾》是鲁迅唯一一本散文集,是他回忆童年、少年和青年时期不同生活经历与体验的文字。
在我们学过的课文中,有表现鲁迅初上学时,跟随寿镜吾老先生在①学习时的情景;有得到第一部《山海经》时,对家中女工②深深的敬意;有在日本留学时,目睹国人麻木的精神状态,最终决定③的经历。
四、文言文阅读(共9分)阅读《邹忌讽齐王纳谏》,完成12~14题。
①邹忌修八尺有余,而形貌昳丽。
朝服衣冠,窥镜,谓其妻曰:“我孰与城北徐公美?”其妻曰:“君美甚,徐公何能及君也?”城北徐公,齐国之美丽者也。
忌不自信,而复问其妾曰:“吾孰与徐公美?”妾曰:“徐公何能及君也?”旦日,客从外来,与坐谈,问之客曰:“吾与徐公孰美?”客曰:“徐公不若君之美也。
”明日徐公来,孰视之,自以为不如;窥镜而自视,又弗如远甚。
暮寝而思之,曰:“吾妻之美我者,私我也;妾之美我者,畏我也;客之美我者,欲有求于我也。
”②于是入朝见威王,曰:“臣诚知不如徐公美。
臣之妻私臣,臣之妾畏臣,臣之客欲有求于臣,皆以美于徐公。
今齐地方千里,百二十城,宫妇左右莫不私王,朝廷之臣,莫不畏王,四境之内莫不有求于王:由此观之,王之蔽甚矣。
”③王曰:“善。
”乃下令:“群臣吏民能面刺寡人之过者,受上赏;上书谏寡人者,受中赏;能谤讥于市朝,闻寡人之耳者,受下赏。
”令初下,群臣进谏,门庭若市;数月之后,时时而间进;期年之后,虽欲言,无可进者。
燕、赵、韩、魏闻之,皆朝于齐。
此所谓战胜于朝廷。
12.解释下列语句中加点词的意思。
(2分)(1)客之美.我者美:(2)能面刺.寡人之过者刺:13.用现代汉语翻译下面的语句。
高中高考-2011东城期末答案

参考答案及评分标准第I 卷 (选择题 共42分)24分,每题2分第II 卷 (非选择题 共58分)19.(12分,每空2分)(1)温度升高,氨在混合气体中的体积分数减小,平衡逆向移动,温度升高平衡向着吸热反应方向移动,故正反应是放热反应(2)N 2(g)+3H 2(g) =2NH 3(g) △H =-92.2 kJ ﹒mol -1 (3)1.5 mol ﹒L -1﹒min -1。
;降低温度 (4) ac20.(11分,除(1)1分外,其余每空2分)(1)过滤 (2)Na +、 AlO 2- 、OH - ; 稀硫酸(3)Al(OH)3+3H +=Al 3++3H 2O 在装置Ⅰ、Ⅱ之间增加一个盛有饱和NaHCO 3溶液的洗气瓶(合理答案给分)(4)2Cu+O 2+2H 2SO 4 =2CuSO 4+2H 2O (合理答案给分) 21.(12分,每空2分) (1)(2)2NH 4Cl+Ca(OH)2CaCl 2+2NH 3↑+2H 2O ;用湿润的红色石蕊试纸接近容器口,观察试纸变蓝,证明已满 (合理答案给分) (3)BaO 2+ H 2SO 4=H 2O 2+BaSO 4↓(4)2H ++2e -=H 2↑;S 2O 82-+2H 2O= H 2O 2+2HSO 4-22.(9分,除电极名称1分外,其余每空2分)(1)铜溶解,生成无色气体,溶液由无色变蓝色。
探究NO 3-在酸、碱性溶液中的氧化性 (2)①正;铁在浓硝酸中迅速氧化,在其表面形成致密的氧化膜,阻碍了内层铁进一步与浓硝酸反应(铁在浓硝酸中钝化)②NO 3-+4H ++3e -= NO↑+2H 2O 23.(14分,每空2分)(1)c (2)NaOH 水溶液;加聚反应;羧基、羟基(3)(4)6 (5)CH 3CH 2CH(OH)COOH△。
2011北京东城中考一模数学(word解析)
2011年东城区中考一模数学试卷一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个是符合题意的. 1.2-的相反数是( ). A .2 B .12 C .12- D .2-2.根据国家统计局的公布数据,2010年我国GDP 的总量约为398000亿元人民币.将398000用科学记数法表示应为( ).A .339810⨯B .60.39810⨯C .53.9810⨯D .63.9810⨯3.如图,直线AB CD ∥,70A ∠=︒,40C ∠=︒,则E ∠等于( ).A .30︒B .40︒C .60︒D .70︒4.如图,在ABC △中,D 、E 分别是BC 、AC 边的中点.若2DE =,则AB 的长度是( ).A .6B .5C .4D .35.甲、乙、丙、丁四名学生10次小测验成绩的平均数(单位:分)和方差如下表:则这四人中成绩最稳定的是( ).A .甲B .乙C .丙D .丁6.已知圆锥的母线长为4,底面半径为2,则圆锥的侧面积等于( ).A .11πB .10πC .9πD .8π7.若从1099 这连续90个正整数中选出一个数,其中每个数被选出的机会相等,则选出的数其十位数字与个位数字的和为9的概率是( ). A .190 B .110 C .19 D .4458.如图,在矩形ABCD 中,5AB =,4BC =,E 、F 分别是AB 、AD 的中点.动点R 从点B 出发,沿B C D F →→→方向运动至点F 处停止.设点R 运动的路程为x ,EFR △的面积为y ,当y 取到最大值时,点R 应运动到( ). A .BC 的中点处 B .C 点处 C .CD 的中点处 D .D 点处 选 手 甲 乙 丙 丁 平均数 92 92 92 92 方差 0.035 0.015 0.0250.027二、填空题(本题共16分,每小题4分) 9.若分式35x +有意义,则x 的取值范围是____________.10.分解因式:22a b ab b -+=_______________.11.已知A 、B 是抛物线243y x x =-+上关于对称轴对称的两点,则A 、B 的坐标可能是 .(写出一对即可)12.如图,直线33y x =,点1A 坐标为(1,0),过点1A 作x 轴的垂线交直线于点1B ,以原点O 为圆心,1OB 长为半径画弧交x 轴于点2A ;再过点2A 作x 轴的垂线交直线于点2B ,以原点O 为圆心,2OB 长为半径画弧交x 轴于点3A ,…,按此做法进行下去,点4A 的坐标为( , );点n A ( , ).三、解答题(本题共30分,每小题5分) 13.计算:084sin45(3)4-︒+-π+-.14.求不等式组46,1(3)22x x +≤⎧⎪⎨->-⎪⎩的整数解.15.先化简,再求值:2232()111x x xx x x +÷---,其中31x =-.16.如图,在四边形ABCD 中,AC 是DAE ∠的平分线,DA CE ∥,AEB CEB ∠=∠.求证:AB CB =.17.列方程或方程组解应用题随着人们节能意识的增强,节能产品进入千家万户,今年1月小明家将天燃气热水器换成了太阳能热水器.去年12月份小明家的燃气费是96元,从今年1月份起天燃气价格每立方米上涨25%,小明家2月份的用气量比去年12月份少10立方米,2月份的燃气费是90元.问小明家2月份用气多少立方米.18.如图,在平行四边形ABCD 中,过点A 分别作AE BC ⊥于点E ,AF CD ⊥于点F . (1)求证:BAE DAF ∠=∠;(2)若4AE =,245AF =,3sin 5BAE ∠=,求CF 的长.四、解答题(本题共20分,每小题5分)19.某中学的地理兴趣小组在本校学生中开展主题为“地震知识知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,划分等级后的数据整理如下表:等级 非常了解 比较了解 基本了解不太了解频数40120n4 频率0.2 m 0.18 0.02(1)表中的m 的值为_______,n 的值为 .(2)根据表中的数据,请你计算“非常了解”的频率在下图中所对应的扇形的圆心角的度数,并补全扇形统计图.(3)若该校有1500名学生,请根据调查结果估计这些学生中“比较了解”的人数约为多少?20.已知:AB 是⊙O 的弦,OD AB ⊥于M 交⊙O 于点D ,CB AB ⊥交AD 的延长线于C . (1)求证:AD DC =;(2)过D 作⊙O 的切线交BC 于E ,若2DE =,1CE =,求⊙O 的半径.21.在平面直角坐标系xOy 中,一次函数1y k x b =+与反比例函数2ky x=的图象交于(1,6)A ,(,3)B a 两点. (1)求1k ,2k 的值;(2)如图,点D 在x 轴上,在梯形OBCD 中,BC OD ∥,OB DC =,过点C 作CE OD ⊥于点E ,CE 和反比例函数的图象交于点P ,当梯形OBCD 的面积为18时,求:PE PC 的值.22.如图1,在ABC △中,已知45BAC ∠=︒,AD BC ⊥于D ,2BD =,3DC =,求AD 的长. 小萍同学灵活运用轴对称知识,将图形进行翻折变换如图1.她分别以AB 、AC 为对称轴,画出ABD △、ACD △的轴对称图形,D 点的对称点为E 、F ,延长EB 、FC 相交于G 点,得到四边形AEGF 是正方形.设AD x =,利用勾股定理,建立关于x 的方程模型,求出x 的值. (1)请你帮小萍求出x 的值.(2)参考小萍的思路,探究并解答新问题:如图2,在ABC △中,30BAC ∠=︒,AD BC ⊥于D ,4AD =.请你按照小萍的方法画图,得到四边形AEGF ,求BGC △的周长.(画图所用字母与图1中的字母对应)图1 图五、解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23.已知关于x 的方程2(1)(21)20m x m x ---+=有两个正整数根. (1)确定整数m 值;(2)在(1)的条件下,利用图象写出方程2(1)(21)2+0mm x m x x---+=的实数根的个数.24.等边ABC △边长为6,P 为BC 边上一点,60MPN ∠=︒,且PM 、PN 分别于边AB 、AC 交于点E 、F .(1)如图1,当点P 为BC 的三等分点,且PE AB ⊥时,判断EPF △的形状;(2)如图2,若点P 在BC 边上运动,且保持PE AB ⊥,设BP x =,四边形AEPF 面积的y ,求y 与x 的函数关系式,并写出自变量x 的取值范围; (3)如图3,若点P 在BC 边上运动,且MPN ∠绕点P 旋转,当2CF AE ==时,求PE 的长.图1 图2 图3A-,B,与y轴交于点C,25.如图,已知二次函数28(0)y ax bx a=++≠的图像与x轴交于点(2,0)ABC∠=.tan2(1)求抛物线的解析式及其顶点D的坐标;(2)设直线CD交x轴于点E.在线段OB的垂直平分线上是否存在点P,使得经过点P的直线PM垂直于直线CD,且与直线OP的夹角为75︒?若存在,求出点P的坐标;若不存在,请说明理由;(3)过点B作x轴的垂线,交直线CD于点F,将抛物线沿其对称轴向上平移,使抛物线与线段EF总有公共点.试探究:抛物线最多可以向上平移多少个单位长度?2011年东城区中考一模数学试卷答案一、选择题(本题共32分,每小题4分)题 号 1 2 3 4 5 6 7 8 答 案ACACBDBB二、填空题(本题共16分,每小题4分)题 号 9 10 11 12 答 案5x ≠2(1)b a -(1,0),(3,0)或 (0,3),(4,3)等839,0 123()3n -,三、解答题:(本题共30分,每小题5分) 13.(本小题满分5分)解:084sin45(3)4-︒+-π+-2=224+1+42-⨯ =5.14.(本小题满分5分) 解:由①得:2x ≤.由②得:34x ->-,解得1x >-.∴原不等式组的解集为12x -<≤. ∴原不等式组的整数解为0,1,2. 15.(本小题满分5分)解:2232()111x x xx x x +÷--- 2321=[](1)(1)1x x x x x x x--⨯-+- 3=21xx -+ 2=1x x -+. 当31x =-时, 原式233=1313x x --==-+.16.(本小题满分5分)-12 0 1CD3∴12∠=∠. 又∵AD EC ∥, ∴23∠=∠. ∴13∠=∠.∴AE CE =.在ABE △和CBE △中, AE CE AEB CEB BE BE =⎧⎪∠=∠⎨⎪=⎩∴ABE CBE ≅△△. ∴AB CB =.17.(本小题满分5分)解:设小明家2月份用气x 立方米,则去年12月份用气(10)x +立方米.根据题意,得90969625%1010x x x -=⨯++. 解这个方程,得30x =. 经检验,30x =是所列方程的根. 答:小明家2月份用气30立方米. 18.(本小题满分5分) 证明:(1)∵四边形ABCD 是平行四边形, ∴B D ∠=∠.又 AE BC ⊥,AF CD ⊥, ∴AEB AFD ∠=∠. ∴BAE DAF ∠=∠.(2)在Rt ABE △中,3sin =5BAE ∠,4AE =,可求5AB =.又∵BAE DAF ∠=∠,∴3sin sin =5DAF BAE ∠=∠.在Rt ADF △中,245AF =,3sin 5DAF ∠=,可求185DF =.∵5CD AB ==. ∴187555CF =-=.四、解答题(本题共20分,每小题5分) 19.(本小题满分5分) 解:(1)0.6;36; (2)72︒;补全图如下:ABCDEF(3)15000.6900⨯=.答:学生中“比较了解”的人数约为900人. 20.(本小题满分5分)(1)证明:在⊙O 中,OD AB ⊥,CB AB ⊥, ∴AM M B =,OD BC ∥. ∴AD DC =.(2)∵DE 为⊙O 切线, ∴OD DE ⊥∴四边形M BED 为矩形. ∴DE AB ∥.∴2M B DE ==,1MD BE EC ===. 连接OB .在Rt OBM △中,222OB OM BM =+.解得52OB =. ⊙O 的半径为52.21.(本小题满分5分) 解:(1)∵点(1,6)A ,(,3)B a 在反比例函数2k y x=的图象上, ∴2166k =⨯=. ∴36a ⨯=,2a =. ∴(2,3)B .由点(1,6)A ,(2,3)B 也在直线1y k x b =+上, 得11623k b k b +=⎧⎨+=⎩ 解得139k b =-⎧⎨=⎩.∴13k =-,26k =.(2)设点P 的坐标为(,)m n .依题意,得13(22)182m m ⨯++-=,6m =.C DxyOEPA BMOABCD E∴(6,3)C ,(6,0)E . ∵点P 在反比例函数6y x=的图象上, ∴1n =.∴:1:2PE PC =.22.(本小题满分5分)解:(1)设AD x =,由题意得,2BG x =-,3CG x =-. 在Rt BCG △中,由勾股定理可得222(2)(3)5x x -+-=. 解得6x =.(2)参考小萍的做法得到四边形AEGF ,60EAF ∠=︒, 120EGF ∠=︒,90AEG AFG ∠=∠=︒,4AE AF AD ===. 连结EF ,可得AEF △为等边三角形. ∴4EF =.∴30FEG EFG ∠=∠=︒. ∴EG FG =.在EFG △中,可求,433EG =, ∴BGC △的周长8233BG CG BC BG CG EB FC EG =++=+++==.五、解答题:(本题共22分,第23题7分,第24题7分,第25题8分) 23.(本小题满分7分)解:由方程2(1)(21)20m x m x ---+=可得2(21)(21)4(1)22(1)m m m x m --±--⨯-⨯=- 2(21)(23)=2(1)m m m -±-- 21(23)2(1)m m m -±+=-111x m =-,2 2.x = ∵1x ,2x 均为正整数,m 也是整数, ∴2m =.(2)由(1)知22320x x x-++=. ∴2232=x x x-+-. 画出函数232y x x =-+,2y x =-的图象,由图象可知,两个函数图象的交点个数是1.Oxy24.(本小题满分7分) (1)EPF △为等边三角形. (2)设=BP x ,则6CP x =-. 由题意可BEP △的面积为238x . CFP △的面积为23(6)2x -. ABC △的面积为93.设四边形AEPF 的面积为y . ∴93y =-238x 23(6)2x --25=363938x x -+-. 自变量x 的取值范围为36x <<.(3)可证EBP PCF ∽△△.∴BP BECF CP =. 设BP x =, 则(6)8x x -=. 解得14x =,22x =.∴PE 的长为4或23. 25.(本小题满分8分) 解:(1)依题意,可知(0,8)C ,则(4,0)B 将(2,0)A -,(4,0)B 代入28y ax bx =++, 4280,16480.a b a b -+=⎧⎨++=⎩ 解得1,2.a b =-⎧⎨=⎩ ∴228y x x =-++配方得2(1)9y x =--+,顶点(1,9)D .(2)假设满足条件的点P 存在,依题意设(2,)P t , 由(0,8)C ,(1,9)D 求得直线CD 的解析式为8y x =+, 它与x 轴的夹角为45︒. 过点P 作PN y ⊥轴于点N .依题意知,30NPO ∠=︒或60NPO ∠=︒. ∵2PN =,∴233ON =或23. ∴存在满足条件的点P ,P 的坐标为23(2,)3和(2,23).(3)由上求得(8,0)E -,(4,12)F .当抛物线向上平移时,可设解析式为228(0)y x x m m =-+++>. 当8x =-时,72y m =-+. 当4x =时,y m =.FP 2M 2N 2P 1N 1M 1HABOxy CD11E∴720m -+≤或12m ≤.由题意可得m 的范围为072m <≤. ∴抛物线最多可向上平移72个单位.2011年东城区中考一模数学试卷答案部分解析一、选择题 1. 【答案】A【解析】2-的相反数是2,故选A .2. 【答案】C【解析】398000用科学记数法表示为53.9810⨯,故选C .3. 【答案】A【解析】∵AB CD ∥,∴70A DFE ∠=∠=︒,∵DFE C E ∠=∠+∠,40C ∠=︒,∴30E ∠=︒,故选A .4. 【答案】C【解析】∵AE CE =,BD CD =,∴122DE AB ==,4AB =,故选C .5. 【答案】B【解析】这四个人10次小测验成绩的平均数相同,方差小的波动越小,成绩越稳定,故选B .6. 【答案】D【解析】圆锥的侧面积等于π24π=8πrl =⨯,故选D .7. 【答案】B【解析】1099 这连续90个正整数中选出的数其十位数字与个位数字的和为9的有18,27,36,45,54,63,72,81,90共9个,所以概率为91=9010,故选B .8. 【答案】B【解析】点R 在运动过程中EF 保持不变,当R 在BC 上运动时,点R 到直线EF 的距离越来越大,即高越来越大,故EFR △的面积也在变大;当R 在CD DF →上运动时,点R 到直线EF 的距离越来越小,即高越来越小,故EFR △的面积也在变小;所以当R 运动到C 点处时,EFR △的面积取到最大值.故选B .二、填空题 9. 【答案】5x ≠【解析】分式35x +有意义,分母不为0,即+50x ≠,5x ≠-. 故答案为:5x ≠.10. 【答案】2(1)b a -【解析】分解因式2222(21)(1)a b ab b b a a b a -+=-+=-. 故答案为:2(1)b a -.11. 【答案】(1,0),(3,0)或(0,3),(4,3)等【解析】令0y =,即243(1)(3)0x x x x -+=--=,11x =,23x =; 令3y =,即243=3x x -+,24(4)0x x x x -=-=,30x =,44x =. 故答案为:(1,0),(3,0)或(0,3),(4,3)等.12. 【答案】839,0;123()3n -,0 【解析】依题可知1(1,0)A ,13(1,)3B ,12233OB OA ==; 即223(,0)3A ,2232(,)33B ,2343OB OA ==; 34(,0)3A ,3443(,)39B ,34839OB OA ==; 有题意可知324123122333n n OA OA OA OA OA OA OA OA -======L , 故n OA 的长度是一个以1为首项,以233为公比的等比数列,故123((),0)3n n A - 故答案为:839,0;123()3n -,0.。
北京市东城区2011学年度第二学期高三综合练习(一)
北京市东城区2011学年度第二学期高三综合练习(一)数学(理科)(东城一模)(时间:120分钟总分:150分)第1卷(选择题共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.””是““4,2.12>>x x 的 ( ) A .充分不必要条件 B .必要不充分条件 C.充要条件 D .既不充分也不必要条件2.已知数列}{n a 为等差数列,且,13,2321=+=a a a 则+4a 65a a +等于 ( )40.A 42.B 43.C 45.D3.已知函数对任意的,R x ∈有,0)()(=--x f x f 且当>x 0时,),1ln()(+=x x f 则函数)(x f 的图象大致为 ( )4.已知平面上不重合的四点P ,A ,B ,C 满足++,,0AP m AC AB =+=且那么实数m 的值为( )2.A3.B4.C5.D5.若下边的程序框图输出的S 是126,则条件①可以为 ( )5.≤n A6.≤n B7.≤n C8.≤n D6.已知,71)4tan(),,2(=+∈παππα那么ααcos sin +的值为 ( ) 51-A 57.B 57.c 43.D 7.已知函数,)21()(31x x f x -=那么在下列区间中含有函数)(x f 的零点的是 ( ))31,0.(A )21,31.(B )32,21.(C )1,32.(D 8.空间内点到平面的距离定义如下:过空间内一点作平面的垂线,这点和垂足之间的距离叫做这个点到这个平面的距离.平面γβα,,两两互相垂直,点,α∈A 点A 到平面γβ,的距离都是3,点P 是α上的动点,且满足P 到β的距离是P 到点A 的距离的2倍,则点P 到平面y 的距离的最小值为 ( )33.-A 3.B 33.+C 6.D第Ⅱ卷(非选择题共110分)二、填空题:本大题共6小题,每小题5分,共30分,把答案填在题中横线上.9.如果)1)((2mi i m ++是实数,那么实数m=10.若曲线C 的参数方程为θθθ(,sin cos 2⎩⎨⎧=+=y x 为参数),则曲线C 上的点到直线0443=+-y x 的距离的最大值为____.11.从某地区随机抽取100名高中男生,将他们的体重(单 位:kg)数据绘制成频率分布直方图(如图).由图中数据 可知体重的平均值为____ kg;若要从身高在[60,70),[70,80),[80,90]三组内的男生中,用分层抽样的 方法选取12人参加一项活动,再从这12人选两人当正、副队长,则这两人身高不在同一组内的概率为____.12.如图,已知圆0的半径为3,从圆O 外一点A 引切线AD 和割线ABC ,若圆心O 到AC 的距离为,3,22=AB则切线AD 的长为13.过抛物线)0(22 >=P Px y 的焦点F 作倾斜角为60的直线与抛物线分别交于A ,B 两点(点A 在x 轴上方),那么=||||BF AF 14.已知数列}{n a 满足:,5,4,3,2,154321=====a a a a a 且当5≥n 时,,1...211-=+n n a a a a 若数列}{n b 满足对任意*,N n ∈有,2222121n n n a a a a a a b ----⋅⋅= 则=5b ;当5≥n 时,=n b三、解答题:本大题共6小题,共80分,解答应写出文字说明,演算步骤或证明过程.15.(本小题共13分)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且满足⋅=-AB a b c cos cos 2 (I )求角A 的大小;(Ⅱ)若,52=a 求△ABC 的面积的最大值.16.(本小题共13分)如图,四棱锥P-ABCD 的底面是菱形,,2,60====∠PD PB AD BCD AC P,3C = 与BD 交于点0.E ,H 分别为PA ,OC 的中点. (I)求证:PC∥平面BDE;(Ⅱ)求证:PH ⊥平面ABCD ;(Ⅲ)求直线CE 与平面PAB 所成角的正弦值.17.(本小题共13分)甲、乙、丙三人参加一家公司的招聘面 试,面试合格者可正式签约,甲表示只要面试合格就签 约,乙、丙则约定:两人面试都合格就一同签约,否则两人都不签约.设甲面试合格的概率为,21乙、丙面试合格的概率都是,31且面试是否合格互不影响. (I)求至少有1人面试合格的概率;(Ⅱ)求签约人数ξ的分布列和数学期望,18.(本小题共14分)已知函数x ex x g x x x f ==)(,ln )(⋅-e 2 (I)求)(x f 在区间[1,3]上的最小值;(Ⅱ)证明:对任意),,0(,+∞∈n m 都有)()(n g m f ≥成立. 19.(本小题共14分)已知椭圆)0(12222>>=+b a bx a y 的离心率为,22且椭圆上的点到两个焦点的距离之和为,22斜率为)0(=/k k 的直线L 过椭圆的上焦点且与椭圆相交于P ,Q 两点,线段PQ 的垂直平分线与y 轴相交于点 M(O ,m).(I)求椭圆的方程;(Ⅱ)求m 的取值范围;(Ⅲ)试用m 表示△MPQ 的面积,并求面积的最大值.20.(本小题共13分)对于),2.*≥∈n N n 定义一个如下数阵:,ln 21222211211⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⋅=m n n n m a a a a a a a a a A 其中对任意的,1,1n j n i ≤≤≤≤当i 能整除j 时,=ij a ;1当i 不能整除J 时,.0=ij a设⋅+++==-∑=nj j n i j ij a a a aj t 211)((I)当n=6时,试写出数阵66A 并计算);(61j t j ∑=(Ⅱ)若[x]表示不超过x 的最大整数,求证:=∑=)(1j t n j ];[1i nn i ∑= (Ⅲ)若,1)(),(.1)(11dx x n g j t n n f n nj ⎰∑===求证:1)(-n g .1)()(+<<n g n f。
北京市东城区2011高三一模理科数学试题及答案(理科详解)(已导入)
北京市东城区2011高三一模理科数学试题及答案(理科详解)(已导入)一、选择题(共8小题;共40分)1. " "是" "的 ( )A. 充分非必要条件B. 必要非充分条件C. 充要条件D. 既不充分也不必要条件2. 已知数列为等差数列,且,,则等于 ( )A. B. C. D.3. 已知函数对任意的有,且当时,,则函数的大致图像为 ( )A. B.C. D.4. 已知平面上不重合的四点,,,满足,且,那么实数的值为 ( )A. B. C. D.5. 若下面的程序框图输出的是,则条件①可为 ( )A. B. C. D.6. 已知,,那么的值为 ( )A. B. C. D.7. 已知函数,那么在下列区间中含有函数零点的是 ( )A. B. C. D.8. 空间点到平面的距离定义如下:过空间一点作平面的垂线,这个点和垂足之间的距离叫做这个点到这个平面的距离.已知平面,,两两互相垂直,点,点到、的距离都是,点是上的动点,满足到的距离是到点距离的倍,则点的轨迹上的点到的距离的最小值是 ( )A. B. C. D.二、填空题(共6小题;共30分)9. 如果是实数,那么实数.10. 已知曲线的参数方程为(为参数),则曲线上的点到直线的距离的最大值为.11. 从某地高中男生中随机抽取名同学,将他们的体重(单位:)数据绘制成频率分布直方图(如图).由图中数据可知体重的平均值为;若要从体重在三组内的男生中,用分层抽样的方法选取人参加一项活动,再从这人选两人当正负队长,则这两人身高不在同一组内的概率为.12. 如图,已知圆的半径为,从圆外一点引切线和割线,圆心到的距离为,,则切线的长为.13. 过抛物线的焦点作倾斜角为的直线,与抛物线分别交于、两点(点在轴上方),则.14. 已知数列满足:,,,,,且当时,,若数列满足对任意,有,则;当时,.三、解答题(共6小题;共78分)15. 在中,角,,的对边分别为、、,且满足.(1)求角的大小;(2)若,求面积的最大值.16. 已知四棱锥的底面是菱形.,,,与交于点,,分别为、的中点.(1)求证:平面;(2)求证:平面;(3)求直线与平面所成角的正弦值.17. (本小题共13分)甲、乙、丙三人参加了一家公司的招聘面试,面试合格者可正式签约,甲表示只要面试合格就签约.乙、丙则约定:两人面试都合格就一同签约,否则两人都不签约.设甲面试合格的概率为,乙、丙面试合格的概率都是,且面试是否合格互不影响.(1)求至少有1人面试合格的概率;(2)求签约人数的分布列和数学期望.18. 已知函数,.(1)求函数在区间上的最小值;(2)证明:对任意,都有成立.19. 已知椭圆的离心率为,且两个焦点和短轴的一个端点是一个等腰直角三角形的顶点.斜率为的直线过椭圆的上焦点且与椭圆相交于,两点,线段的垂直平分线与轴相交于点.(1)求椭圆的方程;(2)求的取值范围;(3)试用表示的面积,并求面积的最大值.20. 对于,定义一个如下数阵:其中对任意的,,当能整除时,;当不能整除时,.设.(1)当时,试写出数阵并计算;(2)若表示不超过的最大整数,求证:;(3)若,,求证:.答案第一部分1. A2. B 【解析】由条件可得公差,.3. D4. B 【解析】.5. B【解析】,;,;,;,;,;,,故若输出,条件①应为.6. A 【解析】,由条件可知在第三象限,由7. B 【解析】,,含有零点的区间是.8. A 【解析】解法一:构造空间长方体,取坐标轴如图所示:由条件可得点坐标为,由到的距离是到点距离的倍可得关系式,当时,右边取得最大值,此时,所以点的轨迹上的点到的距离的最小值为.解法二:仍然取图中的坐标系,点到的距离就是点到轴的距离,所以这个问题可以转化为:在平面内,求到点的距离与到轴的距离的比为的点的轨迹问题.根据椭圆的第二定义,满足条件的点的轨迹是以点为一个焦点,轴为相应准线的椭圆.而且可得解得,,,画出椭圆如图,点的轨迹上的点到的距离为点到轴的距离,由椭圆的基本性质可知,点的轨迹上的点到的距离的最小值为.第二部分9.10.【解析】曲线的普通方程为,问题转化为求圆上的任意一点到直线距离的最大值.11. ;【解析】根据统计图中的数据,名同学体重的平均值为:;根据分层抽样从身高在,三组内的男生中,用分层抽样的方法选取人,则从三组抽取的人数分别为人,人,人,则两人的身高不在同一组的概率为.12.13.【解析】将抛物线与直线的方程联立,得解得.由抛物线的定义,得14. ;【解析】当时,,并结合,得所以第三部分15. (1)由(1),得由正弦定理,得整理,得即由,得,解得因为,所以.(2)由余弦定理,得由,,得即从而三角形的面积为当且仅当时,因此,三角形面积的最大值为.16. (1)因为,分别为、的中点,所以.又平面,平面.所以平面.(2)连接,因为,为的中点,所以.在菱形中,,又因为,所以平面.又平面,所以.在直角三角形中,由于,,则.又,为的中点,所以.又因为,所以平面.(3)过点作,由(2)得平面.如图,以为原点,,,所在直线分别为、、轴,建立空间直角坐标系,则,,,,,从而设是平面的一个法向量,由得取,则.设直线与平面所成的角为,则所以直线与平面所成角的正弦值为.17. (1)用A,B,C分别表示事件甲、乙、丙面试合格.由题意知A,B,C相互独立,且.至少有1人面试合格的概率是(2)的可能取值为0,1,2,3.====∴的分布列是的期望18. (1)由已知,得因为当时,所以在上单调递增,从而所以函数在区间上的最小值为.(2)由,得.当变化时,的变化情况如下:由此,从而当时,由,得当变化时,的变化情况如下:由此,从而当时,因此,对任意,都有成立.19. (1)依题意可得,,.又,可得,.所以椭圆方程为.(2)设直线的方程为,,,线段中点为,联立方程,得整理,得则可得则点的坐标为.由题意有,可得即.又,所以.(3)设椭圆上焦点为,则由,可得,所以又,所以设,则可知在区间单调递增,在区间单调递减.所以,当时,有最大值.此时,的面积有最大值.20. (1)依题意可得,..(2)由题意可知,是数阵的第列的和,因此是数阵所有数的和.而数阵所有数的和也可以考虑按行相加.对任意的,不超过的倍数有,,…,.因此数阵的第行中有个1,其余是,即第行的和为.所以.(3)由的定义可知,,所以.所以.考查定积分,将区间分成等分,则的不足近似值为,的过剩近似值为.所以.所以.所以.所以.。
2011年北京东城初三二模数学试题答案
北京市东城区2010--2011学年第二学期初三综合练习(二)数学试卷参考答案一、选择题(本题共32分,每小题4分)题 号 1 2 3 45 6 7 8 答 案 A D CBD C A A二、填空题(本题共16分,每小题4分)题 号9 10 1112答 案-2圆柱12π三、解答题:(本题共30分,每小题5分) 13.(本小题满分5分)解: 原式222441444x x x x x =+++--- ………………3分23x =- . ………………4分 当332x =时 ,原式233271533244⎛⎫=-=-=⎪ ⎪⎝⎭. ………5分 14.(本小题满分5分) 解:32121=-+--x x x ………………1分去分母得 x-1+1=3(x-2)解得 x=3. ………………4分 经检验:x=3是原方程的根.所以原方程的根为x=3. ………………5分15.(本小题满分5分) 解:(1)A 1 点的坐标为(3,-1),B 1点的坐标为(2,-3),C 1点的坐标为(5,-3);A 2 点的坐标为(-3,-1),B 2点的坐标为(-2,-3),C 2点的坐标为(-5,-3).图略,每正确画出一个三角形给2分.(2)利用勾股定理可求B 2C =65. ………………5分16.(本小题满分5分) 证明:∵ C F AB ∥,∴ ∠A =∠ACF , ∠ADE =∠CFE . -------2分在△ADE 和△CFE 中, ∠A =∠ACF ,∠ADE =∠CFE ,A E E C =,ABCDEF∴ △ADE ≌△CFE . --------4分 ∴ A D C F =. ------5分17.(本小题满分5分)解:设小刚家4、5两月各行驶了x 、y 千米. --------------------------1分依题意,得 ⎪⎩⎪⎨⎧=+-=.2601.01.0,10054y x x y ----------------------------3分 解得 ⎩⎨⎧==.1100,1500y x -------------------------------4分答:小刚家4月份行驶1500千米,5月份行驶了1100千米. -----------5分18.(本小题满分5分)解:(1)由题意可知 点C 的坐标为(1,1).…………………………………1分设直线QC 的解析式为y kx b =+. ∵ 点Q 的坐标为(0,2),∴ 可求直线QC 的解析式为2y x =-+.…2分(2)如图,当点P 在OB 上时,设PQ 交CD 于点E ,可求点E 的坐标为(2a ,1).则522A P A D D E a ++=+,332C EBC B P a ++=-.由题意可得 5323(3)22a a +=-.∴ 1a =. …………………………………4分由对称性可求当点P 在OA 上时,1a =-∴ 满足题意的a 的值为1或-1. …………………………………5分四、解答题(本题共20分,每小题5分) 19.(本小题满分5分)解:(1)证明:∵BD 是∠ABC 的平分线,∴ ∠1=∠2.∵ AD //BC ,∴∠2=∠3. ∴ ∠1=∠3.∴AB=AD . ---------------------2分(2)作AE ⊥BC 于E ,DF ⊥BC 于F .∴ EF=AD=AB .ABD123∵ ∠ABC =60°,BC =3AB , ∴ ∠BAE =30°. ∴ BE =21AB . ∴ BF =23AB=21BC .∴ BD=DC .∴ ∠C =∠2.∵ BD 是∠ABD 的平分线, ∴ ∠1=∠2=30°.∴ ∠C =30°. -------------------------5分20.(本小题满分5分)解:(1)CD 与圆O 相切. …………………1分 证明:连接OD ,则∠AOD =2∠AED =2⨯45︒=90︒. …………………2分 ∵四边形ABCD 是平行四边形,∴AB //DC .∴∠CDO =∠AOD =90︒.∴OD ⊥CD . …………………3分 ∴CD 与圆O 相切.(2)连接BE ,则∠ADE =∠ABE .∴sin ∠ADE =sin ∠ABE =65. …………………4分∵AB 是圆O 的直径,∴∠AEB =90︒,AB =2⨯3=6. 在Rt △ABE 中,sin ∠ABE =ABAE =65.∴AE =5 .21.(本小题满分5分)解:(1)30%; ……………………2分 (2)如图所示. ……………………4分(3)由于月销量的平均水平相同,从折线的走势看,A 品牌的月销量呈下降趋势,而B 品牌的月销量呈上升趋势.所以该商店应经销B 品牌电视机. …………………5分AB CD EOF E D C BA22.(本小题满分5分)解:(1)将图4中的△ABE 向左平移30cm ,△CDF 向右平移30cm ,拼成如图下中的平行四边形,此平行四边形即为图2中的□ABCD .…………………2分(2)由图2的包贴方法知:AB 的长等于三棱柱的底边周长,∴AB =30.∵ 纸带宽为15,∴ sin ∠ABM =151302A M A B==.∴∠AMB =30°. …………………5分五、解答题:(本题共22分,第23题7分,第24题7分,第25题8分) 23.(本小题满分7分) 解:(1) ∵ 关于x 的一元二次方程2220x ax b ++=有实数根,∴ Δ=,04)2(22≥-b a 有a 2-b 2≥0,(a+b )(a-b )≥0.∵ 0,0>>b a ,∴ a+b >0,a-b ≥0.∴ b a ≥. …………………………2分(2) ∵ a ∶b =2∶3,∴ 设2,3a k b k ==.解关于x 的一元二次方程22430x kx k ++=,得 -3x k k =-或.当12,= -3x k x k =-时,由1222x x -=得2k =.当123,= -x k x k =-时,由1222x x -=得25k =-(不合题意,舍去).∴ 4,23a b ==. …………………………5分(3) 当4,23a b ==时,二次函数2812y x x =++与x 轴的交点为、C 的交点坐标分别为A (-6,0)、(-2,0),与y 轴交点坐标为(0,12),顶点坐标D 为(-4,-4).设z =3x -y ,则3y x z =-.画出函数2812y x x =++和3y x =的图象,若直线3y x =平行移动时,可以发现当直线经过点C 时符合题意,此时最大z 的值等于-6 ……………7分24. (本小题满分7分)解:(1)四边形ABCE 是菱形.证明:∵ △ECD 是△ABC 沿BC 方向平移得到的,∴ EC ∥AB ,EC =AB .∴ 四边形ABCE 是平行四边形.321GRQPOEDC BA又∵ AB =BC ,∴四边形ABCE 是菱形. ……………2分(2)①四边形PQED 的面积不发生变化,理由如下: 由菱形的对称性知,△PBO ≌△QEO , ∴ S △PBO = S △QEO∵ △ECD 是由△ABC 平移得到的, ∴ ED ∥AC ,ED =AC =6. 又∵ BE ⊥AC , ∴BE ⊥ED∴S 四边形PQED =S △QEO +S 四边形POED =S △PBO +S 四边形POED =S △B ED=12×BE ×ED =12×8×6=24. ……………4分②如图,当点P 在BC 上运动,使以点P 、Q 、R 为顶点的三角形与△COB 相似. ∵∠2是△OBP 的外角, ∴∠2>∠3.∴∠2不与∠3对应 . ∴∠2与∠1对应 .即∠2=∠1,∴OP =OC =3 .过O 作OG ⊥BC 于G ,则G 为PC 的中点 . 可证 △OGC ∽△BOC . ∴ CG :CO =CO :BC . 即 CG :3=3:5 .∴ CG =95.∴ PB =BC -PC =BC -2CG =5-2×95=75 .∴ BD =PB +PR +RF +DF =x +185+x +185=10.∴ x =75∴ BP =75. ……………7分BCA xy FO D E HM HG H 25.(本小题满分8分) 解:(1)由题意得A (0,2)、B (2,2)、C (3,0).设经过A ,B ,C 三点的抛物线的解析式为y=ax 2+bx +2.则⎩⎨⎧=++=++02390224b a b a解得 ⎪⎪⎩⎪⎪⎨⎧=-=3432b aH∴ 224233y x x =-++.……………2分(2)由224233y x x =-++=228(1)33x --+.∴ 顶点坐标为G (1,83).过G 作GH ⊥AB ,垂足为H .则AH =BH =1,GH =83-2=23.∵ EA ⊥AB ,GH ⊥AB , ∴ EA ∥GH .∴GH 是△BEA 的中位线 .∴EA =3GH =43.过B 作BM ⊥OC ,垂足为M . 则MB =OA =AB .∵ ∠EBF =∠ABM =90°,∴ ∠EBA =∠FBM =90°-∠ABF . ∴ R t △EBA ≌R t △FBM .∴ FM =EA =43.∵ CM =OC -OM =3-2=1,∴ CF =FM +CM =73.……………5分(3)要使四边形BCGH 的周长最小,可将点C 向上 平移一个单位,再做关于对称轴对称的对称点C 1,得点C 1的坐标为(-1,1).可求出直线BC 1的解析式为1433y x =+.直线1433y x =+与对称轴x =1的交点即为点H ,坐标为(1,53).点G 的坐标为(1,23).……………8分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
13. 下列叙述中不正确...的是
A.麦克斯韦证实了电磁波的存在
B.偏振现象说明光是横波
C.光电效应现象说明了光具有粒子性
D.天然放射现象的发现使人们认识到原子核有复杂的结构
14. 如图所示为氢原子的能级图。当氢原子从n = 4 的能级跃
迁到n =2 的能级时,辐射出光子a;当氢原子从n =3 的能级跃
迁到n =1 的能级时,辐射出光子b,则下列说法中正确的是
A.光子a 的折射率大于光子b 的折射率
B.光子a 的波长小于光子b 的波长
C.b 光比 a 光更容易发生衍射现象
D.在同种介质中,a光子的传播速度大于b光子的传播速度
15.如图甲,一弹簧振子在AB间做简谐运动,
O为平衡位置。如图乙是振子做简谐运动时
的位移一时间图象。则关于振子的加速度随
时间的变化规律,下列四个图象中正确的是
16. 为了对火星及其周围的空间环境进行探测,我国预计于2011年10月发射第一颗火星探
测器“萤火一号”。假设探测器在离火星表面高度分别为1h和2h的圆轨道上运动时,周期分
别为1T和2T。火星可视为质量分布均匀的球体,且忽略火星的自转影响,万有引力常量为
G。仅利用以上数据,可以计算出
A.火星的半径和“萤火一号”的质量
B.火星的质量和火星对“萤火一号”的引力
C.火星的密度和火星表面的重力加速度
D.火星表面的重力加速度和火星对“萤火一号”的引力
17.输入电压为220V,输出电压为36V的变压器副线圈烧坏,为获知此变压器原、副线圈匝
数,某同学拆下烧坏的副线圈,用绝缘导线在铁芯上新绕了5匝线圈,如题17图所示,然
后将原线圈接到220V交流电源上,测得新绕线圈的端电压为1V,按理想变压器分析,该变
压器烧坏前的原、副线圈匝数分别为
2
A 1100、360 B 1100、180
C 2200、180 D 220、360
18.如图所示,质量为m的物体置于斜面上,用细绳将一质量为m'的物体跨过定滑轮相连
接,当倾角为45°时物体m处于静止状态,当倾角θ再增大一些,物体m仍然静止(绳子
质量、滑轮摩擦不计)下列说法不正确...的是
A.绳子受的拉力增大
B.物林m对斜面的正压力减小
C.物体m受到的静摩擦力可能增大
D.物体m受到的静摩擦力可能减小
19.电动势为E、内阻为r的电源与定值电阻R1、
R
2
及滑动变阻器R连接成如图所示的电路,当滑动变
阻器的触头由中点滑向b端时,下列说法正确的是
A. 电压表和电流表读数都减小
B. 电压表和电流表读数都增大
C.电压表读数增大,电流表读数减小
D.电压表读数减小,电流表读数增大
20 .静电除尘器是目前普遍采用的一种高效除尘器.某除尘器模型
的收尘板是很长的条形金属板,图中直线ab为该收尘板的横截面.
工作时收尘板带正电,其左侧的电场线分布如图所示;粉尘带负电,
在电场力作用下向收尘板运动,最后落在收尘板上.若用粗黑曲线表
示原来静止于P点的带电粉尘颗粒的运动轨迹,下列4幅图中可能
正确的是(忽略重力和空气阻力)
3
21.(18分)
(1)(4分)某同学利用“插针法”测定玻璃的折射率,所用的玻璃砖两面平行,正确操作
后,作出的光路图及测出的相关角度如图所示,①此玻璃的折射率计算式为n=________(用
图中的θ1、θ2 表示);②如果有几块宽度大小不同的平行玻璃砖可供选择,为了减小误差,
应选用宽度____________(填“大”或“小”)的玻璃砖测量。
(2)(6分)在“用单摆测定重力加速度”的实验中:
①用主尺最小分度为1mm,游标上有20个分度的卡尺测量金属球的直径,结果如图甲
所示,可以读出此金属球的直径为________mm。(2分)
θ
1
θ
2
甲
0 2 3 4 5 6 7 8 1
L/cm
99.00
T2/s2
-1.00
4.00
o
