2010年中考数学压轴题及解答1
2010年中考数学压轴题精选(四)

2010年中考数学压轴题精选(四)★★31、(2010眉山)如图,Rt △ABO 的两直角边OA 、OB 分别在x 轴的负半轴和y 轴的正半轴上,O 为坐标原点,A 、B 两点的坐标分别为(3-,0)、(0,4),抛物线223y x bx c =++经过B 点,且顶点在直线52x =上. (1)求抛物线对应的函数关系式;(2)若△DCE 是由△ABO 沿x 轴向右平移得到的,当四边形ABCD 是菱形时,试判断点C 和点D 是否在该抛物线上,并说明理由;(3)若M 点是CD 所在直线下方该抛物线上的一个动点,过点M 作MN 平行于y 轴交CD 于点N .设点M 的横坐标为t ,MN 的长度为l .求l 与t 之间的函数关系式,并求l 取最大值时,点M 的坐标.解:(1)由题意,可设所求抛物线对应的函数关系式为225()32y x m =-+ ∴2254()32m =⨯-+,∴16m =-, ∴所求函数关系式为:22251210()432633y x x x =--=-+(2)在Rt △ABO 中,OA =3,OB =4,∴5AB == ∵四边形ABCD 是菱形,∴BC =CD =DA =AB =5 ∴C 、D 两点的坐标分别是(5,4)、(2,0).当5x =时,2210554433y =⨯-⨯+= 当2x =时,2210224033y =⨯-⨯+=∴点C 和点D 在所求抛物线上.(3)设直线CD 对应的函数关系式为y kx b =+,则5420k b k b +=⎧⎨+=⎩,解得:48,33k b ==-. ∴4833y x =-,∵MN ∥y 轴,M 点的横坐标为t ,∴N 点的横坐标也为t . 则2210433M y t t =-+, 4833N y t =-,∴22248210214202734()3333333322N M l y y t t t t t t ⎛⎫=-=---+=-+-=--+ ⎪⎝⎭∵203-<, ∴当72t =时,32l =最大,此时点M 的坐标为(72,12).★★32、(2010某某)如图,抛物线y = ax 2+ bx + 4与x 轴的两个交点分别为A (-4,0)、B (2,0),与y 轴交于点C ,顶点为D .E (1,2)为线段BC 的中点,BC 的垂直平分线与x 轴、y 轴分别交于F 、G .(1)求抛物线的函数解析式,并写出顶点D 的坐标;(2)在直线EF 上求一点H ,使△CDH 的周长最小,并求出最小周长;(3)若点K 在x 轴上方的抛物线上运动,当K 运动到什么位置时,△EFK 的面积最大?并求出最大面积.解:(1)由题意,得 ⎩⎨⎧=++=+-,0424,04416b a b a 解得21-=a ,b =-1.所以抛物线的解析式为4212+--=x x y ,顶点D 的坐标为(-1,29).(2)设抛物线的对称轴与x 轴交于点M .因为EF 垂直平分BC ,即C 关于直线EG 的对称点为B ,连结BD 交于EF 于一点,则这一点为所求点H ,使DH + CH 最小,即最小为DH + CH = DH + HB = BD =132322=+DM BM . 而 25)429(122=-+=CD . ∴△CDH 的周长最小值为CD + DR + CH =21335+. 设直线BD 的解析式为y = k 1x + b ,则 ⎪⎩⎪⎨⎧=+-=+,29,021111b k b k 解得 231-=k ,b 1 = 3. 所以直线BD 的解析式为y =23-x + 3.由于BC = 25,CE = BC ∕2 =5,Rt △CEG ∽△COB ,得 CE : CO = CG : CB ,所以 CG = 2.5,GO = 1.5.G (0,1.5). 同理可求得直线EF 的解析式为y =21x +23. 联立直线BD 与EF 的方程,解得使△CDH 的周长最小的点H (43,815). (3)设K (t ,4212+--t t ),x F <t <x E .过K 作x 轴的垂线交EF 于N .则 KN = y K -y N =4212+--t t -(21t +23)=2523212+--t t .所以 S △EFK = S △KFN + S △KNE =21KN (t + 3)+21KN (1-t )= 2KN = -t 2-3t + 5 =-(t+23)2 +429.即当t =-23时,△EFK 的面积最大,最大面积为429,此时K (-23,835).★★33、(2010某某)已知抛物线2142y x bx =-++上有不同的两点E 2(3,1)k k +-+和F 2(1,1)k k ---+.(1)求抛物线的解析式. (2)如图,抛物线2142y x bx =-++与x 轴和y 轴的正半轴分别交于点A 和B ,M 为AB 的中点,∠PMQ 在AB 的同侧以M 为中心旋转,且∠PMQ =45°,MP 交y 轴于点C ,MQ 交x 轴于点D .设AD 的长为m (m >0),BC 的长为n ,求n 和m 之间的函数关系式. (3)当m ,n 为何值时,∠PMQ 的边过点F .解:(1)抛物线2142y x bx =-++的对称轴为122bx b =-=⎛⎫⨯- ⎪⎝⎭. ∵ 抛物线上不同两个点E 2(3,1)k k +-+和F 2(1,1)k k ---+的纵坐标相同, ∴ 点E 和点F 关于抛物线对称轴对称,则 (3)(1)12k k b ++--==,且k ≠-2.∴抛物线的解析式为2142y x x =-++. (2)抛物线2142y x x =-++与x 轴的交点为A (4,0),与y 轴的交点为B (0,4), ∴ AB=AM =BM=在∠PMQ 绕点M 在AB 同侧旋转过程中,∠MBC =∠DAM =∠PMQ =45°,在△BCM 中,∠BMC +∠BCM +∠MBC =180°,即∠BMC +∠BCM =135°,在直线AB 上,∠BMC +∠PMQ +∠AMD =180°,即∠BMC +∠AMD =135°.∴∠BCM =∠AMD .故 △BCM ∽△AMD .∴BC BM AM AD =,即=,8n m =.故n 和m 之间的函数关系式为8n m =(m >0).(3)∵F 2(1,1)k k ---+在2142y x x =-++上,∴221(1)(1)412k k k ---+--+=-+, 化简得,2430k k -+=,∴k 1=1,k 2=3. 即F 1(-2,0)或F 2(-4,-8).①MF 过M (2,2)和F 1(-2,0),设MF为y kx b =+, 则 2220.k b k b +=⎧⎨-+=⎩, 解得,121.k b ⎧=⎪⎨⎪=⎩,∴ 直线MF 的解析式为112y x =+. 直线MF 与x 轴交点为(-2,0),与y 轴交点为(0,1). 若MP 过点F (-2,0),则n =4-1=3,m =83; 若MQ 过点F (-2,0),则m =4-(-2)=6,n =43. ②MF 过M (2,2)和F 1(-4,-8),设MF 为y kx b =+, 则2248.k b k b +=⎧⎨-+=-⎩, 解得,534.3k b ⎧=⎪⎪⎨⎪=-⎪⎩,∴ 直线MF 的解析式为5433y x =-. 直线MF 与x 轴交点为(45,0),与y 轴交点为(0,43-). 若MP 过点F (-4,-8),则n =4-(43-)=163,m =32; 若MQ 过点F (-4,-8),则m =4-45=165,n =52. 故当118,33,m n ⎧=⎪⎨⎪=⎩226,4,3m n =⎧⎪⎨=⎪⎩333,2163m n ⎧=⎪⎪⎨⎪=⎪⎩或4416,552m n ⎧=⎪⎪⎨⎪=⎪⎩时,∠PMQ 的边过点F .★★34、(2010某某)如图1,在△ABC 中,AB=BC ,P 为AB 边上一点,连接CP ,以PA 、PC 为邻边作□APCD ,AC 与PD 相交于点E ,已知∠ABC=∠AEP=α(0°<α<90°). (1)求证:∠EAP=∠EPA ;(2)□APCD 是否为矩形?请说明理由;(3)如图2,F 为BC 中点,连接FP ,将∠AEP 绕点E 顺时针旋转适当的角度,得到∠MEN (点M 、N 分别是∠MEN 的两边与BA 、FP 延长线的交点).猜想线段EM 与EN 之间的数量关系,并证明你的结论.解:(1)证明:在ΔABC 和ΔAEP 中,∵∠ABC=∠AEP,∠BAC=∠EAP ∴ ∠ACB=∠APE,在ΔABC 中,AB=BC ,∴∠ACB=∠BAC,∴ ∠EPA=∠EAP (2)答:□ APCD 是矩形∵四边形APCD 是平行四边形,∴ AC=2EA,PD=2EP∵ 由(1)知 ∠EPA=∠EAP,∴ EA=EP,则 AC=PD ,∴□APCD 是矩形 (3)答: EM=EN , ∵EA=EP ∴ ∠EPA=90°- 12α∴∠EAM=180°-∠EPA=180°-(90°-12α)=90°+12α由(2)知∠CPB=90°,F 是BC 的中点,∴ FP=FB,∴∠FPB=∠ABC=α图1B P∴ ∠EPN=∠EPA+∠APN=∠EPA+∠FPB=90°- 12α+α=90°+12α∴ ∠EAM=∠EPN∵ ∠AEP 绕点E 顺时针旋转适当的角度,得到∠MEN,∴ ∠AEP=∠MEN ∴∠AEP - ∠AEN=∠MEN -∠AEN 即 ∠MEA=∠NEP ∴ ΔEAM≌ΔEPN ∴ EM=EN★★35、(2010某某)26.(14分)如图1,已知点B (1,3)、C (1,0),直线y=x +k 经过点B ,且与x 轴交于点A ,将△ABC 沿直线AB 折叠得到△ABD. (1)填空:A 点坐标为(____,____),D 点坐标为(____,____); (2)若抛物线y=13x 2+b x +c 经过C 、D 两点,求抛物线的解析式;(3)将(2)中的抛物线沿y 轴向上平移,设平移后所得抛物线与y 轴交点为E ,点M 是平移后的抛物线与直线AB 的公共点,在抛物线平移过程中是否存在某一位置使得直线EM ∥x 轴.若存在,此时抛物线向上平移了几个单位?若不存在,请说明理由.(提示:抛物线y=ax 2+b x +c(a ≠0)的对称轴是x =-b 2a ,顶点坐标是(-b 2a ,4a c -b24a)图1备用图解:(1) A(-2,0) ,D(-2,3)(2)∵抛物线y=13 x 2+b x +c 经过C(1,0),D(-2,3)代入,解得:b=- 23 ,c=13∴ 所求抛物线解析式为:y=13 x 2-23x +13(3)答:存在解法一: 设抛物线向上平移H 个单位能使EM∥x 轴,则平移后的解析式为:y=13 x 2-23x +13 +h =31(x -1)² + h此时抛物线与y 轴交点E(0,+h)当点M 在直线y=x +2上,且满足直线EM∥x 轴时 则点M 的坐标为(h h +-31,35) 又 ∵M 在平移后的抛物线上,则有31+h=31(h-35-1)²+h,解得: h=35 或 h=311 (і)当 h=35时,点E (0,2),点M 的坐标为(0,2)此时,点E,M 重合,不合题意舍去。
2010年中考数学压轴题平移旋转对称重点
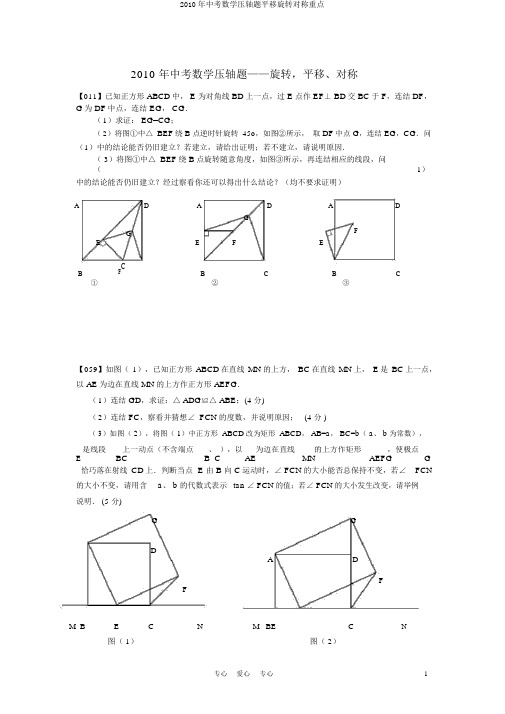
2010 年中考数学压轴题——旋转,平移、对称【011】已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连结DF,G为 DF中点,连结 EG, CG.(1)求证:EG=CG;(2)将图①中△BEF绕B点逆时针旋转 45o,如图②所示,取DF中点G,连结EG,CG.问(1)中的结论能否仍旧建立?若建立,请给出证明;若不建立,请说明原因.( 3)将图①中△BEF绕B点旋转随意角度,如图③所示,再连结相应的线段,问(1)中的结论能否仍旧建立?经过察看你还可以得出什么结论?(均不要求证明)A D A D A DGGEF F EEB F CB C B C①②③【059】如图(1),已知正方形ABCD在直线MN的上方,BC在直线MN上,E是BC上一点,以 AE为边在直线 MN的上方作正方形 AEFG.(1)连结GD,求证:△ADG≌△ABE;(4 分)(2)连结FC,察看并猜想∠FCN的度数,并说明原因; (4 分 )(3)如图( 2),将图( 1)中正方形ABCD改为矩形ABCD,AB=a,BC=b(a、b为常数),E 是线段上一动点(不含端点、),以为边在直线的上方作矩形,使极点G BC B C AE MN AEFG恰巧落在射线CD上.判断当点 E 由 B 向 C运动时,∠ FCN的大小能否总保持不变,若∠FCN的大小不变,请用含a、 b 的代数式表示tan ∠ FCN的值;若∠ FCN的大小发生改变,请举例说明. (5 分)G GDA DFFM B E C N M BE C N 图( 1)图( 2)【062】如图 13-1 至图 13-5 ,⊙O均作无滑动转动,⊙O1、⊙ O2、⊙ O3、⊙ O4均表示⊙ O与线段 AB或 BC相切于端点时辰的地点,⊙ O的周长为 c.阅读理解:( 1)如图 13-1,⊙O从⊙O1的地点出发,沿AB转动到O1O O2⊙ 2 的地点,当AB = c 时,⊙O恰巧自转 1 周.A BO图 13-1( 2)如图13-2 ,∠ABC相邻的补角是n°,⊙ O在∠ ABC外面沿 A- B- C转动,在点B处,一定由O1⊙ O 的地点旋转到⊙ O 的地点,⊙ O绕点 B 旋O2 12转的角∠ O1BO2= n °,⊙ O在点 B 处自转n周.A B n°D360C 实践应用:图 13-2( 1)在阅读理解的(1)中,若AB =2c,则⊙O自转周;若 AB =l ,则⊙ O自转周.在阅读理解的(2)中,若∠ABC = 120°,则⊙O 在点 B 处自转周;若∠ ABC= 60°,则⊙ O 在点 B处自转周.O1O O2O3 A B1O4( 2)如图 13-3 ,∠ABC=90°,AB=BC= c.⊙O从C2⊙O的地点出发,在∠ ABC外面沿 A- B- C转动1图 13-3到⊙ O 的地点,⊙ O自转周.4拓展联想:B( 1)如图 13-4 ,△的周长为l,⊙O从与AB相切于点DABC的地点出发,在△ABC外面,按顺时针方向沿三角形滚O动,又回到与AB 相切于点 D 的地点,⊙ O自转了多少D周?请说明原因.A C图 13-4(2)如图 13-5 ,多边形的周长为l ,⊙ O从与某边相切于点D的地点出发,在多边形外面,按顺时针方向沿多边形转动,又回到与该边相切于点D的地点,直接写..出⊙ O自转的周数.OD图 13-5专心爱心专心2【014】在平面直角坐标中,边长为 2 的正方形OABC的两极点A、 C 分别在 y 轴、x轴的正半轴上,点 O 在原点.现将正方形 OABC 绕 O 点顺时针旋转,当 A 点第一次落在直线y x 上时停止旋转,旋转过程中, AB 边交直线 y x 于点 M , BC 边交x轴于点 N (如图) .y( 1)求边OA在旋转过程中所扫过的面积;y x ( 2)旋转过程中,当MN和AC平行时,求正方形AOABC 旋转的度数;M ( 3)设MBN的周长为p,在旋转正方形OABC B的过程中, p 值能否有变化?请证明你的结论.xO NC(第 26题)【017】如图,已知抛物线y x2bx c 经过 A(10),, B(0,2) 两点,极点为 D .(1)求抛物线的分析式;(2)将△OAB绕点A顺时针旋转 90°后,点B落到点C的地点,将抛物线沿y轴平移后经过点 C ,求平移后所得图象的函数关系式;(3)设( 2)中平移后,所得抛物线与y 轴的交点为B1,极点为 D1,若点N在平移后的抛物线上,且知足△ NBB1的面积是△ NDD 1面积的2 倍,求点N的坐标.yBO A D x【018】如图,抛物线 yax 2 bx 4a 经过 A( 1,0) 、C (0,4) 两点, 与 x 轴交于另一点 B .(1)求抛物线的分析式;(2)已知点 D (m , m 1) 在第一象限的抛物线上,求点D 对于直线 BC 对称的点的坐标;(3)在( 2)的条件下,连结 BD,点 P为抛物线上一点,且DBP 45°P的坐,求点标.yCABOx【053】如下图,在平面直角坐标系中,抛物线y ax 2bx c( a 0)经过A(1,0) ,B(3,0),C (0,3)三点,其极点为 D ,连结 BD ,点 P 是线段 BD 上一个动点(不与B 、 D重合),过点 P 作y轴的垂线,垂足为E ,连结 BE . (1)求抛物线的分析式,并写出极点D 的坐标;( 2)假如 P 点的坐标为 (x ,y), △ PBE 的面积为 s ,求 s 与 x 的函数关系式,写出自变量 x的取值范围,并求出 s的最大值;( 3)在( 2)的条件下,当 s获得最大值时,过点P 作 x的垂线,垂足为F ,连结 EF ,把 △ PEF 沿直线 EF 折叠,点 P 的对应点为 P ,请直接写出 P 点坐标,并判断点 P 能否在该抛物线上.yDC 32E P1BA321O12 3x1【 055】在平面直角坐标系中,现将一块等腰直角三角板ABC放在第二象限,斜靠在两坐标轴上,且点A(0,2),点C ( 10),,如下图:抛物线y ax 2ax 2经过点 B .(1)求点B的坐标;(2)求抛物线的分析式;(3)在抛物线上能否还存在点角三角形?若存在,求全部点yA( 0, 2)BC(- 1, 0)P(点 B 除外),使△ ACP 仍旧是以 AC 为直角边的等腰直P的坐标;若不存在,请说明原因.x(第 25 题)【076】如图,抛物线 y 1 x2mx n 与x轴交于A、B两点,与y轴交于C点,四边形OBHC2为矩形,的延伸线交抛物线于点( 5,2),连结、 .CH D BC AD(1)求 C 点的坐标及抛物线的分析式;(2)将△BCH绕点B按顺时针旋转 90°后再沿x轴对折获得△BEF(点 C与点 E对应),判断点 E 能否落在抛物线上,并说明原因;( 3)设过点 E 的直线交AB边于点 P,交 CD边于点 Q.问能否存在点P,使直线 PQ分梯形 ABCD的面积为1∶3两部分?若存在,求出P 点坐标;若不存在,请说明理由.。
2010年中考数学试题汇编压轴题06

(第24题图)(第24题备用图)R 1(9, 3)R 2(3, 9)R 1(3, 3)AB CE F 0xy2010年中考数学试题分类汇编 压轴题(六)24、(茂名市本题满分8分)如图,在直角坐标系x O y 中,正方形OCBA 的顶点A 、C 分别在y 轴、x 轴上,点B 坐标为(6,6),抛物线c bx ax y ++=2经过点A 、B 两点,且13-=-b a .(1)求a ,b ,c 的值; (3分)(2)如果动点E 、F 同时分别从点A 、点B 出发,分别沿A →B 、B →C 运动,速度都是每秒1个单位长度,当点E 到达终点B 时,点E 、F 随之停止运动.设运动时间为t 秒,EBF ∆的面积为S .①试求出S 及t 之间的函数关系式,并求出S 的最大值;(2分)②当S 取得最大值时,在抛物线上是否存在点R ,使得以E 、B 、R 、F 为顶点的四边形是平行四边形?如果存在,求出点R 的坐标;如果不存在,请说明理由.(3分)解:(1)由已知A (0,6)、B (6,6)在抛物线上,得方程组: ······1分 解得: ·············3分(2)①运动开始t 秒时,EB =t -6,BF =t ,S =tt t t BF EB 321)6(21212+-=-=⋅,··········4分 因为29)3(2132122+--=+-=t t t S , 所以当3=t 时,S 有最大值29.··················5分②当S 取得最大值时,由①知3=t ,所以BF =3,CF =3,EB =6-3=3. 若存在某点R ,使得以E 、B 、R 、F 为顶点的四边形是平行四边形,则EB FR EB FR //11且=,即可得R 1为(9,3)、(3,3);··················6分(第25题备用图)或者BF ER BF ER //22且=,可得R 2为(3,9).·························7分再将所求得的三个点代入,可知只有点(9,3)在抛物线上,因此抛物线上存在点R 1(9,3),使得四边形EBRF 为平行四边形.············8分25、(茂名市本题满分8分)已知⊙O 1的半径为R ,周长为C .(1)在⊙O 1内任意作三条弦,其长分别是1l 、2l 、3l l l l (2)如图,在直角坐标系x O y 中,设⊙O 1的圆心为O 1(R ①当直线l :)0(>+=b b x y 及⊙O 1相切时,求b ②当反比例函数的图象及⊙O 1有两个交点时,求k 的取值范围. (3解:(1)证明:R l 21≤ ,R l 22≤,R l 23≤.1l ∴+2l +3l C R R =⨯<⨯≤223π,2分因此,1l +2l +3l < C . (3)分(2)解:①如图,根据题意可知⊙O 1及及x 轴、y 轴分别相切,设直线l 及⊙O 1相切于点M ,则O 1M ⊥l ,过点O 1作直线NH ⊥x 轴,及l 交于点N ,及x 轴交于点H ,又∵直线l 及x 轴、y 轴分别交于点E (b -,0)、F (0,b ),∴OE =OF =b ,∴∠NEO =45o ,∴∠ENO 1=45o ,在o =R 2,∴点N 的坐标为N (R ,R R +2把点N 坐标代入b x y +=得:b R R R +=+2,解得:b =②如图,设经过点O 、O 1的直线交⊙O 1于点A 、D ,则由已知,直线OO 1:是圆及反比例函数图象的对称轴,当反比例函数的图象及⊙O 1直径AD 相交时(点A 、D 除外),则反比例函数的图象及⊙O 1有两个交点.过点A 作AB ⊥x 轴交x 轴于点B ,过O 1作O 1C ⊥x 轴于点C ,OO 1=O 1C ÷sin45o =R 2,OA =R R +2,所以OB =AB =⋅OA sin45o =,因此点A 的坐标是A ,将点A 的坐标 代入,解得:.····················6分同理可求得点D 的坐标为D ,将点D 的坐标代入,解得: ······7分所以当反比例函数的图象及⊙O 1有两个交点时,k 的取值范围是:22)223()223(R k R +<<-······················· 8分25.(湘西自治州 本题20分)如图,已知抛物线24y ax x c =-+经过点(0,6)A -和(3,9)B -,(1)求出抛物线的解析式;(2)写出抛物线的对称轴方程及顶点坐标;(3)点P (m ,m) 及点Q 均在抛物线上(其中m >0),且这两点关于抛物线的对称轴 对称,求m 的值及点Q 的坐标;(4)在满足(3)的情况下,在抛物线的对称轴上寻找一点M ,使得△QMA 的周长最小.解:(1)依题意有 即 ……2分……4分∴抛物线的解析式为:246y x x =--……5分(2)把246y x x =--配方得,2(2)10y x =--∴对称轴方程为2x = ……7分顶点坐标(2,10)-……10分(3)由点(,)P m m 在抛物线上 有246m m m =--……12分即2560m m --=∴16m = 或21m =-(舍去) ……13分∴(6,6)P∵点P 、Q 均在抛物线上,且关于对称轴2x =对称∴(2,6)Q -……15分(4)连接,AQ AP ,直线AP 及对称轴2x =相交于点M由于,P Q 两点关于对称轴对称,由轴对称性质可知,此时的交点M ,能够使得△QAM 的2010年中考数学试题汇编——压轴题(06) 周长最小.……17分设直线PA 的解析式y kx b =+ ∴有∴∴直线PA 的解析式为:26y x =-……18分设点(2,)M n则有2262n =⨯-=-……19分此时点(2,2)M -能够使得△AMQ 的周长最小.……20分26.(湘潭市 本题满分10分)如图,直线6y x =-+及x 轴交于点A ,及y 轴交于点B ,以线段AB 为直径作⊙C ,抛物线c bx ax y ++=2过A 、C 、O 三点.(1) 求点C 的坐标和抛物线的解析式;(2) 过点B 作直线及x 轴交于点D ,且OB 2=OA·OD ,求证:DB 是⊙C 的切线;(3) 抛物线上是否存在一点P , 使以P 、O 、C 、A 为顶点的四边形为直角梯形,如果存在,求出点P 的坐标;如果不存在,请说明理由.解:(1)A (6,0),B (0,6) ……………………1分 连结OC ,由于∠AOB =90o,C 为AB 的中点,则, 所以点O 在⊙C 上(没有说明不扣分).过C 点作CE ⊥OA ,垂足为E ,则E 为OA 中点,故点C 的横坐标为3. 又点C 在直线y=-x+6上,故C (3,3) ……………………2分 抛物线过点O ,所以c=0,26题图又抛物线过点A 、C ,所以{3930366=+=+a b a b,解得:所以抛物线解析式为 …………………3分 (2)OA =OB =6代入OB 2=OA·OD ,得OD =6 ……………………4分 所以OD =OB =OA ,∠DBA =90o. ……………………5分 又点B 在圆上,故DB 为⊙C 的切线 ……………………6分 (通过证相似三角形得出亦可)(3)假设存在点P 满足题意.因C 为AB 中点,O 在圆上,故∠OCA=90o,要使以P 、O 、C 、A 为顶点的四边形为直角梯形,则 ∠CAP =90o或 ∠COP =90o, ……………………7分 若∠CAP =90o,则OC ∥AP ,因OC 的方程为y =x ,设AP 方程为y =x +b . 又AP 过点A (6,0),则b =-6, ……………………8分方程y =x -6及联立解得:{116x y ==,{2239x y =-=-,故点P 1坐标为(-3,-9) ……………………9分 若∠COP =90o,则OP ∥AC ,同理可求得点P 2(9,-9) (用抛物线的对称性求出亦可)故存在点P 1坐标为(-3,-9)和P 2(9,-9)满足题意.…………10分28.(甘肃省 本小题满分12分)如图,抛物线及x 轴交于A (-1,0)、B (3,0)两点,及y 轴交于点C (0,-3),设抛物线的顶点为D .(1)求该抛物线的解析式及顶点D 的坐标;(2)以B 、C 、D 为顶点的三角形是直角三角形吗?为什么?(3)探究坐标轴上是否存在点P ,使得以P 、A 、C 为顶点的三角形及△BCD 相似?若存在,请指出符合条件的点P 的位置,并直接写出点P 的坐标;若不存在,请说明理由.(1)设该抛物线的解析式为c bx ax y ++=2, 解:由抛物线及y 轴交于点C (0,-3),可知3-=c .即抛物线的解析式为32-+=bx ax y . ………………………1分 把A (-1,0)、B (3,0)代入, 得 解得2,1-==b a .∴ 抛物线的解析式为y = x 2-2x -3. ……………………………………………3分 ∴ 顶点D 的坐标为()4,1-. ……………………………………………………4分说明:只要学生求对2,1-==b a ,不写“抛物线的解析式为y = x 2-2x -3”不扣分.(2)以B 、C 、D 为顶点的三角形是直角三角形. ……………………………5分 理由如下:过点D 分别作x 轴、y 轴的垂线,垂足分别为E 、F.在Rt △BOC 中,OB=3,OC=3,∴ 182=BC . …………………………6分 在Rt △CDF 中,DF=1,CF=OF-OC=4-3=1,∴ 22=CD . …………………………7分 在Rt △BDE 中,DE=4,BE=OB-OE=3-1=2,∴ 202=BD . …………………………8分 ∴ 222BD CD BC =+, 故△BCD 为直角三角形. …………………………9分(3)连接AC ,可知Rt △COA ∽ Rt △BCD ,得符合条件的点为O (0,0). ………10分过A 作AP 1⊥AC 交y 轴正半轴于P 1,可知Rt △CAP 1 ∽ Rt △COA ∽ Rt △BCD , 求得符合条件的点为. …………………………………………11分 过C 作CP 2⊥AC 交x 轴正半轴于P 2,可知Rt △P 2CA ∽ Rt △COA ∽ Rt △BCD ,求得符合条件的点为P 2(9,0). …………………………………………12分 ∴符合条件的点有三个:O (0,0),,P 2(9,0).26.(桂林市本题满分12分)如图,过A(8,0)、B(0,xy3=交于点C.平行于y轴的直线l从原点O出发,以每秒1个单位长度的速度沿x轴向右平移,到C点时停止;l分别交线段BC、OC于点D、E,以DE为边向左侧作等边△DEF,设△DEF及△BCO重叠部分的面积为S(平方单位),直线l的运动时间为t(秒).(1)直接写出C点坐标和t的取值范围;(2)求S及t的函数关系式;(3)设直线l及x轴交于点P,是否存在这样的点P,使得以P、O、F为顶点的三角形为等腰三角形,若存在,请直接写出点P的坐标;若不存在,请说明理由.解(1)C(4,……………………………2分t的取值范围是:0≤t≤4 ……………………………… 3分(2)∵D点的坐标是(t,+E的坐标是(t)∴DE=+=……………………4分∴等边△DEF的DE边上的高为:123t-∴当点F在BO边上时:123t-=t,∴t=3 ……………………5分当0≤t<3时,重叠部分为等腰梯形,可求梯形上底为:- …7分S=)23t+-备用图1= ………………………………8分当3≤t ≤4时,重叠部分为等边三角形S=1)(123)2t - ………………… 9分=2-+……………………10分(3)存在,P (247,0) ……………………12分说明:∵FO≥FP≥OP ≤4∴以P ,O ,F 以顶点的等腰三角形,腰只有可能是FO ,FP ,若FO =FP 时,t =2(12-3t ),t =247,∴P (247,0)30. (江西省南昌市)课题:两个重叠的正多边形,其中的一个绕某一个顶点旋转所形成的有关问题. 实验及论证设旋转角∠A 1A 0B 1=α(α<∠A 1A 0B 1),θ1,θ2,θ3,θ4,θ5,θ6所表示的角如图所示.图1 图2 图3 图4αθ4HB 2B 3A 3A 22A 2B 1A 1A 011(1)用含α的式子表示:θ3=_________,θ4=_________,θ5=_________;(2)图1-图4中,连接A 0H 时,在不添加其他辅助线的情况下,是否存在及直线A 0H 垂直且被它平分的线段?若存在,请选择期中的一个图给出证明;若不存在,请说明理由; 归纳及猜想设正n 边形A 0A 1A 2…A n-1及正n 边形A 0B 1B 2…B n-1重合(其中,A 1及B 1重合),现将正n 边形A 0B 1B 2…B n-1绕顶点A 0逆时针旋转α().(3)设θn 及上述“θ3,θ4,…”的意义一样,请直接写出θn 的度数;(4)试猜想在正n 边形且不添加其他辅助线的情形下,是否存在及直线A 0H 垂直且被它平分的线段?若存在,请将这条线段用相应的顶点字母表示出来(不要求证明);若不存在,请说明理由.解:(1)α-︒60, α, α-︒36. ····················································· 3分说明:每写对一个给1分.(2)存在.下面就所选图形的不同分别给出证明:选图1.图1中有直线H A o 垂直平分12B A ,证明如下:图1方法一: 证明:∵21A A A o ∆及210B B A ∆是全等的等边三角形, ∴1020B A A A =, ∴210120A B A B A A ∠=∠.又∵︒=∠=∠601020H B A H A A .∴ 2112A HB B HA ∠=∠. ∴HB H A 12=.∴点H 在线段12B A 的垂直平分线上.又∵1020B A A A =,∴点0A 在线段12B A 的垂直平分线上∴直线H A o 垂直平分12B A ···················································· 8分方法二: 证明:∵21A A A o ∆及210B B A ∆是全等的等边三角形,∴1020B A A A =, ∴210120A B A B A A ∠=∠. 又HB A H A A 1020∠=∠. ∴2112A B H B HA ∠=∠∴12HB HA =.在H A A 20∆及H B A 10∆中∵1020B A A A =,12HB HA =,H B A H A A 1020∠=∠ ∴H A A 20∆≌H B A 10∆.∴H A B H A A 0102∠=∠ ∴H A o 是等腰三角形102B A A 的顶角平分线.∴直线H A o 垂直平分12B A . ················································· 8分选图2.图2中有直线H A o 垂直平分22B A ,证明如下:图2∵2020A A B A =∴220220B A A A B A ∠=∠又∵︒=∠=∠45320120A A A B B A ,∴ 2222B HA A HB ∠=∠.∴22HA HB =.∴点H 在线段22B A 的垂直平分线上. 又∵2020A A B A =,∴点0A 在线段22B A 的垂直平分线上∴直线H A o 垂直平分22B A . ··································································· 8分说明:(ⅰ)在图2中选用方法二证明的,参照上面的方法二给分;(ⅱ)选择图3或图4给予证明的,参照上述证明过程评分.(3)当n 为奇数时,,当n 为偶数时,αθ=n ··························································· 10分(4)存在.当n 为奇数时,直线H A o 垂直平分2121-+n n B A ,当n 为偶数时,直线H A o 垂直平分22nn B A . ·································· 12分26.(山东省泰安市 本小题满分10分)如图,△ABC 是等腰三角形,AB=AC ,以AC 为直径的⊙O 及BC 交于点D ,DE ⊥AB ,垂足为E ,ED 的延长线及AC 的延长线交于点F 。
2010年中考数学压轴题精选(五)及答案

★★41、(2010深圳)如图10,以点M (-1,0)为圆心的圆与y 轴、x 轴分别交于点A 、B 、C 、D ,直线y =- 33 x - 533 与⊙M 相切于点H ,交x 轴于点E ,交y 轴于点F . (1)请直接写出OE 、⊙M 的半径r 、CH 的长;(3分) (2)如图11,弦HQ 交x 轴于点P ,且DP :PH =3:2,求cos ∠QHC 的值;(3)如图12,点K 为线段EC 上一动点(不与E 、C 重合),连接BK 交⊙M 于点T ,弦AT 交x 轴于点N .是否存在一个常数a ,始终满足MN ·MK =a ,如果存在,请求出a 的值;如果不存在,请说明理由.解:(1)、如图4,OE =5,2r =,CH =2(2)、如图5,连接QC 、QD ,则90CQD ∠=︒,QHC QDC ∠=∠ 易知CHP DQP ∆∆,故DP DQ PH CH =,32DQ=图10 图11图123cos cos 4QD QHC QDC CD ∴∠=∠==; (3)、如图6,连接AK ,AM ,延长AM , 与圆交于点G ,连接TG ,则90GTA ∠=︒34∠=∠,2390︒∴∠+∠=由于390BKO ∠+∠=︒,故,2BKO ∠=∠; 而1BKO ∠=∠,故12∠=∠在AMK ∆和NMA ∆中,12∠=∠;AMK NMA ∠=∠ 故AMK NMA ∆;MN AMAM MK=;即:24MN MK AM ==g 故存在常数a ,始终满足MN MK=g ★★42、(2010(米/秒)与时间t 5),C (135,0). (1)式;(2)计算该同学从家到学校的路程(提示:在OA 和BC 段的运动过程中的平均速度分别等于它们中点时刻的速度,路程=平均速度×时间);(3)如图b ,直线x =t (0≤t ≤135),与图a 的图象相交于P 、Q ,用字母S 表示图中阴影部分面积,试求S 与t 的函数关系式;图6(4)由(2)(3),直接猜出在t 时刻,该同学离开家所超过的路程与此时S 的数量关系. 图 a图b解:(1)1(010)25(10130)135(130135)v t t v t v t t ⎧=≤<⎪⎪=≤<⎨⎪=-≤≤⎪⎩ (2)2.5×10+5×120+2×5=635(米)(3)221(010)4525(10130)1(130135)2S t t S t t S t t ⎧=≤<⎪⎪=-≤<⎨⎪⎪=-≤≤⎩ +135t-8475 (4) 相等的关系;★★43、(2010随州)已知抛物线2(0)y ax bx c a =++≠顶点为C (1,1)且过原点O.过抛物线上一点P (x ,y )向直线54y =作垂线,垂足为M ,连FM (如图).(1)求字母a ,b ,c 的值;(2)在直线x =1上有一点3(1,)4F ,求以PM 为底边的等腰三角形PFM的P 点的坐标,并证明此时△PFM 为正三角形;(3)对抛物线上任意一点P ,是否总存在一点N (1,t ),使PM =PN 恒成立,若存在请求出t 值,若不存在请说明理由.解:(1)a =-1,b =2,c =0(2)过P 作直线x=1的垂线,可求P 的纵坐标为14,横坐标为1+.此时,MP =MF =PF =1,故△MPF 为正三角形. (3)不存在.因为当t <54,x <1时,PM 与PN 不可能相等,同理,当t >54,x >1时,PM 与PN 不可能相等。
2010年中考数学压轴题精选(2)及答案
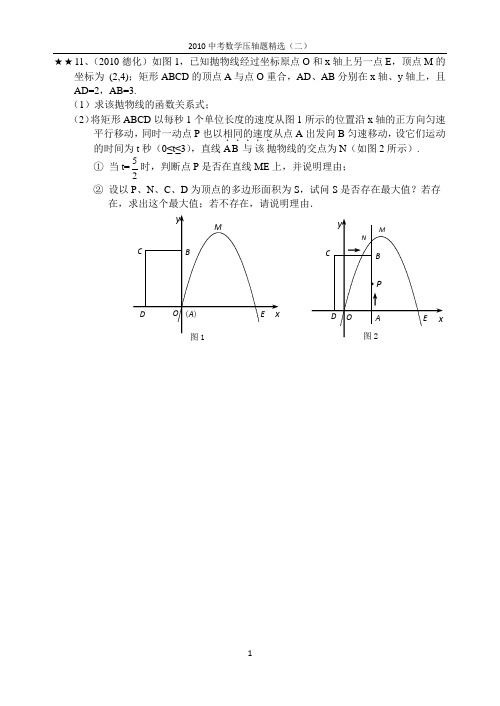
★★11、(2010德化)如图1,已知抛物线经过坐标原点O 和x 轴上另一点E ,顶点M 的坐标为 (2,4);矩形ABCD 的顶点A 与点O 重合,AD 、AB 分别在x 轴、y 轴上,且AD=2,AB=3.(1)求该抛物线的函数关系式; (2)将矩形ABCD 以每秒1个单位长度的速度从图1所示的位置沿x 轴的正方向匀速平行移动,同时一动点P 也以相同的速度.....从点A 出发向B 匀速移动,设它们运动的时间为t 秒(0≤t≤3),直线AB 与该抛物线的交点为N (如图2所示).① 当t=25时,判断点P 是否在直线ME 上,并说明理由;② 设以P 、N 、C 、D 为顶点的多边形面积为S ,试问S 是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.★★12、(2010德州)已知二次函数c bx ax y ++=2的图象经过点A (3,0),B (2,-3),C (0,-3).(1)求此函数的解析式及图象的对称轴;(2)点P 从B 点出发以每秒0.1个单位的速度沿线段BC 向C 点运动,点Q 从O 点出发以相同的速度沿线段OA 向A 点运动,其中一个动点到达端点时,另一个也随之停止运动.设运动时间为t 秒.①当t 为何值时,四边形ABPQ 为等腰梯形;②设PQ 与对称轴的交点为M ,过M 点作x 轴的平行线交AB 于点N ,设四边形ANPQ 的面积为S ,求面积S 关于时间t 的函数解析式,并指出t 的取值范围;当t 为何值时,S 有最大值或最小值.O A BCP Q M N第23题图★★13、(2010东阳)如图,P 为正方形ABCD 的对称中心,A (0,3),B (1,0),直线OP 交AB 于N ,DC 于M ,点H 从原点O 出发沿x 轴的正半轴方向以1个单位每秒速度运动,同时,点R 从O 出发沿OM 方向以2个单位每秒速度运动,运动时间为t 。
求: (1)C 的坐标为 ▲ ; (2)当t 为何值时,△ANO 与△DMR 相似? (3)△HCR 面积S 与t 的函数关系式; 并求以A 、B 、C 、R 为顶点的四边形是梯形 时t 的值及S 的最大值。
2010年中考复习针对性训练+综合压轴题

2010年中考复习针对性训练综合压轴题一、解答题(共7小题,满分0分)1、如图1,已知直线EA与x轴、y轴分别交于点E和点A(0,2),过直线EA上的两点F、G分别作x轴的垂线段,垂足分别为M(m,0)和N(n,0),其中m<0,n>0.(1)如果m=﹣4,n=1,试判断△AMN的形状;(2)如果mn=﹣4,(1)中有关△AMN的形状的结论还成立吗?如果成立,请证明;如果不成立,请说明理由;(3)如图2,题目中的条件不变,如果mn=﹣4,并且ON=4,求经过M、A、N三点的抛物线所对应的函数关系式;(4)在(3)的条件下,如果抛物线的对称轴l与线段AN交于点P,点Q是对称轴上一动点,以点P、Q、N为顶点的三角形和以点M、A、N为顶点的三角形相似,求符合条件的点Q的坐标.考点:二次函数综合题。
专题:代数几何综合题。
分析:(1)根据勾股定理可以求出AM.AN,MN的长度,根据勾股定理的逆定理就可以求出三角形是直角三角形.(2)AM.AN,MN的长度可以用m,n表示出来,根据m,n的关系就可以证明.(3)M、A、N的坐标已知,根据待定系数法局可以求出二次函数的解析式.(4)抛物线的对称轴与x轴的交点Q1符合条件,易证Rt△PNQ1∽Rt△ANM且Rt△PQ2N、Rt△NQ2Q1、Rt△PNQ1和Rt△ANM两两相似,根据相似三角形的对应边的比相等,得到就可以求出Q1Q2得到符合条件的点的坐标.解答:解:(1)△AMN是直角三角形.依题意得OA=2,OM=4,ON=1,∴MN=OM+ON=4+1=5在Rt△AOM中,AM===在Rt△AON中,AN===∴MN2=AM2+AN2∴△AMN是直角三角形(解法不惟一).(2分)(2)答:(1)中的结论还成立.依题意得OA=2,OM=﹣m,ON=n∴MN=OM+ON=n﹣m∴MN2=(n﹣m)2=n2﹣2mn+m2∵mn=﹣4∴MN2=n2﹣2×(﹣4)+m2=n2+m2+8又∵在Rt△AOM中,AM===在Rt△AON中,AN===∴AM2+AN2=4+m2+4+n2=n2+m2+8∴MN2=AM2+AN2∴△AMN是直角三角形.(解法不惟一)(2分)(3)∵mn=﹣4,n=4,∴m=﹣1.方法一:设抛物线的函数关系式为y=ax2+bx+c.∵抛物线经过点M(﹣1,0)、N(4,0)和A(0,2)∴.∴.∴所求抛物线的函数关系式为y=﹣x2+x+2.方法二:设抛物线的函数关系式为y=a(x+1)(x﹣4).∵抛物线经过点A(0,2)∴﹣4a=2解得a=﹣∴所求抛物线的函数关系式为y=﹣(x+1)(x﹣4)即y=﹣x2+x+2.(2分)(4)抛物线的对称轴与x轴的交点Q1符合条件,∵l⊥MN,∠ANM=∠PNQ1,∴Rt△PNQ1∽Rt△ANM∵抛物线的对称轴为x=,∴Q1(,0)(2分)∴NQ1=4﹣=.过点N作NQ2⊥AN,交抛物线的对称轴于点Q2.∴Rt△PQ2N、Rt△NQ2Q1、Rt△PNQ1和Rt△ANM两两相似∴即Q1Q2=∵点Q2位于第四象限,∴Q2(,﹣5)(2分)因此,符合条件的点有两个,分别是Q1(,0),Q2(,﹣5).(解法不惟一)点评:本题主要考查了勾股定理的逆定理,待定系数法求函数的解析式.以及相似三角形的性质,对应边的比相等.考点:二次函数综合题。
2010年部分省市中考数学试题分类汇编 压轴题(五)及答案
2010年部分省市中考数学试题分类汇编压轴题(五)28.(江苏省无锡市本题满分10分)如图1是一个三棱柱包装盒,它的底面是边长为10cm 的正三角形,三个侧面都是矩形.现将宽为15cm的彩色矩形纸带AMCN裁剪成一个平行四边形ABCD (如图2),然后用这条平行四边形纸带按如图3 的方式把这个三棱柱包装盒的侧面进行包贴(要求包贴时没有重叠部分),纸带在侧面缠绕三圈,正好将这个三棱柱包装盒的侧面全部包贴满.(1)请在图2中,计算裁剪的角度∠BAD;(2)计算按图3方式包贴这个三棱柱包装盒所需的矩形纸带的长度.解:(1)由图2的包贴方法知:AB的长等于三棱柱的底边周长,∴AB=30∵纸带宽为15,∴sin∠DAB=sin∠ABM=151302AMAB==,∴∠DAB=30°.(2)在图3中,将三棱柱沿过点A的侧棱剪开,得到如图甲的侧面展开图,C 图甲图1图3A将图甲种的△ABE 向左平移30cm ,△CDF 向右平移30cm ,拼成如图乙中的平行四边形ABCD ,此平行四边形即为图2中的平行四边形ABCD 由题意得,知:BC=BE+CE=2CE=2×cos 30CD =︒∴所需矩形纸带的长为MB+BC=30·cos30°+cm .28.(江苏省宿迁市 本题满分12分)已知抛物线c bx x y ++=2交x 轴于)0,1(A 、)0,3(B ,交y 轴于点C ,其顶点为D .(1)求b 、c 的值并写出抛物线的对称轴; (2)连接BC ,过点O 作直线BC OE ⊥交抛物线的对称轴于点E .求证:四边形ODBE 是等腰梯形; (3)问Q 抛物线上是否存在点Q ,使得△OBQ 的面积等于四边形ODBE 的面积的31?若存在,求出点Q 的坐标;若不存在,请说明理由.解:(1)求出:4-=b ,3=c ,抛物线的对称轴为:x=2 ……3分(2) 抛物线的解析式为342+-=x x y ,易得C 点坐标为(0,3),D 点坐标为(2,-1) 设抛物线的对称轴DE 交x 轴于点F ,易得F 点坐标为(2,0),连接OD ,DB ,BE ∵∆OBC 是等腰直角三角形,∆DFB 也是等腰直角三角形,E 点坐标为(2,2), ∴∠BOE= ∠OBD=45 ∴OE ∥BD∴四边形ODBE 是梯形 ………………5分在ODF Rt ∆和EBF Rt ∆中,(第28题)(第28题2)OD=5122222=+=+DF OF ,BE=5122222=+=+FB EF∴OD= BE∴四边形ODBE 是等腰梯形 ……………7分(3) 存在, ……8分 由题意得:29332121=⨯⨯=⋅=DE OB S ODBE 四边形 ………………9分 设点Q 坐标为(x ,y ), 由题意得:y y OB S OBQ 2321=⋅=三角形=23293131=⨯=ODBE S 四边形 ∴1±=y当y=1时,即1342=+-x x ,∴ 221+=x , 222-=x ,∴Q 点坐标为(2+2,1)或(2-2,1) …………11分 当y=-1时,即1342-=+-x x , ∴x=2, ∴Q 点坐标为(2,-1)综上所述,抛物线上存在三点Q 1(2+2,1),Q 2 (2-2,1) ,Q 3(2,-1) 使得OBQ S 三角形=ODBE S 四边形31. ………………12分EFQ 1 Q 3Q 226.(湖南省长沙市)如图,在平面直角坐标系中,矩形OABC 的两边分别在x 轴和y轴上,OA =cm , OC=8cm ,现有两动点P 、Q 分别从O 、C 同时出发,P 在线段OA 上沿OAcm 的速度匀速运动,Q 在线段CO 上沿CO 方向以每秒1 cm 的速度匀速运动.设运动时间为t 秒. (1)用t 的式子表示△OPQ 的面积S ;(2)求证:四边形OPBQ 的面积是一个定值,并求出这个定值;(3)当△OPQ 与△P AB 和△QPB 相似时,抛物线214y x bx c =++经过B 、P 两点,过线段BP 上一动点M 作y 轴的平行线交抛物线于N ,当线段MN 的长取最大值时,求直线MN 把四边形OPBQ 分成两部分的面积之比.解:(1) ∵CQ =t ,OPt ,CO =8 ∴OQ =8-t∴S △OPQ=21(8)222t t -=-+(0<t <8) …………………3分 (2) ∵S 四边形OPBQ =S 矩形ABCD -S △PAB -S △CBQ=1188)22⨯⨯-⨯⨯=………… 5分 ∴四边形O PBQ 的面积为一个定值,且等于 …………6分(3)当△OPQ 与△P AB 和△QPB 相似时, △QPB 必须是一个直角三角形,依题意只能是∠QPB =90°又∵BQ 与AO 不平行 ∴∠QPO 不可能等于∠PQB ,∠APB 不可能等于∠PBQ ∴根据相似三角形的对应关系只能是△OPQ ∽△PBQ ∽△ABP ………………7分8=解得:t =4经检验:t =4是方程的解且符合题意(从边长关系和速度) 此时P(0)∵B (8)且抛物线214y x bxc =++经过B 、P 两点, 第26题图∴抛物线是212284y x x =-+,直线BP 是:28y x =- …………………8分 设M (m , 28m -)、N (m ,212284m m -+)∵M 在BP 上运动 ∴4282m ≤≤ ∵2112284y x x =-+与228y x =-交于P 、B 两点且抛物线的顶点是P ∴当4282m ≤≤时,12y y > ………………………………9分 ∴12MN y y =-=21(62)24m --+ ∴当62m =时,MN 有最大值是2 ∴设MN 与BQ 交于H 点则(62,4)M 、(62,7)H ∴S △BHM =13222⨯⨯=32 ∴S △BHM :S 五边形QOPMH =32:(32232)-=3:29 ∴当MN 取最大值时两部分面积之比是3:29. ……10分28.(南京市8分)如图,正方形ABCD 的边长是2,M 是AD 的中点,点E 从点A 出发,沿AB 运动到点B 停止,连接EM 并延长交射线CD 于点F ,过M 作EF 的垂线交射线BC 于点G ,连结EG 、FG 。
【配套K12】2010年各地中考数学 压轴题精选
2010中考数学压轴题精选(一)★★1、(2010北京)在平面直角坐标系xOy 中,抛物线y = -41-m x 2+45mx +m 2-3m +2 与x 轴的交点分别为原点O 和点A ,点B (2,n )在这条抛物线上。
(1)求点B 的坐标; (2)点P 在线段OA 上,从O 点出发向点运动,过P 点作x 轴的垂线,与直线OB 交于点E 。
延长PE 到点D ,使得ED =PE ,以PD 为斜边在PD 右侧作等腰直角三角形PCD (当P 点运动时,C 点、D 点也随之运动)当等腰直角三角形PCD 的顶点C 落在此抛物线上时,求OP 的长;若P 点从O 点出发向A 点作匀速运动,速度为每秒1个单位,同时线段OA 上另一 点Q 从A 点出发向O 点作匀速运动,速度为每秒2个单位(当Q 点到达O 点时停止运动,P 点也同时停止运动)。
过Q 点作x 轴的垂线,与直线AB 交于点F 。
延长QF 到点M ,使得FM =QF ,以QM 为斜边,在QM 的左侧作等腰直角三角形QMN (当Q 点运动时,M 点,N 点也随之运动)。
若P 点运动到t 秒时,两个等腰直角三角形分别有一条直角边恰好落在同一条直线上,求此刻t 的值。
★★2、(2010北京)问题:已知△ABC 中,∠BAC =2∠ACB ,点D 是△ABC 内的一点,且AD =CD ,BD =BA 。
探究∠DBC 与∠ABC 度数的比值。
请你完成下列探究过程:先将图形特殊化,得出猜想,再对一般情况进行分析并加以证明。
(1) 当∠BAC =90︒时,依问题中的条件补全右图。
观察图形,AB 与AC 的数量关系为 ; 当推出∠DAC =15︒时,可进一步推出∠DBC 的度数为 ;可得到∠DBC 与∠ABC 度数的比值为 ;(2) 当∠BAC ≠90︒时,请你画出图形,研究∠DBC 与∠ABC 度数的比值是否与(1)中的结论相同,写出你的猜想并加以证明。
★★3、(2010郴州)如图(1),抛物线42y x x =+-与y 轴交于点A ,E (0,b )为y A C B轴上一动点,过点E 的直线y x b =+与抛物线交于点B 、C .(1)求点A 的坐标;(2)当b =0时(如图(2)),ABE 与ACE 的面积大小关系如何?当4b >-时,上述BOC 是以b ;若★★4、(2010滨州)如图,四边形ABCD 是菱形,点D的坐标是(0,3),以点C 为顶点的抛物线c bx ax y ++=2恰好经过x 轴上A 、B 两点.(1)求A 、B 、C 三点的坐标;(2)求过A 、B 、C 三点的抛物线的解析式;(3)若将上述抛物线沿其对称轴向上平移后恰好过D 点,求平移后抛物线的解析式,并指出平移了多少个单位?★★5、(2010长沙)已知:二次函数22y ax bx =+-的图象经过点(1,0),一次函数图象经过原点和点(1,-b ),其中0a b >>且a 、b 为实数. (1)求一次函数的表达式(用含b 的式子表示); (2)试说明:这两个函数的图象交于不同的两点;(3)设(2)中的两个交点的横坐标分别为x1、x2,求| x1-x2 |的范围.★★6、(2010长沙)如图,在平面直角坐标系中,矩形OABC的两边分别在x轴和y轴上,OA , OC=8cm,现有两动点P、Q分别从O、C同时出发,P在线段OA上沿OA cm的速度匀速运动,Q在线段CO上沿CO方向以每秒1cm的速度匀速运动.设运动时间为t秒.(1)用t 的式子表示△OPQ 的面积S ;(2)求证:四边形OPBQ 的面积是一个定值,并求出这个定值;(3)当△OPQ 与△PAB 和△QPB 相似时,抛物线214y x bx c =++经过B 、P 两点,过线段BP 上一动点M 作y 轴的平行线交抛物线于N ,当线段MN 的长取最大值时,求直线MN 把四边形OPBQ 分成两部分的面积之比.★★7、(2010常德)如图9,已知抛物线212y x bx c x =++与轴交于点A (-4,0)和B (1,0)两点,与y 轴交于C 点. (1)求此抛物线的解析式;第26题图(2)设E 是线段AB 上的动点,作EF∥AC 交BC 于F ,连接CE ,当C E F 的面积是BEF 面积的2倍时,求E 点的坐标;(3)若P 为抛物线上A 、C 两点间的一个动点,过P 作y 轴的平行线,交AC 于Q ,当P 点运动到什么位置时,线段PQ 的值最大,并求此时P 点的坐标.★★8、(2010常德)如图10,若四边形ABCD 、四边形CFED 都是正方形,显然图中有AG=CE ,AG⊥CE.(1)当正方形GFED 绕D 旋转到如图11的位置时,AG=CE 是否成立?若成立,请给出证明;图9x若不成立,请说明理由.(2)当正方形GFED 绕D 旋转到如图12的位置时,延长CE 交AG 于H ,交AD 于M. ①求证:AG⊥CH;②当AD=4,CH 的长。
2010年中考数学压轴题精选(五)及答案
★★、(深圳)如图,以点(-)为圆心的圆与轴、轴分别交于点、、、,直线=- -与⊙相切于点,交轴于点,交轴于点. ()请直接写出、⊙的半径、的长;(分)()如图,弦交轴于点,且=,求∠的值;()如图,点为线段上一动点(不与、重合),连接交⊙于点,弦交轴于点.是否存在一个常数,始终满足·=,如果存在,请求出的值;如果不存在,请说明理由.解:()、如图,,,()、如图,连接、,则, 易知,故,,,由于,;()、如图,连接,,延长, 与圆交于点,连接,则,由于,故,;而,故在和中,;故; ;即:故存在常数,始终满足,常数图图图★★、(随州)某同学从家里出发,骑自行车上学时,速度(米秒)与时间(秒)的关系如图,(,),(,),(,).()求该同学骑自行车上学途中的速度与时间的函数关系式;()计算该同学从家到学校的路程(提示:在和段的运动过程中的平均速度分别等于它们中点时刻的速度,路程=平均速度×时间);()如图,直线=(≤≤),与图的图象相交于、,用字母表示图中阴影部分面积,试求与的函数关系式;()由()(),直接猜出在时刻,该同学离开家所超过的路程与此时的数量关系.图图解:()()×××=(米)()() 相等的关系;★★、(随州)已知抛物线顶点为(,)且过原点.过抛物线上一点(,)向直线作垂线,垂足为,连(如图).()求字母,,的值;()在直线=上有一点,求以为底边的等腰三角形的点的坐标,并证明此时△为正三角形;()对抛物线上任意一点,是否总存在一点(,),使=恒成立,若存在请求出值,若不存在请说明理由.解:()=-,=,=()过作直线的垂线,可求的纵坐标为,横坐标为.此时,===,故△为正三角形.()不存在.因为当<,<时,与不可能相等,同理,当>,>时,与不可能相等。
★★、(台州)如图,△中,∠°,,.点,都是斜边上的动点,点从向运动(不与点重合),点从向运动,.点,分别是点,以,为对称中心的对称点,⊥于,交于点.当点到达顶点时,,同时停止运动.设的长为,△的面积为.()求证:△∽△;()求关于的函数解析式并求的最大值;()当为何值时,△为等腰三角形?解:()∵、关于点成中心对称,⊥,∴°,,∴,∴△∽△.()①如图,当时,,,此时.当时,最大值.②如图,当时,,,此时.当时,最大值.∴与之间的函数解析式为的最大值是.()①如图,当时,若,∵,,∴,.显然,不可能;②如图,当时,(第题)(图)(图)若,,;若,此时点,分别与点,重合,;若,则△∽△, ∴,,.∴当的值为时,△是等腰三角形。
2010年部分省市中考数学试题分类汇编 压轴题(四)及答案
2010年部分省市中考数学试题分类汇编压轴题(四)23.(安徽省)如图,已知111ABC A B C △∽△,相似比为k (k >1),且ABC △的三边长分别为a 、b 、c (a>b>c ),111A B C △的三边长分别为1a 、1b 、1c .(1)若c=a 1,求证:a=kc ;[证](2)若c=a 1,试给出符合条件的一对111ABC A B C △和△,使得a 、b 、c 和1a 、1b 、1c 都是正整数,并加以说明;[解](3)若b=a 1,c=b 1,是否存在111ABC A B C △和△使得k =2?请说明理由.[解]解:(1)证:111ABC A B C △∽△,且相似比为11(1).ak k k a ka a >∴=∴=,, 又1.c a a kc =∴=, ··········································································· (3分) (2)解:取11186443 2.a b c a b c ======,,,同时取,, ··············· (8分) 此时1111112a b cABC A B C a b c ===∴,△∽△且1.c a = ······························ (10分) 注:本题也是开放型的,只要给出的ABC △和111A B C △符合要求就相应赋分. (3)解:不存在这样的ABC △和111A B C △.理由如下: 若2k =,则111222.a a b b c c ===,, 又1b a =,1c b =,第23题图112244a a b b c ∴====,2.b c ∴= ························································································ (12分)24b c c c c a ∴+=+<=,而b c a +>,故不存在这样的ABC △和111A B C △,使得 2.k = ··································· (14分) 注:本题不要求学生严格按反证法的证明格式推理,只要能说明在题设要求下2k =的情况不可能即可. 24.(芜湖市 本小题满分14分)如图,在平面直角坐标系中放置一矩形ABCO ,其顶点为A (0,1)、B (-33,1)、C (-33,0)、O (0,0).将此矩形沿着过E (-3,1)、F (-433,0)的直线EF 向右下方翻折,B 、C 的对应点分别为B ′、C ′. (1)求折痕所在直线EF 的解析式;(2)一抛物线经过B 、E 、B ′三点,求此二次函数解析式;(3)能否在直线EF 上求一点P ,使得△PBC 周长最小?如能,求出点P 的坐标;若不能,说明理由.解:(2)设矩形沿直线EF 向右下方翻折后,B 、C 的对应点为1122()()B x y C x y B B A AE AE A ''''''⊥,,,.过作交所在直线于点. 2360B E BE B EF BEF ''==∠=∠=︒,, 6033B EA A E B A '''''∴∠=︒∴=,,.1102(02)A A B y x y B '''∴∴==--与重合,在轴上.,即,.[此时需说明()11B x y y ',在轴上]. ······································································ 6分设二次函数解析式为:2y ax bx c =++抛物线经过()33B -,1、()3E -,1、()0-2B ',.得到233127331c a b c a b c -=⎧⎪-+=⎨⎪-+=⎩解得134332a b c ⎧=-⎪⎪⎪=-⎨⎪=-⎪⎪⎩2143233y x x ∴=---该二次函数解析式. ····················································· 9分(3)能,可以在直线EF 上找到P 点,连接B C EF P BP '交于点,再连接.由于B P BP P C '=,此时点到、B '在一条直线上,故BP PC B P PC '+=+的和最小, 由于BC 为定长,所以满足PBC ∆周长最小. ······················································ 10分 设直线B C '的解析式为:y kx b =+2033bk b-=⎧⎪⎨=-+⎪⎩23:29B C y x '∴=--直线的解析式为. ·································· 12分 182332119103411x y x P B C EF y y x ⎧⎧=-⎪=--⎪⎪'∴⎨⎨⎪⎪=-=+⎩⎪⎩又为直线和直线的交点,解得 18311P ⎛⎫∴- ⎪⎝⎭10点的坐标为,-11. ··································································· 14分 [注:对于以上各大题的不同解法,解答正确可参照评分!]26.( 重庆市綦江县) 已知:抛物线y=ax 2+bx+c(a >0)的图象经过点B(12,0)和C(0,-6),对称轴为x=2.(1)求该抛物线的解析式; (2)点D 在线段AB 上且AD=AC ,若动点P 从A 出发沿线段AB 以每秒1个单位长度的速度匀速运动,同时另一动点Q 以某一速度从C 出发沿线段CB 匀速运动,问是否存在某一时刻,使线段PQ 被直线CD 垂直平分?若存在,请求出此时的时间t (秒)和点Q 的运动速度;若不存在,请说明理由;(3)在(2)的结论下,直线x=1上是否存在点M ,使△MPQ 为等腰三角形?若存在,请求出所有点M 的坐标;若不存在请说明理由. 解:方法一:∵抛物线过C(0,-6) ∴c=-6, 即y=ax 2+bx -6由⎪⎩⎪⎨⎧=-+=-061214422b a a b解得:a=161 ,b=-41∴该抛物线的解析式为y=161x 2-41x -6 -----------------3分 方法二:∵A 、B 关于x=2对称∴A (-8,0) 设y=a(x +8)(x -12)C 在抛物线上 ∴-6=a ×8×(-12) 即a=161 ∴该抛物线的解析式为:y=161x 2-41x -6 --------3分(2)存在,设直线CD 垂直平分PQ,在Rt △AOC 中,AC=2268+=10=AD∴点D 在对称轴上,连结DQ 显然∠PDC=∠QDC ,-----------4分 由已知∠PDC=∠ACD∴∠QDC=∠ACD ∴DQ ∥AC -----------------------------5分 DB=AB -AD=20-10=10∴DQ 为△ABC 的中位线 ∴DQ=21AC=5 -----------------6分 AP=AD-PD=AD-DQ=10-5=5 ∴t=5÷1=5(秒)∴存在t=5(秒)时,线段PQ 被直线CD 垂直平分-----------7分 在Rt △BOC 中, BC=22126+=65 ∴CQ=35∴点Q 的运动速度为每秒553单位长度.------------------8分 (3)存在 过点Q 作QH ⊥x 轴于H ,则QH=3,PH=9在Rt △PQH 中,PQ=2239+=310 --------------------9分 ①当MP=MQ ,即M 为顶点,设直线CD 的直线方程为:y=kx+b(k ≠0),则:⎩⎨⎧+==-b k b 206 解得:⎩⎨⎧=-=36k b ∴y=3x-6当x=1时,y=-3 ∴M 1(1, -3) ------------------------10分 ②当PQ 为等腰△MPQ 的腰时,且P 为顶点. 设直线x=1上存在点M(1,y) ,由勾股定理得: 42+y 2=90 即y=±74∴M 2(1,74) M 3(1,-74) -----------------------11分 ③当PQ 为等腰△MPQ 的腰时,且Q 为顶点.过点Q 作QE ⊥y 轴于E ,交直线x=1于F ,则F(1, -3) 设直线x=1存在点M(1,y), 由勾股定理得: (y +3)2+52=90 即y=-3±65∴M 4(1, -3+65) M 5((1, -3-65) --------------------12分 综上所述:存在这样的五点:M 1(1, -3), M 2(1,74), M 3(1,-74), M 4(1, -3+65), M 5((1, -3-65).25.(山东省滨州市 本题满分l0分)如图,四边形ABCD 是菱形,点D 的坐标是(0,3),以点C 为顶点的抛物线c bx ax y ++=2恰好经过x 轴上A 、B 两点.(1)求A 、B 、C 三点的坐标;(2)求过A 、B 、C 三点的抛物线的解析式;(3)若将上述抛物线沿其对称轴向上平移后恰好过D 点,求平移后抛物线的解析式,并指出平移了多少个单位?解:①由抛物线的对称性可知AM=BM在Rt△AOD和Rt△BMC中,∵OD=MC,AD=BC,∴△AOD≌△BMC.∴OA=MB=MA.………………………………………l分设菱形的边长为2m,在Rt△AOD中,2)22m=+)32((m解得m=1.∴DC=2,OA=1,OB=3.∴A、B、C三点的坐标分别为(1,0)、(3,0)、(2,3)………………… 4分②设抛物线的解析式为y=a(x—2)2+3代入A点坐标可得a=—3抛物线的解析式为y=—3(x—2)2+3……………………………………7分③设抛物线的解析式为y=—3(x一2)2+k代入D(0,3)可得k=53所以平移后的抛物线的解析式为y=—3(x一2)2+53..............................9分平移了53一3=43个单位. 026.(山东省烟台市本题满分14分)如图,已知抛物线y=x2+bx-3a过点A(1,0),B(0,-3),与x轴交于另一点C.(1)求抛物线的解析式;(2)若在第三象限的抛物线上存在点P,使△PBC为以点B为直角顶点的直角三角形,求点P的坐标;(3)在(2)的条件下,在抛物线上是否存在一点Q,使以P,Q,B,C为顶点的四边形为直角梯形?若存在,请求出点Q的坐标;若不存在,请说明理由.解:(1)把A(1,0),B(0,-3)代入y=x2+bx-3a中,得1+b-3a=0-3a=-3a=1解得b=2∴抛物线的解析式为y=x2+2x-3………………………………………4分(2)令y=0,得x2+2x-3=0,解得x1=-3,x2=1∴点C(-3,0) (5)分∵B(0,-3)∴△BOC为等腰直角三角形.∴∠CBO=45°……………………………………………………6分过点P作PD⊥y轴,垂足为D,∵PB⊥BC,∴∠PBD=45°∴PD=BD……………………………8分所以可设点P(x,-3+x)则有-3+x=x2+2x-3,∴x=-1,所以P点坐标为(-1,-4)………………………10分(3)由(2)知,BC⊥BP当BP为直角梯形一底时,由图象可知点Q不可能在抛物线上.若BC为直角梯形一底,BP为直角梯形腰时,∵B(0,-3),C(-3,0),∴直线BC的解析式为y=-x-3…………………………11分∵直线PQ∥BC,且P(-1,-4),∴直线PQ的解析式为y=-(x+1)-3-1即y=-x-5…………………………………………………12分xy OA B CD EP y =-x -5联立方程组得y =x 2+2x -3解得x 1=-1,x 2=-2…………………………………………………………………………13分 ∴x =-2,y =-3,即点Q (-2,-3)∴符合条件的点Q 的坐标为(-2,-3)………………………………………………14分28.(四川省成都市)在平面直角坐标系xOy 中,抛物线2y ax bx c =++与x 轴交于A B 、两点(点A 在点B 的左侧),与y 轴交于点C ,点A 的坐标为(30)-,,若将经过A C 、两点的直线1y kx b =+沿y 轴向下平移3个单位后恰好经过原点,且抛物线的对称轴是直线2x =-.(1)求直线AC 及抛物线的函数表达式;(2)如果P 是线段AC 上一点,设ABP ∆、BPC ∆的面积分别为ABP S ∆、BPC S ∆,且:2:3ABP BPC S S ∆∆=,求点P 的坐标;(3)设Q 的半径为l ,圆心Q 在抛物线上运动,则在运动过程中是否存在Q 与坐标轴相切的情况?若存在,求出圆心Q 的坐标;若不存在,请说明理由.并探究:若设⊙Q 的半径为r ,圆心Q 在抛物线上运动,则当r 取何值时,⊙Q 与两坐轴同时相切?解:(1)∵y kx b =+沿y 轴向下平移3个单位后恰好经过原点,∴3b =,(0 3)C ,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第 1 页 共 30 页 2010年中考数学压轴题及解答1 1、(2010年北京市)24. 在平面直角坐标系xOy中,抛物线y= 41mx245mxm23m2 与x轴的交点分别为原点O和点A,点B(2,n)在这条抛物线上。 (1) 求点B的坐标; (2) 点P在线段OA上,从O点出发向点运动,过P点作x轴的 垂线,与直线OB交于点E。延长PE到点D。使得ED=PE。 以PD为斜边在PD右侧作等腰直角三角形PCD(当P点运动 时,C点、D点也随之运动) 当等腰直角三角形PCD的顶点C落在此抛物线上时,求 OP的长; 若P点从O点出发向A点作匀速运动,速度为每秒1个单位,同时线段OA上另一 点Q从A点出发向O点作匀速运动,速度为每秒2个单位(当Q点到达O点时停止 运动,P点也同时停止运动)。过Q点作x轴的垂线,与直线AB交于点F。延长QF 到点M,使得FM=QF,以QM为斜边,在QM的左侧作等腰直角三角形QMN(当Q 点运动时,M点,N点也随之运动)。若P点运动到t秒时,两个等腰直角三角形分 别有一条直角边恰好落在同一条直线上,求此刻t的值。 【解答】
24. 解:(1) ∵拋物线y= 41mx245mxm23m2经过原点,∴m23m2=0,解得m1=1,m2=2,
由题意知m1,∴m=2,∴拋物线的解析式为y= 41x225x,∵点B(2,n)在拋物线 y= 41x225x上,∴n=4,∴B点的坐标为(2,4)。 (2) 设直线OB的解析式为y=k1x,求得直线OB的解析式为 y=2x,∵A点是拋物线与x轴的一个交点,可求得A点的 坐标为(10,0),设P点的坐标为(a,0),则E点的坐标为 (a,2a),根据题意作等腰直角三角形PCD,如图1。可求 得点C的坐标为(3a,2a),由C点在拋物线上,得
2a= 41(3a)2253a,即49a2211a=0,解得a1=922,a2=0
(舍去),∴OP=922。 依题意作等腰直角三角形QMN,设直线AB的解析式为y=k2xb,由点A(10,0), 点B(2,4),求得直线AB的解析式为y= 21x5,当P点运动到t秒时,两个等腰 直角三角形分别有一条边恰好落在同一条直线上,有以下三种情况: 第一种情况:CD与NQ在同一条直线上。如图2所示。可证△DPQ为等腰直角三 角形。此时OP、DP、AQ的长可依次表示为t、4t、2t个单位。∴PQ=DP=4t,
∴t4t2t=10,∴t=710。 第二种情况:PC与MN在同一条直线上。如图3所示。可证△PQM为等腰直角三 角形。此时OP、AQ的长可依次表示为t、2t个单位。∴OQ=102t,∵F点在 直线AB上,∴FQ=t,∴MQ=2t,∴PQ=MQ=CQ=2t,∴t2t2t=10,∴t=2。 第三种情况:点P、Q重合时,PD、QM在同一条直线上,如图4所示。此时OP、
x y O 1 1
O A B C D E P
y
x 图1 第 2 页 共 30 页
AQ的长可依次表示为t、2t个单位。∴t2t=10,∴t=310。综上,符合题意的 t值分别为710,2, 310。
2、(2010年北京市) 25. 问题:已知△ABC中,BAC=2ACB,点D是△ABC内的一点,且AD=CD,BD=BA。 探究DBC与ABC度数的比值。 请你完成下列探究过程: 先将图形特殊化,得出猜想,再对一般情况进行分析并加以证明。 (1) 当BAC=90时,依问题中的条件补全右图。 观察图形,AB与AC的数量关系为 ; 当推出DAC=15时,可进一步推出DBC的度数为 ; 可得到DBC与ABC度数的比值为 ; (2) 当BAC90时,请你画出图形,研究DBC与ABC度数的比值 是否与(1)中的结论相同,写出你的猜想并加以证明。 【解答】 25. 解:(1) 相等;15;1:3。 (2) 猜想:DBC与ABC度数的比值与(1)中结论相同。 证明:如图2,作KCA=BAC,过B点作BK//AC交CK于点K, 连结DK。∵BAC90,∴四边形ABKC是等腰梯形, ∴CK=AB,∵DC=DA,∴DCA=DAC,∵KCA=BAC, ∴KCD=3,∴△KCD△BAD,∴2=4,KD=BD, ∴KD=BD=BA=KC。∵BK//AC,∴ACB=6, ∵KCA=2ACB,∴5=ACB,∴5=6,∴KC=KB, ∴KD=BD=KB,∴KBD=60,∵ACB=6=601, ∴BAC=2ACB=12021, ∵1(601)(12021)2=180,∴2=21, ∴DBC与AB C度数的比值为1:3。
3、(2010年安徽省芜湖市)23.(本小题满分12分) 如图,BD是⊙O的直径,OA⊥OB,M是劣弧AB⌒上一点,过点M点作⊙O的切线MP交OA的延长线于P点,MD与OA交于N点. (1)求证:PM=PN;
(2)若BD=4,PA= 32 AO,过点B作BC∥MP交⊙O于C点,求BC的长.
A C
B
E x O A B
C
y
P M Q N F
D
图2 x y
O A M (C) B
(E)
D
P Q F N
图3 图4
y x B O Q(P) N
C
D M E
F
D A C
B
图1 B
A C
D
K 1 2
3 4
5
6
图2 第 3 页 共 30 页
【解答】 解:
4、(2010年安徽省芜湖市)24.(本小题满分14分)如图,在平面直角坐标系中放置一矩形ABCO,其顶点为A(0,1)、B(-33,1)、C(-33,0)、O(0,0).将此矩形沿着过E(-3,1)、
F(-433,0)的直线EF向右下方翻折,B、C的对应点分别为B′、C′. (1)求折痕所在直线EF的解析式; (2)一抛物线经过B、E、B′三点,求此二次函数解析式; (3)能否在直线EF上求一点P,使得△PBC周长最小?如能,求出点P的坐标;若不能,说明理由. 第 4 页 共 30 页
【解答】 第 5 页 共 30 页
5、(2010年安徽省) 22.春节期间某水库养殖场为适应市场需求,连续用20天时间,采用每天降低水位以减少捕捞成本的办法,对水库中某种鲜鱼进行捕捞、销售。 九(1)班数学建模兴趣小组根据调查,整理出第x天(201x且x为整数)的捕捞与销售的相关信息如下:
⑴在此期间该养殖场每天的捕捞量与前一末的捕捞量相比是如何变化的? ⑵假定该养殖场每天捕捞和销售的鲜鱼没有损失,且能在当天全部售出,求第x天的收入y(元)与x(天)之间的函数关系式?(当天收入=日销售额—日捕捞成本) 试说明⑵中的函数y随x的变化情况,并指出在第几天y取得最大值,最大值是多少?
【解答】
6、(2010年安徽省)23.如图,已知△ABC∽△111CBA,相似比为k(1k),且△ABC的三边长分别为a、b、c(cba),△111CBA的三边长分别为1a、1b、1c。 ⑴若1ac,求证:kca; ⑵若1ac,试给出符合条件的一对△ABC和△111CBA,使得a、b、c和1a、1b、1c进都是正整数,并加以说明; ⑶若1ab,1bc,是否存在△ABC和△111CBA使得2k?请说明理由。
【解答】 第 6 页 共 30 页
7、(2010年福建省德化县)25、(12分)在△ABC中,AB=BC=2,∠ABC=120°,将△ABC绕点B顺时针旋转角α(0(1)如图①,观察并猜想,在旋转过程中,线段EA1与FC有怎样的数量关系?并证明你的结论; (2)如图②,当=30°时,试判断四边形BC1DA的形状,并说明理由; (3)在(2)的情况下,求ED的长.
【解答】 25、(1)1EAFC;提示证明1ABECBF„„„„„3分
(2)①菱形(证明略)„„„„„„„„„„„„„„„7分 (3)过点E作EG⊥AB,则AG=BG=1
在RtAEG中,123coscos303AGAEA
由(2)知AD=AB=2 ∴2233EDADAE„„„„„12分
8、(2010年福建省德化县)26、(12分)如图1,已知抛物线经过坐标原点O和x轴上另一点E,顶点M的坐标为 (2,4);矩形ABCD的顶点A与点O重合,AD、AB分别在x轴、y轴上,且AD=2,AB=3. (1)求该抛物线的函数关系式; (2)将矩形ABCD以每秒1个单位长度的速度从图1所示的位置沿x轴的正方向匀速平行移动,同时一动点P也以相同的速度.....从点A出发向B匀速移动,设它们运动的时间为t秒(0≤t≤3),直线AB与该抛物线的交点为N(如图2所示).
① 当t=25时,判断点P是否在直线ME上,并说明理由;
② 设以P、N、C、D为顶点的多边形面积为S,试问S是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
C1 A1 F
E D
C
B A 图①
C1 A1 F
E
D
C
B A
图②
图2 B C O A D E
M y x P N
·
图1
B C
O (A)
D E
M y x
