二维热传导方程的解法
数学物理方程2热传导方程

对未来研究的展望
深入研究热传导方程的数学性质
尽管热传导方程已有广泛的研究和应用,但对其数学性质的理解仍不够深入。未来可以进一步研究热传导方程解的唯 一性、稳定性、渐近性等数学问题,以推动数学理论的发展。
拓展热传导方程的应用领域
随着科技的发展,热传导方程的应用领域也在不断拓展。例如,在新能源领域,热传导方程可以用于研究太阳能电池 板的工作原理和优化设计;在环保领域,热传导方程可用于研究污染物在环境中的扩散和迁移规律。
交换。
热传导方程是偏微分方程的一种形式,通常采用傅里叶级数或
03
有限元方法进行求解。
热传导现象的重要性
1
热传导现象在自然界和工程领域中广泛存在,如 气候变化、能源利用、材料科学等。
2
热传导方程的应用有助于深入理解热量传递的机 制,为相关领域的研究提供理论基础。
3
通过求解热传导方程,可以预测温度分布、热量 传递速率等关键参数,为实际问题的解决提供指 导。
04 热传导方程的数值解法
有限元法
有限元法是一种将连续的求解域离散化为有限个小的、互连 的子域(或单元)的方法。在每个单元内,选择合适的基函 数,将待求的解表示为这些基函数的线性组合。通过求解一 系列线性方程组,可以得到原问题的近似解。
有限元法在求解热传导方程时,可以将复杂的几何形状离散 化为有限个简单的几何形状,从而简化计算过程。同时,有 限元法能够处理复杂的边界条件和初始条件,适用于各种类 型的热传导问题。
有限差分法
总结词
有限差分法是一种数值求解偏微分方程的方法,通过将连续的偏微分方程离散化为差分 方程来求解。
详细描述
有限差分法的基本步骤是将偏微分方程中的空间变量离散化为有限个点,然后将偏微分 方程转化为差分方程,最后通过迭代求解差分方程得到原方程的近似解。这种方法适用
2-稳态热传导3

, (m 1, 2, )
sin( ) 0
这样就得到满足方程和边界条件式的无穷多个解
X m Bm sin( m x)
分离变量法
Y Csh( y) Dch( y)
由边界条件式可得Y(0)=0,得D=0。
Y Cm sh( m y)
相应地有
m Cm sin( m x)sh( m y),(m 1, 2, )
Cm sh( m h)
2
0
f1 ( x) sin( m x)dx
即
Cm
2
0
f1 ( x)sin( m x)dx sh( m H )
分离变量法
最后得到原问题的解为
( x, y )
2
m 1
sh(
1 m
sh( H)
m
y ) sin(
m
x) f1 ( x) sin(
2 2 0 2 2 x y y 0, f 0 ( x ) 令 θ=θ1+θ2+θ3+θ4, y H , f1 ( x ) 由于每个问题中都有3个齐次边界条件, x 0, 0 ( y ) 可以分别按以上介绍的方法求得解析解。x , 1 ( y )
d2X 2 X 0 2 dx
d 2Y 2 Y 0 2 dy
分离变量法
它们各自的通解为
X A cos( x) B sin( x)
Y Csh( y) Dch( y )
注意到x方向的两个边界条件都是齐次的,把式
( x, y) X ( x)Y ( y)
代入边界条件式,同样可分离变量得到
热传导方程的导出及其定解问题的导出

热传导方程的导出及其定解问题的导出1. 热传导方程的导出考察空间某物体G 的热传导问题。
以函数u (x ,y ,z ,t )表示物体G 在位置(x ,y ,z )及时刻t 的温度。
依据传热学中的Fourier 实验定律,物体在无穷小时段dt 内沿法线方向n 流过一个无穷小面积dS 的热量dQ 与物体温度沿曲面dS 法线方向的方向导数学成正比,即o n d udQ =-k (x ,y ,z )dSdt (1-1)o n 其中k (x ,y ,z )称为物体在点(x ,y ,z )处的热传导系数,它应取正值。
(1-1)式中负号的出 o u现是由于热量总是从温度高的一侧流向低的一侧,因此dQ 应和异号。
o n在物体G 内任取一闭曲面r ,它所包围的区域记为0,由(1-1)式,从时刻t 到t 流进12此闭曲面的全部热量为Q =f t 2仙k (x ,y ,z)—dS\dt (1-2)4I r O nJ这里表示u沿r 上单位外法线方向n 的方向导数。
o n流入的热量使物体内部的温度发生变化,在实践间隔(t ,t )中物体温度从u (x ,y ,z ,t )121变化到u (x‘y ,z ,t2),它所应该吸收的热量是JU c (x ,y ,z )P (x ,y ,z )[u (x ,y ,z ,t )一u (x ,y ,z ,t )]dxdydz其中c 为比热,P 为密度。
因此就成立 >dt=JfJ C (x ,y ,z )P (x,y ,z)[u (x,y ,z ,12)一U (x ,y ,z ,t i )]dxdydz(1-3)假设函数u 关于变量x ,y ,z 具有二阶连续偏导数,关于t 具有一阶连续偏导数,利用格林公式,可以把(1-3)化为交换积分次序,就得到J t t 12仰(x ,y ,z )护t10O x{k 譽'O x 丿(一O u 、 +—k 二+—°y°y 丿 O z (O u 、k 一>dxdydzdt =c P JI o 丿J 「E O u dtdxdydztO t 丿dxdydzdt =0(1-4)训c P '0、由于t i,t2,0都是任意的,我们得到(1-5)式称为非均匀的各向同性体得热传导方程。
无单元 Galerkin 方法数值求解二维瞬态热传导问题

无单元 Galerkin 方法数值求解二维瞬态热传导问题摘要:采用无单元 Galerkin 方法数值求解具有狄利克雷边界条件的二维瞬态热传导问题。
首先离散该问题的时间变量,将该问题转化为与时间无关的边值问题;然后采用罚函数法处理 Dirichlet 边界条件,得到数值离散方程组,再利用 Matlab 软件求解给出的算例,结果表明该方法得到的数值结果与解析解吻合较好,该方法具有较高的计算精度和较好的收敛性。
关键词:二维瞬态热传导问题;无单元 Galerkin 方法;罚函数法;Matlab 软件中图分类号:G210.7 文献标识码:A 文章编号:20200168685有限差分法(FDM)[1]、有限元法(FEM)[2]、边界元法(BEM)得[3]、无网格法[4]等数值方法是解决瞬态热传导问题的常用方T k1T k1法。
Burlayenko 等人[5]用梯度有限元法计算了梯度材料中的瞬Tk1vd k vd k vdy2y态温度。
Sutradhar 和 Paulino[6]提出了一种简单的边界元法,该法只考虑边界条件,适用于梯度材料中的三维非定常热传导问T k1vd k1Q vdk1vd题。
Sladek 等人[7]用无网格局部边界积分方程方法考虑梯度材料中的不稳定温度场。
无单元 Galerkin 方法是应用最为广泛的无网格方法之一。
本文借鉴文献[8]应用无单元 Galerkin 方法数值求解具有狄利克雷边界条件的二维瞬态热传导问题。
首先离散该问题的时间变量,将该问题转化为与时间无关的边值问题;然后采用罚函数法(7)接下来,根据高斯公式化简(7)式,于是得与混合边值问k1x H1 ,使得,有题(6)等价的变分问题:求T处理 Dirichlet 边界条件,得到数值离散方程组,再利用 Matlab 软件求解给出的算例,最后给出了一个数值算例来验证理论误差a T k1,v(8)T k1vdvQ k1dR k1vd vT k2d结果。
热传导方程求解-分离变量法
牛曼外问题
拉普拉斯方程的狄氏内问题
Q(x, y, z)
拉普拉斯方程的基本解
• 1 三维空间的拉氏方程基本解
将三维空间拉氏方程用球坐标系表示
z
r M(x, y,z)
z
1 r2
r
(r2
u ) r
1
r2 sin
(sin
u )
r2
1
sin2
2u
2
0
A xo
xy
P
y
求其球对称解 u u(r)(解只与r有关,与角度无关)
0
n 0,1, 2,....
X
n
(
x)
sin
2n 2a
1
x
n 0,1, 2....
ux (0, y) u(a, y) 0 u(x, 0) (x) u(x,b) (x)
X (x) X (x) 0
X (0)
X (a)
0
n
(2n 1 2a
)2
0
n 0,1, 2,....
ux (0, y) ux (a, y) 0 u(x,0) (x) u(x,b) (x)
内容回忆
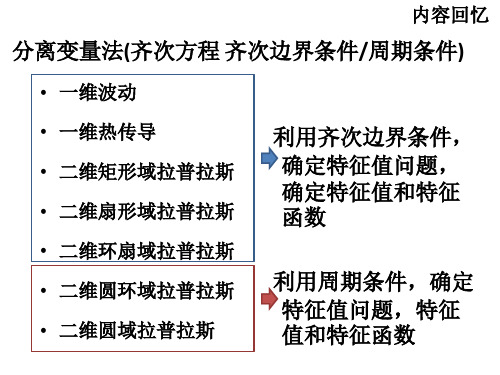
分离变量法(齐次方程 齐次边界条件/周期条件)
• 一维波动
• 一维热传导 • 二维矩形域拉普拉斯 • 二维扇形域拉普拉斯
利用齐次边界条件,
确定特征值问题, 确定特征值和特征 函数
• 二维环扇域拉普拉斯 • 二维圆环域拉普拉斯 • 二维圆域拉普拉斯
利用周期条件,确定
特征值问题,特征 值和特征函数
X (x) X (x) 0
X (0) X (l) 0
n
( n l
)2
0
稳态热传导问题的数值模拟

稳态热传导问题的数值模拟热传导是热能从高温区向低温区传递的过程,在自然界和工程应用中有广泛的应用。
当材料或物体的长度,面积和体积足够大以至于其中的热量可以被视为连续分布时,稳态热传导方程可以用来描述热传导现象。
本文将讨论如何通过数值模拟来解决稳态热传导问题。
1. 稳态热传导方程首先,我们来看一下稳态热传导方程。
稳态热传导方程最常用的形式是二维热传导方程和三维热传导方程。
对于二维情况,可以表示为:$$ \frac{\partial^2 T}{\partial x^2}+\frac{\partial^2 T}{\partial y^2}=0 $$对于三维情况,可以表示为:$$ \frac{\partial^2 T}{\partial x^2}+\frac{\partial^2 T}{\partialy^2}+\frac{\partial^2 T}{\partial z^2}=0 $$其中,T表示温度。
2. 数值模拟方法由于稳态热传导方程在大多数情况下很难用解析方法求解,因此数值模拟方法成为了解决该问题的主要方法之一。
这里我们主要介绍两种数值模拟方法:有限差分法和有限元法。
2.1 有限差分法有限差分法是一种基于迭代计算的数值模拟方法,它将区域离散化为小的网格,并通过有限差分来逼近上述方程。
具体来说,它将偏微分方程近似为差分方程,然后用迭代方法来逼近和求解问题。
在应用有限差分法时,需要将连续的区域离散化为小的网格。
然后,用相邻两个网格点的温度差来逼近该点处的温度。
具体来说,对于二维情况,可以用以下公式来表示:$$ \frac{T(i+1,j)+T(i-1,j)+T(i,j+1)+T(i,j-1)-4T(i,j)}{h^2}=0 $$其中,h表示网格尺寸,i和j分别表示网格的横向和纵向坐标。
通过递归求解该方程,可以得到整个区域内的温度分布。
2.2 有限元法有限元法是一种更通用的数值模拟方法,可以用于解决各种类型的偏微分方程。
热传导方程求解

热传导方程求解
热传导是物体内发生热能转移过程的数学建模,是热力学理论和工程实践中非常重要的部分。
热传导方程旨在帮助我们解决传热传质问题,通过描述温度在时间和空间上的变化,
可以理解热的行为。
根据体热传导数学模型,热传导方程可以总结为:
$$\frac{\partial T}{\partial t} = \kappa \nabla^2T$$
其中T为温度,t为时间,$\kappa$为热传导系数,$\nabla^2T$为拉普拉斯运算。
热传导方程可以用来说明物体内热能如何传播,可以确定物体内沿着空间和时间上的热量流动。
求解热传导方程是帮助我们理解物体热量分布行为的基础。
例如,当求解物体内温度分布的问题时,下式可以用来描述该问题:
$$\begin{cases} \frac{\partial T}{\partial t} = \kappa \nabla^2T \\ T(x,y,z,0)=f(x,y,z) \\
T(x,y,z,t) \rightarrow 0 \ \ \text{当}\ x\rightarrow\infty\end{cases}$$
其中$f(x,y,z)$是初始温度分布函数,$T(x,y,z,t)$表示特定的坐标上的时间t上的温度。
求解热传导方程可以根据实际情况采取各种数值和分析方法,例如有限元法、有限差分法、蒙特卡洛法和自然稳定性分析等。
同时,也可以利用计算机辅助软件对热传导方程进行求解。
热传导方程通过数学建模可以很好地概括物体内热能分布和传递规律,有助于深入理解物体内各种热力现象,为物理、工程以及其他领域的研究提供了有效的理论支撑。
热传导的数学模型与应用

热传导的数学模型与应用热传导是研究热传输过程的一种方法,它基于物质的热运动,描述了热能在空间中沿着温度梯度传导的过程。
在现实世界中,热传导的应用广泛,例如工程传热、地质传热等。
本文将介绍热传导的数学研究领域及其在应用中的一些方法和技术。
一、一维热传导的数学模型考虑一根长为L的均匀导热杆,其温度分布随时间的变化可以描述为以下偏微分方程:$$\frac{\partial u}{\partial t}=k\frac{\partial^2 u}{\partial x^2}$$其中,u表示温度,k是杆的热导率。
这个方程是著名的热传导方程,它描述了热传导现象的基本规律。
对于一维的情况,我们可以设计一些边界条件来求解这个方程。
例如,假设杆的两端分别接触两个热库,温度分别为$u_0$和$u_L$,则可以给出如下的边界条件:$$u(0,t)=u_0,\quad u(L,t)=u_L$$此外,还需确定初始条件,即$t=0$时的温度分布:$$u(x,0)=f(x)$$为了求解这个问题,我们可以采用变量分离法或者傅里叶变换等数学工具求解上述偏微分方程,进而得到温度分布随时间的变化规律。
这个问题在工程中有很多应用,例如热传导计算、材料热处理等。
二、二维热传导的数学模型对于二维的情况,即热传导在一个平面上进行时,我们需要引入两个空间变量$x,y$,此时热传导方程变为:$$\frac{\partial u}{\partial t}=k\left(\frac{\partial^2 u}{\partialx^2}+\frac{\partial^2 u}{\partial y^2}\right)$$同样地,我们还需要给出边界条件和初始条件。
例如,假设平面上存在一个温度分布为$u(x,y,0)=f(x,y)$的初始温度分布,则边界条件可以取如下形式:$$u(x,0,t)=u(x,L,t)=u(0,y,t)=u(W,y,t)=0$$其中,L和W分别表示平面的长度和宽度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二维热传导方程的解法
热传导是指物体内部的热量由高温处向低温处自然传递的现象。
而热传导方程就是描述热传导现象的数学方程。
在物理学中,二
维热传导方程是一个很重要的方程,它可以用来描述各种具有二
维几何形状的物体内部的热传导性质。
本文将介绍二维热传导方
程的解法。
一、二维热传导方程的建立
二维热传导方程的建立需要满足两个条件:
1. 假设物体是均匀的,即密度、比热和热导率在整个物体内是
不变的;
2. 假设物体的热量是由热传导引起的。
根据热传导定律,可以得到二维热传导方程:
$${\partial u\over\partial t} =\ alpha({\partial^2u\over\partial x^2}
+ {\partial^2u\over\partial y^2}) $$
其中,$\alpha$为热扩散系数,$u$为物体内的温度场,$x,y$分别为物体内的两个空间坐标,$t$为时间。
二、格点法
格点法是一种数学工具,它可以通过将物体划分成许多个小区域来离散化二维热传导方程,从而得到数值解。
通过将物体划分成的小区域称为格点,每个格点的温度可以根据它周围格点的温度值进行计算。
使用格点法求解二维热传导方程的基本步骤如下:
1. 将物体划分成 $N\times N$ 个格点,每个格点的大小为
$\Delta x\times\Delta y$;
2. 将时间划分成若干个离散时间步长 $\Delta t$,并设定初值条件 $u(x,y,0)=f(x,y)$;
3. 根据离散化的二维热传导方程对每个格点的温度进行更新,即
$${u_{i,j}^{n+1}-u_{i,j}^n\over\Delta t} ={\alpha\over\Delta
x^2}(u_{i+1,j}^n-2u_{i,j}^n+u_{i-1,j}^n) +{\alpha\over\Delta
y^2}(u_{i,j+1}^n-2u_{i,j}^n+u_{i,j-1}^n) $$
4. 循环迭代,重复步骤 3 直到达到约定的终止条件。
三、有限元法
有限元法是一种数值计算方法,它可以用于解决各种偏微分方程的数值解。
针对二维热传导方程,有限元法也是一种有效的解法。
与格点法不同的是,有限元法将物体划分成若干个小三角形或四边形的元素,而不是平行四边形。
使用有限元法求解二维热传导方程的基本步骤如下:
1. 将物体划分成 $N$ 个小三角形或四边形的有限元网格;
2. 将时间划分成若干个离散时间步长 $\Delta t$,并设定初值条件 $u(x,y,0)=f(x,y)$;
3. 根据元素的形状和尺寸,通过有限元法对每个元素的局部温度场进行逼近,即
$$ u(x,y)\approx\sum_i u_i\phi_i(x,y) $$
其中,$u_i$为节点 $i$ 上的温度值,$\phi_i$为形状函数;
4. 根据离散化的二维热传导方程对每个节点的温度进行更新,即
$$ {u_i^{n+1}-u_i^n\over\Delta t} =\sum_j K_{ij}^{n}\ u_j^n $$其中,
$$ K_{ij}^{n} ={\alpha\over A}\int_A
(\nabla\phi_i\cdot\nabla\phi_j)dA $$
是系统刚度矩阵,$A$是元素的面积。
5. 循环迭代,重复步骤 3 和 4 直到达到约定的终止条件。
四、总结
格点法和有限元法是两种经典的二维热传导方程的解法。
虽然它们在实际应用中有一些差异,但它们都可以得到足够精确的数值解,并且具有很强的普适性。
在实际工程计算中,我们可以根据具体问题的特点选择合适的方法进行求解。
