机械原理(西工大第二版)习题选解
机械原理习题及解答

第二章习题及解答2-1 如题图2-1所示为一小型冲床,试绘制其机构运动简图,并计算机构自由度。
(a)(b)题图2-1解:1)分析该小型冲床由菱形构件1、滑块2、拨叉3和圆盘4、连杆5、冲头6等构件组成,其中菱形构件1为原动件,绕固定点A作定轴转动,通过铰链B与滑块2联接,滑块2与拨叉3构成移动副,拨叉3与圆盘4固定在一起为同一个构件且绕C轴转动,圆盘通过铰链与连杆5联接,连杆带动冲头6做往复运动实现冲裁运动。
2)绘制机构运动简图选定比例尺后绘制机构运动简图如图(b)所示。
3)自由度计算其中n=5,P L=7, P H=0,F=3n-2P L-P H=3×5-2×7=1故该机构具有确定的运动。
2-2 如题图2-2所示为一齿轮齿条式活塞泵,试绘制其机构运动简图,并计算机构自由度。
(a)(b)题图2-2解:1)分析该活塞泵由飞轮曲柄1、连杆2、扇形齿轮3、齿条活塞4等构件组成,其中飞轮曲柄1为原动件,绕固定点A作定轴转动,通过铰链B与连杆2联接,连杆2通过铰链与扇形齿轮3联接,扇形齿轮3通过高副接触驱动齿条活塞4作往复运动,活塞与机架之间构成移动副。
2) 绘制机构运动简图选定比例尺后绘制机构运动简图如图(b)所示。
3)自由度计算其中n=4,P L=5, P H=1F=3n-2P L-P H=3×4-2×5-1=1故该机构具有确定的运动。
2-3 如图2-3所示为一简易冲床的初步设计方案,设计者的意图是电动机通过一级齿轮1和2减速后带动凸轮3旋转,然后通过摆杆4带动冲头实现上下往复冲压运动。
试根据机构自由度分析该方案的合理性,并提出修改后的新方案。
题图2-3解:1)分析2)绘制其机构运动简图(图2-3 b)选定比例尺后绘制机构运动简图如图(b )所示。
3)计算机构自由度并分析其是否能实现设计意图由图b 可知,45200l h n p p p F ''===== 故3(2)34(2520)00l h F n p p p F ''=-+--=⨯-⨯+--=因此,此简易冲床根本不能运动,需增加机构的自由度。
机械原理习题全解
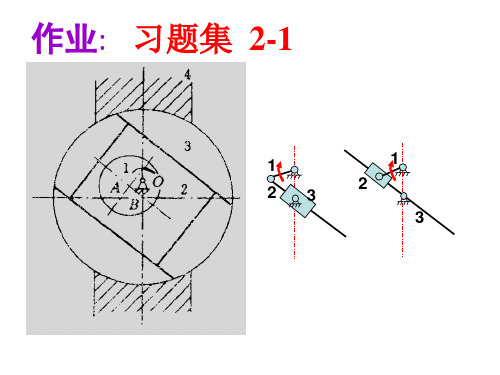
作业: 习题集 2-2
1 2 3 4
5
解: n = 4,pl = 5,ph = 1,F’ = 0,p’ = 0 F= 3n- (2pl+ph-p’ ) - F’ = 1 机构自由度数=机构原动件数 所以,机构具有确定的运动。
2-3 图示为一简易冲床的初拟设计方案。设计者的思路是:动力由 齿轮1输入,使轴A 连续回转;而固装在轴 A 上的凸轮2 与杠杆3 组成 的凸轮机构使冲头 4上下运动,以达到冲压的目的。试绘出其机构 运动简图(各尺寸由图中量取),分析是否能实现设计意图,并提 出修改方案。 3
5
4
解:n 3, P
l
2
(1)
4, Ph 1
F 3 3 (2 4 1 0) 0 0
原方案不可行。 改进措施: 1、增加一个低副和一个活动构件; 2、用一个高副代替低副。
修 改 方 案
3
2
3
5
4
(1)
2
5
4
(1)
习题2-4 图示牛头刨床设计方 案草图。 设计思路为:动力由 曲柄1输入,通过滑块2使 摆动导杆 3 作往复摆动, 并带动滑枕4作往复移动 , 已达到刨削加工目的。 试问图示的构件组合是否 能达到此目的? 如果不 能,该如何修改?
4
F’ = 1
F= 3n- (2pl+ph) - F’ = 1
1
机构自由度数=机构原动件数
所以,机构具有确定的运动。
作业: 习题集 2-2
4 3 2 1 5
6
解: n = 5,pl = 5,ph = 2,F’ = 1,p’ = 0 F= 3n- (2pl+ph-p’ ) - F’ = 2 机构自由度数=机构原动件数 所以,机构具有确定的运动。
机械原理习题解答(第1-3章)

vB
+
vC2B
=
vC3
+
vC2C3
方向
? ?
ω1lAB
?
BC
AB
0
? ∥BC
b
C(C2,C3,C4)
p
C3
C2
d
e
再根据速度影像原理,作△bde ∽ △ BDE 求得d及e,由图可得
b
vD v pd 0.23m / s
C(C2,C3,C4)
p' C '
(3)加速度分析
' C2
3
答:(1)机构所有的瞬心数:K=(N-1)/2=6(6-1)/2=15。 (2)求出如下三个瞬心P16,P36,P13,如下图所示。
P23 K(P13) P36
P12 P16
1 / 3 P P / P P 36 13 16 13
3-11 速度多边形和加速度多边形有哪些特性?试标出图 中VAB、VBC、VCA及VA、VB、VC的方向? 答:速度多边形具有以下特点: (1)作图起点p称为速度多边形的极点p,它代表机构中速 度为零的点。 (2)在速度多边形中,连接p点和任一点的矢量代表该点 在机构图中同名点的绝对速度,其指向是从p点指向该点。
答:速度瞬心是互作平面相对运动的两构件上瞬时相对速 度为零的重合点,也就是具有同一瞬时绝对速度的重合点 (即瞬时绝对速度速度相等的重合点),简称瞬心。若瞬心 处的绝对速度为零,则该瞬心称为绝对瞬心,否则称为相 对瞬心。 3-2 何为三心定理?何种情况下的瞬心需用三心定理来确 定? 答: 三心定理是指三个彼此作平面平行运动的构件的三 个瞬心必位于同一直线上。 对于不通过运动副直接相连的两构件间的瞬心位置,需用 三心定理来确定。
机械原理习题及答案(1-1至4-3)精品PPT课件

同下,其最少齿数为13( 20,ha*1 ).
答:z=13
做人,无需去羡慕别人,也无需去花 时间去 羡慕别 人是如 何成功 的,想 的只要 是自己 如何能 战胜自 己,如 何变得 比昨天 的自己 强大就 行。自 己的磨 练和坚 持,加 上自己 的智慧 和勤劳 ,会成 功的。 终将变 成石佛 那样受 到大家 的尊敬 。
lAB lBC lCD lAD
lAB50 35 30 lAB 15
答:lAB 15mm
2.当AD为机架,此机构为双曲柄机构,
则AD为最短杆,据曲柄存在条件,分两种情况;
(1)若 l AB 为最长杆,则 lAD lAB lBC lCD
30 lAB50 35
lAB55mm
A C lB C lA B 8 0 5 .0m 0 7 2 m 0m
A' C lA B lB C 8 0 5 .0m 0 1 2 m 7
另一解: lAB 21.5mm
lBC 48.5mm
l 0.002 m / mm
图示铰链四杆机构中,已
2-7 知 lAB30mm,lAD60mm,lDE10mm,原
答: z 21( ha *coC s*) 42
4-2: 5-4 一渐开线直齿轮,用卡尺测量其三个齿和两个齿的公法
线齿长根度圆为直W 径3df62.1176m2mm m,W ,齿2 数3z=9.3248m .试,m 齿确顶定圆该直齿径轮的da模2数0m8m,m,
压力角
,齿顶高系数
rb
mzcos
2
rf m(2zha*C*)
机械原理习题答案

pR12 M A
1ω O
ω 21
2
ω 23
3 pR32
B
P
4
2)确定ω21、ω23 的方向(如图)
pR12
A
ω 21
ω
M 1O
ω 23
2
3
B 4
P PR32
3)判断总反力应切于 A、B 处摩擦圆的上方还是下方(如图)
O
ω
1M
PR1
A
ω 21
2
ω 23
3 P
B 4 PR32
2.在图示曲柄滑块机构中 ,曲柄 1 在驱动力矩 M1 作用下等速转动。设已知各转动副的轴颈半径 r=10mm,当量摩擦系数 fv = 0.15 ,移动副中的滑块摩擦系数 f = 0.15 ,lAB = 100 mm,lBC = 350 mm。 各构件的质量和转动惯量忽略不计。当 M1 = 20 Nm 时,试求机构在图示位置所能克服的有效阻力 F3 及
uuur aBt 1 = 1× 55×102 = 5.5 m s2
uuuuur
ak B 2 B1
=
2
×10
×
0.55
=
11m
s2
uur a3
=
µα
.l p 'b2 '
=
0.2 ×
60
=
12
m
s2
4.已 知 图 所 示 的 机 构 的 尺 寸 及 ω 1=
1rad/s,试用图解法求ω3,a3,vD和 aD。
FR 21 Q
=
sin(π + ϕ ) 2
sin(π − α − 2ϕ )
2
FR 21
=
sin 98.53° sin 12.94°
西南交大《机械原理》习题解

机械原理习题解答例4-1 绘制图4-2所示液压泵机构的机构运动简图。
解:该机构由机架1、原动件2和从动件3、4组成,共4个构件,属于平面四杆机构。
机构中构件1、2,构件2、3,构件4、1之间的相对运动为转动,即两构件间形成转动副,转动副中心分别位于A 、B 、C 点处;构件3、4之间的相对运动为移动,即两构件间形成移动副,移动副导路方向与构件3的中心线平行。
构件1的运动尺寸为A 、C 两点间距离,构件2的运动尺寸为A 、B 两点之间的距离,构件3从B 点出发,沿移动副导路方向与构件4在C 点形成移动副,构件4同时又在C 点与构件1形成转动副。
选择与各构件运动平面平行的平面作为绘制机构运动简图的视图平面。
选择比例尺l μ=0.001m/mm ,分别量出各构件的运动尺寸,绘出机构运动简图,并标明原动件及其转动方向,如图4-2所示。
例4-2 绘制图4-3所示简易冲床的机构运动简图。
解:图示机构中已标明原动件,构件6为机架,其余构件为从动件。
需要注意的是,在区分构件时应正确判断图中各构件都包括哪些部分,例如:构件3就包括两部分,如图所示。
该机构中构件1与机架以转动副连接,转动副中心位于固定轴的几何中心A 点处;构件2除与构件1形成回转中心位于C 点的转动副外,又与构件3形成移动副,移动副导路沿BC 方向;构件3也绕固定轴上一点B 转动,即构件3与机架形成的转动副位于B 点,同时图4-3 简易冲床机构l μ=0.001m/mm构件3与构件2形成移动副,又与构件4形成中心位于D 点的转动副;构件4与构件5形成中心位于E 点的转动副;构件5与机架6形成沿垂直方向的移动副。
该机构属于平面机构,因此选择与各构件运动平面平行的平面作为绘制机构运动简图的视图平面。
选择比例尺l μ=0.001m/mm ,量出各构件的运动尺寸,绘出机构运动简图,并标明原动件及其转动方向,如图4-3所示。
4-3 题4-3图为外科手术用剪刀。
机械原理第二章练习题答案

机械原理第二章练习题答案机械原理第二章练习题答案第一题:一个质量为10kg的物体以2m/s的速度向上运动,经过2s后速度变为4m/s,请问这个物体所受到的力是多少?解析:根据牛顿第二定律,力等于质量乘以加速度。
首先计算加速度,加速度等于速度变化量除以时间,即(4m/s - 2m/s) / 2s = 1m/s²。
然后将加速度代入公式,力等于质量乘以加速度,即10kg * 1m/s² = 10N。
所以这个物体所受到的力是10N。
第二题:一个力为20N的物体受到一个与其运动方向相反的恒力作用,物体的加速度为4m/s²,请问物体的质量是多少?解析:根据牛顿第二定律,力等于质量乘以加速度。
将已知数据代入公式,20N = 质量* 4m/s²。
解方程可得质量= 20N / 4m/s² = 5kg。
所以物体的质量是5kg。
第三题:一个质量为2kg的物体受到一个力为10N的作用,物体的加速度是多少?解析:根据牛顿第二定律,力等于质量乘以加速度。
将已知数据代入公式,10N = 2kg * 加速度。
解方程可得加速度 = 10N / 2kg = 5m/s²。
所以物体的加速度是5m/s²。
第四题:一个质量为5kg的物体受到一个力为30N的作用,物体的加速度是多少?解析:根据牛顿第二定律,力等于质量乘以加速度。
将已知数据代入公式,30N = 5kg * 加速度。
解方程可得加速度= 30N / 5kg = 6m/s²。
所以物体的加速度是6m/s²。
第五题:一个质量为10kg的物体受到一个力为50N的作用,物体的加速度是多少?解析:根据牛顿第二定律,力等于质量乘以加速度。
将已知数据代入公式,50N = 10kg * 加速度。
解方程可得加速度= 50N / 10kg = 5m/s²。
所以物体的加速度是5m/s²。
通过以上练习题,我们可以看到牛顿第二定律在解决物体运动问题中的应用。
机械设计 西工大 课后习题_答案

第三章 机械零件的强度习题答案3-1某材料的对称循环弯曲疲劳极限MPa 1801=-σ,取循环基数60105⨯=N ,9=m ,试求循环次数N分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。
[解] MPa 6.373107105180936910111=⨯⨯⨯==--N N σσN MPa 3.324105.2105180946920112=⨯⨯⨯==--N N σσN MPa 0.227102.6105180956930113=⨯⨯⨯==--N N σσN 3-2已知材料的力学性能为MPa 260=s σ,MPa 1701=-σ,2.0=σΦ,试绘制此材料的简化的等寿命寿命曲线。
[解] )170,0('A )0,260(C 012σσσΦσ-=- σΦσσ+=∴-121MPa 33.2832.0117021210=+⨯=+=∴-σΦσσ得)233.283,233.283(D ',即)67.141,67.141(D '根据点)170,0('A ,)0,260(C ,)67.141,67.141(D '按比例绘制该材料的极限应力图如下图所示3-4 圆轴轴肩处的尺寸为:D =72mm ,d =62mm ,r =3mm 。
如用题3-2中的材料,设其强度极限σB =420MPa ,精车,弯曲,βq =1,试绘制此零件的简化等寿命疲劳曲线。
[解] 因2.14554==d D ,067.0453==d r ,查附表3-2,插值得88.1=ασ,查附图3-1得78.0≈σq ,将所查值代入公式,即()()69.1188.178.0111k =-⨯+=-α+=σσσq查附图3-2,得75.0=σε;按精车加工工艺,查附图3-4,得91.0=σβ,已知1=q β,则35.211191.0175.069.1111k =⨯⎪⎭⎫ ⎝⎛-+=⎪⎪⎭⎫ ⎝⎛-+=qσσσσββεK ()()()35.267.141,67.141,0,260,35.2170,0D C A ∴ 根据()()()29.60,67.141,0,260,34.72,0D C A 按比例绘出该零件的极限应力线图如下图3-5 如题3-4中危险截面上的平均应力MPa 20m =σ,应力幅MPa 20a =σ,试分别按①C r =②C σ=m ,求出该截面的计算安全系数ca S 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 机构的结构分析2-11. 图示为一简易冲床的初拟设计方案。
设计者的思路是:动力由齿轮1输入,使轴A 连续回转;而固装在轴A 上的凸轮2与杠杆3组成的凸轮机构使冲头4上下运动,以达到冲压的目的。
试绘出其机构运动简图(各尺寸由图上量取),分析是否能实现设计意图,并提出修改方案(要求用机构示意图表示出来)。
解⑴分析:绘制机构运动简图沿着运动传递的路线,根据各个活动构件参与构成运动副的情况(两构件组成的运动副的类型,取决于两构件之间的相对运动关系),确定表示各个构件的符号,再将各个构件符号连接起来,就得到机构运动简图(或机构示意图)。
构件2:与机架5构成转动副A ;与构件3构成凸轮高副。
所以构件2的符号为图a)。
构件3:与构件2构成凸轮高副;与机架5构成转动副;与机架4构成转动副。
所以构件3的符号为图b)。
构件4:与机架3构成转动副;与机架5构成移动副。
所以构件4的符号为图c)或图d)。
将这些构件符号依次连接起来,就得到机构运动简图,如题2-11答图a)或b)所示。
机构运动简图,如题2-11答图a)或b)所示。
⑵分析:是否能实现设计意图在机构的结构分析中判断该方案否能实现设计意图,应该从以下两点考虑:①机构自由度是否大于零;②机构原动件的数目是否等于机构自由度的数目。
因此,必须计算该机构的自由度F=3n-(2p L +p H )=3×3-(2×4+1)=0。
因为机构的自由度为 F=3n-(2p L +p H )=3×3-(2×4+1)=0 可知,该机构不能运动,不能实现设计意图。
题2-11图图a)图b)图c)题2-11答图a)b)⑶分析修改方案因为原动件的数目为1,所以修改的思路为:将机构的自由度由0变为1。
因此,修改方案应有2种。
方案1:给机构增加1个构件(增加3个独立运动)和1个低副(增加2个约束),使机构自由度增加1,即由0变为1。
如题2-11答图c)、d)、e)所示。
方案2:将机构中的1个低副(2个约束)替换为1个高副(1个约束),使机构中的约束数减少1个,从而使机构自由度增加1,即由0变为1。
如题2-11答图f)所示。
修改方案如题2-11答图c)、d)、e)、f)所示。
题2-2 图a 所示为一小型压力机。
图上,齿轮1与偏心轮1’为同一构件,绕固定轴心O 连续转动。
在齿轮5上开有凸轮轮凹槽,摆杆4上的滚子6嵌在凹槽中,从而使摆杆4绕C 轴上下摆动。
同时,又通过偏心轮1’、连杆2、滑杆3使C 轴上下移动。
最后通过在摆杆4的叉槽中的滑块7和铰链G使冲头8实现冲压运动。
试绘制其机构运动简图,并计算自由度。
解:分析机构的组成:此机构由偏心轮1’(与齿轮1固结)、连杆2、滑杆3、摆杆4、齿轮5、滚子6、滑块7、冲头8和机架9组成。
偏心轮1’与机架9、连杆2与滑杆3、滑杆3与摆杆4、摆杆4与滚子6、齿轮5与机架9、滑块7与冲头8均组成转动副,滑杆3与机架9、摆杆4与滑块7、冲头8与机架9均组成移动副,齿轮1与齿轮5、凸轮(槽)5与滚子6组成高副。
故解法一:7=n 9=l p 2=h p12927323=-⨯-⨯=--=h l p p n F解法二:8=n 10=l p 2=h p 局部自由度 1='F11210283)2(3=--⨯-⨯='-'-+-=F p p p n F h le)题2-11答图题2-3如图a 所示为一新型偏心轮滑阀式真空泵。
其偏心轮1绕固定轴A 转动,与外环2固连在一起的滑阀3在可绕固定轴心C 转动的圆柱4中滑动。
当偏心轮1按图示方向连续转动时,可将设备中的空气按图示空气流动方向从阀5中排出,从而形成真空。
由于外环2与泵腔6有一小间隙,故可抽含有微小尘埃的气体。
试绘制其机构的运动简图,并计算其自由度。
解:1)取比例尺,绘制机构运动简图。
(如图题2-3所示)ABC1234题2-32) 3=n 4=l p 0=h p10423323=-⨯-⨯=--=h l p p n F2-16. 试计算图示各机构的自由度。
图a 、d 为齿轮—连杆组合机构;图b 为凸轮—连杆组合机构(图中在D 处为铰接在一起的两个滑块);图c 为一精压机机构。
并问在图d 所示机构中,齿轮3、5和齿条7为什么?Ca)b)解a) 分析:A 为复合铰链,不存在局部自由度和虚约束。
F=3n -(2p L +p H )=3×4-(2×5+1)=1或F=3n -(2p L +p H -p')-F'=3×4-(2×5+1-0)-0=1 b) 分析:B 、E 为局部自由度。
F=3n -(2p L +p H )=3×5-(2×6+2)=1或F=3n -(2p L +p H -p')-F'=3×7-(2×8+2-0)-2=1注意:该机构在D 处虽存在轨迹重合的问题,但由于D 处相铰接的双滑块为一个Ⅱ级杆组,未引入约束,故机构不存在虚约束。
如果将相铰接的双滑块改为相固联的十字滑块,则该机构就存在一个虚约束。
c) 分析:该机构存在重复结构部分,故存在虚约束。
实际上,从传递运动的独立性来看,有机构ABCDE 就可以了,而其余部分为重复部分,则引入了虚约束。
F=3n -(2p L +p H )=3×5-(2×7+0)=1或F=3n -(2p L +p H -p')-F'=3×11-(2×17+0-2)-0=1d) 分析:A 、B 、C 为复合铰链;D 处高副的数目为2。
不存在局部自由度和虚约束。
F=3n -(2p L +p H )=3×6-(2×7+3)=1或F=3n -(2p L +p H -p')-F'=3×6-(2×7+3-0)-0=1齿轮3与5的中心距受到约束,轮齿两侧齿廓只有一侧接触,另一侧存在间隙,故齿轮高副提供一个约束。
齿条7与齿轮5的中心距没有受到约束,两齿轮的中心可以彼此靠近,使轮齿两侧齿廓均接触,因轮齿两侧接触点处的法线方向并不重合,故齿轮高副提供两个约束。
题2-8 图示为一刹车机构。
刹车时,操作杆1向右拉,通过构件2、3、4、5、6使两闸瓦刹住车轮。
试计算机构的自由度,并就刹车过程说明此机构自由度的变化情况。
(注:车轮不属于刹车机构中的构件。
)解:1)未刹车时,刹车机构的自由度6=n 8=l p 0=h p20826323=-⨯-⨯=--=h l p p n F2)闸瓦G 、J 之一刹紧车轮时,刹车机构的自由度5=n 7=l p 0=h p10725323=-⨯-⨯=--=h l p p n F3)闸瓦G 、J 同时刹紧车轮时,刹车机构的自由度4=n 6=l p 0=h p00624323=-⨯-⨯=--=h l p p n F题2-10 图示为以内燃机的机构运动简图,试计算自由度,并分析组成此机构的基本杆组。
如在该机构中改选EG 为原动件,试问组成此机构的基本杆组是否与前者不同。
解:1)计算此机构的自由度7=n 10=l p 0=h p101027323=-⨯-⨯=--=h l p p n F2)取构件AB 为原动件时机构的基本杆组图2-10(b )所示。
此机构为二级机构。
3)取构件GE 为原动件时机构的基本杆组图2-10(c )所示。
此机构为三级机构。
第三章 平面机构的运动分析3-3. 试求图示各机构在图示位置时全部瞬心的位置。
解 a)通过运动副直接相联的两构件的瞬心:P 12在A 点,P 23在B 点,P 34在C 点,P 14在垂直于移动副导路方向的无穷远处。
不通过运动副直接相联的两构件的瞬心位置,借助三心定理来确定:对于构件1、2、3,P 13必在P 12及P 23的连线上,而对于构件1、4、3,P 13又必在P 14及P 34的连线上,因上述两线平行,故上述两线的交点在无穷远处,即为P 13在垂直于BC 的无穷远处。
对于构件2、3、4,P 24必在P 23及P 34的连线上,而对于构件2、1、4,P 24又必在P 12及P 14的连线上,故上述两线的交点B 即为瞬心P 24。
b)通过运动副直接相联的两构件的瞬心: P 12在A 点,P 23在垂直于移动副导路方向的无穷远处, P 34在B 点,P 14在垂直于移动副导路方向的无穷远处。
不通过运动副直接相联的两构件的瞬心位置,借助三心定理来确定:对于构件1、2、3,P 13必在P 12及P 23的连线上,而对于构件1、4、3,P 13又必在P 14及P 34的连线上,故上述两线的交点即为P 13。
同理,可求得瞬心P 24。
c)通过运动副直接相联的两构件的瞬心:P 12在垂直于移动副导路方向的无穷远处,P 23在A 点,P 34在B 点,P 14在垂直于移动a)b)d) 题3-3图a)∞ b)P 1324 A B12 34 c)副导路方向的无穷远处。
不通过运动副直接相联的两构件的瞬心位置,借助三心定理来确定:对于构件1、2、3,P 13必在由P 12和P 23确定的直线上,而对于构件1、4、3,P 13又必在由P 14和P 34确定的直线上,故上述两直线的交点即为P 13。
对于构件2、3、4,P 24必在由P 23和P 34确定的直线上,而对于构件2、1、4,P 24又必在由P 12及P 14确定的直线上(两个无穷远点确定的直线),故上述两线的交点即为P 24,即P 24在直线AB 上的无穷远处。
d)通过运动副直接相联的两构件的瞬心:P 12必在过A 点的公法线上,同时P 12必在垂直于v M 的直线上,故上述两线的交点即为P 12。
P 23在B 点。
P 34在垂直于移动副导路方向的无穷远处。
P 14在C 点。
不通过运动副直接相联的两构件的瞬心位置,借助三心定理来确定:对于构件1、2、3,P 13必在P 12及P 23的连线上,而对于构件1、4、3,P 13又必在P 14及P 34的连线上,故上述两线的交点即为P 13。
同理,可求得瞬心P 24。
3-6. 在图示的四杆机构中,μL =3 (mm/mm),l AB =60 mm ,l CD =90 mm ,l AD =l BC =120 mm ,ω2=10 rad/s ,φ=165º,试用瞬心法求:⑴点C 的速度v C ;⑵构件3的BC 线上(或其延长线上)速度最小的一点E 的位置及其速度的大小;⑴ 各瞬心如图b 所示(P 12在A 点,P 23在B 点,P 34在C 点,P 14在D 点,P 13在直线AB 与CD 的交点,P 24在直线AD 与BC 的交点)。
