2011年12月考试高等数学(II-2)第三次作业
高等数学(II-1) ( 第3次 )

2015年9月份考试作业高等数学(II-1)第3次
一、填空题
1.
参考答案:
2.
参考答案:
[-1,3]
3.
参考答案:
4.
参考答案:
无穷
5.
参考答案:
12
6.
参考答案:
7.
参考答案:
8.
参考答案:
9.
参考答案:
10.
参考答案:
两边同时对求导,得
,
解出,得
二、计算题
1.
参考答案:
欲使原函数有意义,必须
且,解得
且,
故,原函数的定义域为:
2.
参考答案:
解:因为,所以;
即在处切线斜率为,法线的斜率为;所以切线方程是:;
法线的方程为:。
3.
参考答案:
解:
4.
参考答案:
解:
5.
参考答案:
解:它表示以原点为圆心,半径为的圆的,故
6.
参考答案:
解:,所以在函数处函数连续,
,在处一阶导数不存在,
而在处两边取值异号,故是函数的两个拐点。
7.
参考答案:
评分标准:
8.
参考答案:
,。
三、证明题
1.
参考答案:
证明:
2.
参考答案:
证明:对方程两边取n次方,得到,移项得到,两段开n次方,
得到,反函数为,于是函数
的反函数就是它本身。
2011南京市高三第三次模拟考试数学试卷
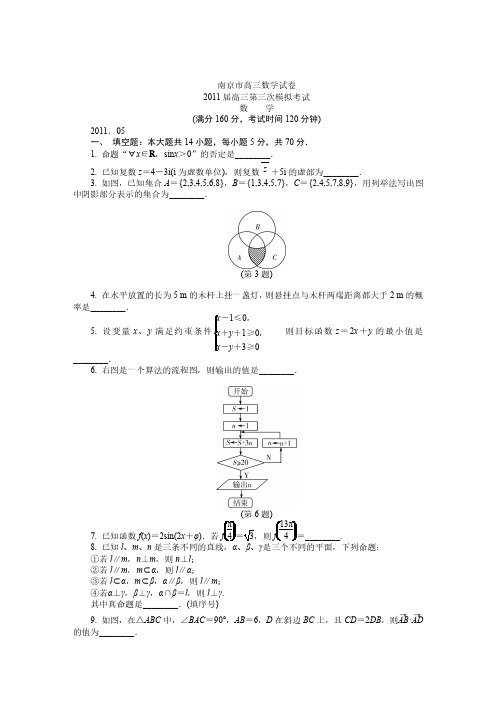
南京市高三数学试卷2011届高三第三次模拟考试数学(满分160分,考试时间120分钟)2011.05一、填空题:本大题共14小题,每小题5分,共70分.1.命题“∀x∈R,sin x>0”的否定是________.2.已知复数z=4-3i(i为虚数单位),则复数z+5i的虚部为________.3.如图,已知集合A={2,3,4,5,6,8},B={1,3,4,5,7},C={2,4,5,7,8,9},用列举法写出图中阴影部分表示的集合为________.(第3题)4.在水平放置的长为5m的木杆上挂一盏灯,则悬挂点与木杆两端距离都大于2m的概率是________.5.设变量x、y满足约束条件-1≤0,+y+1≥0,-y+3≥0则目标函数z=2x+y的最小值是________.6.右图是一个算法的流程图,则输出的值是________.(第6题)7.已知函数f(x)=2sin(2x+φ).若=3,则________.8.已知l、m、n、β、γ①若l∥m,n⊥m,则n⊥l;②若l∥m,m⊂α,则l∥α;③若l⊂α,m⊂β,α∥β,则l∥m;④若α⊥γ,β⊥γ,α∩β=l,则l⊥γ.其中真命题是________.(填序号)9.如图,在△ABC中,∠BAC=90°,AB=6,D在斜边BC上,且CD=2DB,则AB→·AD→的值为________.(第9题)10.已知数列{a n }的前n 项和S n=2n 2+pn ,a 7=11,若a k +a k +1>12,则正整数k 的最小值为________.11.若不等式4x 2+9y 2≥2k xy 对一切正整x 、k 的最大值为________.12.已知直线y =mx (m ∈R )与函数f (x )2-12x ,x ≤0,12x 2+1,x >0的图象恰有3个不同的公共点,则实数m 的取值范围是________.13.已知椭圆x 2a 2+y 2b 2=1(a >b >0)的左、右焦点分别为F 1、F 2,离心率为e ,若椭圆上存在点P ,使得PF 1PF 2=e ,则该椭圆离心率e 的取值范围是________.14.如图,已知正方形ABCD 的边长为1,过正方形中心O 的直线MN 分别交正方形的边AB 、CD 于点M 、N ,则当MN BN 取最小值时,CN =________.(第14题)二、解答题:本大题共6小题,共90分.解答时应写出文字说明、证明过程或演算步骤.15.(本题满分14分)已知a 、b 、c 分别为△ABC 的内角A 、B 、C 的对边,且a cos C +c cos A =2b cos B .(1)求角B 的大小;(2)求sin A +sin C 的取值范围.如图,在矩形ABCD中,AD=2,AB=4,E、F分别为边AB、AD的中点,现将△ADE 沿DE折起,得四棱锥A—BCDE.(1)求证:EF∥平面ABC;(2)若平面ADE⊥平面BCDE,求四面体FDCE的体积.2014年青奥会水上运动项目将在J地举行.截至2010年底,投资集团B在J地共投资100百万元用于房地产和水上运动两个项目的开发.经调研,从2011年初到2014年底的四年间,B集团预期可从三个方面获得利润:一是房地产项目,四年获得的利润的值为该项目投资额(单位:百万元)的20%;二是水上运动项目,四年获得的利润的值为该项目投资额(单位:百万元)的算术平方根;三是旅游业,四年可获得利润10百万元.(1)B集团的投资应如何分配,才能使这四年总的预期利润最大?(2)假设从2012年起,J地政府每年都要向B集团征收资源占用费,2012年征收2百万元,以后每年征收的金额比上一年增加10%.若B集团投资成功的标准是:从2011年初到2014年底,这四年总的预期利润中值(预期最大利润与最小利润的平均数)不低于总投资额的18%,问B集团投资是否成功?在平面直角坐标系xOy中,已知定点A(-4,0)、B(4,0),动点P与A、B连线的斜率之积为-14.(1)求点P的轨迹方程;(2)设点P的轨迹与y轴负半轴交于点C.半径为r的圆M的圆心M在线段AC的垂直平分线上,且在y轴右侧,圆M被y轴截得的弦长为3r.(ⅰ)求⊙M的方程;(ⅱ)当r变化时,是否存在定直线l与动圆M均相切?如果存在,求出定直线l的方程;如果不存在,说明理由.设等比数列{a n }的前n 项和为S n .已知a n +1=2S n +2(n ∈N *).(1)求数列{a n }的通项公式;(2)在a n 与a n +1之间插入n 个数,使这n +2个数组成一个公差为d n 的等差数列.(ⅰ)求证:1d 1+1d 2+1d 3+…+1d n <1516(n ∈N *);(ⅱ)在数列{d n }中是否存在三项d m 、d k 、d p (其中m 、k 、p 成等差数列)成等比数列?若存在,求出这样的三项;若不存在,说明理由.已知函数f(x)=x3+x2-ax(a∈R).(1)当a=0时,求与直线x-y-10=0平行,且与曲线y=f(x)相切的直线方程;(2)求函数g(x)=f(x)x-a ln x(x>1)的单调递增区间;(3)如果存在a∈[3,9],使函数h(x)=f(x)+f′(x)(x∈[-3,b]在x=-3处取得最大值,试求b的最大值.高三数学附加题试卷第页(共2页)2011届高三第三次模拟考试数学附加题(满分40分,考试时间30分钟)21.【选做题】在A、B、C、D四小题中只能选做2题,每小题10分,共20分.解答时应写出文字说明、证明过程或演算步骤.A.选修41:几何证明选讲如图,AB为⊙O的切线,A为切点,过线段AB上一点C作⊙O的割线CED(E在C、D 之间),若∠ABE=∠BDE,求证:C为线段AB的中点.B.选修42:矩阵与变换求曲线C:xy=1在矩阵M=11-11对应的变换作用下得到的曲线C1的方程.C.选修44:坐标系与参数方程在极坐标系中,已知圆C:ρ=22cosθ和直线l:θ=π4(ρ∈R)相交于A、B两点,求线段AB的长.D.选修45:不等式选讲已知a、b都是正实数,且a+b=2,求证:a2a+1+b2b+1≥1.【必做题】第22题、第23题,每小题10分,共20分.解答时应写出文字说明、证明过程或演算步骤.22.在棱长为2的正方体ABCD-A1B1C1D1中,E为棱AB的中点,点P在平面A1B1C1D1内,若D1P⊥平面PCE,试求线段D1P的长.23.假设位于正四面体ABCD顶点处的一只小虫,沿着正四面体的棱随机地在顶点间爬行,记小虫沿棱从一个顶点爬到另一个顶点为一次爬行.小虫第一次爬行由A等可能地爬向B、C、D中的任意一点,第二次爬行又由其所在顶点等可能地爬向其他三点中的任意一点,如此一直爬下去,记第n(n∈N*)次爬行后小虫位于顶点A处的概率为p n.(1)求p2,p3,p4的值,并写出p n的表达式(不要求证明);(2)设S n=p1C1n+p2C2n+p3C3n+…+p n C n n(n∈N*),试求S n(用含n的式子表示).。
2011年春季学期高等数学(II-2)第二次作业

2011年春季学期高等数学(II-2)第二次作业一、单项选择题 (共6题、总分18分、得分18分)1. 设C y x f B y x f A y x f yy xy xx ===),(,),(,),(000000,那么在f(x,y)的驻点处),(00y x 取得极大值的条件是( D ). A 、0,02>>-A AC B B 、0,02<>-A AC B C 、0,02><-A AC BD 、0,02<<-A AC B2. 设D 是矩形闭区域:d y c b x a ≤≤≤≤,,则积分⎰⎰dxdy y g x f D )()(=( D )A 、0B 、⎰dc dy y g )( C 、⎰ba dx x f )(D 、⎥⎦⎤⎢⎣⎡⋅⎥⎦⎤⎢⎣⎡⎰⎰d c b a dy y g dx x f )()( 3. 点 ),(00y x P 是函数 z=f(x,y)的驻点,则( D ) A 、P 是 f(x,y) 的极大值点 B 、P 是f(x,y)的极小值点C 、P 不是f(x,y)的极值点D 、不能确定P 是否为f(x,y)的极值点4. 积分⎰⎰≤++-Dy x R y x D dxay e 22)(21:,22,化为极坐标的二次积分为( A )A 、rdr e d R r ⎰⎰-2202πθ B 、dr e d R r ⎰⎰-202πθC 、dr e d R r ⎰⎰-2202πθ D 、dr e d R r ⎰⎰-2102θ 5. D 是由x 轴、y 轴及直线x+y=1所围成的三角形区域,则等于⎰⎰D xydxdy ( D )A 、14B 、18C 、112D 、1246. 下列二重积分的性质不正确的是( A ) A 、⎰⎰⎰⎰⎰⎰⋅=σσσdxdy y x g dxdy y x f dxdy y x g y x f ),(),(),(),( B 、⎰⎰⎰⎰=σσdxdy y x f k dxdy y x g y x kf ),(),(),(C 、⎰⎰=σσ的面积dxdyD 、⎰⎰⎰⎰⎰⎰±=±σσσdxdy y x g y x f dxdy y x g dxdy y x f )),(),((),(),(二、填空题 (共8题、总分24分、得分0分)1. 设非均质圆形薄板的半径为 R ,其上的面密度与到圆心的距离成正比,比例系数是 K 。
绵阳市高2011级第三次诊断性考试数学(理科)

1 2
5. 已知命题 p : x R, sin x>a ,若 p 是真命题,则实数 a 的取值范围为 A. a<1 B. a 1 C. a 1 D. a 1
数学(理科)试题第 1 页(共 4 页)
6. 已知 a [2,2] ,则函数 f ( x) x 2 2ax 1 有零点的概率为 A.
4 1 3 C4 C1 C4 4 1 P ( 1) , , 4 C5 5 C54 5
甲 5 3 3 9 2 0 1 9 1 7 1 2 3 4 0 7 0 7
乙 4 6 6 0
4
6
P( 0)
∴ ξ 的分布列: ξ 0 1
数学(理科)试题第 5 页(共 4 页)
P
1 5
14. 已知实数 x, y 满足 xy 1 2 x y ,且 x> 1 ,则 ( x 1)( y 2) 的最小值为_______. 15. 已知有限集 A a1 , a2 , a3 ...,an (n≥2).如果 A 中元素 ai (i 1,2,3,...,n) 满足
2
3 3 2 a 时,求锐二面角 D-EF-B 的余弦值. 8
1 1 p1 p2 p3 p4
( III ) 设 hx f x x , 对 任 意 x1 , x2 1,x1 x2 , 证 明 : 不 等 式
x1 x2 > x1 x2 x1 x2 1 恒成立. hx1 hx2
1 2
B.
1 3
C.
1 4
D.
1 5
7. 若抛物线 C1 : y 2 4 x 的焦点 F 恰ห้องสมุดไป่ตู้是双曲线 C2 :
x2 y2 1(a>0, b>0) 的右焦点, a b2
2011年12月考试电工电子技术第三次作业.docx

2011年12月考试电工电子技术第三次作业.docxD3. 一个八位D/A转换器的最小输出电压增量为0.02V,当输入代码为01001101时,输出电压为多少?4. 图示电路中,已知:U S1 =70V ,U S2= 5V ,U S3 =15V ,R 1 =R6 =1 Ω,R 2 =4 Ω,R 3 = 15 Ω,R 4 = 0.5 Ω,R 5= 9.5 Ω,R 7 = 5 Ω。
用基尔霍夫定律求图示电路中的电位V A,V B 和电压U AB 。
5. 在双极型晶体管放大电路中,测得3个晶体管的各个电极电位如图所示。
判断题各晶体管的类型,并区分e、b、c三个电极。
6. 如图电路,试求IR 、IZ、IL和输出电压的平均值u0AV。
7. 某收音机的输出变压器,一次绕组的匝数为230匝,二次绕组的匝数为80匝,原配接8Ω的扬声器,现改用4Ω的扬声器。
问二次绕组的匝数应改为多少?答案:一、填空题(30分,共 15 题,每小题 2 分)1.参考答案:选频环节解题方案:评分标准:正确则满分;错误为0分2.参考答案:幅值、频率、初相位解题方案:评分标准:正确则满分;错误为0分3.参考答案:线性电路解题方案:评分标准:正确则满分;错误为0分4.参考答案:开启电压解题方案:开启电压是N沟道增强型绝缘栅场效应管刚产生导电沟道的栅源电压评分标准:正确则满分;错误为0分5.参考答案:常开触点解题方案:常开触点通电时闭和评分标准:正确则满分;错误为0分6.参考答案:负反馈解题方案:评分标准:正确则满分;错误为0分7.参考答案:8位解题方案:评分标准:正确则满分;错误为0分8.参考答案:交越失真解题方案:评分标准:正确则满分;错误为0分9.参考答案:达到最大值解题方案:评分标准:正确则满分;错误为0分10.参考答案:开环或正反馈解题方案:评分标准:正确则满分;错误为0分11.参考答案:15mA解题方案:评分标准:正确则满分;错误为0分12.参考答案:1500r/min解题方案:定子旋转磁场对定子的转速即为同步转速,n0=50*60/2=1500r/min 评分标准:正确则满分;错误为0分13.参考答案:5 个解题方案:KVL方程数=8-(4-1)=5评分标准:正确则满分;错误为0分14.参考答案:22 欧姆解题方案:功率因数为0.707,所以,XC - XL= R评分标准:正确则满分;错误为0分15.参考答案:1500r/min解题方案:n0=50*60/2=1500r/min评分标准:正确则满分;错误为0分二、计算题(70分,共 7 题,每小题 10 分)1.参考答案:4V解题方案:输出电压=10-6=4V(5分)评分标准:见解题过程2.参考答案:A[SEPARATOR]B解题方案:(每量2分)评分标准:见解题过程3.参考答案:输出电压为:0.02*77=1.54V(3分)解题方案:(01001101)B=(77)D(3分)所以,输出电压为:0.02*77=1.54V(3分)评分标准:见解题过程4.参考答案:解题方案:(每式3分)评分标准:见解题过程5.参考答案:(a)NPN 型硅管① --e, ② --b, ③ --c 。
福建省四地六校2011-2012学年高二数学下学期第三次月考试题 理

“华安、连城、永安、漳平一中、龙海二中、泉港一中”六校联考2011-2012学年下学期第三次月考高二数学(理科)试题(考试时间:120分钟 总分:150分)★友情提示:要把所有答案都写在答题卷上,写在试卷上的答案无效。
一、选择题(本题共10个小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
) 1.计算ii+3的值为( ) A .i 31+ B .i 31-- C .i 31- D .i 31+-2.下表是降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y (吨标准煤)的几组对应数据,根据表中提供的数据,可求出y 关于x 的线性回归方程ˆy=0.7x+0.35,那么表中m 的值为( )A.4B.3.15C.4.5D.33. 5位同学报名参加两个课外活动小组,每位同学限报其中的一个小组,则不同的报名方法共有 ( )A .10种B .20种C .25种D .32种 4.二项式12)2(xx +展开式中的常数项是( )A .第7项B .第8项C .第9项D .第10项5.如图,由函数()xf x e e =-的图象,直线2x =及x 轴所围成的阴影部分面积等于( ) A .221e e --B .22e e - C .22e e -D .221e e -+6.已知222233+=,333388+=,44441515+=,。
,若66a a b b+= , (,a b ∈R ) , 则( )A.a =5,b =24B.a =6,b =24C.a =6,b =35D.a =5,b =357.袋中装有6个不同的红球和4个不同的白球,不放回地依次摸出2个球,在第1次摸出红球的条件下,第2次摸出的也是红球的概率为( ) A .59B .49C .29D .238.函数)(x f y =的图像如图所示,下列数值排序正确的是( )A. )2()3()3()2(0f f f f -<'<'<B. )2()2()3()3(0f f f f '<-<'<C. )2()3()2()3(0f f f f -<'<'<D. )3()2()2()3(0f f f f '<'<-<9. 箱子里有5个黑球,4个白球,每次随机取出一个球,若取出黑球,则放回箱中,重新取球;若取出白球,则停止取球,那么在第4次取球之后停止的概率为 ( )A .315445C C C B .354()99⨯ C .5194⨯ D .13454()99C ⨯⨯ 10. 如图所示,()f x 是定义在区间[, ]c c (0c )上的奇函数,令()()g x a f x b ,并有关于函数()g x 的四个论断: ①若0a,对于[1, 1]内的任意实数, m n (mn ), ()()0g n g m n m恒成立;②函数()g x 是奇函数的充要条件是0b ;③若1a ≥,0b,则方程()0g x 必有3个实数根;④a R ∀∈,()g x 的导函数)(x g '有两个零点; 其中所有正确结论的序号是( ).A. ①②B. ①②③C. ①④D. ②③④ 二、填空题(本题共5小题,每小题4分,共20分)11.设随机变量ξ服从正态分布(,9)N u ,若 (3)(1)p p ξξ>=<,则u =12. 若X ~B (20,p),当p=21且P(X=k)取得最大值时,k=________.13. 现有一个关于平面图形的命题,如图所示,同一个平面内有两个 边长都是a 的正方形,其中一个的某顶点在另一个的中心,则这两个正方形重叠部分的面积恒为42a .类比到空间,有两个棱长均为a 的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为 .14. 设复数z=cos θ+i sin θ,0θπ≤≤,则1+z 的最大值为 .15. 已知数组:1()1,12(,)21,123(,,)321,1234(,,,)4321,,1231(,,,,,),1221n nn n n ---记该数组为:123456(),(,),(,,),,a a a a a a 则2012a = .三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 16. (本题满分13分)已知甲袋装有1个红球,4个白球;乙袋装有2个红球,3个白球,所有球大小都相同,现从甲袋中任取2个球,乙袋中任取2个球. (1)求取到的4个球全是白球的概率;(2)求取到的4个球中红球个数不少于白球个数的概率.17.(本题满分13分)某同学参加科普知识竞赛,需回答3个问题.竞赛规则规定:答对第一、二、三个问题分别得100分、100分、200分,答错得零分.假设这名同学答对第一、二、三个问题的概率分别为0.8,0.7,0.6,且各题答对与否相互之间没有影响. (1)求这名同学得300分的概率; (2)求这名同学至少得300分的概率.18.(本题满分13分)设函数32()2338f x x ax bx c =+++在1x =及2x =处取得极值. (Ⅰ)求a 、b 的值;(Ⅱ)当2c =-时,求函数()f x 在区间[03],上的最大值. 19.(本小题满分13分)当*n N ∈时,111111234212n S n n=-+-++-- , 11111232n T n n n n=+++++++.(Ⅰ)求1S ,2S ,1T ,2T ;(Ⅱ)猜想n S 与n T 的大小关系,并用数学归纳法证明.20.(本题满分14分) 张先生家住H 小区,他在C 科技园区工作,从家开车到公司上班有L 1,L 2两条路线(如图),L 1路线上有A 1,A 2,A 3三个路口,各路口遇到红灯的概率均为21;L 2路线上有B 1,B 2两个路口,各路口遇到红灯的概率依次为43,53. (1)若走L 1路线,求最多遇到1次红灯的概率; (2)若走L 2路线,求遇到红灯次数X 的数学期望; (3)按照“平均遇到红灯次数最少”的要求,请你帮助张 先生从上述两条路线中选择一条最好的上班路线,并说明理由.21. (本小题满分14分) 已知函数1()ln f x a x x=-,a ∈R .(1)若曲线()y f x =在点(1,(1))f 处的切线与直线20x y +=垂直,求a 的值; (2)求函数()f x 的单调区间;(3)当1a =,且2x ≥时,证明:(1)25f x x --≤.“华安、连城、永安、漳平一中、龙海二中、泉港一中”六校联考2011-2012学年下学期第三次月考 高二数学(理科)试题参考答案二、填空题(本题共5小题,每小题4分,共20分)11. 2 12. 10 13. 38a14. 2 15.559三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 16.(本题满分13分)解:基本事件为“从甲袋中任取2个球,乙袋中任取2个球”,故基本事件的总数N =2255C C ⋅;………………2分 (1)设“取到的4个球全是白球”为事件A ,则事件A 中包含的基本事件数为n 1=2243C C ⋅;………………4分∴P(A)=1n 9N 50=. ………………6分 (2)设“取到的4个球中红球个数不少于白球个数”为事件B ,则事件B 中包含的基本事件数为:1111221122142342142n C C C C C C C C C 34,=++=………………10分∴P(B)=2n 17N 50= ………………13分. 17(本小题满分13分)解:17.设事件A 为“答对第一题”,事件B 为“答对第二题”,事件C 为“答对第三题”,则P(A)=0.8,P(B)=0.7,P(C)=0.6. ………………2分 (1)这名同学得300分可表示为(A ∩B ∩C)∪(A ∩B ∩C). 所以P((A ∩B ∩C)∪(A ∩B ∩C)),=P(A ∩B ∩C)+P(A ∩B ∩C)=P(A )·P(B)·P(C)+P(A)·P(B )·P(C) =(1-0.8)×0.7×0.6+0.8×(1-0.7)×0.6=0.228. ………………7分 (2)这名同学至少得300分包括得300分或400分. 该事件表示为(A ∩B ∩C)∪(A ∩B ∩C)∪(A ∩B ∩C), 所以P((A ∩B ∩C)∪(A ∩B ∩C)∪(A ∩B ∩C)) =P((A ∩B ∩C)∪(A ∩B ∩C))+P(A ∩B ∩C) =0.228+0.8×0.7×0.6=0.564.………13分 18. (本小题满分13分)解:①解: 2()663f x x ax b '=++,………………1分因为函数()f x 在1x =及2x =取得极值,则有(1)0f '=,(2)0f '=.………………3分即6630241230a b a b ++=⎧⎨++=⎩,.………………4分解得3a =-,4b =.………………6分 ②由(Ⅰ)可知,32()29128f x x x x c =-++,2()618126(1)(2)f x x x x x '=-+=--.………………7分当(01)x ∈,时,()0f x '>; 当(12)x ∈,时,()0f x '<; 当(23)x ∈,时,()0f x '>.………………9分 所以,当1x =时,()f x 取得极大值(1)58f c =+, 又(0)8f c =,(3)98f c =+.………………11分则当[]03x ∈,时,()f x 的最大值为(3)987f c =+=-.…13分19. (本小题满分13分) 解:(1) 1112S T ==,22712S T ==;………………2分 (2)猜想:n n S T =(*n N ∈)………………4分 证明:(1)当1n =时,11S T =; (2)假设当n k =时,k k S T =,即11111111112342121232k k k k k k -+-++-=++++-+++,………………6分 当1n k =+时111111112342122122k k k k -+-++-+--++111111()12322122k k k k k k =+++++-+++++………………8分 111111()()12223221k k k k k k =-++++++++++………………10分 111112322122k k k k k =+++++++++,即11k k S T ++=,………………12分 结合(1)(2),可知*n N ∈,n n S T =成立.………………………13分 20. (本小题满分14分)解: (Ⅰ)设走L 1路线最多遇到1次红灯为A 事件,则0312331111()=()()2222P A C C ⨯+⨯⨯=. ………………3分所以走L 1路线,最多遇到1次红灯的概率为21.………4分 (II )依题意,X 的可能取值为0,1,2………………5分)0(=X p =(1-43))531(-⨯=101)531(43)1(-⨯==X P +20953)431(=⨯-2095343)2(=⨯==X P ………………7分2027220120010=⨯+⨯+⨯=EX …………9分(Ⅲ)设选择L 1路线遇到红灯次数为Y ,随机变量Y 服从二项分布,1(3,)2Y B ,…11分所以13322EY =⨯=. ………………13分因为EX EY <,所以选择L 2路线上班最好. ………………14分21. (本大题满分14分)解:(1)函数()f x 的定义域为{}|0x x >,21()a f x x x '=+. 又曲线()y f x =在点(1,(1))f 处的切线与直线20x y +=垂直, 所以(1)12f a '=+=,即1a =.--------- 4分(2)由于21()ax f x x +'=.--------- 5分 当0a ≥时,对于(0,)x ∈+∞,有()0f x '>在定义域上恒成立, 即()f x 在(0,)+∞上是增函数.--------- 7分 当0a <时,由()0f x '=,得1(0,)x a =-∈+∞.当1(0,)x a∈-时,()0f x '>,()f x 单调递增;当1(,)x a∈-+∞时,()0f x '<,()f x 单调递减.------- 10分(3)当1a =时,1(1)ln(1)1f x x x -=---,[)2,x ∈+∞. 令1()ln(1)251g x x x x =---+-.2211(21)(2)()21(1)(1)x x g x x x x --'=+-=----. 当2x >时,()0g x '<,()g x 在(2,)+∞单调递减.又(2)0g =,所以()g x 在(2,)+∞恒为负. ------- 12分 所以当[2,)x ∈+∞时,()0g x ≤.即1ln(1)2501x x x ---+-≤. 故当1a =,且2x ≥时,(1)25f x x --≤成立.----- 14分。
2011年高考数学 最后5天练第三天
FCΒιβλιοθήκη CE CFE , 故 Rt△A1 AC ∽ Rt△FCE , AAC 1
EF . CFE 与 FCA1 互余.于是 AC 1 A1C 与平面 BED 内两条相交直线 BD,EF 都垂直,
用心 爱心 专心
H E G D A F B C
所以 A1C 平面 BED . ··························· 6 分 (Ⅱ)作 GH DE ,垂足为 H ,连结 A1 H .由三垂线定理知 A1H DE , 故 A1 HG 是二面角 A1 DE B 的平面角. ·················· 8 分
用心
爱心
专心
4.(满分 12 分)设函数 f ( x) 2 x 3(a 1) x 1(a 1)
3 2
(1)求 f ( x) 的单调区间; (2)讨论 f ( x) 的极值。
5. ( 满 分 12 分 ) 设 a n 使 等 差 数 列 , bn 是 各 项 都 为 正 数 的 等 比 数 列 , 且
∴函数 g ( x) 是偶函数. 3. (满分 12 分) 证明: (1)在直三棱柱 ABC A1 B1C1 , ∵底面三边长 AC 3 , AB 5 , BC 4 ∴ AC BC , 又直三棱柱 ABC A1 B1C1 中
AC CC1 ,
且 BC CC1 C , BC,CC1 平面BCC1 B1 ∴ AC 平面BCC1 B1 ∴ AC BC1 ; (2)设 CB1 与 C1 B 的交点为 E ,连结 DE , 而 BC1 平面BCC1 B1
12 分
3 2 301 n n, 1 ≤ n ≤ 50, 2 2 综上所述, Sn 3 n 2 299 n 7500, 51 ≤ n ≤ 100. 2 2
2011级高等数学二期末试题及解答A(少学时、经管类)
2011级本科高等数学(二)期末试题及解答A(少学时、经管类)一、单项选择题(本大题共5小题,每小题3分,共15分) 1. [少学时]设直线方程为000:x x y y z z L m n p---==, 平面方程为:0Ax By Cz D π+++=, 若直线与平面平行或直线在平面上,则 ( A ).(A) 充要条件是:0Am Bn Cp ++=; (B) 充要条件是:A B Cm n p==; (C) 充分但不必要条件是: 0Am Bn Cp ++=; (D) 充分但不必要条件是:A B C m n p==. [经管类]已知()y x f ,在()b a ,处偏导数存在,则()(),,limh f a h b f a h b h→+--=( A ).(A) ()b a f x ,2' ; (B) ()b a f x ,2' ; (C) ()b a f x ,' ; (D) 0 . 2.设(,)z z x y =是由方程z x y z e ++=所确定的隐函数, 则zx∂=∂ ( C ). (A)11z e -; (B) 21z e -; (C) 11ze--; (D)1ze -. 3.函数33(,)3f x y x y xy =+-的极小值为 ( B ). (A) 1 ; (B) 1-; (C) 0; (D) 3-.4.下列说法正确的是 ( D ).(A) 若lim 0n n u →∞=, 则级数1n n u ∞=∑必收敛;(B) 若级数1n n u ∞=∑ 发散, 则必有lim 0n n u →∞≠;(C) 若级数1n n u ∞=∑发散, 则lim n n S →∞=∞;(D) 若lim 0n n u →∞≠, 则级数1n n u ∞=∑必发散.5.设(,)f x y 具有一阶连续偏导数,且(1,1)2f =,(,)x f m n m n =+,(,)y f m n m n =⋅,令()(,(,))g x f x f x x =,则(1)g '=( C ).(A) 3 ; (B) 6 ; (C) 9 ; (D) 12 .二、填空题(本大题共5小题,每小题3分,共15分)6.[少学时]设(1,3,2)a =,(2,,4)b y = ,且a b ⊥ ,则y =103-.[经管类]级数)21)1(1(1n n n n -+∑∞=的和为 0 .7.函数221(,,)u x y z z x y=-- 的间断点是22{(,,)}x y z z x y =+. 8.设函数22z x y y =+, 则dz =22(2)xydx x y dy ++. 9.微分方程0ydx xdy +=的通解是xy C = . 10.【少学时】曲线sin (0)2y x x π=≤≤与2x π=及0y =所围的平面图形绕y 轴旋转所成旋转体的体积为2π .【经管类】曲线x y e =与0x =、1x =及0y =所围的平面图形绕y 轴旋转所成旋转体的体积为2π .三、解答题(本大题共6小题,每小题8分,共48分) 11.求极限2011cos()lim1x yx y xy e→→--.解:2011cos()lim 1x y x y xy e →→--22011()2lim x y xy x y →→= (4分) 01lim2x y y →→=12=. (8分) 12.设2(,)tan()2x y f x y xy e =-,求(0,1)x f ,(0,1)y f . 解:22sec ()4x yx f y xy xye=- (3分)222sec ()2x y y f x xy x e =- (6分) (0,1)1x f =,(0,1)0y f =. (8分)13.设223(,,)u x y z xy y z x z =++,求)1,1,1(du .解:223x u y x z =+,22y u xy yz =+,23z u y x =+ (3分)(1,1,1)4x u =,(1,1,1)4y u =,(1,1,1)2z u = (5分) (1,1,1)442du dx dy dz =++ . (8分)14.设(,)z f u v =而,u y v xy ==,且f 具有二阶连续偏导数,求2zx y∂∂∂.解: '.zy f x∂=⋅∂2 (4分) ()'''''z f y f f x x y∂=++⋅∂∂222122'''''.f yf xyf =++22122 (8分)15.判别正项级数122n n n ∞=+∑的敛散性. 解: lim lim n n n n n n u n u n ++→∞→∞⎛⎫+=⋅ ⎪+⎝⎭113222 (3分) lim .()n n n →∞+==<+311222(6分) 所以原级数收敛. (8分) 16.计算二重积分22xy De d σ+⎰⎰,其中D 是由圆周224x y +=所围成的闭区域.解:x y Ded d ed πρσθρρ+=⋅⎰⎰⎰⎰2222200 (4分)().e d e e ρρπρππ⎡⎤===-⎣⎦⎰222224001212(8分)四、解答题(本大题共2小题,每小题6分,共12分)17.[少学时]设一平面经过原点及点(6,3,2)M -且与平面428x y z -+=垂直, 求此平面方程.解: 所求平面的法向量(,,),(,,)n n OM ⊥-⊥=-412632. (2分)则 (,,)(,,)(,,)-⨯-=-412632446.取 (,,)n =-223. (4分)故所求平面方程为: x y z+-=2230. (6分)[经管类]求差分方程153x x y y +-=07()3y =的特解.解:因5,3a C ==,故通解为3514x x x C y Aa A a =+=-+⋅- (2分) 又03743y A =-+=,则3712A = (4分)故所求特解为3375412x x y=-+⋅ . (6分) 18.设幂级数 11n n nx ∞-=∑.(1). 求收敛半径及收敛区间 . (2). 求和函数.解: (1). lim lim .n n n na n a n ρ+→∞→∞+===111所以收敛半径.R =1 (1分)当x=1时,n n ∞=∑1发散;当x =-1时,()n n n ∞-=-∑111 发散.所以收敛区间为: (,)-11. (2分) (2). 设和函数为: ()n n S x nx ∞-==∑11. (3分)()xxx n n n n S x dx nx dx nx dx ∞∞--==⎛⎫== ⎪⎝⎭∑∑⎰⎰⎰1100011.x n nn n x x x x ∞∞==⎡⎤===⎣⎦-∑∑1101 (4分)故 '().().()x S x x x x ⎛⎫==-<< ⎪--⎝⎭211111(6分)五、证明题(本大题共2小题,每小题5分,共10分)19.)(t f 为连续函数,求证11123001()()3x dx x f y dy t f t dt =⎰⎰⎰.证明:111220()()yxdx x f y dy dy x f y dx =⎰⎰⎰⎰ (2分)13001()3yf y x dy =⎰ (4分) 11330011()()33f y y dy t f t dt ==⎰⎰. (5分) 20.设110,0,(1,2,)n n n n n n a b a b n a b ++>>≤= ,且级数1n n b ∞=∑收敛,证明级数1n n a ∞=∑收敛.证明:由已知110,0,(1,2,)n n n n n na b a b n a b ++>>≤= 得: 1111n n n n a a ab b b ++≤≤≤ (2分) 于是 11n n a a b b ≤,1,2,n = (4分) 又级数1n n b ∞=∑收敛,所以级数1n n a ∞=∑收敛. (5分)。
YT2010-2011高数(二)练习题-20110607
A. f ( x, y ) 在 (0 , 0) 处不连续; C. f ( x, y ) 在 (0 , 0) 处不可微;
B. f x (0 , 0) = f y (0 , 0) = 0 ; D. f x ( x, y ), f y ( x, y ) 在 (0 , 0) 处连续.
(2)设 f x ( x 0 , y 0 ) = 0 , f y ( x 0 , y 0 ) = 0 ,则( A . 二元函数 f ( x, y ) 在 ( x0 , y 0 ) 处连续;
高等数学(二) 练习题
一、填空题(5 题) 1.(1)直线过点 ( 0 , 2 , − 3) ,且与平面 x − y + 4 z + 1 = 0 垂直,则该直线的方程是. x − 2 y z +1 ●过点 (1,−1,−2) 且平行于直线 的直线方程为. = = 2 1 4
●直线 L :
x−7 y −4 z −5 与平面 π : 3 x − y + 2 z − 5 = 0 的交点 = = 5 1 4 x +1 y + 2 z + 3 垂直,则该平面的方程是 = = 4 1 −3
x2 + y 2 + z 2 =R2
∫∫
R 2 dxdy = R 2 ⋅ π R 2 .
(2)以下计算中错误的是 (
A.
).
Ω
∫∫∫ Ω ( x
2
+ y 2 + z 2 ) dv = R 2 ∫∫∫
4 dv = R 2 ⋅ πR 2 , 其中 Ω : x 2 + y 2 + z 2 ≤ R 2 ; 3
⎛ y⎞ ⎟ ; ⎝x⎠
2
) .
A. ( x + y ) − ⎜ C. x
山东省实验中学2011届高三第三次诊断性测试理科数学试题(WORD版)
A. ①和②
B.②和③
C.③和④
D. ①和④
()
x2 y2 9.已知 F1 , F2 是双曲线 a2 b2 1,(a b 0) 的左、右焦点,过 F1 且垂直于 x 轴的直线与双曲线的左支交于
A 、 B 两点 △ ABF 2 是正三角形,那么双曲线的离心率为
()
A. 2
B. 3
C.2
D.3
10.已知 A 、 B、 C 是锐角 △ ABC 的三个内角,向量 p ( sin A,1)q (1, cosB) ,则 p与 q 的夹角是 ( )
| BM | | BN |?若存在,求出直线 l 的方程;若不存在,说明理由。
22.(本小题满分 14 分 )
设 f ( x) a x ln x, g( x) x2 x2 3. x
(1)当 a 2 时,求曲线 y f ( x)在 x 1处的切线方程;
(2)如果存在 x1, x2 [0,2] 使得 g (x 1 ) g( x2 ) M 成立,求满足上述条件的最大整数 M ; 1
①若
,
,则 a// ;
② 若a / / ,a b, 则b ; ③若 a / /b,l , 则l b ; ④
,
,则 / /
以上命题正确的个数是
A.1
4.设 0,函数 y 2
A.
3
B.2
sin( x ) 3
4
B.
3
C.3
2 的图像向右平移 3
C.
2
D.4
4 个单位后与原图像重合,则 3
D.3
5.设 a log5 4,b (log5 3)2 , c log 4 5 ,则
()
A.{5 , 7}
B.{2 ,4}
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2011年12月考试高等数学(II-2)第三次作业
答案:
一、填空题(30分,共 10 题,每小题 3 分)
1. 可分离量的微分方程
2.
3. 阶数
4. 发散
5. y=-x+1
6.
7.
8. 2dx+dy
9. 45 度或135度
10. 2;0
二、计算题(40分,共 5 题,每小题 8 分)
1.
2.
3.
4.
由于 ,而级数
绝对收敛,所以原级数也是绝对收敛。
5.
三、证明题(30分,共 2 题,每小题 15 分)
1.
2.
