回归正交试验设计
正交试验设计因素选择与优化策略

正交试验设计因素选择与优化策略正交试验设计是一种常用的统计方法,用于确定影响某一产出指标的多个因素之间的关系。
通过使用正交试验设计,可以在少量实验中获得充分的信息,从而帮助优化产品或过程。
然而,正确选择和优化正交试验设计的因素是关键的。
本文将探讨正交试验设计因素选择与优化策略。
1. 因素选择在确定正交试验设计的因素时,需要考虑以下几个方面:1.1 问题定义首先,需要明确研究的问题定义。
确定您感兴趣的产出指标,并确定可能影响该指标的因素。
1.2 因素类型确定因素的类型是选择正交试验设计的重要一步。
因素可以是定性的或定量的。
定性因素是指不能被精确测量的因素,如颜色或形状;而定量因素是可以被准确测量的,如温度或时间。
确保正确识别因素的类型,以便正确选择设计。
1.3 因素数量确定正交试验设计中的因素数量是很重要的。
较少的因素数量可以减少实验规模,但可能无法完全掌握因素之间的相互作用。
较多的因素数量可能会增加实验的复杂性。
根据实验的目标和可用资源,选择适当的因素数量。
2. 优化策略在确定正交试验设计的因素之后,需要考虑如何优化设计以获得可靠的结果。
以下是几个常用的优化策略:2.1 L型表设计L型表是正交试验设计中常用的设计类型之一。
它可以用于确定每个因素的水平对产出指标的影响,并确定因素之间的相互作用。
通过选择适当的L型表设计,并根据实验结果进行分析,可以获得最佳的因素水平组合。
2.2 随机化在正交试验设计中,随机化是必不可少的。
它可以减少可能存在的偏差,并提高实验结果的可信度。
通过随机化因素水平的选择和实验的顺序,可以降低因素之间的干扰效应。
2.3 统计分析使用适当的统计方法对实验数据进行分析也是优化正交试验设计的重要策略。
通过运用方差分析、回归分析等方法,可以确定哪些因素对产出指标具有显著影响,并进一步优化设计。
2.4 反应面法反应面法是一种基于正交试验设计结果的建模方法。
通过构建数学模型,可以预测产出指标在不同水平组合下的表现。
正交试验设计PPT课件

验设计方法提供依据。
03
扩展正交试验设计的应用领域
研究正交试验设计在其他领域的应用可能性,如社会科学、人文科学等。
谢谢
THANKS
正交表的选择与设计
根据试验目的和因素数量选择合 适的正交表。
确定水平数,即各因素的取值数 量。
确定试验次数,即正交表的行数。
试验方案的制定
根据正交表,确定每个因素的取值组合。 确定试验的顺序,以避免误差的积累。
制定详细的试验步骤和操作规程。
试验数据的收集与分析
按照试验步骤进行试验,并记 录每个试验的结果。
降低试验成本
通过优化试验次数,可以减少 人力、物力和时间的投入,从 而降低试验成本。
加速试验进程
较少的试验次数意味着更短的 时间和更快的反馈,有助于加
速产品研发和优化进程。
因素水平的优化
确定关键因素
在正交试验设计中,首先需要明确哪 些因素是关键因素,并针对这些因素 进行优化。
选择合适水平
针对每个关键因素,选择合适的水平 进行试验,以获得最佳的试验效果。
CHAPTER
人工智能与机器学习在正交试验设计中的应用
机器学习算法优化正交试验设计过程
01
通过机器学习算法,可以自动分析历史数据,预测最佳试验条
件,从而减少试验次数,提高试验效率。
数据挖掘与知识发现
02
利用机器学习技术对大量试验数据进行挖掘,发现隐藏的模式
和关系,为后续试验提供指导。
自动化与智能化
03
结合人工智能技术,实现正交试验设计的自动化和智能化,减
少人为干预,提高试验精度和可靠性。
多目标优化问题的正交试验设计研究
1 2 3
多目标决策理论的应用
单因素考察和正交实验设计

单因素考察和正交实验设计实验设计是科学研究中的重要环节,通过设计合理的实验,可以根据实验结果得出准确可靠的结论。
其中,单因素考察和正交实验设计是两种常用的实验设计方法。
一、单因素考察:1.确定研究对象和考察因素:首先确定研究对象,明确要考察的因素是什么。
例如,研究对象是植物生长,考察因素可以是施肥量。
2.设置试验组和对照组:确定不同水平的因素水平组合,通常需要设计不同的试验组和对照组。
例如,考察植物生长的施肥量,可以设置不同施肥量的处理组,以及不施肥的对照组。
3.进行实验:根据设计好的试验组和对照组,对研究对象进行实验操作。
4.收集数据:实验结束后,需要对每个试验组和对照组进行数据收集。
通常,需要对多次实验进行统计分析,以得出可靠的结论。
5.分析结果:对收集到的数据进行统计分析,比较不同组之间的差异。
可以使用方差分析等统计方法来判断差异是否显著。
如果结果有统计学意义,就可以得出该因素对结果的影响程度。
二、正交实验设计:正交实验设计是一种多因素试验设计方法,通过设计合理的试验矩阵,同时考察若干因素对结果的影响,可以得到更加全面和可靠的结论。
正交实验设计的特点是通过有限的试验次数和样本数,解决多因素试验中的混淆问题。
具体步骤如下:1.确定研究对象和考察因素:同样需要明确研究对象和考察因素,例如研究对象是其中一种陶瓷材料的强度,考察因素可以是温度、压力和时间等。
2.选择正交表:根据研究因素的水平数目,选择合适的正交表。
正交表通过独立随机性和均匀分布性,让各个因素水平之间的关系尽可能平均。
3.设置试验组和对照组:根据正交表的要求,设置合理的试验组和对照组。
通常,在每个试验组中,考察因素的水平之间是相互独立的。
4.进行实验:按照正交表中给定的试验组进行实验操作。
5.收集数据:实验结束后,对每个试验组和对照组进行数据收集。
6.分析结果:通过对数据进行统计分析,可以得出各个因素及其交互作用对结果的影响程度。
可以使用方差分析、回归分析等方法进行分析。
4、高级实验设计—回归的旋转设计(Regressional Rotary Design)

x
i,j =1,2„P;
待定参数
以上为 P 元二次回归旋转设计的旋转性条件。
此外,为了使旋转设计成为可能,还必须使信
息矩阵 A 不退化,为此,必须有不等式:
4 p 2 2 P 2
上式为 P 元二次回归的非退化条件。 已证明,只要使 N 个试验点不在同一个球面上, 就能满足非退化条件。或者说只要使 N 个试验点至少 分布于两个半径不等的球面上,就有可能获得旋转设
P 2 2 ˆ D y P 2 4 PN
4 1 2 P 1 4 P 1 4 1 2 2 4 P 2 4 4
(4.11) 由式(4.11)经研究表明,只有采用恰当的方法 确定 4 ,才能满足通用性的要求。如何确定 4 ?对 4 有什么要求呢?总的来说,它必须使上式中 i处的
ˆ 的 二次旋转组合设计具有同一球面预测值 y
方差相等的优点,但回归统计数的计算较繁琐,
若使它获得正交性就能简化计算手续。
在二次旋转组合计划中,一次项和交互项的 回归系数 bj ,bij 仍保持正交,但 b0 与 bjj 之间,
以及 bii 与 bjj 之间都存在相关,即不具正交性,
它们之间的相关矩分别为:
计方案。
为了获得 P 元二次旋转设计方案,就要求既要
满足非退化条件式,又要满足旋转性条件式。
如何才能满足这两方面的条件呢?这主要借助
于组合设计来实现,因为组合设计中 N 个试验点:
N mc m m0
分布在三个半径不相等的球面上:
mc 个点分布在半径为 P 的球面上; c m 个点分布在半径为 的球面上; m0 个点分布在半径为 0 0 的球面上;
一次回归正交设计、二次回归正交设计、二次回归旋转设计
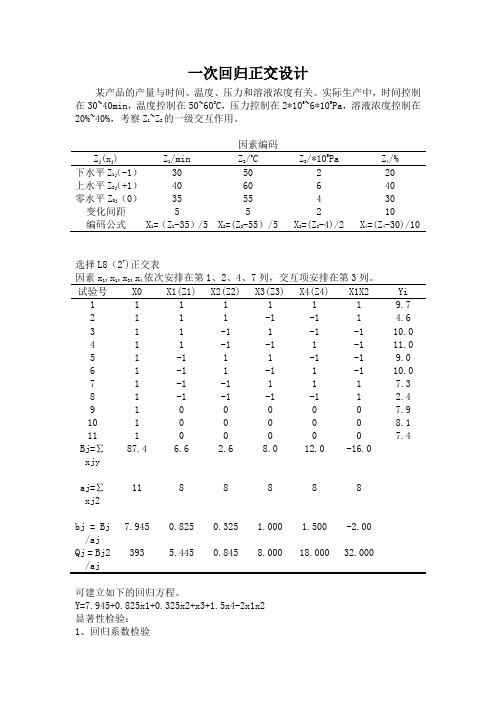
一次回归正交设计某产品的产量与时间、温度、压力和溶液浓度有关。
实际生产中,时间控制在30~40min,温度控制在50~600C,压力控制在2*105~6*105Pa,溶液浓度控制在20%~40%,考察Z1~Z2的一级交互作用。
因素编码Z j (xj) Z1/min Z2/o C Z3/*105Pa Z4/%下水平Z1j(-1)30 50 2 20上水平Z2j(+1)40 60 6 40零水平Z0j(0)35 55 4 30 变化间距 5 5 2 10编码公式X1=(Z1-35)/5 X2=(Z2-55)/5 X3=(Z3-4)/2 X4=(Z4-30)/10选择L8(27)正交表因素x1,x1,x3,x4依次安排在第1、2、4、7列,交互项安排在第3列。
试验号X0 X1(Z1) X2(Z2) X3(Z3) X4(Z4) X1X2 Yi1 1 1 1 1 1 1 9.72 1 1 1 -1 -1 1 4.63 1 1 -1 1 -1 -1 10.04 1 1 -1 -1 1 -1 11.05 1 -1 1 1 -1 -1 9.06 1 -1 1 -1 1 -1 10.07 1 -1 -1 1 1 1 7.38 1 -1 -1 -1 -1 1 2.49 1 0 0 0 0 0 7.910 1 0 0 0 0 0 8.111 1 0 0 0 0 0 7.4 Bj=∑xjy87.4 6.6 2.6 8.0 12.0 -16.0aj=∑xj211 8 8 8 8 8bj = Bj/aj7.945 0.825 0.325 1.000 1.500 -2.00Qj = Bj2/aj393 5.445 0.845 8.000 18.000 32.000可建立如下的回归方程。
Y=7.945+0.825x1+0.325x2+x3+1.5x4-2x1x2显著性检验:1、回归系数检验回归关系的方差分析表变异来源SS 平方和 Df 自由度 MS 均方 F 显著水平x 1 5.445 1 5.445 76.25 0.01x 2 0.845 1 0.845 11.83 0.05x 3 8.000 1 8.000 112.04 0.01x4 18.000 1 18.000 252.10 0.01x1x2 32.000 1 32.000 448.18 0.01回归 64.29 5 12.858 180.08 0.01 剩余 0.357 5 0.0714 失拟0.09730.03230.25<1误差e 0.26 2 0.13总和 64.647 10经F 检验不显著的因素或交互作用直接从回归方程中剔掉,不必再重新进行回归分析。
正交试验设计多层次模型建立与分析

正交试验设计多层次模型建立与分析在统计学和实验设计中,正交试验设计是一种有效的方法,可用于研究多个因素对某个过程或系统的影响。
本文将介绍正交试验设计的多层次模型建立与分析方法。
一、什么是正交试验设计?正交试验设计是一种通过系统地变化多个因素,以观察和分析其对特定过程或系统的影响的方法。
它的目标是在有限的试验次数内,得到尽可能多的信息,并避免因素之间的相互影响。
正交试验设计通过合理地选取试验方案,可以减少试验误差,提高结果的可信度。
二、正交试验设计的多层次模型建立在正交试验设计中,多层次模型是用来描述多个因素对响应变量的影响的数学模型。
多层次模型的建立是正交试验设计的关键步骤。
1. 确定因素与水平首先,需要确定影响研究对象的各个因素,以及每个因素的水平。
例如,对于某个产品的质量测试,可能需要考虑温度、湿度和压力等因素,并确定每个因素的几个水平。
2. 构建正交表接下来,根据因素的个数和水平数,构建正交表。
正交表是一种特殊的设计矩阵,可以保证每个因素的每个水平在试验中均匀分布,避免因素之间的相互干扰。
3. 收集数据按照正交表的设计,进行试验,收集各个因素在不同水平下的响应变量数据。
4. 建立多层次模型利用收集到的数据,对于每个因素的每个水平,建立多层次模型,通过回归分析等统计方法,确定每个因素的影响程度和显著性。
三、正交试验设计的多层次模型分析在建立多层次模型后,需要进行模型分析,以了解各个因素对响应变量的影响情况。
1. 方差分析通过方差分析,可以判断每个因素的水平对响应变量的影响是否显著。
方差分析可以将观测到的方差分解为因素之间的方差、误差的方差以及交互作用的方差。
2. 估计效应通过估计效应,可以定量地评估每个因素的影响程度。
估计效应的大小表示该因素对响应变量的影响大小,可以帮助研究人员优化设计,提高产品或过程的性能。
3. 优化设计根据模型分析的结果,可以优化试验设计,进一步提高产品或过程的性能。
通过调整因素的水平,可以最大程度地减少响应变量的波动,提高整体质量。
正交试验法
DOCS SMART CREATE
CREATE TOGETHER
DOCS
01
正交试验法的基本概念与原理
正交试验法的定义与背景
正交试验法是一种实验设计方法
• 用于研究多个因素对实验结果的影响
• 通过正交表安排实验,提高实验效率
源于20世纪初的统计学家
• 罗德里格斯(A. A. Rodrigues)
• 费雪(R. A. Fisher)
• 邓肯(F. Y. Duncan)等
正交试验法在实验设计中的重要性
• 提高实验效率
• 减少实验误差
• 便于数据分析与优化
⌛️
正交试验法的原理与特点
正交试验法的原理
正交试验法的特点
• 利用正交表安排实验
• 实验次数较少
• 考虑因素间的交互作用
• 因素水平分布均匀
优化策略
优化技巧
• 找出最优实验方案
• 利用正交表进行实验设计
• 分析因素间的交互作用
• 结合实际情况调整实验方案
• 调整实验因素与水平
• 考虑实验误差的影响
正交试验法的误差分析与控制
误差来源分析
误差控制方法
• 实验操作误差
• 提高实验操作水平
• 测量误差
• 采用准确的测量方法
• 数据处理误差
• 数据处理时进行误差修正
反应条件优化
• 反应温度、压力、物料配比等条件
• 考虑因素间的交互作用
• 优化反应条件,提高反应效率
催化剂性能评价
• 催化剂活性、选择性、稳定性等性能评价
• 研究催化剂组成与工艺条件对性能的影响
• 优化催化剂组成与工艺条件,提高催化剂性能
正交试验设计(内容详尽)
示。
存在期望值时:
n
S 2 ( xi )2 i 1
不存在期望值时:
n
S 2 ( xi x)2 i 1
自由度指的是关系式中独立数据的个数,通常用 f 表示。
例如,在计算偏差平方和的过程中,若表达式中使用
的是期望值 ,则 f n;若表达式中使用的是平均值 x ,
n
则因为存在约束条件 ( xi x) 0 而使独立数据的个数少 i 1
其他:
★ 标示因素
★ 区组因素
★ 信号因素
★ 误差因素
正交试验设计
⑷ 因素的水平 试验中因素变化的状态和条件称为因素的水平或位数,
简称水平。水平用数字(1,2,3…)表示。 试验中设计过程中水平的选取原则是:
◆ 宜选用三水平,以有利于实验结果的分析; ◆ 水平通常取等间隔,特殊情况下取对数间隔; ◆ 水平应该具体。水平应该是可控的,其变化对试验指 标有影响。
◆ 确定出各因素对试验指标的影响规律,得知哪些因素的 影响是主要的、哪些因素的影响是次要的、哪些因素之间 存在相互影响; ◆ 选出各因素的一个水平组合来确定最佳生产条件。
正交试验设计的基础是正交表。
7.1.3 基本概念
■ 过程或系统
人、机器、实验条件等资源的组合。
正交试验设计
可控因素
x1 x2
xp
通常用 表示,即
存在期望值时:
V
1 n
n i 1
( xi
)2
不存在期望值时:
V
1 n1
n i 1
( xi
x)2
正交试验设计
7.2.2 样本及其分布
■ 总体、个体与样本 总体(population):被研究对象的全体。 个体(individual):组成总体的每个单元。
正交实验
应用实例-2:
• 过去生产乙酰胺苯,产率一直保持在65%
左右,为了提高产量,根据工人经验,提 出反应温度、反应时间、硫酸浓度和操作 方法四个因素(子)的两个水平的研究题目。
•
1、正交表选择
• 根据原则,确定最少需超过实验次数=(21)×4+(2-1)(2-1)×1+1=6,也由于研究 条件A,B,C,D因子均是2水平的,因此 选入L8(27)表较为适宜。
表头设计
• 表头设计原则: • 第一,注意不要让主效应之间、主效应
实 例 分 析
因素 A —— 人 参 B —— 白 术 C —— 干 姜 D —— 甘 草 (k-1)m +1=5
交互作用 人参与白术 —— A×B 人参与干姜 —— A×C 1+1+1=3
白术与干姜 —— B×C n=8
L8 (27 ) 确定正交表
n=8
2、表头设计 要求: 没有交互作用时,可随意安排因素在各列中; ① ②有交互作用时,不能随意安排,要优先安排 具有交互作用的因素,A、B、C因素先考虑;
交互作用的定义 ——
在影响试验结果的诸因素中,有些因素不仅单独对效应 起作用,而且还与其它一个或多个因素联合起来影响响应值 (效应值)。这种联合作用就称为“交互作用”。如果两个 因素联合则称为双因子交互作用;如果三个因素联合则称为 叁因子交互作用;如果多个因素联合则称为多因子交互作用, 或称为高级交互作用;一般情况下,高级交互作用通常可以 忽略。
表示正交表意思
L4 (23 )
L8 (27 )
L9 (34 )
常见正交表
L8 (41 24 )
L (61 36 ) 18
常见正交表
考察最小试验组数
《2024年正交试验设计和分析方法研究》范文
《正交试验设计和分析方法研究》篇一一、引言正交试验设计是一种常用的统计分析方法,广泛应用于各个领域的研究与实践中。
它通过正交性原则,合理安排试验因素和水平,使得各因素间的效应能够独立可加,从而实现全面而经济的试验目的。
本文将对正交试验设计及其分析方法进行深入探讨和研究。
二、正交试验设计基本原理正交试验设计基于数理统计理论,根据实验需求选取不同的试验因素和水平,并运用正交表来安排实验。
正交表是一种特殊的表格,它具有整齐可比性、均衡分散性等特点,能够有效地减少试验次数,提高试验效率。
正交试验设计的核心在于正交性原则,即各因素间的效应能够独立可加,从而使得试验结果具有明显的规律性和可预测性。
三、正交试验设计步骤1. 明确试验目的和要求:确定试验的目标、任务和预期结果,为后续的试验设计提供依据。
2. 选取试验因素和水平:根据试验目的和要求,选择合适的试验因素和水平。
3. 制定正交表:根据选定的试验因素和水平,制定合适的正交表。
4. 实施试验:按照正交表进行实验,记录实验数据。
5. 数据分析与结果解释:对实验数据进行统计分析,解释各因素对实验结果的影响。
四、正交试验分析方法1. 极差分析:极差分析是一种简单而有效的正交试验分析方法。
它通过计算各因素在不同水平下的实验结果极差,来评价各因素对实验结果的影响程度。
2. 方差分析:方差分析是一种更为精确的正交试验分析方法。
它通过计算各因素引起的实验结果方差,来评估各因素对实验结果的贡献程度。
3. 回归分析:回归分析是一种将实验结果与各因素进行数学建模的分析方法。
它通过建立回归方程,揭示各因素与实验结果之间的数量关系,为优化实验提供依据。
五、实例分析以某企业生产过程中的工艺参数优化为例,通过正交试验设计,选取了温度、时间、压力等三个关键工艺参数作为试验因素,并设定了不同的水平。
然后根据正交表进行实验,记录各组实验结果。
通过对实验结果进行极差分析和方差分析,发现温度对产品性能的影响最为显著,其次是时间和压力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
规范变量z 规范变量 j 上星号臂γ 上星号臂 上水平1 上水平 零水平0 零水平 下水平-1 下水平- 下星号臂- 下星号臂-γ 变化间距 变化间距 j
②确定合适的二次回归正交组合设计 参考表8-22 参考表
正交表的选用 因素数m 因素数 2 3 4(1/2实施) ( 实施 实施) 4 5(1/2实施) ( 实施 实施) 5 选用正交表 L4(23) L8(27) L8(27) L16(215) L16(215) L32(231) 表头设计 1,2列 , 列 1,2,4列 , , 列 1,2,4,7列 , , , 列 1,2,4,8列 , , , 列 1,2,4,8,15列 , , , , 列 1,2,4,8,16列 , , , , 列 mc 22= 4 23= 8
(3)回归方程的建立 ) m0=0,n=mc=8 , = 计算表 计算各回归系数 写出y与规范变量 写出 与规范变量zj的回归方程 与规范变量 根据偏回归系数绝对值大小, 根据偏回归系数绝对值大小,确定因素和交互作用主次 根据偏回归系数正负, 根据偏回归系数正负,得到各因素对试验指标的影响方向 (4)方差分析 ) 与自然变量x (5)回归方程的回代:得到试验指标 与自然变量 j的回归 )回归方程的回代:得到试验指标y与自然变量 方程
1 m0 SSe1 = ∑ ( y0i y 0 ) 2 = ∑ y0i2 (∑ y0i ) 2 m0 i =1 i =1 i =1
m0
m0
重复试验误差的自由度: 重复试验误差的自由度: ②回归方程失拟部分: 回归方程失拟部分: 失拟平方和 :
df e1 = m0 1
SS Lf = SST SS R SS e1 = SS e SS e1
回归平方和 : SS R = ∑ SS 一次项 + ∑ SS 交互项 残差平方和 :
SS e = SST SS R
②自由度 dfT=n―1 各种偏回归平方和的自由度= 各种偏回归平方和的自由度=1 回归平方和的自由度 :
df R = ∑ df一次项 + ∑ df交互项
残差自由度: 残差自由度:
df e = df T df R
(3)星号臂长度与二次项的中心化 ) ①星号臂长度 与因素数m,零水平试验次数m 星号臂长度γ与因素数 ,零水平试验次数 0及二水平试 验数m 验数 c有关
γ的确定
公式计算
γ=
(mc + 2m + m0 )mc mc 2
参考表8-18 参考表
二次回归正交组合设计γ 二次回归正交组合设计γ值表 m0 1 2 3 4 5 6 7 8 9 10 因素数m 因素数 2 1.000 1.078 1.147 1.210 1.267 1.320 1.369 1.414 1.457 1.498 3 1.215 1.287 1.353 1.414 1.471 1.525 1.575 1.623 1.668 1.711 4(1/2实施) ( 实施 实施) 1.353 1.414 1.471 1.525 1.575 1.623 1.668 1.711 1.752 1.792 4 1.414 1.483 1.547 1.607 1.664 1.719 1.771 1.820 1.868 1.914 5(1/2实施) ( 实施 实施) 1.547 1.607 1.664 1.719 1.771 1.820 1.868 1.914 1.958 2.000 5 1.596 1.662 1.724 1.784 1.841 1.896 1.949 2.000 2.049 2.097
8.1 一次回归正交试验设计及结果分析
建立试验指标( ) 个试验因素x 建立试验指标(y)与m个试验因素 1,x2,…,xm之间的 个试验因素 , 一次回归方程 例:m=3时,一次回归方程: = 时 一次回归方程: y=a+b1x1+b2x2+b3x3+b12x1x2+b13x1x3+b23x2x3 = பைடு நூலகம் 其中x , , 表示3个因素 个因素; 其中 1,x2,x3表示 个因素;x1x2,x1x3,x2x3表示交互作用 , , 若不考虑交互作用,为三元一次线形回归方程: 若不考虑交互作用,为三元一次线形回归方程: y=a+b1x1+b2x2+b3x3 = +
全实施: 全实施:mc=2m
- 1/2实施:mc=2m-1 实施: 实施 - 1/4实施:mc=2m-2 实施: 实施
星号试验: 星号试验:
与原点(中心点)的距离都为 与原点(中心点)的距离都为γ mγ=2m 零水平试验: 零水平试验: 各因素水平编码都为零时的试验 试验次数m 试验次数 0
8.2.2 二次回归正交组合设计的应用
(1)基本步骤 ) ①因素水平编码 试验因素的水平被编为- ,-1, , , 试验因素的水平被编为-γ,- ,0,1,γ 变化间距:j=上水平-零水平=零水平-下水平 上水平-零水平=零水平- 变化间距:
x jγ x j 0
j =
γ
因素水平的编码表
自然变量x 自然变量 j x1 x1γ x12=x10+1 x10 x11=x10-1 x-1γ 1 x2 x2γ x22=x20+2 x20 x21=x20-2 x-2γ 2 … … … … … … … xm xmγ xm2=xm0+m xm0 xm1=xm0-m x-mγ m
编码目的: 编码目的: 使每因素的每水平在编码空间是“平等” 使每因素的每水平在编码空间是“平等”的,规范变量 zj的取值范围都是 -1,1] 的取值范围都是[- , 编码能将试验结果y与因素 编码能将试验结果 与因素xj(j=1,2,…,m)之间 与因素 = , , , ) 的回归问题,转换成试验结果y与编码值 与编码值z 的回归问题,转换成试验结果 与编码值 j之间的回归问 题
②二次项的中心化
1 n 2 对二次项的每个编码进行中心化处理 : z ji ' = z ji2 ∑ z ji n i =1 (二次项编码 -(二次项编码算术平均值 二次项编码)- 二次项编码算术平均值 二次项编码算术平均值) 二次项编码
二元二次回归正交组合设计编码表 试验号 1 2 3 4 5 6 7 8 9 z1 1 1 -1 -1 1 -1 0 0 0 z2 1 -1 1 -1 0 0 1 -1 0 z1 z2 1 -1 -1 1 0 0 0 0 0 z12 1 1 1 1 1 1 0 0 0 z22 1 1 1 1 0 0 1 1 0 z1’ 1/3 1/3 1/3 1/3 1/3 1/3 -2/3 -2/3 -2/3 z2’ 1/3 1/3 1/3 1/3 -2/3 -2/3 1/3 1/3 -2/3
(2)因素水平的编码 ) 编码( ):将因素 编码(coding):将因素 j的各水平进行线性变换: ):将因素x 的各水平进行线性变换:
zj =
x j xj0 j
zj:因素 j的编码 ,称为规范变量 因素x xj:自然变量 上水平x 上水平 j2的编码 :zj2=1 下水平x 的编码: =-1 下水平 j1的编码:zj1=- 零水平x 的编码: 零水平 j0的编码:zj0=0
n
bj =
∑z
i =1
ji
yi
j=1,2,…,m = , , ,
mc
n i =1 k j i
bkj =
说明: 说明:
∑ (z z ) y
mc
i
j>k, k=1,2,…,m-1 > = , , , -
求得的回归系数直接反映了该因素作用的大小 回归系数的符号反映了因素对试验指标影响的正负
8.1.3 回归方程及偏回归系数的方差分析
8.1.2 一次回归方程的建立
总试验次数为n 总试验次数为 : n=mc+m0 = mc:二水平试验次数 m0:零水平试验次数 一次回归方程系数的计算: 一次回归方程系数的计算: 常数项: 常数项:a 一次项系数: 一次项系数:bj 交互项系数: 交互项系数: bjk
1 n a = ∑ yi = y n i =1
二元二次回归正交组合设计
(2) 三元二次回归正交组合设计试验方案 ) 三元二次回归方程: 三元二次回归方程:
2 2 y = a +bx1 +b2x2 +b3x3 +b12x1x2 +b13x1x3 +b23x2x3 +b11x12 +b22x2 +b33x3 1
试验方案
三元二次回归正交组合设计
8.1.3.1 无零水平试验时 ①平方和: 平方和: 总平方和: 总平方和:
1 n SST = Lyy = ∑ ( yi y) = ∑ y (∑ yi )2 n i =1 i =1 i =1
2 2 i
j
n
n
一次项偏回归平方和 : S S
= m cb 2 j
2 SS kj = m c bkj 交互项偏回归平方和: 交互项偏回归平方和:
失拟平方和自由度: 失拟平方和自由度: d f = d f d f Lf e e1
③失拟检验 :
FL f =
SS L f d f L f S S e 1 df e 1
对于给定的显著性水平α(一般取 ) 对于给定的显著性水平 (一般取0.1) 当FLf<Fα(dfLf,dfe1)时,就认为回归方程失拟不显 失拟平方和SS 是由随机误差造成的, 著,失拟平方和 Lf是由随机误差造成的,所建立的回 归方程是拟合得很好 例8-2
8.2 二次回归正交组合设计
回归方程的建立: 回归方程的建立: 根据最小二乘法原理得到正规方程组 求解正规方程组, 求解正规方程组,得回归系数 要求:试验次数>回归方程的项数 要求:试验次数> 回归正交组合设计: 回归正交组合设计:在一次回归正交试验设计的基础上 再增加一些特定的试验点, 再增加一些特定的试验点,通过适当的组合形成试验方 案
(3)一次回归正交设计表 ) 将二水平的正交表中“ 用 将二水平的正交表中“2”用“-1”代换 ,例: 代换
