二维线性系统和离散图像的线性变换
第三讲 图像变换

傅立叶级数:非正弦周期函数
为了研究非正弦周期函数,可以将周期为T=2π/ ω的周期 函数用一系列以T为周期的正弦函数的级数来表示,记为:
fT (t) A0 An sin(nt n) n1
其中A0,An, φn 是常数,n=1,2,3……
当输入信号沿时间轴平移T,有:
x(t-T)->y(t-T)
则称该线性系统具有移不变性
二维线性位移不变系统
如果对二维函数施加运算T[·] ,满足
T f x, y T[ f x, y] T f1 x, y f2 x, y T f1 x, y T f2 x, y
2
则周期函数可表示为:
f (x) a0 (an cos nx bn sin nx)
2 n1
傅立叶级数
三角函数系的正交性
即:sinx,cosx,sin2x,cos2x,…,sinnx,cosnx,…在区 间[-π,π]上正交,就是指在三角函数系中任何两个 函数的乘积在区间[-π,π]上的积分等于零。
图像与图像变换
图像的表示
空间域 频率域
将图像看成是线性叠加系统
图像由像素组成,像素在图像空间中按某种规律排 列的,图像在空间域上具有很强的相关性。
图像变换是将图像从空间域变换到其它域如频 率域的数学变换
图像变换的目的在于:
①使图像处理问题简化; ②有利于图像特征提取; ③有助于从概念上增强对图像信息的理解。
Taf x, y aT f x, y
则称该运算为二维线性运算。由它描述的系统,称为二维 线性系统。
06-二维线性系统分析2-傅里叶变换定理、线
1 x
0
F.T.
1
f
0
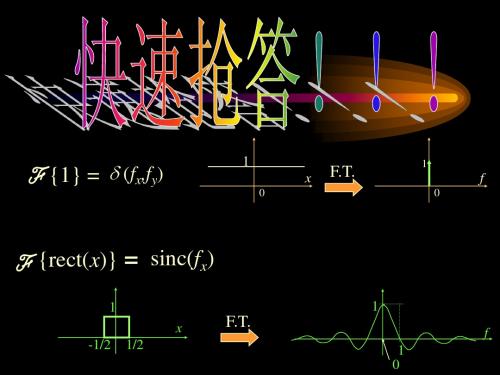
{rect(x)} = sinc(fx)
1 x -1/2 1/2 1
F.T.
1 0
f
§1-2 二维傅里叶变换 2-D Fourier Transform
傅里叶变换和傅里叶逆变换
F ( f x , f y ) = ∫ ∫ f ( x, y ) exp[ j 2π ( f x x + f y y )]dxdy
§1-2 二维傅里叶变换Fourier Transform
定理的证明 四, F.T.定理 -- Parseval定理的证明 定理
∫
+∞
∞
g ( x) dx = ∫ g ( x) g * ( x)dx
2 ∞ +∞
+∞
+ ∞G ( f ) exp( j 2πfx )df + ∞G * ( f ' ) exp( j 2πf ' x)df ' dx = ∫ ∫ ∫∞ ∞ ∞
{g(x,y) . h(x,y)}= G(fx,fy) * H(fx,fy)
将时,空域的卷积运算,化为频域的乘积运算,特别有用 将时,空域的卷积运算,化为频域的乘积运算,特别有用. 亦可用于求复杂函数的F.T.和复杂函数的卷积 和复杂函数的卷积 亦可用于求复杂函数的
§1-2 二维傅里叶变换Fourier Transform
1 {cos(2πf 0 x)} = [δ ( f x f 0 ) + δ ( f x + f 0 )] 2 1 {sin(2πf 0 x)} = [δ ( f x f 0 ) δ ( f x + f 0 )] 2j
二维离散傅里叶变换计算过程

二维离散傅里叶变换计算过程傅里叶变换是信号处理中非常重要的数学工具,可以将一个时域信号转换为频域表示。
而二维离散傅里叶变换(2D DFT)则是将二维离散信号转换为二维频域表示。
本文将介绍二维离散傅里叶变换的计算过程。
1. 二维离散傅里叶变换的定义二维离散傅里叶变换是将一个二维离散信号(图像)转换为二维频域表示的数学变换。
假设有一个大小为M×N的二维离散信号f(x, y),其中x和y分别表示信号的行和列,那么二维离散傅里叶变换的定义可以表示为:F(u, v) = ΣΣf(x, y) * exp(-j2π(ux/M + vy/N))其中F(u, v)表示变换后的频域信号,u和v分别表示频域的行和列,j表示虚数单位,M和N分别表示信号的行数和列数。
2. 二维离散傅里叶变换的计算过程二维离散傅里叶变换的计算过程可以分为两个步骤:首先进行行变换,然后进行列变换。
2.1 行变换对于给定的二维离散信号f(x, y),我们首先对每一行进行变换。
对于第i行,我们可以将其看作一个一维离散信号,然后对其进行一维离散傅里叶变换。
假设第i行的变换结果为F(i, v),其中v 表示频域的列,那么F(i, v)的计算公式为:F(i, v) = Σf(i, y) * exp(-j2πvy/N)其中y表示该行的列索引。
2.2 列变换在完成行变换后,我们继续对每一列进行变换。
对于每一列,我们可以将其看作一个一维离散信号,然后对其进行一维离散傅里叶变换。
假设第j列的变换结果为F(u, j),其中u表示频域的行,那么F(u, j)的计算公式为:F(u, j) = ΣF(i, j) * exp(-j2πiu/M)其中i表示该列的行索引。
3. 二维离散傅里叶变换的计算复杂度二维离散傅里叶变换的计算复杂度较高,为O(MN(M+N))。
其中M和N分别表示信号的行数和列数。
由于计算复杂度较高,通常会采用快速傅里叶变换(FFT)算法来加速计算过程。
二维离散余弦变换解法

二维离散余弦变换(2D-DCT)是一种在图像处理中常用的技术,尤其在图像压缩领域,如JPEG压缩算法中。
其基本思想是将二维信号(如图像)分解为不同频率的余弦函数的叠加。
二维离散余弦变换的数学表达式通常如下:X(u,v) = C(u)C(v) ∑∑ x(m,n)cos((2m+1)uπ/(2M))cos((2n+1)vπ/(2N))其中,X(u,v)表示变换后的系数,x(m,n)表示原始信号的像素值,C(u)和C(v)是归一化因子,M和N分别表示原始信号的宽度和高度,u和v表示频域的坐标。
但是,上述公式并没有提供具体的解法步骤,因为它本身就是定义了二维离散余弦变换的计算方式。
在实际应用中,我们通常会使用特定的算法或库函数(如Python中的numpy.fft.dct2)来计算二维离散余弦变换。
对于具体的计算步骤,以下是一种可能的简化描述:1.获取输入图像(或二维信号)的所有像素值,即x(m,n)。
2.初始化输出矩阵X(u,v)为零矩阵,其大小与输入图像相同。
3.对输入图像的每一个像素位置(m,n),计算其对应的余弦项cos((2m+1)uπ/(2M))cos((2n+1)vπ/(2N))。
4.将步骤3中计算得到的余弦项乘以该像素位置的像素值x(m,n)。
5.对步骤4中得到的乘积进行累加,累加到输出矩阵X(u,v)的对应位置。
6.对输出矩阵X(u,v)的每一个元素,乘以对应的归一化因子C(u)C(v)。
以上步骤描述了如何计算二维离散余弦变换的一种可能方法,但请注意这并非唯一的实现方式。
具体的实现可能会根据具体的应用场景和优化需求进行调整。
另外,对于二维离散余弦变换的逆变换(即从频域系数恢复原始图像),其计算过程与上述过程类似,但方向相反。
具体来说,就是将频域系数乘以对应的归一化因子,然后进行反余弦变换,最后得到恢复后的图像。
双线性变换法

双线性变换法双线性变换法(bilinear transofrmation method)是一种通过变换以分析和解决非线性系统的复杂方法。
它最初由Collins,Mitroff和Zinnes提出,其主要特点是将非线性系统转化为线性系统来进行分析。
它把一个非线性系统映射到一个线性系统可以使一些复杂的非线性图像变成简单的线性图像,从而形成简单的表达式来解决复杂的问题。
一、双线性变换法定义双线性变换法是指通过线性常数和相关系数,将一维和多维数据变换为更简单的线性形式,以模拟复杂的非线性系统的运算的一种变换方法。
二、双线性变换法的应用(1)控制论领域。
双线性变换可以将复杂的非线性系统转变为简单的线性系统,使得这些复杂的系统容易控制。
(2)视觉领域。
双线性变换可以解决计算机视觉中的误差传播问题,将非线性的图像识别问题转变为简单的线性问题来处理;另外,在图像处理领域用双线性变换可以实现图像的变换,从而实现复杂的图像变换;(3)机器学习领域。
双线性变换可以将非线性的机器学习问题变换为线性的问题,让算法可以更加简单有效地解决复杂的机器学习问题。
三、双线性变换法的局限性(1)双线性变换法还有一些困难。
例如,当非线性系统出现很多两个变量或多个变量间有联系时,双线性变换也会受到很大影响。
(2)双线性变换法也会遇到数值不稳定的问题,在遇到非线性系统的情况下,很多变量的变化对结果的影响会变得很大,因此会产生数值不稳定的现象。
(3)双线性变换只是一种模拟,它并不能完全模拟出非线性系统的真实行为,因此很多时候双线性变换的结果可能不太准确。
双线性变换法是一种实用性很强的方法,它可以帮助我们更准确地分析和解决非线性系统问题,它也应用于控制论、视觉和机器学习等领域,但由于它有一些限制,如数值不稳定性和无法完全模拟非线性系统,因此我们需要更加谨慎地运用双线性变换法来真正发挥它的优势。
二元函数的离散二维傅里叶变换与离散二维傅里叶变换的应用

二元函数的离散二维傅里叶变换与离散二维傅里叶变换的应用二元函数的离散二维傅里叶变换(Discrete Two-dimensional Fourier Transform)是一种将二维离散信号转换到频域的重要数学工具。
在数字图像处理、通信系统和信号处理等领域中得到了广泛应用。
本文将介绍二元函数的离散二维傅里叶变换的定义、性质以及其在数字图像处理中的应用。
一、离散二维傅里叶变换的定义和性质离散二维傅里叶变换是二维信号的频域表示,它将一个二元函数表示为两个离散变量的函数。
设f(m,n)是一个m×n的离散二维信号,则它的离散二维傅里叶变换F(u,v)定义为:F(u,v)=∑[∑f(m,n)e^(-j2π(um/M+vn/N))] (1)其中,u和v是频率变量,范围在[0,M-1]和[0,N-1]之间,M和N分别表示信号的行数和列数。
离散二维傅里叶变换有以下性质:1. 线性性质:设f1(m,n)和f2(m,n)是两个m×n维的离散二维信号,α和β是常数,则有F(αf1(m,n)+βf2(m,n))=αF(f1(m,n))+βF(f2(m,n))。
2. 变换的逆运算:假设一个信号F(u,v)经过离散二维傅里叶变换得到一个函数f(m,n),则信号F(u,v)通过逆变换可以得到相应的函数f(m,n),即f(m,n)=∑[∑F(u,v)e^(j2π(um/M+vn/N))]。
3. 位移性质:对于一个二维离散信号f(m,n)的傅里叶变换F(u,v),其在频域中的相对位移可以引起在空域中的相位变换。
即若f(m,n)经过水平或垂直平移变换,则其傅里叶变换F(u,v)也会在相应的方向上发生相位变化。
4. 共轭对称性:离散二维傅里叶变换满足共轭对称性质,即对于一个二维离散信号f(m,n)的傅里叶变换F(u,v),有F(u,v) = F*(-u,-v),其中F*(-u,-v)表示F(u,v)的共轭复数。
二、离散二维傅里叶变换在数字图像处理中的应用离散二维傅里叶变换在数字图像处理中有广泛的应用,包括图像滤波、边缘检测、图像增强等。
二维离散余弦变换的一种新的快速算法
二维离散余弦变换的一种新的快速算法二维离散余弦变换(2DDiscreteCosineTransform,2D-DCT)是一种常见的无损压缩算法,用于存储和传输信号和图像等非常重要的功能。
本文介绍了一种新的2D-DCT快速算法,深入分析了其理论基础以及其优势和缺点,详细介绍了其实现过程。
一、2D-DCT算法基本原理2D-DCT是一种基于余弦函数的线性数学变换,其中余弦函数是一种用于描述无穷期信号的函数。
这种变换能够将图像或信号的信息从空间域转换到频域,在该变换过程中,信息的量化率可以大大提高。
2D-DCT的基本原理是,将一幅图像看作一个由许多小块组成的矩阵,每个小块即为一个像素点。
然后将每个小块矩阵进行余弦变换,根据信号的不同,对每个像素点进行相应的处理,使得其可以有更高的有效分辨率以及更小的数据大小,从而实现无损压缩。
二、新的2D-DCT快速算法为了提高2D-DCT的运行效率,提出了一种新的2D-DCT快速算法。
它主要通过一系列的基于字典的运算将2D-DCT的运算复杂度降低到O(N * log(N))。
该算法的具体步骤如下:1、首先,对原始图像进行划分,将图像分为8 8的块,以便于后续步骤中进行处理。
2、然后,根据2D-DCT的理论基础,首先将划分好的块按行排列,然后将每行应用一维DCT变换,以将空间域信号转换到频域。
3、最后,将每列按照其在一维DCT变换中获得的信号值排序,然后将排序后的矩阵再次进行一维DCT变换,最终得到余弦变换的最终结果。
三、优势和缺点新的2D-DCT快速算法具有一定的优势和缺点,优势主要表现在更低的运算复杂度以及更高的时间效率上,由于它的运算效率更高,因此可以大大降低实际应用中的成本。
但是,相比于其他算法,新的2D-DCT快速算法在能量损失率方面仍存在一定缺点,这意味着它不能完全捕捉图像或视频中的所有信息,因此在任何图像或视频处理中都不会提供最佳性能。
四、算法实现过程新的2D-DCT快速算法可以通过下述方法实现:1、首先,将原始图像分割为8 8的块,每个小块即为一个像素点,然后根据2D-DCT的理论基础,对每个像素点进行一维DCT变换,以将空间域信号转换到频域。
图像的线性变换
实验二 图像的线性变换实验学时:2学时实验类型:综合实验要求:必修一、实验目的通过掌握图像直方图的绘制方法,深入理解图像直方图对于观察图像的意义。
通过掌握灰度变换的方法,并深入了解图形经过灰色变换后,动态范围扩大,图像层次显得清晰,图像特征明显,更有利于对图像的目视观察。
二、实验内容(1)编程实现图像的直方图。
(2)编程并实现窗口灰度变换,分段线性变换,显示图像的直方图和灰度图,观察图像灰度的结果。
(3)在实验过程中,改变线性分段范围,观察图像灰度变换后的目视效果变化情况。
三、实验原理、方法和手段(1)灰度的线性变换若()[(,)]g x T f x y =是一个线性或分段线性的单值函数,灰度变换方程为: ()[(,)](,)g x T f x y af x y b ==+ 则由它确定的 灰度变换为灰度变换,简称线性变换。
(2)窗口灰度变换在曝光不足或曝光过度的情况下,或景物本身灰度级很少,图像的灰度可能会局限在一定的很小的范围内。
当图像中大部分的灰度级在[,]L U 范围内,少部分像素分布在小于L 和大于U 的区间内时,限定一个窗口范围,该窗口中的灰度值保持不变,对小于该窗口下限的灰度值直接设置为0;大于该窗口上限的灰度值直接设置为255,将有效地改善图像视觉效果。
灰度窗口变换函数表达式如下:0()255f x x ⎧⎪=⎨⎪⎩x L L x U x U <≤≤>图1其中L和U分别是图中窗口的下限和上限。
(3)分段线性变换分段线性变换和灰度的线性变换有点类似,都用到了灰度的线性变换。
但不同之处在于分段线性变换不是完全的线性变换,而是分段进行线性变换,将图像灰度区间分成两段甚至多段,分别作线性变换称之为分段线性变换。
分段线性变换的优点是可以根据用户的需要,拉伸特征物体的灰度细节,相对抑制不感兴趣的灰度级。
图2灰度变换函数如下:112112112222/()()()/()(255)()/(255)y x x f x y y x x x x y y x x x y ⋅⎧⎪=---+⎨⎪---+⎩1122x x x x x x x <≤≤> 其中,11(,)x y 和 22(,)x y 是图中两个转折点坐标。
二维线性系统
H(fx,fy)的模称振幅传递函数. H(fx,fy)的复角称相位传递函数. 的模称振幅传递函数 振幅传递函数. 的复角称相位传递函数 相位传递函数.
2.2. 3. 二维线性不变系统的本征函数: 二维线性不变系统的本征函数 本征函数
若ℜ{f(x ,y)}=a f(x ,y), 式中a为复常数,则称 ,y) 为算 , 式中a为复常数,则称f(x }表征的系统的本征函数 表征的系统的本征函数。 符ℜ{ }表征的系统的本征函数。 系统的本征函数是一特定的输入函数, 系统的本征函数是一特定的输入函数,输入输出之间仅差 别一个复常数,复指数基元就是线性空不变系统的本征函数。 别一个复常数,复指数基元就是线性空不变系统的本征函数。
叠加积分 一般写成
)
∫
∞
−∞
f (ξ 2 , η 2 )h ( x 2 − ξ 2 , y 2 − η 2 ) d ξ 2 d η 2
= f ( x2 , y2 ) ∗ h( x2 , y2 )
g(x, y) = f (x, y) ∗ h(x, y)
线性空不变系统
2.2. 2. 二维线性不变系统的传递函数: 二维线性不变系统的传递函数 传递函数
F( f x , f y ) = ∫
逆变换: 逆变换
若输入空间域函数f(x,y),其付里变换为: ,其付里变换为 若输入空间域函数
∫ f ( x, , y) = ∫ ∫
∞
∞
−∞ −∞ ∞ ∞
f ( x, y) exp − j2π ( f x x + f y y) dxdy
[
−∞ −∞
F( f x , f y )exp j2π ( f x x + f y
[
] y)]df df
离散状态空间模型
§10-3 离散状态空间模型一个物理系统的数学模型可以用不同方法来描述。
对于线性离散系统可以直接用差分方程来表示,也可以用脉冲传递函数或离散状态空间模型来表示。
传递函数模型在经典控制理论中是常用的,它适用于线性、定常系统,但不适于非线性和时变系统的分析。
状态空间模型是现代控制理论的基础,是一种时域分析方法,它比较适合于多输入多输出、时变和准线性系统的分析和设计。
在引入状态变量和状态空间概念后,系统的数学模型就变成很规则的形式,为系统的理论分析和设计综合带来方便。
一个系统的状态变量的选择不是唯一的,表达同一线性系统的不同状态空间模型之间存在着线性变换关系。
一、线性离散系统的状态空间模型线性时不变离散系统的状态空间表达式为)()()()( )()1(k DU k CX k Y k U k X k X +=Γ+Φ=+ (10.59)式中把kT 和T k )1(+略记为k 和1+k ,即把采样周期T 看成基本时间单位。
(10.59)中的第一个方程称为状态方程,第二个方程称为输出方程或测量方程。
Y U X ,,分别表示n 维状态列向量,m 维输入列向量和p 维输出列向量;Φ是n n ⨯维矩阵,称为状态矩阵或系统矩阵;Γ是m n ⨯维矩阵,称为输入矩阵或驱动矩阵;C 是n p ⨯维矩阵,称为状态矩阵;D 是m p ⨯维矩阵,称为直传矩阵或传输矩阵。
(10.59)式所代表的离散系统可用图10-13表示,图中1-Z表示单位延迟。
图10-13 线性时不变离散系统的状态空间模型从图中可以看出,状态空间法把系统的特征用D C ,,,ΓΦ四个矩阵表示,从而把系统的描述规格化了,为分析研究带来方便。
)(k Y )(k X )1(+k X )(k U DCφ1-Z Γ用迭代法就可以求出(10.59)式的解,)()0()1()1()0()0()()1()0()0()1()1()2()0()0()1(101212i U X k U U U X k X U U X U X X U X X k i i k kk k k ΓΦ+Φ=-Γ++ΓΦ+ΓΦ+Φ=Γ+ΦΓ+Φ=Γ+Φ=Γ+Φ=∑-=----(10.60)此解由两部分组成:第一部分取决于初始状态,第二部分是控制作用的结果,它是控制信号的加权和。
