2011年全国初中数学竞赛试题(初试与复试)及参考答案
2011年全国初中数学联赛决赛试卷及其答案

2011年全国初中数学联赛决赛试卷(4月10日 上午8:45——11:15)考生注意:1.本试卷共三大题(13个小题),全卷满分140分.2.用圆珠笔、签字笔或钢笔作答. 3.解题书写不要超出装订线. 4.不能使用计算器.一、选择题(本题满分42分,每小题7分)1.一个凸多边形的每一个内角都等于150°,则这个凸多边形所有对角线的条数总共有( ) A .42条 B .54条 C .66条 D .78条2.如图,矩形ABCD 的对角线相交于O ,AE 平分∠BAD 交BC 于E .若∠CAE=15°,则∠BOE =( )A .30°B .45°C .60°D .75°3.设方程()()0x a x b x ---=的两根是c ,d ,则方程()()0x c x d x --+=的分根 是( )A .a ,bB .-a ,-bC .c ,dD .-c ,-d 4.若不等式2133x x a -+-≤有解,则实数a 的最小值是( )A .1B .2C .4D .65.若一个三角形的任意两条边都不相等,则称它为“不规则三角形”.用一个正方体上的任意三个顶点构成的所有三角形中,“不规则三角形”的个数是( ) A .18 B .24 C .30 D .36 6.不定方程2225x y -=的正整数解(x ,y )的组数是( ) A .0组 B .2组 C .4组 D .无穷多组. 二、填空题(本大题满分28分,每小题7分) 本题共有4小题,要求直接将答案写在横线上.1.二次函数22y x ax =-+的图象关于直线x =1对称,则y 的最小值是__________. 2.已知1a ,则20122011201022a a a +-的值为_____________.3.已知△ABC 中,ABBC =6,CAM 是BC 的中点,过点B 作AM 延长线的垂线,垂足为D ,则线段BD 的长度是_______________.4.一次棋赛,有n 个女选手和9n 个男选手参赛,每位选手都与其余10n -1个选手各对局一次.计分方式为:胜者得2分,负者得0分,平局各得1分.比赛结束后统计发现,所有男选手的得分总和是所有女选手得分总和的4倍.则n 的所有可能值是__________. 三、解答题(本题共三小题,第1题20分,第2、3题各25分) 1.(本题满分20分)已知x 1,x 2是关于x 的一元二次方程22(31)210x a x a +-+-=的两个实数根,使得1212(3)(3)80x x x x --=-成立.求实数a 的所有可能值.O EDB A2.(本题满分25分)抛物线2y ax bx c =++的图象与x 轴有两个交点M (x 1,0),N (x 2,0),且经过点A (0,1),其中0<x 1<x 2.过点A 的直线l 与x 轴交于点C ,与抛物线交于点B (异于点A ),满足△CAN 是等腰直角三角形, 且S △BMN =52S △AMN .求该抛物线的解析式. 3.(本题满分25分)如图,AD 、AH 分别是△ABC (其中AB >AC )的角平分线、高线,M 是AD 的中点.△MDH 的外接圆交CM 于E .求证:∠AEB =90°.EH MD C B A2011年全国初中数学联合竞赛试题参考答案说明:评阅试卷时,请依据本评分标准:选择题和填空题只设7分和0分两档;其余各题,请严格按照本评分标准规定的评分档次给分,不要再增加其他中间档次.如果考生的解答方法和本解答不同,只要思路合理,步骤正确,在评卷时请参照本评分标准划分的档次,给予相应的分数.一、选择题(本题满分42分,每小题7分)1、B2、D3、A4、C5、B6、A 二、填空题(本题满分28分,每小题7分) 1、1 2、0 3、234、1 三、解答题(本题共三小题,第1题20分,第2、3题各25分) 1、(本题满分20分)已知21,x x 是关于x 的一元二次方程012)13(22=-+-+a x a x 的两个实数根,使得80)3)(3(2121-=--x x x x 成立。
2011年全国初中数学竞赛试题(A)

2011年全国初中数学竞赛试题(A 卷)一、选择题(每小题7分,共35分)1、设17-=a ,则代数式12612322--+a a a 的值为().A、24B、25C、1074+D、1274+2、对于任意实数d c b a ,,,,定义有序实数对()()d c b a ,,与之间的运算⊗为:()()()bc ad bd ac d c b a ++=⊗,,,,若对于任意实数v u ,都有()()()v u y x v u ,,,=⊗,则()y x ,为().A、()1,0B、()01,C、()01-,D、()1-0,3、若,0,1>>y x 且满足,,3y y x y x x xy ==则y x +的值为().A、1B、2C、29D、2114、已知点D、E 分别在ΔABC 的边AB、AC 上,BE 与CD 交于点F,设,,,,4321S S S S S S S S CEF BCF BDF EADF ====则4231S S S S 与大小关系为().A、4231S S S S <B、4231S S S S =C、4231S S S S >D、无法确定5、设333991......2111+++=S ,则S 4的整数部分等于().A、4B、5C、6D、7二、填空题(每小题6分,共30分)6、若关于x 的方程()()0422=+--m x x x 有三个根,且这三个根恰好可以作为一个三角形的三边长,则m 的取值范围是________.7、一枚质地均匀的正方体骰子的六个面上的数字分别是1,2,2,3,3,4,另一枚质地均匀的正方体骰子的六个面上的数字分别是1,3,4,5,6,8,同时掷出两枚骰子,则其朝上的面两数字之和为5的概率是_______.8、如图,已知点A、B 在直线x y =上,过A、B 分别作y 轴的平行线交双曲线()01>=x xy 于点C、D,若BD=2AC,则22-4OD OC 的值为______________.9、若21-1-+=x x y 的最大值为a ,最小值为b ,则22b a +的值为_______.10、如图,已知在RtΔABC 中,斜边AB 的长为35,正方形CDEF 内接于ΔABC,且其边长为12,则ΔABC 的周长为_________.三、解答题(每小题15分,共60分)11、已知关于x 的一元二次方程02=++a cx x 的两个整数根恰好比方程02=++b ax x 的两个根都大1,求c b a ++的值.12、如图,已知点H 为ΔABC 的垂心,以AB 为直径的⊙1O 与ΔBCH 的外接圆⊙2O 交于点D,延长AD 与CH 交于点P,求证:P 为CH 的中点.13、如图,已知A 为y 轴正半轴上一点,点A、B 关于x 轴对称,过A 任作直线与抛物线232x y =交于P、Q 两点.(1)求证:∠ABP=∠ABQ;(2)若点()1,0A ,且∠PBQ=。
2011年全国初中数学竞赛天津赛区复赛试题[1]2011年全国初中数学竞赛天津赛区复赛试题[1]
![2011年全国初中数学竞赛天津赛区复赛试题[1]2011年全国初中数学竞赛天津赛区复赛试题[1]](https://img.taocdn.com/s3/m/857a989f011ca300a7c39045.png)
“《数学周报》杯”2011年全国初中数学竞赛天津赛区复赛试卷(3月20日上午 9∶30~11∶30)一、选择题(本题共5小题,每小题7分,满分35分.每小题均给出了代号为A 、B 、C 、D 的四个选项,其中只有一个选项是正确的.请将正确选项的代号填入题后的括号里)(1)设32x =,则代数式(1)(2)(3)x x x x +++的值为( ). (A )0(B )1(C )﹣1(D )2(2)已知x y z ,,为实数,且满足253x y z +-=,25x y z --=-,则222x y z ++的最小值为( ).(A )111(B )0(C )5 (D )5411(3)若1x >,0y >,且满足3yy xxy x x y==,,则x y +的值为( ). (A )1 (B )2(C )92(D )112(4)设333311111232011S =++++,则4S 的整数部分等于( ). (A )4 (B )5(C )6(D )7(5)点D E ,分别在△ABC 的边AB AC ,上,BE CD ,相交于点F ,设1234BDF BCF CEF EADF S S S S S S S S ∆∆∆====四边形,,,,则13S S 与24S S 的大小关系为( ).(A )1324S S S S < (B )1324S S S S = (C )1324S S S S >(D )不能确定得分 评卷人二、填空题(本题共5小题,每小题7分,满分35分.把答案填在题中横线上)(6)两条直角边长分别是整数a b ,(其中2011b <),斜边长是1b +的直角三角形的个数为 . (7)一枚质地均匀的正方体骰子的六个面上的数字分别是1,2,2,3,3,4;另一枚质地均匀的正方体骰子的六个面上的数字分别是1,3,4,5,6,8. 同时掷这两枚骰子,则其朝上的面两数之和为7的概率是 . (8)若112y x x =-+-的最大值为a ,最小值为b ,则22a b +的值为 .(9)如图,双曲线xy 2=(x >0)与矩形OABC 的边CB , BA 分别交于点E ,F ,且AF=BF ,连接EF , 则△OEF 的面积为 .第(10)题(10)如图,在Rt△ABC中,斜边AB的长为35,正方形CDEF内接于△ABC,且其边长为12,则△ABC的周长为 .三、解答题(本题共4小题,每小题20分,满分80分,解答应写出文字说明,演算步骤或证明过程)(11)(本小题满分20分)已知关于x 的一元二次方程20x cx a ++=的两个整数根恰好比方程20x ax b ++=的两个根都大1,求a b c ++的值.得分评卷人(12)(本小题满分20分)如图,点H为△ABC的垂心,以AB为直径的⊙1O和△BCH的外接圆⊙2O相交于点D,延长AD交CH于点P,求证:点P为CH的中点.得分 评卷人(13)(本小题满分20分)如图,点A 为y 轴正半轴上一点,A B ,两点关于x 轴对称,过点A 任作直线交抛物线223y x于P ,Q 两点.(Ⅰ)求证:∠ABP =∠ABQ ; (Ⅱ)若点A 的坐标为(0,1),且 ∠PBQ =60º,试求所有满足条件的直线PQ 的函数解析式.(14)(本小题满分20分)已知0122011i a i >=,, , , ,且122011a a a <<<,证明:122011a a a ,,,中一定存在两个数i j a a i j <,(),使得(1)(1)2010i j j i a a a a ++-<.。
2011年全国初中数学竞赛预赛试题含答案
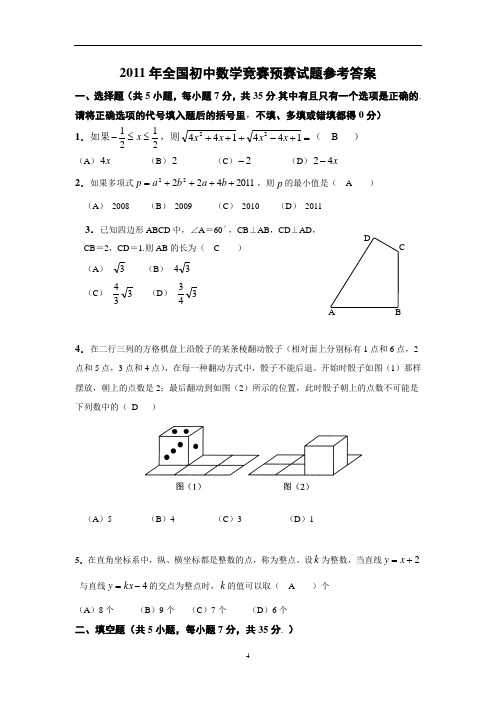
2011年全国初中数学竞赛预赛试题参考答案一、选择题(共5小题,每小题7分,共35分.其中有且只有一个选项是正确的. 请将正确选项的代号填入题后的括号里,不填、多填或错填都得0分) 1.如果2121≤≤-x ,则=+-+++14414422x x x x ( B ) (A )x 4 (B )2 (C )2- (D )x 42-2.如果多项式201142222++++=b a b a p ,则p 的最小值是( A )(A ) 2008 (B ) 2009 (C ) 2010 (D ) 20113.已知四边形ABCD 中,∠A =60 ,CB ⊥AB ,CD ⊥AD ,CB =2,CD =1.则AB 的长为( C ) (A ) 3 (B ) 34(C )334 (D ) 3434.在二行三列的方格棋盘上沿骰子的某条棱翻动骰子(相对面上分别标有1点和6点,2点和5点,3点和4点),在每一种翻动方式中,骰子不能后退。
开始时骰子如图(1)那样摆放,朝上的点数是2;最后翻动到如图(2)所示的位置,此时骰子朝上的点数不可能是下列数中的( D )(A )5 (B )4 (C )3 (D )15.在直角坐标系中,纵、横坐标都是整数的点,称为整点。
设k 为整数,当直线2+=x y 与直线4-=kx y 的交点为整点时,k 的值可以取( A )个 (A )8个 (B )9个 (C )7个 (D )6个二、填空题(共5小题,每小题7分,共35分. )BACD6.从分数组{}111111,,,,,24681012中删去两个分数,使剩下的数之和为1,则删去的两个数是 . 解:11810与7.如果我们把y x *定义为)1)(1(++=*y x y x ,2*x 定义为x x x *=*2,那么多项式12)(32+*-**x x ,当2=x 时的值为 .解:328.将54321,,,,这五个数字排成一排,最后一个数是奇数,且使得其中任意连续三个数之和都能被这三个数中的第一个数整除,那么满足要求的排法有 种。
2011年全国初中数学竞赛解答题汇编(含答案)

O A BCDEM第17题图H y九年级实验班数学竞赛试卷15.已知关于x 的方程x 3-ax 2-2ax +a 2-1=0有且只有一个实数根. 求实数a 的取值范围.16.如图所示,在平面直角坐标系中有点A (-1,0)、点B (4,0),以AB 为直径的半圆交y 轴正半轴于点C 。
(1)求点C 的坐标;(2)求过A 、B 、C 三点的抛物线的解析式;(3)在(2)的条件下,若在抛物线上有一点D ,使四边形BOCD 为直角梯形,求直线BD的解析式。
17.如图,⊙O 为△ABC 的外接圆,∠BAC=60°,H 为边AC 、AB 上高BD 、CE 的交点,在BD 上取点M ,使BM=CH 。
(1)求证:∠BOC=∠BHC ; (2)求证:△BOM ≌△COH ; (3)求MHOH的值.18.一个棋盘有13行17列,每个小方格里都写了一个数,从左上角开始,第一行依次为1, 2, ⋅⋅⋅, 17;第二行依次为18, 19, ⋅⋅⋅, 34; ⋅⋅⋅,一直写到最后一行,现将此棋盘里的数重写,从左上角开始,第一列从上到下依次为1, 2, ⋅⋅⋅ , 13;第二列从上到下依次为14, 15, ⋅⋅⋅, 26;⋅⋅⋅,一直写到最后一列,这样有一些小方格在两种写法里有相同的数,求所有这些小方格里(有相同数的)的数之和是多少?15、将原方程视为a 的一元二次方程,即a 2-( x 2+2x )a +x 3-1=0. 分解因式得[a -(x -1)][a-(x 2+x +1)]=0. 则x =a +1或x 2+x +1-a =0①.(6分)因x =a +1不是方程①的根,所以,当方程①无实根时,原方程有且只有一个实根. 于是△=1-4 ( 1-a )<0. 解得a <34.(6分) 16、(1)解:如图,连结AC ,CB 。
依相交弦定理的推论可得OC 2=OA ·OB ,解得OC=2。
2000年到2011年全国初中数学竞赛历考答案(12份)-716

中国教育学会中学数学教学专业委员会 “《数学周报》杯”2011年全国初中数学竞赛试题题 号 一 二 三总 分1~5 6~10 11 12 13 14 得 分 评卷人 复查人答题时注意:1.用圆珠笔或钢笔作答; 2.解答书写时不要超过装订线; 3.草稿纸不上交.一、选择题(共5小题,每小题7分,共35分. 每道小题均给出了代号为A ,B ,C ,D 的四个选项,其中有且只有一个选项是正确的. 请将正确选项的代号填入题后的括号里,不填、多填或错填都得0分)1.设71a =-,则代数式32312612a a a +--的值为( ).(A )24 (B )25 (C )4710+ (D )4712+ 2.对于任意实数a b c d ,,,,定义有序实数对a b (,)与c d (,)之间的运算“△”为:(a b ,)△(c d ,)=(ac bd ad bc ++,).如果对于任意实数u v ,, 都有(u v ,)△(x y ,)=(u v ,),那么(x y ,)为( ).(A )(0,1) (B )(1,0) (C )(﹣1,0) (D )(0,-1)3.若1x >,0y >,且满足3y y xxy x x y==,,则x y +的值为( ).(A )1 (B )2 (C )92 (D )1124.点D E ,分别在△ABC 的边AB AC ,上,BE CD ,相交于点F ,设1234BDF BCF CEF EADF S S S S S S S S ∆∆∆====四边形,,,,则13S S 与24S S 的大小关系为( ).(A )1324S S S S < (B )1324S S S S = (C )1324S S S S > (D )不能确定 5.设3333111112399S=++++,则4S 的整数部分等于( ). (A )4 (B )5 (C )6 (D )7二、填空题(共5小题,每小题7分,共35分)6.若关于x 的方程2(2)(4)0x x x m --+=有三个根,且这三个根恰好可 以作为一个三角形的三条边的长,则m 的取值范围是 .7.一枚质地均匀的正方体骰子的六个面上的数字分别是1,2,2,3,3,4;另一枚质地均匀的正方体骰子的六个面上的数字分别是1,3,4,5,6,8. 同时掷这两枚骰子,则其朝上的面两数字之和为奇数的概率是 .8.如图,点A B ,为直线y x =上的两点,过A B ,两点分别作y 轴的平行线交双曲线1y x=(x >0)于C D ,两点. 若2BD AC =,则224OC OD - 的值为 .9.若112y x x =-+-的最大值为a ,最小值为b ,则22a b +的值为 .10.如图,在Rt △ABC 中,斜边AB 的长为35,正方形CDEF 内接于△ABC ,且其边长为12,则△ABC 的周长为 .三、解答题(共4题,每题20分,共80分)11.已知关于x 的一元二次方程20x cx a ++=的两个整数根恰好比方程(第8题)(第10题)20x ax b ++=的两个根都大1,求a b c ++的值.12.如图,点H 为△ABC 的垂心,以AB 为直径的⊙1O 和△BCH 的外接圆⊙2O 相交于点D ,延长AD 交CH 于点P ,求证:点P 为CH 的中点.13.如图,点A 为y 轴正半轴上一点,A B ,两点关于x 轴对称,过点A 任作直线交抛物线223yx =于P ,Q 两点. (1)求证:∠ABP =∠ABQ ;(2)若点A 的坐标为(0,1),且∠PBQ =60º,试求所有满足条件的直线PQ 的函数解析式.14.如图,△ABC 中,60BAC ∠=︒,2AB AC =.点P 在△ABC 内,且352PA PB PC ===,,,求△ABC 的面积.(第13题)(第12题)中国教育学会中学数学教学专业委员会“《数学周报》杯”2011年全国初中数学竞赛试题参考答案一、选择题 1.A解:因为71a =-, 17a +=, 262a a =-, 所以322312612362126261261260662126024.a a a a a a a a a a a +--=-+---=--+=---+=()()()2.B解:依定义的运算法则,有ux vy u vx uy v +=⎧⎨+=⎩,,即(1)0(1)0u x vy v x uy -+=⎧⎨-+=⎩,对任何实数u v ,都成立. 由于实数u v ,的任意性,得(x y ,)=(1,0).3.C解:由题设可知1y y x -=,于是341y y x yx x -==,所以 411y -=, 故12y =,从而4x =.于是92x y +=. 4.C解:如图,连接DE ,设1DEF S S ∆'=,则1423S S EF S BF S '==,从而有1324S S S S '=.因为11S S '>,所以1324S S S S >.5.A解:当2 3 99k =,,,时,因为(第14题)(第4题)()()()32111112111k k k k k k k ⎡⎤<=-⎢⎥-+-⎣⎦, 所以 3331111115111239922991004S ⎛⎫<=++++<+-< ⎪⨯⎝⎭. 于是有445S <<,故4S 的整数部分等于4.二、填空题 6.3<m ≤4解:易知2x =是方程的一个根,设方程的另外两个根为12 x x ,,则124x x +=,12x x m =.显然1242x x +=>,所以122x x -<, 164m ∆=-≥0,即 ()2121242x x x x +-<,164m ∆=-≥0,所以1642m -<, 164m ∆=-≥0,解之得 3<m ≤4.7.19解: 在36对可能出现的结果中,有4对:(1,4),(2,3),(2,3),(4,1)的和为5,所以朝上的面两数字之和为5的概率是41369=. 8.6解:如图,设点C 的坐标为a b (,),点D 的坐标为c d (,),则点A 的坐标为a a (,),点B 的坐标为.c c (,) 因为点C D ,在双曲线1y x=上,所以11ab cd ==,. 由于AC a b =-,BD c d =-, 又因为2BD AC =,于是22222242c d a b c cd d a ab b -=--+=-+,(),所以 22224826a b c d ab cd +-+=-=()(),即224OC OD -=6.9.32(第8题)解:由1x -≥0,且12x -≥0,得12≤x ≤1.22213113122()2222416y x x x =+-+-=+--+. 由于13124<<,所以当34x =时,2y 取到最大值1,故1a =. 当12x =或1时,2y 取到最小值12,故22b =.所以,2232a b +=. 10.84解:如图,设BC =a ,AC =b ,则22235a b +==1225. ①又Rt △AFE ∽Rt △ACB ,所以FE AFCB AC=,即1212b a b-=,故 12()a b ab +=. ② 由①②得2222122524a b a b ab a b +=++=++()(),解得a +b =49(另一个解-25舍去),所以493584a b c ++=+=.三、解答题11.解:设方程20x ax b ++=的两个根为αβ,,其中αβ,为整数,且α≤β,则方程20x cx a ++=的两根为11αβ++,,由题意得()()11a a αβαβ+=-++=,,两式相加得 2210αβαβ+++=, 即 (2)(2)3αβ++=,所以 2123αβ+=⎧⎨+=⎩,; 或232 1.αβ+=-⎧⎨+=-⎩,(第10题)解得 11αβ=-⎧⎨=⎩,; 或53.αβ=-⎧⎨=-⎩,又因为[11]a b c αβαβαβ=-+==-+++(),,()(),所以 012a b c ==-=-,,;或者8156a b c ===,,,故3a b c ++=-,或29.12.证明:如图,延长AP 交⊙2O 于点Q , 连接 AH BD QB QC QH ,,,,.因为AB 为⊙1O 的直径, 所以∠ADB =∠BDQ =90°, 故BQ 为⊙2O 的直径. 于是CQ BC BH HQ ⊥⊥,.又因为点H 为△ABC 的垂心,所以.AH BC BH AC ⊥⊥,所以AH ∥CQ ,AC ∥HQ ,四边形ACQH 为平行四边形. 所以点P 为CH 的中点.13.解:(1)如图,分别过点P Q , 作y 轴的垂线,垂足分别为C D , . 设点A 的坐标为(0,t ),则点B 的坐标为(0,-t ). 设直线PQ 的函数解析式为y kx t =+,并设P Q ,的坐标分别为 P P x y (,),Q Q x y (,).由223y kx t y x =+⎧⎪⎨=⎪⎩,, 得 2203x kx t --=,于是 32P Q x x t =-,即 23P Q t x x =-.(第12题)(第13题)于是222323P P Q Qx t y t BC BD y t x t ++==++22222()333.222()333P P Q P P Q P Q Q P Q Q Q P x x x x x x x x x x x x x x --===--- 又因为P Q x PCQD x =-,所以BC PC BD QD=. 因为∠BCP =∠90BDQ =︒,所以△BCP ∽△BDQ , 故∠ABP =∠ABQ .(2)解法一 设PC a =,DQ b =,不妨设a ≥b >0,由(1)可知∠ABP =∠30ABQ =︒,BC =3a ,BD =3b ,所以 AC =32a -,AD =23b -.因为PC ∥DQ ,所以△ACP ∽△ADQ . 于是PC ACDQ AD=,即3223a a b b -=-, 所以3a b ab +=.由(1)中32P Q x x t =-,即32ab -=-,所以33322ab a b =+=,,于是可求得2 3.a b == 将32b =代入223y x =,得到点Q 的坐标(32,12).再将点Q 的坐标代入1y kx =+,求得3.3k =- 所以直线PQ 的函数解析式为313y x =-+. 根据对称性知,所求直线PQ 的函数解析式为313y x =-+,或313y x =+. 解法二 设直线PQ 的函数解析式为y kx t =+,其中1t =. 由(1)可知,∠ABP =∠30ABQ =︒,所以2BQ DQ =.故 222(1)Q QQ x x y =++. 将223Q Q y x =代入上式,平方并整理得 4241590Q Q x x -+=,即22(43)(3)0Q Q x x --=.所以 32Q x =或 3. 又由 (1)得3322P Q x x t =-=-,32P Q x x k +=. 若32Q x =,代入上式得 3P x =-, 从而 23()33P Q k x x =+=-.同理,若3Q x =, 可得32P x =-, 从而 23()33P Q k x x =+=.所以,直线PQ 的函数解析式为313y x =-+,或313y x =+. 14.解:如图,作△ABQ ,使得QAB PAC ABQ ACP ∠=∠∠=∠,,则△ABQ ∽△ACP . 由于2AB AC =,所以相似比为2. 于是22324AQ AP BQ CP ====,.60QAP QAB BAP PAC BAP BAC ∠=∠+∠=∠+∠=∠=︒.由:2:1AQ AP =知,90APQ ∠=︒,于是33PQ AP ==.所以 22225BP BQ PQ ==+,从而90BQP ∠=︒. 于是222()2883AB PQ AP BQ =++=+ .故 213673sin 60282ABC S AB AC AB ∆+=⋅︒==.(第14题)。
2011年全国初中数学竞赛试题 (2)

2011年全国初中数学竞赛试题考试时间.2011年3月20日9.30——11.30 满分.150分答题时注意.1、用圆珠笔或钢笔作答;2、解答书写时不要超过装订线;3、草稿纸不上交。
一、选择题(共5小题,每小题7分,共35分。
每道小题均给出了代号为A 、B 、C 、D 的四个选项,其中有且只有一个选项是正确的。
请将正确选项的代号填入题后的括号里,不填、多填或错填都得0分)1、设x =,则代数式(1)(2)(3)x x x x +++的值为( ) A 、0 B 、1 C 、﹣1 D 、22、对于任意实数a, b, c, d, 定义有序实数对(a, b )与(c, d)之间的运算“△”为.(a, b )△(c, d )=(ac+bd, ad+bc )。
如果对于任意实数u, v,都有(u, v )△(x, y )=(u, v ),那么(x, y )为( )A 、(0, 1)B 、(1, 0)C 、(﹣1, 0)D 、(0, ﹣1)3、已知A,B 是两个锐角,且满足225sin cos 4A B t +=,2223cos sin 4A B t +=,则实数t 所有可能值的和为( )A 、83- B 、53- C 、1 D 、1134、如图,点D 、E 分别在△ABC 的边AB 、AC 上,BE 、CD 相交于点F,设1EADF S S 四边形=,2BDF S S ∆=,3BCF S S ∆=,4CEF S S ∆=,则13S S 与24S S 的大小关系为( )A 、13S S ﹤24S SB 、13S S =24S SC 、13S S ﹥24S SD 、不能确定 F BC ED A5、设33331111++++1232011S =,则4S 的整数部分等于( ) A 、4 B 、5 C 、6 D 、7二、填空题(共5小题,每小题7分,共35分)6、两条直角边长分别是整数a, b (其中b<2011),斜边长是b+1的直角三角形的个数为 .7、一枚质地均匀的正方体骰子的六个面上的数字分别是1,2,2,3 ,3,4;另一枚质地均匀的正方体骰子的六个面上的数字分别是1,3,4,5,6,8。
2011年“数学周报杯”全国初中数学竞赛试卷

2011年“数学周报杯”全国初中数学竞赛试卷一、选择题(共5小题,每小题6分,满分30分)1.设a= ,则323a +12a -6a-12=( )A . 24B .25C . +10D .+122.规定”△”为有序实数对的运算,如果(a ,b )△(c ,d )=(ac+bd ,ad+bc ).如果对任意实数a ,b 都有(a ,b )△(x ,y )=(a ,b ),则(x ,y )为( )A .(0,1)B .(1,0)C .(-1,0)D .(0,-1)3.若x >1,y >0,且满足xy=y x ,3y x =x y ,则x+y 的值为( ) A . 1 B .2 C .92 D .1124.点D ,E 分别在△ABC 的边AB ,AC 上,BE ,CD 相交于点F ,设S 四边形EADF=S1,S △BDF=S2,S △BCF=S3,S △CEF=S4,则S1S3与S2S4的大小关系为( )A .S1S3<S2S4B .S1S3=S2S4C .S1S3>S2S4D .不能确定5.设S=33331111+++......+12399,则4S 的整数部分等于( )A .4B .5C .6D .7二、填空题(共5小题,每小题6分,满分30分)6.若关于x 的方程(x-2)(2x -4x+m )=0有三个根,且这三个根恰好可以作为一个三角形的三条边的长,则m 的取值范围是_____________.7.一枚质地均匀的正方体骰子的六个面上的数字分别是1,2,2,3,3,4;另一枚质地均匀的正方体骰子的六个面上的数字分别是1,3,4,5,6,8.同时掷这两枚骰子,则其朝上的面两数字之和为奇数5的概率是_____________8.如图,点A ,B 为直线y=x 上的两点,过A ,B 两点分别作y 轴的平行线交双曲线y=1x (x >0)于C ,D 两点.若BD=2AC ,则224OC OD 的值为____________.9.若y= 的最大值为a,最小值为b,则22a+b的值为10.如图,在Rt△ABC中,斜边AB的长为35,正方形CDEF内接于△ABC,且其边长为12,则△ABC的周长为三、解答题(共4小题,满分10分)11.已知关于x的一元二次方程2x+cx+a=0的两个整数根恰好比方程2x+ax+b=0的两个根都大1,求a+b+c的值.和△BCH的外接圆⊙O2相交12.如图,点H为△ABC的垂心,以AB为直径的⊙O1于点D,延长AD交CH于点P,求证:点P为CH的中点.13.如图,点A为y轴正半轴上一点,A,B两点关于x轴对称,过点A任作直线交抛物线y=23x2于P,Q两点.(1)求证:∠ABP=∠ABQ;(2)若点A的坐标为(0,1),且∠PBQ=60°,试求所有满足条件的直线PQ的函数或a=-(α+β)=-[(-5)+(-3)]=8,b=αβ=(-5)×(-3)=15,c=-[(α+1)+(β+1)]=-[(-5+1)+(-3+1)]=6,∴a=0,b=-1,c=-2;或者a=8,b=15,c=6,∴a+b+c=0+(-1)+(-2)=-3或a+b+c=8+15+6=29,故a+b+c=-3,或29.(20分)12 略,13 略,14 略。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
共8页,第1页 2011年全国初中数学竞赛试题及参考答案 说明:评阅试卷时,请依据本评分标准.第一试,选择题和填空题只设7分和0分两档;第二试各题,请按照本评分标准规定的评分档次给分.如果考生的解答方法和本解答不同,只要思路合理,步骤正确,在评卷时请参照本评分标准划分的档次,给予相应的分数.
第一试 一、选择题:(本题满分42分,每小题7分)
1.已知2ba,4)1()1(22abba,则ab的值为 ( ) A.1. B.1. C.21. D.21. 【答】B.
由4)1()1(22abba可得abbbaa4)1()1(22,
即04)(2)(3322abbababa, 即222222()2()40abaabbab,即2240abab,所以1ab. 2.已知△ABC的两条高线的长分别为5和20,若第三条高线的长也是整数,则第三条高线长的最大值为 ( ) A.5. B.6. C.7. D.8. 【答】B.
设△ABC的面积为S,所求的第三条高线的长为h,则三边长分别为hSSS2,202,52.显然20252SS,于是由三边关系,得
,252202,522202hSSSShSS
解得3204h.
所以h的最大整数值为6,即第三条高线的长的最大值为6. 3.方程)2)(324(|1|2xx的解的个数为 ( ) A.1个 B.2个 C.3个 D.4个 【答】C.
当1||x时,方程为)2)(324(12xx,即0349)324(2xx,解得13x,2433x,均
满足1||x. 当1||x时,方程为)2)(324(12xx,即0347)324(2xx,解得332x,满足1||x. 综上,原方程有3个解. .4.今有长度分别为1,2,„,9的线段各一条,现从中选出若干条线段组成“线段组”,由这一组线段恰好可以拼接成一个正方形,则这样的“线段组”的组数有 ( ) 共8页,第2页
A.5组. B.7组. C.9组. D.11组. 【答】C. 显然用这些线段去拼接成正方形,至少要7条.当用7条线段去拼接成正方形时,有3条边每边都用2条线段连接,而另一条边只用1条线段,其长度恰好等于其它3条边中每两条线段的长度之和.当用8条线段去拼接成正方形时,则每边用两条线段相接,其长度和相等.
又因为45921,所以正方形的边长不大于45[]114.由于 4352617; 5362718; 546372819;
64738291; 65748392.
所以,组成边长为7、8、10、11的正方形,各有一种方法;组成边长为9的正方形,有5种方法。 故满足条件的“线段组”的组数为1×4+5=9. 5.如图,菱形ABCD中,3AB,1DF,60DAB,15EFG,BCFG,则AE ( )
A.21. B.6. C.132. D.31. 【答】 D. 过F作AB的垂线,垂足为H.∵60DAB,2FDADAF,
∴30AFH,1AH,3FH, 又∵15EFG, ∴EFGAFHAFGEFH45153090,
从而△FHE是等腰直角三角形,所以HE=FH=3,
∴ 31HEAHAE. 6.已知2111zyx,3111xzy,4111yxz,则zyx432的值为 ( ) A.1. B.23. C.2. D.25. 【答】C.
由已知等式得2zyxzxxy,3zyxxyyz,4zyxyzzx,所以29zyxzxyzxy.
于是,25zyxyz,23zyxzx,21zyxxy.所以 35xy,3yz,35xy,即xyz53。 代入2111zyx,得2153511xxx,解得1023x. 所以 2523543532432xxxxzyx. 二、填空题:(本题满分28分,每小题7分) 1.在△ABC中,已知AB2,322,2ABBC,则A .
HGCBADFE共8页,第3页
【答】 15。 延长AB到D,使BD=BC,连线段CD,则12DBCDABCA,所以CA=CD。 作ABCE于点E,则E为AD的中点,故 111()(2232)23222AEDEADABBD,
(223)(23)3BEABAE.
在Rt△BCE中,3cos2EBEBCBC,所以30EBC,故 1521ABCA. 2.二次函数cbxxy2的图象的顶点为D,与x轴正方向从左至右依次交于A,B两点,与y轴正方向交于C点,若△ABD和△OBC均为等腰直角三角形(O为坐标原点),则cb2 . 【答】 2.
由已知,得),0(cC,)0,24(2cbbA,)0,24(2cbbB,)44,2(2cbbD.
过D作ABDE于点E,,则ABDE2,即cbcb444222,得cbcb42422, 所以042cb或242cb.又042cb,所以242cb. 又OBOC,即242cbbc,得2422cbcb. 3.能使2562n是完全平方数的正整数n的值为 . 【答】 11. 当8n时,)21(225628nnn,若它是完全平方数,则n必为偶数.
若2n,则65225622n;若4n,则17225624n;若6n,则5225626n;若8n,则2225628n。所以,当8n时,2562n都不是完全平方数.
当8n时,)12(2256288nn,若它是完全平方数,则128n为一奇数的平方。 设28)12(12kn(k为自然数),则)1(210kkn.由于k和1k一奇一偶,所以1k,于是2210n,故11n. 4.如图,已知AB是⊙O的直径,弦CD与AB交于点E,过点A作圆的切线与CD的延长线交于点F,如果CEDE43,58AC,D为EF的中点,则AB= . 【答】 24. 设yAExCE,4,则xEFxDEDF6,3.
DEBACDF
BOACE共8页,第4页
连AD,BC.因为AB为⊙O的直径,AF为⊙O的切线,所以DAFACDEAF,90. 又因为D为Rt△AEF的斜边EF的中点, ∴ DFDEDA,∴ AFDDAF,
∴ AFDACD,∴ 58ACAF.
在Rt△AEF中,由勾股定理得 222AFAEEF,即 3203622yx. 设zBE,由相交弦定理得 BEAEDECE,即21234xxxyz, ∴ yzy33202 ① 又∵ DEAD, ∴ AEDDAE. 又BECAEDBCEDAE,,∴ BECBCE,从而zBEBC.
在Rt△ACB中,由勾股定理得 222BCACAB,即22320)(zzy, ∴ 32022yzy. ② 联立①②,解得16,8zy. 所以24BEAEAB. 第二试 (A)
一、(本题满分20分)已知三个不同的实数cba,,满足3cba,方程012axx和02cbxx有一个相同的实根,方程2x0xa和02bcxx也有一个相同的实根.求cba,,的值. 解 依次将题设中所给的四个方程编号为①,②,③,④.
设1x是方程①和方程②的一个相同的实根,则,0,01121121cbxxaxx 两式相减,可解得bacx11. „„„„„„„„5分 设2x是方程③和方程④的一个相同的实根,则,0,0222222bcxxaxx两式相减,可解得12cbax。
所以 121xx. „„„„„„„„10分 又方程①的两根之积等于1,于是2x也是方程①的根,则01222axx。 又 0222axx,两式相减,得 1)1(2axa. „„„„„„„„15分 若1a,则方程①无实根,所以1a,故12x. 于是 1,2cba.又3cba,解得 3,2bc. „„„„„„„„20分 共8页,第5页
二.(本题满分25分)如图,在四边形ABCD中,已知60BAD,90ABC,120BCD,对角线BDAC,交于点S,且SBDS2,P为AC的中点.求证:(1)30PBD;(2)DCAD. 证明 (1)由已知得 90ADC,从而DCBA,,,四点共圆,AC为直径,P
为该圆的圆心. „„„„„„„„5分 作BDPM于点M,知M为BD的中点,所以BPM=12BPD=60A,从而30PBM. „„„„„„„„10分
(2)作BPSN于点N,则12SNSB.
又BDMBDMSBDS21,2, ∴ SNSBSBSBDMDSMS21232, „„„„„„„„15分 ∴ Rt△PMS≌Rt△PNS,∴ 30NPSMPS, 又PBPA,所以1152PABNPS,故DCADAC45,所以DCAD. „„„„„„„„25分 三.(本题满分25分)已知pnm,,为正整数,nm.设(,0)Am,(,0)Bn,(0,)Cp,O为坐标原点.若90ACB,
且)(3222OCOBOAOCOBOA. (1)证明:3pnm; (2)求图象经过CBA,,三点的二次函数的解析式. 解 (1)因为90ACB,ABOC,所以2OCOBOA,即2pmn. 由)(3222OCOBOAOCOBOA,得)(3222pnmpnm.„„„„„„„5分 又)(2)(2222mpnpmnpnmpnm)(2)(22mpnpppnm )(2)(2pnmppnm))((pnmpnm
,
从而有3pnm,即3pnm. „„„„„„„„10分 (2)由2pmn,3pnm知nm,是关于x的一元二次方程 0)3(22pxpx ①
的两个不相等的正整数根,从而04)]3([22pp,解得31p。 又p为正整数,故1p或2p. „„„„„„„„„15分 当1p时,方程①为0142xx,没有整数解.
